Irreversible Incremental Behavior in a Granular Material
Abstract
We test the elasticity of granular aggregates using increments of shear and volume strain in a numerical simulation. We find that the increment in volume strain is almost reversible, but the increment in shear strain is not. The strength of this irreversibility increases as the average number of contacts per particle (the coordination number) decreases. For increments of volume strain, an elastic model that includes both average and fluctuating motions between contacting particles reproduces well the numerical results over the entire range of coordination numbers. For increments of shear strain, the theory and simulations agree quite well for high values of the coordination number.
pacs:
81.05.Rm, 81.40.Jj, 83.80.FgGranular materials have received the attention of many researchers in the last decade because of unsolved problems with direct relevance to chemistry, physics and engineering. The behavior of a granular material can range between that of a gas and that of a solid, depending on the applied loading and the regime of deformation considered. Significant progresses have been made with the introduction of numerical tools (e.g. Cundall.Strack.1979 ) that permit the detailed analysis of an aggregate of particles. Although such simulations have provided information about inter-particle interactions, such as their elasticity, sliding, and deletion, and statistical measures of their cooperative behavior, such as induced anisotropy and force chains, it is still unclear how to incorporate these informations in a predictive theoretical model.
Attempts to do this have been made in the context of the effective medium theory (EMT) (e.g. Digby ; Walton ) in which the contact displacements are given by the applied average strain. However, the predicted shear and bulk moduli are far from those measured in numerical simulations (e.g. Cundall.Jenkins.1989 ; Makse.Gland.1999 ). In order to improve the theoretical prediction, particle displacements are given by the sum of an average and the fluctuation components (e.g. Koend ; Misra ). In particular, better predictions of the shear and bulk moduli have been obtained in a recent work that employs pair fluctuations Luigi ; LaRaJen . However, Agnolin and Roux Ivana point out that such predictions fail when the the coordination number, , is low and close to the isostatic limit at which the aggregate is statically determinate. They suggest that for low coordination number, more complicated models are needed that account for collective deformations among particles. That is, the assumption of pair fluctuations is not sufficient to capture the response of poorly coordinate aggregates of particles. Here, we address this issue and provide an alternative interpretation of the failure of an elastic description at low coordination numbers.
We carry out numerical simulations using a distinct element method and focus on the first incremental response of an isotropically compressed random aggregate that consists of identical, elastic, frictional spheres. We consider dense aggregates, with solid volume fractions near , that have different . Previous work Ivana ; Ell ; vanHecke have considered poorly coordinated aggregates and found that the shear modulus is proportional to , where is equal to four for a packing of frictional spheres. Here, we find that when decreases, there is an irreversible behavior of the aggregate that involves local, coordinated, irreversible motions of the particles that are not resisted by forces. These motions result in a reduction of the apparent stiffness of the aggregate (e.g. Mouk ). That is, the initial configuration of a poorly coordinated aggregate can not sustain any incremental strain unless a change in the geometry of the packing occurs. When such irreversible changes are present, simple elastic theory can not reproduce the response of the aggregate and the utility of the elastic moduli is questionable.
We introduce measures of these irreversible deformations which vary with the coordination number. For increments in volume strain, the number of irreversible motions is so small that their effect is negligible and the response of the aggregate can be assumed to be elastic. More importantly, for shear increments, the strength of the irreversibility persists even at high and increases as decreases towards its isostatic value, indicating that elasticity does not describe the aggregate response.
Our numerical simulations consider particles, each with diameter , randomly generated in a periodic cubic cell. We employ material properties typical of glass spheres: a shear modulus and a Poisson’s ratio, . The interaction between particles is a non-central contact force in which the normal component is the non-linear Hertz interaction and the tangential component is bilinear: an initial elastic displacement followed by Coulomb sliding (e.g.Makse.Gland.1999 ). We create different initial isotropic states by varying the coefficient of friction between particles during the preparation (e.g. Magna ); all initial states have a solid volume fraction and a confining pressure that varies from to
For all packings, we evaluate the response of the aggregate to homogeneous increments in volume and shear strain by setting the particle coefficient of friction high enough to prevent sliding. Because of the random positions of the particles and their different initial contact stiffnesses, the subsequent particle motions are the sum of the homogeneous applied strain and a fluctuation that relaxes the particles towards a new equilibrium state. When this relaxation involves a rearrangement of particles, the incremental response is irreversible.
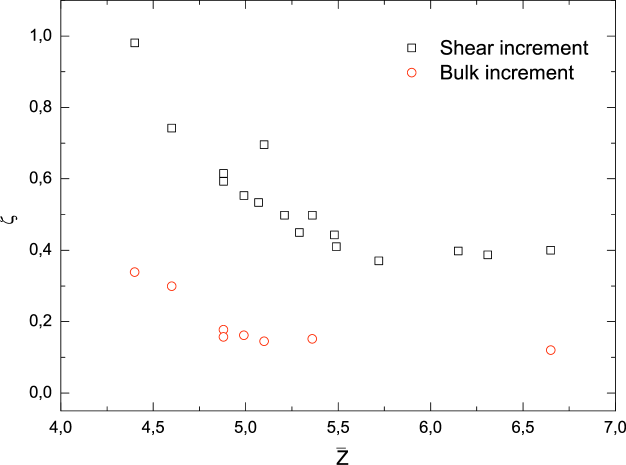
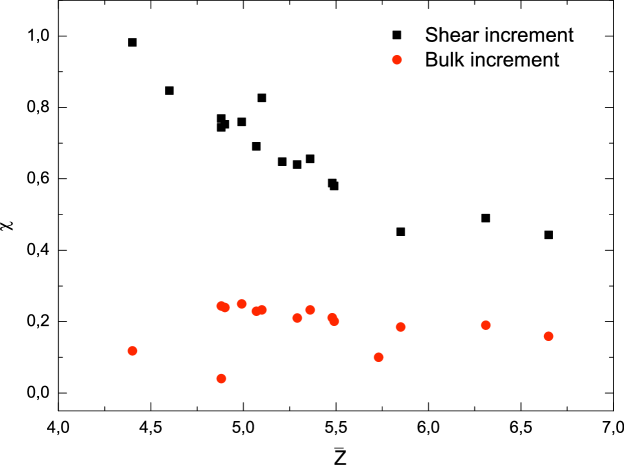
We attempt to characterize the particle rearrangement and introduce two measures of the strength of the irreversibility: the first is related to contact displacement, and the second is associated with contact forces. We apply a forward increment in strain followed by an identical backward strain in which the reference configuration should be recovered if the deformation were perfectly elastic.
We define the parameter as the average over all contacts of the ratio of the absolute values of the contact displacements after and before the backward increment in strain. A parameter, , is similarly defined in terms of the contact forces. Both parameters would be zero for perfectly elastic behavior.
We measure and in all of the packings for increments in both shear and volume strain. We apply increments of strain with magnitudes that depend on the confining pressure; the ratio of the associated volume strain with the confining pressure is constant at about . The results are plotted in Figs. 1 and 2, displaying and as functions of .
Figs. 1 and 2 show small variations in and associated with increments in volume strain. The strength of the irreversibility is almost negligible, with slight increases as is approached. We conclude that an approximate elastic response for the aggregate is obtained for increments of volume strain, independent of the coordination number.
For increments in shear strain, both and increase as is approached. We believe that these irreversible motions are associated with the presence of local instability (e.g. Mouk ). Moreover, both and are non-zero for high values of the coordination number, in contrast to what we find for increments in volume strain. The aggregate seems to experience rearrangements over the entire range of the coordination number, with the irriversibility becoming stronger as isostaticity is approached.
The condition of isostaticity has been an object of great interest for many researchers (Makse.Gland.1999 ; Wyart ; Silbert ; Ell ; vanHecke ; brito ). The contact forces in an aggregate are uniquely determined in terms of the applied loads, independent of the contact stiffness, when the aggregate is both statically and kinematically determinate (e.g. Pelle ). The condition for static determinacy, often referred to as Maxwell s condition Max , insures the equality between the number of unknowns and the number of equilibrium equations. In a granular aggregate, this necessitates that . The condition for kinematic determinacy insures that there are no inextensional mechanisms in the aggregate; then a rigid aggregate is able to sustain any external self-equilibrated perturbation without changing the relative positions of its particle centers.
The kinematic condition is not often taken into account in recent work on granular aggregates (e.g. Wyart2 ) and sometimes has been emphasized in a different way. For example, Moukarzel Mouk , in his description of network rigidity, defines an isostatic system to be one in which the rank K of the rigidity matrix that relates the contact forces to the applied forces always equals to the number of equations, rather than one in which the simple Maxwell condition is satisfied. Then, when K is less than the number of equations, the network is flexible; this can occur when .
The presence of irreversibility in all of our aggregates, even in the limit that (see Figs. 1 and 2) indicates that the kinematic condition does not hold. Consequently, inextensional mechanisms and the associated soft or floppy vibrational modes are possible. This situation may occur whatever the value , if particles location do not correspond to those of a rigid network. In particular, in packing characterized as isostatic by (e.g. Wyart ; Silbert ; Ell ), soft modes can occur as long as the kinematic condition is not satisfied. However, we should emphasize that the initial states that we employ are constructed in a much different way than those constructed to insure an initial, stable, elastic response (e.g. O'Hern ).
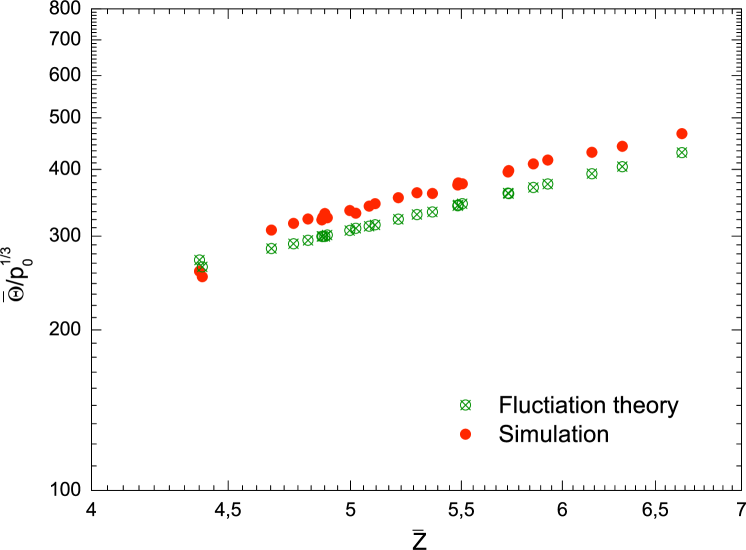
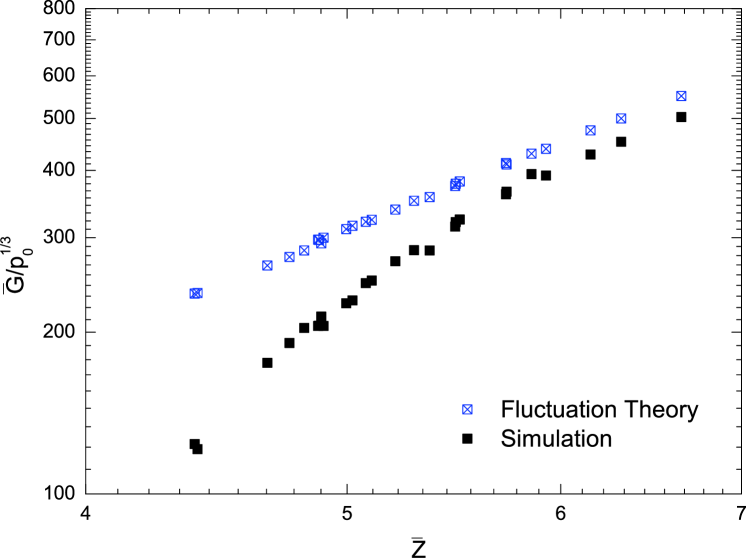
We now turn from irreversibility to elasticity and report results from numerical simulation for the bulk modulus, , and the shear modulus, , where is the average stress tensor, the average strain tensor, and is the volume of the aggregate. When a shear increment is applied to poorly coordinated systems, the irreversibility increases and the material response deviates from elasticity. That is, an elastic theory can only be considered as providing an upper bound on the shear modulus.
To make predictions of the moduli, we adopt the fluctuation theory developed by LaRaJen . This theory improves upon the simplest average strain models Digby ; Walton , because contacting particles are assumed to move with both the average deformation and fluctuations and because the statistics of the aggregate are taken in account. The theory employs force and moment equilibrium for a typical pair of particles to evaluate the fluctuations, and then uses them to determine the stress in the aggregate. However, at low values of the coordination number, the simple statistical model introduced to describe the variability of the neighborhood of contacting pairs of particles is probably too simple, (e.g. Agn_08 ) and the initial distribution contact forces (e.g.TA ) is not taken into account.
Here we repair the second deficiency and assume that the distribution, of the normal component of the contact force, is exponential (e.g.Cundall.Jenkins.1989 ):
| (1) |
where, by definition,
From the effective medium theory (e.g.Jen-Strack ), the confining pressure can be expressed as function of ,
and the relation between the normal component of the contact displacement, and is
| (2) |
| (3) | |||||
where is the Gamma function.
So the average normal contact stiffness becomes
| (4) |
The average shear stiffness is .
Taking in account the initial distribution of forces in this way, we obtain a new solution for the fluctuations; with this, the resulting expressions for the bulk modulus and the shear modulus are, respectively,
| (5) |
| (6) | |||||
where a relation between the rms value of the fluctuation in the number of contacts per particle and its average value has been adopted Magna . At the upper limit of validity of equations (5,6), , we recover the average strain prediction Digby ; Walton . This limit results from the modeling of the statistical distribution of particles in the assembly.
Comparison between the predictions of the bulk and shear moduli and measurements in the numerical simulation are shown in Figs. 3 and 4. There is agreement at high values of the coordination number for the shear modulus; the slight difference may be attributed to the irreversibility. However, when the comparison is extended to lower values of the prediction strongly deviate from the simulations, as also seen by others Ivana . Here, we conclude that this discrepancy is due to the observed irreversible motions and that an elastic theory is not able to capture the behavior of the system for low values of . For the bulk modulus, the theory works quite well over the entire range of , because the irreversibility, measured by and , can be neglected.
In conclusion, we have measured the irreversible motions in a granular aggregate subjected to incremental strains and determined their influence on the mechanical response of the material. We found that particles may experience rearrangements in their geometry and contact forces, even when small perturbations are applied and that these rearrangements are sensitive to the coordination number. The strength of this irreversibility is negligible for increments in volume strain, while it strongly increases for increments in shear strain as approaches . The presence of irreversible motions in the aggregates indicates a deviation from elastic behavior. That is, an elastic theory is appropriate to describe the material behavior only if mechanisms do not play an important role in the displacements of the particles.
La Ragione, Magnanimo, and Jenkins are grateful for support from Strategic Plan-119, Regione Puglia (Italy) and Gruppo Nazionale della Fisica Matematica. Makse acknowledges support from DOE and NSF.
References
- (1) P. A. Cundall and O. D. L. Strack, Gé otechnique 29, 47 (1979).
- (2) P. J. Digby, J. Appl. Mech. 48, 803 (1981).
- (3) K. Walton, J. Mech. Phys. Solids 35, 213 (1987).
- (4) J. T. Jenkins, P. A. Cundall, and I. Ishibashi, in Powder and Grains, Ed. Biarez and Gourvès, Balkema, Rotterdam (1989).
- (5) H. A. Makse, N. Gland, D. L. Johnson, and L. Schwartz, Phys. Rev. Lett. 83, 5070 (1999); ibid, Phys.Rev. E 70, 061302 (2004).
- (6) M.A. Koenders Acta Mech. 70, 31 (1987).
- (7) A. Misra and C.S. Chang Int. J. Solids Struc. 30, 2547 (1993).
- (8) J. Jenkins, D. Johnson, L. La Ragione, and H. A. Makse, J. Mech. Phys. Solids 53, 197 (2005).
- (9) L. La Ragione and J. T. Jenkins, Proc. Roy. Soc. London A, 463, 735 (2007).
- (10) I. Agnolin and J.N. Roux. I, II, III Phys. Rev. E 76, 061302, 061303, 061304 (2007).
- (11) W. G. Ellenbroek, E. Somfai, M. van Hecke,and W. van Saarloos, Phys.Rev. Lett 97, 258001 (2006).
- (12) E. Somfai, M. van Hecke, W. G. Ellenbroek, K. Shundyak and W. van Saarloos, Phys. Rev. E 75, 020301(R) (2007).
- (13) C. F. Moukarzel, Phys.Rev. Lett 81, 1634 (1998); ibid Gran. Matter, 3, 41 (2001).
- (14) V. Magnanimo, L. La Ragione, J.T. Jenkins, P. Wang and H. A. Makse. Europhys. Lett. 81, 34006 (2008).
- (15) M. Wyart, L.E. Silbert, S.R. Nagel and T.A Witten, Phys. Rev. E. 72, 051306 (2005).
- (16) L.E. Silbert, A.J. Liu, S.R. Nagel, Phys. Rev. Lett. 95, 098301 (2005).
- (17) C. Brito and M. Wyart, Europhys. Lett. 76,149 (2006).
- (18) S. Pellegrino, C.R., Calladine, Inter. Jour. of Sol. and Str. 22(4), 409-428 (1986)
- (19) J.C., Maxwell, Philos. Mag.27,294-299 (1864)
- (20) M. Wyart, H. Liang, A. Kabla, and L., Mahadevan, Phys.Rev. Lett 101, 215501 (2008)
- (21) C.S. O’Hern, L.E. Silbert, A.J. Liu and S.R.Nagel, Phys. Rev. E. 68, 011306 (2003).
- (22) I. Agnolin, N. Kruyt and J.N. Roux, in EM08 18-21 May 2008 Minneapolis (USA).
- (23) C. Thornton and S.J. Antony. Phil. Trans. Roy. Soc. London A, 356 (1998).
- (24) J.T. Jenkins and O.D.L. Strack, Mech. Matls.16 , 25 (1993).