Present address: ]University of Jyvaskyla, Department of Physics, P. O. Box 35, FI-40014 University of Jyvaskyla, Finland
Present address: ]Lawrence Livermore National Laboratory, 7000 East Ave, Livermore, CA 94550, USA
Present address: ]Department of Physics, University of Washington, Seattle, WA 98195, USA
Present address: ]TRIUMF, 4004 Wesbrook Mall, Vancouver, BC, V6T 2A3, Canada
Present address: ]Department of Physics, Simon Fraser University, Burnaby, BC, V5A 1S6, Canada
Present address: ]Department of Physics, Lund University, 22100 Lund, Sweden
Present address: ]Department of Physics, Pierce College Puyallup, Washington, WA 98374, USA
Present address: ]Department of Physics, University of Chicago, Chicago, Illinois 60637, USA
Isospin symmetry in values: Coulomb excitation study of 21Mg
Abstract
The = nucleus 21Mg has been studied by Coulomb excitation on 196Pt and 110Pd targets. A 205.6(1)-keV -ray transition resulting from the Coulomb excitation of the ground state to the first excited state in 21Mg was observed for the first time. Coulomb excitation cross-section measurements with both targets and a measurement of the half-life of the state yield an adopted value of = 13.3(4) W.u. A new excited state at 1672(1) keV with tentative assignment was also identified in 21Mg. This work demonstrates large difference of the values between = , = 21 mirror nuclei. The difference is investigated in the shell-model framework employing both isospin conserving and breaking USD interactions and using modern ab initio nuclear structure calculations, which have recently become applicable in the shell.
I Introduction
Nuclei around the N = Z line serve as a laboratory to investigate the level to which isospin symmetry is conserved in nature. Traditionally isospin symmetry and its breaking have been investigated by comparing the energies of excited states in mirror nuclei or their masses Bentley and Lenzi (2007). In order to further the understanding of isospin symmetry breaking effects and develop the existing nuclear models, a range of spectroscopic data is required, including values, in addition to level energies and nuclear masses. Nuclear structure studies in the shell are particularly interesting since this region is accessible by nuclear theory through phenomenological and ab initio methods.
The phenomenological isospin symmetric USD interaction Brown and Wildenthal (1988) was successful in reproducing experimental data, but required additional corrections to reproduce the mirror energy difference (MED) systematics of the 2+ states in = 18-36, = 1,2 nuclei Doornenbal et al. (2007). The main modification of the USD interaction was the use of experimental single-particle energies derived from the = 17, = mirror pair, which implicitly introduce isospin symmetry breaking since the excitation energies in 17O and 17F are likely influenced by the Thomas-Ehrman shift Ehrman (1951); Thomas (1952) and other Coulomb effects. Additional corrections to the calculation were performed separately for the nuclei lying in the lower ( = 18-28) and higher ( = 28-36) shells Doornenbal et al. (2007) yielding a very good agreement with experimental MED.
Subsequently, the modified USD interaction (USD) was applied to calculate both MED and values in = 1,,2 -shell mirror pairs Wendt et al. (2014). The MED values in these systems are experimentally well known. Experimental and values for = 1,2 and = nuclei, respectively, are also available at or near the valley of stability. However, for neutron-deficient = ,2 nuclei the available experimental data are scarce. For example, information on the values in = nuclei was limited to 33Ar Wendt et al. (2014) prior to the present work.
The MED values in = 19-37, = mirror pairs have been reasonably well reproduced by the USD interaction. The same is also true for the values in = 1, and 2 nuclei between mass ranges of = 18-38, 21-37 and 20-36, respectively. The first experimental value for the = nucleus 33Ar was found to be in excellent agreement with the USD prediction. However, it is unclear if the USD interaction is actually required to reproduce data like it clearly is in the case of MED. Moreover, the USD calculation predicted a large difference between values in = 21, = mirror nuclei (21Mg/21F) Wendt et al. (2014), but it was not quantified what fraction of this difference, if any, had its origin in isospin breaking interactions.
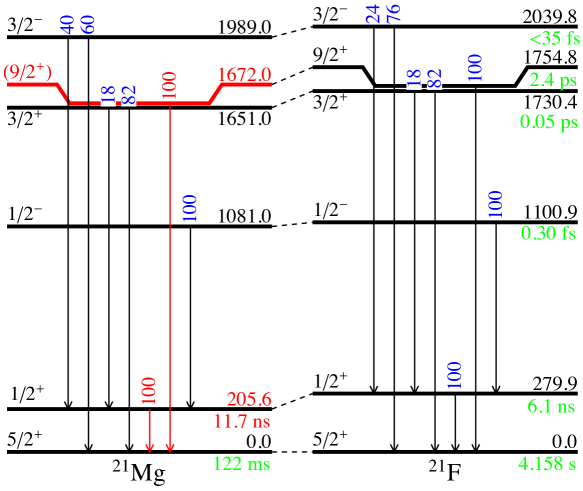
The low-lying level schemes of 21Mg and 21F with available spectroscopic information, including new data from the present work, are presented in Fig. 1. Prior to this work, no -ray transition from the lowest-lying state had been observed. In the present work the value in 21Mg is extracted for the first time using both Coulomb excitation and electronic timing. The obtained value together with other available data for = mirror nuclei are compared to the USD prediction, but also to the isospin conserving USDB calculation. Aim is to investigate the importance of the isospin symmetry breaking modifications of the USD interaction specifically on values. Predictions obtained from modern ab initio calculations that include isospin symmetry breaking at the nucleon-nucleon interaction level will also be compared to the available experimental data.
II Experimental setup and details
The experiment was performed at the TRIUMF - ISAC-II facility in Vancouver, Canada. A proton beam with 70-A intensity, accelerated with TRIUMF’s main cyclotron to 500-MeV energy, impinged on a SiC target Dombsky and Kunz (2014). Spallation reaction products were ionized using the TRIUMF Resonant Ionization Laser Ion Source (TRILIS) Bricault et al. (2014) to enhance the 21Mg yield with respect to the three orders of magnitude higher 21Na yield. The 21Na contamination was heavily suppressed by mass selection in the ISAC mass separator after which the ions were injected to the ISAC and ISAC-II linear accelerator chain. The post-accelerated 21Mg ions were delivered to the TIGRESS Hackman and Svensson (2014) experimental station with two different beam energies; 95 MeV was used with a 2.93-mg/cm2 thick 196Pt target enriched to 94.6 %, while 67 MeV was used with a 2.94-mg/cm2 thick 110Pd foil enriched to 97.6 %. Data were collected with the 196Pt and 110Pd targets for 66 h and 24 h, respectively. The average 21Mg intensity at the TIGRESS target position was approximately 5 105 particles/s. The beam composition was monitored by employing a Bragg detector Marchetto et al. (2012). The 21Na contamination was found to vary between 16-19 % of the total beam intensity.
The 21Mg ions were Coulomb excited on the 196Pt and 110Pd targets housed within the BAMBINO chamber located at the center of the TIGRESS Hackman and Svensson (2014) germanium-detector array. For the 196Pt target, 95 MeV is the highest safe bombarding energy for which the Coulomb excitation process is still purely electromagnetic at all angles according to the Cline criterion Cline (1986). For the 110Pd target, 67-MeV energy is safe up to the center-of-mass angle 145∘. Coulomb excitation induced rays from the beam and target nuclei were detected with 14 HPGe clover detectors each equipped with BGO and CsI(Tl) Compton suppressors. The TIGRESS detectors were arranged in the high-efficiency configuration providing absolute photopeak efficiency of 11.3(7) % at 1.3 MeV. Scattered 21Mg projectiles were detected with the BAMBINO array consisting of two 150-m thick annular Micron S3-type silicon detectors Hurst et al. (2009); Kwan et al. (2014); mic located 30 mm up- and downstream from the target position. The BAMBINO detectors cover laboratory angles between 20.1∘-49.9∘ and 130.6∘-159.9∘.
The TIGRESS digital data acquisition system Hackman and Svensson (2014) was used to acquire data in particle singles and particle- coincidence trigger modes. Preamplifier waveforms (traces) from all detectors were recorded on an event-by-event basis. Traces were fitted offline to improve the electronic timing resolution Rizwan (2015). A linear fit is made to the baseline while quadratic and linear fits are applied to the rising edges of the Ge and Si traces, respectively. Time of a radiation event is extracted with 1 ns accuracy from the intersection of the two fits. Depending on the -ray energy, tens of ns timing resolution for the prompt Ge-Si coincidences was obtained.
III Analysis and Results
The -ray energy spectra with the Doppler correction (black curve) and without it (red (gray) curve) observed in coincidence with the = 21 (21Mg and 21Na) projectiles scattered downstream from the 196Pt and 110Pd targets are presented in Fig. 2 a) and b), respectively. Previous studies have identified a state at 200 keV in 21Mg, but -ray transitions from this state were not observed Kubono et al. (1992); Diget et al. (2008). Ref.Kubono et al. (1992) suggests assignment for this state based on the measured angular distributions of three-particle transfer. The 21Mg ground-state spin is measured to be Krämer et al. (2009) and comparison with 21F suggests positive parity. The non-observation of the -ray transition in Ref. Diget et al. (2008) was attributed to the isomeric nature of the state. The analogue state in 21F has a half-life of t1/2 = 6.1(2) ns Warburton and Olness (1970).
In the present work, a -ray line was observed at 205.6(1) keV labeled with the red (gray) solid diamonds in Fig. 2. This transition must originate from 21Mg since it was not observed when the TRILIS lasers were blocked. The measured energy is in agreement with the previously measured state energies of 208(10) keV Kubono et al. (1992) and 201(4) keV Diget et al. (2008). Since the 205.6(1)-keV transition was observed without employing the Doppler correction, the half-life of the initial state has to be sufficiently long for the excited projectile to reach the S3 detector, where the -ray emission takes place. Consequently, the observed 205.6(1)-keV line signifies the first direct observation of the -ray transition in 21Mg. The other -ray lines in Fig. 2 labeled with open red (gray) symbols arise from the Coulomb excitation of the target nuclei and from 20Ne, which is populated in the -delayed proton decay of 21Mg.
Figure 2 shows also the -ray energies, which have been Doppler corrected on an event-by-event basis for 21Mg and 21Na using the position information obtained from the Si and Ge detectors. This results in an energy resolution of 20 keV at 1.384 MeV. The two lines at 332.0(3) keV and 1384(1) keV labeled with open black diamonds correspond to the and transitions in 21Na, respectively. The 1672(1)-keV line labeled in Fig. 2 with the solid black diamond is assigned to originate from 21Mg because there are no corresponding transitions in the target nuclei or in 21Na.
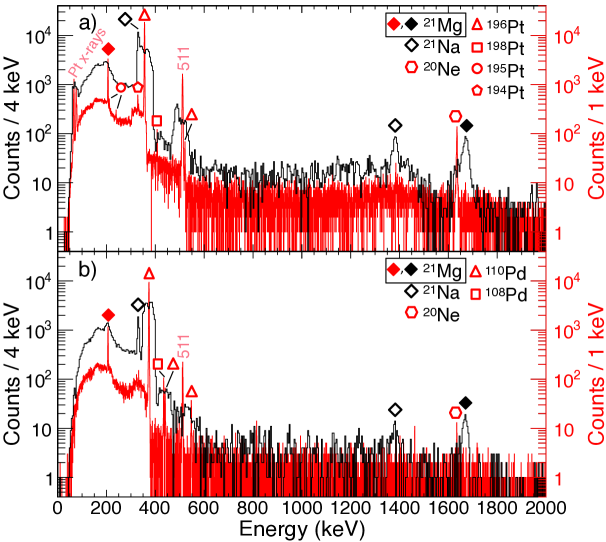
As shown in Fig. 1, there are and states at 1730 keV and 1755 keV, respectively, in 21F with only 25-keV energy difference Kozub et al. (1983); VonMoss et al. (2015). A state at 1651(10) keV has been previously identified in 21Mg Kubono et al. (1992); Diget et al. (2008). This state is the isobaric analogue of the 1730-keV state in 21F with identical decay branching ratios. It seems likely that the newly observed 1672(1)-keV -ray transition originates from a state in 21Mg, which is the isobaric analogue of the state in 21F. The new state at 1672(1) keV lies 21 keV above the previously identified state in good agreement with the mirror nucleus. Consequently, this work demonstrates the first experimental observation of the state in 21Mg.
In order to extract the values in 21Mg, the Coulomb excitation data were divided into six subsets corresponding to six ranges of projectile scattering angles covered by the downstream S3 detector. Data collected with the 196Pt and 110Pd targets were analyzed separately. The intensities of the and -ray transitions in 21Mg for each subset of data were extracted and corrected for the detection efficiency and the target impurity Zielińska et al. (2016). The intensity of the 205.6(1)-keV line was extracted initially from the decays occurring in the downstream S3 detector since the in-flight decay component could not be observed in the Doppler corrected spectra. The intensities of the -ray lines resulting from the target excitations were extracted and corrected for the detection efficiency and the beam impurity Zielińska et al. (2016). The detection efficiency of TIGRESS was measured at the target position and at the locations of the S3 detectors using 152Eu and 133Ba sources.
Corrected 21Mg and target -ray yields were analyzed using the GOSIA2 code Zielińska et al. (2016); Czosnyka et al. (1983); gos . The 21Mg matrix elements were fitted relative to the 196Pt and 110Pd target -ray yields. Matrix elements of the low-lying transitions in both targets are known with good precision together with other spectroscopic data Xiaolong (2007); Gürdal and Kondev (2012), which allow them to be used as an absolute normalisation for the beam excitations. For 21Mg the two observed states and their matrix elements in addition to a buffer state above the state were included in the analyses. The presently measured state half-life was not utilized in the GOSIA2 analyses in order to ensure the independence of the analyses.
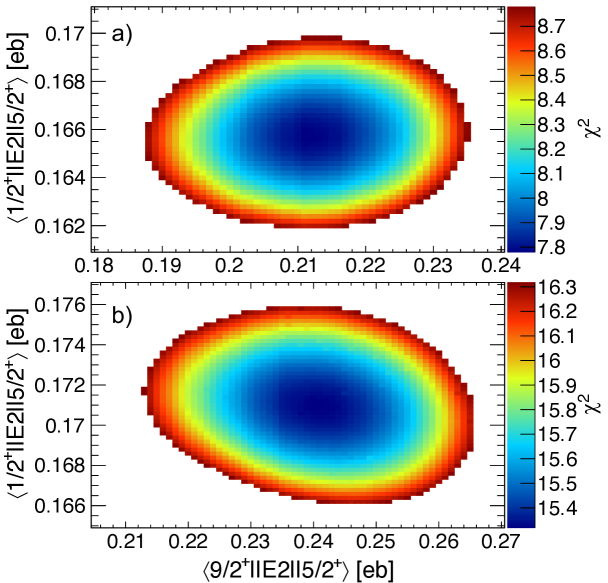
In the GOSIA2 fitting procedure and were scanned simultaneously resulting in a two-dimensional surface. The minimum value () represents the best fit of the matrix elements to the experimental -ray yields Zielińska et al. (2016). This analysis was performed iteratively since the state decays partly between the target and the S3 detector reducing the true -ray yield. The obtained matrix element from the first (previous) step was employed to compute the half-life of the state, which was then used to correct the -ray transition intensities for in-flight decay losses for the next analysis round. The values converged rapidly after 4 analysis steps for both 196Pt and 110Pd data increasing the non-corrected matrix elements by 4 % and 3 %, respectively.
The surfaces with applied 1 cuts are shown in Fig. 3 a) and b) for the 196Pt and 110Pd target data, respectively, after the convergence was reached. The 1-uncertainty contour is the part of the surface for which . The uncertainties of the matrix elements are obtained by projecting the 1 contour on the corresponding matrix element axis Zielińska et al. (2016). Matrix elements and values with errors are presented in Table 1. The obtained matrix elements from different measurements are in good agreement within uncertainties.
| 21Mg | 196Pt target | 110Pd target | from t1/2 |
|---|---|---|---|
| [eb] | 0.166(4) | 0.171(5) | 0.162(4) |
| [W.u.] | 13.3(6) | 14.2(8) | 12.7(6) |
| [eb] | 0.21(2) | 0.24(3) | |
| [W.u.] | 22(5) | 28(7) |
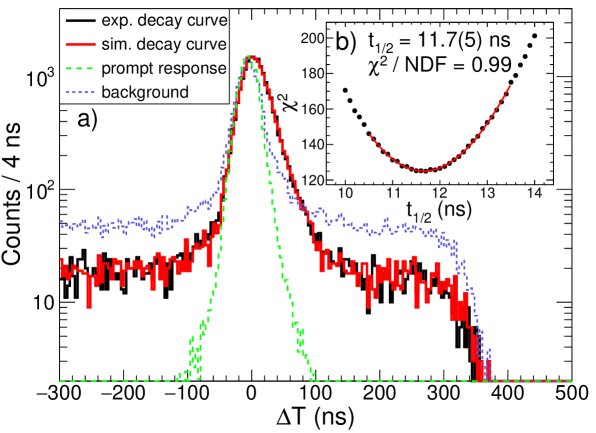
The decay curve of the state with 2.2 104 events was obtained from the GeS3 time difference distribution gating on the 205.6(1)-keV rays (black line in Fig. 4 a)). This was then compared to simulated decay curves (red (solid gray)) generated by sampling 1.3 104 decay events (= area of the 205.6(1)-keV peak) from the experimental prompt response distribution (green (dashed gray)) and 0.9 104 events from the background distribution (violet (short dashed gray)) with different half-lives. A value was computed for each simulated curve. The prompt response was extracted from the GeS3 time differences by gating on the 356-keV rays originating from 196Pt, state with = 34.15(15) ps Xiaolong (2007). The width of the distribution was further modified as the timing resolution decreases towards lower -ray energies. The background distribution was obtained by setting gates on both sides of the 205.6(1)-keV peak. Minimum was found at = 11.7(5) ns as shown in Fig. 4 b).
IV Discussion
In the present work, the value in 21Mg is obtained from three independent measurements from the Coulomb excitation cross section measurements on 196Pt and 110Pd targets and from the half-life measurement of the state. From these measurements the adopted value of = 13.3(4) W.u. is obtained using the expected value method Birch and Singh (2014) in V.AveLib software vav . This result yields the second data point for the value systematics of = nuclei in the shell. A value of = 25(4) W.u. is also obtained in the present work.
The experimental data for = nuclei are compared to various theoretical predictions in Fig. 5 a) and b). The USD calculation (taken from Ref. Wendt et al. (2014)) with an isoscalar polarization charge of = 0.35 e ( = 1.35 e, = 0.35 e) is in good agreement with the experimental values. The isospin conserving USDB calculation with = 0.35 e yields similar agreement with experiment. This indicates that the values, unlike MED, are largely insensitive to the phenomenological isospin symmetry breaking modifications of the USD interaction introduced in Ref. Doornenbal et al. (2007). The USDB calculation with = 0.5 e is also shown in Fig. 5 to demonstrate values’ sensitive reliance on the effective charges. The values of the A = 21 mirror pair were further investigated with the USDB-cdpn interaction Ormand and Brown (1989), which includes Coulomb and charge-dependent interactions, yielding less than 1 % increase in the strength in comparison to USDB.
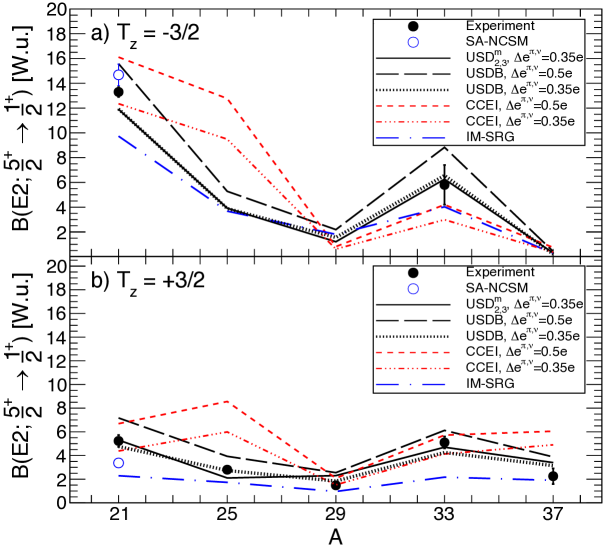
Ab initio methods have recently become available to study the spectroscopic properties of the shell nuclei. In Fig. 5 the experimental values are compared to the coupled-cluster effective interaction (CCEI) Jansen et al. (2016), the in-medium similarity renormalization group (IM-SRG) Tsukiyama et al. (2012); Bogner et al. (2014); Stroberg et al. (2017), and the symmetry-adapted no-core shell model (SA-NCSM) Launey et al. (2016); Dytrych et al. (2013) calculations. The CCEI, IM-SRG and SA-NCSM methods have been previously applied to calculate the level energies in and shell nuclei Stroberg et al. (2016); Jansen et al. (2016, 2014); Launey et al. (2016); Dytrych et al. (2013).
In the present work the IM-SRG calculation was performed using the EM 1.8/2.0 chiral interaction Hebeler et al. (2011) in a harmonic oscillator (HO) basis of = 20 MeV, including 13 major shells. The CCEI calculation employed a similar interaction Jansen et al. (2016). The IM-SRG calculation uses a consistently transformed transition operator Parzuchowski et al. (2017) and does not incorporate effective charges while the CCEI calculation uses a bare transition operator with phenomenological effective charges. The SA-NCSM calculations, not employing effective charges, were performed using the N2LO chiral potential Ekström et al. (2013) with HO frequency range of = 1020 MeV in a model space of 5 to 13 major shells and three symmetry-based model space selections. For each of these selections, calculations were performed with increasing number of shells to ensure convergence. The results are reported for = 15 MeV and 13 major shells, while the quoted uncertainties arise from the variation of the values with respect to the number of shells and the value of used in the calculation. Isospin symmetry breaking is included in the IM-SRG, CCEI and SA-NCSM approaches at the level of the chiral interaction. The interactions include the Coulomb force and the smaller non-Coulomb effects due to the different pion masses.
The CCEI calculation is found to agree better with experiment with = 0.35 e and it reproduces the experimental values at A = 21 correctly as shown in Fig. 5. The CCEI results deviate from the other models at A = 25 since CCEI favours different dominant configurations for the states in 25Si and 25Na.
The IM-SRG calculation underpredicts the strength for the majority of = nuclei. The same has been observed with = 1, shell mirror pairs Henderson et al. (2018), but the discrepancy was found to be much larger than observed here. The improved agreement achieved here for the values might result from the state configurations, which are likely dominated by single-particle excitations. In particular, IM-SRG is in good agreement with the USD and USDB predictions at A = 25 and A = 29 where the Z, N = 14, 16 subshell closures are likely to further suppress collectivity. Nevertheless, the trend for increasing difference of the values between A = 21 mirror nuclei is correctly reproduced. This difference is also obtained in the SA-NCSM calculations, which yield larger values in comparison to IM-SRG, but lower and larger values than measured for 21F and 21Mg, respectively.
Under the assumption of isospin symmetry, values from the A = 21 mirror pair can be used to calculate experimental and theoretical isoscalar () and isovector () matrix elements according to, e.g., Refs. Brown et al. (1982); Orce and Velázquez (2006). This analysis implies that the dominant component is correctly reproduced by SA-NCSM, while the component is overestimated by about 50 % indicating a larger difference between the associated proton matrix elements in comparison to the experimental . Similar analysis with the IM-SRG results reveals that the situation is the opposite - the component is only slightly overestimated while the component is clearly underestimated. Whether these observations arise from the characteristic features of the SA-NCSM and IM-SRG approaches remains an open question.
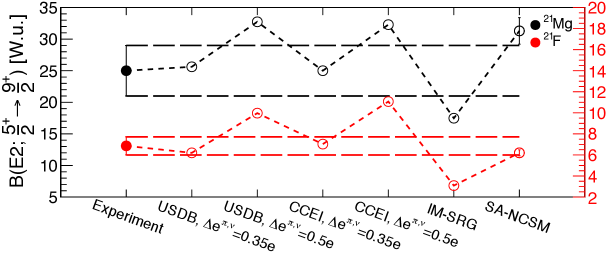
According to USDB calculation a dominant part (73 %) of the state in 21Mg is based on configuration, which may alternatively be interpreted to arise from a coupling of an odd neutron to the first excited 2+ state in 20Mg. Figure 6 shows how the different calculations compare with the experimental value between the collective state and the ground state in 21Mg (and 21F). The USDB and CCEI approaches reproduce well the experimental values for both nuclei with = 0.35 e. The SA-NCSM calculation lies close to the experimental value in 21Mg, given the quoted uncertainties, while the IM-SRG calculation underpredicts the experimental value by 30 %.
V Summary
The = nucleus 21Mg was studied in Coulomb excitation enabling the first direct observations of the and -ray transitions. The and values were measured and the results are compared to shell-model and ab initio nuclear structure calculations. The value in 21Mg is found to be more than two times larger than the corresponding value in its mirror nucleus 21F. Shell-model calculations employing modified USD and standard USDB interactions reproduce this difference equally well indicating that the associated values do not signal significant isospin symmetry breaking. The IM-SRG ab initio approach is found to underpredict both newly measured values in 21Mg, while the SA-NCSM ab initio calculations yield a slight overprediction.
Acknowledgements.
This work has been supported by the Natural Sciences and Engineering Research Council of Canada (NSERC), The Canada Foundation for Innovation and the British Columbia Knowledge Development Fund. TRIUMF receives federal funding via a contribution agreement through the National Research Council of Canada. The work at LLNL is under contract DE-AC52-07NA27344. The work at JYFL-ACCLAB has been supported by the Academy of Finland under the Finnish Center of Excellence Programme (2012-2017). The work at Colorado School of Mines has been supported by the U.S. Department of Energy under Grant No. DE-SC0017649. This work has been partly supported by the U.S. National Science Foundation (OIA-1738287, ACI-1713690). This work benefitted from computing resources provided by Blue Waters and LSU (www.hpc.lsu.edu). The Blue Waters sustained-petascale computing project is supported by the National Science Foundation (awards OCI-0725070 and ACI-1238993) and the state of Illinois, and is a joint effort of the University of Illinois at Urbana-Champaign and its National Center for Supercomputing Applications.References
- Bentley and Lenzi (2007) M. Bentley and S. Lenzi, Prog. Part. Nucl. Phys. 59, 497 (2007), URL http://www.sciencedirect.com/science/article/pii/S0146641006000743.
- Brown and Wildenthal (1988) B. A. Brown and B. H. Wildenthal, Annu. Rev. Nucl. Part. Sci. 38, 29 (1988), URL https://doi.org/10.1146/annurev.ns.38.120188.000333.
- Doornenbal et al. (2007) P. Doornenbal, P. Reiter, H. Grawe, T. Otsuka, A. Al-Khatib, A. Banu, T. Beck, F. Becker, P. Bednarczyk, G. Benzoni, et al., Phys. Lett. B 647, 237 (2007), URL http://www.sciencedirect.com/science/article/pii/S0370269307001499.
- Ehrman (1951) J. B. Ehrman, Phys. Rev. 81, 412—416 (1951), URL https://link.aps.org/doi/10.1103/PhysRev.81.412.
- Thomas (1952) R. G. Thomas, Phys. Rev. 88, 1109 (1952), URL https://link.aps.org/doi/10.1103/PhysRev.88.1109.
- Wendt et al. (2014) A. Wendt, J. Taprogge, P. Reiter, P. Golubev, H. Grawe, S. Pietri, P. Boutachkov, A. Algora, F. Ameil, M. A. Bentley, et al., Phys. Rev. C 90, 054301 (2014), URL https://link.aps.org/doi/10.1103/PhysRevC.90.054301.
- Firestone (2015) R. Firestone, Nuclear Data Sheets 127, 1 (2015), URL http://www.sciencedirect.com/science/article/pii/S0090375215000241.
- Kozub et al. (1983) R. L. Kozub, J. Lin, J. F. Mateja, C. J. Lister, D. J. Millener, J. W. Olness, and E. K. Warburton, Phys. Rev. C 27, 158 (1983), URL https://link.aps.org/doi/10.1103/PhysRevC.27.158.
- VonMoss et al. (2015) J. M. VonMoss, S. L. Tabor, V. Tripathi, A. Volya, B. Abromeit, P. C. Bender, D. D. Caussyn, R. Dungan, K. Kravvaris, M. P. Kuchera, et al., Phys. Rev. C 92, 034301 (2015), URL https://link.aps.org/doi/10.1103/PhysRevC.92.034301.
- Dombsky and Kunz (2014) M. Dombsky and P. Kunz, Hyperfine Interactions 225, 17 (2014), URL https://doi.org/10.1007/s10751-013-0879-5.
- Bricault et al. (2014) P. G. Bricault, F. Ames, M. Dombsky, P. Kunz, and J. Lassen, Hyperfine Interactions 225, 25 (2014), URL https://doi.org/10.1007/s10751-013-0880-z.
- Hackman and Svensson (2014) G. Hackman and C. E. Svensson, Hyperfine Interactions 225, 241 (2014), URL https://doi.org/10.1007/s10751-013-0905-7.
- Marchetto et al. (2012) M. Marchetto, F. Ames, P. Bender, B. Davids, N. Galinski, A. Garnsworthy, G. Hackman, O. Kirsebom, R. Laxdal, D. Miller, et al., in Proceedings of LINAC2012, edited by M. Draper, C. Calri, J. Poole, L. Liljeby, and S. Lupu (JACoW, 2012), p. 1059, URL http://accelconf.web.cern.ch/AccelConf/LINAC2012/papers/fr1a04.pdf.
- Cline (1986) D. Cline, Annu. Rev. Nucl. Part. Sci. 36, 683 (1986), URL https://doi.org/10.1146/annurev.ns.36.120186.003343.
- Hurst et al. (2009) A. Hurst, C. Wu, J. Becker, M. Stoyer, C. Pearson, G. Hackman, M. Schumaker, C. Svensson, R. Austin, G. Ball, et al., Physics Letters B 674, 168 (2009), ISSN 0370-2693, URL http://www.sciencedirect.com/science/article/pii/S0370269309002822.
- Kwan et al. (2014) E. Kwan, C. Wu, N. Summers, G. Hackman, T. Drake, C. Andreoiu, R. Ashley, G. Ball, P. Bender, A. Boston, et al., Physics Letters B 732, 210 (2014), ISSN 0370-2693, URL http://www.sciencedirect.com/science/article/pii/S0370269314002056.
- (17) Micron semiconductor ltd. - silicon catalogue, http://79.170.44.80/micronsemiconductor.co.uk/wp-content/uploads/2017/01/2017-MSL-Catalogue.pdf.
- Rizwan (2015) U. Rizwan, Master’s thesis, Simon Fraser University (2015), URL http://summit.sfu.ca/item/15733.
- Kubono et al. (1992) S. Kubono, Y. Funatsu, N. Ikeda, M. Yasue, T. Nomura, Y. Fuchi, H. Kawashima, S. Kato, H. Miyatake, H. Orihara, et al., Nucl. Phys. A 537, 153 (1992), URL http://www.sciencedirect.com/science/article/pii/037594749290162D.
- Diget et al. (2008) C. A. Diget, P. Adrich, D. Bazin, M. D. Bowen, B. A. Brown, C. M. Campbell, J. M. Cook, A. Gade, T. Glasmacher, K. Hosier, et al., Phys. Rev. C 77, 064309 (2008), URL https://link.aps.org/doi/10.1103/PhysRevC.77.064309.
- Krämer et al. (2009) J. Krämer, K. Blaum, M. D. Rydt, K. Flanagan, C. Geppert, M. Kowalska, P. Lievens, R. Neugart, G. Neyens, W. Nörtershäuser, et al., Phys. Lett. B 678, 465 (2009), URL http://www.sciencedirect.com/science/article/pii/S037026930900776X.
- Warburton and Olness (1970) E. K. Warburton and J. W. Olness, Phys. Rev. C 2, 2235 (1970), URL https://link.aps.org/doi/10.1103/PhysRevC.2.2235.
- Zielińska et al. (2016) M. Zielińska, L. P. Gaffney, K. Wrzosek-Lipska, E. Clément, T. Grahn, N. Kesteloot, P. Napiorkowski, J. Pakarinen, P. Van Duppen, and N. Warr, The Eur. Phys. J. A 52, 99 (2016), URL https://doi.org/10.1140/epja/i2016-16099-8.
- Czosnyka et al. (1983) T. Czosnyka, D. Cline, and C. Wu, Bull. Am. Phys. Soc. 28, 745 (1983).
- (25) Gosia user’s manual, http://www.pas.rochester.edu/~cline/Gosia/Gosia_Manual_20120510.pdf.
- Xiaolong (2007) H. Xiaolong, Nuclear Data Sheets 108, 1093 (2007), ISSN 0090-3752, URL http://www.sciencedirect.com/science/article/pii/S0090375207000488.
- Gürdal and Kondev (2012) G. Gürdal and F. Kondev, Nuclear Data Sheets 113, 1315 (2012), ISSN 0090-3752, URL http://www.sciencedirect.com/science/article/pii/S0090375212000415.
- Birch and Singh (2014) M. Birch and B. Singh, Nucl. Data Sheets 120, 106 (2014), URL http://www.sciencedirect.com/science/article/pii/S0090375214004712.
- (29) Visual averaging library (v.avelib) user manual, https://www-nds.iaea.org/public/ensdf_pgm/utility/vavelib/AveLib_userManual.pdf.
- Ormand and Brown (1989) W. Ormand and B. Brown, Nucl. Phys. A 491, 1 (1989), URL http://www.sciencedirect.com/science/article/pii/0375947489902030.
- Jansen et al. (2016) G. R. Jansen, M. D. Schuster, A. Signoracci, G. Hagen, and P. Navrátil, Phys. Rev. C 94, 011301(R) (2016), URL https://link.aps.org/doi/10.1103/PhysRevC.94.011301.
- Tsukiyama et al. (2012) K. Tsukiyama, S. K. Bogner, and A. Schwenk, Phys. Rev. C 85, 061304(R) (2012), URL https://link.aps.org/doi/10.1103/PhysRevC.85.061304.
- Bogner et al. (2014) S. K. Bogner, H. Hergert, J. D. Holt, A. Schwenk, S. Binder, A. Calci, J. Langhammer, and R. Roth, Phys. Rev. Lett. 113, 142501 (2014), URL https://link.aps.org/doi/10.1103/PhysRevLett.113.142501.
- Stroberg et al. (2017) S. R. Stroberg, A. Calci, H. Hergert, J. D. Holt, S. K. Bogner, R. Roth, and A. Schwenk, Phys. Rev. Lett. 118, 032502 (2017), URL https://link.aps.org/doi/10.1103/PhysRevLett.118.032502.
- Launey et al. (2016) K. D. Launey, T. Dytrych, and J. P. Draayer, Prog. Part. Nucl. Phys. 89, 101 (2016), URL http://www.sciencedirect.com/science/article/pii/S0146641016000338.
- Dytrych et al. (2013) T. Dytrych, K. D. Launey, J. P. Draayer, P. Maris, J. P. Vary, E. Saule, U. Catalyurek, M. Sosonkina, D. Langr, and M. A. Caprio, Phys. Rev. Lett. 111, 252501 (2013), URL https://link.aps.org/doi/10.1103/PhysRevLett.111.252501.
- Stroberg et al. (2016) S. R. Stroberg, H. Hergert, J. D. Holt, S. K. Bogner, and A. Schwenk, Phys. Rev. C 93, 051301(R) (2016), URL https://link.aps.org/doi/10.1103/PhysRevC.93.051301.
- Jansen et al. (2014) G. R. Jansen, J. Engel, G. Hagen, P. Navratil, and A. Signoracci, Phys. Rev. Lett. 113, 142502 (2014), URL https://link.aps.org/doi/10.1103/PhysRevLett.113.142502.
- Hebeler et al. (2011) K. Hebeler, S. K. Bogner, R. J. Furnstahl, A. Nogga, and A. Schwenk, Phys. Rev. C 83, 031301(R) (2011), URL https://link.aps.org/doi/10.1103/PhysRevC.83.031301.
- Parzuchowski et al. (2017) N. M. Parzuchowski, S. R. Stroberg, P. Navrátil, H. Hergert, and S. K. Bogner, Phys. Rev. C 96, 034324 (2017), URL https://link.aps.org/doi/10.1103/PhysRevC.96.034324.
- Ekström et al. (2013) A. Ekström, G. Baardsen, C. Forssén, G. Hagen, M. Hjorth-Jensen, G. R. Jansen, R. Machleidt, W. Nazarewicz, et al., Phys. Rev. Lett. 110, 192502 (2013), URL https://link.aps.org/doi/10.1103/PhysRevLett.110.192502.
- Henderson et al. (2018) J. Henderson, G. Hackman, P. Ruotsalainen, S. Stroberg, K. D. Launey, F. A. Ali, N. Bernier, M. A. Bentley, M. Bowry, R. Caballero-Folch, et al., Phys. Lett. B 782, 468 (2018), URL http://www.sciencedirect.com/science/article/pii/S0370269318304283.
- Brown et al. (1982) B. A. Brown, B. H. Wildenthal, W. Chung, S. E. Massen, M. Bernas, A. M. Bernstein, R. Miskimen, V. R. Brown, and V. A. Madsen, Phys. Rev. C 26, 2247 (1982), URL https://link.aps.org/doi/10.1103/PhysRevC.26.2247.
- Orce and Velázquez (2006) J. Orce and V. Velázquez, Nucl. Phys. A 764, 205 (2006), URL http://www.sciencedirect.com/science/article/pii/S0375947405011346.