The ALADIN2000 Collaboration
Isotopic Dependence of the Nuclear Caloric Curve
Abstract
The dependence of projectile fragmentation at relativistic energies has been studied with the ALADIN forward spectrometer at SIS. A stable beam of 124Sn and radioactive beams of 124La and 107Sn at 600 MeV per nucleon have been used in order to explore a wide range of isotopic compositions. Chemical freeze-out temperatures are found to be nearly invariant with respect to the of the produced spectator sources, consistent with predictions for expanded systems. Small Coulomb effects ( MeV) appear for residue production near the onset of multifragmentation.
pacs:
25.70.Mn, 25.70.Pq, 25.75.-qThe isotopic dependence of the nuclear caloric curve, the temperature-energy relation of excited nuclear systems poch95 ; kelic06 , is of interest for several reasons. It is, at first, of practical importance for isotopic reaction studies, presently conducted in many laboratories and conceived under the assumption that the basic reaction processes remain unchanged if only the isotopic composition of the collision partners is varied. One expects that specific effects related to the isotopic dependence of the nuclear forces can be isolated in this way colonna06 ; baoan08 . For example, in the statistical interpretation of isoscaling, analytic relations between the measured parameters and the symmetry term in the equation of state can be derived if the freeze-out temperatures can be assumed to be identical for the reactions one compares colonna06 ; botv02 . A significant isotopic dependence of the caloric curve would here present a complication.
From a theoretical point of view, the isotopic behaviour of the caloric curve is useful for investigating its connection with limiting temperatures, i.e. the maximum temperatures nuclei can sustain before they become unbound bonche85 ; besp89 . These limiting temperatures have been found to be correlated with the critical temperature of nuclear matter, in fact nearly linearly in mean-field calculations with Skyrme forces song91 . Experimental information on limiting temperatures will thus permit tests of microscopic calculations of the nuclear equation of state at finite temperature which cannot be easily obtained by other means baldo04 ; wang05 .
In the calculations considering excited compound nuclei in equilibrium with their surrounding vapor, their stability was found to be strongly dependent on the Coulomb pressure generated by the protons they contain bonche85 ; besp89 . The limiting temperatures decrease along the valley of stability because the effect of the increasing atomic number is stronger than that of the decreasing charge-to-mass ratio of heavy nuclei. A systematic mass dependence of measured breakup temperatures in multifragmentation reactions has, therefore, led to the suggestion that they may be identified with the predicted stability limits nato95 ; nato02 . In this case, since Coulomb effects should be even more pronounced along chains of isotopes or isobars, one would expect a significant isotopic dependence of the caloric curve kelic06 .
On the other hand, statistical models for multifragmentation, based on calculating the accessible phase space in expanded volumes gross86 ; bond95 , predict only small temperature differences for neutron-rich and neutron-poor systems ogul02 . To some extent, the isotopic behaviour of the caloric curve thus turns into a test of the reaction mechanism, indicating whether the observed disintegrations are primarily caused by a Coulomb instability limiting the existence of compound nuclei or by the opening of the partition space.
Experiment S254, conducted at the SIS heavy-ion synchrotron at GSI Darmstadt, was devoted to the study of isotopic effects in projectile fragmentation at relativistic energies. Besides stable 124Sn beams, neutron-poor secondary Sn and La beams were used in order to extend the range of isotopic compositions beyond that available with stable beams alone. The radioactive beams were produced at the fragment separator FRS frs92 by fragmenting primary 142Nd projectiles with energies near 900 MeV/nucleon in a thick beryllium target. The FRS was set to select 124La and, subsequently, 107Sn projectiles which were directed onto natSn targets of 500 mg/cm2 areal density at the ALADIN setup. All three beams had a laboratory energy of 600 MeV/nucleon. At this energy, the acceptance of the ALADIN forward spectrometer is about 90% for projectile fragments with , increases with , and exceeds 95% for schuett96 .
In order to reach the necessary beam intensity of about 103 particles/s with the smallest possible mass-to-charge ratio , it was found necessary to accept a distribution of neighbouring nuclides together with the requested 124La or 107Sn isotopes. The mean compositions of the nominal 124La (107Sn) beams were = 56.8 (49.7) and = 2.19 (2.16), respectively luk08 . Model studies confirm that these values are also representative for the spectator systems emerging after the initial stages of the reaction botv02 ; lef05 .
The obtained mass resolution is about 7% (FWHM) for projectile fragments with and decreases to 3% for . Masses are thus individually resolved for fragments with atomic number . The elements are individually resolved over the full range of atomic numbers up to with the resolution (FWHM) obtained with the TP-MUSIC IV detector schuett96 .
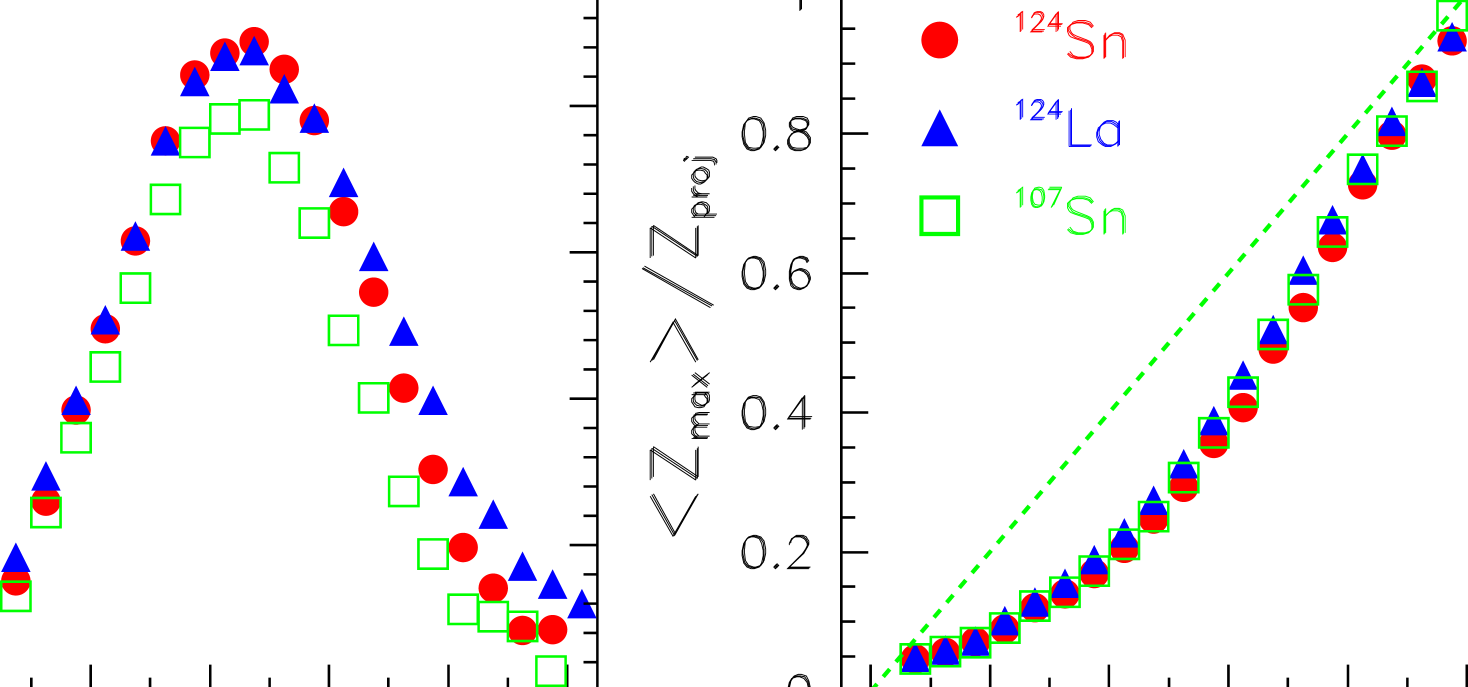
Global fragmentation observables were found to depend only weakly on the isotopic composition. This is shown in Fig. 1 for the mean multiplicity of intermediate-mass fragments () and for , both as a function of . Here denotes the largest atomic number within a partition while the sorting variable with represents the of the spectator system, apart from emitted hydrogens.
The multiplicities exhibit the universal rise and fall of fragment production schuett96 , and only a slightly steeper slope in the rise section () distinguishes the neutron-rich 124Sn from the two other cases. The difference can be related to the evaporation properties of excited heavy nuclei sfienti_prag . Neutron emission as the prevailing deexcitation mode of neutron-rich residue nuclei does not affect . The emission of hydrogen isotopes reduces since they are not counted therein. The same effect produces small differences in the correlation of with (Fig. 1, right panel). There, the transition from predominantly residue production to multifragmentation appears as a reduction of with respect to which occurs between 0.6 and 0.8.
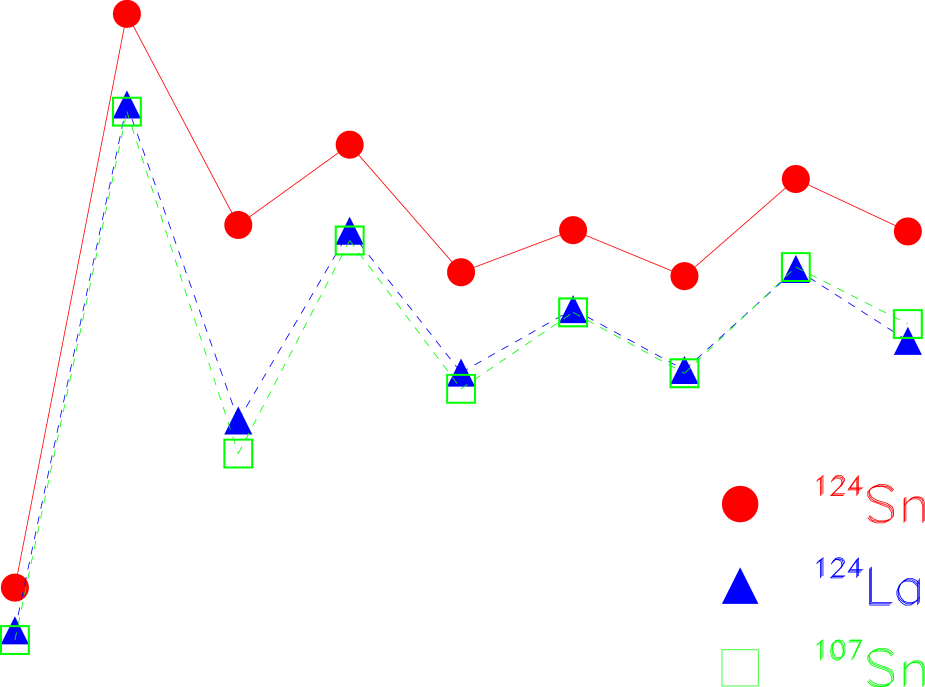
The mean neutron-to-proton ratios / of light fragments exhibit nuclear structure effects characteristic for the isotopes produced as well as a significant memory of the isotopic composition of the emitting system (Fig. 2). The mean neutron numbers are larger for the fragments of 124Sn by, on average, . The values for have been corrected for the missing yields of unstable 8Be fragments by smoothly interpolating over the measured yields of 7,9-11Be. This has a negligible effect for 124La and 107Sn with / but lowers the value for 124Sn from 1.23 to 1.16 which makes the systematic odd-even variations as a function of the fragment more clearly visible. Apparently, the strongly bound even-even nuclei attract a large fraction of the product yields ricci04 .
Two temperature observables, deduced from the resolved isotope yields, are shown in Fig. 3 as a function of the normalized . Besides the frequently used
| (1) |
(left panel, Ref. poch95 ), also
| (2) |
deduced from Li and Be fragment yields is displayed (right panel, Ref. traut07 ). The apparent temperatures, as given by the formulae, are shown, i.e. without corrections for secondary decays feeding the ground states of these nuclei. Including such corrections will raise the temperature values by 10 to 20% poch95 ; traut07 . The dependence of the secondary-decay corrections on has been quantitatively studied with two models, the SMM bond95 and the Quantum Statistical Model of Hahn and Stöcker hahn88 but significant effects ( keV) were not found.
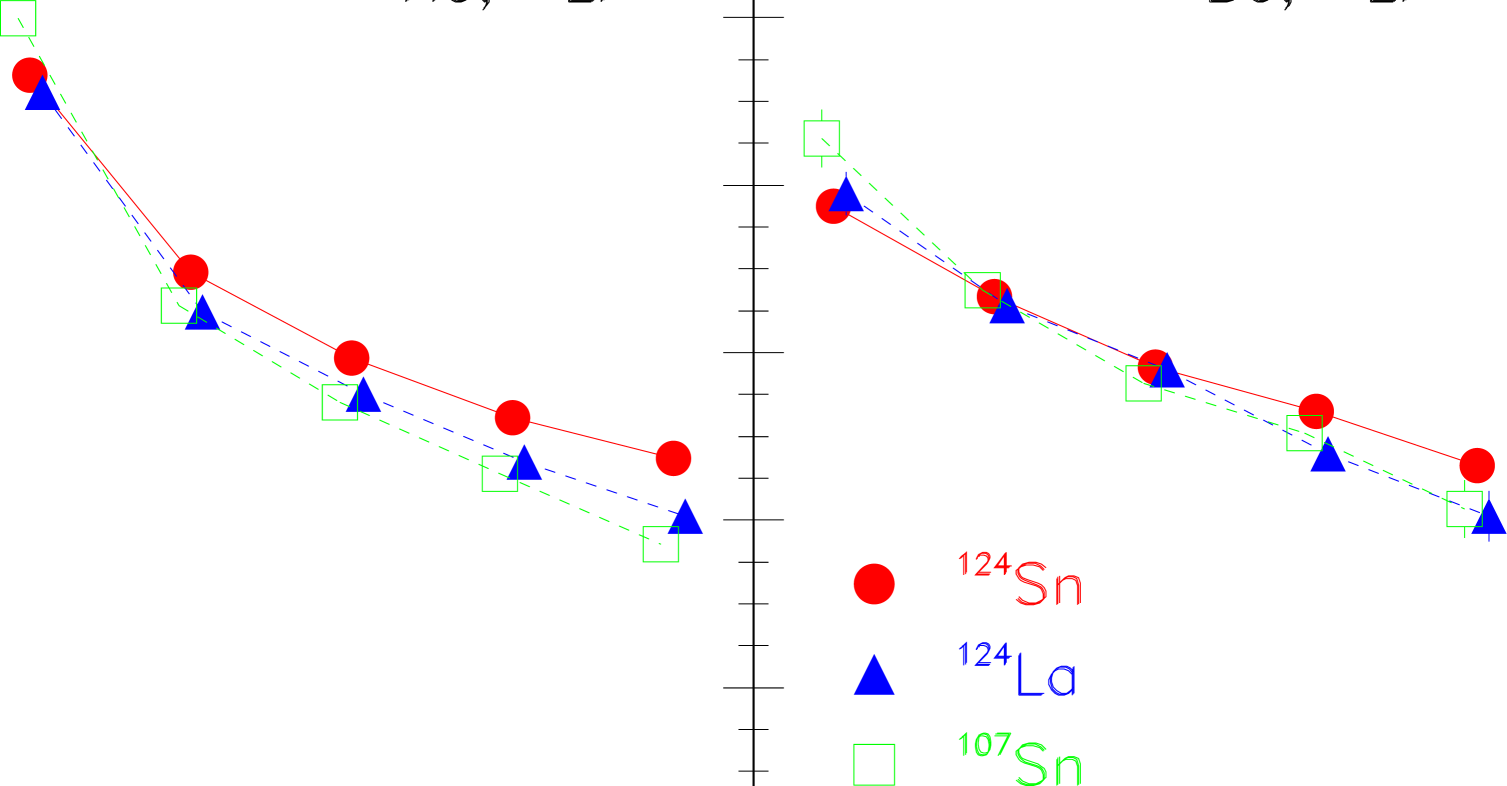
Both temperature observables show the same smooth rise with increasing centrality that is familiar from earlier studies of 197Au fragmentations traut07 ; xi97 . The dependence on the isotopic composition is rather weak. The mean temperature differences between the neutron-rich and neutron-poor systems amount to MeV and MeV in the bin of maximum fragment production, , and become negligible at smaller . This translates into a similar invariance for the nuclear caloric curve as may serve as a measure of the deposited energy . The latter is expected on the basis of the participant-spectator geometry but also confirmed by the observation that the degree of fragmentation, known to depend on tamain06 , is strongly related to (Fig. 1). At larger , in the regime of predominantly residue production ( and above), the temperatures of 124Sn decays exceed those for the neutron-poor systems by about 0.6 MeV.
Within these limits, and particularly in the regime of multifragmentation, the deduced temperatures are consistent with the overall observation that the reaction processes are not strongly affected by a variation of the system . Only the fragment mass distributions react sensitively to this parameter (Fig. 2). Comparing to the theoretical predictions, we find that the global behavior of the breakup temperatures is in good agreement with the SMM calculations for 124Sn and 124La nuclei of Ogul and Botvina ogul02 . The differences obtained for these cases are negligible in the multifragmentation regime and reach a maximum MeV in the transition region where the equilibrium temperature for the more proton-rich 124La system is slightly lower.
Rather small isotopic variations of the caloric curve have also been predicted with Thomas-Fermi-type calculations in which expansion kolomietz01 ; hoel07 ; samaddar07 and shape degrees of freedom de06 have been considered. The obtained temperatures of 5 to 8 MeV are within the present range but it is not obvious that the experimental temperatures of fragmented systems at chemical freeze-out can be considered as representative for uniform spherical nuclei, even after expansion.
For a quantitative comparison with the expectations for limiting-temperatures of compound nuclei, the region of transition from residue production to multifragmentation () seems best suited. The residue channels associated with the highest temperatures are found here. They may be separated from the fragmentation events in the same bin by applying an additional condition on . Furthermore, in order to account for the above-mentioned effects of evaporation and to select equivalent degrees of fragmentation, slightly lower limits were chosen for the neutron-poor projectiles (by 0.05 on the reduced scale, cf. Fig. 1).
| Projectile | ||||
|---|---|---|---|---|
| 124Sn | 8.2 | 9.2 | 6.27 0.04 | 5.96 0.08 |
| 124La | 6.3 | 7.6 | 5.89 0.05 | 5.59 0.11 |
| 107Sn | 6.6 | 8.2 | 5.79 0.05 | 5.22 0.09 |
In Table 1, a summary of the experimental values for these event classes is given together with the Hartree-Fock results of Besprosvany and Levit besp89 . Besides the predictions for the nominal projectiles, also those for nuclei with the same but only 75% of the projectile mass are included. These are the spectator systems most likely populating this bin poch95 . Their limiting temperatures are higher than those of the nominal nuclei while their difference is slightly smaller.
The displayed experimental temperatures contain a 20% side-feeding correction. The additional condition on reduces the mean experimental temperature by MeV (last column of Table 1). Less violent processes associated with smaller energy deposits are selected poch95 . With the same condition, also the difference between the neutron-rich and neutron-poor spectator systems changes, rising by a small amount from to MeV (statistical errors).
It is obvious that Coulomb effects on the scale of MeV as exhibited by the Hartree-Fock limiting temperatures are not observed. On the other hand, the large difference in average magnitude of the predicted and measured temperatures is not as crucial as it may appear at first sight. As noted already by Natowitz et al. nato95 , the predictions depend sensitively on the type of force used in the calculations baldo04 . The experimental average MeV for nuclei is close to the results obtained with the SkM∗ force by Song and Su song91 who, however, have not studied the dependence on . If these low values, including the corresponding critical temperature MeV for infinite nuclear matter song91 , can be shown to be realistic a link may be established between the limits of dynamic compound stability and the onset of multifragmentation. Otherwise, and as suggested by the SMM results ogul02 , also the transition to multifragmentation is predominantly governed by the properties of the fragmentation phase space.
In summary, the study of projectile fragmentation over wide ranges of , up to presently available limits for proton-rich beams, has shown that the overall isotopic dependence is weak. In particular, the breakup temperatures entering the nuclear caloric curve were found to be identical within a few hundreds of keV, compatible with the assumption of identical reaction trajectories usually made in isotopic reaction studies, and in good agreement with the SMM predictions for a statistical population of the asymptotic phase space including the partition degree of freedom. The temperature differences reach a value of about 0.6 MeV in selected channels of residue production. The temperature MeV measured for these processes represents a lower bound for the limiting temperature of compound nuclei in the region.
The authors thank J. B. Natowitz for valuable comments and discussion. C. Sf. acknowledges the receipt of an Alexander-von-Humboldt fellowship. This work has been supported by the European Community under contract No. HPRI-CT-1999-00001 and by the Polish Ministry of Science and Higher Education under Contracts No. 1 P03B 105 28 (2005 - 2006) and N202 160 32/4308 (2007-2009).
References
- (1) J. Pochodzalla et al., Phys. Rev. Lett. 75, 1040 (1995).
- (2) for a review see, e.g., A. Kelić, J. B. Natowitz, and K.-H. Schmidt, Eur. Phys. J. A 30, 203 (2006).
- (3) M. Colonna and M. B. Tsang, Eur. Phys. J. A 30, 165 (2006), and references therein.
- (4) Bao-An Li, Lie-Wen Chen, and Che Ming Ko, Phys. Rep. 464, 113 (2008).
- (5) A. S. Botvina, O. V. Lozhkin, and W. Trautmann, Phys. Rev. C 65 044610 (2002).
- (6) P. Bonche, S. Levit, and D. Vautherin, Nucl. Phys. A436, 265 (1985).
- (7) J. Besprosvany and S. Levit, Phys. Lett. B 217, 1 (1989).
- (8) H. Q. Song and R. K. Su, Phys. Rev. C 44, 2505 (1991).
- (9) M. Baldo, L. S. Ferreira, and O. E. Nicotra, Phys. Rev. C 69, 034321 (2004).
- (10) P. Wang et al., Nucl. Phys. A748, 226 (2005).
- (11) J. B. Natowitz et al., Phys. Rev. C 52, R2322 (1995).
- (12) J. B. Natowitz et al., Phys. Rev. C 65, 034618 (2002).
- (13) D. H. E. Gross, Zhang Xiao-ze, and Xu Shu-yan, Phys. Rev. Lett. 56, 1544 (1986).
- (14) J. P. Bondorf et al., Phys. Rep. 257, 133 (1995).
- (15) R. Ogul and A. S. Botvina, Phys. Rev. C 66, 051601(R) (2002).
- (16) H. Geissel et al., Nucl. Instr. and Meth. B 70, 286 (1992).
- (17) A. Schüttauf et al., Nucl. Phys. A607, 457 (1996).
- (18) J. Łukasik et al., Nucl. Instr. and Meth. A 587, 413 (2008).
- (19) A. Le Fèvre et al., Phys. Rev. Lett. 94, 162701 (2005).
- (20) C. Sfienti et al., Nucl. Phys. A749, 83c (2005).
- (21) M. V. Ricciardi et al., Nucl. Phys. A733, 299 (2004).
- (22) W. Trautmann et al., Phys. Rev. C 76, 064606 (2007).
- (23) D. Hahn and H. Stöcker, Nucl. Phys. A476, 718 (1988).
- (24) Hongfei Xi et al., Z. Phys. A 359, 397 (1997); erratum in Eur. Phys. J. A 1, 235 (1998).
- (25) B. Tamain, Eur. Phys. J. A 30, 71 (2006).
- (26) V. M. Kolomietz, A. I. Sanzhur, S. Shlomo, and S. A. Firin, Phys. Rev. C 64, 024315 (2001).
- (27) C. Hoel, L. G. Sobotka, and R. J. Charity, Phys. Rev. C 75, 017601 (2007).
- (28) S. K. Samaddar, J. N. De, X. Viñas, and M. Centelles, Phys. Rev. C 76, 041602(R) (2007).
- (29) J. N. De et al., Phys. Lett. B 638, 160 (2006).