11email: {xavier.coiteux.roy,stefan.wolf}@usi.ch
Key Agreement and Oblivious Transfer
from Free-Energy Limitations
Abstract
We propose one of the very few constructive consequences of the second law of thermodynamics. More specifically, we present protocols for secret-key establishment and multiparty computation the security of which is based fundamentally on Landauer’s principle. The latter states that the erasure cost of each bit of information is at least (where is Boltzmann’s constant and is the absolute temperature of the environment). Albeit impractical, our protocols explore the limits of reversible computation, and the only assumption about the adversary is her inability to access a quantity of free energy that is exponential in the one of the honest participants. Our results generalize to the quantum realm.
August 12, 2025
Keywords: Reversible computation, quantum information, information-
theoretic security, key establishment, oblivious transfer.
1 Introduction
1.1 Motivation
In the past decades, several attempts were made to achieve cryptographic security from physical properties of communication channels: Most prominently, of course, quantum cryptography [BB84, Eke91]; other systems made use of noise in communication channels [Wyn75] or bounds on the memory space accessible by an adversary [Mau92]. These schemes have in common that no limit is assumed on the opponent’s computational power: They are information-theoretically secure.
Our schemes for achieving confidentiality (key agreement or, more precisely, key expansion) as well as secure coöperation (multiparty computation, i.e., oblivious transfer) rely solely on a bound on the accessible free energy111Free energy is “free” in the sense that it can be used to do work — it is not “entrapped” in a system. of an adversary. More specifically, we propose schemes the security of which follows from Landauer’s principle, which is a quantification of the second law of thermodynamics: In a closed system, “entropy” does not decrease (roughly speaking).
Landauer’s principle states that the erasure of information unavoidably costs free energy, the amount of which is proportional to the length of the string to be erased. On the “positive” side, the converse of the principle states that the all- string of length has a free-energy value proportional to . More precisely, the erasure cost and work value are both quantified by , where is Boltzmann’s constant (in some sense the nexus between the micro- and macroscopic realms), and is the absolute temperature of the environmental heat bath.
Our result can be seen as one episode in a series of results suggesting information-theoretic security to be, in principle, achievable under the assumption that at least one in a list of physical theories, such as quantum mechanics or special relativity, is accurate: We add to this list the second law of thermodynamics — to which not much glamour has been attached before.
1.2 Contributions
We base the “free-energy-bounded model” of information-theoretic cryptography upon the observation that the second law of thermodynamics has a cryptographically useful corollary: “Copying information has a fundamental cost in free energy.” Bounding the free energy of an adversary forces them into picking parsimoniously what to copy, and that can be exploited in a reversible-computing context to ensure information-theoretic security. Our secret-key establishment protocol demonstrates how bounds in free energy can lead to cryptographic mechanisms similar to the ones used in quantum-key distribution and in the bounded-storage model, while our oblivious-transfer protocol exemplifies the novelty of our model.
This is an overview of our article: In Section 2, we review the subjects of information-theoretic cryptography and of reversible computing. In Section 3, we introduce, based on reversible computing, a novel model of computation and interaction that captures the consumption and the production of free energy in Turing machines. In Section 4, we establish some prerequisites: we prove a version of Landauer’s principle in our framework, and construct a game that is basically equivalent to a thermodynamical “almost-no-cloning theorem,” which we later use in our security proofs. In Sections 5 and 6, we offer protocols for secret-key establishment and oblivious transfer, respectively; their information-theoretical security is based fundamentally on Landauer’s principle. It is assured against adversaries whose bound in free energy is exponential compared to the one of the honest players. While the present work focuses on classical information, we sketch in Section 7 how all our results generalize in presence of quantum adversaries.
2 State of the Art
2.1 Information-theoretic cryptography from physical assumptions
In parallel to the development of computationally secure cryptography — and somewhat in its shadow —, attempts were made to obtain in a provable fashion stronger, information-theoretic security, based not on the hardness of obtaining the (uniquely determined) message in question, but on the sheer lack of information. Hereby, the need for somehow “circumventing” Shannon’s pessimistic theorem of perfect secrecy is met by some sort of physical limitation. The latter can come in the form of simple noise in a communication channel, a limitation on accessible memory, the uncertainty principle of quantum theory, or the non-signalling postulate of special relativity.
The first system of the kind, radically improving on the perfectly secret yet impractical one-time pad, has been Aaron Wyner’s wiretap channel [Wyn75]: Here, information-theoretic secret-key establishment becomes possible — under the assumption, however, that the legitimate parties already start with an advantage, more specifically, that the adversary only has access to a non-trivially degraded version of the recipient’s pieces of information. A broadcast scenario was proposed by Csiszár and Körner [CK78] — where, again, an initial advantage in terms of information proximity or information quality was required by the legitimate partners versus the opponent. A breakthrough was marked by the work of Maurer [Mau93], who showed that the need for such an initial advantage on the information level can be replaced by interactivity of communication: Maurer, in addition, conceptually simplified and generalized the model by separating the noisily correlated data generation from public yet authenticated communication, the latter being considered to be for free. The model shares its communication setting with both public-key as well as quantum cryptography. Maurer and Wolf [MW96] have shown that in the case of independent-channel access to a binary source, key agreement is in fact possible in principle in all non-trivial cases, i.e., even when Eve starts with a massive initial advantage in information quality.
In the same model, it has also been shown that multiparty computation becomes possible, namely bit commitment and (the universal primitive of) oblivious transfer [CK88, Cré97]. More generally, oblivious transfer has also been achieved from unfair noisy channels, where the error behaviour is prone to be influenced in one way or another by the involved, distrusting parties willing to coöperate.
The public-randomizer model by Maurer [Mau92] has generally been recognized as the birth of the idea of “memory-bounded models,” based on the fact that the memory an opponent or cheater (depending on the context) can access is limited. Specifically, Maurer assumes the wire-tapper can obtain a certain fraction of the physical bits. This was generalized to arbitrary types of information by Dziembowski and Maurer [DM02]. Analogously, also oblivious transfer has been shown achievable with a memory-bounded receiver [CCM98, DHRS04]. The main limitation to the memory-bounded model, for both secret-key establishment and multiparty computation, is that the memory advantage of the honest participants over the adversaries is at most quadratic [DM04].
The idea to use quantum physics for cryptographic ends dates back to Wiesner, who, for instance, proposed to use the uncertainty principle to realize unforgeable banknotes. His “conjugate coding” [Wie83] resembles oblivious transfer; the latter — even bit commitment, actually — we know now to be unachievable from quantum physics only [May97, LC98]. A breakthrough has been the now famous “BB84” protocol for key agreement by communication through a channel allowing for transmitting quantum bits, such as an optic fibre, plus a public yet authenticated classical channel [BB84].
A combination of the ideas described is the “bounded quantum-storage model” [DFSS08]: Whereas no quantum memory is needed at all for the honest players, a successful adversary can be shown to need more than of the communicated quantum bits. The framework has been unified and generalized to the “noisy” model by König, Wehner, and Wullschleger [KWW12].
Very influential has been a proof-of-principle result by Barrett, Hardy, and Kent [BHK05]: The security in key agreement that stems from witnessing quantum correlations can be established regardless of the validity of quantum theory, only from the postulate of special relativity that there is no superluminal signalling. The authors combined Ekert’s [Eke91] idea to obtain secrecy from proximity to a pure state, guaranteed by close-to-maximal violation of a “Bell inequality,” with the role this same “nonlocality” plays in the argument that the outcomes of quantum measurements are, in fact, random and not predetermined: In the end, reasoning results that are totally independent of the completeness of quantum theory. Later, efficient realizations of the paradigm were presented [HRW, MPA11]. Conceptually, an interesting resulting statement is that information-theoretic key agreement is possible if either quantum mechanics OR relativity theory are complete and accurate “descriptions of nature.” Another point of interest is that trust in the manufacturer is not even required: “device independence” [VV14].
Kent also demonstrated that bit commitment can be information-theoretically secure thanks to special relativity alone [Ken99]. On the other hand, oblivious transfer cannot be information-theoretically secure even when combining (without further assumptions) the laws of quantum mechanics and special relativity [Col07].
2.1.1 Now — the free-energy-bounded model:
We add to this list the novel free-energy-bounded model. Unlike the assumptions in memory-bounded models, thermodynamics does not in principle prohibit free-energy-bounded players from computing on memories of exponential size (in some security parameter), but it does prohibit those players from erasing a significant portion of such memories. If the players only have access to memories in initial states of maximal entropy, as is assumed in equilibrium in thermodynamics, the erasing restriction becomes a copying restriction (because one cannot copy without a blank memory to write the copy onto) and opens the way to a novel foundation of physics-based information-theoretic security that is different from the bounded-storage model.222In particular, the free-energy-bounded model offers fresh mechanisms, coming from reversible computing, to build information-theoretic protocols (e.g., our oblivious-transfer protocol). Another important difference is that in our protocols, the advantage of honesty in free-energy consumption is exponential in the security parameter, while in the bounded-storage model (which is not based on reversible computing but arguably more practical), it is polynomial.
2.2 Reversible computing
2.2.1 The cost of computation.
Security in cryptography relies on a cost discrepancy between honest and malicious actors. While fundamental thermodynamical limits to the cost of computation have been well-studied (for example, see [FDOR15] for a quantum-informational analysis and [BW19] for an algorithmic-information-theoretical analysis), they have never before333Let us mention the (questionable) conjecture in [HS03] that the heat-flow equation of thermodynamics is a computational one-way function. been considered as a means for cryptography — we address that.
2.2.2 The second law of thermodynamics.
The modern view of the second law of thermodynamics is due to Ludwig Boltzmann, who defined the entropy of a macrostate — roughly speaking, the natural logarithm of the number of microstates in the
macrostate in question — and stated that the entropy of a closed system does not decrease with time. The second law has constantly been subject to discourse, confusion, and dispute; its most serious challenge was “Maxwell’s demon” who apparently violates the law by adaptive acts, i.e., by a sorting procedure.
Charles Bennett [Ben87] explained that Maxwell’s paradox actually disappears when the demon’s internal state (its “brain”) is taken into consideration. More specifically, the erasure of the stored information requires free energy that is then dissipated as heat to the environment. This is Landauer’s principle [Lan61]; it did not only help to resolve the confusion around Maxwell’s demon, but turned out to be an important manifestation of the second law with respect to information processing in its own right: Erasure of information — or, more generally, any logically irreversible computing step, has a thermodynamic cost. Logical irreversibility (information is lost)
implies thermodynamic irreversibility (free energy is “burnt” to heat up the environment).
2.2.3 Energy-neutral (thermodynamically reversible) computation.
Landauer’s principle serves as a strong motivation to ask for the possibility whether computing can always be (made) reversible, i.e., forced to not “forget” along the way any information about the past (previous computation). More specifically, can every Turing-computable function also be computed by a reversible Turing machine (the latter was introduced in [Lec63]; see Chapter 5 of [Mor17] for a more modern account)? In the early 1970s, Charles Bennett answered this question to the affirmative; the running time is also at most doubled, essentially — a very encouraging result [Ben73]: The imperative reversibility of microphysics can, at least in principle, be carried over to macrocomputing. Bennett’s idea was that the reversible Turing machine would allocate part of its tape to maintain a history of its computation. While the latter needs to be gotten rid of in order to have the whole be “sustainable,” that cannot be done by “crude” erasure of that history — all won would be lost again. It can, however, be done by un-computing: After copying the output, the reversible Turing machine reverts step by step the original computation, undoing its history tape in a “controlled” and reversible way until the output is computed back to the input. An idea similar to Bennett’s elegant trick also works for circuits: Any irreversible circuit can be transformed into a reversible one, computing the same function, and having essentially only double depth.
All in all, this means that logical reversibility — which Landauer tells us to be a necessary condition for thermodynamic reversibility — can be achieved; remains the question whether it is also a sufficient condition for energy-neutral computation. The answer is yes, as exemplified by Fredkin and Toffoli [FT82] and their Gedankenexperiment of a “ballistic computer” which carries out its computations through elastic collisions between balls and balls, and balls and walls.
In the end, we get an optimistic picture for the future of computing: Any computable function can be computed also without
the transformation of free energy into heating of the environment. (Clearly, a “loan” of free energy is necessary to start the computation, but no law of physics prevents its complete retrieval, alongside the result of the computation, when the latter concludes.)
Reversible computing is at the core of our model.444Reversible computing is of paramount importance in the context of Moore’s and Koomey’s laws about the future of computation, because their continuation is threatened by physical walls and the most important one comes from thermodynamics (and not quantum mechanics). Reversible computing can in principle solve the problem completely by enabling computation without dissipation of heat.
2.2.4 The energy value of redundancy.
The converse of Landauer’s principle states that all physical representations of the all-0 string have work value. More generally, all redundant (i.e., compressible in a lossless fashion) strings have work value, which is essentially their length minus their best compression [Ben82]. A bound in free energy is therefore a bound on the redundancy of information; a principle we use in this work to construct cryptographic protocols.

In the light of Landauer’s principle and of its converse, the all-0 string can be used as a proxy for free-energy (see Fig. 1). This allows us to abstract the thermodynamics completely from the model we present in Section 3, which is then formulated purely in terms of (logically reversible) Turing machines.
3 Turing Machines with Polynomial Free-Energy Constraints
In the following, we have this classical555The classical setting is used for all sections but Section 7, which approaches the quantum generalization. setting in mind: Alice, Bob, and Eve have their own secure labs, where they can store and manipulate exponentially long (in some security parameter ) bit strings. Those strings start in uniformly random666This randomness is motivated by the equipartition assumption of classical thermodynamics. states; we can think of them as the information about the specific microstate that describes the position and momentum of an exponential number of particles floating in their labs. We assume that technology is advanced enough to consider these exponentially long bit strings as static (even if the system starts in a random state, it does not get re-randomized at every time step), either because their evolution is tractable (it evolves according to the logically reversible laws of physics) or because the players can act on them quickly enough that it does not matter. The physical restriction on the honest and malicious players concerns their available free energy: For some security parameter , malicious players are bounded exponentially (more precisely, by ), while honest players need only an asymptotically amount. These bounds are constraining because any computation that is not logically reversible has a free-energy cost; a malicious agent cannot for example erase a -long segment of random information — by Landauer’s principle, doing so would cost a quantity of free energy exceeding their free-energy bound. We formalize this computation model in Section 3.1.
Communicationwise, the players are allowed to broadcast -length bit strings in the traditional sense using a public authenticated channel, or to transfer -long bit strings through a private-but-insecure777By “insecure,” we mean here that it is vulnerable to Eve-in-the-middle attacks. SWAP channel, This channel, which swaps two bit strings at no energy cost, can also be substituted by an insecure physical channel. Both views are informationally equivalent, and are defined in Section 3.2.
In particular, our model differs from the bounded-storage model — both the players and the adversary have more power.
3.1 Computation model
The fundamental laws of physics are logically reversible. We hence base our formal notion of player (or adversary) on reversible Turing machines.
Definition 1 (TTM).
A thermodynamical Turing machine (TTM) is a logically reversible, deterministic, universal, prefix-free Turing machine with the following semi-infinite tapes:
-
1.
An input-only instruction tape.
-
2.
An initially blank computation tape that must be returned blank when the machine halts.
-
3.
An initially random memory tape.
-
4.
An initially blank free-energy tape.
The free-energy tape of a TTM imitates a “reservoir” of free energy:
Definition 2 (consumption).
The free-energy input is quantified888More precisely, it is bounded from below., when the machine halts, by the distance, on the initially blank free-energy tape, between the extremity and the last cell with a (after this cell, the tape contains only 0s).
For example, if a machine always manages to return the free-energy tape as blank as it was — it uses no free energy and computes both logically and thermodynamically reversibly; if a machine writes, and leaves, some information on the first cells of the initially blank free-energy tape, we say it consumes an amount of free-energy. (In this work we have set .)
Our security proofs will rely on a concept we name proof-of-work.
Definition 3 (production).
We say a TTM produces a proof-of-work of value if it halts with a number of s at the beginning of its (initially random) memory tape.
We consider agents (TTMs) with bounds, in the security parameter , on the free-energy input.
Definition 4 (BFE).
An -BFE agent — an agent who is bounded in free energy by the function , where is a security parameter — is modelled by a TTM that can only consume a quantity of free energy.
In other words, every time a -BFE agent reaches a halting state, the non-blank portion of its free-energy tape ends at a distance at most from the extremity, by definition.
In our protocols, the honest players are asymptotically -BFE, while the adversary is assumed exactly -BFE. An important limitation of -BFE agents is given by the following theorem, to which the security of our protocols will be reduced.
Theorem 3.1.
For all , an -BFE player cannot produce an proof-of-work, except with probability .
3.2 Communication and reversible transfer
Our cryptographic model can be formalized further by integrating BFE parties into a multi-round interactive protocol that uses reversible computing, however, let us focus on how Alice and Bob can exchange information. There are of two distinct resources:
-
•
Standard communication for messages of length .
-
•
Reversible transfer for longer messages, up to length .
3.2.1 Standard communication.
We consider that Alice and Bob have access to a public authenticated communication channel in the traditional sense: Alice broadcasts a message (making, therefore, inevitably many copies of its information content) and Bob receives it. Because Alice and Bob are -BFE, this information-duplicating channel can only be used for messages of length .
3.2.2 Reversible transfer.
To send states of length more than , Alice and Bob have to resort to reversible computing. Reversible transfer differs from standard communication in the sense that, in order to implement the process at no free energy cost, the sender must forget the information content of the message they send. (They could, of course, preëmptively make a partial copy of that information, but copying is not free and is thus limited by the free energy assumption.) There are two different physical ways to picture such reversible transfer.
The first way is to implement, over a given distance, a reversible SWAP: In essence, this operation simply swaps two bit strings of equal length in a logically and thermodynamically reversible way — Alice gets Bob’s string and Bob gets Alice’s string. Since we are only interested in the string that Alice (the sender) sends, Bob (the receiver) can input junk in exchange. The SWAP allows -BFE players to transfer between themselves bits of information (without copying them).
The second way to implement reversible communication is to simply consider that Alice is sending the whole physical system encoding her string (e.g., she puts a canister of gas with entropy on a frictionless cart and pushes it toward Bob). For the cart as for the SWAP channel, since the information is never copied, it can be transferred from Alice to Bob at no thermodynamical cost. This is not dissimilar to how it is in practice cheaper to send hard drives directly by mail rather than to send their content through a cable.
These two pictures (the SWAP channel and the physical channel) are from an information point of view equivalent — we adopt the SWAP channel for this work.
4 Technical Preliminaries
We introduce some notation and introduce some of the techniques used later in the security proof of our main protocols.
4.1 Smooth min-entropy
Most of our formal propositions rely on the variational distance.
Definition 5.
The variational distance between two random variables and is defined as
| (1) |
It is operationally very useful because it characterizes the impossibility to distinguish between and — using any physical experiment whatsoever. More precisely, given either or with probability , the optimal probability to correctly guess which one it is is .
Definition 6.
The conditional min-entropy is defined as
| (2) |
It is the optimal probability of correctly guessing given side information .
Smoothing entropies [RW04, RW05] is done to ignore events that are typically unlikely. We will typically use smoothing with a parameter . We denote by the functions that are negligible in , meaning asymptotically bounded from above by the inverse of every function that is polynomial in .
Definition 7.
The smooth conditional min-entropy is defined as
| (3) |
where is the set of all events.
Smooth conditional min-entropy is used mainly for privacy amplification.
4.2 Proof of Theorem 3.1
We define and prove formally a version of Landauer’s principle (Theorem 3.1), which is the claim in Section 3 that BFE players modelled as thermodynamical Turing machines cannot produce more free energy than they consume, except with exponentially vanishing probability. The theorem follows from the logical reversibility of a TTM — the existence of a thermodynamically free logically irreversible physical process would be a violation of the second law of thermodynamics. We introduce some algorithmic-information-theory notation along the way; a more exhaustive introduction is the excellent book by Li and Vitányi [LV+08].
Theorem 4.1 (technical).
Given infinite tapes , a -BFE TTM cannot produce a proof-of-work, except with probability .
are, respectively, the representation of the instruction, memory, and (blank) free-energy tapes, at the beginning of the computation.
We start with the simpler case of assuming that all of these tapes are finite (but arbitrarily long), and then generalize our analysis to the infinite case.
4.2.1 The finite case.
Let be a thermodynamical Turing machine as described in Definition 1: universal, prefix-free, deterministic and logically reversible. The program is taken from the read-only instruction tape (which can be taken long but finite); the (initially random) memory tape starts in , with taken arbitrary but finite; the free-energy tape starts with blank content , where is also finite.
The logical-reversibility condition means if and only if .
We use a counting argument. We consider the set of all couples of lengths fixed. There are of them and they are all equally probable. We then consider the subset
| (4) |
where is an arbitrary padding string of appropriate length, and denotes a concatenation. Intuitively, bounds the free-energy input and is the minimum number of bits that get randomized on the initially blank free-energy tape ; bounds the free-energy output and is the maximum number of erased bits on the initially random memory tape . (Those erased bits constitute the proof-of-work.)
Lemma 1.
| (5) |
Proof.
Because of logical reversibility, the input-couples are at most999“At most” because not all programs halt and some output-couples might not be in the image of . as numerous as the output-couples . We count the maximum number of such output-couples by summing the lengths of all “ positions”; there are at most of them.∎
The probability of drawing at random such a couple is therefore
| (6) |
Proposition 1.
Given finite and , a -BFE TTM (therefore with free-energy input ) is limited in its production of free energy by
| (7) |
4.2.2 The infinite case.
We now reduce the infinite case to the finite case that we just analyzed.
We take again a TTM. Let us consider , where each bit is perfectly random. Let us also set . Since is fixed, it is enough to again consider it finite. The prefix-free condition implies that the behaviour of is well defined even on infinite tapes because its programs101010“Program” is taken here in the general sense and includes arguments and . are self-delimited.
Definition 8.
Let
| (8) |
be the halting probability of (i.e, Chaitin’s constant [Cha75]), where the sum is over all self-delimited programs 111111We assume to be fixed; by “program” we mean the random input ..
We also define its partial sum.
Definition 9.
| (9) |
Note first that since is a monotonically increasing function that converges to , it holds that
| (10) |
Definition 10.
Let be the time-busy-beaver function, which returns the maximum running time that a halting program of length can take before halting.
Observe that it implies that, for all halting programs of length , the infinite part of each tape that comes after the bit is never read or modified by the TTM (moving there is by definition too long).
Proposition 2.
A TTM with infinite tapes behaves with arbitrarily high probability exactly as if these infinite tapes were (extremely long but) finite:
, such that
| (11) |
where the subset notation is used to split and .
Proof.
Taking Eq. 10 with , with the consideration about busy beaver above (any machine that halts affects only a finite amount of tape).∎
4.3 The exhaustive and sampled memory games
We detail here in a game format a reduction that we later use in our security proofs. Our memory games involve an adversary against a verifier. The adversary sends, using a reversible channel SWAP, an exponentially long string to the verifier, but is also asked to try to keep a copy of it; the verifier then interrogates the adversary about either all of that string (in the exhaustive variant), or about a random linear-size subset of it (in the sampled variant); we show that the adversary has limited advantage in guessing as compared to a trivial strategy, unless they made an accurate copy of the whole string of exponential length — a process that requires, in light of Landauer’s principle, an exponential amount of either luck or free energy. We formalize this intuition, starting with the non-sampled version of the game.
Definition 11.
The exhaustive memory game is defined as follows for security parameters and :
-
1.
The adversary isolates (by taking it from the environment of their lab for example) a system . All the rest of their available information is modelled as .
-
2.
The adversary (modelled as a TTM) makes some computation on the systems .
-
3.
Through a noiseless reversible channel (e.g., SWAP), the adversary sends to the verifier.
-
4.
The verifier provides the adversary a blank tape of length , and asks the adversary to correctly print on it all of .
Proposition 3.
For any -BFE adversary, the advantage at the exhaustive memory game, compared to a trivial coin-flip strategy, is bounded by
| (13) |
Proof.
We reduce a violation of Theorem 1 (i.e., Landauer’s principle) to a large advantage at the exhaustive memory game. During the game, instead of sending to the verifier, the adversary deviates and XORs onto their best guess for given side information . If the adversary guesses correctly, it turns into an all- string. This proof-of-work of length violates Theorem 1 if it is created with probability higher than ; therefore, it does not.∎
The constraint also holds if the adversary is quizzed only on a random subset of positions.
Definition 12.
The sampled memory game is defined as follows for free-energy bound , security parameter , and sample size :
-
1.
The adversary isolates (by taking it from the environment of their lab for example) a system . All the rest of their available information is modelled as .
-
2.
The adversary (modelled as a TTM) makes some computation on the systems .
-
3.
Through a noiseless reversible channel (e.g., SWAP), the adversary sends to the verifier.
-
4.
The verifier chooses at random sample positions and sends a description of these positions to the adversary, who must correctly guess .
Theorem 4.2.
For any -BFE adversary, the advantage at the sampled memory game, compared to a trivial coin-flip strategy, is bounded, for all , by
| (14) |
4.4 Universal hashing
Universal hashing is useful for both privacy amplification and authentication.
Definition 13 (2-universal hashing [CW79, WC81]).
Let be a set of hash functions from . is 2-universal if, given any distinct elements and any (not necessarily distinct) elements , then
| (16) |
Lemma 2 (Leftover hash lemma [BBR88, ILL89, HILL93, BBCM95]).
Let be a 2-universal hash function. If , then
| (17) |
is a short uniformly random seed and is the variable whose randomness is to be amplified. is the uniform distribution of appropriate dimension. The symbol is used to represent the joint probability of independent distributions.
5 Secret-Key Establishment
Secret-key establishment (SKE) is a fundamental primitive for two-way secure communication because it allows for a perfectly secure one-time-pad encryption between Alice and Bob about which Eve knows nothing (otherwise the protocol aborts).
5.1 Definitions (SKE)
Definition 14.
A secret-key-establishment scheme is sound if, at the end the protocol, Alice and Bob possess the same key with overwhelming probability in the security parameter :
| (18) |
Definition 15.
A secret-key-establishment scheme is information-theoretically secure (i.e., almost perfectly secret) if the key is uniformly random even given all of the adversary’s side information , except with probability at most negligible in the security parameter :
| (19) |
In what follows, the variables are strings from registers of length roughly , while denote strings from registers of length .
5.2 Protocol (SKE)
Theorem 5.1.
The following secret-key-establishment protocol is information-theoretically sound and secure against any eavesdropper whose free energy is bounded by . Alice and Bob need a quantity of free energy that is asymptotically .
is the binary entropy.
Note that for any fixed (as long as it is not trivially ), Alice and Bob can choose a security parameter for which the protocol will be secure for that value of . That is unlike, for example, the BB84 quantum-key-distribution protocol, which only tolerates error rates less than (any more and Eve can intercept the whole quantum state).
5.2.1 The intuition.
Because she is -bounded in free energy, Eve cannot copy to her memory the whole -long string that she sends to Bob, on which Bob will later base the raw key. Alice circumvents this limitation by already knowing the raw-key positions at the moment she sends ( becomes, after Eve’s potential tampering, ) and thus need not store more than an asymptotically -long segment of the -long string. As in quantum key distribution, Eve can force the protocol to abort.
5.3 Soundness analysis (SKE)
5.3.1 Parameter estimation.
We first estimate (using upper bounds) between Alice and Bob the global error rate and the non-tested rawkey error rate . The former quantity is important for the privacy amplification analyzed in Section 5.4, while the second is needed to analyze information reconciliation.
Proposition 4.
Alice and Bob can accurately estimate the error rate by sampling on the positions the error rate :
| (20) |
Proof.
is computed from the Hamming weight . Chernoff’s inequality bounds .∎
Proposition 5.
Alice and Bob can accurately estimate from :
| (21) |
Proof.
We insert in Eq. 20 and isolate .∎
5.3.2 Information reconciliation (error correction).
Once they have a good estimate of , Alice and Bob achieve information reconciliation by applying error correction on that unused subset of bits.
Note that it is important that the established key be based on Bob’s string, rather than on Alice’s, because the reasoning (see the security analysis in Section 5.4) using the sampled memory game only directly bounds from above the mutual information between Bob and Eve, not the one between Alice and Eve.
Proposition 6.
For any non-trivial constant , Alice and Bob can transform the samples into the (non-necessarily secret) keys for which
| (22) |
They can do so with (the exact value is given below) bits of authenticated public communication.
We present one standard construction to correct an arbitrary error rate on the bits of rawkey that were not used during the parameter-estimation phase.
Asymptotically optimal protocol for information reconciliation [BS93]:
Let ;
-
1.
Bob picks at random a hash function from a 2-universal family and computes .
-
2.
Bob communicates and to Alice, using the authenticated public channel.
-
3.
Alice computes .
Here, is the Hamming distance; determines efficiency and is the security parameter.
Proof.
We first count, in the uniform distribution, the smooth number of strings with length that contains approximately : Let ; from the asymptotic equipartition property, we have ,
| (23) |
Because is 2-universal, the probability of obtaining a correct hash from a non-correct candidate in is bounded by . By the union bound, the protocol is therefore sound except with probability at most , which is .∎
While the above ideal information reconciliation protocol is optimal, it offers no (known) efficient way (in the computational complexity sense) for Alice to decode Bob’s codeword. While we are in this work only concerned with thermodynamic (rather than computational) efficiency, we refer to [BS93], or to the theory of Shannon-optimal efficient algebraic codes, such as convoluted codes, for asymptotically ideal information-reconciliation protocols that are also computationally efficient.
5.4 Security analysis (SKE)
If the protocol does not abort, Eve has negligible information about the key at the end. This security resides on the fact that even if Eve intercepts (which was sent from Alice to Bob) and replaces it with , she cannot keep roughly more than a fraction of the information about . Thus, since the key is based on , Eve has limited knowledge about it.
Formally, this can be analyzed with the sampled memory game in Section 4.3. Theorem 4.2 thereat guarantees a good starting point — Eve (who is -BFE) must have limited information about Bob’s raw key of length :
| (24) |
The next step is to go from low information to essentially no information.
5.4.1 Privacy amplification.
Privacy amplification turns a long string about which the adversary has potentially some knowledge into a shorter one about which the adversary has essentially none.
In secret-key establishment, Eve’s partial information can come from eavesdropping (and as shown, this quantity is roughly a fraction ) or from the public information leaked by the information reconciliation protocol, which is easily characterized.
Privacy amplification can be realized in an information-theoretically secure manner with 2-universal hashing (see Section 4.4).
Proposition 7.
After privacy amplification, is approximately of length , and Eve has essentially no knowledge about it.
Proof.
Let quantify the number of bits about exchanged publicly during the information-reconciliation (IR) protocol. We note that , hence
| (25) |
Therefore, taking guarantees after hashing ( is the security parameter for the Leftover hash lemma; see Section 4.4) information-theoretic security on those remaining bits.∎
Note that for any fixed , the parameters and can be selected as to make a positive quantity when the protocol does not abort (as a result of too many errors). Also note that the parameters and must not be too small.
6 1-out-of-2 Oblivious Transfer
Oblivious transfer (OT) is a cryptographic primitive that is universal for two-party computation [Rab81, Kil88]. It comes in many flavours, but they are all equivalent [Cré87]. We concern ourselves with 1-out-of-2 OT (or 1–2 OT). Informally: Alice sends two envelopes to Bob; Bob can open one to read the message in it, but he cannot open both; Alice cannot know which message Bob read.
6.1 Definitions (OT)
Definition 16.
A 1–2 OT protocol is perfectly sound if, when Alice and Bob are honest, the message received by Bob is with certainty the message sent by Alice, for his choice of :
| (26) |
Definition 17.
A 1–2 OT protocol is information-theoretically secure-for-Alice if Bob cannot learn something non-negligible about both of Alice’s messages simultaneously: For any -BFE Bob,
| (27) |
denotes all of (a potentially malicious) Bob’s side information. And similarly for in regards to Alice.
Definition 18.
A 1–2 OT protocol is information-theoretically secure-for-Bob if Alice cannot learn anything non-negligible about Bob’s choice : For any -BFE Alice,
| (28) |
An OT protocol is information-theoretically secure when it is information-theoretically secure for both Alice and Bob.
6.2 Protocol (OT)
Theorem 6.1.
The following 1–2 OT protocol is perfectly sound and information-theoretically secure against -BFE adversaries. The free-energy requirement of the honest players is asymptotically .
The perfect soundness is straightforward. Security is analyzed in Section 6.3.
6.2.1 The intuition.
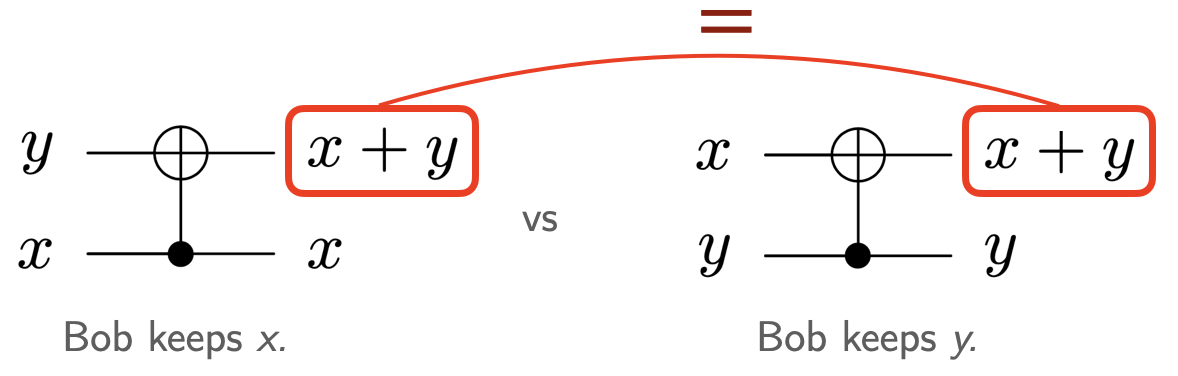
In addition to the previously exploited impossibility to copy exponential quantities of information without using corresponding quantities of free energy or violating Landauer’s principle, the oblivious-transfer protocol makes use of another key feature of reversible computing: As long as Bob is in possession of , the maximally random variables and have conditionally exactly the same information content; but once is returned to Alice, and revert to being uncorrelated. In other words, although sending back to Alice forces Bob to forget information about the couple (enabling 1-out-of-2 transfer), it does not uniquely specify which information he forgot (Alice remains oblivious).
6.3 Security analysis (OT)
6.3.1 Security for Bob.
From Alice’s point of view, Bob’s behaviour (i.e., sending back to Alice) is identical whether he chooses message or message ; the scheme is therefore perfectly secure for Bob.
6.3.2 Security for Alice.
We prove that a malicious Bob cannot learn anything non-negligible about a second message as soon as he learns something non-negligible about a first message.
Proof.
We pose without a loss of generality that is the event corresponding to “Bob learns something non-negligible about .” Because he is -bounded in free energy, a malicious Bob’s success at the sampled memory game (on state and sample raw) is bounded by Theorem 4.2:
| (29) |
By subadditivity, we have
| (30) | |||
| (31) | |||
| (32) |
We apply the Leftover hash lemma (Lemma 2) with . The two privacy-amplification steps succeed (except by the union bound with probability ) if, respectively,
| (33) | |||
| (34) |
We assume by contradiction that they are both unsuccessful with non-negligible probability. It implies
| (35) |
which contradicts Eq. 29 for small .∎
7 From classical adversaries to quantum adversaries
Up to here, the notion of information that has been used — in the protocols for secret-key establishment and oblivious transfer, as well as in their analyses — is purely classical. But as scrutinised by thorough experiments (notably, the extensive serie of Bell experiments [FC72, ADR82, HBD+15, GVW+15, SMSC+15]), nature is quantum-physical. The aim of this section is to bring our work one step closer to the quantum realm. Namely, we investigate whether our (classical131313All classical operations can be viewed as quantum operations restricted to diagonal density matrices.) protocols are secure against quantum adversaries. We find that our SKE protocol (Section 5.2) is secure against a quantum Eve as it is. On the other hand, to retain security against a malicious quantum Alice, our OT protocol (Section 6.2) has to be slightly updated — the patched protocol presented below in Section 7.4 is quantum-safe but remains classical for honest players. Our work’s conclusion, therefore, fully extends to the quantum world of Maxwell demons (given arbitrarily large but random environments): It is — on paper — information-theoretically cryptographically friendly.
7.1 The setting made quantum
Our model described in Section 3 is based on Alice, Bob, and Eve being classical computers with thermodynamical restrictions (we call them Thermodynamical Turing Machines) interacting through classical channels (a standard authenticated channel and a SWAP channel).
In a quantum setting, Alice, Bob, and Eve are upgraded to universal quantum computers [Deu85] and their communication channels can carry states in quantum superposition. A quantum computer cannot compute more than a classical computer could (given exponential computational time, a classical computer can simulate a quantum computer). Quantum computing cannot either be used to evade Landauer’s principle [FDOR15]. As such, once all elements are properly defined, a quantum version of our Theorem 3.1 holds.
Proposition 8 (Thm. 3.1 in the quantum realm (sketch)).
For all , a player modelled by a quantum computer with a bound in free energy cannot erase more than initially completely mixed qubits, except with probability .
The ability to send and receive quantum states does enable new possibilities for both honest and malicious agents — we investigate next how this affects the security of our previous SKE and OT protocols.
7.2 The quantum exhaustive and sampled memory games
We extend the proof method developed in Section 4.3 to the quantum world.
First, the bound on the success of an adversary at the exhaustive memory game (Proposition 3) is unaffected by the transition from classical to quantum information.
Proposition 9 (Prop. 3 with quantum side-information).
For any quantum adversary with a bound in free energy, the advantage at the exhaustive memory game, compared to a trivial coin-flip strategy, is bounded by
| (36) |
The next step is to sample from (Theorem 4.2).
Proposition 10 (Thm. 4.2 with quantum side-information).
For any quantum adversary with a bound in free energy, the advantage at the sampled memory game, compared to a trivial coin-flip strategy, is bounded, for all , by
| (37) |
7.3 The classical SKE protocol is already quantum-resistant
The information-theoretical security of the SKE protocol from Section 5 depends uniquely on the one of privacy amplification and on Theorem 4.2.
Since in presence of quantum side information, universal-2 hashing (Lemma 2) remains a universally composably secure way of achieving privacy amplification [RK05, TSSR11], and that, as we just argued, so is the case of Theorem 4.2, the SKE scheme presented in Section 5.2 is secure against quantum adversaries.
Fundamentally different from standard quantum key distribution, the result is nevertheless an information-theoretically secure key distribution scheme for a quantum world in which entropy is exponentially cheaper than free energy.
7.4 A quantum-resistance patch for the OT protocol
Given that the above SKE protocol is quantum-resistant, and that the same argument applies to the security-for-Alice part of our oblivious-transfer protocol, it would be natural for our previously detailed scheme to be also quantum-resistant. But it is not: The security-for-Bob, which is trivial in the classical case (because , see Fig. 2), can be broken by a malicious quantum Alice. The reason is that if Alice acts maliciously and sends the superposed quantum states and to Bob (for some random and ), she can discriminate between the state sent back by Bob when he does (to keep ) compared to when he does (to keep ). This attack is illustrated in Fig. 3.
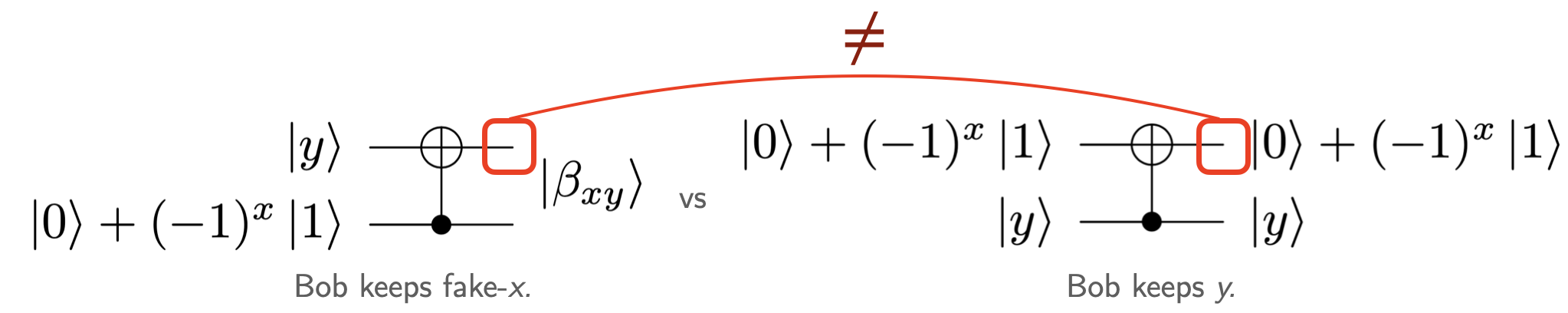
But there is a simple patch for this attack, or, in fact, for all quantum attacks by a malicious Alice. Alice’s extra power comes from the fact she can send states in superposition, but Bob can in return preëmptively “classicize” the possibly quantum states and by CNOT-ing each bit to a different bit of the totally mixed environments and . Given control of a large enough environment (of dimension ), Bob can do so at no free energy cost. The resulting state, when traced over that environment, is then undistinguishable from a (possibly noisy) state sent by a malicious-but-classical Alice. Even if misbehaviour from Alice’s part might affect the protocol’s correctness (which is allowed for a malicious Alice), it leaves the perfect security intact: a quantum Alice can still not gain any information about Bob’s choice.
The above step reduces the security for Bob in the quantum case to the one of the classical case. The updated protocol does not require the honest players to make any quantum operations per se.
8 Concluding remarks
We propose a free-energy-bounded model of cryptography, in which we have derived information-theoretically secure protocols for secret-key establishment and oblivious transfer.
Even if the rationale behind its security is totally different: Our secret-key-establishment protocol is similar to standard quantum key distribution. Our oblivious-transfer protocol, on the other hand, is novel in itself: The mechanism that allows Alice to check that Bob honestly forgets information is proper to reversible computing.
Our schemes are not practical at this point: Current technology is still far from computing with memories that are large enough for Landauer’s principle to become the main obstacle (it is worth noting that Boltzmann’s constant, which we have in this work conveniently set to , is in fact ); and whereas no laws of physics forbid it, implementing reversible computation on such states is for now science fiction. Our result is rather to be seen as part of the quest of distinguishing what physical phenomena allow for realizing cryptographic functionalities in principle, and which do not. In this spirit, our protocols add another element to the longer and longer list of physical laws from which cryptographic security can directly be derived: We can now claim that information-theoretic key agreement is theoretically possible as soon as one of the fundamental limits conjectured by either quantum theory or special relativity or the second law of thermodynamics is correct. Concerning the novel appearance of a thermodynamic law in this list, we remark first that according to Albert Einstein, thermodynamics is the only physical theory that will survive future development in Physics. Second, the second law is rather pessimistic in nature, and to see it being linked to a constructive application is refreshing. We are, in fact, not aware of many uses, besides our protocols, of the law. In summary, we can say, somewhat ironically: One small step for cryptography — one giant leap for the second law.
Acknowledgement
We thank Charles Alexandre Bédard and Cecilia Boschini for helpful comments about earlier version of this work. We also thank Renato Renner and two anonymous referees for some interesting remarks regarding the physicality of the model. This research was supported by the Swiss National Science Foundation (SNF).
References
- [ADR82] Alain Aspect, Jean Dalibard, and Gérard Roger. Experimental test of Bell’s inequalities using time-varying analyzers. Physical Review Letters, 49(25):1804, 1982.
- [BB84] Charles H Bennett and Gilles Brassard. Quantum cryptography: Public key distribution and coin tossing. In Proc. IEEE Int. Conf. Computers, Systems, and Signal Processing, Bangalore, India, 1984, pages 175–179, 1984.
- [BBCM95] Charles H Bennett, Gilles Brassard, Claude Crépeau, and Ueli M Maurer. Generalized privacy amplification. IEEE Transactions on Information Theory, 41(6):1915–1923, 1995.
- [BBR88] Charles H Bennett, Gilles Brassard, and Jean-Marc Robert. Privacy amplification by public discussion. SIAM Journal on Computing, 17(2):210–229, 1988.
- [Ben73] Charles H Bennett. Logical reversibility of computation. IBM journal of Research and Development, 17(6):525–532, 1973.
- [Ben82] Charles H Bennett. The thermodynamics of computation: a review. International Journal of Theoretical Physics, 21(12):905–940, 1982.
- [Ben87] Charles H Bennett. Demons, engines and the second law. Scientific American, 257(5):108–117, 1987.
- [BHK05] Jonathan Barrett, Lucien Hardy, and Adrian Kent. No signaling and quantum key distribution. Physical Review Letters, 95(1):010503, 2005.
- [BS93] Gilles Brassard and Louis Salvail. Secret-key reconciliation by public discussion. In Workshop on the Theory and Application of of Cryptographic Techniques, pages 410–423. Springer, 1993.
- [BW19] Ämin Baumeler and Stefan Wolf. Free energy of a general computation. Physical Review E, 100(5):052115, 2019.
- [CCM98] Christian Cachin, Claude Crépeau, and Julien Marcil. Oblivious transfer with a memory-bounded receiver. In Proceedings 39th Annual Symposium on Foundations of Computer Science (Cat. No. 98CB36280), pages 493–502. IEEE, 1998.
- [Cha75] Gregory J Chaitin. A theory of program size formally identical to information theory. Journal of the ACM (JACM), 22(3):329–340, 1975.
- [CK78] Imre Csiszár and Janos Körner. Broadcast channels with confidential messages. IEEE Transactions on Information Theory, 24(3):339–348, 1978.
- [CK88] Claude Crépeau and Joe Kilian. Achieving oblivious transfer using weakened security assumptions. In FOCS, volume 88, pages 42–52, 1988.
- [Col07] Roger Colbeck. Impossibility of secure two-party classical computation. Physical Review A, 76(6):062308, 2007.
- [Cré87] Claude Crépeau. Equivalence between two flavours of oblivious transfers. In Conference on the Theory and Application of Cryptographic Techniques, pages 350–354. Springer, 1987.
- [Cré97] Claude Crépeau. Efficient cryptographic protocols based on noisy channels. In International Conference on the Theory and Applications of Cryptographic Techniques, pages 306–317. Springer, 1997.
- [CW79] J Lawrence Carter and Mark N Wegman. Universal classes of hash functions. Journal of Computer and System Sciences, 18(2):143–154, 1979.
- [Deu85] David Deutsch. Quantum theory, the church–turing principle and the universal quantum computer. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 400(1818):97–117, 1985.
- [DFSS08] Ivan B Damgård, Serge Fehr, Louis Salvail, and Christian Schaffner. Cryptography in the bounded-quantum-storage model. SIAM Journal on Computing, 37(6):1865–1890, 2008.
- [DHRS04] Yan Zong Ding, Danny Harnik, Alon Rosen, and Ronen Shaltiel. Constant-round oblivious transfer in the bounded storage model. In Theory of Cryptography Conference, pages 446–472. Springer, 2004.
- [DM02] Stefan Dziembowski and Ueli Maurer. Tight security proofs for the bounded-storage model. In Proceedings of the thiry-fourth annual ACM Symposium on Theory of Computing, pages 341–350, 2002.
- [DM04] Stefan Dziembowski and Ueli Maurer. On generating the initial key in the bounded-storage model. In International Conference on the Theory and Applications of Cryptographic Techniques, pages 126–137. Springer, 2004.
- [Eke91] Artur K Ekert. Quantum cryptography based on Bell’s theorem. Physical Review Letters, 67(6):661, 1991.
- [FC72] Stuart J Freedman and John F Clauser. Experimental test of local hidden-variable theories. Physical Review Letters, 28(14):938, 1972.
- [FDOR15] Philippe Faist, Frédéric Dupuis, Jonathan Oppenheim, and Renato Renner. The minimal work cost of information processing. Nature communications, 6(1):1–8, 2015.
- [FT82] Edward Fredkin and Tommaso Toffoli. Conservative logic. International Journal of theoretical physics, 21(3):219–253, 1982.
- [GVW+15] Marissa Giustina, Marijn AM Versteegh, Sören Wengerowsky, Johannes Handsteiner, Armin Hochrainer, Kevin Phelan, Fabian Steinlechner, Johannes Kofler, Jan-Åke Larsson, Carlos Abellán, et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Physical Review Letters, 115(25):250401, 2015.
- [HBD+15] Bas Hensen, Hannes Bernien, Anaïs E Dréau, Andreas Reiserer, Norbert Kalb, Machiel S Blok, Just Ruitenberg, Raymond FL Vermeulen, Raymond N Schouten, Carlos Abellán, et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature, 526(7575):682–686, 2015.
- [HILL93] Johan Håstad, Russell Impagliazzo, Leonid A Levin, and Michael Luby. Construction of a pseudo-random generator from any one-way function. In SIAM Journal on Computing, 1993.
- [HRW] Esther Hänggi, Renato Renner, and Stefan Wolf. Efficient device-independent quantum key distribution. EUROCRYPT 2010, pages 216–234.
- [HS03] Norbert Hungerbühler and Michael Struwe. A one-way function from thermodynamics and applications to cryptography. Elemente der Mathematik, 58(2):49–64, 2003.
- [ILL89] Russell Impagliazzo, Leonid A Levin, and Michael Luby. Pseudo-random generation from one-way functions. In Proceedings of the twenty-first annual ACM Symposium on Theory of Computing, pages 12–24, 1989.
- [Ken99] Adrian Kent. Unconditionally secure bit commitment. Physical Review Letters, 83(7):1447, 1999.
- [Kil88] Joe Kilian. Founding crytpography on oblivious transfer. In Proceedings of the twentieth annual ACM Symposium on Theory of Computing, pages 20–31, 1988.
- [KR11] Robert König and Renato Renner. Sampling of min-entropy relative to quantum knowledge. IEEE Transactions on Information Theory, 57(7):4760–4787, 2011.
- [KRS09] Robert König, Renato Renner, and Christian Schaffner. The operational meaning of min-and max-entropy. IEEE Transactions on Information theory, 55(9):4337–4347, 2009.
- [KWW12] Robert König, Stephanie Wehner, and Jürg Wullschleger. Unconditional security from noisy quantum storage. IEEE Transactions on Information Theory, 58(3):1962–1984, 2012.
- [Lan61] Rolf Landauer. Irreversibility and heat generation in the computing process. IBM Journal of Research and Development, 5(3):183–191, 1961.
- [LC98] Hoi-Kwong Lo and Hoi Fung Chau. Why quantum bit commitment and ideal quantum coin tossing are impossible. Physica D: Nonlinear Phenomena, 120(1-2):177–187, 1998.
- [Lec63] Yves Lecerf. Machines de Turing réversibles. Comptes Rendus hebdomadaires des séances de l’Académie des Sciences, 257:2597–2600, 1963.
- [LV+08] Ming Li, Paul Vitányi, et al. An introduction to Kolmogorov complexity and its applications, volume 3. Springer, 2008.
- [Mau92] Ueli M Maurer. Conditionally-perfect secrecy and a provably-secure randomized cipher. Journal of Cryptology, 5(1):53–66, 1992.
- [Mau93] Ueli M Maurer. Secret key agreement by public discussion from common information. IEEE Transactions on Information Theory, 39(3):733–742, 1993.
- [May97] Dominic Mayers. Unconditionally secure quantum bit commitment is impossible. Physical Review Letters, 78(17):3414, 1997.
- [Mor17] Kenichi Morita. Theory of reversible computing. Springer, 2017.
- [MPA11] Lluís Masanes, Stefano Pironio, and Antonio Acín. Secure device-independent quantum key distribution with causally independent measurement devices. Nature communications, 2(1):1–7, 2011.
- [MW96] Ueli Maurer and Stefan Wolf. Towards characterizing when information-theoretic secret key agreement is possible. In International Conference on the Theory and Application of Cryptology and Information Security, pages 196–209. Springer, 1996.
- [Rab81] Michael O Rabin. How to exchange secrets by oblivious transfer. Technical Memo TR-81, 1981.
- [RK05] Renato Renner and Robert König. Universally composable privacy amplification against quantum adversaries. In Theory of Cryptography Conference, pages 407–425. Springer, 2005.
- [RW04] Renato Renner and Stefan Wolf. Smooth Rényi entropy and applications. In International Symposium on Information Theory, 2004. ISIT 2004. Proceedings., page 233. IEEE, 2004.
- [RW05] Renato Renner and Stefan Wolf. Simple and tight bounds for information reconciliation and privacy amplification. In International conference on the theory and application of cryptology and information security, pages 199–216. Springer, 2005.
- [SMSC+15] Lynden K Shalm, Evan Meyer-Scott, Bradley G Christensen, Peter Bierhorst, Michael A Wayne, Martin J Stevens, Thomas Gerrits, Scott Glancy, Deny R Hamel, Michael S Allman, et al. Strong loophole-free test of local realism. Physical Review Letters, 115(25):250402, 2015.
- [TSSR11] Marco Tomamichel, Christian Schaffner, Adam Smith, and Renato Renner. Leftover hashing against quantum side information. IEEE Transactions on Information Theory, 57(8):5524–5535, 2011.
- [Vad04] Salil P Vadhan. Constructing locally computable extractors and cryptosystems in the bounded-storage model. Journal of Cryptology, 17(1):43–77, 2004.
- [VV14] Umesh Vazirani and Thomas Vidick. Fully device-independent quantum key distribution. Physical Review Letters, 113:140501, Sep 2014.
- [WC81] Mark N Wegman and J Lawrence Carter. New hash functions and their use in authentication and set equality. Journal of Computer and System Sciences, 22(3):265–279, 1981.
- [Wie83] Stephen Wiesner. Conjugate coding. ACM Sigact News, 15(1):78–88, 1983.
- [Wyn75] Aaron D Wyner. The wire-tap channel. Bell System Technical Journal, 54(8):1355–1387, 1975.