Koebe uniformization of nondegenerate domains with bounded gap-ratio
Abstract.
Koebe uniformization is a fundemental problem in complex analysis. In this paper, we use transboundary extremal length to show that every nondegenerate and uncountably connected domain with bounded gap-ratio is conformally homeomorphic to a circle domain.
Key words and phrases:
Koebe uniformization, transboundary extremal length, nondegenerate, gap-ratio2020 Mathematics Subject Classification:
Primary 30C20; Secondary 30C351. Introduction
A connected domain on the Riemannian sphere is called a circle domain if each component of is either a closed disk or a point. In 1909, P. Koebe [15] posed the following conjecture, known as the Kreisnormierungsproblem:
Conjecture 1.1 (Koebe’s conjecture).
Any plane domain is conformally homeomorphic to a circle domain in .
In the 1920’s, P. Koebe [16] himself proved the following theorem, which was able to confirm the conjecture in the finitely connected case:
Theorem 1.1.
Let be a finite multi-connected domain. Then is conformally homeomorphic to a circle domain.
Later, P. Koebe [17] showed that the conjecture is true for a class of domains with some symmetry. For domains with various conditions on the “limit boundary components”, one can see [1, 6, 8, 9, 18, 19, 22, 24, 25].
In 1993, Z.X. He and O. Schramm [12] proved that the Koebe’s conjecture holds for countably connected domains, which is a major breakthrough. Recently, K. Rajala [21] presented a new proof for this case by the idea of exhaustion.
For uncountablly connected cases, O. Schramm [23] introduced the tool of transboundary extremal length, which has played a central role in recent developments on the uniformization of fractal metric spaces, see [2, 4, 5, 10]. Then he prescribed the boundary shapes by studying the so called “cofat domains”:
Definition 1.1.
Let be some constant. A set will be called fat, if for every and for every disk centered at that does not contain we have . A connected domain is cofat, if each connected component of its complement is fat for some .
By the tool of transboundary extremal length, Schramm established the following.
Theorem 1.2.
Every cofat domain in is conformally homeomorphic to a circle domain.
Resently X.G. Wang and Y. Zhong demonstrate that any infinitely connected attracting Fatou domain of a geometrically finite rational map is conformally homeomorphic to a cofat domain [26]. More resent results related to the Koebe uniformization problem can be found in [3, 11, 13, 14, 20, 27]. However, the conjecture is still open.
1.1. Main results
Since the boundary components can be quite complicated, domains do not usually satisfy the “cofat” condition. It is natural to study a class of more general domains. We will mention some necessary definitions herein to make the presentation clear and accessible.
Definition 1.2.
Let be some constant. A connected set with positive area is called nondegenerate if
A connected domain is called nondegenerate if all its complementary components are nondegenerate for some .
Let be a nondegenerate connected subset in . We denote
Clearly, when is a closed disk; otherwise we must have . Recall definition 1.1, it is easy to show that a cofat domain is also a nondegenerate domain.
The method used in establishing Koebe uniformization of cofat domains can not be applied directly to nondegenerate domains. The reason for this limitation lies in the more complicated boundary behavior exhibited by the complementary of nondegenerate domains. In section 3, we will introduce a new quentity named gap-ratio to describe the distribution of those complementary components. By using transboundary extremal length and exploring the geometrical properties of such domains, we show that the bounded gap-ratio property will overcome the obstacle induced by its irregular boundary. Consequently, we obtain the main theorem of this paper:
Theorem 1.3.
Every nondegenerate domain in with bounded gap-ratio is conformally homeomorphic to a circle domain.
1.2. Outline of the paper
This paper is organized as follows. In section 2 we provide some preliminaries. Section 3 is devoted to prove that a domain with bounded gap-ratio has well-distributed property, and we established the extended Carathéodory kernel convergence theorem for this case in section 4. The remaining part of the proof, arranged in section 5, will proceed naturally.
The author would like to express his gratitude to Xiaoguang Wang for many useful comments during the formative period of this work in Zhejiang University.
2. Preliminaries
Let be a multi-connected domain and , where if and only if and belong to the same connected component of . The space is the ends compactification of and we define as the complementary space of . Let be the quotient map. The notation will stand for when or . We say is a non-trivial complementary component if its diameter . Otherwise, is a trivial complementary component. The space of trivial and non-trivial complementary components will be denoted by and .
2.1. Transboundary extremal length
Let the area measure on the space be equal to Lebesgue measure on and equal to counting measure on . An extended metric for the domain is a Borel measurable function . The area of is
The extended metric is allowable if . Let be an interval, define be a curve in , then the length of is
Let be a collection of curves in . For any extended metric , we set
be the length of . Then the transboundary extremal length of is defined as
where the supremum is taken over all allowable extended metrics on .
Lemma 2.1 (Invariance of transboundary extremal length ([23])).
Let be a conformal homeomorphism between domains in , and let be a collection of curves in . Set . Then .
2.2. Well-distributed property
Clearly, the transboundary extremal length is a generialization of traditional extremal length. We want to apply it to consider the distance betwenn two subsets in a multi-connected domain.
For each and , let be a Jordan curve in that separates from in , be the connected component of that contains and be all the Jordan curves in satisfying: (i) separate from ; or (ii) and separate from . Let be the transboundary extremal length of . We introduce the following definition:
Definition 2.1 (Well-distributed).
Let be a multi-connected domain with . For each and for any , there is some such that for all and all , which is a union of and some components of , the transboundary extremal length when the distance between and is less than . Then we say is well-distributed or has well-distributed property.
We note that the proof of theorem 1.3 relies on the key observation that under what condition a nondegenerate domain has well-distributed property. In the following section, we will present the notion of gap-ratio and prove that is well-distributed when is a nondegenerate domain with bounded gap-ratio.
3. Bounded gap-ratio implies well-distributed property
Let us consider a connect compact set as shown in figure 1. Given some point . If , we can use the distance to discribe the relevant location bewteen them. Here we introduce a new quantity to measure the relationship between the shape of and the distance from to . Let
We define as the gap-ratio of to . It is easy to know that for all , we have as . Particularly, if is a single point and if is a circle or an arc cetered at .
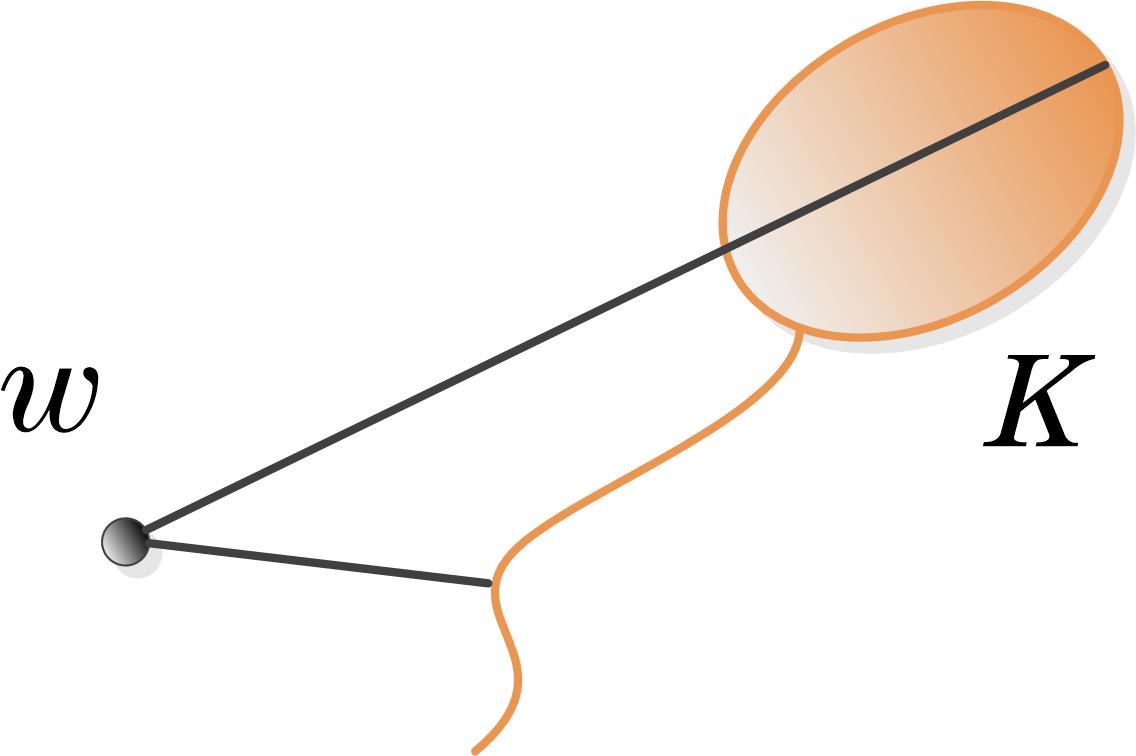
Definition 3.1.
Let be a multi-connected domain with . For any , the gap-ratio of to is
Particularly, if we set and to be concentric circles, then
for arbitrarily small .
Definition 3.2.
Let be a multi-connected domain with . We call has bounded gap-ratio if for each , there is a such that for all satisfying
there must be
| (3.1) |
where is a constant.
We note that there is a subtle difference between the conditions of bounded gap-ratio and uniformly relative separation for nondegenerate domains. Let be fixed and tend to zero, the uniformly relative separation claims that the diameter of () tends to zero. However, the condition (3.1) allows big . For instance, we take to be a disk, to be an anulus sharing the same center of , then has a lower bound as tends to zero.
Theorem 3.1.
Let be a nondegenerate domain with bounded gap-ratio and . Then is well-distributed.
Proof.
Let be an arbitary domain that combined with some components of . For each , recall that is the connected component of containing . Take and , let be the circle of radius cetered at such that . Since , the complementary components intersecting will not intersect . Hence they must be contained in . Let be the components that intersect both and . Clearly, for each , we have . This implies that . However, the area of is limited, we can conclude that is a finite set. Generally, we denote as the collection of complementary components of that intersect both and , where The setting of ensures that there is no complementary component intersecting both and .
Now we consider a subset of , where . Suppose that is inside the circle for some positive integer . We take and let be the circle of radius centered at . Moreover, we let , then separates from . Set , we have . For any extended metric on such that , we infer from the definition of length that
| (3.2) |
where is defined as if and if . Let be the annulus bounded by and . In order to prevent the double counting of complementary components in the subsequent deduction, we integrate (3.2) from to for . Then we have
By Cauchy’s inequality,
Since the complementary components that intersect must be contained in , the sum of their area is controlled by the area of . Then we have
This implies
Recall that
There is at least one complementary component intersecting both and , but it does not contain any inner point of the disk bounded by , see figure 2.
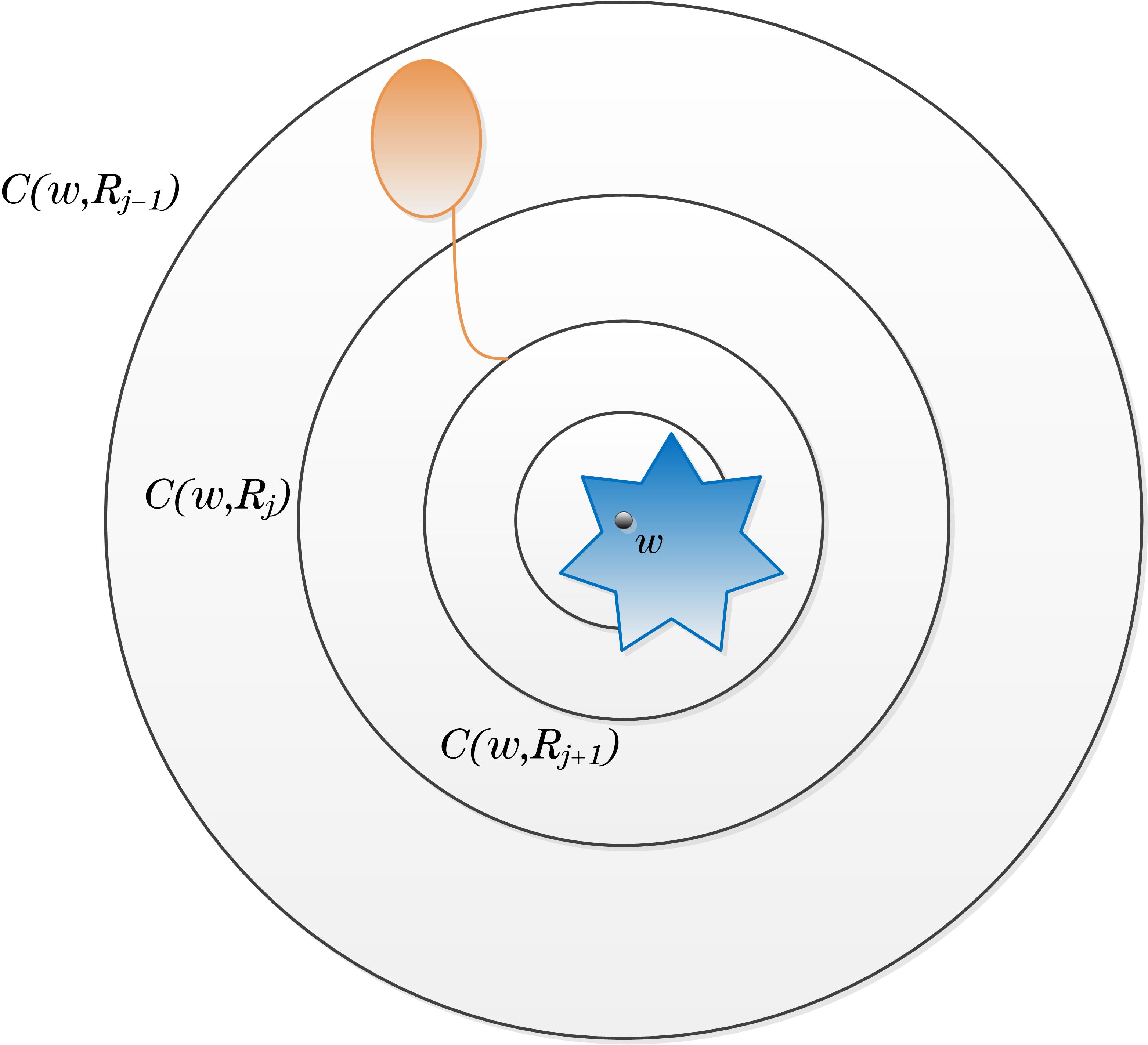
Since is a domain with bounded gap-ratio, we take the first sufficiently small so that the gap-ratios of all complementary components inside to are uniformly bounded. Hence we have
where is a constant. It then follows that
| (3.3) |
We indicate that the complementary components intersecting must be contained in , then for each , there is at most one such that . We add (3.3) from to , to get
This implies . Hence
| (3.4) |
Given , we can choose sufficiently large so that the right hand of (3.4) is less than . Then we have for each , there is a such that when . According to the compactness of , the proof is completed. ∎
At the end of this section, we have derived from Möbius invariance of fatness([23]) and Möbius invariance of crossratio that:
Theorem 3.2 (Möbius invariance of gap-ratio).
Let be a nondegenerate domain with bounded gap-ratio, and let be a Möbius transformation. Then is also a nondegenerate domain with bounded gap-ratio.
4. The extended Carathéodory kernel convergence theorem
The Carathéodory kernel convergence theorem([7]) tells us what the image is. However, it does not give much informatin about for any . This section is devoted to establish the extended Carathéodory kernel convergence theorem for nondegenerate domains.
Theorem 4.1.
Let be a nondegenerate domain with bounded gap-ratio. Given a sequence of conformal maps with the limit . Suppose that for each , there is a domain containing such that
-
•
is a union of and a collection of connected components of ;
-
•
is at most countable;
-
•
extends to a conformal mapping , and each is a nondegenerate domain.
Let . Then is the complement of the connected component of that contains , where is any Hausdorff limit of a subsequence of . Moreover, we have is a singleton if is.
Proof.
We first normalize the sequence by requiring and due to theorem 3.2. Without loss of generality, we assume that is the Hausdorff limit of the sequence . Let be the complement of the connected component of that contains . Our goal is to show that . According to the Carathéodory kernel convergence theorem, we have . Hence we only need to show that .
Striving for a contradiction, we assume . Let as shown in figure 3. Set , and . (It is possible that or .) Since , it follows that the distance in between and tends to zero as . (Otherwise, we consider a Jordan curve in which separates from for infinite many , then the image of this curve under will separate from .)
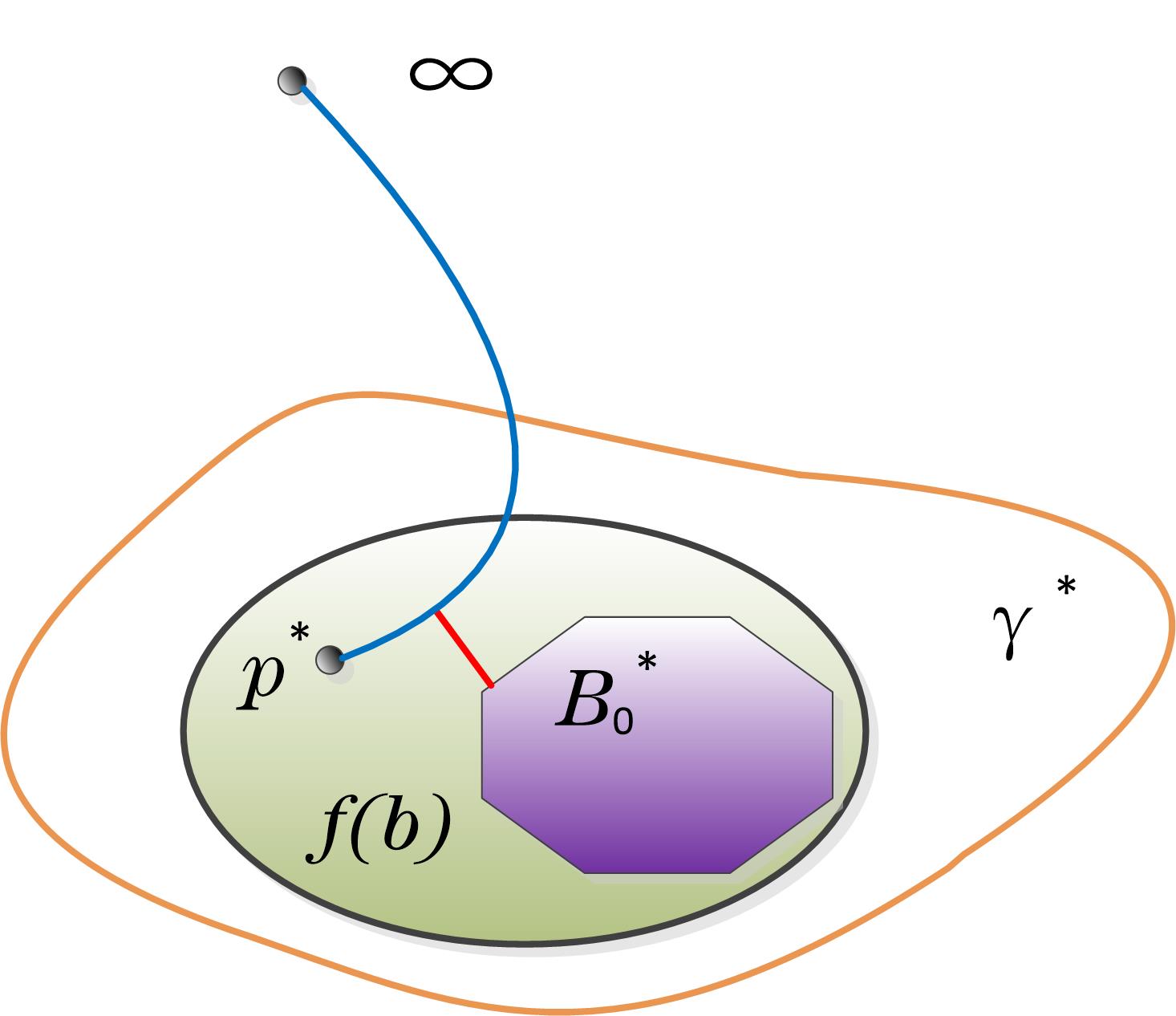
Part I: Prove that as .
Recall that is a Jordan curve that separates from in , and is the connencted component of that contains . Similarly, we let be the connencted component of that contains . Let be the collection of all Jordan curves satisfies either of the following conditions:
-
•
separates from ;
-
•
and separates from .
Let .
Part II: Fix an extended metric to get a positive lower bound of .
It follows from the normalization that there is some radius so that for all . We now define for all :
and for :
It is clear that is an extended metric on . In the following we will show that the ratio is strictly greater than zero under the metric for any , so that the transboundary extremal length is bounded away from zero as .
Since , there is a curve that connects and as shown in figure 3. Let be a number that smaller than the distance from to . It is obvious that for sufficiently large we have for all .
Let , and for any , set . It is easy to know that is a non-negative real valued function and covers the interval . Parametering as , where is an interval. It is clear that is a collection of connected components of . We denote the collection of connected components as . Then for each , we have
On the other hand, for each , it follows that
Since the set of such and is countable, and the interval is covered by the sets
this implies
Since are chosen arbitrarily, we conclude that
| (4.1) |
Moreover, we note that is nondegenerate. Then for each non-trival component , we have
| (4.2) |
Thus for and for . Moreover, we have
| (4.3) |
According to the conformal invariance of transboundary extremal length, we infer from the result in Part I that . This contradiction establishes that .
Part III: Show that is a singleton if is.
We first suppose that is a singleton and is a fixed positive integer. Let be the collection of all Jordan curves in that separates from and . We have from definition 2.1. By the invariance of transboundary extremal length, we also have . This implies is a single point. Since this holds for every and is the Haussdorff limit of , must be a single point. Thus we have is a singleton. ∎
5. Proof of the main theorem
Recall that a circle domain is a connected domain in such that every boundary component is either a cirlce or a point, hence it is nondegenerate.
Proof of theorem 1.3.
Let be a nondegenerate domain with bounded gap-ratio. Due to theorem 3.2, we assume for normalization. It is clear that the space must be countable. Let be a sequence of finite subsets of such that . For each , let . By Koebe’s finite connected uniformization theorem there is a conformal homeomorphism such that and is a circle domain. Let be the limitation of on , thus we obtain a normal family . Without loss of generality, we assume converges to . It is clear that is conformal on and satisfies the normalization. According to theorem 4.1, we have is a round disk for each , and is a single point for each . This implies is a circle domain. ∎
References
- [1] L. Bers, Uniformization by Beltrami equations, Communications on Pure and Applied Mathematics, 14(3): 215-228, 1961, .
- [2] M. Bonk, Uniformization of Sierpiński carpets in the plane, Inventiones mathematicae, 186(3): 559-665, 2011, .
- [3] M. Bonk, Uniformization by square domains, The Journal of Analysis, 24: 103-110, 2016.
- [4] M. Bonk and S. Merenkov, Quasisymmetric rigidity of square Sierpiński carpets, Annals of Mathematics, 177(2): 591-643, 2013.
- [5] M. Bonk and S. Merenkov, Square Sierpiński carpets and Lattès maps, Mathematische Zeitschrift, 296: 695-718, 2020.
- [6] R. Denneberg, Konforme Abbildung einer Klasse unendlich vielfach zusammenhängender schlichter Bereiche auf Kreisbereiche, Diss., Leipziger Berichte, 84: 331-352, 1932.
- [7] G.M. Goluzin, Geometric Theory of Functions of a Complex Variable, Translations of Mathematical Monographs, American Mathematical Society, 1969.
- [8] H. Grötzsch, Eine Bemerkung zum Koebeschen Kreisnormierungsprinzip, Leipziger Berichte, 87: 319-324, 1935.
- [9] A. Haas, Linearization and mappings onto pseudocircle domains, Transactions of the American Mathematical Society, 282(1): 415-429, 1984.
- [10] H. Hakobyan and W. Li, Quasisymmetric embeddings of slit Sierpiński carpets, Transactions of the American Mathematical Society, 376: 8877-8918, 2023.
- [11] S. Hildebrandt and H. von der Mosel, Conformal mapping of multuply connected Riemann domains by a variational approach, Advances in Calculus of Variations, 2: 137-183, 2009.
- [12] Z.-X. He and O. Schramm, Fixed points, Koebe uniformization and circle packings, Annals of Mathematics, 137: 369-406, 1993.
- [13] Z.-X. He and O. Schramm, Rigidity of circle domains whose boundary has finite linear measure, Inventiones mathematicae, 115(3): 297-310, 1994,.
- [14] Z.-X. He and O. Schramm, Koebe Uniformization for “Almost Circle Domains”, American Journal of Mathematics, 117(3): 653-667, 1995.
- [15] P. Koebe, Über die Uniformisierung beliebiger analytischer Kurven III, Nachr. Ges Wiss. Gott., 337-358, 1908,.
- [16] P. Koebe, Abhandlungen zur Theorie der Konformen Abbildung: VI. Abbildung mehrfach zusammenhängender Bereiche auf Kreisbereiche, etc., Mathematische Zeitschrift, 7: 235-301, 1920.
- [17] P. Koebe, Über die Konforme Abbildung Endlich- und Unendlich-Vielfach Zusammenhängender Symmetrischer Bereiche auf Kreisbereiche, Acta Mathematica, 43: 263-287, 1922.
- [18] H. Meschowski, Über die konformen Abbildung gewisser Bereiche von unendlich hohen Zusammenhang auf Vollkreisbereiche. I, Mathematische Annalen, 123(1): 392-405, 1951.
- [19] H. Meschowski, Über die konformen Abbildung gewisser Bereiche von unendlich hohen Zusammenhang auf Vollkreisbereiche. II, Mathematische Annalen, 124(1): 178-181, 1952.
- [20] D. Ntalampekos and M. Younsi, Rigidity theorems for circle domains, Inventiones mathematicae, 220(1): 129-189, 2020.
- [21] K. Rajala, Uniformization of planar domains by exhaustion, Preprint, arXiv:2111.00845, 2021.
- [22] L. Sario, Über Riemannsche Flachen mit hebbarem Rand, Annales Academiae Scientiarum Fennicae. Series AI, 50: 1-79, 1948.
- [23] O. Schramm, Transboundary extremal length, Journal d’Analyse Mathématique, 66: 307-329, 1995.
- [24] K.L. Sterbel, Über das Kreisnormierungsproblem der konformen Abbildung, Annales Academiae Scientiarum Fennicae, 1: 1-22, 1951.
- [25] K.L. Sterbel, Über die konformen Abbildung von Gebieten unendlich hohen Zusammenhangs, Commentarii Mathematici Helvetici, 27: 101-127, 1953.
- [26] X.G. Wang and Y. Zhong, Koebe uniformization for infinitely connected attracting Fatou domains, Preprint, arXiv:2406.13524, 2024.
- [27] M. Younsi, Removability, rigidity of circle domains and Koebe’s conjecture, Advances in Mathematics, 303: 1300-1318, 2016.