Kondo Breakdown in Topological Kondo Insulators
Abstract
Motivated by the observation of light surface states in SmB6, we examine the effects of surface Kondo breakdown in topological Kondo insulators. We present both numerical and analytic results which show that the decoupling of the localized moments at the surface disturbs the compensation between light and heavy electrons and dopes the Dirac cone. Dispersion of these uncompensated surface states are dominated by inter-site hopping, which leads to a much lighter quasiparticles. These surface states are also highly durable against the effects of surface magnetism and decreasing thickness of the sample.
Kondo insulators are a class of strongly correlated electron material in which the screening of local moments by conduction electrons gives rise to an insulating gap at low temperatures Fisk et al. (1995); Coleman (2007). The first Kondo insulator, SmB6, discovered more than 40 years agoMenth et al. (1969), has attracted renewed interest due to its unusual surface transport properties: while its insulating gap develops around K, the resistivity saturates below a few KelvinAllen et al. (1979). Although this excess conductivity was originally ascribed to mid-gap impurity statesNickerson et al. (1971), renewed interest derives from the proposal that SmB6 is a topological Kondo insulator, developing protected conducting surface states at low temperatures Dzero et al. (2010, 2012); Alexandrov et al. (2013); Lu et al. (2013). ExperimentsWolgast et al. (2013); Zhang et al. (2013); Kim et al. (2013, 2014) have since confirmed that the plateau conductivity derives from surface states, and these states have been resolved by angle-resolved photoemission spectroscopy (ARPES) Jiang et al. (2013); Neupane et al. (2013); Xu et al. (2013); Frantzeskakis et al. (2013). The most recent spin-ARPES experiments have also resolved the helicoidal spin polarization of the surface quasiparticles expected from topologically protected Dirac conesXu et al. (2014).
Yet, despite this success, certain aspects of these materials remain unexplained. A particularly notable problem, is that both quantum oscillationLi et al. (2013) and ARPESNeupane et al. (2013); Jiang et al. (2013); Xu et al. (2013); Frantzeskakis et al. (2013); Kim et al. (2014); Xu et al. (2014) studies show that the surface quasiparticles are light, with Fermi velocities , ranging from Jiang et al. (2013) to Neupane et al. (2013); yet current theoriesDzero et al. (2010, 2012); Alexandrov et al. (2013); Lu et al. (2013) predict heavy Dirac quasiparticles with velocities , an order of magnitude slower.
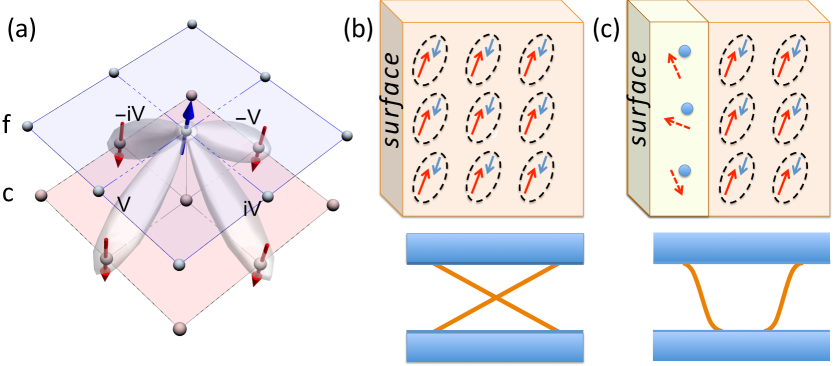
Here we propose a resolution to this problem, by taking into account of the breakdown of the Kondo effect at the surface. The essence of our theory is based on the observation that the reduced co-ordination of the Sm3+ ions at the surface causes a marked reduction in the surface Kondo temperature , so that the screening of local moments at the surface is either suppressed to much lower temperatures, or fails completely due to an intervention of surface magnetic order. “Kondo breakdown”Si et al. (2001); Coleman et al. (2001); Senthil et al. (2003); Pépin (2007); Paul et al. (2007) liberates unquenched moments at the surface, and has the effect of shifting the mixed valence of the surface Sm ions towards the higher entropy, (3+) configuration of the unquenched moments, as observed in X-ray absorption spectroscopy Phelan et al. (2014). Most importantly, Kondo breakdown will liberate a large number of carriers previously bound inside Kondo singlets at the surface (see Fig1(b) and (c)): this process localizes -holes, driving up the electron count in the surface states to form large spin-polarized Fermi surfaces determined by the Luttinger sum rule
| (1) |
where is the total Fermi surface area of the singly-degenerate surface states, is the change the valence, i.e. for Sm , , in units where the lattice constant . A detailed analysis presented later, shows that the dispersion of these highly doped surface states are dominated by a quadratic inter site hopping term
| (2) |
where is the effective hopping, while and are functions that depend on the surface scattering phase shift , as defined later. The quadratic term, absent in a conventional topological surface state, appears when the perfect compensation between heavy and light electrons is disrupted at the surface by Kondo breakdown: this term increases the velocity of the surface states by about an order of magnitude, providing a natural explanation to the light surface states observed in experiments. Moreover, the heavy doping of the surface states shifts the Dirac point into the valence band, leading to an unusual protection of surface states against decreasing thickness and surface magnetism. We will show that the interaction of the local moments and the light surface states is described by a new kind of “chiral Kondo lattice” with the potential for a rich phase diagram of competing interacting surface states.
Model: We introduce a simplified lattice model for topological Kondo insulators, described by the periodic Anderson model:
| (3) |
where the and respectively create conduction and f electrons at site , with corresponding hopping matrix elements and . is the onsite Coulomb repulsion of f-electrons. and are the bare hybridization and level position. The form-factor
| (4) |
describes the spin-orbit coupled hybridization between neighboring and electrons. This simplified form factor captures the important vectorial spatial structure of hybridization between f and d states, whose orbital angular momenta differ by one unit. The hybridization is odd-parity and vanishes onsite because the heavy and light orbitals have opposite spatial parity. Fig. 1(a) shows a schematic of our model. Note that it explicitly includes an dispersionColeman (2007), which is required for a fully gapped spectrum. Microscopically these terms are expected to result from the indirect hopping of f-electrons via the p-orbitals of the Boron ions.
To describe the large limit we adopt a slave-boson mean-field theory and carry out a saddle point approximation in the bulk, giving rise to the mean-field Hamiltonian Coleman (1987).
| (5) | |||||
| (6) |
Here, is the renormalized hybridization, where is the slave boson projection amplitude. The f-hopping now becomes . We consider a general nearest neighbor and next nearest neighbor dispersion, while , where, for simplicity, we have taken the ratio between the - and electron hoppings to be a single fixed constant for both nearest neighbor and second-neartest neighbor hoppings. The quantity is the constraint field that imposes the mean-field constraint , where is the local conserved charge associated with the slave boson treatment of the infinite limit, here taken to be ; is the total number of sites. In momentum space the form factor of the hybridization now takes the form , where , which reduces to at small k. This odd-parity hybridization is reminiscent of the gap function in topological superfluid 3He-3B. This model can be regarded as an adiabatic continuation from small to large at infinite spin-orbit coupling. Band crossing between the odd and even parity bands generates the topological band structureHasan and Kane (2010); Qi and Zhang (2011) with protected surface states.
In order to obtain the surface state spectrum, we adopt Volovik’s approach, mapping the reflection at the boundary onto transmission through an interface where the hybridization changes signVolovik (2009). This method enables us to solve for the surface states using a linearized Hamiltonian. For pedagogical purposes, we take . We can treat the surface eigenstate at as a one-dimensional problem, and since the main surface scattering effect takes place close to the Fermi surface, we can linearize the dispersion(5) normal to the surface and obtain the surface eigenstates at . The two interface eigenstates at are given by
| (7) |
where and . and denote the orbital and the spin component of the wave function. The corresponding energy of a state at the Dirac point is . The transverse dispersion that develops at finite is then treated using first order degenerate perturbation theory, projecting the full Hamiltonian onto the surface bound-states, . This leads to the dispersion
| (8) |
where . Since , the surface states are composed of heavy quasiparticles. Note that at this stage, the quadratic term is absent.
Surface Kondo breakdown: The reduced co-ordination number of the f-electrons, plus the internal gapping of the bulk states lowers the effective Kondo coupling constant. If we assume crudely that the Kondo coupling constant is reduced by a factor of th, the reduced Kondo temperature is then
| (9) |
For example, if we take the bulk Kondo temperature with half band-width , this gives a surface Kondo temperature of . In practice, the gapping of the bulk states makes this an upper bound. This effect has been recently explored in 1DAlexandrov and Coleman (2014); Lobos et al. (2014). However, unlike one dimension, where the spin-decoupled phase is no longer topologicalAlexandrov and Coleman (2014), in two and three dimensions, the topological insulator is protected by time reversal symmetry and the spin-decoupled state remains topological in the bulk. With these considerations in mind, we model the surface Kondo breakdown as the suppression of the slave boson amplitude to zero on the surface layer of the TKI.
Surface Kondo breakdown localizes mobile -quasiparticles at the surface, removing them from the Fermi sea. In SmB6, this is equivalent to a shift in the effective f-valence from at the surface. This is a reduction in the number of f-holes, that corresponds to an increase in the density of electrons on the surface. From Luttinger’s sum rule (eq. 1), the area enclosed by the Fermi surface is equal to the total electron density. The Fermi surface area observed in ARPES is 0.3-0.35Neupane et al. (2013); Jiang et al. (2013); Xu et al. (2013); Frantzeskakis et al. (2013); Kim et al. (2014); Xu et al. (2014), in agreement with Luttinger sum rule.
Next we examine the effect of Kondo breakdown on the dispersion of the surface states. The effect of Kondo breakdown can be incorporated by introducing a scattering phase shift into the component of the surface state wave function, which ensures that surface node of the part of the wave function is shifted one lattice unit in towards the bulk, depleting the surface of mobile f-electrons (see supplementary information for detailssupplementary material (2014)). In Volovik’s approach, becomes a transmission phase shift. The unperturbed energy of the surface bound-state is now modified and the dispersion becomes
| (10) |
Note the appearance of a term, driven by an increase the conduction electron content of the surface states. The subleading linear term is also modified, containing the renormalization of order one: . Substituting and in eq. 10 leads to eq. 2. This analytic result provides a natural explanation to the light quasiparticles in SmB6. For a parameter choice of , , consistent with band structure calculationsLu et al. (2013), and the value of which leads to the experimentally observed gap we obtain surface state velocity without surface Kondo breakdown and with surface Kondo breakdown in agreement with the measured by ARPES experimentsNeupane et al. (2013). Here the quoted surface velocities were calculated at the mid-gap energy of the Dirac point in the absence of Kondo breakdown. We can not however, account for the much larger surface velocity meV reported in quantum oscillations Li et al. (2013).
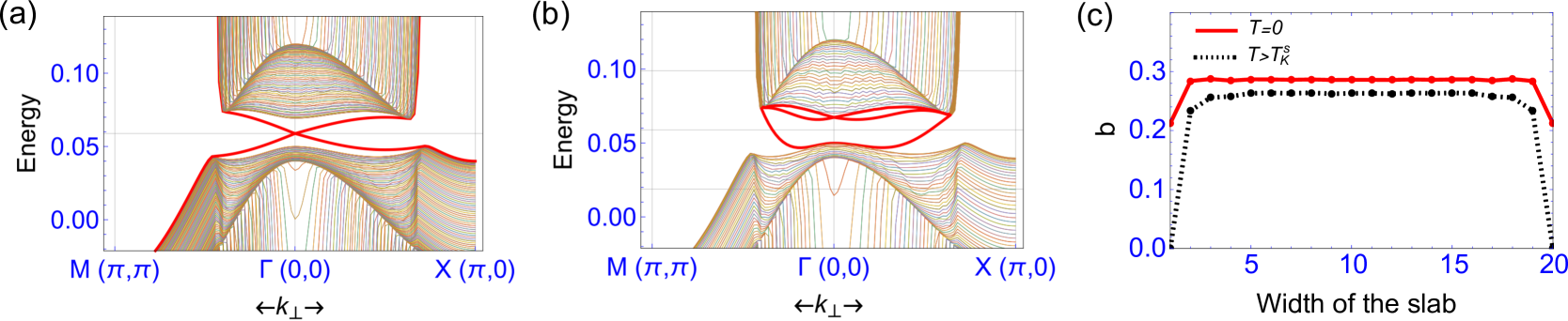
To confirm the results of our simplified analytical calculations, we have carried out a series of slab calculations with and without Kondo breakdown. As a first check, we simulated Kondo breakdown by setting the amplitude of the surface slave boson field to zero. Without surface Kondo breakdown (Fig 2(a)), the surface states are heavy, but as expected, when the slave boson amplitude is suppressed to zero on the surface, the topological states become much lighter as shown in Fig. 2(b). Moreover, the area of the light Fermi surface is significantly enhanced, corresponding to the extra density of carriers on the surface.
Next, to confirm that the assumption of surface Kondo breakdown we performed a fully self-consistent mean field calculation in which both and were allowed to vary along the direction. In this self-consistent calculation, we chose parameters where the heavy and light bands cross at the three X-points, as seen SmB6 Jiang et al. (2013); Neupane et al. (2013); Xu et al. (2013); Frantzeskakis et al. (2013); from a technical stand-point, the crossing at the three points is required to enhance the f-character, achieving the Kondo limit while still in the strong topological insulator phase. We achieve this crossing in our model by taking , such that the heavy and light bands cross at the 3 different points. We note that for the simpler choice , bands cross at the point, restricting the strong topological insulating behavior to the region to . Fig 2 (c) presents the results of these calculations. We find as expected, that the self-consistently determined slave boson amplitude is depressed at the surface, corresponding to a reduction of the surface Kondo temperature. In our model calculation, for which found that is depressed by at the surface, corresponding to , a result consistent with equation (8). We also found that as the temperature is raised above the the surface Kondo temperature , the surface collapses to zero, even though it is still finite in the bulk. The dispersion displays a corresponding transition between heavy and light surface states as the temperature is raised through . In practice, the possible intervention of magnetism or other instabilities may permanently prevent the low-temperature re-establishment of the Kondo effect at the surface.
Chiral Kondo lattice: The consequences of surface Kondo breakdown are rather interesting. The decoupled f-electrons now interact with the chiral surface states to form a new kind of Kondo lattice in which the conduction sea of chiral electrons is now singly degenerate, interacting with the local moments via a Hamiltonian
where is the Kondo coupling, is the decoupled local moment and where creates a chiral, spin polarized surface states whose dispersion is given in eq. 10. The localized two-component electron field at site ,
| (11) |
is constructed from the spin-polarized surface states by combining orbital and spin angular momentum. is the antiferromagnetic Heisenberg exchange between the local moments which is derived by a Schrieffer-Wolff transformation of eq. S19. The ground-state of the chiral Kondo lattice can be either magnetically ordered state or a heavy fermion liquid where the local moments are screened by chiral fermions. As in conventional heavy fermion systems, near the quantum critical point that separates these two limits, there is the possibility of strange metal behavior and superconducting ground-states. A 2D version of a similar model with 1D edge states have been explored recentlyAltshuler et al. (2013).
Even the magnetic phase diagram of this lattice is expected to be rich. The RKKY interaction in a chiral Kondo lattice gives rise to Heisenberg, Dzyaloshniskii-Moriya and compass anisotropy terms Zhu et al. (2011) of strength , and respectively. For the ground state is an in-plane ferromagnet whereas for , it is a spiral of variable pitch set by Banerjee et al. (2013). Such a spiral state evolves into a skyrmion crystal in applied magnetic fieldBanerjee et al. (2014). Experimentally, in SmB6, indications of magnetism have been observed as hysteresis in magnetoresistance experimentsNakajima et al. (2013); Eo et al. (2014). The absence of ordered ferromagnetic moment in XMCD experimentsPhelan et al. (2014) suggests that the ground state might be a spiral with no net moment. Magnetic order breaks the time reversal symmetry and can in principle gap the surface states. We note that of the most recent single crystals show no plateau in resistivityPhelan et al. (2014) indicating that magnetism may play a crucial role in the topological behavior. Better sample quality and tuning the chiral Kondo lattice through a quantum critical point opens up the possibility of exotic superconductivity on the surface of topological Kondo insulators.
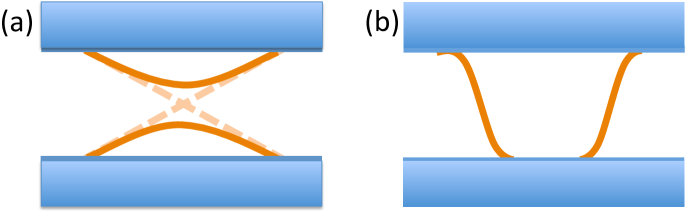
Thickness dependence of surface states: Perfect topological protection of the surface states requires an infinite bulk. When the thickness of the system is comparable to the decay length, of the surface states, the two surface states on each surface mix, giving rise to a gap in the spectrum. Since the mixing is a zero-momentum transfer process, the gap opens at the doubly degenerate Dirac point as shown in Fig. 3(a). This effect has been observed in conventional topological insulators like where the surface states get gapped for thickness 3-5 quintuple layersZhang et al. (2010). However with surface Kondo breakdown, the Dirac point shifts in the valence band, giving rise to a unique protection against decreasing thickness of the sample (Fig. 3(b)). Recent transport experiments on films about L=100-200nm thicknesses observe topological surface states Yong et al. (2014). We predict that the topological states will persist even in ultra-thin samples, , making a perfect candidate for thin film applications. This mechanism also gives rises to protection against small time reversal symmetry breaking effects such as weak magnetism at the surface.
Conclusion: To conclude, we have addressed the origin of the light surface states of topological Kondo insulators as a simple consequence of surface Kondo breakdown. Our results appear to reconcile the observation of light surface states and the peculiar shift of valence in observed in X-ray measurements. This theory also predicts an increased stability of the the surface states against finite thickness and magnetism may be important in thin film device fabrication. We have also argued that the interaction of the surface spins with spin-polarized light surface states is described by a chiral Kondo lattice: a two dimensional Kondo lattice with strong parity violation, with the potential for a rich phase diagram in the vicinity of its magnetic quantum critical point. The detailed character of the surface states at low temperatures, with the possibility of a wide variety of magnetic or other orderings Efimkin and Galitski (2014); Roy et al. (2014) remains a fascinating topic for future research.
Note added: We recently became aware of low temperature magneto thermo-electric transport measurementsLuo et al. (2014) which indicate the development of a very heavy surface Fermi liquid below 3K, with quasiparticle group velocities in the range , consistent with the development of a low-temperature surface Kondo effect.
Acknowledgments: We gratefully acknowledge stimulating conversations with Jim Allen, Tzen Ong, Kai Sun, George Sawatzky and David Vanderbilt. This work is supported by Department of Energy grant DE-FG02-99ER45790.
References
- Fisk et al. (1995) Z. Fisk et al., Physica B 206 & 207, 798 (1995).
- Coleman (2007) P. Coleman, Handbook of Magnetism and Advanced Magnetic Materials (John Wiley and Sons, Ltd., 2007).
- Menth et al. (1969) A. Menth, E. Buehler, and T. H. Geballe, Phys. Rev. Lett. 22, 295 (1969).
- Allen et al. (1979) J. W. Allen, B. Batlogg, and P. Wachter, Phys. Rev. B 20, 4807 (1979).
- Nickerson et al. (1971) J. C. Nickerson et al., Phys. Rev. B 3 (1971).
- Dzero et al. (2010) M. Dzero, K. Sun, V. Galitski, and P. Coleman, Phys. Rev. Lett. 104, 106408 (2010).
- Dzero et al. (2012) M. Dzero, K. Sun, P. Coleman, and V. Galitski, Phys. Rev. B 85, 045130 (2012).
- Alexandrov et al. (2013) V. Alexandrov, M. Dzero, and P. Coleman, Phys. Rev. Lett. 111, 226403 (2013).
- Lu et al. (2013) F. Lu et al., Phys. Rev. Lett. 110, 096401 (2013).
- Wolgast et al. (2013) S. Wolgast et al., Phys. Rev. B 88, 180405 (2013).
- Zhang et al. (2013) X. Zhang et al., Phys. Rev. X 3, 011011 (2013).
- Kim et al. (2013) D. J. Kim et al., Scientific Reports 3, 3150 (2013).
- Kim et al. (2014) D. J. Kim, J. Xia, and Z. Fisk, Nature Materials 13, 466 (2014).
- Jiang et al. (2013) J. Jiang et al., Nat. Comm. 4, 3010 (2013).
- Neupane et al. (2013) M. Neupane et al., et al., Nat. Comm. 4, 2991 (2013).
- Xu et al. (2013) N. Xu et al., Phys. Rev. B 88, 121102 (2013).
- Frantzeskakis et al. (2013) E. Frantzeskakis, N. de Jong, B. Zwartsenberg, Y. K. Huang, Y. Pan, X. Zhang, J. X. Zhang, F. X. Zhang, L. H. Bao, O. Tegus, et al., Phys. Rev. X 3, 041024 (2013).
- Xu et al. (2014) N. Xu, P. K. Biswas, J. H. Dil, G. Landolt, S. Muff, C. E. Matt, X. Shi, N. C. Plumb, M. Radavic, E. Pomjakushina, et al., Nature Comm. 5, 4566 (2014).
- Li et al. (2013) G. Li et al., arXiv p. 1306.5221 (2013).
- Si et al. (2001) Q. Si, S. Rabello, K. Ingersent, and J. L. Smith, Nature 413, 804 (2001).
- Coleman et al. (2001) P. Coleman, C. Pépin, Q. Si, and R. Ramazashvili, J. Phys.: Condens. Matter 13, 723 (2001).
- Senthil et al. (2003) T. Senthil, S. Sachdev, and M. Vojta, Phys. Rev. Lett. 90, 216403 (2003).
- Pépin (2007) C. Pépin, Phys. Rev. Lett. 98, 206401 (2007).
- Paul et al. (2007) I. Paul, C. Pépin, and M. Norman, Phys. Rev. Lett. 98, 026402 (2007).
- Phelan et al. (2014) W. A. Phelan et al., Phys. Rev. X 4, 031012 (2014).
- Coleman (1987) P. Coleman, Phys. Rev. B 35, 5072 (1987).
- Hasan and Kane (2010) M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010).
- Qi and Zhang (2011) X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys. 83, 1057 (2011).
- Volovik (2009) G. E. Volovik, JETP Letters 90, 398 (2009).
- Alexandrov and Coleman (2014) V. Alexandrov and P. Coleman, Phys. Rev. B 90, 115147 (2014).
- Lobos et al. (2014) A. M. Lobos, A. O. Dobry, and V. Galitski, arXiv p. 14115357 (2014).
- supplementary material (2014) See Supplemental Material [url], which includes Ref. [33].
- Andrei et al. (1983) N. Andrei, K. Furuya, and J. Lowenstein, Rev. Mod. Phys 55, 331 (1983).
- Altshuler et al. (2013) B. L. Altshuler, I. L. Aleiner, and V. I. Yudson, Phys. Rev. Lett. 111, 086401 (2013).
- Zhu et al. (2011) J.-J. Zhu, D.-X. Yao, S.-C. Zhang, and K. Chang, Phys. Rev. Lett. 106, 097201 (2011).
- Banerjee et al. (2013) S. Banerjee, O. Erten, and M. Randeria, Nat. Phys 9, 626 (2013).
- Banerjee et al. (2014) S. Banerjee, J. Rowland, O. Erten, and M. Randeria, Phys. Rev. X 4, 031045 (2014).
- Nakajima et al. (2013) Y. Nakajima et al., arXiv p. 1312.6132 (2013).
- Eo et al. (2014) Y.-S. Eo et al., arXiv p. 14107430 (2014).
- Zhang et al. (2010) Y. Zhang et al., Nat. Phys. 6, 584 (2010).
- Yong et al. (2014) J. Yong et al., arXiv p. 1408.5413 (2014).
- Efimkin and Galitski (2014) D. K. Efimkin and V. Galitski, Phys. Rev. B 90, 081113 (2014).
- Roy et al. (2014) B. Roy et al., arXiv p. 14101868 (2014).
- Luo et al. (2014) Y. Luo et al., Phys. Rev. B 91, 075130 (2015).
Supplementary material for ‘Kondo Breakdown In Topological Kondo Insulators’
This supplementary material presents the details of the surface state calculations. We first describe the Volovik methodVolovik (2009) and then apply it to our model, with and without Kondo breakdown.
I Volovik method
Surface states are evanescent solutions of the Hamiltonian which are nucleated by the boundary. The surface state wave function in the presence of a hard wall consists of an incoming and an outgoing wave moving in opposite directions whose superposition vanishes at the boundary as shown in Fig 1(a). Volovik’s methodVolovik (2009) “unfolds” the reflection process into a transmission problem, with incoming and outgoing waves moving in the same direction (see Fig. 1b). Similar “unfolding” techniques have been applied in wide variety of problems including the Kondo impurity modelAndrei et al. (1983). The Volovik transformation is made by applying the reflection operator to the eigenvalue equation governing the incoming waves: under this a transformation, the odd parity terms in the Hamiltonian reverse sign at the boundary: in our particular, model the only odd parity term in the Hamiltonian is the hybridization, , which in the Volovik mapping now changes sign at the boundary as shown in Fig1(b). The Volovik method has the advantage that the ingoing and outgoing waves carry the same momentum; it also brings out the close analogy between surface states and Jackiw-Rebbi domain wall bound-states, with the additional technical advantage that it can handle cases where .
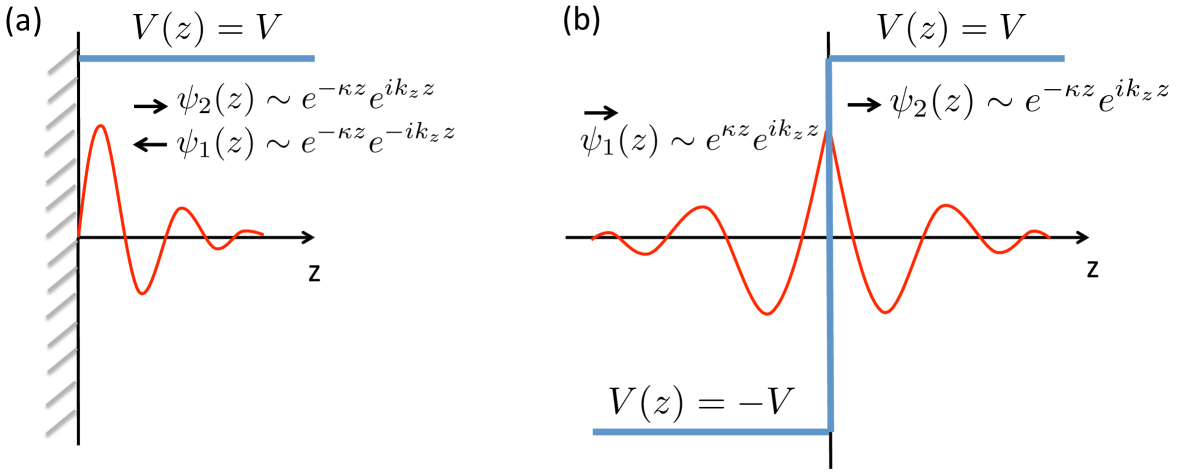
To be more specific, consider first a reflection boundary problem. The wavefunction consists of incoming and outgoing waves
| (S1) |
Here are eigenstates of the bulk Hamiltonian defined on the half-line and is a spinor. The full wavefunction is given by
| (S2) |
The boundary condition is satisfied by the fact that .
The Volovik method obtains an equivalent transmission problem by applying the parity operator to the eigenvalue equation of the incoming wave , to obtain
| (S3) |
where is the parity reversed Hamiltonian. The corresponding transmission problem is then given by
| (S4) |
Here
| (S5) |
is a symmetric domain-wall bound-state. In our particular problem the right and left hand Hamilonians are simply obtained by reversing the sign of the hybridization: .
II Continuum model
Our starting point is , the mean field Hamiltonian, eq. 5 in the main text. We replace and expand to quadratic order in so that
| (S6) |
where
| (S7) |
Here the - index refers to the conduction/f-electron degree of freedom, so that describes a conduction electron while describes an f-electron. The Pauli matrices carry the spin degree of freedom. We seek bound-state solutions of the form
| (S8) |
where .
We will be interested in the small values of the transverse momenta, where . This allows us to expand the Hamiltonian in in powers of , where
| (S9) | |||
| (S10) | |||
| (S11) |
Our procedure is to first obtain the eigenvalues of the zeroth order Hamiltonian, and then to carry out perturbation theory on the remaining components . This corresponds to first solving for the bound-state at .
We need to treat positive and negative separately. In the positive half-plane, () the eigenvalue condition gives
| (S12) |
We may simultaneously diagonalize both energy and , defining “up” and “down” eigenstates . For , the reduced eigenvalue equation is
| (S13) |
where we have dropped the orbital index for clarity. The solution for can be written in the form of an evanescent wave.
| (S14) |
where is a normalization constant and and are defined as follows
| (S15) | |||
| (S16) | |||
| (S17) |
Similarly, the solution is
| (S18) |
Following the same procedure, the decaying solutions for are
| (S19) | |||||
| (S20) |
II.1 Without Kondo breakdown
We first consider the case the boundary conditions in the absence of Kondo breakdown. We need to match and at . This gives the condition: . We then find , and for .
| (S21) | |||
| (S22) | |||
| (S23) |
So far we have considered the case. The solution for can be obtained by
| (S24) |
The remainder of the Hamiltonian is treated within perturbation for small . The effective Hamiltonian derived by projecting on to the surface states: , where are spin indices. The quadratic part of the Hamiltonian cancels exactly: . The remaining linear part gives
| (S25) |
where the normalization takes the form . The effective Hamiltonian is then
| (S26) |
where and the corresponding dispersion is
| (S27) |
where is defined as .
II.2 Kondo breakdown
In the presence of Kondo breakdown, the hybridization vanishes at the first site. As a result, and bands are subject to different boundary conditions. This effect can be captured by a simple phase shift , such that the boundary condition is modified to
| (S28) |
Now the previous condition of r=0 is modified to . Hence the energy and the decay length takes the form
| (S29) | |||
| (S30) |
As before we consider the rest of Hamiltonian as perturbation . The effective Hamiltonian is then However, the quadratic part () of no longer cancels exactly and gives the diagonal part of the effective Hamiltonian
| (S31) |
where
| (S32) |
where
| (S33) |
leading to
| (S34) |
While the linear part gives
| (S35) |
The effective Hamiltonian is then
| (S36) |
Combining all the pieces together we can diagonalise the effective Hamiltonian to get the energy:
| (S37) |
References
- Volovik (2009) G. E. Volovik, JETP Letters 90, 398 (2009).
- Andrei et al. (1983) N. Andrei, K. Furuya, and J. Lowenstein, Rev. Mod. Phys 55, 331 (1983).