La curva de Fargues–Fontaine:
Una motivación al estudio de la teoría de representaciones de Galois -ádicas
Resumen.
Este artículo proporciona una revisión comprensiva sobre la curva de Fargues-Fontaine, una pieza central en la teoría de Hodge -ádica, y su papel crucial en la clasificación de las representaciones de Galois -ádicas. Nos enfocamos en sintetizar los desarrollos fundamentales en torno a esta curva, subrayando cómo conecta conceptos avanzados de geometría aritmética con la teoría práctica de representaciones. Analizamos en detalle los anillos de periodos de Fontaine (), abordando sus propiedades algebraicas y aritméticas esenciales, y cómo estos anillos contribuyen a la construcción y definición de la curva. Además, exploramos la teoría de las representaciones de Galois -ádicas admisibles y discutimos cómo, una vez definida la curva, esta se relaciona con la teoría de Harder-Narasimhan.
Key words and phrases:
Curva de Fargues-Fontaine, Geometría Aritmética, Representaciones de Galois -ádicas, Anillos de Peridos, TeorÃa de Hodge -ádica.1991 Mathematics Subject Classification:
11F85, 11S15, 11S20, 11F80.1. Introducción
La geometría aritmética ha experimentado un impulso significativo en los últimos años gracias al uso de métodos -ádicos. Uno de sus grandes avances ha sido el descubrimiento de la curva de Fargues–Fontaine que ha generado gran interés debido a las diversas relaciones que tiene con distintas áreas de las matemáticas [10].
Fue descubierta en el año 2009 por los matemáticos franceses Laurent Fargues y Jean Marc-Fontaine mediante una serie de correos electrónicos y en el transcurso de una semana de conferencias en Trieste, Italia. Pierre Colmez documenta este intercambio de mensajes y nos aporta el contexto mediante el cual se realizó dicho descubrimiento [7]. Fargues y Fontaine discutían un artículo de Berger [2] donde aseguraba que el anillo de periodos era un anillo de Bezout. Fontaine, incrédulo de esta afirmación, indaga aún más llegando a una conclusión inesperada, el hecho que es de ideales principales. Fascinado por este anillo, Fontaine plantea a Colmez y Fargues una serie de preguntas cuyas respuestas desembocarían en relaciones con la teoría de filtraciones de Harder-Narasimhan en el contexto -ádico. Estas relaciones darían pié al descubrimiento de la curva de Fargues–Fontaine revelándonos una conexión importante, la relación de las fibras vectoriales de la curva con la teoría de Harder-Narasimhan, que a su vez, tiene relación con las representaciones de Galois -ádicas y los llamados anillos de periodos de Fontaine.
La teoría de Hodge -ádica provee una forma de clasificar representaciones de Galois -ádicas de campos locales de característica cero con campo residual de característica (también llamados campos de característica mixta). Esta teoría tiene sus inicios en los trabajos de Serre y Tate quienes estudiaban los módulos de Tate sobre variedades abelianas y las representaciones de Hodge-Tate. Estas representaciones están relacionadas a ciertas descomposiciones de cohomologías -ádicas, análogas a la descomposición de Hodge. Futuros avances en el área se inspiraron por las representaciones de Galois -ádicas que nacen de la cohomología étale de variedades. Es en este contexto donde Jean-Marc Fontaine introduce los anillos de periods.
La estructura del artículo es el siguiente: En la sección 2 presentamos notación e información preliminar que se usará a lo largo del texto. En la sección 3 se plantea una introducción a la idea de Fontaine sobre la clasificación de representaciones de Galois -ádicas para dar paso en la sección 4 a la definición de los anillos periodos y mencionar sus propiedades algebraicas y aritméticas más importantes. En la sección 5 retomamos lo comentado en la sección 3 con más detalle para explicar de manera más precisa el papel que toman los anillos de periodos en la clasificación de las representaciones de Galois -ádicas. En la sección 6 presentamos la construcción de la curva de Fargues-Fontaine usando como analogía las ideas para la construcción de la esfera de Riemann. Finalmente, en la sección 7 describimos la conexión entre las fibras vectoriales de la curva de Fargues-Fontaine con las representaciones de Galois -ádicas mediante el teorema de Harder-Narasimhan.
2. Notación y Preliminares
Sea un primo fijo. El campo de los números -ádicos (denotado como ) se puede definir como sigue: Para sea la máxima potencia de que divide al entero . Extendiendo esto a definimos . Así podemos definir una norma en como
Dicha norma induce una distancia en la cual no es completa (no toda sucesión de Cauchy converge). A la completación de respecto a esta distancia es lo llamados el campo de los número -ádicos.
Denotamos por a una extensión finita de , su anillo de enteros, su único ideal maximal y su campo residual. Denotamos por a la máxima extensión no ramificada [20] de dentro de . Fijamos una cerradura algebraica de y sea su grupo de Galois absoluto. Notar que es también una cerradura algebraica de y por lo tanto no depende . Sea la extensión maximal no ramificada de en Análogamente definimos a Como es no ramificado sobre es la extensión máxima no ramificada de en y por lo tanto también es independiente de .
Denotemos por a la completación ádica de y por a su anillo de enteros. Fijamos al parámetro uniformizador de , es decir, un generador del ideal principal .
Se dirá que un campo de característica es perfecto si el morfismo de Frobenius es un isomorfismo.
3. La idea de Fontaine.
Desde finales de la década de 1970, J.M. Fontaine desarrolló un programa destinado a clasificar y describir las representaciones del grupo de Galois absoluto, , de una extensión finita de los racionales -ádicos , i.e., los espacios vectoriales de dimensión finita dotados de una acción lineal continua de [1].
La estrategia de Fontaine parte de la siguiente observación: si tenemos un anillo topológico , dotado de una acción continua de y estructuras adicionales estables bajo la acción de podemos asociar a cualquier representación de un invariante de .
Entonces es un –módulo equipado con estructuras adicionales heredadas de , y que es a menudo más fácil de describir que la representación de la que partimos. El anillo permite descomponer la sub–categoría de representaciones admisibles (aquellas para los cuales es trivial, i.e., isomorfa a , como - representación). Tales anillos topológicos son los llamados anillos de periodos de Fontaine. A continuación presentamos la construcción de dichos anillos así como de algunas de sus propiedades.
4. Teoría de Hodge -ádica
La teoría de Hodge -ádica, como lo describe [13], puede verse desde dos puntos de vista: el aritmético y el geométrico.
Desde el punto de vista aritmético, es el estudio de las representaciones de Galois -ádicas, es decir, representaciones continuas donde es extensión finita de . Específicamente, esta teoría busca construir un diccionario que relacione buenas categorías de representaciones de con categorías de objetos algebraicos semilineales. Un ejemplo de esto es el estudio de los módulos de Tate de una curva elíptica sobre (que son representaciones de ) con buena reducción junto con los llamados isocristales (es decir, -espacios vectoriales de dimensión finita equipados con un automofismo de Frobenius semilineal).
Desde el punto de vista geométrico, la teoría de Hodge -ádica es el estudio de la geometría de una variedad (suave) sobre un campo -ádico . En particular estamos interesados es varias teorías de cohomología relacionadas a como la cohomología étale (, la cohomología de DeRham () y la cohomología cristalina (). Uno de los resultados mas relevantes de esta teoría es derivado del caso clásico en sobre la descomposición de Hodge de una variedad suave :
Tate observó que existía una descomposición análoga para la cohomología étale de una variedad abeliana sobre con buena reducción, lo que lo llevo a conjeturar (y tiempo después Faltings lo demostraría) la descomposición de Hodge-Tate [6] :
donde es una variedad suave sobre y es un isomorfismo de representaciones de Galois -ádicas .
En este sentido, Fontaine realiza una serie de conjeturas, ahora teoremas, conocidos como ‟teoremas de comparación˝en donde relaciona a las distintas cohomologías de la variedad, siendo necesario extender los coeficientes a los llamados anillos de periodos de Fontaine.
Teorema 1.
En esta sección nos centraremos en estudiar los anillos de periodos, en particular, mostraremos sus construcciones y las propiedades aritméticas y algebraicas que nos servirán para la construcción de la curva de Fargues-Fontaine. En el presente texto no se estudiará la relación con las cohomologías como en el teorema 4.1. Para el lector interesado en este aspecto puede consultar [1].
4.1. Anillos de Periodos
En geometría algebraica la palabra ‟periodo˝se suele referir a un número complejo que puede ser expresado como integral de una función algebraica sobre un dominio algebraico [14]. Uno de ellos es donde es el círculo unitario en el plano complejo. La teoría de Hodge -ádica nos permite diseñar un análogo -ádico de los periodos, trabajo que realizó Fontaine creando anillos específicos [11, 9, 8, 10], los cuales además están estrechamente relacionados con distintos tipos de cohomologías. Estos anillos forman parte fundamental en la construcción de la curva de Fargues-Fontaine y las representaciones de Galois -ádicas.
En esta sección se dará una introducción a los anillos de periodos como en [3], en particular estudiaremos a los anillos , y , sus respectivas construcciones y algunas de sus propiedades algebraicas y analíticas.
4.1.1. El anillo
Denotemos como el morfismo de Frobenius actuando en el cociente y notemos que es un homomorfismo de anillos. Sea el límite del sistema proyectivo de anillos:
Específicamente, un elemento de es una sucesión de elementos en , que satisfacen la propiedad de compatibilidad es un anillo perfecto de característica .
El anillo esta equipado con una valuación que se definirá a continuación: notemos que si la valuación –ádica de no depende del levantamiento de La valuación induce una función bien definida en el cociente donde Así, para en definimos
La condición de compatibilidad Implica que la sucesión es eventualmente constante y el límite está bien definido.
A continuación se hará uso de una estructura algebraica conocida como el anillo de vectores de Witt y cuya idea es la de construir extensiones no ramificadas.
Definición 2.
Definimos como donde es el funtor de vectores de Witt y la localización en en
Para definimos el representante de Techmüller en como . Dado que es de valuación discreta, todo elemento de puede ser escrito de manera única como
De manera similar, todo elemento de se puede escribir de manera única de la forma
donde puede ser negativo y depende de
Además, cuenta con estructuras adicionales:
-
tiene una acción de Frobenius dado por:
-
está equipado con una acción de dado por:
Fijamos una raíz primitiva –ésima de la unidad en Escojamos a como raíz primitiva –ésima de Entonces es raíz primitiva –ésima de la unidad. Repitiendo este proceso, construimos elementos tales que Sea la clase de Por la propiedad de compatibilidad,
Definición 3.
Para definimos donde es un levantamiento de en .
La función es inyectiva y multiplicativa. Por las propiedades de los vectores de Witt, la función ‟sharp˝se extiende a un homomorfismo inyectivo de álgebras que conmuta con la acción de Está dado por
La siguiente proposición nos dice que el kernel de es principal y nos muestra explícitamente a un generador del mismo.
Proposición 4 ([3], Lema:3.1.5).
Sea elemento tal que y Entonces genera como ideal de En particular, el elemento
satisface las condiciones.
4.1.2. El anillo
Para definir el anillo necesitamos tener la noción de elementos de la forma y para ello daremos un breve preámbulo a las llamadas potencias divididas. Se considerará
Definición 5.
Sea un anillo (conmutativo con unidad), un ideal Una colección de aplicaciones y definido como , es llamado una estructura de potencias divididas en si para todos y se tiene:
-
1)
-
2)
-
3)
-
4)
-
5)
Notemos que y además, ya que cuenta el número de maneras de dividir un grupo de objetos en grupos de elementos.
Lema 6.
Sea un anillo, un ideal de . Si es una estructura de potencias divididas en , entonces para todo y .
Este lema se puede demostrar por inducción. Así, en el anillo tendríamos la noción de dividir entre , cuestión que no siempre es posible si .
Volviendo a los anillos de periodos, dado denotamos como la sub –álgebra de generada por las potencias divididas.
Definición 7.
Definimos como la completación –ádica de donde es un generador de Denotamos por a la localización en de .
Como es un generador de , se tiene que , donde denota la completación –ádica. Otro generador de también es el elemento .
El siguiente lema nos da una condición sobre cuándo cualesquiera dos elementos en producen la misma sub -álgebra generada por las potencias divididas.
Lema 8.
Si entonces
Usando el lema, se tendría que .
Como está definida como completación –ádica es natural equipar y con la topología –ádica. Con esta topología, la inclusión es continua al igual que la inclusión .
Frobenius se extiende canónicamente a un endomorfismo ya que es estable bajo Frobenius. En efecto,
Invirtiendo se obtiene Frobenius para Análogamente, extiende la acción a
contiene un periodo para el caracter ciclotómico, i.e., un elemento en el cuál Galois actúa por multiplicación por , el caracter ciclotómico. Este elemento es
Frobenius actúa como y actúa como Tomando logaritmos, y Así, es un periodo del caracter ciclotómico.
4.1.3. El anillo
Definición 9.
Definimos como la completación de respecto a la topología –ádica, es decir
Como está definido como una completación, la topología natural en este anillo es la topología ádica. Una sucesión de elementos de elementos en converge a si y sólo si para todo la sucesión es eventualmente constante.
Definición 10.
Definimos el anillo
Como es un anillo de valuación discreta con uniformizador , se tiene que es el campo de fracciones de , es decir, este anillo es de hecho un campo.
5. Representaciones de Galois -ádicas
Una vez que hemos construído los anillos de periodos, regresamos a la idea de Fontaine para clasificar las representaciones de Galois -ádicas. En esta sección se hablará primero de la -admisibilidad de una representación para luego dar paso a un ejemplo concreto: como el anillo de periodo nos dará más información sobre la representación. La bibliografía que se seguirá en esta sección es [1].
5.1. Representaciones admisibles
Sea un campo y un grupo. Sea una –álgebra, dominio equipado con una –acción (como –álgebra) y asuma que la sub –álgebra es un campo.
No se imponen estructuras topológicas en o El objetivo en usar a para construir un funtor de representaciones de –lineales de dimensión finita a –espacios vectoriales de dimensión finita equipados con estructuras adicionales que dependen de
Sea y actúa en de manera natural, i.e.,
Definición 11.
Decimos que es –regular si y si para todo cuyo espacio generado –lineal es –estable se tiene que es unidad en
Notemos que si es un campo, entonces es –regular.
Definición 12.
Si es un dominio –regular y denóta el campo entonces para cualquier objeto de representaciones –lineales de dimensión finita definimos
es decir, es un –espacio vectorial equipado con un mapeo canónicoo
Definición 13.
Si se tiene la igualdad se dirá que es una representación –admisible.
El siguiente teorema nos indica que el -espacio vectorial es de hecho de dimensión finita y que al restringirnos a las representaciones -admisibles, se tiene un funtor exacto y fiel.
Teorema 14.
Fijamos como antes.
-
i)
El mapeo es siempre inyectivo y La igualdad se da y si sólo si es un isomorfismo.
-
ii)
Sea la subcategoría de representaciones –admisibles. El funtor contravariante es exacto y fiel.
En particular, considerando a un campo –ádico, i.e., extensión finita de y tenemos que:
-
Si , se dice que la representación es de DeRham.
-
Si , se dice que la representación es cristalina.
-
Si , se dice que la representación es semiestable.
5.2. Representaciones de deRham
Analizaremos un poco más a detalle las representaciones de DeRham. Como es –regular con , la formalización general de representaciones admisibles provee de una buena clase de representaciones -ádicas, los que son -admisibles.
Definición 15.
Definimos el funtor covariante a la categoría de –espacios vectoriales de dimensión finita como En el caso que diremos que es una representación de deRham.
El codominio del funtor anterior tiene estructuras -lineales adicionales (que vienen de la estructura adicional de la -álgebra ), específicamente una filtración -lineal que surge de la filtración –lineal en el campo de fracciones del anillo de valuación discreto completo sobre
Para el -espacio vectorial tiene estructura natural de objeto en Como tiene una filtración –lineal, estable dado por obtenemos una filtración –lineal, –estable en y este induce una filtración en de elementos –invariantes, explícitamente
6. Construcción de la Curva de Fargues-Fontaine.
La curva de Fargues–Fontaine es un objeto de la teoría de números descubierta en 2009 por Laurent Fargues y Jean Marc–Fontaine, donde en su geometría codifica mucha información sobre la aritmética de los números –ádicos. Se ha convertido rápidamente en un tema de investigación en la teoría de Hodge -ádica y el programa de Langlands.
En esta sección motivamos la definición de la curva usando una analogía con la esfera de Riemann. Luego, construimos la curva desde dos puntos de vista distintos, uno desde el punto de vista del álgebra conmutativa y otro desde los espacios de ‟Tilts y Untilts˝[16, 5].
6.1. La esfera de Riemann.
Para motivar la definición de la curva, analizaremos una curva más familiar, la esfera de Riemann , a la cual le podemos asociar anillos
-
Primero, el anillo de funciones meromorfas sobre sin polos fuera del punto al infinito es el álgebra de polinomios donde denota el parámetro local habitual en el origen.
-
Mirando los desarrollos de Laurent en el punto al infinito de todas las funciones meromórficas en encontramos el anillo donde es un parámetro local para el punto al infinito.
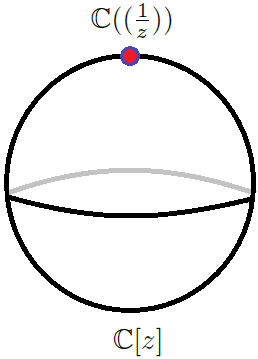
Recíprocamente, podemos reconstruir la esfera de Riemann a partir de los anillos
Más aún, si entonces
La idea de la curva de Fargues–Fontaine es emular la construcción de la esfera de Riemann con los anillos ; pero en los números –ádicos y usando a los anillos donde
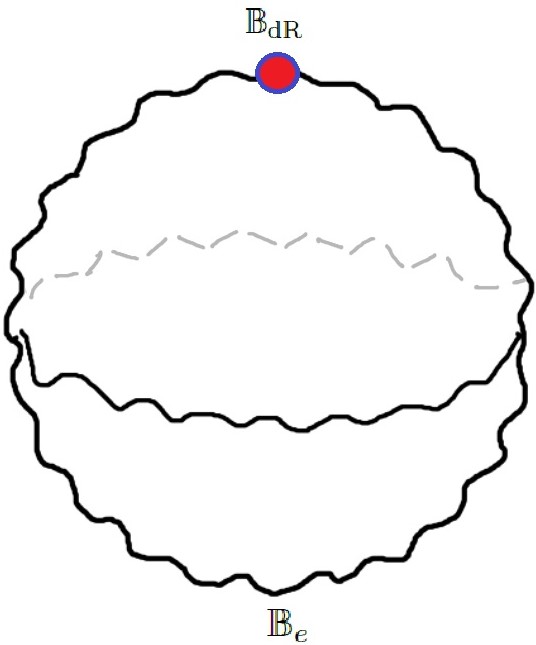
A esta curva la denotaremos como Concretamente, Fargues y Fontaine demostraron que [7]:
Teorema 16 (FF).
Existe un esquema regular, noetheriano, conexo, separado de dimensión uno, , sobre ; tal que tiene un punto al infinito y, el anillo de funciones meromorfas sin polos fuera del infinito es el anillo
En este caso, si entonces la curva de FF se define como Además, de manera análoga al caso de la esfera de Riemann, tenemos que:
6.2. Otro punto de vista: Tilts y Untilts.
A continuación presentamos otra forma de construir la curva de Fargues-Fontaine mediante lo llamados tilts y untilts. Esta sección está basado en la sección 2.1 de [15].
Sea un campo algebraicamente cerrado que contiene a y es completo respecto a un valor absoluto no arquimediano que extiende el valor absoluto -ádico en (Un ejemplo es los complejos -ádicos).
Definición 17.
El ‟tilt ˝ de es un campo algebraicamente cerrado que contiene a y es completo respecto a un valor absoluto no arquimediano no trivial
Como conjunto,
La multiplicación se define término a término y la suma como donde
Recíprocamente, sea con los hipótesis de la definición de tilt.
Definición 18.
Un ‟untilt˝de es un par donde es un campo algebraicamente cerrado que contiene a y es completo respecto a un valor absoluto no arquimediano que extiende el valor absoluto -ádico en y es un isomorfismo de campos valuados.
Decimos que dos untilts son equivalentes si existe un isomorfismo tal que el isomorfismo inducido entre sus tilts es compatible con y , es decir, si existe isomorfismo tal que el diagrama conmuta:
donde
Definición 19.
Sea el conjunto de clases de equivalencia de untilts de
Dado un untilt de podemos construir nuevos untilts para todo donde es el automorfismo de Fronbenius.
Definición 20.
Decimos que dos untilts son Frobenius equivalentes si existe tal que y son equivalentes.
Al conjunto de clases de equivalencia de untilts Frobenius equivalentes está dado por el cociente
donde el grupo cíclico infinito actúa en via
El siguiente resultado cuya demostración puede ser consultado en [15] nos dá la relación entre este conjunto de clase de equivalencia y las curva de Fargues-Fontaine.
Teorema 21.
Existe una curva cuyos puntos están en biyección con
7. La curva y las representaciones de Galois -ádicas.
En esta última sección se muestra la relación de la curva de Fargues-Fontaine, específicamente sus fibrados vectoriales, con las representaciones de Galois -ádicas, haciendo uso del teorema de Harder-Narasimhan. En los fibrados vectoriales se tiene lo siguiente:
Definición 22.
Sea una superficie de Riemann. Para cualquier fibrado vectorial de asociamos dos invariantes:
-
Su rango,
-
Su grado, definido como el grado de su ‟determinant line bundle˝. El grado de un fibrado lineal se define identificando a con un divisor de Weil y definimos
De los dos invariantes anteriores se define un tercero, su pendiente
Se dice que es semiestable si para todo subfibrado vectorial de
Enunciaremos ahora el teorema principal de este sección cuya demostración puede ser consultada en [15].
Teorema 23 (Harder-Narasimhan (H-N)).
Sea un fibrado vectorial de Entonces tiene una única filtración de sub-fibrados
tales que:
-
El fibrado cociente es semiestable para todo
-
En general hay otras categorías en las cuales existe un análogo al teorema de H-N. Mencionaremos alguna de estas.
-
Fibrados vectoriales de una curva
Sea una superficie de Riemann. Sea la categoría de fibrados en Equipado con las nociones definidas anteriormente de rango y grado, dicha categoría satisface el teorema H-N. -
Los pares -algebraicos completos. Antes de definir estos objetos necesitaremos la definición de una función casi euclidiana.
Definición 24.
Una función casi euclidiana de un dominio entero es una función que cumple las siguientes propiedades:
-
1.
-
2.
Para se tiene que
-
3.
Si entonces es unidad.
-
4.
Si con entonces existen tales que y
Definición 25.
Un par -algebraico es un par que consiste es un anillo de ideales principales y una valuación tal que es una función casi euclidiana en Decimos que el par el completo si
para todo donde corre sobre todos los ideales primos distintos del cero de y denota la valuación –ádica asociada en
Sea un par –algebraico completo. Un ‟fibrado vectorial en ˝se define como un par donde es un –módulo libre de rango finito y es un –retículo dentro del espacio vectorial de dimensión finita donde es la completación de respecto a y es el anillo de enteros.
-
•
El rango de es el rango del módulo
-
•
El grado se define comparando bases de y
Así, la categoría de fibrados vectoriales de un par -algebraico cumple el teorema H-N.
En particular, para el par -algebraico completo de la curva de Fargues-Fontaine, los –pares solo son llamados -pares. Aquí un fibrado vectorial es un par tal que-
•
es un –módulo libre de rango finito.
-
•
es un –retículo dentro de
La siguiente proposición relaciona las dos categorías antes mencionadas. Su demostración puede ser consultada en [15].
Proposición 26.
La categoría de –pares se identifica con la categoría de fibrados vectoriales de la curva de Fargues–Fontaine.
-
1.
-
Espacios vectoriales con filtraciones.
Dada una extensión de campos sea la categoría de pares donde es un –espacio vectorial de dimensión finita y es una filtración en separada y exhaustiva.-
•
-
•
Así, esta categoría cumple con el teorema H-N.
-
•
-
Isocristales.
Sea campo perfecto de característica y Un isocristal sobre es un par donde es un –espacio vectorial de dimensión finita y es un isomorfismo –semilineal (esto es, para todo y )-
•
-
•
donde de un isocristal de rango uno se define escogiendo un elemento básico luego para algún y ya que es campo de valuación discreta.
Así, esa categoría cumple con el teorema de H-N. A esta categoría se le suele denotar como
Sea donde y Podemos definir un isocristal como
-
•
con elementos básicos
-
•
como el único endomorfismo semilineal que satisface:
El isocristal tiene rango grado y pendiente
Lema 27.
Sea isocristal sobre Entonces el par
es un fibrado vectorial con rango y grado dado por el rango y grado del isocristal.
Este lema asocia a un isocristal fibrado un fibrado vectorial en denotado por En particular, en el caso del isocristal con escribimos Por el lema, tiene rango grado y pendiente si con y
Teorema 28 (De clasificación de fibrados vectoriales en ).
Sea un fibrado vectorial en Entonces existe una única sucesión de racionales tales que es isomorfo a
Corolario 29.
-
•
El funtor es esencialmente sobreyectivo.
-
•
Sea un fibrado vectorial de y Entonces es semiestable de pendiente si y sólo si es isomorfo a para algún
-
•
La categoría de fibrados vectoriales de semiestables y de pendiente cero equivalente a la categoría de –espacios vectoriales de dimensión finita vía
-
•
-
Esta es la categoría de los tripletes donde-
•
es un –espacio vectorial de dimensión finita.
-
•
isomorfismo -lineal.
-
•
es una filtración en separada y exhaustiva.
Es decir, y Definimos:
-
•
-
•
De esta forma, esta categoría cumple con el teorema de H-N.
-
•
Como si es representación cristalina entonces es de deRham y Así el funtor
es completamente fiel.
Fontaine conjeturó que todo isocristal filtrado estaba en la imagen esencial de si y sólo si era débilmente admisible [7, Capítulo 8: classification des fibrés vectoriels: le cas algébriquement clos] , que en este caso, es equivalente a pedir que sea semiestable y de pendiente cero. Esto demuestra que
donde denota ‟weakly admissible˝(débilmente admisible) es una equivalencia de categorías. También es posible demostrar que la categoría de representaciones semiestables se puede describir como isocristales filtrados débilmente admisibles con operador de monodromía [7].
Finalmente, hemos llegado a uno de los objetivos de la teoría de Hodge -ádica, describir clases de representaciones de Galois -ádicas en términos de pura álgebra lineal.
8. Epílogo
El estudio de la curva de Fargues-Fontaine es actualmente un tema de investigación muy activo dentro del área de la geometría aritmética. Trabajos como los de Peter Scholze de perfectoides [19] o de Fargues respecto al programa de Langlands [12] son muestra del actual avance en este tópico. Otro punto de vista que particularmente estamos estudiando son los sistemas dinámicos de funciones racionales sobre la curva: estudiar puntos periódicos o los conjuntos de Fatou y Julia podrían llevarnos a descubrir aún más información acerca de este objeto matemático tan importante.
AGRADECIMIENTOS
El primer autor expresa su gratitud a CONAHCyT por la beca obtenida para estudiar el doctorado en el CIMAT y con el cual fue posible el desarrollo del presente artículo.
Referencias
- [1] Olivier Brinon and Brian Conrad. Cmi summer school notes on p-adic hodge theory. (2009).
- [2] Laurent Berger. Construction de (phi, gamma)-modules: représentations p-adiques et b-paires. Algebra and Number Theory, 2(1):91-120, (2008).
- [3] Xavier Caruso. An introduction to p-adic period rings. (2019).
- [4] CIMPA. Research school on hodge theory and p-adic hodge theory, (2021).
- [5] Pierre Colmez. Le programme de fontaine. L’Enseignement Mathématique, 65(3/4):487-531, (2019).
- [6] Gerd Faltings. p-adic hodge theory. J. Amer. Math. Soc, 1(1):255-299, (1988).
- [7] Laurent Fargues and Jean Marc Fontaine. Courbes et fibrés vectoriels en théorie de Hodge p-adique. Société mathématique de France, (2018).
- [8] Jean Marc Fontaine and Luc Illusie. p-adic periods: A survey. Université de Paris-sud, Département de mathématiques, (1990).
- [9] J-M Fontaine. p-adic periods and p-adic étale cohomology. In Current trends in arithmetical algebraic geometry, Proceedings of the AMS-IMS-SIAM joint summer research conference, Humboldt State Univ., Arcata, Calif., 1985, pages 179-207. Amer. Math. Soc., (1987).
- [10] Jean-Marc Fontaine. Le corps des périodes p-adiques. Astérisque, 223:59-111, (1994).
- [11] Jean-Marc Fontaine. Représentations p-adiques semi-stables. Astérisque, 223:113-184, (1994).
- [12] Laurent Fargues and Peter Scholze. Geometrization of the local langlands correspondence. arXiv preprint arXiv:2102.13459, (2021).
- [13] Serin Hong. Notes on p-adic hodge theory. (2020).
- [14] Maxim Kontsevich and Don Zagier. Periods. Springer, (2001).
- [15] Matthew Morrow. The Fargues-Fontaine curve and diamonds. Séminaire BOURBAKI, (1150), (2018).
- [16] Matthew Morrow. Raconte moi. . . la courbe de Fargues-Fontaine. Gazette des Mathematiciens, (163):36-41, (2020).
- [17] Jesus Rogelio Perez Buendia. A crystalline criterion for good reduction on semi-stable k3-surfaces over a p-adic field. PhD thesis, Concordia University, (2014).
- [18] J. Rogelio. Pérez-Buendía. Curse: p-adic galois representations. https://youtu.be/-KoXxop6X1Y?feature=shared, CIMPA Research School on Hodge Theory and p-adic Hodge Theory. Online, CIMAT-Gto, México, (2021)
- [19] Peter Scholze. Perfectoid spaces and their applications. In Proceedings of the ICM, volume 2014, (2014).
- [20] Jean-Pierre Serre. Local Fields. Graduate Texts in Mathematics;67. Springer Verlag New York Inc, (1979).
- [21] O. Hyodo and K. Kato, “Semi-stable reduction and crystalline cohomology with logarithmic poles,” Astérisque, vol. 223, pp. 221–268, 1994, [Paris: Société Mathématique de France, 1973-].
| Dirección del autor: |
|---|
| Centro de Investigación en Matemáticas (CIMAT), |
| Unidad Mérida, |
| Parque Científico y Tecnológico de Yucatán Km 5.5 Carretera Sierra Papacal |
| Chuburná Puerto Sierra Papacal; CP 97302, Mérida, Yucatán. |
| e-mail: jorge.robles@cimat.mx |
| Dirección del coautor: |
|---|
| Centro de Investigación en Matemáticas (CIMAT), |
| Unidad Mérida, |
| Parque Científico y Tecnológico de Yucatán Km 5.5 Carretera Sierra Papacal |
| Chuburná Puerto Sierra Papacal; CP 97302, Mérida, Yucatán. |
| e-mail: rogelio.perez@cimat.mx |