La ecuación de Burgers como un paso previo al estudio de los fluidos incompresibles

Rafael Granero Belinchón

{}^{\mbox{{\footnotesize 1}}}

y José Manuel Moreno Valderrama

{}^{\mbox{{\footnotesize 2}}}

Resumen

En este artículo se presentan las ecuaciones de Euler y de Navier-Stokes, las más básicas de las ecuaciones de los fluidos incompresibles, así como unos modelos simplificados de dichos problemas como pueden ser la ecuación quasigeostrófica u otros escalares activos. Las técnicas matemáticas para obtener que estas ecuaciones están bien puestas en el sentido de Hadamard y otras propiedades cualitativas (Principios del Máximo, formación de singularidades…) se ilustran en el caso sensiblemente más sencillo de la ecuación de Burgers con disipación no-local. Se adjunta una sección dedicada a los métodos numéricos usados para aproximar soluciones a estos problemas. Este trabajo tiene su origen en una serie de clases que impartimos en la escuela JAE-Intro del CSIC durante el verano del curso 2010-2011 y por lo tanto se centra en la popularización y divulgación de la física involucrada y en la explicación detallada de las ideas más abstractas en los argumentos puramente matemáticos.

¹¹footnotetext: Email: r.granero@icmat.es
Consejo Superior de Investigaciones Científicas
Instituto de Ciencias Matemáticas (CSIC-UAM-UC3M-UCM)
C/Nicolás Cabrera, 13-15,
Campus de Cantoblanco,
28049 - Madrid²²footnotetext: Email: josemanuel.moreno@estudiante.uam.es
Universidad Autónoma de Madrid
Campus de Cantoblanco,
28049 - Madrid

Palabras clave: Ecuaciones de Euler, ecuaciones de Navier-Stokes, ecuación quasi-geostrófica, medios porosos, Ley de Darcy, interfase.

Agradecimientos: R.Granero está financiado por el proyecto MTM2008-03754 del Ministerio de Ciencia e Innovación (MICINN).

1 Introducción y motivación

El estudio de las ecuaciones de los fluidos incompresibles tiene cada vez un mayor interés, tanto desde el punto de vista más teórico (integrales singulares…) como desde el enfoque más aplicado (simulaciones numéricas…).

Las ecuaciones que aparecen modelizando problemas de mecánica de fluidos son variadas, pero las más importantes son las de Euler y Navier-Stokes. De hecho por demostrar (o refutar) la existencia global de solución clásica para Navier-Stokes el Instituto Clay otorga un premio de un millón de dólares.

Consideramos como dominio espacial el plano o el espacio enteros, $i\mathchar 314\relax e\mathchar 314\relax\;\mathbb{R}^{d}$ con $d=2,3$ y exigimos que la velocidad del fluido sea cero en el infinito. Sea además $f$ el campo de velocidades inicial. Entonces las ecuaciones de Euler (1707-1783) para la velocidad $u$ de un fluido incompresible son

\left\{\begin{array}[]{l}\stackrel{{\scriptstyle\text{Masa}}}{{\overbrace{\rho}}}\stackrel{{\scriptstyle\text{Aceleraci\'{o}n}}}{{\overbrace{(\partial_{t}u+(u\cdot\nabla)u)}}}=\stackrel{{\scriptstyle\text{Fuerzas internas}}}{{\overbrace{-\nabla p}}}+\stackrel{{\scriptstyle\text{Fuerzas externas}}}{{\overbrace{F}}}\;\;(\text{Conservaci\'{o}n del momento}),\\ \nabla\cdot u=0,\;\;(\text{Conservaci\'{o}n de la masa})\mathchar 314\relax\end{array}\right\mathchar 314\relax

(1)

con $\nabla=(\partial_{x_{1}},\mathchar 314\relax\mathchar 314\relax\mathchar 314\relax,\partial_{x_{d}})$ y $u=(u_{1},\mathchar 314\relax\mathchar 314\relax\mathchar 314\relax,u_{d})$ . Este sistema de ecuaciones es la segunda ley de Newton en el caso de un continuo de partículas.

Las ecuaciones de Navier (1785-1836) y Stokes (1819-1903) para un fluido incompresible con densidad $\rho$ son

\left\{\begin{array}[]{l}\stackrel{{\scriptstyle\text{Masa}}}{{\overbrace{\rho}}}\stackrel{{\scriptstyle\text{Aceleraci\'{o}n}}}{{\overbrace{(\partial_{t}u+(u\cdot\nabla)u)}}}=\stackrel{{\scriptstyle\text{Fuerzas internas}}}{{\overbrace{-\nabla p+\nu\Delta u}}}+\stackrel{{\scriptstyle\text{Fuerzas externas}}}{{\overbrace{F}}}\;\;(\text{Conservaci\'{o}n del momento}),\\ \nabla\cdot u=0,\;\;(\text{Conservaci\'{o}n de la masa}),\end{array}\right\mathchar 314\relax

(2)

donde $\Delta=\sum_{i=1}^{d}\partial_{x_{i}}^{2}$ .

En las ecuaciones de Navier-Stokes se ha añadido el rozamiento entre partículas del fluido modelizándolo con un laplaciano.

Observamos que es un sistema de evolución ’extraño’ en el sentido de que la derivada temporal de la presión $p$ no aparece. Eso nos indica que la presión se puede obtener de la velocidad $u$ . Para ver esto basta tomar la divergencia de la ecuación de conservación del momento,

\nabla\cdot((u\cdot\nabla)u)=-\Delta p\mathchar 314\relax

Ahora podemos utilizar la función de Green para el Laplaciano (que para $\mathbb{R}^{d}$ es conocida) y obtener $p=G(u)$ . Tomamos el gradiente en esta expresión y obtenemos un sistema de ecuaciones no-locales cerrado para $u$ (donde ahora nos restringimos a velocidades incompresibles). Además hemos obtenido que la presión actúa como un multiplicador de Lagrange para la restricción $\nabla\cdot u=0$ . Los resultados de los que se dispone cierran la teoría en $d=2$ . En el plano se conoce la existencia global (en tiempo) de soluciones clásicas. Para el problema completo $d=3$ se tiene un teorema de existencia local (en tiempo) de solución clásica (ver [19]). Esta diferencia es porque las ecuaciones en los casos bidimensional y tridimensional son sensiblemente distintas. Para verlo necesitamos definir una cantidad que nos de información sobre cuánto ’gira’ el fluido. Esta cantidad que denotaremos $\omega$ se llama vorticidad y es el rotacional de la velocidad, $i\mathchar 314\relax e\mathchar 314\relax$

\text{rot }u=\omega,

con $u$ el campo de velocidades del fluido. En concreto se tiene que las ecuaciones para la vorticidad son distintas: para un fluido no viscoso e incompresible¹¹1Estos fluidos se conocen como fluidos ideales., es decir, que sigue las ecuaciones de Euler, en el caso $d=2$ se tiene

\partial_{t}\omega+u\cdot\nabla\omega=0,

(3)

que es una ecuación de transporte, mientras que en el caso $d=3$ se tienen las siguientes ecuaciones

\partial_{t}\omega+(u\cdot\nabla)\omega=(\omega\cdot\nabla)u\mathchar 314\relax

(4)

En el caso de considerar un fluido viscoso se ha de añadir un término $\Delta\omega$ .

La diferencia entre ambos casos aparece también en las longitudes de onda que están íntimamente relacionadas con el fenómeno de la ’turbulencia’ (ver [13]). La turbulencia tiene como efecto principal facilitar que dos fluidos se mezclen, por lo tanto, llegados a este punto podemos ’experimentar’ un teorema. Para este pequeño juego necesitamos dos vasos pequeños llenos hasta arriba uno de ellos de agua y el otro de vino. La cuestión es: ¿cómo conseguimos cambiar los líquidos de vaso sin usar un tercer recipiente y sin que se mezclen? Para responder a esta pregunta hemos de conocer cómo es la turbulencia en tres dimensiones y qué diferencia hay con dos dimensiones. Así, si conseguimos una manera de reducir el problema tridimensional a uno bidimensional hemos acabado, porque en dos dimensiones ’no hay turbulencia’ y ésta es la culpable de que los líquidos se mezclen. Para conseguir esta reducción en las dimensiones lo que hacemos es tapar el vaso de agua con un carné y colocarlo con cuidado encima del vaso de vino. Si lo hemos hecho bien no se ha salido ni una gota. Ahora abrimos una rendija minúscula entre los vasos y el carné. El agua es más densa, por lo tanto comenzará a bajar mientras que el vino subirá…¡y todo esto sin mezclarse! (ver Figura 1)

Refer to caption — Figura 1: Experimento.

Tras esta excursión por las ciencias experimentales volvamos a las matemáticas. La vorticidad $\omega$ es una cantidad que aparece en el conocido criterio de existencia global de Beale-Kato-Majda (ver [4]).

Teorema 1 (Beale-Kato-Majda).

Sean $T^{*}$ y $M$ dos constantes tales que

\int_{0}^{T}||\omega||_{L^{\infty}}\leq M\;\;\forall T<T^{*},

entonces una solución clásica de las ecuaciones de Euler (1) existe al menos hasta tiempo $T^{*}$ . Además, si $T^{max}$ es el tiempo máximo de existencia (es decir, aparece una singularidad), entonces

\mathop{\operator@font l\acute{{\imath}}m}_{T\rightarrow T^{max}}\int_{0}^{T}||\omega||_{L^{\infty}}\rightarrow\infty\mathchar 314\relax

Este teorema nos dice que si controlamos ’lo que gira’ el fluido entonces no hay singularidades, por lo tanto conocer cómo se comporta la vorticidad es crucial para intentar entender qué hace el fluido. En efecto, también es interesante porque si la conocemos podemos recuperar la velocidad gracias a la fórmula de Biot-Savart (ver [3]). En el caso bidimensional la ley de Biot-Savart es

u=\int_{\mathbb{R}^{2}}K(x-y)\omega(y)dy=K(\omega),

(5)

con

K(x)=\frac{1}{2\pi}\left(\frac{-x_{2}}{|x|^{2}},\frac{x_{1}}{|x|^{2}}\right)\mathchar 314\relax

Ahora bien, con lo que acabamos de mencionar podemos ver que el problema de las ecuaciones de Euler (1) en el caso bidimensional podemos formularlo de manera equivalente como un ’escalar activo’, es decir, un escalar que es transportado por el fluido de manera que además podemos recuperar la velocidad del fluido si conocemos el escalar. En efecto: recordemos que teníamos la ecuación para la vorticidad (que en dos dimensiones es un escalar) (3), esto unido a $u=K(\omega)$ cierra el problema para la vorticidad. Además si asumimos que nuestro dato inicial está acotado, usando el Teorema 1, tenemos que la solución clásica del sistema (1) existe globalmente.

El estudio matemático de los escalares activos tiene una gran relevancia en cuanto que son sistemas sencillos que conservan el carácter no local de un fluido incompresible. Además de que hay multitud de aplicaciones donde el problema físico se puede modelizar con un escalar activo. Por ejemplo tenemos el caso de la ecuación Quasigeostrófica (ver [5], [8], [16], [7] y las referencias allí expuestas) o de la Ley de Darcy (ver [10],[11], [12], [9], [1], [20]). La ecuación quasigeostrófica modeliza la evolución de la temperatura de grandes masas de aire en grandes escalas espaciales y es muy estudiada como modelo de la ’frontogénesis’ (la formación de frentes de aire a distinta temperatura). Este problema es de interés en meteorología, porque ya se sabe que

La falta de acierto de quienes predicen el tiempo se ha hecho ya proverbial, y sin embargo no hay ningún meteorólogo competente que no opine que los procesos atmosféricos están causalmente determinados.

Max Planck (extraído de [21])

La ecuación quasigeostrófica en dos dimensiones espaciales es

\left\{\begin{array}[]{l}\partial_{t}\theta+u\cdot\nabla\theta=0,\\ u=R^{\perp}u=(-R_{2}\theta,R_{1}\theta),\end{array}\right\mathchar 314\relax

(6)

donde $R_{i}$ es la transformada de Riesz $i-$ ésima (ver [22]) y $\theta$ es la temperatura del aire.

La Ley de Darcy modeliza un fluido incompresible que se mueve a bajas velocidades por un medio poroso. Así si $\rho(x,t)$ es la densidad del fluido se tiene el problema

\left\{\begin{array}[]{l}\partial_{t}\rho+u\cdot\nabla\rho=0,\\ u=-(\nabla p+ge_{2}\rho),\\ \nabla\cdot u=0\mathchar 314\relax\end{array}\right\mathchar 314\relax

Este problema puede reducirse a un escalar activo tomando el rotacional dos veces en la ecuación, obteniendo

\left\{\begin{array}[]{l}\partial_{t}\rho+u\cdot\nabla\rho=0,\\ u=(-\Delta)^{-1}(\text{rot rot }ge_{2}\rho)\mathchar 314\relax\\ \end{array}\right\mathchar 314\relax

(7)

Podemos modelizar la transferencia de calor interno del fluido en un medio poroso con la misma ecuación (7) si a $\rho$ le damos el sentido de una temperatura (ver [2]). Por lo tanto, tanto en el caso de la ecuación (6) y de (7) puede interesarnos añadir un término de difusión del calor. Sin embargo estos términos de difusión no tienen por qué ser el típico laplaciano, puede ser necesario añadir una ’potencia fraccionaria del laplaciano’. El laplaciano en el espacio de Fourier (con variables $\xi$ ) tiene una expresión sencilla, es un multiplicador:

\widehat{-\Delta u}=|\xi|^{2}\hat{u}\mathchar 314\relax

Podemos definir el operador $\Lambda=\sqrt{-\Delta}$ de la siguiente manera

\widehat{\Lambda u}=|\xi|\hat{u},

(8)

y equivalentemente

\widehat{\Lambda^{\alpha}u}=|\xi|^{\alpha}\hat{u}\mathchar 314\relax

(9)

Notemos que también podemos escribir el resultado de aplicar el laplaciano fraccionario como la siguiente convolución:

\Lambda^{\alpha}u(x)=\beta({\alpha},d)\text{P.V.}\int_{\mathbb{R}^{d}}\frac{u(x)-u(y)}{|x-y|^{d+\alpha}}dy

(10)

donde $\beta(\alpha,d)$ es una constante de normalización. Los operadores (8) y (9) (o su versión (10)) son lo que nosotros entendemos por ’potencias fraccionarias del laplaciano’. Así las ecuaciones (6) y (7) con difusión no local son

\left\{\begin{array}[]{l}\partial_{t}\theta+u\cdot\nabla\theta=-\gamma\Lambda^{\alpha}\theta,\\ u=R^{\perp}u=(-R_{2}\theta,R_{1}\theta),\end{array}\right\mathchar 314\relax

(11)

\left\{\begin{array}[]{l}\partial_{t}\rho+u\cdot\nabla\rho=-\gamma\Lambda^{\alpha}\rho,\\ u=(R_{1}R_{2},-R_{1}^{2})\rho\mathchar 314\relax\\ \end{array}\right\mathchar 314\relax

(12)

Para irnos aproximando a estos problemas podemos plantearnos otros más sencillos o simplificados. Por ejemplo, consideremos un escalar activo

\left\{\begin{array}[]{l}\partial_{t}\eta+u\cdot\nabla\eta=-\gamma\Lambda^{\alpha}\eta,\\ u=T(\eta),\\ \end{array}\right\mathchar 314\relax

(13)

donde $T$ es un operador integral singular que además nos garantiza que $\nabla\cdot u=0$ . Queremos simplificar este problema de manera que sea fácilmente abordable, pero no tiene que estar tan simplificado que no nos de ninguna información. Lo primero que hacemos es reducir el número de variables espaciales a una, por lo tanto $\nabla=\partial_{x}$ . Además podemos simplificar $T$ tomándolo igual a la identidad, es decir, pierde su carácter integral singular. La ecuación resultante de estas simplificaciones es la ecuación de Burgers viscosa si $\gamma>0$ y la ecuación de Burgers no viscosa si $\gamma=0$ (ver [17] y [14]):

\partial_{t}\eta+\eta\partial_{x}\eta=-\gamma\Lambda^{\alpha}\eta\mathchar 314\relax

(14)

Como la condición $\nabla\cdot u=0$ en una dimensión no tiene sentido físico (en una dimensión no hay choques) con esta ecuación tenemos un modelo unidimensional de las ecuaciones (1) y (2). Así nuestra ecuación (14) es el modelo más sencillo que nos da información tanto sobre las ecuaciones (1), (2) como (13).

Este texto está organizado de la siguiente manera: en la sección 2 probaremos la existencia local de solución clásica para toda la familia de ecuaciones (14). En la sección 3 obtendremos una ley de conservación y unos principios del máximo que se tienen para las soluciones clásicas de la ecuación (14). En la sección 4 daremos un criterio de existencia de solución clásica análogo al de Beale-Kato-Majda. En la sección 5 veremos que hay blow up para $\gamma=0$ en (14) y en la sección 6 haremos simulaciones numéricas de la solución de (14).

2 Existencia local de la solución clásica

El problema que estudiaremos en esta sección y las siguientes es la ecuación (14) (donde cambiamos la notación $\eta$ por la más corriente $u$ ):

\left\{\begin{array}[]{l}\partial_{t}u+u\partial_{x}u=-\gamma\Lambda^{\alpha}u,\;\;(t,x)\in[0,T]\times\mathbb{R}\\ u(0,x)=f(x),\\ \end{array}\right\mathchar 314\relax

(15)

donde $T>0$ es el tiempo de existencia, $0<\alpha\leq 2$ y $\gamma\geq 0$ . Sobre el dato inicial impondremos las condiciones necesarias cuando veamos el teorema de existencia local, pero por el momento podemos suponer que $f\in C^{2}$ . Nos restringiremos a las soluciones clásicas o soluciones fuertes. Este tipo de soluciones es tan suave como sea necesario para dar el sentido usual a las derivadas parciales que aparecen en la ecuación. Así para la ecuación de Burgers queremos que $u$ tenga al menos una derivada en $t$ y dos en $x$ . Es decir, queremos que $u\in C^{2,1}_{x,t}$ .

En esta sección probaremos la existencia local de solución clásica para la ecuación (15) con $\gamma\geq 0$ y $\alpha\in(0,2]$ si el dato inicial está en un cierto espacio de funciones. Para ello utilizaremos el método de la energía de Leray (ver [19]). El argumento de Leray ya es un argumento clásico. Nosotros trataremos de aplicarlo con todo detalle en el ejemplo sencillo de la ecuación (15).

La idea del método es conseguir una sucesión de problemas regularizados para la ecuación (15). Para todos los problemas regularizados se demuestra la existencia utilizando el Teorema de Picard en un espacio de Banach adecuado. Se concluye el argumento observando que la familia de soluciones regularizadas forma una sucesión de Cauchy, y por lo tanto convergente en algún espacio. El espacio de Banach que vamos a usar es $H^{s}(\mathbb{R})$ , $s\geq 3$ porque utilizando la inmersión de Sobolev tenemos que entonces $u\in C^{2}(\mathbb{R})$ .

2.1 Estimaciones a priori

Para utilizar el método de Leray hemos de conseguir unas cotas a priori para ciertas cantidades. Es decir, suponiendo que hay solución.

Si pensamos en $u$ como en la velocidad de un fluido incompresible nos interesa conocer qué ocurre con la ’energía cinética’ del fluido, es decir, la norma $L^{2}$ de $u$ .

Proposición 1 (Principio del máximo para $||\cdot||_{L^{2}}$ ).

Sea $u$ una solución clásica de (15). Entonces se tiene que:

a)

Si $\gamma=0$ ,

$||u||_{L^{2}}(t)=||f||_{L^{2}},$
b)

Si $\gamma>0$ ,

$||u||_{L^{2}}(t)\leq||f||_{L^{2}}\mathchar 314\relax$

Demostración.

Observamos que

\frac{1}{2}\frac{d}{dt}||u||^{2}_{L^{2}}=\int_{\mathbb{R}}u\partial_{t}udx=-\int_{\mathbb{R}}u^{2}\partial_{x}udx-\gamma\int_{\mathbb{R}}u\Lambda^{\alpha}udx\\ =-\frac{1}{3}\int_{\mathbb{R}}\partial_{x}(u^{3})dx-\gamma\int_{\mathbb{R}}\Lambda^{\alpha}uudx=-\gamma\int_{\mathbb{R}}\Lambda^{\alpha}uudx\mathchar 314\relax

De aquí se concluye la parte a) del resultado. Para obtener la parte b) hemos de utilizar el Teorema de Plancherel:

\int_{\mathbb{R}}\Lambda^{\alpha}uudx=\int_{\mathbb{R}}|\xi|^{\alpha}\hat{u}\bar{\hat{u}}d\xi=\int_{\mathbb{R}}\left(\Lambda^{\alpha/2}u\right)^{2}dx\mathchar 314\relax

De esta última igualdad (que no es más que la prueba de que el operador $\Lambda^{\alpha}$ es simétrico) se concluye el resultado. ∎

En el caso de que la solución $u$ no sea lo bastante regular como para ser solución clásica entonces la norma $L^{2}$ no se conserva. Esto en las ecuaciones de Euler es una serie de celebrados artículos (ver [18]). Las soluciones débiles de (1) en tres dimensiones o de (15) con $\gamma=0$ no siempre tienen sentido físico. Lo que implica físicamente es que un fluido perfecto que estuviese inicialmente en reposo puede comenzar a agitarse a lo loco sin haber mediado fuerza externa alguna, siempre y cuyo la velocidad $u$ no tenga la suficiente regularidad como para ser solución clásica. Matemáticamente esta ’paradoja’ física se traduce en que no hay unicidad de soluciones débiles para el sistema de ecuaciones (1) en tres dimensiones. En el caso de (15) sin viscosidad ( $\gamma=0$ ) lo que ocurre es que se da un choque de curvas características y después no hay una manera única de continuar la solución. Enlaza esto con las condiciones de Rankine-Hugoniot y las soluciones de entropía (ver [15]). Además, si consideramos el problema viscoso

\partial_{t}u^{\gamma}+u^{\gamma}\partial_{x}u^{\gamma}=-\gamma\Lambda^{\alpha}u^{\gamma},

pero tomamos $\gamma\rightarrow 0$ recuperamos la solución de entropía para la ecuación de Burgers no viscosa como límite, es decir, $u^{0}=\mathop{\operator@font l\acute{{\imath}}m}_{\gamma\rightarrow 0}u^{\gamma}$ (ver Figura 2).

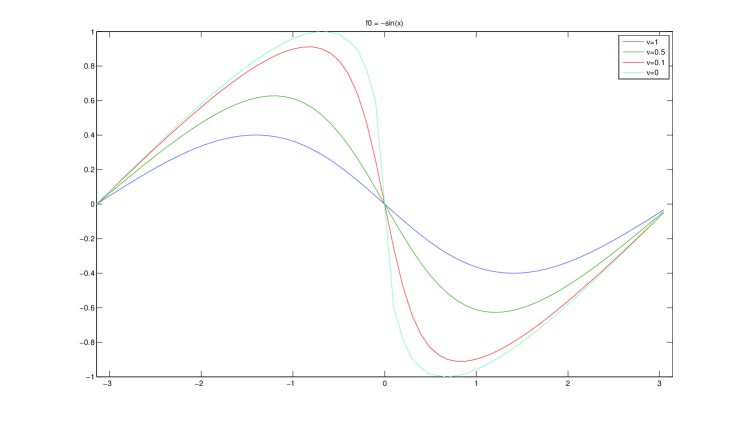
Ya tenemos una cota a priori para la norma $L^{2}$ . Como mencionamos antes queremos que nuestra solución esté en el espacio de Sobolev $H^{3}$ , por lo que sólo falta estimar la norma $L^{2}$ de $\partial_{x}^{3}u$ .

Proposición 2.

Sea $u$ una solución clásica del problema (15) con un dato inicial $f\in H^{3}(\mathbb{R})$ . Entonces se tiene la siguiente cota

||u||_{H^{3}}(t)\leq\frac{||f||_{H^{3}}}{1-c||f||_{H^{3}}t}\mathchar 314\relax

(16)

Demostración.

Se tiene que

\frac{1}{2}\frac{d}{dt}||\partial_{x}^{3}u||^{2}_{L^{2}}=\int_{\mathbb{R}}\partial_{x}^{3}u\partial_{x}^{3}\partial_{t}udx,

por lo que hemos de derivar tres veces la ecuación (15), obteniendo

\partial_{x}^{3}\partial_{t}u=-\gamma\Lambda^{\alpha}\partial_{x}^{3}u-3(\partial_{x}^{2}u)^{2}+4\partial_{x}u\partial_{x}^{3}u+u\partial_{x}^{4}u\mathchar 314\relax

Introducimos esta expresión en nuestra expresión y logramos

	$\displaystyle\frac{1}{2}\frac{d}{dt}\|\|\partial_{x}^{3}u\|\|^{2}_{L^{2}}$	$\displaystyle=$	$\displaystyle-\gamma\int_{\mathbb{R}}\partial_{x}^{3}u\Lambda^{\alpha}\partial_{x}^{3}udx-3\int_{\mathbb{R}}(\partial_{x}^{2}u)^{2}\partial_{x}^{3}udx+\int_{\mathbb{R}}4\partial_{x}u(\partial_{x}^{3}u)^{2}dx$
			$\displaystyle+\int_{\mathbb{R}}u\partial_{x}^{4}u\partial_{x}^{3}udx=I_{1}+I_{2}+I_{3}+I_{4}\mathchar 314\relax$

Usando el Teorema de Plancherel se obtiene que

I_{1}=-\gamma\int_{\mathbb{R}}|\xi|^{\alpha}\hat{\partial_{x}^{3}u}\bar{\hat{\partial_{x}^{3}u}}d\xi=-\gamma\int_{\mathbb{R}}\left(\Lambda^{\alpha/2}\partial_{x}^{3}u\right)^{2}dx=-\gamma||\Lambda^{\alpha/2}\partial_{x}^{3}u||_{L^{2}}^{2}\leq 0\mathchar 314\relax

La segunda integral se anula por las condiciones de borde impuestas

I_{2}=-\int_{\mathbb{R}}\partial_{x}\left[(\partial_{x}^{2}u)^{3}\right]=0\mathchar 314\relax

Las integrales que faltan son las más singulares por tener el mayor número de derivadas, sin embargo sólo nos hemos de preocupar de $I_{3}$ , porque $I_{4}$ es igual. En efecto

I_{4}=\frac{1}{2}\int_{\mathbb{R}}u\partial_{x}\left[(\partial_{x}^{3}u)^{2}\right]=-\frac{1}{2}\int_{\mathbb{R}}\partial_{x}u(\partial_{x}^{3}u)^{2}\mathchar 314\relax

Por lo tanto sólo hemos de acotar la integral $I_{3}$ . Se tiene que

I_{3}\leq c||\partial_{x}u||_{L^{\infty}}||\partial_{x}^{3}u||_{L^{2}}^{2}\leq||u||_{H^{3}}^{3},

y concluímos que

\frac{d}{dt}||\partial_{x}^{3}u||^{2}_{L^{2}}\leq c||u||_{H^{3}}^{3}\mathchar 314\relax

Usando la Proposición 1 obtenemos

\frac{d}{dt}||u||_{H^{3}}\leq c||u||_{H^{3}}^{2}\mathchar 314\relax

Sin más que integrar la EDO se concluye la primera parte del resultado. ∎

Comentario 1 Es más, si $f\in H^{k}(\mathbb{R})$ , $k>3$ se tiene la siguiente cota

||u||_{H^{k}}(t)\leq\frac{||f||_{H^{k}}}{1-c||f||_{H^{k}}t}\mathchar 314\relax

(17)

2.2 Regularización del problema

Consideremos una función $\rho\in C^{\infty}_{c}$ , $\rho(x)=\rho(|x|)$ , $\rho\geq 0$ y $\int_{\mathbb{R}}\rho=1$ . Un ejemplo de tal $\rho$ puede ser la función

\rho(x)=\frac{e^{-\frac{1}{1-x^{2}}}}{\int_{-1}^{1}e^{-\frac{1}{1-y^{2}}}dy}\mathchar 314\relax

Ahora, para cualquier $\epsilon$ positivo, consideramos las funciones

\rho_{\epsilon}=\frac{1}{\epsilon}\rho\left(\frac{x}{\epsilon}\right)\mathchar 314\relax

(18)

Observamos que $\rho_{\epsilon}$ siguen teniendo las mismas propiedades que $\rho$ . Dada una función $g\in L^{p}$ , si ahora hacemos la convolución $g_{\epsilon}=\rho_{\epsilon}*g$ , obtenemos que $g_{\epsilon}\in C^{\infty}$ y, gracias a la desigualdad de Young:

||\rho_{\epsilon}*g||_{L^{r}}\leq||\rho_{\epsilon}||_{L^{q}}||g||_{L^{p}},\quad\frac{1}{r}+1=\frac{1}{p}+\frac{1}{q},

(19)

tenemos que

||\rho_{\epsilon}*g||_{L^{p}}\leq||g||_{L^{p}}\mathchar 314\relax

Además $\mathop{\operator@font l\acute{{\imath}}m}_{\epsilon\rightarrow 0}g_{\epsilon}=g$ . Pueden verse más propiedades de estos núcleos $\rho_{\epsilon}$ en [3].

El primer paso del método es regularizar el problema de manera que podamos demostar existencia de los problemas regularizados y también podamos usar las estimaciones a priori. Para ello utilizarmos la convolución con $\rho_{\epsilon}$ . Así consideramos la familia de problemas

\left\{\begin{array}[]{l}\partial_{t}u_{\epsilon}=-\rho_{\epsilon}*\left(\rho_{\epsilon}*u_{\epsilon}\right)\partial_{x}\left(\rho_{\epsilon}*u_{\epsilon}\right)-\rho_{\epsilon}*\left(\gamma\Lambda^{\alpha}\rho_{\epsilon}*u_{\epsilon}\right),\;\;(t,x)\in[0,T]\times\mathbb{R},\epsilon>0\\ u_{\epsilon}(0,x)=f(x)\mathchar 314\relax\\ \end{array}\right\mathchar 314\relax

(20)

Esta regularización particular se ha elegido pensando en obtener las mismas estimaciones de la Proposición 17. Por ser $\rho_{\epsilon}$ una función radial tenemos que

\int f\rho_{\epsilon}*g=\int\int f(x)\rho_{\epsilon}(x-y)g(y)dydx=\int\int f(x)\rho_{\epsilon}(y-x)g(y)dydx=\int g\rho_{\epsilon}*f,

e integrando por partes tenemos unas estimaciones para $u_{\epsilon}$ como las de la Proposición 17.

Proposición 3.

Sea $u_{\epsilon}$ solución de (20) con dato inicial $f\in H^{k}(\mathbb{R})$ , $k\geq 3$ . Entonces se tiene la siguiente cota

||u_{\epsilon}||_{H^{k}}(t)\leq\frac{||f||_{H^{k}}}{1-c||f||_{H^{k}}t}\mathchar 314\relax

(21)

2.3 Existencia para los problemas regularizados

Para demostrar la existencia de los problemas regularizados (20) vamos a utilizar el teorema de Picard en el espacio $H^{k}(\mathbb{R})$ . Hemos de ver entonces que para todo $\epsilon$ se tiene que

F_{\epsilon}=-\rho_{\epsilon}*\left(\rho_{\epsilon}*u_{\epsilon}\right)\partial_{x}\left(\rho_{\epsilon}*u_{\epsilon}\right)-\rho_{\epsilon}*\left(\gamma\Lambda^{\alpha}\rho_{\epsilon}*u_{\epsilon}\right)

es localmente (es decir, si $||u||_{H^{k}}<\lambda$ para cierto $\lambda$ ) Lipschitz con respecto a la norma $H^{k}$ . Para empezar hemos de asegurarnos que no perdemos derivadas al aplicar $F_{\epsilon}$ . Esto se consigue porque en lugar de derivar $u_{\epsilon}$ derivamos el núcleo $\rho_{\epsilon}$ , de manera que $u_{\epsilon}$ no pierde derivadas. Veamos que $F_{\epsilon}$ es Lipschitz:

Lema 1.

Sea $\lambda>0$ , entonces para todo $\epsilon>0$ $F_{\epsilon}$ es una función Lipschitz en $\{g:g\in H^{k}(\mathbb{R}),||g||_{H^{k}}\leq\lambda\}$ con $k\geq 3$ .

Demostración.

Se tiene que

||F_{\epsilon}(u)-F_{\epsilon}(v)||_{H^{k}}=||-\rho_{\epsilon}*\left(\rho_{\epsilon}*u\right)\partial_{x}\left(\rho_{\epsilon}*u\right)-\rho_{\epsilon}*\left(\gamma\Lambda^{\alpha}\rho_{\epsilon}*u\right)\\ +\rho_{\epsilon}*\left(\rho_{\epsilon}*v\right)\partial_{x}\left(\rho_{\epsilon}*v\right)+\rho_{\epsilon}*\left(\gamma\Lambda^{\alpha}\rho_{\epsilon}*v\right)||_{H^{k}}\mathchar 314\relax

Vamos a agrupar las partes difusivas de $u$ con la de $v$ :

||\rho_{\epsilon}*\left(-\gamma\Lambda^{\alpha}\rho_{\epsilon}*u+\gamma\Lambda^{\alpha}\rho_{\epsilon}*v\right)||_{H^{k}}\leq\gamma||\rho_{\epsilon}*(v-u)||_{H^{k+\alpha}}\leq L_{1}(\gamma,\alpha,\epsilon)||u-v||_{H^{k}}\mathchar 314\relax

Queda probar la estimación para la parte convectiva:

||\rho_{\epsilon}*(-\rho_{\epsilon}*u\partial_{x}\left(\rho_{\epsilon}*u\right)+\rho_{\epsilon}*v\partial_{x}(\rho_{\epsilon}*v))||_{H^{k}}\\ \leq||-\rho_{\epsilon}*u\partial_{x}\left(\rho_{\epsilon}*u\right)\pm\rho_{\epsilon}*u\partial_{x}\left(\rho_{\epsilon}*v\right)+\rho_{\epsilon}*v\partial_{x}(\rho_{\epsilon}*v)||_{H^{k}}\\ \leq||\rho_{\epsilon}*u\partial_{x}\left(\rho_{\epsilon}*(v-u)\right)+(\rho_{\epsilon}*(v-u))\partial_{x}(\rho_{\epsilon}*v)||_{H^{k}}\\ \leq||\rho_{\epsilon}*u\partial_{x}\left(\rho_{\epsilon}*(v-u)\right)||_{H^{3}}+||(\rho_{\epsilon}*(v-u))\partial_{x}(\rho_{\epsilon}*v)||_{H^{k}}\mathchar 314\relax

Utilizamos ahora que, si $s>1/2$ , $H^{s}(\mathbb{R})$ es un álgebra de Banach, es decir, que se cumple

||fg||_{H^{s}}\leq||f||_{H^{s}}||g||_{H^{s}}\mathchar 314\relax

Gracias a esta propiedad de los espacios de Sobolev tenemos que

||\rho_{\epsilon}*u\partial_{x}\left(\rho_{\epsilon}*(v-u)\right)||_{H^{k}}+||(\rho_{\epsilon}*(v-u))\partial_{x}(\rho_{\epsilon}*v)||_{H^{k}}\\ \leq||\rho_{\epsilon}*u||_{H^{k}}||\partial_{x}\left(\rho_{\epsilon}*(v-u)\right)||_{H^{k}}+||\partial_{x}(\rho_{\epsilon}*v)||_{H^{k}}||(\rho_{\epsilon}*(v-u))||_{H^{k}}\\ \leq L_{2}(\epsilon,\lambda)||u-v||_{H^{k}}\mathchar 314\relax

Para concluir hemos de elegir $L=\mathop{\operator@font m\acute{a}x}\{L_{1},L_{2}\}$ . ∎

Por lo tanto, dado un dato inicial $f\in H^{k}$ , si aplicamos el Teorema de Picard tenemos que existe una sucesión $u_{\epsilon}\in C^{1}([0,T_{\epsilon}],H^{k}(\mathbb{R}))$ . Además, por las propiedades de los núcleos $\rho_{\epsilon}$ , se puede demostrar que $T_{\epsilon}=\infty\mathchar 314\relax$

Tenemos así el siguiente resultado:

Lema 2.

Dado una dato inicial $f\in H^{k}$ con $k\geq 3$ el problema (20) tiene una única solución $u_{\epsilon}\in C^{1}([0,\infty),H^{k})$ .

2.4 Paso al límite $\epsilon\rightarrow 0$

Veremos que $u_{\epsilon}\in C^{1}([0,T],H^{k})$ forma una sucesión de Cauchy en el espacio $C([0,T],H^{s})$ , $0\leq s<k$ donde $T<T^{*}=\frac{1}{c||f||_{H^{k}}}$ (ver Proposición 21). Para ello tenemos que ver que en $L^{2}$ es Cauchy y entonces utilizando las estimaciones de la Proposición 21 concluiremos que es una sucesión de Cauchy en $H^{s}$ con $s<k$ . El caso extremo de $s=k$ lo trataremos al final.

Lema 3.

$u_{\epsilon}$ es una sucesión de Cauchy en $C([0,T],H^{s})$ , con $0\leq s<k$ .

Demostración.

Veremos primero que $u_{\epsilon}$ es Cauchy en $C([0,T],L^{2})$ . Sean $\epsilon,\delta$ dos números positivos. Entonces se tiene

$\displaystyle\frac{1}{2}\frac{d}{dt}\|\|u_{\epsilon}-u_{\delta}\|\|_{L^{2}}^{2}$	$\displaystyle=$	$\displaystyle-\gamma\int_{\mathbb{R}}(\rho_{\epsilon}(\Lambda^{\alpha}\rho_{\epsilon}u_{\epsilon})-\rho_{\delta}(\Lambda^{\alpha}\rho_{\delta}u_{\delta}))(u_{\epsilon}-u_{\delta})dx$
		$\displaystyle-\int_{\mathbb{R}}(\rho_{\epsilon}(\rho_{\epsilon}u_{\epsilon}(\partial_{x}(\rho_{\epsilon}u_{\epsilon})))-\rho_{\delta}(\rho_{\delta}u_{\delta}(\partial_{x}(\rho_{\delta}u_{\delta}))))(u_{\epsilon}-u_{\delta})dx$
	$\displaystyle=$	$\displaystyle I_{1}+I_{2}\mathchar 314\relax$

Veamos el caso de los operadores difusivos:

I_{1}=-\gamma\int_{\mathbb{R}}(\rho_{\epsilon}*(\Lambda^{\alpha}\rho_{\epsilon}*u_{\epsilon})-\rho_{\delta}*(\Lambda^{\alpha}\rho_{\delta}*u_{\delta}))(u_{\epsilon}-u_{\delta})dx\\ =-\gamma\int_{\mathbb{R}}(\rho_{\epsilon}*(\Lambda^{\alpha}\rho_{\epsilon}*u_{\epsilon})\pm\rho_{\delta}*(\Lambda^{\alpha}\rho_{\delta}*u_{\epsilon})-\rho_{\delta}*(\Lambda^{\alpha}\rho_{\delta}*u_{\delta}))(u_{\epsilon}-u_{\delta})dx\\ =-\gamma\int_{\mathbb{R}}((\rho_{\epsilon}*(\Lambda^{\alpha}\rho_{\epsilon})-\rho_{\delta}*(\Lambda^{\alpha}\rho_{\delta}))*u_{\epsilon}+\rho_{\delta}*(\Lambda^{\alpha}\rho_{\delta}*(u_{\epsilon}-u_{\delta}))(u_{\epsilon}-u_{\delta})dx\mathchar 314\relax

Integrando por partes el segundo sumando obtenemos que

-\gamma\int_{\mathbb{R}}((\rho_{\epsilon}*(\Lambda^{\alpha}\rho_{\epsilon})-\rho_{\delta}*(\Lambda^{\alpha}\rho_{\delta}))*u_{\epsilon}+\rho_{\delta}*(\Lambda^{\alpha}\rho_{\delta}*(u_{\epsilon}-u_{\delta}))(u_{\epsilon}-u_{\delta})dx\\ \leq-\gamma\int_{\mathbb{R}}(\rho_{\epsilon}*(\Lambda^{\alpha}\rho_{\epsilon})-\rho_{\delta}*(\Lambda^{\alpha}\rho_{\delta}))*u_{\epsilon}(u_{\epsilon}-u_{\delta})\\ \leq\gamma||u_{\epsilon}-u_{\delta}||_{L^{2}}||(\rho_{\epsilon}*(\Lambda^{\alpha}\rho_{\epsilon})-\rho_{\delta}*(\Lambda^{\alpha}\rho_{\delta}))*u_{\epsilon}||_{L^{2}},

y por lo tanto, usando las propiedades de las suavizaciones (ver [3])

$\displaystyle\|\|\Lambda^{\alpha}((\rho_{\epsilon}(\rho_{\epsilon})-\rho_{\delta}(\rho_{\delta}))*u_{\epsilon})\|\|_{L^{2}}$	$\displaystyle\leq$	$\displaystyle\|\|(\rho_{\epsilon}(\rho_{\epsilon})-\rho_{\delta}(\rho_{\delta}))*u_{\epsilon}\|\|_{H^{\alpha}}$
	$\displaystyle=$	$\displaystyle\|\|(\rho_{\epsilon}(\rho_{\epsilon})-\rho_{\delta}(\rho_{\delta}))u_{\epsilon}\pm\rho_{\epsilon}u_{\epsilon}\pm\rho_{\delta}*u_{\epsilon}\|\|_{H^{\alpha}}$
	$\displaystyle\leq$	$\displaystyle\|\|\rho_{\epsilon}(\rho_{\epsilon}u_{\epsilon})-\rho_{\epsilon}*u_{\epsilon}\|\|_{H^{\alpha}}$
		$\displaystyle+\|\|\rho_{\delta}(\rho_{\delta}u_{\epsilon})-\rho_{\delta}*u_{\epsilon}\|\|_{H^{\alpha}}$
		$\displaystyle+\|\|\rho_{\epsilon}u_{\epsilon}-\rho_{\delta}u_{\epsilon}\|\|_{H^{\alpha}}$
	$\displaystyle\leq$	$\displaystyle c\epsilon\|\|\rho_{\epsilon}u_{\epsilon}\|\|_{H^{1+\alpha}}+c\delta\|\|\rho_{\delta}u_{\epsilon}\|\|_{H^{1+\alpha}}$
		$\displaystyle+\|\|\rho_{\epsilon}u_{\epsilon}\pm u_{\epsilon}-\rho_{\delta}u_{\epsilon}\|\|_{H^{\alpha}}$
	$\displaystyle\leq$	$\displaystyle c\epsilon\|\|\rho_{\epsilon}u_{\epsilon}\|\|_{H^{1+\alpha}}+c\delta\|\|\rho_{\delta}u_{\epsilon}\|\|_{H^{1+\alpha}}$
		$\displaystyle+(c\epsilon+c\delta)\|\|u_{\epsilon}\|\|_{H^{1+\alpha}}$
	$\displaystyle\leq$	$\displaystyle c\mathop{\operator@font m\acute{a}x}\{\epsilon,\delta\}\|\|u_{\epsilon}\|\|_{H^{3}}$

Recordemos que, fijo $T<T^{*}$ , tenemos la cota uniforme $||u_{\epsilon}||_{H^{3}}\leq C(T,||f||_{H^{3}})$ y por lo tanto tenemos que

I_{1}\leq C(T,||f||_{H^{3}},\gamma)||u_{\epsilon}-u_{\delta}||_{L^{2}}\mathop{\operator@font m\acute{a}x}\{\epsilon,\delta\}\mathchar 314\relax

Para la integral $I_{2}$ se hace igual. Hay que sumar y restar los términos

\rho_{\delta}*(\rho_{\epsilon}*u_{\epsilon}\partial_{x}(\rho_{\epsilon}*u_{\epsilon})),\;\;\rho_{\delta}*(\rho_{\delta}*u_{\epsilon}\partial_{x}(\rho_{\epsilon}*u_{\epsilon})),\;\;\rho_{\delta}*(\rho_{\delta}*u_{\delta}\partial_{x}(\rho_{\epsilon}*u_{\epsilon}))\mathchar 314\relax\mathchar 314\relax\mathchar 314\relax

y aplicar las mismas desigualdades (Sobolev, Cauchy-Schwartz…).

Una vez que hemos probado que $u_{\epsilon}$ es una sucesión de Cauchy en $C([0,T],L^{2})$ , utilizando la cota uniforme en $\epsilon$ (Proposición 21)

||u_{\epsilon}||_{H^{k}}\leq C(T,||f||_{H^{k}}),

podemos interpolar (ver [3]) entre el espacio $H^{0}=L^{2}$ y $H^{k}$ , de manera que $u_{\epsilon}$ es de Cauchy para todo $H^{s}$ con $s<k$ . Podemos así asegurar la existencia de $u\in C([0,T],H^{s})$ como el límite de $u_{\epsilon}$ en la topología usual de ese espacio. ∎

Además podemos mejorar el resultado para cubrir el caso extremo $s=k$ . Así hemos de ver que $u=\mathop{\operator@font l\acute{{\imath}}m}_{\epsilon\rightarrow 0}u_{\epsilon}$ está en el espacio $H^{k}$ .²²2Podemos elegir la noción de límite de cualquier espacio $C([0,T],H^{s})$ con $s<k$ .

Lema 4.

La función $u$ definida como el límite anterior está en $C([0,T],H^{k})$ .

Demostración.

Para probarlo hemos de razonar con análisis funcional. Como $\{u_{\epsilon}\}$ está acotada en $H^{k}$ (Proposición 21) tiene una subsucesión que converge débilmente en este espacio. Es decir

<u_{\epsilon},z>\rightarrow<v,z>,\;\;\forall z\in H^{-k}\mathchar 314\relax

En principio no podemos asegurar que $u=v$ . Para concluir la igualdad utilizamos las convergencias débiles, pues la convergencia fuerte implica la convergencia débil, en los espacios $H^{s}$ con $s<k$ además del hecho de que $H^{k}\subset H^{s}\Rightarrow H^{-k}\supset H^{-s}$ y obtenemos que si $u\neq v$ tenemos una contradicción. ∎

2.5 Regularidad de $u$

Gracias a los lemas anteriores podemos demostrar el siguiente resultado:

Teorema 2 (Existencia local de solución clásica).

Sea $f\in H^{k}$ , $k\geq 3$ . Entonces existe una única $u\in C([0,T],H^{k})\cap C^{1}([0,T],H^{k-2})$ , definida como el límite uniforme en compactos de $\mathbb{R}$ de $u_{\epsilon}$ , solución clásica del problema (15) con $\gamma\geq 0$ y $0<\alpha\leq 2$ .

Demostración.

Existencia: De los lemas anteriores se obtiene la existencia de $u\in C([0,T],H^{k})$ como límite uniforme en compactos de $u_{\epsilon}$ . Para obtener la regularidad temporal necesaria para $u$ observamos que $\partial_{t}u_{\epsilon}$ tiende como distribución a la derivada débil de $u$ (que denotamos por $\partial_{t}u$ ). En efecto, para toda función test $\phi$ , se tiene que

\int_{\mathbb{R}}\int_{0}^{T}\phi\partial_{t}u_{\epsilon}dtdx=-\int_{\mathbb{R}}\int_{0}^{T}\partial_{t}\phi u_{\epsilon}dtdx\rightarrow-\int_{\mathbb{R}}\int_{0}^{T}\partial_{t}\phi udtdx=\int_{\mathbb{R}}\int_{0}^{T}\phi\partial_{t}udtdx\mathchar 314\relax

Además $\partial_{t}u_{\epsilon}\rightarrow-\gamma\Lambda^{\alpha}u-u\partial_{x}u$ en $C([0,T],C(\mathbb{R}))$ (y por lo tanto también en sentido distribucional). Esto es una consecuencia de las propiedades de los núcleos suavizantes.

Ahora estamos en condiciones de conseguir una mejor estimación para $\partial_{t}u$ :

||\partial_{t}u||_{C([0,T],C(\mathbb{R}))}=\mathop{\operator@font m\acute{a}x}_{0\leq t\leq T}\mathop{\operator@font m\acute{a}x}_{x\in U;\newline U\subset\subset\mathbb{R}}|-\gamma\Lambda^{\alpha}u-u\partial_{x}u|\leq\mathop{\operator@font m\acute{a}x}_{0\leq t\leq T}\left(c||u||_{C^{2}}+||u||_{C^{2}}^{2}\right)\\ \leq c||u||_{C([0,T],H^{3}(\mathbb{R}))}+||u||_{C([0,T],H^{3}(\mathbb{R}))}^{2}\leq C(||f||_{H^{k}},T,\gamma)\mathchar 314\relax

En particular si $u\in C([0,T],H^{k})$ con $k\geq 3$ se concluye que $u$ es solución clásica de la ecuación de Burgers.

Para concluir que $u\in C^{1}([0,T],H^{k-2})$ tenemos que obtener una cota para $||\partial_{t}u||_{H^{k-2}}$ :

||\partial_{t}u||_{H^{k-2}}\leq\gamma||\Lambda^{\alpha}u||_{H^{k-2}}+||u||_{H^{k-2}}||\partial_{x}u||_{H^{k-2}}\leq C(||f||_{H^{k}},T,\gamma),

y entonces

||u||_{C^{1}([0,T],H^{k-2})}=\mathop{\operator@font m\acute{a}x}_{0\leq t\leq T}||u||_{H^{k-2}}+||\partial_{t}u||_{H^{k-2}}\\ \leq\mathop{\operator@font m\acute{a}x}_{0\leq t\leq T}||u||_{H^{k-2}}+\mathop{\operator@font m\acute{a}x}_{0\leq t\leq T}\gamma||\Lambda^{\alpha}u||_{H^{k-2}}+\mathop{\operator@font m\acute{a}x}_{0\leq t\leq T}||u||_{H^{k-2}}||\partial_{x}u||_{H^{k-2}}\leq C(||f||_{H^{k}},T,\gamma),

donde en la última desigualdad hemos usado (17).

Unicidad: Supongamos que hubiese dos soluciones, $u$ y $v$ en el espacio $H^{k}$ con $k\geq 3$ del problema (15) con el mismo dato inicial. Entonces

$\displaystyle\frac{1}{2}\frac{d}{dt}\|\|u-v\|\|_{L^{2}}^{2}$	$\displaystyle=$	$\displaystyle-\gamma\|\|\Lambda^{\alpha/2}(u-v)\|\|_{L^{2}}^{2}-\int_{\mathbb{R}}(u-v)(u\partial_{x}u-v\partial_{x}v)dx$
	$\displaystyle\leq$	$\displaystyle-\frac{1}{2}\int_{\mathbb{R}}(u-v)\partial_{x}(u^{2}-v^{2})dx$
	$\displaystyle\leq$	$\displaystyle\frac{-1}{2}\int_{\mathbb{R}}(u-v)\partial_{x}((u+v)(u-v))dx$
	$\displaystyle\leq$	$\displaystyle\frac{-1}{2}\int_{\mathbb{R}}(u-v)^{2}\partial_{x}(u+v)dx-\frac{1}{2}\int_{\mathbb{R}}(u-v)\partial_{x}(u-v)(u+v)dx$
	$\displaystyle\leq$	$\displaystyle c\int_{\mathbb{R}}(u-v)^{2}\partial_{x}(u+v)dx$
	$\displaystyle\leq$	$\displaystyle c(\|\|u\|\|_{H^{k}},\|\|v\|\|_{H^{k}})\|\|u-v\|\|_{L^{2}}^{2}$
	$\displaystyle\leq$	$\displaystyle c(T,\|\|f\|\|_{H^{k}})\|\|u-v\|\|_{L^{2}}^{2},$

y usando Gronwall se obtiene la unicidad. ∎

3 Propiedades de las soluciones

En esta sección encontraremos algunas propiedades básicas que deberá tener una solución de la ecuación de Burgers.

Como la ecuación (15) modeliza un escalar que es transportado por un fluido donde la velocidad del fluido la hemos hecho proporcional al escalar (14) es de esperar que la masa total, i.e. se conserva. En efecto,

Proposición 4 (Conservación de la masa).

Sea $u$ una solución clásica de la ecuación (15) entonces se tiene que

\int_{\mathbb{R}}u(t,x)dx=\int_{\mathbb{R}}f(x)dx\mathchar 314\relax

Demostración.

Integrando la ecuación (15) en espacio

\frac{d}{dt}\int_{\mathbb{R}}u(t,x)dx=\int\partial_{t}u(t,x)dx=\int_{\mathbb{R}}-\frac{1}{2}\partial_{x}(u(t,x)^{2})-\gamma\Lambda^{\alpha}u(t,x)dx=I_{1}+I_{2}\mathchar 314\relax

Por las condiciones de borde para $u$ la integral $I_{1}$ se anula.

Para ver que la integral $I_{2}$ se anula razonamos utilizando la transformada de Fourier. Dada un función $g(x)$ se cumple que

\int_{\mathbb{R}}g(x)dx=\hat{g}(0)\mathchar 314\relax

Como $\Lambda^{\alpha}$ en el espacio de Fourier es el multiplicador de la definición (9) obtenemos que

I_{2}=-\gamma\int_{\mathbb{R}}\Lambda^{\alpha}u(t,x)dx=-\gamma\widehat{\Lambda^{\alpha}u}(0)=0\mathchar 314\relax

∎

Otra cantidad de la que es interesante ver la evolución es la norma $L^{\infty}$ de la solución:

Proposición 5 (Principio del máximo para $||\cdot||_{L^{\infty}}$ ).

Sea $u$ una solucion clásica de (15) tal que $\mathop{\operator@font m\acute{a}x}_{x\in\mathbb{R}}u(t,x)\geq 0$ , $\mathop{\operator@font m\acute{{\imath}}n}_{x\in\mathbb{R}}u(t,x)\leq 0$ y $\alpha\in(0,2]$ , entonces se tienen los siguientes resultados

a)

Si $\gamma=0$ ,

$||u||_{L^{\infty}}(t)=||f||_{L^{\infty}},$
b)

Si $\gamma>0$ ,

$||u||_{L^{\infty}}(t)\leq||f||_{L^{\infty}}\mathchar 314\relax$

Demostración.

Observamos que la función $M(t)=\mathop{\operator@font m\acute{a}x}_{x\in\mathbb{R}}u(t,x)=u(t,x_{t})$ es Lipschitz. En efecto:

\mathop{\operator@font m\acute{a}x}_{x}|u(t_{1},x)|=\mathop{\operator@font m\acute{a}x}_{x}(|u(t_{1},x)-u(t_{2},x)+u(t_{2},x)|)\leq\mathop{\operator@font m\acute{a}x}_{x}(|u(t_{1},x)-u(t_{2},x)|)+\mathop{\operator@font m\acute{a}x}_{x}|u(t_{2},x)|,

de donde

|\mathop{\operator@font m\acute{a}x}_{x}u(t_{1},x)-\mathop{\operator@font m\acute{a}x}_{x}u(t_{2},x)|\leq\mathop{\operator@font m\acute{a}x}_{x}(|u(t_{1},x)-u(t_{2},x)|)=\mathop{\operator@font m\acute{a}x}_{x}(|\partial_{t}u(s,x)||t_{1}-t_{2}|)\\ \leq\mathop{\operator@font m\acute{a}x}_{s\in(t_{2},t_{1})}\mathop{\operator@font m\acute{a}x}_{x}(|\partial_{t}u(s,x)|)|t_{1}-t_{2}|\mathchar 314\relax

(22)

Para concluir que la función es Lipschitz observamos que debemos restringirnos a un intervalo temporal $[0,T]$ con $T>0$ fijo. Ahora nos aseguramos de que $(t_{1},t_{2})\subset[0,T]$ y obtenemos

|\mathop{\operator@font m\acute{a}x}_{x}u(t_{1},x)-\mathop{\operator@font m\acute{a}x}_{x}u(t_{2},x)|\leq\mathop{\operator@font m\acute{a}x}_{s\in[0,T]}\mathop{\operator@font m\acute{a}x}_{x}(\partial_{t}u(s,x))(t_{1}-t_{2})=L(t_{1}-t_{2})\mathchar 314\relax

Usando el Teorema de Radamacher tenemos que $M(t)$ es derivable en casi todo punto,

$\displaystyle M^{\prime}(t)$	$\displaystyle=$	$\displaystyle\mathop{\operator@font l\acute{{\imath}}m}_{h_{j}\rightarrow 0}\frac{M(t+h_{j})-M(t)}{h_{j}}=\mathop{\operator@font l\acute{{\imath}}m}_{h_{j}\rightarrow 0}\frac{u(x_{t+h_{j}},t+h_{j})-u(x_{t},t)}{h_{j}}$
	$\displaystyle=$	$\displaystyle\mathop{\operator@font l\acute{{\imath}}m}_{h_{j}\rightarrow 0}\frac{u(x_{t+h_{j}},t+h_{j})\pm u(x_{t+h_{j}},t)-u(x_{t},t)}{h_{j}}=\partial_{x}u(t,x_{t})+\partial_{t}u(x_{t},t)$
	$\displaystyle=$	$\displaystyle\partial_{t}u(x_{t},t)\mathchar 314\relax$

De manera que, si $\gamma=0$ ,

M^{\prime}(t)=\partial_{t}u(x_{t},t)=-u(x_{t},t)\partial_{x}u(x_{t},t)=-\frac{1}{2}\partial_{x}(u^{2}(x_{t},t))=0

donde en la última igualdad hemos usado que $u(x_{t},t)$ es máximo. En el caso en el que $\gamma\geq 0$ tenemos que dar signo al término $-\gamma\Lambda^{\alpha}u(t,x_{t})$ . Usaremos la expresión como una convolución (10). Se tiene que

-\gamma\Lambda^{\alpha}u(x_{t},t)=c\text{P.V.}\int_{\mathbb{R}}\frac{u(y,t)-u(x_{t},t)}{|x-y|^{1+\alpha}}dy\leq 0\mathchar 314\relax

En el caso en el que $\alpha=2$ el resultado se reduce a conocer qué signo tiene la segunda derivada en un punto de máximo.

Para el mínimo se hace de manera análoga. ∎

4 Un resultado análogo al de Beale-Kato-Majda

El lector atento se habrá percatado de que la ecuación de Burgers (15) tiene una especie de Teorema de Beale-Kato-Majda. Recordemos que en una dimensión espacial lo más parecido a $\omega$ es la primera derivada espacial $\partial_{x}u$ . Entonces tenemos el siguiente resultado:

Proposición 6.

Sea $T>0$ . Entonces, si

\int_{0}^{T}||\partial_{x}u||_{L^{\infty}}(s)ds<\infty,

existe $u$ solución clásica de (15) al menos hasta tiempo $T$ .

Demostración.

En la prueba de la proposición de las estimaciones a priori (Proposición 17) logramos la cota

\frac{d}{dt}||\partial_{x}^{3}u||_{L^{2}}^{2}\leq c||\partial_{x}u||_{L^{\infty}}||\partial_{x}^{3}u||_{L^{2}}^{2}\mathchar 314\relax

De esta expresión obtenemos

\frac{d}{dt}||u||_{H^{3}}\leq c||\partial_{x}u||_{L^{\infty}}||u||_{H^{3}},

y aplicando la desigualdad de Gronwall (es decir, integramos la EDO) conseguimos el resultado. ∎

5 Buscando singularidades

Consideramos la ecuación (15) con $\gamma=0$ . Esta ecuación es una ecuación de transporte unidimensional no-lineal, por lo tanto es susceptible de aplicarle el método de las características. Esa técnica aplicada a esta ecuación se puede encontrar en casi todos los manuales de ecuaciones diferenciales. Nosotros utilizaremos una técnica similar a la que utilizamos para probar el Principio del Máximo en la sección 2. Queremos encontrar una singularidad para $u$ . Por la Proposición 5 tenemos que $u$ no explota, por lo tanto si hay una singularidad debe estar en alguna de las derivadas espaciales de $u$ . Como estamos en el caso no viscoso solamente tenemos una derivada espacial, así que $\partial_{x}u$ es nuestra candidata a cantidad que explota.

Así sea $u\in H^{3}(\mathbb{R})$ una solución clásica de (15). Por la inmersión de Sobolev se tiene que $\partial_{x}u\in C^{1}(\mathbb{R})$ . Ahora la idea es aplicar el Teorema de Rademacher a $\partial_{x}u$ . De manera análoga a la de la demostración de la Proposición 5 se demuestra que si $m_{x}(t)=\mathop{\operator@font m\acute{{\imath}}n}_{x\in\mathbb{R}}\partial_{x}u=\partial_{x}u(x_{t},t)$ se tiene que

m^{\prime}_{x}(t)=\partial_{t}\partial_{x}u(x_{t},t)=-(\partial_{x}u(x_{t},t))^{2}-u(x_{t},t)\partial_{x}^{2}u(x_{t},t)\mathchar 314\relax

Como $x_{t}$ es el punto de máximo de $\partial_{x}u$ tenemos que $\partial_{x}^{2}u=0$ , por lo que la ecuación para la evolución del máximo es

m_{x}^{\prime}=-m_{x}^{2}\mathchar 314\relax

Si ahora resolvemos la EDO obtenemos que

m_{x}(t)=\frac{m_{x}(0)}{1+tm_{x}(0)}\mathchar 314\relax

(23)

Hemos obtenido el siguiente resultado

Proposición 7 (Singularidad).

Sea $f\in H^{3}$ tal que $\mathop{\operator@font m\acute{{\imath}}n}_{x\in\mathbb{R}}\partial_{x}f(x)<0$ . Entonces $u$ solución clásica de (15) con $\gamma=0$ desarrolla una singularidad en tiempo finito.

5.1 Interpretando la singularidad

El tipo de singularidad que se produce se conoce como ’choque’³³3Del inglés ’shock’. y es una discontinuidad en $u$ , o lo que es lo mismo $\partial_{x}u(x,T^{*})=-\infty$ . Si pensamos en $u$ como la altura de la superficie de una ola unidimensional lo que ocurre es que las partículas del fluido que integran la ola se mueven más rápido cuanto más altas estén, por lo que las más altas van a acercarse a las más bajas. Entonces cuando las alcancen se produce este choque. Esta discontinuidad previene que nuestra interfase $u$ deje de ser un grafo, porque si pensamos en la física de la ola tenemos que las partículas más rápidas sobrepasan a las más lentas (ver Figura 3).

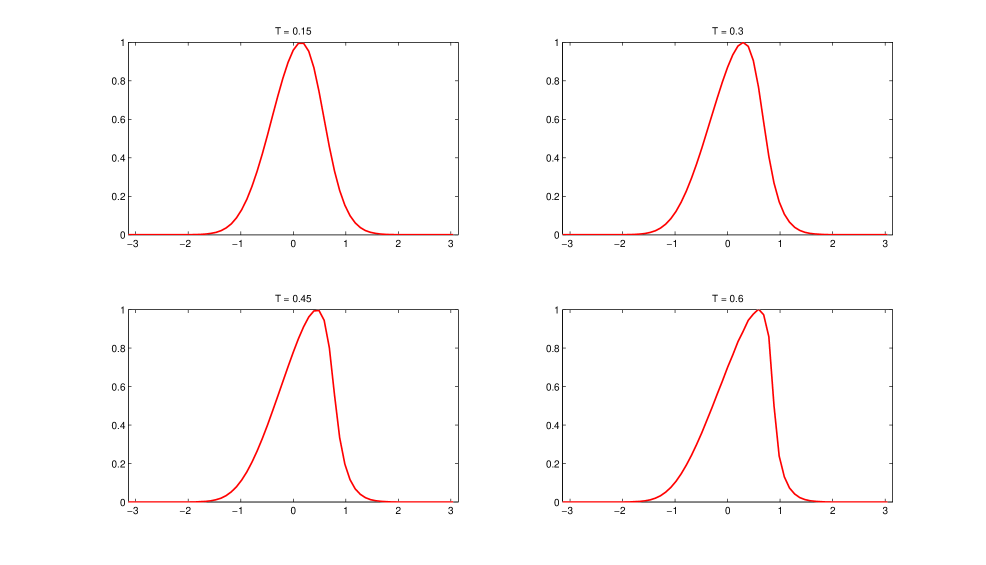
Hemos mencionado que la ecuación de Burgers podía ser entendida como una ola, lo que no es completamente descabellado.

Si $y=u(x,t)$ es la superficie del agua (entonces la ola viene dada por la curva $(x,u(x,t))$ ), y $v=(v_{1},v_{2})$ es el campo de velocidades del agua, entonces la ecuación de la interfase entre el agua y el aire es

\partial_{t}u=-\partial_{x}uv_{1}(x,u(x,t),t)+v_{2}(x,u(x,t),t)=(-\partial_{x}u,1)\cdot v\mathchar 314\relax

Ahora observamos que en las olas la parte más alta se mueve a mayor velocidad que la parte más baja. Por lo tanto parece natural (al menos como primera aproximación) hacer la hipótesis $v_{1}(x,u(x,t),t)=cu(x,t)$ (la constante $c$ podemos tomarla igual a 1 si hacemos un cambio de variables). Así si despreciamos la velocidad vertical, $v_{2}(x,u(x,t),t)\approx 0$ , tenemos la ecuación de Burgers no viscosa como modelo del perfil de una ola. Podemos razonar también que la curva cambia según sea su curvatura, de manera que $v_{2}(x,u(x,t),t)\approx\kappa[u]$ con $\kappa[u]$ la curvatura de la curva $u$ . Además si suponemos curvas suaves de amplitud pequeña podemos linealizar la curvatura obteniendo el operador $\gamma\partial_{x}^{2}u(x,t)$ . Así, con hipótesis razonables al menos en primera aproximación, obtenemos la ecuación de Burgers viscosa como modelo simplificado del perfil de una ola.

Una ola unidimensional con unas ciertas características (longitud de onda, amplitud…) puede modelizarse en un mejor nivel de aproximación con la ecuación KdV siguiente:

\partial_{t}u+\partial_{x}uu=\partial_{x}^{3}u\mathchar 314\relax

(24)

Veamos de manera muy resumida cómo puede derivarse formalmente esta ecuación. Para describir una ola consideramos que el agua bajo la superfie tiene un flujo irrotacional, $i\mathchar 314\relax e\mathchar 314\relax$ $v=\nabla\phi$ para cierta función escalar $\phi$ . Si suponemos válidas las ecuaciones de Euler para el agua bajo la superficie tenemos que $\phi$ sigue la ley

\partial_{t}\phi+\frac{1}{2}|\nabla\phi|^{2}+p+gy=0\mathchar 314\relax

Además, por la incompresibilidad se tiene $\Delta\phi=0$ .

Figura 4: Una ola y sus parámetros característicos

La coordenada $y$ se distingue de la $x$ en que actúa la gravedad, por lo tanto parece natural hacer un desarrollo de $\phi$ en potencias de $y$ , $\phi=\sum_{n=0}^{\infty}y^{n}\phi_{n}(x,t)$ . Si consideramos olas pequeñas en amplitud con respecto a la longitud de onda, entonces tenemos que despreciar los términos de orden grande en $y$ en nuestra expresión para $\phi$ .

Si además suponemos que $\partial_{x}\phi_{0}\approx u$ podemos concluir la ecuación (24). Esta hipótesis se motiva por los desarrollos en serie de potencias anteriores.

Observamos que la hipótesis para obtener la ecuación de Korteveg-de Vries es menos restrictiva que para obtener la ecuación de Burgers, pues exclusivamente suponemos que $\partial_{x}\phi_{0}(x,t)=u(x,t)$ no que $\partial_{x}\phi(x,f(x,t),t)=v_{1}(x,f(x,t),t)=u(x,t)$ . Consideramos por lo tanto discrepancias en los ordenes mayores.

6 Método numérico

En la siguiente sección nos proponemos dar una aproximación numérica al problema (14) propuesto en $\mathbb{T}$ .

6.1 Discretización espacial

La forma natural de abordar el problema es usando la transformada de Fourier discreta (DFT) (ver [6] y [23]). Sea $\mathbb{T}^{\star}_{N}$ una discretización de $\mathbb{T}$ , con un número par $N$ de puntos, dada por,

x_{j}=\frac{\pi}{N}(2j-N),\quad j=0,\ldots,N-1

La idea es sustituir el valor de $u(\cdot,x)=u(x)$ en los nodos, $u(x_{j})$ , por su interpolante trigonométrico,

	$\displaystyle I_{N}u(x)$	$\displaystyle=$	$\displaystyle\sum_{k={-N/2}}^{N/2-1}\tilde{u}_{k}e^{ikx}$
	$\displaystyle I_{N}u(x_{j})$	$\displaystyle=$	$\displaystyle u(x_{j}),\quad j=0,\ldots,N-1$

Es decir, dado un vector con los valores nodales de $u$ , $U=[u_{0}\cdots u_{N-1}]$ , la DFT nos proporciona $\tilde{U}=[\tilde{u}_{-N/2}\cdots\tilde{u}_{N/2-1}]$ . Estos coeficientes vienen dados por,

\tilde{u}_{k}=\frac{1}{N}\sum_{j=0}^{N-1}u(x_{j})e^{ikx_{j}},\quad j=0,\ldots,N-1

y puede demostrarse que están relacionados con los coeficientes $\hat{u}_{k}$ de la serie de Fourier de $u(x)$ mediante,

\tilde{u}_{k}=\hat{u}_{k}+\sum_{m\neq 0,m=-\infty}^{\infty}\hat{u}_{k+Nm},\quad k=-N/2,\ldots,N/2-1

Sabiendo como aproximar $u(x)$ , es importante saber como aproximar $\partial_{x}u(x)$ . Para ello derivamos el interpolante trigonométrico anterior obteniendo,

\partial_{x}I_{N}u(x)=\sum_{k=-N/2}^{N/2-1}ik\tilde{u}_{k}e^{ikx}

Nuestra aproximación de $\partial_{x}u(x)$ en $x_{l}$ vendrá dada por lo que nosotros llamaremos,

(\mathcal{D}_{N}u)_{l}=\sum_{k=-N/2}^{N/2-1}ik\tilde{u}_{k}e^{-ikx_{l}},\quad l=0,\ldots,N-1

De la misma forma, parece apropiado aproximar el operador $\Lambda^{\alpha}=(-\partial_{x}^{2})^{\alpha/2}$ mediante,

(\mathcal{E}_{N}^{\alpha}u)_{l}=\sum_{k=-N/2}^{N/2-1}|ik|^{\alpha}\tilde{u}_{k}e^{-ikx_{l}},\quad l=0,\ldots,N-1\mathchar 314\relax

6.2 Discretización temporal

Para la aproximación de la derivada temporal en la ecuación utilizaremos el método de Runge-Kutta explícito de orden $4$ , también denominado RK4.

Sea $T^{\star}=\{t_{0},\ldots,t_{M}\}$ una discretización del dominio temporal $[0,T]$ . Así si $U_{s}=[u(x_{1},t_{s})\ldots u(x_{N},t_{s})]$ es la aproximación de la solución a nuestro problema en tiempo $t=t_{s}$ se tiene que $U_{s}$ verifica la ecuación

\frac{d}{dt}U_{s}=F(U_{s},t_{s}),

con $F=-u\partial_{x}u-\gamma\Lambda^{\alpha}u$ .

Entonces,

\displaystyle U_{s+1}=U_{s}+\frac{1}{6}\Delta t(K_{1}+2K_{2}+2K_{3}+K_{4}),

donde,

$K_{1}$	$=$	$F(U_{s},t_{s})$ ,
$K_{2}$	$=$	$F(U_{s}+\frac{1}{2}\Delta tK_{1},t_{s}+\frac{1}{2}\Delta t)$ ,
$K_{3}$	$=$	$F(U_{s}+\frac{1}{2}\Delta tK_{2},t_{s}+\frac{1}{2}\Delta t)$ ,
$K_{4}$	$=$	$F(U_{s}+\Delta tK_{3},t_{s}+\Delta t)$ .

Referencias

[1] J. Bear, Dynamics of Fluids in Porous Media, American Elsevier, New York, 1972.
[2] A. Bejan y D. Nield, Convection in Porous Media, Springer, New York, 1992.
[3] A.L. Bertozzi y A.J. Majda. Vorticity and the Mathematical Theory of Incompresible Fluid Flow. Cambridge Press, 2002.
[4] J.T. Beale, T. Kato y A. Majda Remarks on the breakdown of smooth solutions for the 3-D Euler equations. Comm. Math. Phys. 94, no. 1, 61-66, 1984.
[5] L. Cafarelli y A. Vasseur. Drift diffusion with fractional diffusion y de quasi-geostrophic equation. To appear in Annals of Mathematics,
[6] C. Canuto, M.Y. Hussaini, A. Quarteroni, T.A. Zang, Spectral Methods, Springer-Verlag, 2006
[7] P. Constantin, D. Córdoba y J. Wu, On the critical dissipative quasigeostrophic equation, Indiana Univ. Math., 50, 97-107, 2001.
[8] A. Córdoba y D. Córdoba, A maximum principle applied to Quasi-geostrophic equations, Comm. Math. Phys. 249, no. 3, 511-528, 2004.
[9] A. Córdoba, D. Córdoba y F. Gancedo, Interface evolution: the Hele-Shaw y Muskat problems. To appear in Annals of Math.
[10] D. Córdoba y F. Gancedo, Contour dynamics of incompressible 3-D fluids in a porous medium with different densities. Comm. Math. Phys. 273 (2007), no. 2, 445–471.
[11] D. Córdoba y F. Gancedo, A maximum principle for the Muskat problem for fluids with different densities. Comm. Math. Phys. 286 (2009), no. 2, 681–696.
[12] D. Córdoba, F. Gancedo y R. Orive, A note on the interface dynamics for convection in porous media. Physica D 237 (10-12), (2008), pp. 1488–1497.
[13] C.R. Doering y J.D. Gibbon Applied Analysis of the Navier-Stokes Equations, Cambridge text in applied mathematics.
[14] H. Dong, D. Du, y D. Li,. Finite time singularities and global well-posedness for fractal Burgers equations. Indiana University Math. J., Vol 58, No.2, 807–821, 2009.
[15] L.C. Evans, Partial Diferential Equations, AMS, 2008.
[16] F. Gancedo. Existence for the $\alpha$ -patch model and the QG sharp front in Sobolev spaces. Adv. Math., Vol 217/6: 2569-2598, 2008.
[17] A. Kiselev, F. Nazarov, y R. Shterenberg,. Blow up and regularity for fractal Burgers equation. Partial Differ. Equ., Vol 5, 211–240, 2008.
[18] C. De Lellis y L. Székelyhidi Jr. The Euler equations as a differential inclusion. Ann. Math., Vol 170, 3, 1417-1436, 2009.
[19] J. Leray. Sur le mouvement d’un liquide viscoux emplissant l’espace. Acta. Math., Vol 63,No.1,193-248, 1934.
[20] M. Muskat, The flow of homogeneous fluids through porous media. New York, 1937.
[21] M. Planck Autobiografía científica y últimos escritos, Nivola, 2000.
[22] E.M. Stein Singular integrals y differentiability properties of functions, Princeton University Press, 1970.
[23] L.N. Trefethen Spectral methods in Matlab, SIAM, 2000.

$\displaystyle\|\|\Lambda^{\alpha}((\rho_{\epsilon}(\rho_{\epsilon})-\rho_{\delta}(\rho_{\delta}))*u_{\epsilon})\|\|_{L^{2}}$	$\displaystyle\leq$	$\displaystyle\|\|(\rho_{\epsilon}(\rho_{\epsilon})-\rho_{\delta}(\rho_{\delta}))*u_{\epsilon}\|\|_{H^{\alpha}}$
	$\displaystyle=$	$\displaystyle\|\|(\rho_{\epsilon}(\rho_{\epsilon})-\rho_{\delta}(\rho_{\delta}))u_{\epsilon}\pm\rho_{\epsilon}u_{\epsilon}\pm\rho_{\delta}*u_{\epsilon}\|\|_{H^{\alpha}}$
	$\displaystyle\leq$	$\displaystyle\|\|\rho_{\epsilon}(\rho_{\epsilon}u_{\epsilon})-\rho_{\epsilon}*u_{\epsilon}\|\|_{H^{\alpha}}$
		$\displaystyle+\|\|\rho_{\delta}(\rho_{\delta}u_{\epsilon})-\rho_{\delta}*u_{\epsilon}\|\|_{H^{\alpha}}$
		$\displaystyle+\|\|\rho_{\epsilon}u_{\epsilon}-\rho_{\delta}u_{\epsilon}\|\|_{H^{\alpha}}$
	$\displaystyle\leq$	$\displaystyle c\epsilon\|\|\rho_{\epsilon}u_{\epsilon}\|\|_{H^{1+\alpha}}+c\delta\|\|\rho_{\delta}u_{\epsilon}\|\|_{H^{1+\alpha}}$
		$\displaystyle+\|\|\rho_{\epsilon}u_{\epsilon}\pm u_{\epsilon}-\rho_{\delta}u_{\epsilon}\|\|_{H^{\alpha}}$
	$\displaystyle\leq$	$\displaystyle c\epsilon\|\|\rho_{\epsilon}u_{\epsilon}\|\|_{H^{1+\alpha}}+c\delta\|\|\rho_{\delta}u_{\epsilon}\|\|_{H^{1+\alpha}}$
		$\displaystyle+(c\epsilon+c\delta)\|\|u_{\epsilon}\|\|_{H^{1+\alpha}}$
	$\displaystyle\leq$	$\displaystyle c\mathop{\operator@font m\acute{a}x}\{\epsilon,\delta\}\|\|u_{\epsilon}\|\|_{H^{3}}$

La ecuación de Burgers como un paso previo al estudio de los fluidos incompresibles

Resumen

1 Introducción y motivación

Teorema 1 (Beale-Kato-Majda).

2 Existencia local de la solución clásica

2.1 Estimaciones a priori

Proposición 1 (Principio del máximo para ||⋅||L2||\cdot||_{L^{2}}).

Demostración.

Proposición 2.

Demostración.

2.2 Regularización del problema

Proposición 3.

2.3 Existencia para los problemas regularizados

Lema 1.

Demostración.

Lema 2.

2.4 Paso al límite ϵ→0\epsilon\rightarrow 0

Lema 3.

Demostración.

Lema 4.

Demostración.

2.5 Regularidad de uu

Teorema 2 (Existencia local de solución clásica).

Demostración.

3 Propiedades de las soluciones

Proposición 4 (Conservación de la masa).

Demostración.

Proposición 5 (Principio del máximo para ||⋅||L∞||\cdot||_{L^{\infty}}).

Demostración.

4 Un resultado análogo al de Beale-Kato-Majda

Proposición 6.

Demostración.

5 Buscando singularidades

Proposición 7 (Singularidad).

5.1 Interpretando la singularidad

6 Método numérico

6.1 Discretización espacial

6.2 Discretización temporal

Referencias

Proposición 1 (Principio del máximo para $||\cdot||_{L^{2}}$ ).

2.4 Paso al límite $\epsilon\rightarrow 0$

2.5 Regularidad de $u$

Proposición 5 (Principio del máximo para $||\cdot||_{L^{\infty}}$ ).