Università di Roma “La Sapienza”, Dipartimento di Matematica, Piazzale Aldo Moro 2, 00185 Roma, Italy
1
LANGUAGE CLASSES ASSOCIATED WITH AUTOMATA OVER MATRIX GROUPS
Abstract.
We investigate the language classes recognized by group automata over matrix groups. For the case of matrices, we prove that the corresponding group automata for rational matrix groups are more powerful than the corresponding group automata for integer matrix groups. Finite automata over some special matrix groups, such as the discrete Heisenberg group and the Baumslag-Solitar group are also examined. We also introduce the notion of time complexity for group automata and demonstrate some separations among related classes. The case of linear-time bounds is examined in detail throughout our repertory of matrix group automata.
Key words and phrases:
group automata, time complexity1991 Mathematics Subject Classification:
68Q45, 68Q051. Introduction
Many extensions of the classical finite automaton model have been examined. One such variant is the group automaton (finite automaton over groups), which is a nondeterministic finite automaton equipped with a register that holds an element from a group [18]. The register is initialized to the identity element of the group, and a computation is deemed successful if the register is equal to the identity element at the end of the computation after being multiplied at every step. This setup generalizes various models such as nondeterministic blind multicounter automata [8] and finite automata with multiplication [13].
The theory of group automata has been essentially developed in the case of free groups [5, 4, 14], and in the case of free Abelian groups [7, 6], where strong theorems allow to characterize the power of such models and the combinatorial properties of the languages recognized by these automata. For groups that are not of the types mentioned above, even in the case of groups of matrices of low dimension, the study of group automata quickly beomes nontrivial, and there are remarkable classes of linear groups for which little is known about the automaton models that they define.
In this paper, we present several new results about the classes of languages recognized by finite automata over matrix groups. We focus on matrix groups with integer and rational entries. For the case of matrices, we prove that the corresponding group automata for rational matrix groups are more powerful than the corresponding group automata for integer matrix groups. We also explore finite automata over some special matrix groups, such as the discrete Heisenberg group and the Baumslag-Solitar group. The “zoo” of language classes associated with different groups is presented, visualizing known relationships and open problems.
We also introduce the notion of time complexity for group automata, and use this additional dimension to analyze the relationships among the language families of various automata using different groups. We develop a method for proving that automata over matrix groups where the growth rate of the group and the time are bounded can not recognize certain languages, even if one uses a very weak definition of time-bounded computation, and use this to demonstrate some new relationships between time-bounded versions of our language classes. The case of linear-time bounds is examined in detail throughout our repertory of matrix groups.
2. Preliminaries
2.1. Notation and terminology
The following notation will be used throughout the paper: is the set of states, denotes the initial state, denotes the set of accepting states, and is the input alphabet.
By , we represent the reverse of the string . The length of is denoted by .
, , and denote the families of regular languages, context-free languages, and recursively enumerable languages, respectively.
We assume a familiarity with some basic notions from algebra and group theory (see [9],[17] for references on this topic). For a finitely generated group and a set of generators, the word problem language of is the language over which consists of all words that represent the identity element of . Most of the time, the statements about the word problem are independent of the generating set and in these cases the word problem language is denoted by . For a string , where each represents a generator.
2.2. Group automata
Group automata first appear explicitly in the paper [18] under the name of extended finite automaton. The definition is formally given as follows.
Let be a group under the operation denoted by with the neutral element denoted by . An extended finite automaton over the group is a 6-tuple
where the transition function is defined as
means that when reads the symbol (or empty string) in state , it can move to state , and write in the register, where is the old content of the register. The initial value of the register is the neutral element of the group . The string is accepted if, after completely reading the string, enters an accept state with the content of the register being equal to the neutral element of .
We will prefer using the name group automaton (-automaton) instead of extended finite automaton over group .
Monoid automata are defined analogously where the group is replaced by some monoid .
The class of languages recognized by -automata will be denoted as .
3. Matrix groups and associated language classes
In this section, we are going to prove some new results about the classes of languages recognized by finite automata over various groups, focusing on linear groups.
3.1. Basic results
We will denote the free group over generators by . Note that is the trivial group, and is isomorphic to , the additive group of integers. The class of regular languages is characterized as the set of languages recognized by finite automata over the trivial group in [5].
The relation between the classes of languages recognized by free group automata is summarized as follows.
Fact \thethrm.
[5] .
A characterization of context-free languages by group automata was first stated by Dassow and Mitrana [5], and proven in [4]. Let us note that contains any free group of rank [17].
We will denote by the additive group of integer vectors of dimension . This group is isomorphic to the free Abelian group of rank , and -automata are equivalent to nondeterministic blind -counter automata [11].
The following result states the hierarchy between the classes of languages recognized by -automata. This result also follows from the hierarchy between the class of languages recognized by nondeterministic blind -counter automata.
Fact \thethrm.
[3] for .
We denote by the multiplicative group of positive rational numbers, which is isomorphic to a free Abelian group of infinite rank. A -automaton is also equivalent to a nondeterministic finite automaton with multiplication without equality (1NFAMW) of Ibarra et al. [13].
The following fact characterizes the class of languages recognized for the case where the alphabet is unary,
Fact \thethrm.
[13] All 1NFAMW-recognizable languages over a unary alphabet are regular.
Let us mention that the class of context-free languages and the class of languages recognized by nondeterministic blind counter automata are incomparable.
Fact \thethrm.
and are incomparable for all .
Proof.
Consider the language which is a context-free language. Since context-free languages are closed under star, is a context-free language whereas it cannot be recognized by any -automaton for all by [11]. On the other hand, the non-context-free language can be recognized by a -automaton. ∎
3.2. Automata on groups of and matrices
We denote by the general linear group of degree two over the field of integers, that is, the group of invertible matrices with integer entries. Note that these matrices have determinant . Restricting the matrices in to those that have determinant 1, we obtain the special linear group of degree two over the field of integers, .
Let be the group generated by the matrices
There exists an isomorphism from onto by [15]. Note that and are integer matrices with determinant 1, which proves that is a subgroup of .
Now the question is whether and correspond to larger classes of languages than the class of context-free languages. We are going to use the following fact to prove that the answer is negative.
Fact \thethrm.
[4] Suppose is a finitely generated group and is a subgroup of finite index. Then .
Now we are ready to state our theorem.
.
Proof.
Let us now investigate the group , the group of integer matrices with determinant .
We start by looking at an important subgroup of , the discrete Heisenberg group. The discrete Heisenberg group is defined as , where is the commutator of and .
Any element can be written uniquely as .
It is shown in [19] that the languages , and can be recognized by -automata, using the special multiplication property of the group.
Correcting a small error in [19], we rewrite the multiplication property of the elements of .
We can make the following observation using the fact that contains non-context-free languages.
.
Proof.
The following result is a direct consequence of Fact 3.2.
.
Proof.
Since is a finitely generated group and has finite index in , the result follows by Fact 3.2. ∎
We have talked about the discrete Heisenberg group H. Now let us look at a subgroup of generated by the matrices and , which we will call .
is a free Abelian group of rank 2, and therefore it is isomorphic to .
We conclude the following about the language recognition power of and .
.
Proof.
Now let us move on to the discussion about matrix groups with rational entries.
Let us denote by the general linear group of degree two over the field of rational numbers, that is, the group of invertible matrices with rational entries. Restricting the matrices in to those that have determinant 1, we obtain the special linear group of degree two over the field of rationals, .
We will start by proving that allowing rational entries enlarges the class of languages recognized by matrices with determinant 1.
.
Proof.
It is obvious that . We will prove that the inclusion is proper.
Let us construct an -automaton recognizing the language . The state diagram of and the matrices are given in Figure 1. Without scanning any input symbol, first multiplies its register with the matrix . then multiplies its register with the matrix successively until nondeterministically moving to the next state. After that point, starts reading the string and multiplies its register with the matrix for each scanned . At some point, nondeterministically stops reading the rest of the string and multiplies its register with the matrix . After successive multiplications with , nondeterministically decides moving to an accept state.
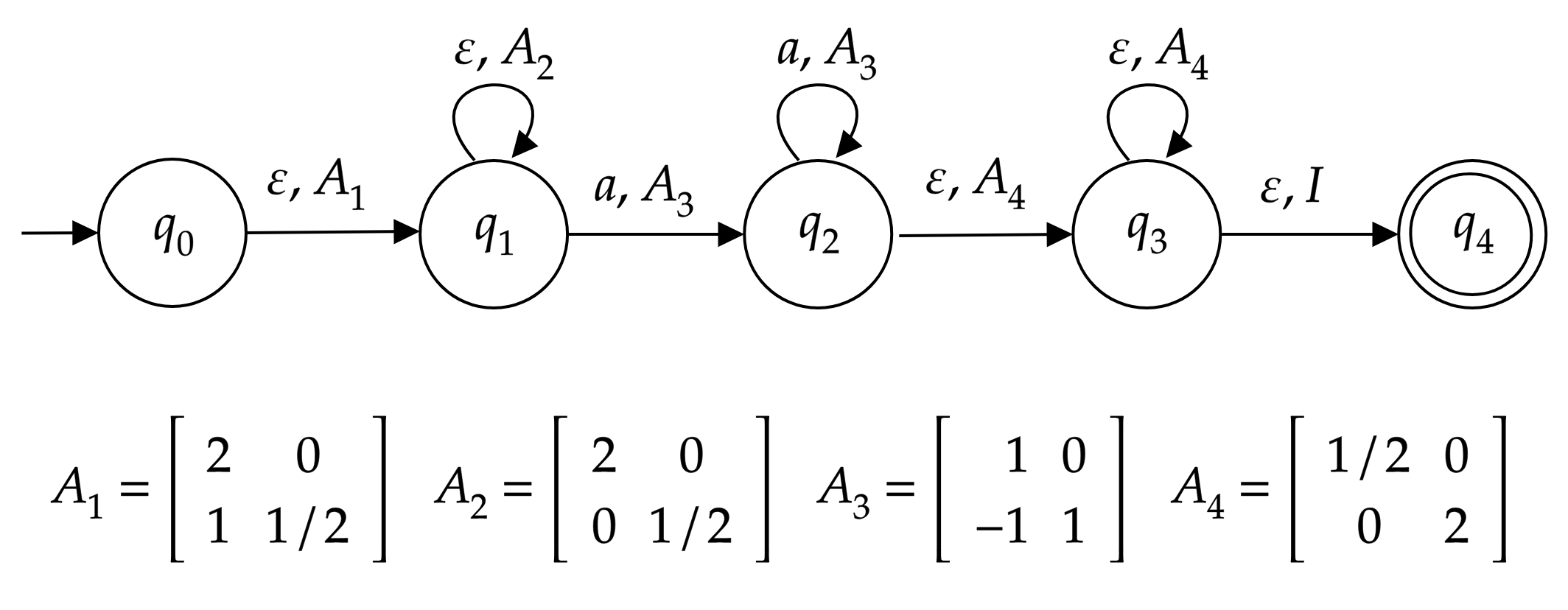
Let us trace the value of the register at different stages of the computation. Before reading the first input symbol, the register has the value
as a result of the multiplications with the matrix and times the matrix . Multiplication with each leaves and unchanged while subtracting from for each scanned . As a result of multiplications with , the register will have the value
For the rest of the computation, will multiply its register with until nondeterministically moving to the final state. As a result of multiplications with , the register will have the value
The final value of the register is equal to the identity matrix when and , which is possible only when the length of the input string is for some . In the successful branch, the register will be equal to the identity matrix and will end up in the final state having successfully read the input string. For input strings which are not members of , either the computation will end before reading the whole input string, or the final state will be reached with the register value not equaling the identity matrix.
Since the matrices used during the computation are 2 by 2 rational matrices with determinant 1, . contains a unary nonregular language, which is not true for by Theorem 3.2 and we conclude the result. ∎
Let us note that the set of languages recognized by -automata is a proper subset of the set of languages recognized by -automata, which can be concluded with the help of the following fact.
.
Proof.
Let and let be a -automaton recognizing . We will construct an -automaton recognizing . Let be the set of elements multiplied with the register during the computation of . We define the mapping as follows.
The elements are rational matrices with determinant 1. Let and be the transition functions of and respectively. We let for every , and . The resulting recognizes .
We will now look at a special subgroup of .
For two integers and , the Baumslag-Solitar group is defined as . We are going to focus on .
Consider the matrix group generated by the matrices
Consider the isomorphism , . The matrices and satisfy the property ,
and we conclude that is isomorphic to .
We will prove that there exists a -automaton which recognizes a non-context-free language.
.
Proof.
Let us construct a -automaton recognizing the language . The state diagram of and the matrices are given in Figure 2. Without scanning any input symbol, multiplies its register with the matrix successively. nondeterministically moves to the next state reading the first input symbol without modifying the register. After that point, starts reading the string and multiplies its register with the matrix for each scanned . At some point, nondeterministically stops reading the rest of the string and multiplies its register with the element . After successive multiplications with , nondeterministically decides to move to an accept state.
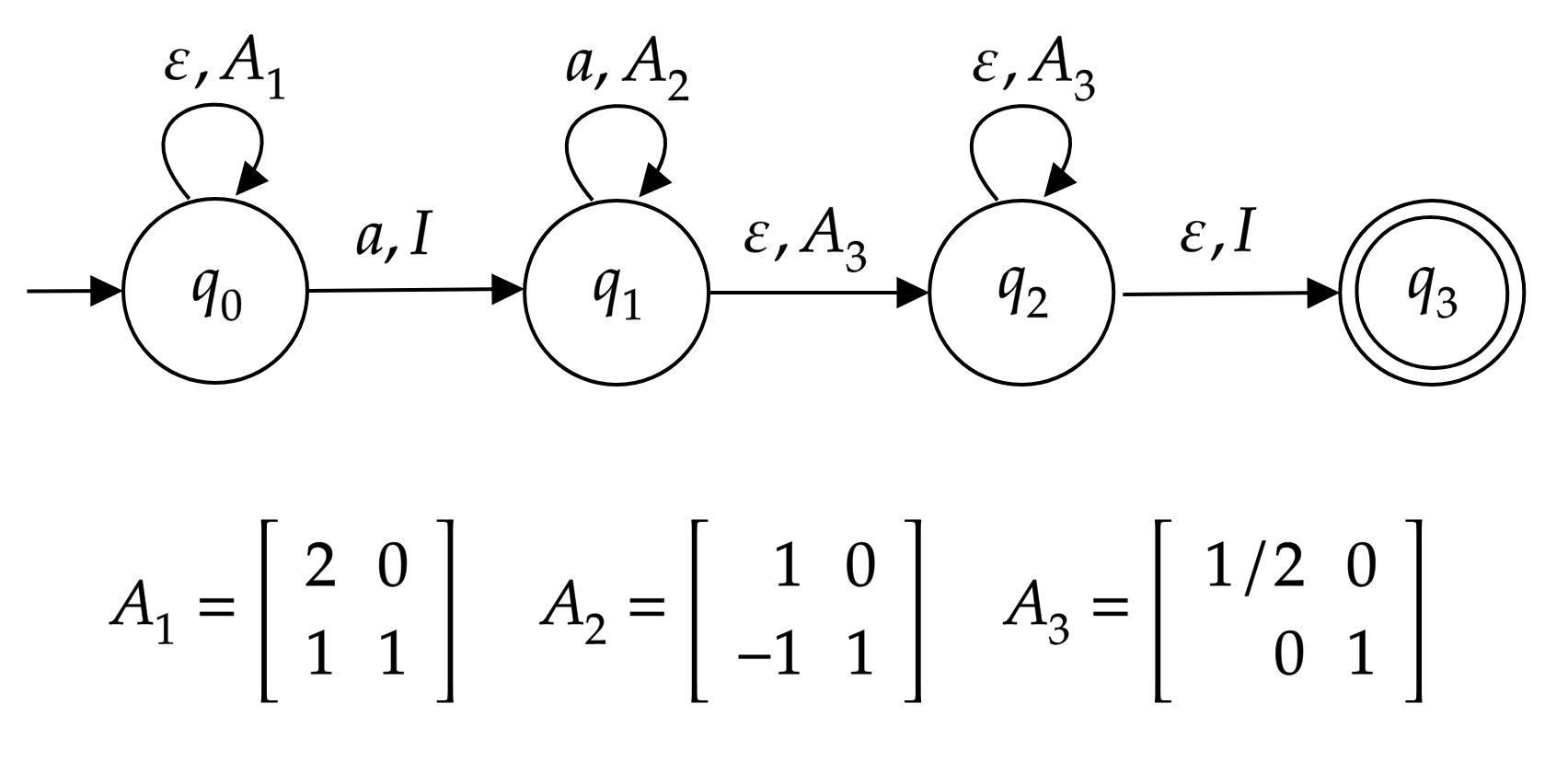
As a result of multiplications with , the register has the value
before reading the first input symbol. Multiplication with each leaves unchanged while subtracting 1 from for each scanned . The register will have the value
as a result of multiplications with the matrix .
For the rest of the computation, will multiply its register with resulting in the register value
since each multiplication with divides by 2.
The register contains the identity matrix at the end of the computation if and which is possible if the input string is of the form . In the successful branch, the register will be equal to the identity matrix and will end up in the final state having successfully read the input string.
For input strings which are not members of , either the computation will end before reading the whole input string or the final state will be reached with the register value being different from the identity matrix. Note that , and , where and are the generators of the group and recall that is isomorphic to . Since is a unary nonregular language, it is not context-free and we conclude the result. ∎
Note that since the subgroup generated by in is isomorphic to and contains a unary nonregular language.
3.3. Automata on matrices of higher dimensions
In [18], it is proven that -automata are as powerful as Turing machines.
Fact \thethrm.
[18] is the family of recursively enumerable languages.
We make the following observation.
.
Proof.
The first equality is Fact 3.3. Recall from Section 3.2 that is an isomorphism from onto , the matrix group generated by the matrices and . Let be the following group of matrices
We will define the mapping as for all which is an isomorphism from onto .
This proves that is isomorphic to a subgroup of . The fact that is the set of recursively enumerable languages helps us to conclude that is the set of recursively enumerable languages for . ∎
Let us also state that the classes of languages recognized by automata over supergroups of such as or are also identical to the class of recursively enumerable languages. {thrm} , where is any matrix group whose matrix entries are computable numbers and is a subgroup of .
Proof.
Note that any finite automaton over a matrix group can be simulated by a nondeterministic Turing machine which keeps track of the register simply by multiplying the matrices and checking whether the identity matrix is reached at the end of the computation, provided that the matrix entries are computable numbers. Since and contains as a subgroup, is the set of recursively enumerable languages. ∎
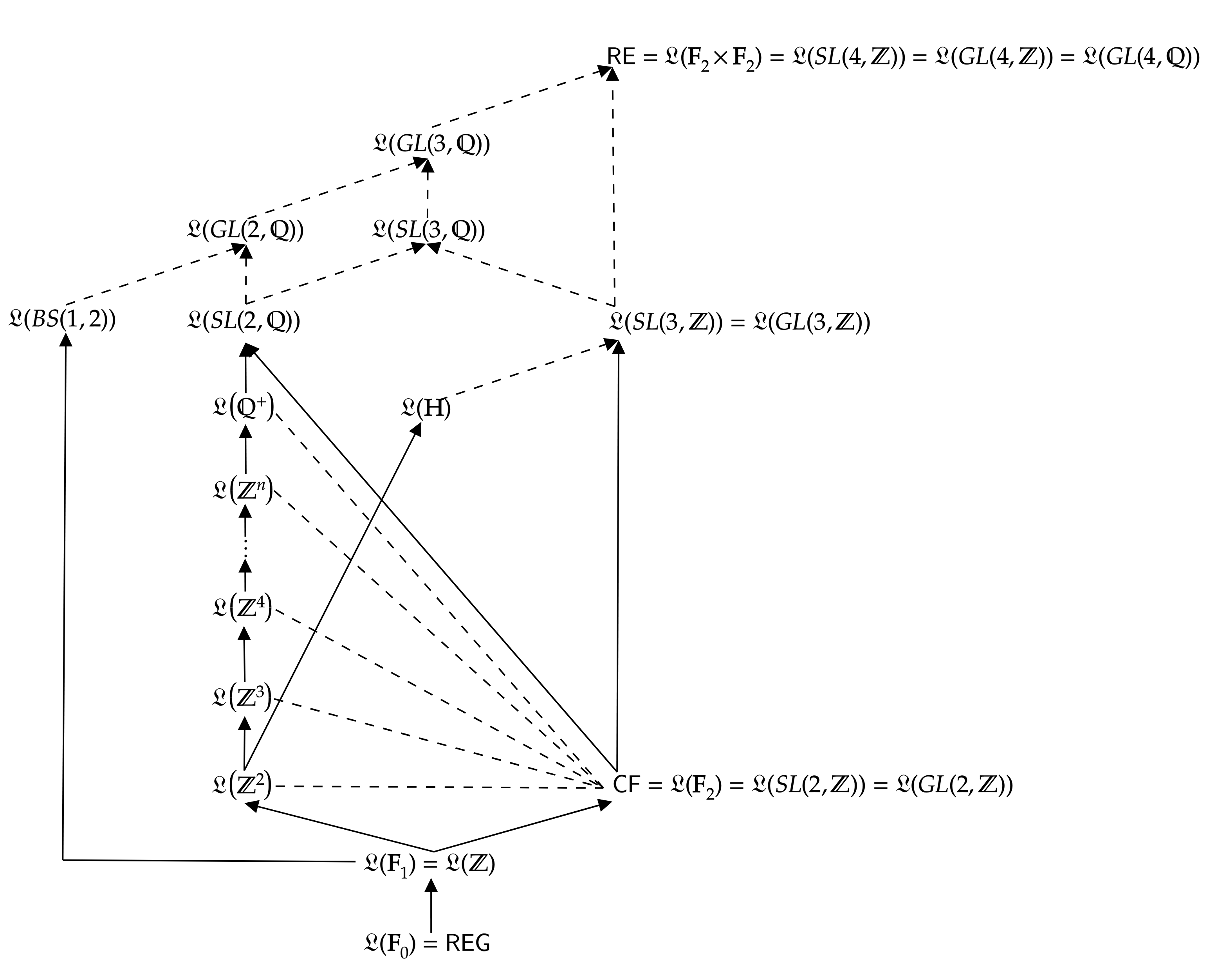
We summarize the results in Figure 3. Solid arrows represent proper inclusion, dashed arrows represent inclusion and dashed lines represent incomparability.
4. Time complexity
In the previous section, we compared various automaton models solely on the basis of the groups they employed as a computational resource. The theory of computational complexity deals with various different types of such resources, the allowed runtime of the machines being the most prominent among them. Some of the automata we saw in Section 3 (e.g. Figure 2) have arbitrarily long computations, and it is a legitimate question to ask whether our results, for instance, the relationships in Figure 3, would still hold if one imposed common time bounds on the automata. We study such questions in this section.
4.1. Definitions
A group automaton recognizing language is said to be strongly time-bounded if for any input string with , every computation of on takes at most steps. We will denote the set of languages recognized by strongly -time bounded -automata by .
Although the strong mode of recognition defined above is standard in studies of time complexity, we will be able to prove the impossibility results of the next subsection even when the machines are subjected to the following, looser requirement:
A group automaton recognizing language is said to be weakly time-bounded if for each accepted input string with , has a successful computation which takes at most steps. So any input string is allowed to cause longer computations, as long as none of those are accepting for inputs which are not members of . We will denote the set of languages recognized by weakly -time bounded -automata by .
A machine is real-time if every transition consumes an input symbol.
Note that the statement is true by definition.
Let be a generator set for the group . The length of , denoted , is the length of the shortest representative for in . Let be the set of all elements in which can be represented by a word of length at most . The growth function of a group with respect to a generating set , denoted , is the cardinality of the set , that is . The growth function is asymptotically independent of the generating set, and we will denote the growth function of a group by .
For a positive integer , two strings are -dissimilar for if , , and there exists a string with , such that iff . Let be the maximum such that there exist distinct strings that are pairwise -dissimilar.
A finite set of strings is said to be a set of uniformly -dissimilar strings for if for each string , there exists a string such that and and for any string such that , and . Let be the maximum such that there exist distinct strings that are uniformly -dissimilar.
Note that the following is always true by definition, since the strings in a uniformly -dissimilar set are pairwise -dissimilar.
for all .
4.2. Limitations of machines on slow groups running in short time
Let be a group with growth function . if .
Proof.
Suppose for a contradiction that there exists a weakly time-bounded -automaton recognizing in time . For a sufficiently large , let be the set of uniformly -dissimilar strings such that . For every string , there exists a string such that and for all with .
Let be the set of accepted extended strings of the form with where and for all with and . Let be the set of time bounded accepting computation paths for the strings in . The computation on the string can be written as
where represents the computation up to the end of the prefix and represents the rest of the computation on the string .
A configuration of a group automaton is a pair consisting of a state and a group element. Let us count the number of configurations that can be reached at the end of the computation . Since the number of states is constant, the number of configurations that can be reached is dependent on the number of different group elements that can appear in the register. After reading a prefix with , the product of the labels on the edges can be given by for some , since the computation in consideration is time bounded. can be expressed as a product of generators, where is at most for some constant , since each group element labeling a transition in is composed of at most some constant number of generators, which is independent of the length of the string. The number of elements in which can be represented as a product of at most generators is given by by the definition of the growth function of . Hence, the number of different values that can appear in the register after reading a string of length exactly is less than or equal to . Since and and , we can conclude that
Now it is easy to see that the number of different configurations that can be reached at the end of a computation is . Note that the cardinality of the set , and thus that of , is equal to . Due to the pigeonhole principle, the same configuration must be reached at the end of two computations and for some . This will result in the acceptance of the strings and , which are not members of . We arrive at a contradiction and conclude that cannot be recognized by any weakly time-bounded -automaton. ∎
In the next lemma, we set a lower bound on maximum cardinality of the set of uniformly -dissimilar strings in the word problem language of some group .
Let be a finitely generated group with growth function . Then .
Proof.
Let be the generator set of . The number of distinct elements in which can be represented by a word of length less than or equal to is , which is the cardinality of the set . Let be the set containing the string representations of the elements in . Every can be extended with so that the extended string represents the identity element of and has length less than or equal to . Since the strings in are those which belong to and represent the identity element of , the extended string . For every string such that , since it is not possible for to represent the identity element of . We conclude that the set is uniformly -dissimilar. Since , it follows that . ∎
The following theorem is about the language recognition power of finite automata over polynomial-growth groups which are weakly polynomial time-bounded. {thrm} Let and be groups with polynomial and exponential growth functions and , respectively. For any polynomial , .
Proof.
Let be a group with a polynomial growth function. For any polynomial , .
Proof.
4.3. Group automata under linear time bounds
In this section, we focus on linear-time computation.
Let be a generator set. For each symbol , the functions and are defined as follows.
Let be the submonoid of all partial functions on generated by and for all . is called the polycyclic monoid on . A -automaton is equivalent to a pushdown automaton, where and can be interpreted as pushing and popping symbols on the stack. The equivalence between the two models is due to the nature of the functions and , and is described in detail in [14]. The resemblance between the free group and is used to prove that in [14] and [4].
Our aim is to show that -automata working in linear time can recognize all context-free languages. It is stated in [21] that -automata which consume at least one input symbol at each step are as powerful as -automata without any time bound. However, it is not straightforward to see whether the same is true for -automata.
.
Proof.
We are going to use the construction of Kambites [14] to prove that any context-free language can be recognized by a weakly linear-time bounded -automaton.
Let be a context-free language and let be a polycyclic monoid automaton recognizing . is the polycyclic monoid on where the cardinality of the set is for some . Let be the identity element of . The construction of Kambites provides an -automaton recognizing the language . The generator set for is , where .
Let us analyze the construction in more detail.
-
•
where and
-
•
= where .
-
•
.
-
•
if where is a positive generator for all .
-
•
if where is a negative generator for all .
-
•
if for all .
-
•
for each .
-
•
for each .
We will prove that actually runs in linear time. There are two transitions where the automaton is allowed to move without consuming any input symbols.
For each state , there are two states and in which are connected with an edge labeled . These transitions do not change the register value, and cannot contribute more than half of the runtime of the machine, since at least one input symbol has to be consumed between any two executions of such transitions.
-loops exist in the machine for each state where the loop is labeled by . Although this looks worrisome at first for the purpose of bounding the runtime, the number of times these loops are traversed is actually bounded, as the following argument suggests. Suppose that the register is multiplied with , , , while reading some input string of length , resulting in the register value , where , at the end of the computation. If is accepted by the machine, should satisfy the following, as well as being equal to the identity element:
This is called a permissible padding in [14]. By looking at the transition function of , one can see that the register is multiplied by a only when an input symbol is consumed. Hence, the number of ’s that occur in is less than or equal to the length of the string. The register is multiplied with without consuming any input symbol. In order for the ’s and ’s to cancel each other, they should be equal in number. Therefore, it can be concluded that the -loops are traversed at most times.
We can conclude that any context-free language can be recognized by a weakly linear-time bounded free group automaton. Since contains every free group of countable rank, the proof is complete. ∎
Suppose is a finitely generated group and is a subgroup of finite index. Then .
Proof.
Now we can show that Theorem 3.2 also holds for linear-time bounded group automaton.
.
By using the results proven in Subsection 4.2, we can demonstrate the language recognition power of weakly linear-time bounded -automata.
.
Proof.
i. For , and are incomparable.
ii. and are incomparable.
Proof.
i. In [19], a weakly linear-time bounded -automaton which recognizes the language is constructed. The language can not be recognized by any -automaton, since any bounded language in is semilinear by [13].
In [10], it is implicitly proven there exists a uniformly -dissimilar set of size for the language for all integers . For , there exists a uniformly -dissimilar set of size for the language and . Since is a polynomial of order 4 [16] and , . By Theorem 4.2, we conclude the result.
The language is not a context-free language. Since has a polynomial growth function [16], there exists a context-free language which can not be recognized by any -automaton in polynomial-time by Theorem 4.2.
∎
Let us note that can be recognized by a -automaton in real time. The existence of the languages can be used to prove the linear-time nondeterministic counter hierarchy, with the help of Theorem 4.2.
for .
Proof.
The language can be recognized by a -automaton in real time. While scanning the first segments of ’s, the ’th counter is increased for each scanned as is read. In the remainder of the computation, the ’th counter is decreased for each scanned when is read.
A celebrated result of the field of computational complexity, the nondeterministic time hierarchy theorem, will enable us to demonstrate that the computational power -automata is dependent on the time allotted for their execution.
Fact \thethrm.
[20] If is a time-constructible function, and , then there exists a language which cannot be recognized by any nondeterministic Turing machine in time , but can be recognized by a nondeterministic Turing machine in time .
Assume that any recursively enumerable language can be recognized by some linear-time -automaton. One can easily build a nondeterministic Turing machine that simulates such a -automaton with only a polynomial slowdown. But this would mean that any recursively enumerable language can be recognized by some nondeterministic TM in polynomial time, contradicting Fact 4.3, which implies that there exist languages which can only be recognized by nondeterministic Turing machines which run in at least exponential time. We have proven the following theorem.
.
Using the ability of Turing machines to simulate any finite automaton over a computable matrix group, the statement of the above theorem can be extended as follows.
for any matrix group whose matrix entries are computable numbers.
Proof.
In Theorem 3.3, we have mentioned that Turing machines can simulate any finite automaton over a computable matrix group. By the nondeterministic time hierarchy theorem, it can be shown that there exist some languages which can not be recognized by any finite automata over matrix groups in linear time. ∎
.
Proof.
It is obvious that an -automaton can be simulated by an -automaton. by Theorem 4.3. The inclusion is proper since the non-context-free language can be recognized by an -automaton in real time by using the two registers as two counters. ∎
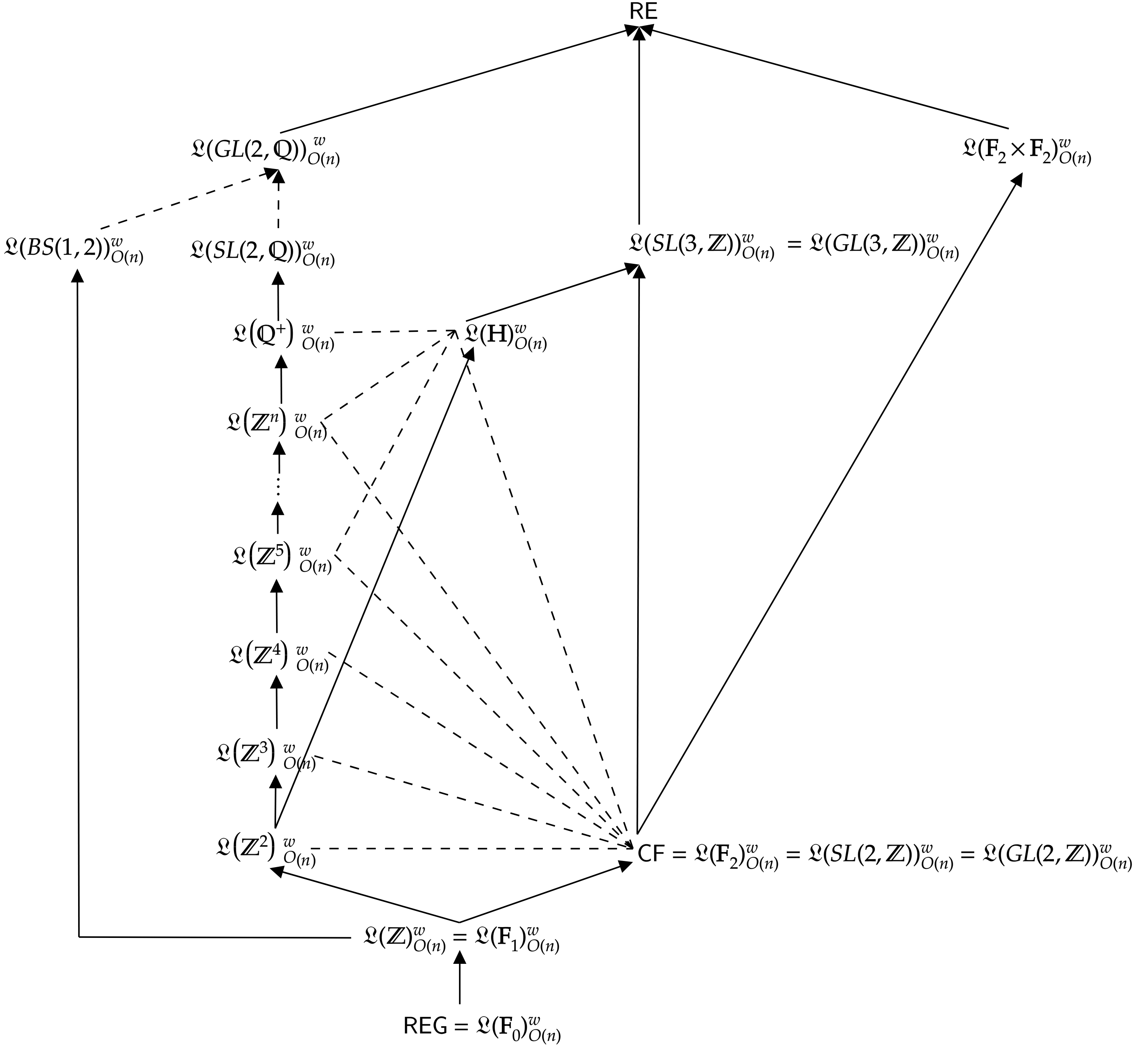
In the rest of the section, the linear-time counterparts of the relationships in Figure 3 will be stated.
-
i.
.
-
ii.
.
-
iii.
.
-
iv.
.
-
v.
and are incomparable for all .
-
vi.
.
-
vii.
.
Proof.
Analogous results where no time bound was imposed on the machines were proven in Theorems 3.2, 3.2, 3.2, and 3.2, respectively. The group automata recognizing the witness languages , and operate in weakly linear time in all cases.
v. The equivalent result for the general case is given in Fact 3.1. The non-context-free language can be recognized by a -automaton in real time.
vi. The equivalent result for the general case is given in Theorem 3.2. The result follows by Theorem 4.3.
vii. The equivalent result for the general case is given in Fact 3.1. is the trivial group, and any regular language can be recognized by a deterministic finite automaton, which can be seen as finite automaton over , in real time. Since is isomorophic to , the equality is obvious. Since the nonregular language can be recognized by a -automaton in real time, the proper inclusion follows. Lastly, since is equivalent to by Theorem 4.3, the last proper inclusion is still valid. ∎
The results are summarized in Figure 4.
5. Open questions
Does there exist an -automaton recognizing ? 111Corollary 2 of [3] states that the word problem of a finitely generated Abelian group is recognized by a -automaton if and only if has a finite index subgroup isomorphic to a subgroup of . That corollary could be used to give an affirmative answer to this open question. Unfortunately, the corollary is wrong: Let be an Abelian group and let . contains the word problem of any finitely generated Abelian group. Since is finitely generated, any finite index subgroup of is also finitely generated. Any finite index subgroup of is either free or has a subgroup of finite index that is a direct product of free groups [1]. Any subgroup of an Abelian group is again Abelian. Hence, it is not possible that has a finite index subgroup isomorphic to a subgroup of .
Can we prove a stronger version of Theorem 4.2, which is independent of the time component? For instance, for the case of , is it true that in general?
Can we describe the necessary properties of a group so that contains ?
Little is known about -automata. Does contain every context-free language?
Which, if any, of the subset relationships in Figure 3 are proper inclusions?
Can we add other classes above RE in Figure 3 by examining groups on matrices with uncomputable entries?
Theorem 4.2 uses the definition of uniform -dissimilarity requiring that . Would the theorem be still true if we replace by ? The gap between and might be large as mentioned in [10]. Consider the language . It is stated in [10] that a set of uniformly -dissimilar strings for can not contain more than two strings. However, , since is not a regular language.
Can real-time -automata recognize every context-free language?
References
- [1] Gilbert Baumslag and James E Roseblade. Subgroups of direct products of free groups. Journal of the London Mathematical Society, 2(1):44–52, 1984.
- [2] Nathanial Patrick Brown and Narutaka Ozawa. C*-algebras and finite-dimensional approximations, volume 88. American Mathematical Soc., 2008.
- [3] Sean Cleary, Murray Elder, and Gretchen Ostheimer. The word problem distinguishes counter languages. arXiv preprint math/0606415, 2006.
- [4] Jon M. Corson. Extended finite automata and word problems. International Journal of Algebra and Computation, 15(03):455–466, 2005.
- [5] Jürgen Dassow and Victor Mitrana. Finite automata over free groups. International Journal of Algebra and Computation, 10(06):725–737, 2000.
- [6] Murray Elder, Mark Kambites, and Gretchen Ostheimer. On groups and counter automata. International Journal of Algebra and Computation, 18(08):1345–1364, 2008.
- [7] Gillian Z. Elston and Gretchen Ostheimer. On groups whose word problem is solved by a counter automaton. Theoretical Computer Science, 320(2–3):175 – 185, 2004.
- [8] Patrick C. Fischer, Albert R. Meyer, and Arnold L. Rosenberg. Real time counter machines. In Proceedings of the 8th Annual Symposium on Switching and Automata Theory (SWAT 1967), FOCS ’67, pages 148–154, 1967.
- [9] J.B. Fraleigh and V.J. Katz. A first course in abstract algebra. Addison-Wesley world student series. Addison-Wesley, 2003.
- [10] Ian Glaister and Jeffrey Shallit. Automaticity iii: Polynomial automaticity and context-free languages. Computational Complexity, 7(4):371–387, 1998.
- [11] S. A. Greibach. Remarks on blind and partially blind one-way multicounter machines. Theoretical Computer Science, 7:311–324, 1978.
- [12] Rostislav I Grigorchuk. On growth in group theory. In Proceedings of the International Congress of Mathematicians, volume 1, pages 325–338, 1990.
- [13] Oscar H. Ibarra, Sartaj K. Sahni, and Chul E. Kim. Finite automata with multiplication. Theoretical Computer Science, 2(3):271 – 294, 1976.
- [14] Mark Kambites. Formal languages and groups as memory. Communications in Algebra, 37(1):193–208, 2009.
- [15] Mikhail I. Kargapolov and Ju. I. Merzljakov. Fundamentals of the Theory of Groups. Springer-Verlag, 1979.
- [16] Pierre De La Harpe. Topics in geometric group theory. The University Of Chicago Press, Chicago, 2000.
- [17] Roger C. Lyndon and Paul E. Schupp. Combinatorial Group Theory. Springer-Verlag, 1977.
- [18] Victor Mitrana and Ralf Stiebe. The accepting power of finite automata over groups. In New Trends in Formal Languages, pages 39–48. Springer-Verlag, 1997.
- [19] Elaine Render. Rational monoid and semigroup automata. PhD thesis, University of Manchester, 2010.
- [20] Stanisław Żak. A Turing machine time hierarchy. Theoretical Computer Science, 26(3):327 – 333, 1983.
- [21] Georg Zetzsche. Silent transitions in automata with storage. In International Colloquium on Automata, Languages, and Programming, pages 434–445. Springer Berlin Heidelberg, 2013.