Large Mass Inflow Rates in Saturn’s Rings due to Ballistic Transport and Mass Loading
Abstract
The Cassini mission provided key measurements needed to determine the absolute age of Saturn’s rings, including the extrinsic micrometeoroid flux at Saturn, the volume fraction of non-icy pollutants in the rings, and the total ring mass. These three factors constrain the ring age to be no more than a few 100 Myr [54]. Observations during the Cassini Grand Finale also showed that the rings are losing mass to the planet at a prodigious rate. Some of the mass flux falls as “ring rain” at high latitudes. However, the influx in ring rain is considerably less than the total measured mass influx of to kg s-1 at lower latitudes [90].
In addition to polluting the rings, micrometeoroid impacts lead to ballistic transport, the mass and angular momentum transport due to net exchanges of meteoroid impact ejecta. Because the ejecta are predominantly prograde, they carry net angular momentum outward. As a result, ring material drifts inward toward the planet. Here, for the first time, we use a simple model to quantify this radial mass inflow rate for dense rings and find that, for plausible choices of parameters, ballistic transport and mass loading by meteoroids can produce a total inward flux of material in the inner B ring and in the C ring that is on the order of a few to a few kg s-1, in agreement with measurements during the Cassini Grand Finale. From these mass inflow rates, we estimate that the remaining ring lifetime is 15 to 400 Myr. Combining this with a revised pollution age of 120 Myr, we conclude that Saturn’s rings are not only young but ephemeral and probably started their evolution on a similar timescale to their pollution age with an initial mass of one to a few Mimas masses.
In addition to showing that meteoroid impacts can produce a large sustained mass inflow through the B and C rings, this paper addresses various uncertainties and considers possible contributions by additional transport mechanisms and by external torques. We also map out a set of future research projects, including global simulations.
keywords:
Saturn, rings , Planetary rings , Interplanetary dust1 Introduction
One of the impressive results of the Cassini Grand Finale was the measurement of a surprisingly large mass inflow into Saturn from the rings [90, 48, 63], as summarized in Perry et al. [72]. This inflow is at least an order of magnitude or more than the ring rain inferred from observations of Saturn’s upper atmosphere (see Section 2.2). The Cassini mission overall, including the final orbits, has also improved our knowledge of parameters and processes critical to assessing how strongly meteoroid bombardment affects the rings. In particular, meteoroid bombardment causes the rings to evolve due to mass deposition by the meteoroids (mass loading, hereafter ML) and due to exchanges between different ring regions of mass and angular momentum through impact ejecta produced by the meteoroids (ballistic transport, hereafter BT). What we demonstrate in this paper is that these processes can plausibly produce a mass inflow through the B and C rings toward Saturn of the magnitude observed.
This paper is organized as follows. Section 2 details the motivation for this work, especially the large mass inflow into Saturn detected from the rings and the other new constraints on ring properties and environment derived from the Cassini Grand Finale. In Section 3, we review some basics of transport due to meteoroid bombardment. In Section 4, we develop simple models for the mass inflow expected from BT and ML, and we apply these models to Saturn’s rings in Section 5, along with an estimate for the mass inflow rate due to viscosity. Section 6 presents a discussion of the mass influx rates, the absolute ring age, and the expected ring lifetime, and we summarize our conclusions and planned future work in Section 7.
2 Background and Motivation
2.1 Ring Age and Pollution by Meteoroids
Saturn’s rings are continuously subjected to bombardment by extrinsic micrometeoroids. This affects the rings in two principal ways. First, incoming impactors can lead to structural evolution of the rings because the copious ejecta produced by impacts cause mass and angular momentum exchanges between different ring regions [50, 51, 19, 23, 21, 22, 29, 30, hereafter I83, I84, D84, D89, D92, D96, E15 and E18]. The meteoroids can also deposit mass and exert net torques on a global scale (I84; D96; E15; E18). Second, the predominantly icy rings become more and more polluted because the incoming material, which has a large non-icy component, darkens the rings over time [15, hereafter CE98]. In particular, lower mass surface density and/or optical depth regions such as the C ring and Cassini division darken faster than the denser, more massive A and B rings. The susceptibility of the rings to the effects of micrometeoroid bombardment comes about in no small measure because of the rings’ massive surface-area-to-mass ratio, about a factor of times more than for a moon of equal mass (E15).
Key parameters, such as the rate of deposition of extrinsic material, the ring mass, and the current level of ring pollution, as well as an understanding of the physics of how material is redistributed in the rings over time, provide a powerful age-dating tool for the rings. Prior to the Cassini Grand Finale, some of these parameters remained the subject of debate and speculation. That the rings might in fact be younger than previously thought was first suggested by Voyager measurements showing that the albedo in the A and B rings were inconsistent with the fraction of pollutant they would have obtained over the age of the Solar System given the accepted micrometeoroid influx at the time [18, CE98]. The idea was considered unpopular because there was no apparent statistically plausible way to form the rings so long after the Late Heavy Bombardment if the rings were only a few hundred million years old [see, e.g., 17, 8]. Thus, the view that the rings cannot be young persisted until Cassini could provide definitive evidence.
Analyzing Cassini radiometer measurements, Zhang et al. [92, 93] found that the non-icy material volume fractions in the C ring and Cassini division were , whereas the fractions in the relatively more massive A and B rings were . These fractions are consistent with HST [16] and VIMS results [9] if the pollutant is intramixed in fine grains and shadowing is allowed for. While visible and IR wavelengths only sample the surface layers of the particles, the microwave measurements sample the bulk of the ring particles, so that the radial variation of pollutants across the rings indeed indicates that the rings overall are not very polluted and, moreover, exhibit a distinct contrast in the level of pollution between low- and high- regions. Although low- regions darken faster than high- regions, this contrast diminishes over long times because the darker regions become the dominant source for darkening of the brighter higher- regions due to ballistic transport [E15; 28]. While there is evidence that the middle C ring is polluted with non-icy material to higher levels than the rest of the C ring, Zhang et al. [93] showed that this can be explained by rubble from a captured Centaur that has become mixed into this region over the last few to ten million years or so. It does not affect the estimate of an overall pollution age.
In another caution about pollution ages, the Conclusions Section of Buratti et al. [7] asserts that their evidence for icy E ring dust accumulating on the surfaces of outer ring moons may invalidate young ring ages. Actually, what these authors find is that Pan in the Keeler gap has the same red color as the surrounding rings and that the reddening diminishes outward systematically as the distance of ring moons from Saturn increases. This suggests that the icy E ring dust, or whatever else may be the source of the icy material, is being deposited only in the outermost ring region and does not penetrate as far as Pan. Pollution age analyses are not sensitive to the outer few thousand kilometres of the rings but rely on comparisons between optically thick and thin regions much closer to Saturn. The orbital dynamics of E ring dust [38, 39, 40] make it unlikely that it would penetrate deeply into the main rings. So, while a refined treatment of pollution should probably consider sources of icy material, it is unlikely to affect ages based on meteoroid pollution for the bulk of the rings (see, however, Section 6.4.2).
Another key piece of data for estimating pollution ages is the input rate from meteoroids. Several authors estimated the mass flux of meteoroids at Saturn prior to Cassini [e.g., 65, 37, 14, hereafter CD90]. After a careful review of this work, CE98 showed in their Figure 17 that their improved estimate (the solid histogram in the figure) agreed with Pioneer and Ulysses data for 10 m sized particles and smaller. They concluded that the CD90 value for a one-sided interplanetary flux of 4.5 10-17 g cm-2 s-1 for small meteoroids at Saturn, the value used in ballistic transport and pollution calculations up to that time, was good to within a factor of three up or down. Here, “one-sided” means the flux measured passing through an area only from one side to the other. The Cassini Cosmic Dust Analyzer (CDA) experiment has now measured the meteoroid flux at Saturn and infers an interplanetary flux at 10 AU a factor of two less than the CD90 value [2, 1, 55, 54, see Section 5.1].
Furthermore, CDA finds, through orbit reconstruction, that the population of impactors is consistent with Edgeworth-Kuiper Belt (EKB) projectiles, not the Oort Cloud source that had been previously assumed (CD90; CE98). Particles from this dynamical population have much lower velocities as they enter Saturn’s Hill sphere (which we call “at infinity”) than cometary particles, and thus are about ten times more focused gravitationally by the planet. In other words, for a given micrometeoroid flux at infinity, the impact flux on the rings is an order of magnitude higher than previously assumed, thus lowering age estimates by about the same factor. This is illustrated by Figure 9.5 of E18, where the computation of CD90 was redone using a meteoroid velocity at infinity at Saturn of 3 km s-1 instead of the 14.4 km s-1 used in CD90. The increase in the ejecta intensity is an order of magnitude111The actual mean velocity at infinity as derived by CDA is km s-1 lowering the estimate of Estrada et al. [30, who estimated a factor of higher] by a factor of , but still overall an order of magnitude in ejecta intensity.. A similar factor can be obtained by applying the various gravitational focusing formulae referenced in Appendix B of CE98. All these computations involve approximations. A more careful treatment of gravitational focusing is needed but would be a substantial project. However, the order of magnitude difference in focusing between the two meteoroid populations is almost certainly valid and has been accepted for some time [e.g., 65].
Finally, the total ring mass plays a critical role in determining the exposure age of the rings. The post-Voyager estimate for the rings was roughly a Mimas mass [25], but if the ring mass surface density, say in the opaque, dense B ring core were an order of magnitude higher – an idea that seemed plausible from discovery of the rings’ clump-and-gap structure in which density waves could hide large amounts of mass [86, 79] – then the rings would be much more resistant to pollution and could be ancient [24]. However, from gravity field measurements in the final orbits of the Cassini Grand Finale, the mass of the rings has been determined to be Mimas masses [49], even lower than the post-Voyager estimate and similar to estimates from wavelet-based analyses of several density waves in the B ring [45].
Taken together, the direct bulk pollution measurements, the characterization of the meteoroid impactors, and the determination of the ring mass unambiguously suggest a youthful age for the rings. As discussed in detail by E18, with the new observational constraints, the ages deduced for the rings from meteoroid bombardment based on various global, structural, and pollution considerations all seem to agree on an age on the order of at most a few yrs. Rings with ages few yrs are consistent with the ring age calculated by Kempf et al. [54].
2.2 Ring Rain, Mass Inflow, and the Grand Finale
The end of the Cassini mission provided a unique opportunity to determine additional constraints for the rings. Observations conducted in its final 22 orbits, when the spacecraft flew through the 2000 km-wide region that separates the rings from Saturn’s upper atmosphere, measured the amount of ring material falling into the planet, thereby providing another means by which to constrain not only how old the rings are but also estimate how long their remaining lifetime may be. These final orbits also allowed for the determination of the composition of the ring material and to test the so-called “ring rain” hypothesis. In this scenario, some fraction of the ejected material resulting from micrometeoroid impacts (in the form of ions or nanometer-to-sub-micron-sized grains), which can be charged either by micrometeoroid impact-produced plasma or photoionization, travel along magnetic field lines and fall into Saturn’s (preferentially southern) atmosphere [11, 69, 53, 52]. The transport of this ejected material, presumed to be mostly water, into the Saturnian atmosphere is thought to explain the latitudinal pattern of ionospheric H infrared emission [e.g., 71, 64].
Cassini’s Magnetospheric Imaging Instrument (MIMI) which measured neutral atoms, ions and electrons was deployed, in part, to test the ring rain hypothesis. MIMI detected a very small flux of nm radius grains (assuming the density of ice) precipitating into Saturn’s atmosphere through the process of atmospheric drag due to kinetic collisions with exospheric H and H2. Modeling of the data indicate that the grains, likely originating from the D68 ringlet at the inner edge of the D ring and mostly confined within of the ring plane, precipitate at a rate of kg s-1 [63]. These authors also find that the charged component of these grains is relatively low in the midplane, but reaches a maximum in the wings of the distribution at higher latitudes () consistent with transport along magnetic field lines associated with ring rain. This flux is small, but may not be surprising given that MIMI only samples the low end of the particle size distribution, whereas larger particles dominate the mass density [48].
The CDA, which is sensitive to larger particles222 The CDA instrument has multiple impact targets that allow for sensitivity to a range of particle size [see 85]., was also active in the final orbits and found that the primary flux into the planet arises from grains nm in radius entering at moderate latitudes. Larger grains (hundreds of nm) are also seen confined to a band within a few hundred km of the midplane and with a lower abundance [48]. Their simulations indicate that the observed population of nanograins are fast ejecta released from the surfaces of the rings due to micrometeoroid impacts. These nanoparticles travel along magnetic field lines and are deposited in the atmosphere over a latitudinal range of . Hsu et al. [48] estimate an ejection rate for these tens of nanometer-sized particles to be 1800 to 6800 kg s-1 of which 18% arrive at Saturn as ring rain, or roughly 320 to 1200 kg s-1. Of this fraction, 70% is deposited near the midplane, while 30% (100 to 380 kg s-1) is deposited in the mid-latitude ring rain regions.
The measured mass inflow rate is over an order of magnitude more than the 3 to 20 kg s-1 of water product initially thought to be needed to account for the H emission [64]. However, a new analysis of the ground-based Keck II data [71], in which the temperature, density, and cooling rate parameters for H were directly derived, now estimates that the required mass flux is 432 to 2800 kg s-1 of charged water products [70]. This is interesting in that the composition of the nanograins measured by CDA were found to be that of water and silicates, with the measured silicate mass fractions ranging from 8 to 30% and the silicate fraction being maximum approaching the ring rain latitudes. Since the rings are by mass % water ice, the depletion of water in the CDA data suggests a mechanism at work to erode water ice from the grains, but the ultimate fate of that water is not clear. These recent results suggest that the water lost from these grains may indeed be ending up in the atmosphere333The measured mass fraction in the midplane is close to C ring composition in terms of volume fraction (%) as derived by Zhang et al. [93]..
The Cassini Ion Neutral Mass Spectrometer (INMS) experiment, which measured the composition of Saturn’s equatorial upper atmosphere and its interactions with material originating from the rings, found a surprisingly large mass influx of between 4800 and 45000 kg s-1 within a latitude band 8o near the equator [90]. In addition to observing the infall of water, substantial amounts of volatiles and impact fragments of organic nanoparticles were also measured. These authors concluded that this large mass flux likely requires the regular transfer of material from the C ring to the D ring. Unlike CDA and MIMI, which were sensitive to a specific range of particle radii, INMS sampled remnants of infalling material regardless of original particle size and so may offer a more appropriate measure of the total mass influx from the rings into the planet. The minimum and maximum values of the equatorial mass flux, which were derived from three low altitude revs, are significantly larger than the influxes estimated by MIMI and CDA and larger than the amount of influx needed to explain the ring rain effect.
It is the source of this large overall mass influx that we endeavor to explain in this paper as a natural by-product of outward angular momentum transport by BT and of meteoroid mass loading. Specifically, our aim is, for the first time, to quantify the inward drift of ring material from the main rings into regions close to the planet due to micrometeoroid bombardment and to determine how this compares with the overall mass influx of material measured in the final orbits of the Cassini Grand Finale. If they are comparable, it would provide another confirmation of the importance of meteoroid bombardment for ring dynamics and a consistency check for age dating the rings.
3 Ballistic Transport and Mass Loading
Our own theoretical treatment of ballistic transport and mass loading in Saturn’s rings was developed in a series of papers over two decades ago (D84; D89; D92; D96) and was recently reviewed in depth by E15 and E18. The reader should consult these references for details beyond the summary provided in this section.
Our formulation of the response of a ring to meteoroid bombardment, as described below, only applies to dense rings, like the A, B, and C rings of Saturn, and not to sparse or gossamer rings like the D ring, where other processes are likely to dominate the behavior [46]. We discuss the D ring and the problem of spanning the gap between the D ring and Saturn in Section 6.4.1. The purpose of this paper is to demonstrate that ballistic transport and mass loading can sustain mass inflow toward Saturn through the B and C rings of the magnitude observed flowing onto Saturn.
3.1 Basics
Saturn’s rings are subject to impacts by small meteoroids, with the bulk of the incoming mass in the form of micron-to-tens-of-micron-sized particles of interplanetary origin [CD90; 55, 1, 54]. The dust strikes the ring particles at hypervelocity with speeds of 10’s km s-1. The primary result of impact is release of a high yield of small ejecta particles with speeds relative to their ring particle of origin that range up to 100’s m s-1 or more. This is true whether the impacts are cratering events or cause disruption of the ring particle. The fragments of a disrupted ring particle can formally be treated in BT as ejecta. The ejecta that escape their radius of origin arc above the rings on ballistic elliptical trajectories which carry them to ring regions separated in radius by a few to a few thousands of km. Depending on the relative optical depths of the regions where the ballistic trajectories intersect the ring plane, some or all of the ejecta are absorbed by the rings at a radius different from their radius of origin.
A characteristic time scale associated with BT, called the “gross erosion time” (D84), is defined as the time it would take a ring region to erode away completely if all locally produced ejecta were lost and no ejecta were gained from elsewhere. It is given by
| (1) |
where is the surface mass density of the rings at radius from the center of Saturn, is the (two-sided) mass emission rate of ejecta per unit area, is the (two-sided) mass rate of meteoroid impacts per unit area, and is the typical yield, i.e., the typical ratio of ejected mass to meteoroid mass for an impact. “Two-sided” here means that inflow onto both sides of the rings, North and South, is included. As discussed below, is on the general order of 104 to 105 yr. This is much longer than the local collision time for ring particles, typically a half to several orbit periods (hours to days), but short compared to the Solar System lifetime.
BT usually manifests itself on a time scale longer than because not all ejecta from are lost and ejecta are also absorbed from other ring regions. It is the net effect of ejecta exchanges between ring regions that produces transport of mass and angular momentum. Net mass exchange leads to what we call a “direct” change in the surface mass density of the rings. In addition, because the ejecta generally have specific angular momentum different from their parent ring particles and also different from the ring particles that absorb them, ejecta exchanges cause the specific orbital angular momentum of the local ensemble of ring particles to change. The result is a slow drift to a different ring radius. The divergence of this local mass flux also changes the ring surface density.
The following equation from E18 describes the result of these two effects on the evolution of the ring surface density ,
| (2) |
Here we have adopted the same notation found in E18. is the gain rate of mass per unit area at due to absorption of ejecta from elsewhere, and is the loss rate of mass per unit area due to ejecta emitted at and absorbed elsewhere. The first term on the RHS of Eq. (2) is the change in due the divergence of the radial mass flux. represents the net local direct gain of mass per unit area due to ejecta exchanges. The last term on the RHS of (2) is the mass loading, the mass deposited locally by the meteoroids themselves. Here we assume no meteoroid mass is lost.
The radial drift speed in Eq. (2)
| (3) |
is caused by at least three processes, namely, from left to right, ballistic transport, viscosity, and mass loading. We will not concern ourselves here with the viscous radial drift . An estimate for viscously driven mass inflow will be given in Section 5.4. The radial drift due solely to ejecta exchanges is given by
| (4) |
where and are the gain and loss rates of angular momentum per unit area at due to ejecta gained and lost and is the specific orbital angular momentum at required for a circular orbit around Saturn. Basically, it is assumed that, as its specific orbital angular momentum changes, the ensemble of ring particles at drifts to a radius where its new value of allows it collectively to follow a circular orbit. Note that and have different units from and , g cm-2 s-1 and g s-2, respectively.
The radial drift due to mass loading and associated torques is given by
| (5) |
where is the torque caused by the meteoroids and is usually negative due to aberration of the meteoroids by the orbital motions of Saturn and of the ring particles (CD90). Note that, even if there were no aberration, i.e., , the meteoroid mass loading by itself will cause inward radial drift. In fact, mass loading tends to dominate the meteoroid torque at least for Oort cloud projectiles (see D96).
3.2 The Ejecta Distribution
There are a few features of the expected angular and speed distributions of ejecta that are worth noting before we consider approximations to the gain and loss integrals.
Predominance of Prograde Ejecta. Because of the aberration of the meteoroid influx by the ring particle orbital motion (CD90), impacts tend to occur on the leading hemispheres of ring particles. So the ejecta velocities from non-disruptive impacts tend to have a prograde sense with respect to the ring particle orbital velocity. The vertical thickness of the ensemble of ring particles is only tens of meters [10] with random speeds of less than a cm s-1, much smaller than the ejecta speeds. So, as discussed in D84, D89, and D92, prograde ejecta follow elliptical orbits that arc above the ring plane and re-intersect it at a larger radial distance . Prograde ejecta carry away more specific angular momentum than required for a circular orbit at but arrive at with less specific angular momentum than needed there for a circular orbit. Retrograde ejecta have the opposite signs of angular momentum differences. Because the cratering ejecta are predominantly prograde, they represent a net outward transport of angular momentum. However, both prograde ejecta lost from to and those gained at from an interior radius decrease the specific angular momentum at and , and so cause an inward drift at both locations.
As shown in Fig. 12 and Eqs. (41) to (46) of CD90, the prograde ejecta outweigh retrograde ejecta by a considerable factor when the impactors are predominantly Oort Cloud cometary dust. The ratio can be seen to be about 2.5 to 1 for the approximations used in Fig. 3 of Latter et al. [58]. The Cassini Dust Analyzer (CDA) results [55, 1, 54] show that the bulk of impactors on Saturn’s rings are not cometary in origin but have the dynamics of dust originating in the Edgeworth-Kuiper Belt, i.e., low-to-moderate eccentricity and low, prograde inclinations in the heliocentric frame. Unlike the cometary population that is isotropic in the heliocentric frame, the EKB population tends to be isotropic in the frame of the planet and is characterized by a much lower speed at the Hill radius of Saturn compared to Oort Cloud projectiles. As a result, the EKB micrometeoroids are much more gravitationally focused at the rings (Section 2.1). E18 redid the CD90 analysis for EKB impactors in an approximate manner and found that the resultant angular distribution of the ejecta is even more prograde than the cometary one, with a ratio of prograde to retrograde ejecta of more like 7 to 1 (see Figs. 9.4 and 9.5 of E18), thus accentuating the radial inward drifts.
Power-Law Speed Distribution. We characterize ejecta speeds by the parameter , where is the local circular orbit speed. As discussed in E15 and E18, the speed distribution from non-disruptive hypervelocity impacts is likely to be a steep power law with between 2 and 3, and the speeds in this distribution are likely to span the range from a few to up to several 100 m s-1. For example, the cumulative ejecta speed distributions from laboratory experiments [47] suggest values of 2.1 to 2.7 for a wide range of target strengths (higher ’s) and porosity (lower ’s), and the hypervelocity impact experiments of Koschny and Grün [56, 57] using ice and ice/silicate targets produce maximum velocities of order several 100 m s-1.
As shown by the 2 and 3 curves in Figure 9.10 of E18, such -values combined with a speed distribution ranging up to a few100 m s-1 are probably required to produce the observed features called “ramps”, which are linear in normal optical depth and exist just inside the steep A and B ring inner edges (see Figs. 9.1, 9.2, and 9.10 of E18). Production of ramps for = 3 was also discussed extensively in D92 and E15.
One possible complication is that Koschny and Grün [56, 57] found the maximum velocity of ejection depended on the angle of ejection. CD90 included an ejecta cone model for impacts, including how the cone varied with angle of incidence of impact. The CD90 results ended up being averaged over all possible impacts, and much of this detail washes out. CD90 did not include variation of the ejecta speed with ejection angle. This could be done but would wash out by the time impacts at all incidence angles were considered. Thought should be given to effects like this when the CD90 computations are redone in the future, but what probably matters more is the average overall ejecta velocity distribution. The BT mass inflow results of Section 4.2 are more sensitive to the lower ejecta speed cutoff of the power law, not the upper cutoff. The upper cutoff matters more for explaining the extent of the observed ramps.
Although disruptive impacts are also likely to occur, we have not yet tried to characterize them or their BT implications in detail. Such impacts will probably include a cratering component of high-speed ejecta from the initial impact plus a high yield of slower moving, possibly more retrograde ejecta due to the breakup of the ring particle. In this paper, we focus on the higher-speed prograde yield from cratering events, which in fact will be most effective at producing radial mass influx in the rings. We offer the ramps as observational evidence that a prograde power-law component does dominate BT at higher speeds.
3.3 The Gain and Loss Integrals
The gain and loss terms in Eqs. (2) and (4) are given by Eqs. (13), (14), (16), and (17) of E15. We describe them in this subsection only qualitatively. They involve triple integrals, two integrals over the solid angle of the angular ejecta emission function and one over the ejecta speed distribution. The emission angles and speeds determine, for the ’s, where ejecta that are absorbed at have come from and, for the ’s, where ejecta emitted at re-intersect the ring plane. In addition, these integrals include a probability function that uses the optical depths at the radii of emission and re-intersection to determine what fraction of ejecta get reabsorbed at rather than at . In general, this function depends on the direction in which the ejecta are launched, because the probabilities are determined by slant path optical depths. At low to moderate ’s, ejecta may execute more than one orbit before being absorbed at one or the other of these radii.
3.4 Ejecta Emission Rate
The loss and gain integrals also contain an ejecta emission rate function which depends on and . As given by Eq. (9.6) of E18, CD90 found that a good approximation to the and dependence of the local ejecta mass emission rate per unit area444This function was determined for Oort Cloud projectiles. It will probably differ somewhat for the EKB population (see Sec. 5.1). is
| (6) |
where . is the ejecta mass emission rate per unit area as . Note that the -dependent function in Eq. (6) peaks at where 1.135 As , 0.933 . In the limit of small , as ,
| (7) |
To an approximation good enough for our purposes,
| (8) |
where RS ( km is Saturn’s equatorial radius) and is the one-sided flat plate meteoroid influx in a heliocentric frame far from Saturn (for cometary projectiles) or in the Saturn reference frame far from Saturn (for the EKB projectiles). The “gravitational focusing factor” is meant to characterize the focusing expected for an assumed population of meteoroid impactors. As discussed in Section 5.1 and E18, it is expected to be of order 3 for cometary meteoroids and 30 for EKB meteoroids (see also Appendix B of CE98). The factor is adopted from CD90, based on a fit to CD90 results, as an estimate for how the gravitational focusing depends on (see also Section 4.2 of CE98).
4 Mass Influx Models for Ballistic Transport and Mass Loading
Previous papers on BT and ML mostly concerned how structure in the rings can be produced near edges (D89; D92; D96; E15; E18) or due to instabilities [20, 58, 59, 60]. This paper focuses instead on a more fundamental feature of BT and ML, namely that both mechanisms can drive significant mass inflow. Inflow due to ML was discussed in D96, E15, and E18 in the context of the lifetime of the current C ring.
4.1 BT in a Quasi-Steady Uniform Ring
We first address BT by considering the special case of a disk with constant and . As demonstrated in D89, E15, and E18, this results in a steady-state behavior to a high degree of approximation away from boundaries, with deviations only to second order in . Even the largest ejection speeds in the power-law distribution are expected to be only 100’s m s-1, leading to or to . In other words, it would take about to to see large deviations from the steady state, a time comparable to or greater than a Solar System lifetime. Just as for a steady-state gaseous accretion disk, the uniform ring case is only an idealization and is significantly affected by the imposition of realistic boundary conditions.
We explore this analytically by making some approximations similar to those made by Lissauer [61] and Durisen [20, herafter D95]. First suppose that there is only one ejecta speed, characterized by , and that all the ejecta are prograde. Suppose further that the re-intersection radii of the prograde ejecta are distributed uniformly from their radius of origin to , where is the maximum “throw distance” from that an ejectum can reach. To first order in , D89 showed, using Keplerian orbits, that . This drastically simplifies the angle and speed integrations in the ’s and ’s.
The gain and loss integrals also contain relative probabilities of absorption at and . As discussed in D95 [see also 58], a reasonable approximation to this probability function for a uniform ring is
| (9) |
as applied at , where represents a typical slant path through the ring. This allows to be taken outside the angle integration.
There are two limiting cases of Eq. (9). For the probabilities are 1/2. An ejectum emitted at is just as likely to be reabsorbed at or . For , on the other hand, the probability of absorption at is unity and the probability of reabsorption at is zero. We will consider these two limiting cases, and then the results for a general .
The expressions in Eqs. (10) to (15) below are cited by reference to equations from appendices in D92 and E18. The reader who wishes to verify these results can use the linearized gain and loss integrals given, in slightly different notation, by Eqs. (22) to (30) of D95555A factor of is erroneously missing from the RHS’s of the angular momentum loss and gains integrals in Eqs. (24) and (25) of D95. This omission is a typo and does not affect any other results in D95.. Set and in those equations and adopt from 0 to 1 and otherwise. The in D95 is given above, with 1/2 for very low and 1 for very high . The zero-order terms cancel when the gain and loss integrals are subtracted, and the first-order terms lead to the RHS’s of Eqs. (10) to (15) below.
Insight into the physics can be gained from understanding the terms in the equations of D95. The factor in comes from the flat disk geometry of the rings, which causes the ring area elements for emitted ejecta to be smaller than the ring area elements that they are transported to. Hence, for prograde ejecta, to order because ejecta emission annuli have less area than the absorption annuli. In other words, less mass is gained from inner ring regions than is lost to outer regions for purely prograde ejecta, leading to a decrease in due to direct mass exchange. The difference in the angular momentum exchange integrals is that there is an extra factor in due to the and dependence of the ejecta angular momentum. So the radial mass influx is non-zero to order . For a uniform ring, the divergence of the radial flux exactly cancels the mass deposition to order .
Low Optical Depth. For a uniform ring, far from any boundaries, with these approximations, Appendix B of D92 and Appendix A of E18 show that we get, with , to first order in ,
| (10) |
and
| (11) |
If these expressions are put into Eq. (2) with the mass loading term set to zero, for simplicity, we get that is constant to first order in .
High Optical Depth. In the limit , these same expressions become, to first order in ,
| (12) |
and
| (13) |
General Optical Depth. The general case has the -dependent function.
| (14) |
and
| (15) |
4.2 Inflow Rates for the Uniform Ring
If we multiply (15) on both sides by , we get mass inflow in units of mass per unit length of circumference per unit time. So, multiplying by gives the total mass inflow rate ,
| (16) |
Strictly speaking, Eq. (16) is valid only for a single value of , but, when there is an -distribution, each will contribute to the influx according to Eq. (16) but with appropriate weighting. Let’s assume that obeys an power law from a lower limit up to an upper value much like what is assumed in D92 and E15. Then, for , the average weighted by the power law is , and we get the case for general and an power law as
| (17) |
Inserting the appropriate limiting cases for and , we get, for ,
| (18) |
and, for ,
| (19) |
While these mass inflow rates as , it is important to realize that the BT radial inward drift speed does not as . The terms involving the ’s and ’s in the second bracket on the RHS of Eq. (4) are proportional to at low and hence, at constant opacity, to , while the first factor on the RHS contains a . So, as , the and -dependences cancel out in the expression for . This same effect applies to .
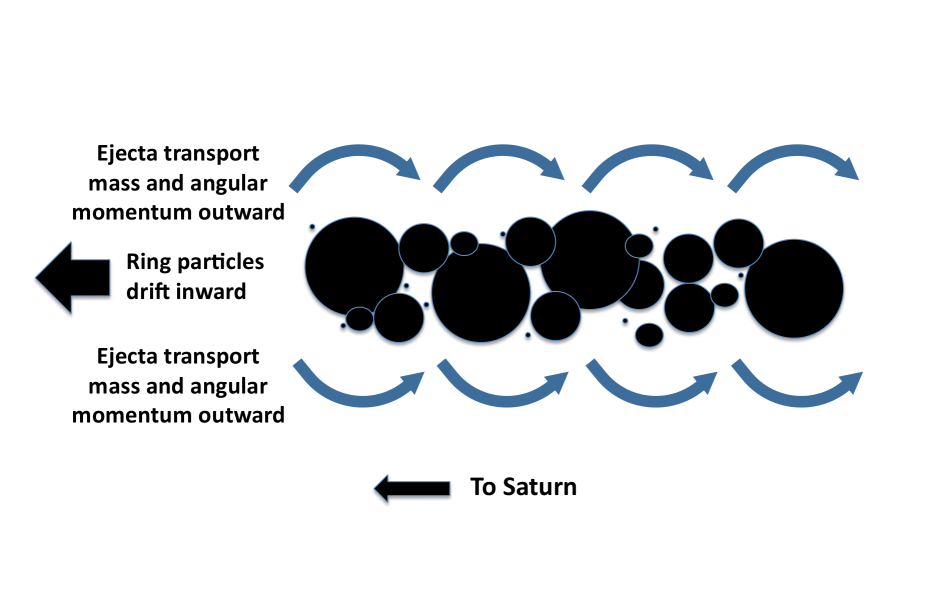
4.3 The Uniform Ring as Analog to a Steady-State Accretion Disk
The uniform ring resembles a steady-state viscous accretion disk [see, e.g., 42]. In both cases, angular momentum is transported outward while mass flows inward without changing the local surface density. In the BT uniform ring, as illustrated in Figure 1, ejecta flying mostly outward above the ring plane carry mass and angular momentum outward and cause changes in the local surface density and specific angular momentum. Because angular momentum is transported inexorably outward by the prograde ejecta, the specific angular momentum of the ensemble of ring particles in the ring plane decreases so that it drifts inward en masse. The combined effect is that remains constant locally in a uniform ring system to a high degree of approximation. The entire ensemble of ring particles consequently moves inward like a conveyor belt because angular momentum is being transported outward. The analogy is not perfect of course. In a viscous accretion disk, it is viscous stresses that carry angular momentum outward, and the steady-state surface density profile depends on the viscosity law.
Realistically, there will be inner and outer boundaries where the BT uniform ring approximation will not apply. Still, the inner boundary region, whatever it is – perhaps the atmosphere of the planet or a region where other mechanisms operate effectively to remove mass – must accommodate the mass inflow. Similarly, the angular momentum carried outward by the ejecta must accumulate somewhere or be removed by other processes. Similar boundary condition issues arise for a viscous accretion disk.
4.4 Mass Loading
The direct deposition of mass and angular momentum by meteoroids sets a lower bound on the radially inward drift speed and mass inflow rate that is independent of uncertain parameters like and . Fig. 1 of D96, which is based on CD90, demonstrates the non-zero inward radial drift speed as due to mass loading and meteoroid torque. It also shows that the meteoroid torque effect on radial drift at low is only about 1/4 that of mass loading alone. So, for a first estimate of inflow rate and speed due to meteoroid deposition, we consider only the direct deposition of mass and not the meteoroid torque. In other words, we ignore the term in Eq. (5).
D96 made analytic fits, given by their Eqs. (7) and (8), to the numerical results of CD90 for cometary dust to get as a function of and . Here we adopt the D96 work but use simpler analytic forms that still reflect what we know about the expected dependences on variables , and and on the parameter . We replace the with by calling out the assumption in D96 that the ring opacity has a constant value of about 0.01 cm2 g-1. Also, the -dependence of should be the same as the -dependence of given by Eq. (2) in E15 (see also Eq. [1] of D96), also based on fits to CD90 computations. We have simplified the D96 -dependence by setting the and parameters that appear in the D96 equations equal to one. The linear -dependence in Eq. (8) of D96 is actually just a crude approximation to the power-law -dependence of the focussing. Here we more accurately reflect that -dependence of focussing explicitly.
The result of all these modifications is a more generally applicable and versatile expression, which represents the CD90 computations as accurately as do Eqs. (7) and (8) of D96. The revised equation is
| (20) |
where ,
| (21) |
and the “CD” refers to the CD90 paper, in which Oort Cloud meteoroid projectiles were assumed, giving . The factor of in Eq. (21) properly includes the factor from Eq. (8) due to the radial dependence of the gravitational focusing. Note that, because is proportional to for constant opacity, has its largest magnitude as , with important implications for ring lifetimes (see Section 5.3).
5 Application to Saturn’s Rings
5.1 Input Parameters
The RHS’s of Eqs. (17), (18), and (19) depend on location in the rings , the optical depth at , the typical impact yield , the characterizing the low end of the power-law ejecta speed distribution, the meteoroid influx at large distance from Saturn , and the strength of the gravitational focusing , which in turn depends on the meteoroid source population. It is worth noting that the RHS’s depend only on , not on . Parametrically, what matters for mass inflow is the efficiency of meteoroid absorption, through , not the particle size distribution, particle porosity, ring texture, or ring opacity. This inflow rate is also independent of viscosity.
On the other hand, the factor is likely to depend on ring particle properties, but exactly how is not well understood. Let without brackets denote the nominal yield for cratering impacts with normal incidence at a speed of 14.4 km s-1. Previous models of the rings’ structural evolution showed that was required to maintain the sharpness of the inner B ring edge and to form the linear ramp that connects it to the C ring (D92; E15). These calculations, however, employed the old cometary flux. The most recent models using the more focused EKB flux adopted in this paper only require [27, 28, E18]. Moreover, analyses of ring pollution ages (E15; E18) seem roughly consistent with to . Thus we adopt as our fiducial value for this work, and this is equivalent to choosing to be about the same value.
In BT simulations, we have typically adopted . This parameter is not well constrained, but is roughly consistent with matching structures near the inner edge of Saturn’s B ring (E15). In terms of the nature of impacts on the rings, both and especially are uncertain by up to an order of magnitude, possibly more, and could vary with location depending on ring particle properties like shape and porosity.
The CDA observations [55, 1, 54] indicate that dust-sized meteoroid impacts are dominated by an EKB source and that the value of the micrometeoroid flux at infinity is g cm-2 s-1. This value is lower by a factor of two compared to earlier estimates for the influx of small meteoroids at Saturn of g cm-2 s-1 (Grün et al., 1985; CD90; CE98; Sec. 2.1), where again “CD” refers to the value adopted in CD90, and is generally consistent with measurements of the interplanetary meteoroid flux by the New Horizons Student Dust Detector [73, 74, 75]. For simplicity, in this paper, we assume the influx at Saturn is constant over relevant time scales.
The CDA measurements also give information about the velocity distribution of the meteoroids as they enter the Saturn system. We have not yet performed a detailed re-computation of the focusing and aberration for EKB meteoroids along the lines of CD90. However, E15 and E18 estimated that the focusing factor is for these objects rather than the three or four assumed by CD90 and CE98 for cometary dust, because the EKB particles enter Saturn’s Hill sphere with smaller speeds relative to Saturn (see CD90; CD98; and the discussion in Section 2.1). The exact functional form of , based here on CD90, is likely to change due to a different degree of aberration for EKB particles, but we suspect this probably only affects results by factors of order unity.
The values of used here are rather large but, as explained in E18, are adopted based on pollution models and fits to ring structure, especially the outer C ring and inner B ring regions. As noted above, using cometary meteoroids, D92 and D96 argued for to match the edge/ramp structure. In their laboratory experiments for impacts onto ice and ice/silicate targets, Koschny and Grün [56] found it was difficult to justify being as large as and suggested that other highly uncertain parameters in ballistic transport modelling might have to be adjusted to bring the required yield down.
The CDA results already move in the right direction. The increase in due to the EKB nature of the impactors has now reduced the estimated for structural fits by about an order of magnitude (E15;E18). With remaining uncertainties in viscosity, in the upper and lower limits of the ejecta velocity power law, and in the exact value of the power law index , plus the absence of a proper and complete treatment of meteoroid focusing and aberration, the value of the structurally required could drop further and be brought more in line with laboratory results.
Another concern raised by Koschny and Grün [56] is illustrated by their Eq. (7) and Table III. Using parameters appropriate for icy projectiles and targets, their experimentally determined yields for a normal impact at 14 km s-1 can be approximately fit by , where is the radius of the impactor. The particles detected by CDA are generally less than 100 m666One grain considerably larger than 100 m was detected which would increase the magnitude of , but was not included in the estimate of the flux for reasons discussed in Kempf et al. [54]. These authors also discuss the probabilities of non-detection of larger grains due to insufficient detector exposure time., implying yields from this fit of less than about 5103. Here we adopt values of compatible with the inner edge results of BT evolutions. It should be noted that it is actually the combination that matters for matching inner edge structures (E15; E18). Any deficiency in the actual could be compensated by an increase in . We should also keep in mind that, despite best efforts, the laboratory impact results may not apply well to ring particles with regoliths and with complex substructure that are in free-fall at cryogenic temperatures.
Another concern is how well our inflow models may apply to parts of the B ring where observations suggest high porosity of the ring particles [e.g., 78, 92], and similarly for observations in the A and C rings [76, 66, 93]. High porosity may imply lower yields so that possibly the inflow rate in the central part of the B ring is actually lower. Pollution models and BT structural arguments do not constrain in the middle B ring. However, this would not affect our explanation of how mass flows from the inner B ring and through the C ring toward the planet, which is the main focus of this paper. On the other hand, the yield in regions of porous particles may well be just as large as elsewhere if the typical compacted components of the porous particle aggregates are significantly larger than the size of the impacting meteoroids. Then impacts by meteoroids could produce yields corresponding to the individual components of the aggregate, not the porous aggregate as a whole.
So, with all these caveats, we here consider a range of from to .
5.2 Mass Inflow due to Ballistic Transport
| (22) |
and
| (23) |
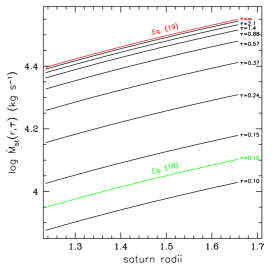
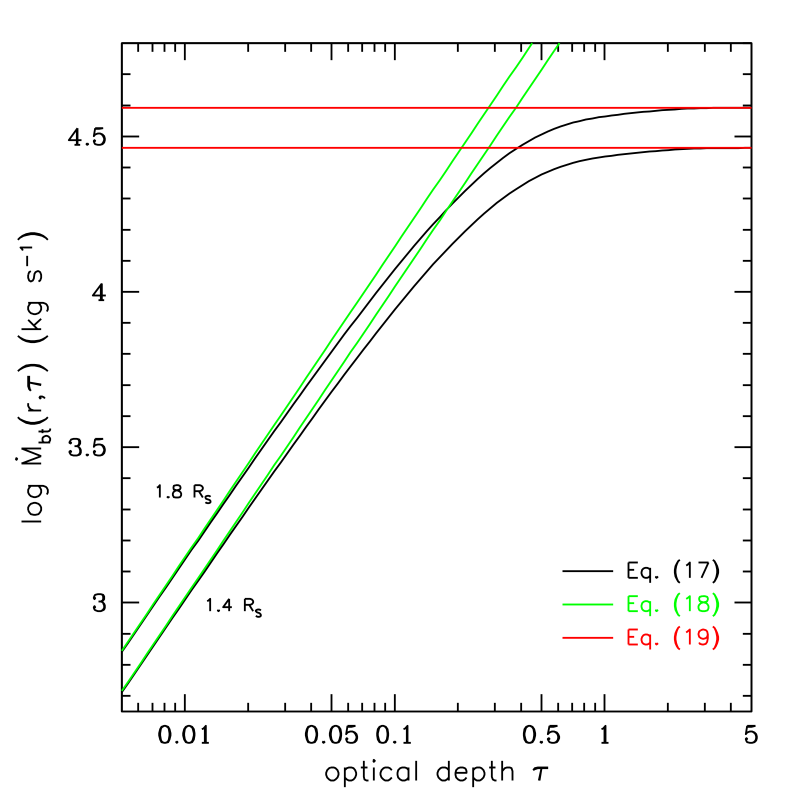
Although, given the uncertainties in the parameters, the true inflow values could be up to an order of magnitude higher or lower, these mass inflow rates capture the principal point of this paper, namely that, for reasonable parameters, mass inflow driven by BT alone is comparable to the mass inflow into Saturn measured by Cassini during its final orbits, few to a few kg s-1. The high optical depth result is appropriate for the B ring, and the low optical depth result is appropriate, in an average sense, for the C ring.
More generally, Figure 2 shows Eq. (17) computed for a variety of ’s as a function of for the same nominal parameter choices used in Eqs. (22) and (23). Note that the inflow rate asymptotes to a finite value as . The result is that we expect a rather constant high value of for a region where optical depths are generally greater than unity, like the B ring. Figure 3 shows how well the low- and high- limiting expressions match the inflow results for general .
As a supplemental result, which will aid in later discussion, the gross erosion time in the inner B ring for the same parametrization is
| (24) |
For this calculation, we have used the derived estimate for the B ring mass of Mimas masses [49] spread out over the radial extent of the B ring from 92,000 to 117,580 km to obtain an average surface density of 52 g cm-2.
5.3 Mass Inflow due to Mass Loading
Eq. (20) gives the mass loading influx rate for cometary dust. For EKB impacting meteoroids, we make the approximation that the gravitational focusing should be about a factor of ten higher (E18). Adopting instead of 3 for EKB impactors, as well as a correction factor to account for the CDA flux , Eqs. (20) and (21) become
| (25) |
Multiplying by , gives the mass inflow rate driven by mass loading for EKB impactors
| (26) |
Eq. (26) assumes zero meteoroid torque. It is likely that the meteoroid torque is not so negligible for EKB impactors, due to their greater aberration. This could increase the inflow rate noticeably and will be the subject of future research.
Figure 4 shows the result of evaluating Eq. (26) for a variety of ’s as a function of . Comparing this with Fig. 2 reveals that is roughly an order of magnitude smaller than , and is, by itself, slightly smaller than the lower estimate of the mass inflow into Saturn observed by INMS. If we reduce our choice of from to , the inflow rates for BT and mass loading are comparable in magnitude, and in tandem are consistent with the lower bound of the mass inflow. Overall, the total mass inflow rate is quite large for and and is consistent with the INMS upper estimate for the mass inflow.
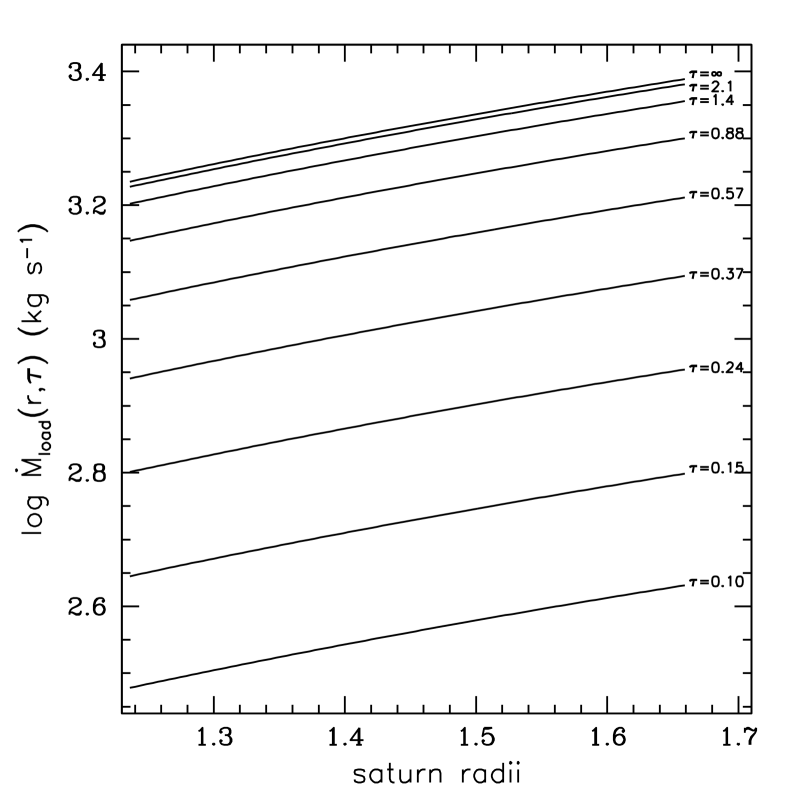
Note that the -dependence for both effects is the same and is due to the combined effects of thin disk geometry and gravitational focusing. While the BT inflow depends on the uncertain parameters and , which characterize the lowest speeds in the power-law ejecta speed distribution and the impact yield, respectively, mass loading depends only on the influx rate of meteoroids and their degree of focusing. With BT added, the mass influxes are larger by an order of magnitude for . We remind the reader that this value of is adopted here on the basis of BT structural arguments (Sec. 5.1).
In Figure 5, we show the inward radial drift velocities due to mass loading alone (solid curves) and due to BT alone (dashed curves) for characteristic locations in the C and B rings at 1.4 RS (red curves) and 1.8 RS (black curves), respectively, as a function of optical depth. In generating these curves, we use Eq. (25) for mass loading and Eq. (15) integrated over the standard -distribution for BT. We also assume that and use an opacity cm2 g-1 for the C ring and cm2 g-1 for the B ring [see, e.g., CE98; 4, 43, 92, 93]. For fixed opacity, the radial drift speeds increase to a nonzero asymptotic value as optical depth and surface density decrease, even though the mass inflow rate goes to zero.
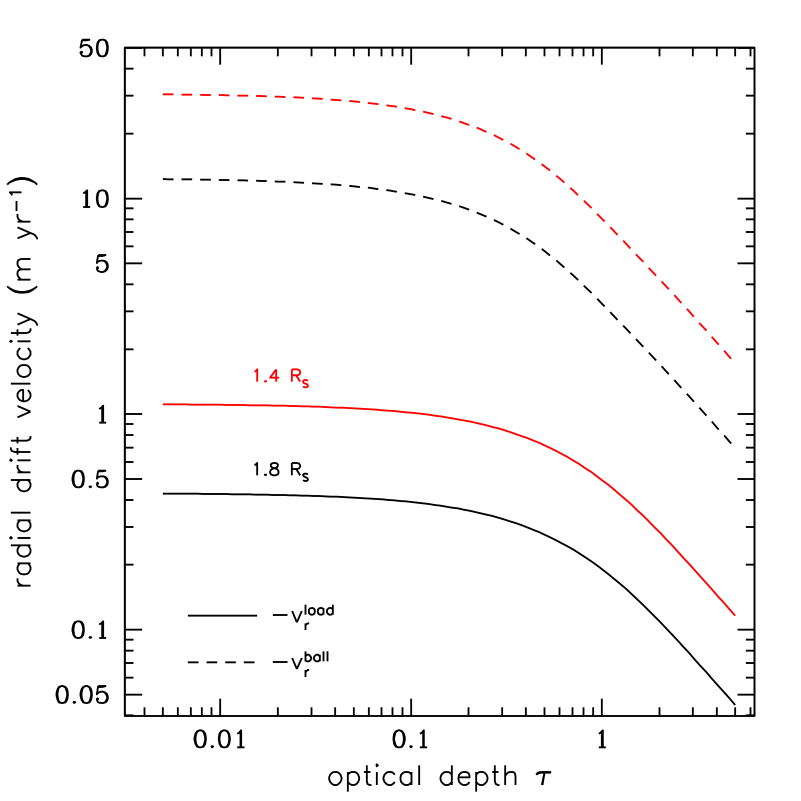
Based on Fig. 5, we expect the low- base of the inner edge of an initially high- ring to spread inwards more quickly than the high- bulk of the ring. Such sharp high- inner edges do occur in global viscous evolutions of rings like those of Salmon et al. [81] and Crida and Charnoz [13]. The implication is that the C ring may have been created from the original B ring inner edge due to BT or even to mass loading alone [see 26].
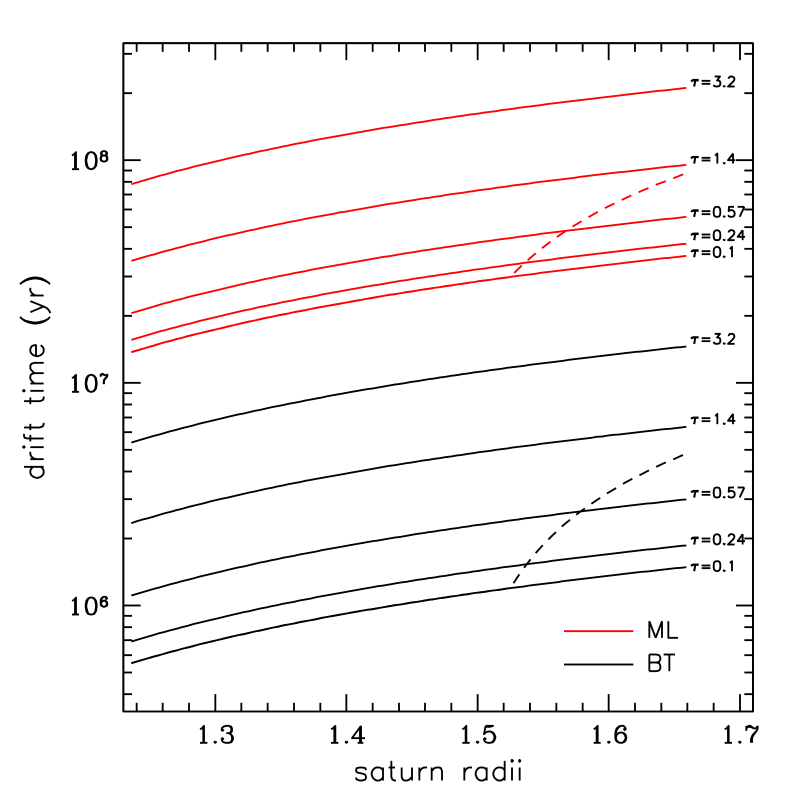
These radial drift speeds can be used to estimate a time scale for ring material located at some radial distance to fall into Saturn. Figure 6 shows this time scale for mass loading (red curves) and BT (black curves) for several . To generate these curves, we have again used Eq. (25) and Eq. (15) integrated over to obtain inward drift speeds. We then integrate the drift speeds over assuming constant optical depth and surface density and using the C ring opacity in the previous paragraph. Drift times are much shorter for low and consistent with previous estimates that the C ring could be lost (or “recycled”) in years by mass loading alone. These times are much shorter for BT, but would be comparable to mass loading for . We also see that becomes longer with increasing optical depth (or ), so that, in an initially massive ring evolving due to strong viscosity, the effects of mass loading and ballistic transport are probably overwhelmed by viscosity until the ring mass decreases significantly.
The dashed curves in Fig. 6 are for a case in which we model the C ring and inner B ring as a step function with g cm-2 for RS, and g cm-2 for RS (Sec. 5.2), representative of current values. For the B ring, this corresponds to taking . For the dashed curves loss time estimates, and at a given are kept constant with time, but the co-moving values change as the mass elements cross the inner B ring edge. Note that the residence time for a mass element in the inner B ring is quite short – less than a few million years for BT with high or a few tens of millions of years for mass loading alone.
It is important to notice in Fig. 5 that the inward drift speeds increase as . So, if we start with a ring of finite mass and radial extent, we expect ML alone to empty the entire B ring onto the planet in a finite time, on the order of a factor of a few times the largest drift times given in Fig. 6 in red (which are the times on which individual annuli of the rings drift all the way to Saturn). Global ring simulations performed in a companion paper verify this [26]. The case for BT alone is more complicated, because angular momentum is conserved, which means that some material must be left behind in orbit, but the bulk of mass elements will flow into Saturn on the times suggested by the black curves for . Also recognise that these drift times do not apply to narrow, dusty rings or sparse debris belts. The drift times presented here are indicative of how long a broad, dense ring can last. The true final behaviour of such a ring system is a separate and interesting question. Perhaps it leads to a long-lived sparse system of dust belts and narrow ringlets.
5.4 Viscous Mass Inflow
It is interesting to compare the mass inflow in the rings expected from viscosity with those derived above. Using the approximation of a steady-state viscous accretion disk with a constant kinematic viscosity , the mass inflow rate is
| (27) |
when the disk is assumed to be Keplerian [see, e.g., 42].
The proper value of viscosity in the rings is a complicated story, and expectations vary theoretically depending on the particle size distribution and whether or not gravitational wakes occur [see, e.g., 83, 82]. Values of the kinematic shear viscosity between 1 and 100 cm2 s-1 generally result, with low optical depth regions tending toward the lower end of the range and higher optical depth regions toward the higher end (see discussions in E15 and E18). We adopt values of 10 cm2 s-1 and 100 cm2 s-1, respectively, which probably overestimate the viscosity [see, e.g., 88, 87]. For estimates of at low and high , we use the same values adopted in Section 6.2 below.
So, for a low- region like the C ring, we get
| (28) |
For parameters more representative of the B ring,
| (29) |
6 Discussion
There are two important implications of our results: 1) The high mass inflow rates through the rings for ballistic transport and mass loading using plausible parameter choices are large enough to explain the large inflow rate into Saturn actually observed by Cassini at the innermost edge of the rings [90]. 2) The age and future lifetime of the rings are likely to be much shorter than the age of the Solar System. Both the age and lifetime are probably at most only a few hundred million years. The first three subsections below elaborate on these points. The last subsection offers some caveats and speculations.
6.1 Mass Inflow to Saturn
The mass inflow rates from the rings into Saturn’s atmosphere as measured by various Cassini instruments in the Grand Finale orbits cover a considerable range (Sec. 2.2). Our general picture is that meteoroid effects drive a large inflow rate towards Saturn with the bulk of the inflow delivered equatorially through the rings. Various erosion processes along the way cause some significant flow into Saturn at high Saturn latitude in the form of ring rain as was measured by CDA, but these measurements are restricted to a narrow range of grain sizes. Such erosion mechanisms were suggested originally by Cook and Franklin [12, see review in D84], before there were many relevant observations.
According to Hsu et al. [48], the tens-of-nanometer grains they detected with CDA are ejected from the main rings at speeds of few - m s-1 with 50% from the C ring, 40% from the B ring, and the remaining fraction from the Cassini Division, A and D rings. The ejecta speeds for these small charged grains are larger than typical speeds assumed for the micron-sized particles which dominate the impact ejecta size distribution in BT (CD90; D92; CE98; Sec. 3.2), but are consistent with experimental [3, 84] and theoretical [69] studies for smaller grains.
It is informative to compare the total ejecta rate of to kg s-1 derived by Hsu et al. [48] for these nanograins to the total ejecta production rate due to micrometeoroid impacts for all particle sizes across the rings. To estimate the total impact ejecta emission rate from the main rings, we integrated the impact flux over each ring assuming mean optical depths of for the C ring and Cassini division, for the B ring and for the A ring to determine impact probabilities. The result is
| (30) |
which is roughly the equivalent of a m radius object with the density of ice every second. Thus the measured CDA nanograin flux, whose contribution spans the entire ring system, is probably no more than of the total ejecta production rate. Of this only 18% arrives at the planet as ring rain (the rest presumably returns to the main rings), and so the CDA nanograins represent only a small fraction of the typical impact yield times the mass of the impactor. In fact, the total mass of such fast charged nanograins emitted in an impact are comparable in mass to the impactor itself. This minute component of small grains with very high ejection speeds appears to be consistent with the correlation between fragment size and ejection speeds [80].
As pointed out in Section 2.2, the kg s-1 of the CDA flux deposited at the ring rain latitudes in the form of charged, solid nanograin particles are apparently not sufficient to explain the kg s-1 required to account for the observed H infrared emission pattern [70]. However, the silicate-to-ice mass fraction at the ring rain latitudes being as high as % [48] implies that a significant fraction of water has been liberated from these nanograins. If one imagines “reconstituting” the CDA grain population with sufficient water so that it is similar to C ring material (% non-icy by mass), this gives an inflow of to kg s-1 of additional water, not too dissimilar from the estimate of O’Donoghue et al. [70].777It should be acknowledged that this agreement may be coincidental because the CDA flux originates predominantly from the C and B rings, whereas the mass flux estimated from the O’Donoghue et al. [70] analysis comes overwhelmingly from the C ring.
Most of the ejecta mass from impacts (Eq. [30]) should be in larger grains, too large to be charged significantly, which is consistent with the flux measured from CDA (and MIMI) only representing a small fraction of the total inflow. The total midplane loss rate from these instruments is on the order of to kg s-1, far less than the equatorial loss rate of to kg s-1 measured by INMS, which should sample the full range of sizes [90]. Because the origin of this material appears to be the D ring, it implies that the C ring must replenish the D ring material at a similar rate assuming a steady-state scenario. Likewise, the C ring must also be replenished from the B ring at a roughly similar rate.
From our analysis, for our nominal choice of parameters, the mass inflow rate through the B ring and the C ring due to ballistic transport and mass loading is consistent with the observed mass inflow rates near Saturn as measured by INMS. For nominal parameters, the C ring mass inflow rate is predicted to be a factor of several lower than that through the B ring. We find that even decreasing one of the critical parameters, like reducing to 104, which remains in a plausible range of parameters, the mass inflow rates for both rings stay within range of the lower bound estimate for inflow from the INMS measurements. Our main point here is that the observed mass inflow rates toward Saturn through the rings can, in principle, be sustained by ballistic transport plus mass loading without straining parameters. Some complications are addressed below in Section 6.4.
6.2 The Age and Remaining Lifetime of Saturn’s Rings
We have argued for many years that the rings must be substantially younger than the Solar System owing to consequences of meteoroid bombardment, based on both structural and pollution effects (D92; D96; CE98; E15; E18). By determining some key parameters required to assess the importance of meteoroid bombardment, the Cassini Grand Finale has substantially strengthened the arguments for a young age (E18). In addition, the measurement of the large inflow from the rings into Saturn combined with a well-determined ring mass now also permits estimates for the future lifetime of the rings (see also the discussion at the end of Section 5.3).
First consider the age. The structural evolution of the rings due to BT occurs on time scales that vary from a few up to hundreds or thousands of (Eqs. [1] and [24]) depending on the structure being modelled (E18). The ages depend on the uncertain impact yield parameter but are always less than the direct deposition time scale for reasonable choices of . The time itself does not depend on , and we expect the evolution of the rings to their current state of pollution to be some fraction of . Thus, age estimates based on pollution are more reliable measures of absolute ring age than estimates based on BT structures alone.
As revisited by Kempf et al. [54], an absolute exposure time for the rings can be obtained by assuming they began as pure water ice and darkened to their current state [15, E15, E18]. The rate per unit area at which the ring annulus at some with surface density is impacted is given by , so that the mass density of pollutant accumulated in a time is , where the factor allows for the possibility that not all of the impactor survives the impact as absorbing material (CE98; E15). The mass fraction of pollutant after this time is . Measured values derived from Cassini RADAR for the amount of non-icy material in the rings are reported as volume fractions of the solid component [92, 93]. So, in terms of the mass fraction, where the mean solid density of a ring particle is . The density of ice g cm-3, and we take the solid density of the incoming pollutant to be 2.8 g cm-3, which represents a volume mixture of 30% carbonaceous and 70% silicate material [91, 54]. The time to acquire the non-icy material then is
| (31) |
For the B ring where is very large, we found that the average surface density is 52 g cm-2 based on the derived mass for the rings during the Cassini Grand Finale [49, Sec. 5.2], while the measured volume fraction of pollutant is to % [93], with the lowest values found in the very opaque B ring core. Using the median value for and the average , we find that at RS
| (32) |
For the C ring, we can do a similar calculation, except the low continuum optical depth, , means that the probability of absorption of a meteoroid, which is , must be taken into account. A typical value for the surface density away from plateaus and the anomalous “rubble belt” in the middle C ring is g cm-2 [4, 44, 93]. Taking % we get at RS a similar time scale
| (33) |
In Eqs. (32) and (33), we have adopted a conservative value of for grains with little or no volatile content [91, 54].
Both these time scales are in agreement with those derived in Kempf et al. [54]. These time scales will be modestly longer if the rings began with a larger mass, as implied by the currently observed mass loss rates. Thus, given the complete suite of available Cassini data, the case appears fairly solid that the rings were formed a few 100 Myr ago, in agreement with arguments based on pollution and structural models presented in previous works [18, CE98; E15; E18].
We establish this young ring age using the ring mass [49], micrometeoroid flux at Saturn [54], and the volume fractions of pollutants [92, 93]. Combined with measurements of the mass loss rates into Saturn during the Cassini Grand Finale, we can now also estimate the turnover time of the C and D rings and the remaining lifetime of the rings as a whole.
The mass loss rate of nanograins measured by CDA is a not a reasonable gauge for remaining ring lifetime because of the limited particle size range to which it is sensitive. On the other hand, the mass flux of charged water products as calculated recently by O’Donoghue et al. [70] may be more representative because the ring rain effect is probably caused by a contribution from all particle sizes. Based on their estimates for the mid-latitude mass loss rate, these authors get a ring lifetime ranging from 150 to 1,100 Myr. with a likely value of 300 Myr, just from the ring rain. This is an upper limit because it does not include the equatorial losses detected in the INMS data [90].
Waite et al. [90] do not estimate an overall remaining lifetime for the main rings, but they do estimate the lifetime of the D and C rings from their mass inflow rates and obtain to yr for the D ring, and to yr for the C ring. Their calculation for the D ring assumes that its mass is % of the kg C ring mass. Their D ring lifetime estimate is based on the assumption that the D ring has a similar particle size distribution to the C ring so that the difference in surface density is simply the optical depth ratio between the D and C ring (). However, meter-size particles dominating the mass in the D ring may not be a reasonable assumption. Particles sizes in the D ring of only tens of microns may be more appropriate [46]. This would significantly lower the mass so that the current mass inflow rates would dissolve the D ring in only about a year. If so, this would tend to support the idea of episodic repopulation of the D ring from the C ring. Waite et al. [90] also posit that the D ring could be repopulated sporadically by large impact events like the one that tilted the D and C ring plane [43].
From our own estimates of the mass inflow rates due to BT alone in Eqs. (22) and (23), we can calculate the remaining ring lifetime. Taking the current ring mass to be Mimas masses [49], or kg, we find that the range of times for the remaining mass of the rings to fall into the planet is 15 to 40 Myrs for the case when , or 150 to 400 Myrs for . This assumes that the mass inflow rate remains constant over that time. The lifetime estimate would be shorter at the tens of percent level or less, depending on parameter choices, if we include contributions due to mass loading and meteoroid torques. They can also be shorter if the slope of the ejecta velocity distribution is flatter so that more ejecta mass is placed at higher speeds or if there is an accentuation of the inward drift rate of material due to the Goertz et al. [36] mechanism (see Section 6.4.4). Our lower bound estimate for the lifetime is naturally similar to what would be inferred from the upper bound for the mass inflow measured by INMS because BT produces mass inflow rates of the same order as observed for our nominal parameter choices. The future lifetimes estimated here based on ring mass and inflow rates are similar within a factor of a few to the inward drift times in Fig. 6 of Section 5.3, as they should be.
The lower bound estimate of 15 Myr seems exceedingly short, perhaps suggesting that the yield or other parameters vary across the rings and/or is generally lower than what we adopt. Even if the influence of BT alone is not as great as computed here, our results show that mass loading alone, which is not far off from the lower bound measured by INMS, represents a relatively firm upper bound on the ring lifetime, similar to the upper bound estimated above for the low- BT case, namely 400 Myr. It could also be that, if the upper estimate of the mass inflow rate by INMS is correct, the inflow just happened to be exceedingly high at the time of observation due to some recent event [90].
6.3 Initial Ring Mass
The mass inflow rates rates from our BT analysis indicate that the ring mass was substantially larger in the past. Given our estimate for the current ring age of years based on pollution, this would imply that the initial ring mass was greater by few tenths to a few Mimas masses. The inclusion of mass loading increases these numbers by tens of percent. So, as we argue in more detail in our companion paper [26], the deduced initial ring mass is consistent with a recent origin scenario in which the rings start significantly more massive ( one to several Mimas masses) and are polluted by micrometeoroids as they evolve to their current mass and darkened state.
The mass inflow rates measured by Cassini, as well as those that we calculate here, suggest that relatively massive rings are ephemeral when subjected to micrometeoroid bombardment888BT may not be so influential in less massive and sparse ring systems such as Uranus and Neptune in which the rings and arcs are radially thin.. Previously, for evolution by viscosity alone, it was found that a massive ring evolves until its surface density drops to the point where the viscous spreading time becomes exceedingly long [8]. The ring mass then approaches an asymptotic limit [81]. The current ring mass is close to that asymptotic limit. However, this result only applies in the absence of other mass loss mechanisms. Given the results of observations and our analysis here, it seems that the ring mass being similar to the Salmon et al. [81] theoretically-derived asymptotic mass may be a coincidence.
6.4 Caveats and Speculations
6.4.1 The C and D rings
Eqs. (22), (23), and (26) plus Figures 2 to 4 show that, at high for nominal parameters, mass loading and ballistic transport can cause mass inflow rates through the B and C ring consistent with observations. Even though the mass inflows for both mechanisms are somewhat weaker at low (i.e., at decreasing surface density), the radial inward drift speeds due to these mechanisms asymptote to large nonzero values (Fig. 5) leading to short loss time scales for ring particles in the C ring and inner B ring (Fig. 6). The low- C ring does not extend all the way down to Saturn, but, for our nominal set of parameters, the mass inflow rate is roughly sufficient to account for the amount of mass that is pouring into Saturn’s atmosphere. On the other hand, if or are considerably smaller than we assume, the C ring mass inflow rate might not be sufficient, especially for the case where the upper estimate for the observed mass inflow rate is correct. Then something important may be missing.
in the C ring can be made to match the full range of the observed mass inflow rates by adopting yields between and . As we discussed in Sec. 5.1, structural models of the inner B ring edge and its transition into the low- C ring require yields for a cometary meteoroid source in order to keep the edge relatively sharp, maintain roughly its observed width, and produce a ramp (D92; E15). The updated BT models using the EKB meteoroid source determined by CDA [54] demonstrate the same morphology but only require yields of to maintain the B ring edge and ramp [27, E18]. So there is indirect evidence that the BT mass inflow may be on the order suggested by Eq. (22). However, it may be the case that is smaller away from the inner edge and/or other properties of the ring particles conspire to reduce the mass inflow rate.
Alternatively, inflow from the D ring into Saturn could be episodic or highly variable with a duty cycle of a third to a tenth, and Cassini happened to sample a much higher than average inflow. How the C ring’s structure changes with time may also have an effect on the mass inflow rate. Structures such as plateaus may be long-lived even if material is drifting through them, or they may change and/or drift inwards on relatively short time scales. There are some gaps in the C ring which might serve temporarily as barriers to mass inflow, but the throw distances of ejecta vary from 10’s up to 1000’s of km, so that some ejecta can “hop” over gaps in both directions. They can hop inwards as well as outwards because some fraction of impact ejecta are always thrown inwards (CD90). Curiously, most of the gaps in the C ring have optical depth spikes at their outer edges, possibly a pile up of material that would be expected if there was a net inward drift rate of material. Properly evaluating how the mass flow behaves under these structural conditions will require future detailed numerical simulations.
The mass loading result is independent of any assumptions about the nature of the transport, but the stronger BT mass inflow rates are computed using the simple model of a constant, nearly steady-state ring. As noted in the previous paragraph, the real rings exhibit gaps, sharp edges, and structure on a variety of scales, so the quasi-steady solution applies at best only as an overall ballpark estimate. While many ejecta can leap across much of the small scale structure, the assumption of a uniform ring clearly breaks down. While the A and B rings probably experience a large overall mass inflow rate, on the order of our estimates, especially across their more uniform regions, there is clearly a need for global BT simulations that include more complexity.
Our inflow model is incomplete in the sense that our formulation of ML and BT does not apply to the D ring itself, which is extremely optically thin and possibly dusty, nor does it address what happens in the gap between the D ring and Saturn, which is wider than a typical ejecta throw distance. A complete discussion goes beyond the scope of this paper, but we point out some considerations. As material flows into the inner C ring, the higher velocities of meteoroids and ring particles make the impacts more catastrophic, with more smaller particles, vapor, and ions being produced. Ejecta velocities are likely to be higher. Once a ring begins to suffer net erosion rather than loading, typical particle sizes are likely to shrink. Small charged ejecta particles and ions will move along magnetic field lines into Saturn’s atmosphere. Larger charged ejecta lose angular momentum to Saturn’s magnetic field (see Section 6.4.4). The occurrence of ring rain, which falls at moderate latitudes, presumably along magnetic field lines, demonstrates that processes like these are indeed occurring in the D and inner C ring [48, 90, 63]. Ring particles eroded and shattered to smaller sizes will become subject to plasma drag as they approach the upper layers of Saturn’s atmosphere [46]. Detailed theoretical or computation studies of the fate of ring material as it gets close to Saturn is difficult but certainly worthy of further research.
6.4.2 Composition of the Inflow
The composition of the inflowing material as seen by CDA appears to be consistent with both C ring composition and the amount of charged water products needed to account for the ring rain phenomenon in Saturn’s atmosphere, if one reconstitutes for the missing water (Sec. 6.1). However, the measured INMS composition has a non-icy mass fraction of % far in excess of bulk ring composition; moreover, the INMS flux is restricted to a narrow equatorial band, and thus must apparently originate from the midplane with inner C or D ring material providing the source [90]. Indeed, if one were to reconstitute the inflow to mean C ring composition (% volume fraction), it would imply a mass flux of kg s-1. BT in principle could provide such large mass influxes for impact yields (Sec. 5.2), but then where does the water go? It may be possible that a higher fraction of ejecta could be vaporized due to much higher micrometeoroid impact velocities in the D and inner C ring deep in the planet’s potential well, which subsequently may recondense on the rings, but it would seem unlikely that such a large fraction of vapor (%) would be produced in this way. If the latter were the case, it might suggest that meteoroid bombardment is actually purifying the ring composition, and not polluting it. For now, we consider this idea entirely speculative and hope to address it more extensively in a future paper. The fact that there is an order of magnitude contrast in the level of darkening between the C ring and B ring, which is consistent with direct deposition of micrometeoroid pollutants (E15, E18), argues against a purification process. It is made even more implausible given that BT tends to produce a more uniform distribution of non-icy material if allowed to act over long enough time scales.
Nevertheless, we note that the composition of the volatiles as observed by INMS appears similar to that of comets. Perhaps material from the icy progenitor moon (or moons) that formed the rings was composed of mostly unprocessed, primitive ices [90]. Cassini INMS found, from flying through plumes, that Enceladus and comets are chemically very similar [89], which suggests that the material that formed Enceladus (and likely all the Saturnian moons) came from heliocentric bodies. This is consistent with the idea that the primary source of solids for the subnebulae of giant planets like Jupiter and Saturn is ablation and capture of planetesimals crossing their circumplanetary disks [31, 32, 67, also see Mousis and Gautier [68]].
Another possibility, perhaps the simplest, is that, given the short lifetime of the C ring (see Figure 6), the admixture of Centaur material into the middle C ring in the last few tens of million years [as suggested by 93]999These authors also discuss the possibility that the rubble could be the last remnants of a ring progenitor moon’s core. may now be dominating what is accreting into Saturn.
6.4.3 Satellite Torques
It has been known for some time that torques exerted through orbital resonances with Mimas and the various inner and embedded satellites have a substantial effect on ring structure, producing density and bending waves and sharp edges [e.g., 62, 6, 41]. These torques also transfer angular momentum from the rings to external satellites and produce short orbit evolution time scales for some satellites [e.g., 77]. The radial drift due to pure mass loading does not involve angular momentum transport, but the inward drift of mass in the steady-state BT solution is caused by the outward transport of angular momentum through the predominance of prograde ejecta. A natural question to ask is where that angular momentum goes in a real ring with edges.
The so-called “box car” evolution, an initially constant- ring between two sharp edges, is illustrative. Figure 10 of D89 shows that, for prograde ejecta, even though the entire box car drifts inward, a peak develops near the outer edge to conserve angular momentum. In real rings, which do not extend outward infinitely at constant , there will be similar effects due to edges or boundary conditions. For a free outer boundary, the BT-driven mass inflow will restructure the rings to conserve angular momentum. How this will affect the rings globally over long times will be the subject of future research.
What we can say is that the various satellite torques, as given in Table 2 of Tajeddine et al. [87], are insufficient by several orders of magnitude to remove the outward angular momentum flux due to BT. The satellite torques are typically few Nm, while a BT mass inflow of only kg s-1 implies angular momentum outflow resulting in an equivalent torque approaching Nm. The satellite torques simply cannot keep up with the BT-driven angular momentum outflow, although they can balance angular momentum outflow due to viscosity, as in Tajeddine et al. [87], because the viscous flow is orders of magnitude smaller. The smaller angular momentum outflow for viscosity is reflected in the correspondingly lower viscous mass inflows, Eqs. (28) and (29), calculated for the steady-state case (see Section 5.4). We currently draw no simple conclusion about this difference between the BT-driven angular momentum outflow and satellite torques. As mentioned in Section 7.3, once we have included proper ballistic transport in global simulations, we will study what happens near outer edges.
While not now sufficient to balance the net BT angular momentum transfer, satellite torques still probably dominate locally for balancing viscous edge spreading on very short length scales. For the expected ejection velocities of between a few to a few times 100 m s-1, the radial ejecta throw distances range from a few 10’s to a few 1,000’s km. So BT transfer is probably not important over extremely sharp edges nor over the relatively short wavelengths of the spiral structure induced by resonances. The huge disparity of the dynamic and gross erosion times also implies that BT should not affect the physics of spiral density waves. On the other hand, it will be interesting to see, in future BT simulations, how BT affects regions of 100’s to 1000’s km width inside sharp edges.
In some global ring evolution scenarios, a proto-Mimas may once have been much closer to the outer A ring edge. There may have been an early, more massive phase of the rings when considerable angular momentum was transferred to Mimas leading to the formation of the Cassini division [5]. Looking to the future, the current rings may be stuck with close to their current total angular momentum, even as they lose mass. The end state of such an evolution needs to be addressed.
6.4.4 Electromagnetic Effects
It seems likely that ring rain and other high latitude mass inflows from the rings into Saturn are due in part to grain charging and electromagnetic effects (see Section 2.2), which cause tiny charged grains or ions to move along Saturn’s magnetic field lines. As indicated by Eq. (30), the production rate of ejecta by meteoroid bombardment is prodigious. It would take only a small fraction of a percent of ejecta to be small enough and to become charged enough in order to explain ring rain and the other high latitude inflows.
Goertz et al. [36] pointed out that somewhat larger charged grains would not reach the planet and would instead lose (gain) angular momentum as they travel due to magnetic torques exerted inside (outside) the corotation radius ( 1.86 ) with Saturn’s magnetic field. When these grains lose their charge or otherwise rejoin the ring material, they would be reabsorbed in the rings at locations with different specific angular momentum. The interesting point for application to mass inflow is that this could enhance the inward mass inflow by providing another angular momentum loss mechanism over the C ring and the inner two-thirds of the B ring. Goertz et al. [36] estimated that the torques were comparable to or stronger than those due to viscosity. A full re-evaluation involves using modern Cassini data to estimate production rates of charged grains of the appropriate size and the radial distances they are likely to travel. This goes beyond the scope of the current paper but might be a fruitful avenue of future research.
As a follow up to Goertz et al. [36], Goertz and Morfill [35] showed that the Goetz et al. effect could produce an instability leading to wavelike structure, similar to the BT linear instability [D95; 58, 59, 60]. As a possible indication that the Goertz et al. mechanism really operates in the rings, we point out that the Goertz and Morfill instability offers a plausible explanation for why the undulations in the C ring have a long wavelength and are sustained at a nonlinear amplitude without propagating quickly into Saturn, as would be expected if BT alone were the cause [58, 59, 60, E15; E18].
6.4.5 Non-Detection of Systematic Inward Drift
Over the roughly forty years between the Voyager missions and the Cassini Grand Finale, the inward drift speeds for the C ring in Fig. 5 should lead to radial material shifts of between about 0.04 km for ML alone and about 1.2 km for BT with . In principle, the BT drifts are large enough to detect if appropriate ring features can be identified to track the flow. French et al. [33] performed a comprehensive study of the radial positions of over a hundred relatively sharp ring features distributed across the rings as determined by stellar occultations. The derived radii of most features do not differ by more than a few hundredths of a km between fits that include only Cassini data and fits that include Voyager and Earth-based data. This suggests little overall drift detected in the chosen features. When compared with the pre-Cassini radial scale determined by French et al. [34], the subset of individual features common to both studies do show radius discrepancies of up to several kilometres, outside the formal error bars, but these are as often positive as negative and not indicative of overall inward drift.
It is incorrect to conclude from this that must be considerably less than 105. The problem is that ML and BT do not necessarily cause identifiable ring features to co-move with the inward flow.
To illustrate this, consider the two long BT simulations for the inner B ring edge region in Figs. 8 of E15 using and cometary impactors (). For one simulation (dark line), the inward motion of the inner edge feature is less than about 10 km over 7106 yr. For the other simulation (red line), which differs only in assumptions about ring opacity, the edge moves inward by 100 km in that time. These inward shifts are orders of magnitude slower than the inward drift of mass elements in the simulations. The relatively sharp inner B ring edge is maintained by BT but is more like a waveform than a material structure. Mass flows inward through the edge much faster than the edge itself moves. The set of shorter simulations with in Fig. 9 of E15 re-enforces the point that mass inflow does not have to result in inward motion of features. All the simulations start with an inner B ring edge centered at 1.52 , but the edge can move either inward or outward, depending only on the exponent of in the ejecta speed distribution (see Section 3.2).
It is interesting to note that some of the largest differences between the French et al. [34] and French et al. [33] fits, as shown in the 2017 paper’s Table 5, are associated with the edges of the plateaus in the C ring. As we discuss in E15 and E18, ballistic transport may play some role in the evolution of these features, even if it is not their cause. Intriguingly, in the work by the French group, all the inner edges of plateaus shift systematically outward by about 1 to 2 km and the outer edges shift inward by about 1 to 2 km. The magnitude is on the order of the BT radial drift in our Fig. 5, but the opposite signs are perplexing. These shifts do not directly reflect a systematic inward flow but could reflect the magnitude of ballistic transport effects acting on the plateaus.
7 Conclusions
7.1 Mass Inflow Rates
The main conclusion of this paper is that, in light of new determinations of key parameters by Cassini, ballistic transport and mass loading due to meteoroid bombardment can plausibly explain the magnitude of the mass inflow from the rings into Saturn as observed during the Grand Finale. For our nominal choices of parameters, we show that these mechanisms can drive mass inflow through the B and C rings with rates that fall within the range determined by INMS [90].
The mass loading inflow rates computed in Section 5.3 depend only on the product of the Saturn Hill radius meteoroid influx and the gravitational focusing factor . This product is now determined by CDA measurements of dust impacts [54]. So the mass loading results are pretty secure. At moderate to high values of , mass loading alone is comparable to (a factor of two smaller) the lower range of the INMS inflow measurement.
For ballistic transport, we use the approximate steady-state solution developed in Section 4 to estimate mass inflow rates. In addition to the factors and , the ballistic transport mass inflow (Section 5.2) depends on the less well-determined factors of typical impact yield and average normalized ejecta speed . The ballistic transport inflow rates are roughly compatible with the lower and upper estimates of the observed mass inflow rates reported by INMS for impact yields to , respectively. While it is unclear how well the steady-state solution applies to the real rings locally, it probably gives a useful global estimate for inflow. The meteoroid-driven mass inflows are several orders of magnitude greater than mass flows due to viscosity (Section 5.4).
Regardless of the various uncertainties, discussed in some detail in Section 6.4, this paper shows that mass should be driven inward toward Saturn in the B ring at rates high enough to explain the observed mass inflows into Saturn. Even though mass inflow rates in the C ring can also be large enough under reasonable assumptions, the situation in the C ring is not as clear because it contains a lot of unexplained complex structure and the detailed loss mechanisms operating close to Saturn are not yet well enough understood.
7.2 Ring Age, Lifetime, and Initial Mass
The mass inflow rates driven by ballistic transport and mass loading do not in themselves dictate a ring age. Instead, in Section 6.2, we used modern data to estimate a ring age due to pollution by meteoroids of only 170 Myr. Also in Section 6.2, we showed that the ballistic transport mass inflow rates in Eqs. (22) and (23) suggest future ring lifetimes of as little as 15 to as much as 400 Myr using the specific examples of impact yields of and . These lifetimes are reduced by tens of percent when mass loading is included. The range of measured mass inflow rates from INMS, which are consistent with our results here, if steady, are large enough to deplete the C ring in only to 7 Myr.
As discussed in Section 6.3, the ballistic transport mass inflow rates for nominal parameters operating over our estimated 120 Myr age for the rings suggest that a few tenths to several Mimas masses have already been lost into Saturn. Adding mass loading increases the numbers modestly.
7.3 Future Work
Although it will probably make differences of a factor of a few at most, the CD90 analysis of focusing and aberration effects for meteoroid impactors with a cometary source needs to be repeated for the EKB source determined by Kempf et al. [54]. E18 estimated the changes with simple approximations but did not redo the CD90 analysis in detail. The various -dependences for impactor absorption probabilities, ejecta emission rates, and mass loading drift are likely to be affected by the change from a cometary to an EKB source. For instance, the in Eq. (6) will probably be smaller due to the greater aberration of the EKB impactors leading to increased slant path optical depths experienced by the meteoroids at the rings. It is also likely that meteoroid torques will play a larger role for EKB impactors for similar reasons. So, we plan to redo the CD90 analysis for EKB projectiles and derive proper ejecta distribution functions and -dependencies.
It is clear, by comparing the viscous mass inflow rates in Eqs. (28) and (29) with the ballistic transport rates in Eqs. (22) and (23) and the mass loading rate in Eq. (26) that the inclusion of mass loading and ballistic transport in global ring simulations is necessary. In our companion paper [26], we show that adding just mass loading to global viscous evolutions leads to finite lifetimes for massive rings rather than the asymptotic mass found in purely viscous simulations [81].
Adding ballistic transport correctly to global simulations is computationally involved but should shorten the expected lifetimes further and have interesting implications for the current mass distribution of the rings because of the outward angular momentum transport involved. Global pollution evolutions could be run simultaneously, and the possibility of a changing composition due to selective retention of water during the inflow process should be considered. Once global simulations with proper ballistic transport become possible, it will be interesting to include satellite torques, especially in scenarios where a proto-Mimas forms outside the Roche radius and then recedes due to resonant torques. Other mass and angular momentum transport processes, like the Goertz et al. [36] mechanism could also be considered. In addition to global simulations, localized ballistic transport simulations will be needed to study how mass inflow is affected by gaps and other ring structures, especially in the C ring.
Acknowledgements
We thank Josh Colwell, Jeff N. Cuzzi, Joe Burns, and Glen Stewart for useful discussions. This work was supported by a grant from NASA’s Cassini Data Analysis Program (PRE) and a Cassini IDS grant (PRE) to Jeff N. Cuzzi. We are also extremely grateful to two anonymous referees for thorough and thoughtful reviews that led to extensive revisions of the manuscript.
References
- Altobelli et al. [2018] Altobelli, N., Kempf, S., Postberg, F., Fisher, C., Albin, T., Poppe, A., Srama, R., 2018. Exogenous dust at Saturn observed Cassini-CDA. Presented at the Cassini Science Symposium, 12-17 August, LASP, Boulder, CO.
- Altobelli et al. [2015] Altobelli, N., Kempf, S., Postberg, F., Horanyi, M., Srama, R., 2015. Dust Populations in the Outer Solar System: 10 years of monitoring by CASSINI-CDA. European Planetary Science Congress 10, EPSC2015–577.
- Arakawa and Higa [1996] Arakawa, M., Higa, M., 1996. Measurements of ejection velocities in collisional disruption of ice spheres. Planet. Space Sci. 44, 901–908. doi:10.1016/0032-0633(95)00119-0.
- Baillié et al. [2011] Baillié, K., Colwell, J.E., Lissauer, J.J., Esposito, L.W., Sremčević, M., 2011. Waves in Cassini UVIS stellar occultations. 2. The C ring. Icarus 216, 292–308. doi:10.1016/j.icarus.2011.05.019.
- Baillié et al. [2019] Baillié, K., Noyelles, B., Lainey, V., Charnoz, S., Tobie, G., 2019. Formation of the Cassini Division - I. Shaping the rings by Mimas inward migration. Mon. Not. R. Astron. Soc. doi:10.1093/mnras/stz548.
- Borderies et al. [1989] Borderies, N., Goldreich, P., Tremaine, S., 1989. The formation of sharp edges in planetary rings by nearby satellites. Icarus 80, 344–360. doi:10.1016/0019-1035(89)90145-0.
- Buratti et al. [2019] Buratti, B.J., Thomas, P.C., Roussos, E., Howett, C., Seiß, M., Hendrix, A.R., Helfenstein, P., Brown, R.H., Clark, R.N., Denk, T., Filacchione, G., Hoffmann, H., Jones, G.H., Khawaja, N., Kollmann, P., Krupp, N., Lunine, J., Momary, T.W., Paranicas, C., Postberg, F., Sachse, M., Spahn, F., Spencer, J., Srama, R., Albin, T., Baines, K.H., Ciarniello, M., Economou, T., Hsu, H.W., Kempf, S., Krimigis, S.M., Mitchell, D., Moragas-Klostermeyer, G., Nicholson, P.D., Porco, C.C., Rosenberg, H., Simolka, J., Soderblom, L.A., 2019. Close Cassini flybys of Saturn’s ring moons Pan, Daphnis, Atlas, Pandora, and Epimetheus. Science 364, eaat2349. doi:10.1126/science.aat2349.
- Charnoz et al. [2009] Charnoz, S., Dones, L., Esposito, L.W., Estrada, P.R., Hedman, M.M., 2009. Origin and Evolution of Saturn’s Ring System, in: Dougherty, M.K., Esposito, L.W., Krimigis, S.M. (Eds.), Saturn from Cassini-Huygens, p. 537. doi:10.1007/978-1-4020-9217-6-17.
- Ciarniello et al. [2019] Ciarniello, M., Filacchione, G., D’Aversa, E., Capaccioni, F., Nicholson, P.D., Cuzzi, J.N., Clark, R.N., Hedman, M.M., Dalle Ore, C.M., Cerroni, P., Plainaki, C., Spilker, L.J., 2019. Cassini-VIMS observations of Saturn’s main rings: II. A spectrophotometric study by means of Monte Carlo ray-tracing and Hapke’s theory. Icarus 317, 242–265.
- Colwell et al. [2009] Colwell, J.E., Nicholson, P.D., Tiscareno, M.S., Murray, C.D., French, R.G., Marouf, E.A., 2009. The Structure of Saturn’s Rings, in: Dougherty, M.K., Esposito, L.W., Krimigis, S.M. (Eds.), Saturn from Cassini-Huygens, p. 375. doi:10.1007/978-1-4020-9217-6-13.
- Connerney [1986] Connerney, J.E.P., 1986. Magnetic connection for Saturn’s rings and atmosphere. Geophys. Res. Lett. 13, 773–776. doi:10.1029/GL013i008p00773.
- Cook and Franklin [1970] Cook, A.F., Franklin, F.A., 1970. The Effect of Meteoroidal Bombardment on Saturn’s Rings. Astron. J. 75, 195. doi:10.1086/110963.
- Crida and Charnoz [2012] Crida, A., Charnoz, S., 2012. Formation of Regular Satellites from Ancient Massive Rings in the Solar System. Science 338, 1196. doi:10.1126/science.1226477.
- Cuzzi and Durisen [1990] Cuzzi, J.N., Durisen, R.H., 1990. Meteoroid bombardment of planetary rings; general formulation and effects of oort cloud projectiles. Icarus 84, 47–501.
- Cuzzi and Estrada [1998] Cuzzi, J.N., Estrada, P.R., 1998. Compositional evolution of saturn’s rings due to meteoroid bombardment. Icarus 132, 1–35.
- Cuzzi et al. [2018] Cuzzi, J.N., French, R.G., Hendrix, A.R., Olson, D.M., Roush, T., Vahidinia, S., 2018. HST-STIS spectra and the redness of Saturn’s rings. Icarus 309, 363–388. doi:10.1016/j.icarus.2018.02.025.
- Dones [1991] Dones, L., 1991. A recent cometary origin for Saturn’s rings? Icarus 92, 194–203. doi:10.1016/0019-1035(91)90045-U.
- Doyle et al. [1989] Doyle, L.R., Dones, L., Cuzzi, J.N., 1989. Radiative transfer modeling of Saturn’s outer B ring. Icarus 80, 104–135. doi:10.1016/0019-1035(89)90163-2.
- Durisen [1984] Durisen, R.H., 1984. Transport effects due to particle erosion mechanisms, in: Greenberg, R., Brahic, A. (Eds.), IAU Colloq. 75: Planetary Rings, pp. 416–446.
- Durisen [1995] Durisen, R.H., 1995. An instability in planetary rings due to ballistic transport. Icarus 115, 66–85. doi:10.1006/icar.1995.1079.
- Durisen et al. [1992] Durisen, R.H., Bode, P.W., Cuzzi, J.N., Cederbloom, S.E., Murphy, B.W., 1992. Ballistic transport in planetary ring systems due to particle erosion mechanisms. II - Theoretical models for Saturn’s A- and B-ring inner edges. Icarus 100, 364–393. doi:10.1016/0019-1035(92)90106-H.
- Durisen et al. [1996] Durisen, R.H., Bode, P.W., Dyck, S.G., Cuzzi, J.N., Dull, J.D., White, II, J.C., 1996. Ballistic Transport in Planetary Ring Systems Due to Particle Erosion Mechanisms. III. Torques and Mass Loading by Meteoroid Impacts. Icarus 124, 220–236. doi:10.1006/icar.1996.0200.
- Durisen et al. [1989] Durisen, R.H., Cramer, N.L., Murphy, B.W., Cuzzi, J.N., Mullikin, T.L., Cederbloom, S.E., 1989. Ballistic transport in planetary ring systems due to particle erosion mechanisms. I - Theory, numerical methods, and illustrative examples. Icarus 80, 136–166. doi:10.1016/0019-1035(89)90164-4.
- Esposito [2008] Esposito, L., 2008. History of Saturn’s rings from Cassini UVIS observations, in: European Planetary Science Congress 2008, p. 757.
- Esposito [1984] Esposito, L.W., 1984. Structure and dynamics of Saturn’s rings as seen by the Voyager stellar occultation, in: Brahic, A. (Ed.), Planetary Rings, pp. 229–250.
- Estrada and Durisen [2023] Estrada, P.R., Durisen, R.H., 2023. Constraints on the initial mass, age and lifetime of Saturn’s rings from viscous evolutions that include pollution and transport due to micrometeoroid bombardment. Icarus 400, 115296. doi:10.1016/j.icarus.2022.115296.
- Estrada et al. [2016] Estrada, P.R., Durisen, R.H., Cuzzi, J.N., 2016. The Evolution of Saturn’s Rings Under the Influence of the Edgeworth-Kuiper Belt Micrometeoroid Flux: Tightening the Constraints on Ring Age, in: AAS/Division for Planetary Sciences Meeting Abstracts #48, p. 114.05.
- Estrada et al. [2017] Estrada, P.R., Durisen, R.H., Cuzzi, J.N., 2017. Ballistic Transport: After the Cassini Grand Finale, is there a Final Consensus on Ring Origin and Age? AGU Fall Meeting Abstracts .
- Estrada et al. [2015] Estrada, P.R., Durisen, R.H., Cuzzi, J.N., Morgan, D.A., 2015. Combined structural and compositional evolution of planetary rings due to micrometeoroid impacts and ballistic transport. Icarus 252, 415–439. doi:10.1016/j.icarus.2015.02.005.
- Estrada et al. [2018] Estrada, P.R., Durisen, R.H., Latter, H.N., 2018. Meteoroid Bombardment and Ballistic Transport in Planetary Rings, in: Tiscareno, M.S., Murray, C.D. (Eds.), Planetary Ring Systems. Properties, Structure, and Evolution, pp. 198–224. doi:10.1017/9781316286791.009.
- Estrada and Mosqueira [2006] Estrada, P.R., Mosqueira, I., 2006. A gas-poor planetesimal capture model for the formation of giant planet satellite systems. Icarus 181, 486–509. doi:10.1016/j.icarus.2005.11.006.
- Estrada et al. [2009] Estrada, P.R., Mosqueira, I., Lissauer, J.J., D’Angelo, G., Cruikshank, D.P., 2009. Formation of Jupiter and Conditions for Accretion of the Galilean Satellites, in: Pappalardo, R.T., McKinnon, W.B., Khurana, K.K. (Eds.), Europa, p. 27.
- French et al. [2017] French, R.G., McGhee-French, C.A., Lonergan, K., Sepersky, T., Jacobson, R.A., Nicholson, P.D., Hedman, M.M., Marouf, E.A., Colwell, J.E., 2017. Noncircular features in Saturn’s rings IV: Absolute radius scale and Saturn’s pole direction. Icarus 290, 14–45. doi:10.1016/j.icarus.2017.02.007.
- French et al. [1993] French, R.G., Nicholson, P.D., Cooke, M.L., Elliot, J.L., Matthews, K., Perkovic, O., Tollestrup, E., Harvey, P., Chanover, N.J., Clark, M.A., Dunham, E.W., Forrest, W., Harrington, J., Pipher, J., Brahic, A., Grenier, I., Roques, F., Arndt, M., 1993. Geometry of the Saturn System from the 3 July 1989 Occultation of 28 Sgr and Voyager Observations. Icarus 103, 163–214. doi:10.1006/icar.1993.1066.
- Goertz and Morfill [1988] Goertz, C.K., Morfill, G., 1988. A new instability of Saturn’s ring. Icarus 74, 325–330. doi:10.1016/0019-1035(88)90044-9.
- Goertz et al. [1986] Goertz, C.K., Morfill, G.E., Ip, W.H., Grun, E., Havnes, O., 1986. Electromagnetic angular momentum transport in Saturn’s rings. Nature 320, 141–143. doi:10.1038/320141a0.
- Grün et al. [1985] Grün, E., Zook, H.A., Fechtig, H., Giese, R.H., 1985. Collisional balance of the meteoritic complex. Icarus 62, 244–272. doi:10.1016/0019-1035(85)90121-6.
- Hamilton [1993a] Hamilton, D.P., 1993a. Erratum: ”motion of Dust in a Planetary Magnetosphere: Orbit-Averaged Equations for Oblateness, Electromagnetic, and Radiation Forces with Application to Saturn’s E-Ring. Icarus 103, 161. doi:10.1006/icar.1993.1065.
- Hamilton [1993b] Hamilton, D.P., 1993b. Motion of Dust in a Planetary Magnetosphere: Orbit-Averaged Equations for Oblateness, Electromagnetic, and Radiation Forces with Application to Saturn’s E Ring. Icarus 101, 244–264. doi:10.1006/icar.1993.1022.
- Hamilton and Burns [1994] Hamilton, D.P., Burns, J.A., 1994. Origin of Saturn’s E Ring: Self-Sustained, Naturally. Science 264, 550–553. doi:10.1126/science.264.5158.550.
- Hanninen and Salo [1992] Hanninen, J., Salo, H., 1992. Collisional simulations of satellite Lindblad resonances. Icarus 97, 228–247. doi:10.1016/0019-1035(92)90130-Y.
- Hartmann [2009] Hartmann, L., 2009. Accretion Processes in Star Formation: Second Edition. Cambridge University Press.
- Hedman et al. [2011] Hedman, M.M., Burns, J.A., Evans, M.W., Tiscareno, M.S., Porco, C.C., 2011. Saturn’s Curiously Corrugated C Ring. Science 332, 708. doi:10.1126/science.1202238.
- Hedman and Nicholson [2013] Hedman, M.M., Nicholson, P.D., 2013. Kronoseismology: Using Density Waves in Saturn’s C Ring to Probe the Planet’s Interior. Astron. J. 146, 12. doi:10.1088/0004-6256/146/1/12.
- Hedman and Nicholson [2016] Hedman, M.M., Nicholson, P.D., 2016. The B-ring’s surface mass density from hidden density waves: Less than meets the eye? Icarus 279, 109–124. doi:10.1016/j.icarus.2016.01.007.
- Hedman et al. [2018] Hedman, M.M., Postberg, F., Hamilton, D.P., Renner, S., Hsu, H.W., 2018. Dusty Rings, in: Tiscareno, M.S., Murray, C.D. (Eds.), Planetary Ring Systems. Properties, Structure, and Evolution, pp. 308–337. doi:10.1017/9781316286791.012.
- Housen and Holsapple [2011] Housen, K.R., Holsapple, K.A., 2011. Ejecta from impact craters. Icarus 211, 856–875. doi:10.1016/j.icarus.2010.09.017.
- Hsu et al. [2018] Hsu, H.W., Schmidt, J., Kempf, S., Postberg, F., Moragas-Klostermeyer, G., Seiß, M., Hoffmann, H., Burton, M., Ye, S., Kurth, W.S., Horányi, M., Khawaja, N., Spahn, F., Schirdewahn, D., O’Donoghue, J., Moore, L., Cuzzi, J., Jones, G.H., Srama, R., 2018. In situ collection of dust grains falling from Saturn’s rings into its atmosphere. Science 362, aat3185. doi:10.1126/science.aat3185.
- Iess et al. [2019] Iess, L., Militzer, B., Kaspi, Y., Nicholson, P., Durante, D., Racioppa, P., Anabtawi, A., Galanti, E., Hubbard, W., Mariani, M.J., 2019. Measurement and implications of Saturn’s gravity field and ring mass. Science 364, aat2965. doi:10.1126/science.aat2965.
- Ip [1983] Ip, W.H., 1983. Collisional interactions of ring particles - The ballistic transport process. Icarus 54, 253–262. doi:10.1016/0019-1035(83)90195-1.
- Ip [1984] Ip, W.H., 1984. Ring torque of Saturn from interplanetary meteoroid impact. Icarus 60, 547–552. doi:10.1016/0019-1035(84)90163-5.
- Ip et al. [2016] Ip, W.H., Liu, C.M., Pan, K.C., 2016. Transport and electrodynamical coupling of nano-grains ejected from the Saturnian rings and their possible ionospheric signatures. Icarus 276, 163–169. doi:10.1016/j.icarus.2016.04.004.
- Jontof-Hutter and Hamilton [2012] Jontof-Hutter, D., Hamilton, D.P., 2012. The fate of sub-micron circumplanetary dust grains I: Aligned dipolar magnetic fields. Icarus 218, 420–432. doi:10.1016/j.icarus.2011.09.033.
- Kempf et al. [2023] Kempf, S., Altobelli, N., Schmidt, J., Cuzzi, J.N., Estrada, P.R., Srama, R., 2023. Micrometeoroid infall onto saturn’s rings constrains their age to no more than a few hundred million years. Science Advances 9, eadf8537. doi:10.1126/sciadv.adf8537.
- Kempf et al. [2017] Kempf, S., Altobelli, N., Srama, R., Cuzzi, J.N., Estrada, P.R., 2017. The Age of Saturn’s Rings Constrained by the Meteoroid Flux Into the System. AGU Fall Meeting Abstracts .
- Koschny and Grün [2001a] Koschny, D., Grün, E., 2001a. Impacts into Ice-Silicate Mixtures: Crater Morphologies, Volumes, Depth-to-Diameter Ratios, and Yield. Icarus 154, 391–401. doi:10.1006/icar.2001.6707.
- Koschny and Grün [2001b] Koschny, D., Grün, E., 2001b. Impacts into Ice-Silicate Mixtures: Ejecta Mass and Size Distributions. Icarus 154, 402–411. doi:10.1006/icar.2001.6708.
- Latter et al. [2012] Latter, H.N., Ogilvie, G.I., Chupeau, M., 2012. The ballistic transport instability in Saturn’s rings - I. Formalism and linear theory. Mon. Not. R. Astron. Soc. 427, 2336–2348. doi:10.1111/j.1365-2966.2012.22122.x.
- Latter et al. [2014a] Latter, H.N., Ogilvie, G.I., Chupeau, M., 2014a. The ballistic transport instability in Saturn’s rings - II. Non-linear wave dynamics. Mon. Not. R. Astron. Soc. 441, 2760–2772. doi:10.1093/mnras/stu737.
- Latter et al. [2014b] Latter, H.N., Ogilvie, G.I., Chupeau, M., 2014b. The ballistic transport instability in Saturn’s rings - III. Numerical simulations. Mon. Not. R. Astron. Soc. 441, 2773–2781. doi:10.1093/mnras/stu657.
- Lissauer [1984] Lissauer, J.J., 1984. Ballistic transport in Saturn’s rings - an analytic theory. Icarus 57, 63–71. doi:10.1016/0019-1035(84)90008-3.
- Lissauer et al. [1981] Lissauer, J.J., Shu, F.H., Cuzzi, J.N., 1981. Moonlets in Saturn’s rings. Nature 292, 707–711. doi:10.1038/292707a0.
- Mitchell et al. [2018] Mitchell, D.G., Perry, M.E., Hamilton, D.C., Westlake, J.H., Kollmann, P., Smith, H.T., Carbary, J.F., Waite, J.H., Perryman, R., Hsu, H.W., Wahlund, J.E., Morooka, M.W., Hadid, L.Z., Persoon, A.M., Kurth, W.S., 2018. Dust grains fall from Saturn’s D-ring into its equatorial upper atmosphere. Science 362, aat2236. doi:10.1126/science.aat2236.
- Moore et al. [2015] Moore, L., O’Donoghue, J., Müller-Wodarg, I., Galand, M., Mendillo, M., 2015. Saturn ring rain: Model estimates of water influx into Saturn’s atmosphere. Icarus 245, 355–366. doi:10.1016/j.icarus.2014.08.041.
- Morfill et al. [1983] Morfill, G.E., Fechtig, H., Gruen, E., Goertz, C.K., 1983. Some consequences of meteoroid impacts on Saturn’s rings. Icarus 55, 439–447. doi:10.1016/0019-1035(83)90114-8.
- Morishima et al. [2016] Morishima, R., Spilker, L., Brooks, S., Deau, E., Pilorz, S., 2016. Incomplete cooling down of Saturn’s A ring at solar equinox: Implication for seasonal thermal inertia and internal structure of ring particles. Icarus 279, 2–19. doi:10.1016/j.icarus.2015.06.025.
- Mosqueira et al. [2010] Mosqueira, I., Estrada, P.R., Charnoz, S., 2010. Deciphering the origin of the regular satellites of gaseous giants - Iapetus: The Rosetta ice-moon. Icarus 207, 448–460. doi:10.1016/j.icarus.2009.10.018.
- Mousis and Gautier [2004] Mousis, O., Gautier, D., 2004. Constraints on the presence of volatiles in Ganymede and Callisto from an evolutionary turbulent model of the Jovian subnebula. Planet. Space Sci. 52, 361–370. doi:10.1016/j.pss.2003.06.004.
- Northrop and Connerney [1987] Northrop, T.G., Connerney, J.E.P., 1987. A micrometeorite erosion model and the age of Saturn’s rings. icarus 70, 124–137. doi:10.1016/0019-1035(87)90079-0.
- O’Donoghue et al. [2019] O’Donoghue, J., Moore, L., Connerney, J., Melin, H., Stallard, T.S., Miller, S., Baines, K.H., 2019. Observations of the chemical and thermal response of ’ring rain’ on Saturn’s ionosphere. Icarus 322, 251–260. doi:10.1016/j.icarus.2018.10.027.
- O’Donoghue et al. [2013] O’Donoghue, J., Stallard, T.S., Melin, H., Jones, G.H., Cowley, S.W.H., Miller, S., Baines, K.H., Blake, J.S.D., 2013. The domination of Saturn’s low-latitude ionosphere by ring ‘rain’. Nature 496, 193–195. doi:10.1038/nature12049.
- Perry et al. [2018] Perry, M.E., Waite, J.H., Mitchell, D.G., Miller, K.E., Cravens, T.E., Perryman, R.S., Moore, L., Yelle, R.V., Hsu, H.W., Hedman, M.M., Cuzzi, J.N., Strobel, D.F., Hamil, O.Q., Glein, C.R., Paxton, L.J., Teolis, B.D., McNutt, R.L., 2018. Material Flux From the Rings of Saturn Into Its Atmosphere. Geophys. Res. Lett. 45, 10,093–10,100. doi:10.1029/2018GL078575.
- Poppe [2016] Poppe, A.R., 2016. An improved model for interplanetary dust fluxes in the outer Solar System. Icarus 264, 369–386. doi:10.1016/j.icarus.2015.10.001.
- Poppe et al. [2019a] Poppe, A.R., Lisse, C.M., Piquette, M., Zemcov, M., Horányi, M., James, D., Szalay, J.R., Bernardoni, E., Stern, S.A., 2019a. Constraining the Solar System’s Debris Disk with In Situ New Horizons Measurements from the Edgeworth-Kuiper Belt. Astrophys. J. Lett. 881, L12. doi:10.3847/2041-8213/ab322a.
- Poppe et al. [2019b] Poppe, A.R., Lisse, C.M., Piquette, M., Zemcov, M., Horányi, M., James, D., Szalay, J.R., Bernardoni, E., Stern, S.A., 2019b. Erratum: “Constraining the Solar System’s Debris Disk with In Situ New Horizons Measurements from the Edgeworth-Kuiper Belt”. Astrophys. J. Lett. 882, L14. doi:10.3847/2041-8213/ab3c6f.
- Porco et al. [2008] Porco, C.C., Weiss, J.W., Richardson, D.C., Dones, L., Quinn, T., Throop, H., 2008. Simulations of the Dynamical and Light-Scattering Behavior of Saturn’s Rings and the Derivation of Ring Particle and Disk Properties. Astron. J. 136, 2172–2200. doi:10.1088/0004-6256/136/5/2172.
- Poulet and Sicardy [2001] Poulet, F., Sicardy, B., 2001. Dynamical evolution of the Prometheus-Pandora system. Mon. Not. R. Astron. Soc. 322, 343–355. doi:10.1046/j.1365-8711.2001.04128.x.
- Reffet et al. [2015] Reffet, E., Verdier, M., Ferrari, C., 2015. Thickness of Saturn’s B ring as derived from seasonal temperature variations measured by Cassini CIRS. Icarus 254, 276–286. doi:10.1016/j.icarus.2015.04.006.
- Robbins et al. [2010] Robbins, S.J., Stewart, G.R., Lewis, M.C., Colwell, J.E., Sremčevíc, M., 2010. Estimating the masses of Saturn’s A and B rings from high-optical depth N-body simulations and stellar occultations. Icarus 206, 431–445. doi:10.1016/j.icarus.2009.09.012.
- Sachse et al. [2015] Sachse, M., Schmidt, J., Kempf, S., Spahn, F., 2015. Correlation between speed and size for ejecta from hypervelocity impacts. J. Geophys. Res. 120, 1847–1858. doi:10.1002/2015JE004844.
- Salmon et al. [2010] Salmon, J., Charnoz, S., Crida, A., Brahic, A., 2010. Long-term and large-scale viscous evolution of dense planetary rings. Icarus 209, 771–785. doi:10.1016/j.icarus.2010.05.030.
- Schmidt et al. [2016] Schmidt, J., Colwell, J.E., Lehmann, M., Marouf, E.A., Salo, H., Spahn, F., Tiscareno, M.S., 2016. On the Linear Damping Relation for Density Waves in Saturn’s Rings. Astrophys. J. 824, 33. doi:10.3847/0004-637X/824/1/33.
- Schmidt et al. [2009] Schmidt, J., Ohtsuki, K., Rappaport, N., Salo, H., Spahn, F., 2009. Dynamics of Saturn’s Dense Rings, in: Dougherty, M.K., Esposito, L.W., Krimigis, S.M. (Eds.), Saturn from Cassini-Huygens, p. 413. doi:10.1007/978-1-4020-9217-6-14.
- Shimaki and Arakawa [2012] Shimaki, Y., Arakawa, M., 2012. Low-velocity collisions between centimeter-sized snowballs: Porosity dependence of coefficient of restitution for ice aggregates analogues in the Solar System. Icarus 221, 310–319. doi:10.1016/j.icarus.2012.08.005.
- Srama et al. [2004] Srama, R., Ahrens, T.J., Altobelli, N., Auer, S., Bradley, J.G., Burton, M., Dikarev, V.V., Economou, T., Fechtig, H., Görlich, M., Grande, M., Graps, A., Grün, E., Havnes, O., Helfert, S., Horanyi, M., Igenbergs, E., Jessberger, E.K., Johnson, T.V., Kempf, S., Krivov, A.V., Krüger, H., Mocker-Ahlreep, A., Moragas-Klostermeyer, G., Lamy, P., Landgraf, M., Linkert, D., Linkert, G., Lura, F., McDonnell, J.A.M., Möhlmann, D., Morfill, G.E., Müller, M., Roy, M., Schäfer, G., Schlotzhauer, G., Schwehm, G.H., Spahn, F., Stübig, M., Svestka, J., Tschernjawski, V., Tuzzolino, A.J., Wäsch, R., Zook, H.A., 2004. The Cassini Cosmic Dust Analyzer. Space Sci. Rev. 114, 465–518. doi:10.1007/s11214-004-1435-z.
- Stewart et al. [2007] Stewart, G.R., Robbins, S.J., Colwell, J.E., 2007. Evidence for a Primordial Origin of Saturn’s Rings, in: AAS/Division for Planetary Sciences Meeting Abstracts #39, p. 420.
- Tajeddine et al. [2017] Tajeddine, R., Nicholson, P.D., Longaretti, P.Y., El Moutamid, M., Burns, J.A., 2017. What Confines the Rings of Saturn? Astrophys. J. Suppl. S 232, 28. doi:10.3847/1538-4365/aa8c09.
- Tiscareno et al. [2007] Tiscareno, M.S., Burns, J.A., Nicholson, P.D., Hedman, M.M., Porco, C.C., 2007. Cassini imaging of Saturn’s rings. II. A wavelet technique for analysis of density waves and other radial structure in the rings. Icarus 189, 14–34. doi:10.1016/j.icarus.2006.12.025.
- Waite et al. [2017] Waite, J.H., Glein, C.R., Perryman, R.S., Teolis, B.D., Magee, B.A., Miller, G., Grimes, J., Perry, M.E., Miller, K.E., Bouquet, A., Lunine, J.I., Brockwell, T., Bolton, S.J., 2017. Cassini finds molecular hydrogen in the Enceladus plume: Evidence for hydrothermal processes. Science 356, 155–159. doi:10.1126/science.aai8703.
- Waite et al. [2018] Waite, J.H., Perryman, R.S., Perry, M.E., Miller, K.E., Bell, J., Cravens, T.E., Glein, C.R., Grimes, J., Hedman, M., Cuzzi, J., Brockwell, T., Teolis, B., Moore, L., Mitchell, D.G., Persoon, A., Kurth, W.S., Wahlund, J.E., Morooka, M., Hadid, L.Z., Chocron, S., Walker, J., Nagy, A., Yelle, R., Ledvina, S., Johnson, R., Tseng, W., Tucker, O.J., Ip, W.H., 2018. Chemical interactions between Saturn’s atmosphere and its rings. Science 362, aat2382. doi:10.1126/science.aat2382.
- Wooden et al. [2017] Wooden, D.H., Ishii, H.A., Zolensky, M.E., 2017. Cometary dust: the diversity of primitive refractory grains. Phil. Trans. R. Soc. A 375, 20160260. doi:10.1098/rsta.2016.0260.
- Zhang et al. [2017a] Zhang, Z., Hayes, A.G., Janssen, M.A., Nicholson, P.D., Cuzzi, J.N., de Pater, I., Dunn, D.E., 2017a. Exposure age of Saturn’s A and B rings, and the Cassini Division as suggested by their non-icy material content. Icarus 294, 14–42.
- Zhang et al. [2017b] Zhang, Z., Hayes, A.G., Janssen, M.A., Nicholson, P.D., Cuzzi, J.N., de Pater, I., Dunn, D.E., Estrada, P.R., Hedman, M.M., 2017b. Cassini microwave observations provide clues to the origin of Saturn’s C ring. Icarus 281, 297–321.