Large-scale Collaborative Filtering with Product Embeddings
Abstract
The application of machine learning techniques to large-scale personalized recommendation problems is a challenging task. Such systems must make sense of enormous amounts of implicit feedback in order to understand user preferences across numerous product categories. This paper presents a deep learning based solution to this problem within the collaborative filtering with implicit feedback framework. Our approach combines neural attention mechanisms, which allow for context dependent weighting of past behavioral signals, with representation learning techniques to produce models which obtain extremely high coverage, can easily incorporate new information as it becomes available, and are computationally efficient. Offline experiments demonstrate significant performance improvements when compared to several alternative methods from the literature. Results from an online setting show that the approach compares favorably with current production techniques used to produce personalized product recommendations.
1 INTRODUCTION
Helping users discover content and products in increasingly complex digital marketplaces is crucial for e-commerce companies like Amazon. In order to accomplish this task, large-scale recommendation systems must model the preference relationships between millions of users and items. Collaborative filtering methods, which aim to model user preferences based on previous user-item interactions, are frequently employed to solve such problems (Linden et al., 2003). In particular, latent factor models, such as those based on matrix factorization, have seen widespread success (Slaney, 2011).
Unfortunately, traditional recommender systems that learn embeddings for both users and items (Koren et al., 2009; Hu et al., 2008) scale at best linearly with the combined number of users and items, and are not appropriate when the numbers of users and items can be in the tens or hundreds of millions (in this work, 40 million users and 10 million items). In such large-scale settings, matrix factorization based approaches to collaborative filtering require sophisticated techniques to overcome the computational and memory strains they pose (Gemulla et al., 2011; Tan et al., 2016).
Furthermore, in real-world settings, numerous related problems which require understanding items, users, and preferences are likely being worked on simultaneously. Repeatedly solving such problems from scratch introduces operational inefficiencies and slows rates of innovation due to the diversion of resources from dealing with the unique aspects of an individual domain. While it may be possible to reclaim these resources by limiting scope, for example, building category specific recommender systems that simply ignore user-item interactions deemed to be out of domain, doing so introduces new to category cold-start problems (Schein et al., 2002) that would not exist if one had modeled a broader view of user tastes and preferences.
One way to overcome the deficiencies outlined above is to decompose the recommendation problem into distinct item representation and user preference modeling phases. Reusing a shared set of highly informative pre-trained item embeddings significantly reduces computational costs, and allows us to focus our efforts on experimentally measuring the effectiveness of downstream collaborative filtering models. While there has been a number of item embedding algorithms proposed in the literature (Grbovic and Cheng, 2018; Grbovic et al., 2015; Biswas et al., 2017; Wu et al., 2017; Vasile et al., 2016), to the best of our knowledge, methods of leveraging such pre-trained item embeddings for user preference modeling have not been extensively studied.
In this work, we explore a number of methods which use pre-trained item embeddings within the large-scale collaborative filtering within implicit feedback setting. Our primary contribution is the novel use of an attention mechanism to select relevant pieces of information from a user’s historical behavior given a particular query item. As such, the proposed method is better described as jointly representing the compatibility between a specific user-item pair, rather that learning distinct user and item representations in a common latent space. We demonstrate that this architecture is extremely well-suited to leveraging such pre-trained distributed representations of items for user preference modeling.
To learn representations of items, any suitable representation learning algorithm could be used (Grbovic et al., 2015; Biswas et al., 2017; Wu et al., 2017; Vasile et al., 2016). In this work, we employ well-known algorithms, originally developed for learning distributed representations of words (Mikolov et al., 2013), which have recently been adapted to the collaborative filtering setting (Grbovic and Cheng, 2018). These pre-trained item representations can be reused to quickly bootstrap machine learning approaches for a variety of e-commerce related tasks such as similarity search, deduplication, or user preference modeling. The generic vector based form of the representations allows them to be easily shared by researchers and practitioners, and provides for a clear point of delineation between systems. As a result, any improvements made to the representation learning framework can immediately benefit downstream tasks without requiring the refactoring of complex production machine learning pipelines (McMahan et al., 2013; Ng, 2016).
After providing background and reviewing related work in Section 2, we describe the components of our approach in Sections 3 and 4. We demonstrate their efficacy on large-scale offline experiments using Amazon user-item interaction data in Section 5, and a production setting in Section 6. In both cases, we show impressive performance against a range of alternative approaches.
2 BACKGROUND AND RELATED WORK
Our model builds upon a rich body of work in collaborative filtering and representation learning. Collaborative filtering systems for implicit feedback data attempt to predict future user behavior based on previously observed interactions. Let and be sets of users and items respectively. For user and item , let if user has interacted with item , and otherwise. The set of all observed item interactions for user is denoted . The collaborative filtering task is then to predict for previously unseen items .
2.1 Latent Factor based Approaches
A commonly employed approach to collaborative filtering is to associate vectors of latent factors with each user and item. The degree to which some query item is relevant for a specific user is taken to be a function of the inner product between these vectors (Koren et al., 2009),
| (1) |
We can then formulate the problem as recovering the observed interactions and estimate parameters by minimizing some suitable loss function,
Common choices of loss include weighted least squares (Hu et al., 2008) or the logistic loss (Johnson, 2014).
While such linear embedding approaches to collaborative filtering perform well in a variety of settings, there are a number of factors that make it difficult to apply in a large-scale recommendation setting like the one considered here.
First and foremost is the sheer number of parameters one must estimate. For example, the dataset used in this work consists of 40 million users and 10 million items. Using dimensional embeddings would require estimating over three billion parameters.
Furthermore, since the number of observed interactions tends to grow linearly with the number of users, the user-item interaction matrix becomes increasingly sparse. Latent factor models operating in this regime require careful regularization to ensure models generalize appropriately to unseen interactions (Mnih and Salakhutdinov, 2008).
Lastly, since latent factor models are transductive in nature, i.e. they do not generalize to new users or items, rapidly incorporating new information into the system can be problematic. For example, incorporating new item interactions into the user representation typically requires solving an optimization problem (Johnson, 2014).
2.2 Learning Nonlinear Encodings of users
The transductive nature of latent factor models can be ameliorated by replacing the linear embedding, , in (1) with a nonlinear embedding of user features,
| (2) |
A number of deep learning based recommendation systems have been proposed, that use a neural network to capture this nonlinear embedding (Dziugaite and Roy, 2015; Salakhutdinov et al., 2007). A common focus of these works is devising methods which are able to exploit various types of side information which are difficult to incorporate when using tranditional matrix factorization based techniques. In recommendation contexts, such side information often requires special handling as it may be very sparse (search queries, geographic location) (Cheng et al., 2016; Wang et al., 2017; Guo et al., 2017), or temporally structured (session or browsing history) (Quadrana et al., 2017).
Historical user behavior is commonly incorporated into deep learning based recommendation systems using a bag-of-words style encoding of past user-item interactions, i.e, summing or averaging item embeddings (Sedhain et al., 2015; Covington et al., 2016; Zheng et al., 2016b). Several recent works have explicitly explored order-independent combination operators operating over sets (Iyyer et al., 2015; Zaheer et al., 2017; Santoro et al., 2017), and surprisingly good performance can be achieved using simple sums, averages, and TF-IDF style weighted averages of word embeddings (White et al., 2015; De Boom et al., 2016) in an NLP context. The use of vector averaging is especially appealing due its simplicity, ability to deal with variable sized user behavior histories, and the ease with which new information can be incorporated.
However, as we show experimentally in Section 5, using a static combination operation may be suboptimal in some settings and significant improvements can be achieved using learned combination operators that can adapt to the context at hand.
2.3 Nonlinear Functions of Items and users
Despite modeling users using flexible nonlinear embeddings, most deep learning based recommender systems share the common architectural feature of modeling relevance as the inner product between a separate user and item vector, as in (2). While this may be sufficient given a large enough number of factors and training dataset, simply enlarging this latent space may be suboptimal both from a generalization and a computational perspective. An alternative, which is explored in this work, is to assume that relevance is some nonlinear function of both the user and the query item.
This idea has been explored by a number of authors. Weston et al. (2013) propose learning multiple vectors for each user and select among them using a max operation. A learned weighting of individual user and item factors is proposed in He et al. (2017). In both cases, these models require learning distinct representations of users and suffer from similar problems as matrix factorization based approaches. Closer in spirit to our work is that of Vartak et al. (2017), which proposes a deep learning based recommender system motivated by a meta-learning perspective (Lake et al., 2015). Their model outputs a relevance score given a query item vector and two user vectors computed by averaging the vectors for items in the sets and . Our approach offers greater flexibility, moving beyond simple averages and using a more flexible functional form.
Another related approach was recently explored by Grbovic and Cheng (2018). Like the work presented here, the techniques presented in Grbovic and Cheng (2018) rely on item representations learned using a word2vec (Mikolov et al., 2013) like procedure. Unlike this work, Grbovic and Cheng’s training procedure simultaneously learns a user type representation while learning item embeddings. Specific users are then mapped to user types by manually derived rules. Ultimately, these representations are used to derive relevance features (cosine distances) which are input into a decision tree based personalization model. In contrast, our approach leverages item embeddings directly to model user prefeences by learning a parametrized model operating over the items a user has previously interacted with. Decoupling these procedures and treating the embeddings as inputs sidesteps the need to define heuristic rules to map from users to types, and allows models to easily incorporate new behavioral signals without retraining.
2.4 Neural Attention Mechanisms for Combining Representations
In addition to summing or averaging item representations, we explore the use of neural attention mechanism to combine item representations. Neural attention mechanisms (Olah and Carter, 2016; Graves et al., 2014; Bahdanau et al., 2015; Kim et al., 2017) provide a method by which neural networks can focus processing on particular portions of the input data and ignore those which may be irrelevant in the current context. Although most commonly used to augment recurrent neural networks, attention mechanisms can also be used as an alternative to convolution (Kim, 2014) or recurrence when dealing with variable size structured inputs such as sequences, trees, or sets (Vaswani et al., 2017). The model we propose is related to this line of work, largely inspired by Memory-Networks and their derivatives (Weston et al., 2014; Sukhbaatar et al., 2015).
The use of attention mechanisms specifically in recommender system contexts has also been recently explored. In (Chen et al., 2017a), an attention mechanism is used to select the most important historical item interactions given a particular user. Because the attention mechanism conditions explicitly on the user rather than the query item, the attention weights applied to past item interactions, and the resulting user representation, remain constant for a particular user. More similar to our work, is the concurrent approach of (Fu et al., 2018), which applies a matching network (Vinyals et al., 2016) like averaging of past item ratings to predict ratings for unseen items. Unlike our work, (Fu et al., 2018) introduce an additional matrix factorization component to improve performance. Thus, both methods require learning an embedding for each user, something we explictly avoid for the reasons described in Section 1.
3 PRODUCT REPRESENTATIONS
Our nonlinear collaborative filtering method, described in Section 4, takes as input a set of pre-trained item embeddings. In the context of this paper, items correspond to products available on an e-commerce site. Numerous techniques for learning product embeddings have been explored in the literature. A common theme is for these methods to focus on representing products via a specific modality such as images (Nedelec et al., 2017), text (Biswas et al., 2017), audio (Van den Oord et al., 2013), or combinations thereof. In our setting, we do not assume access to side-information, so representations are learned based purely on user/item interaction data. If such features were also available, this information can easily be incorporated into the item representation learning process (Vasile et al., 2016; Vartak et al., 2017).
In particular, the embeddings used in this work were created using a straightforward adaptation of the skip-gram method of Mikolov et al. (2013) to the product embedding setting. This is done by replacing sequences of words with temporally ordered sequences of user actions (Vasile et al., 2016). Each sequence consists of a single user’s purchases, product views, and digital video and music streams. A window slides over each sequence and co-occurring pairs within the window are recorded. For each item , this yields a neighborhood of co-occurring context items. In addition to the positive examples of co-occurring context items in , we sample a collection of negative samples randomly from some distribution over items. We wish to learn embeddings that map frequently co-occurring items to similar locations in the embedding space, while maintaining separation between dissimilar items. This is achieved by optimizing the parameters of the embedding to minimize
where are the embeddings for item and context , and is the logistic function. The resulting embeddings are used as inputs to all the models presented in the remainder of this work. Importantly, the embeddings are left fixed and not updated when training downstream collaborative filtering models.
An alternative to using pre-trained would be to jointly learn these embeddings as part of our recommender model (Zheng et al., 2016b; Sedhain et al., 2015; Covington et al., 2016). However, such an approach would significantly increase the complexity of the inference problem, making it infeasible for our large-scale setting. For example, the experiments in Section 5 use a relatively compact model containing just under 200,000 trainable parameters. In comparison, the number of parameters in the item embedding matrix is over 500 million. Splitting the two components simplifies the problem space, and allows the two model components to be learned independently. This is particularly important in large-scale recommendation settings where models must be continuously updated.
While this choice does limit model capacity, the degree to which this will actually hinder performance is unclear. For example, previous results in NLP demonstrated significant performance improvements when using static word embeddings as input, rather than randomly initialized words embeddings trained jointly with the model (Kim, 2014). The use of fixed embeddings also helps to ensure differences in experimental measurements are due to differences in architecture, and not the result of effects such as over specialization of the embeddings during training (a problem has the the potential to be particularly acute given the extremely large number of items in our dataset). For these reasons, this paper focuses exclusively on the use of static item representations and leaves further exploration of this issue as future work.
4 COLLABORATIVE FILTERING WITH ATTENTION
Many large-scale e-commerce datasets feature user interactions with a variety of item types and categories. Tasked with determining if a given item is relevant to a user in this setting, it would be reasonable to assume that only a small subset of the user’s past interactions provide useful information about the problem. Further, the appropriate subset is likely to vary across items. A representation of past item interactions produced using a static combination operator, such as summation or averaging, does not possess this sort of selectivity. We posit that an alternate combination operator, that uses a query dependent weighted average (attention), will provide a more appropriate inductive bias.
4.1 Model
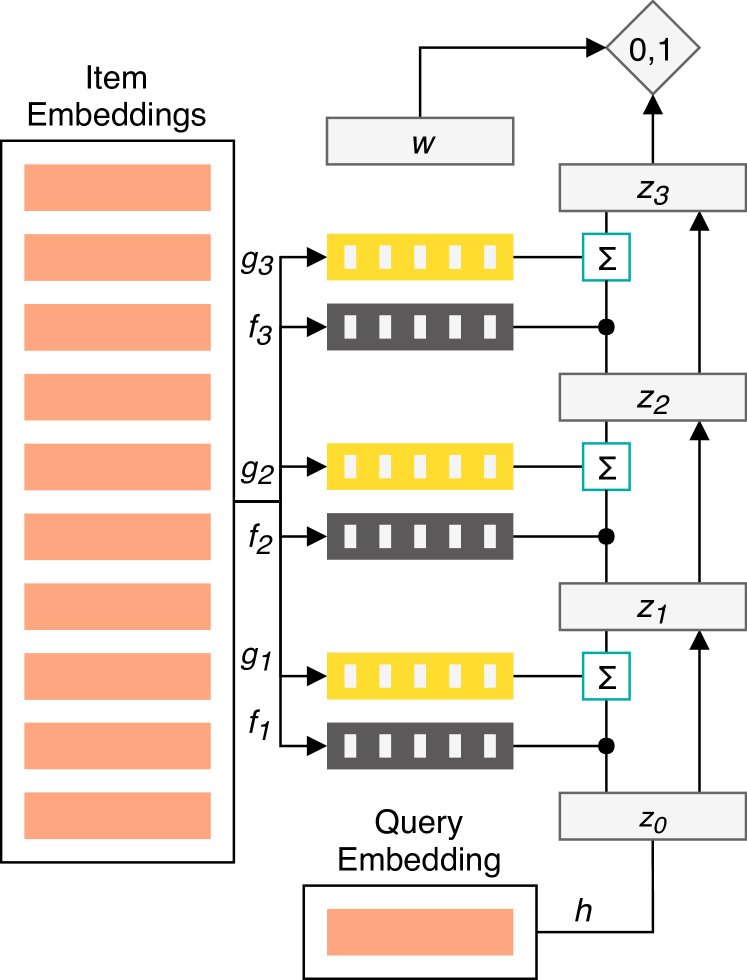
We take a probabilistic approach to ranking and aim to model the probability that user will interact with item based on observed historical user-item interactions . The first step in our model is transforming the embeddings of candidate item and each previously observed item via parametrized functions and respectively. The transformed representation of is then compared to each item a user has previously interacted via a dot product. The result of these comparisons is normalized using the softmax function to yield a vector of attention weights,
Next, the embeddings of the items in are reduced to a single -dimensional vector by transforming them using a third parameterized function , and taking a convex combination with weights ,
Multiple layers of this basic motif are stacked. Information is integrated across layers by adding the query and output of the attention mechanism and using the result as the query in the next layer (Sukhbaatar et al., 2015). A depth- version of the resulting architecture may be written as
where . The resulting joint representation of the query item and the user’s historical item interactions is reduced to a single score
| (3) |
where is the logistic function, and is a weight vector that is shared across all user/query pairs. Figure 1 provides a visual representation of the described architecture.
The use of distinct , , and is similar to the Key-Value Memory Network of Miller et al. (2016), and allows the underlying item embeddings to be adapted for the various purposes they serve within the model, without requiring us to learn multiple new representations of millions of items. Parameters are not shared between layers, so each may potentially focus on different aspects of similarity. In the experiments presented here, , , and take the form of single-layer linear neural networks
4.2 Objective
To optimize the parameters of the model, we temporally partition each user’s item interactions into a set of future and observed item interactions, denoted by and respectively. Predicting a set of future interactions from past interactions reduces the problem to multi-label classification, which could be solved by minimizing the negative log-likelihood,
| (4) |
Unfortunately, in practice is quite large. This makes the sum over each item in (Eqn. 4) computationally difficult. To alleviate this issue we employ a negative sampling technique (Chen et al., 2017b; Pan et al., 2008; Mikolov et al., 2013). For each user, we sample a set of negative items, , , from a smoothed empirical distribution obtained by raising the probability of each item occurring in the training data to a fractional power and renormalizing,
| (5) |
To sample negatives while training, we employ the alias method, which allows us to sample from a categorical distribution in time (Kronmal and Peterson Jr, 1979; Dahl et al., 2012). We also employ a weighting scheme in our loss which gives equal weight to the positive and negative items associated with each training instance. This keeps the scale of the loss independent of the number of positive and negative items that appear in each instance. We found this made tuning hyperparameters easier. Having done this, we arrive at the following loss
4.3 Training Details
The propsed model is fully differentiable and can be trained end-to-end using backpropagation. We use the Adam (Kingma and Ba, 2015) optimizer with , , minibatches of size 64, and an initial learning rate of 0.002. We scale the gradient vector to have norm 10 when it exceeds this value (Pascanu et al., 2013). Model performance is assessed on a small holdout set of users every 5,000 updates, and the learning rate is reduced by a factor of 0.8 when the objective does not improve after 5 consecutive assessments (Jozefowicz et al., 2015). Training is terminated once this occurs 20 times. Parameters are initialized using the orthogonal initialization scheme of Saxe et al. (2014). We use to smooth the empirical sampling distribution, holdout items, and negative samples for each training instance. Unless otherwise mentioned, we use a depth version of our model with hidden layers of size . We tune hyper-parameters on the same set of users used for early stopping, although in many cases found that our initial settings gave reasonable performance and did not explore others. The model is implemented in the PyTorch (Paszke et al., 2017) framework. Training takes around 12 hours on a single GPU.
5 EXPERIMENTS
To thoroughly evaluate the performance of the proposed attention based approach and our modeling choices, we perform a number of large-scale offline experiments using several model settings. We compare our approach to several alternative methods for leveraging item embeddings that have been proposed in the collaborative filtering literature.
5.1 Datasets
Training datasets were constructed by randomly selecting 40 million anonymized Amazon users and aggregating their product purchases and digital content streams over a 120 day period. To assess the performance of models we measured their ability to predict product interactions in the 7 days immediately following the end of the training period. We also removed any items that a user previously interacted with during the training period, choosing to focus exclusively on predicting new item interactions. Because all models use the same set of pre-trained item embeddings, we did not constrain the datasets described here such that all test items appear in the training data. The embeddings are trained on significantly larger datasets, which confers extremely high coverage to downstream algorithms.
5.2 Baselines
We compare against several baselines inspired by the existing literature. Since our data does not include side-information, we do not compare against content-based or hybrid content/collaborative filtering methods such as (Cheng et al., 2016; Wang et al., 2017; Guo et al., 2017; Chen et al., 2017a). Furthermore, we do not compare to methods that require learning an embedding for each user such as (Oard and Kim, 1998; Johnson, 2014; Fu et al., 2018; He et al., 2017; Dziugaite and Roy, 2015), as doing so would be computationally difficult and distract from our primary focus, modeling user preferences with a parametric function of a user’s past item interactions.
Popularity:
A non-personalized algorithm that ranks items according to their frequency in the training data.
Last Item:
An item-based approach which ranks items by cosine similarity (in embedding space) with the last item a user interacted with (Grbovic and Cheng, 2018).
Weighted Sum:
A weighted average of item embeddings a user has previous interacted with. Weights are set using various heuristics based on factors including time, nature, and type of interaction, and tuned using CMA-ES (Hansen et al., 2003).
Deep Averaging Network (DAN):
A deep learning model which uses vector averaging to combine embeddings of items a user has previously interacted with (Iyyer et al., 2015; Vartak et al., 2017; Covington et al., 2016). This input is then passed through a standard feedforward neural network in order to make a relevance determination.
Let be the average of item vectors which user has interacted with, and be some feedforward neural network. We explored two methods for incorporating a user’s past item interactions into the model. The first method adds the average vector to the query vector and passes it through a neural network to produce a relevance score, . The second takes the relevance score to be the inner item of the query vector with the average vector after being processed by the neural network, . We present results for the latter as we found it performed better in our setting. We used the same training and hyperparameter tuning procedures as described in Section 4.3. The best settings we discovered used two layers of 128 rectified linear units.
This baseline is representative of the most commonly used method of incorporating historical user-item interactions in deep learning recommender systems, and allows us to better understand the importance of the attention mechanism in our approach. In particular, the architecture is nearly identical to that of the Collaborative Filtering Neural Autoregressive Distribution Estimator (Zheng et al., 2016a, b), User-Autorec (Sedhain et al., 2015), and Non-Linear Bias Adaptation (Vartak et al., 2017) recommender systems, modified to use a pre-trained embedding. Concretely, since multiplying a matrix of pre-trained item embeddings by a sparse-binary vector of observed previous interactions is equivalent to simply summing the item embeddings, the first layer of the DAN model is equivalent (up to a scaling constant) to the first layer of these models. We explore multiple layers of nonlinearities in the DAN, as well as several variants of the exact functional form, suggesting it is largely representative of the best-case performance one would obtain using these methods with fixed item embeddings.
5.3 Evaluation Metrics
We evaluated models with normalized discounted cumulative gain (NDCG) (Wang et al., 2013; Chen et al., 2009) and Recall@K. NDCG allows us to measure the quality of the entire ranked list, while still putting most of the emphasis on items near the top. Recall@K, which has the benefit of being highly interpretable, is the fraction of items ranked amongst the top that were actually interacted with by the user.
Because we had to rank an extremely large number of items for each user (our dataset contains several orders of magnitude more items than the widely used Netflix dataset (Bennett et al., 2007)), we followed the common practice of ranking the set of items the user interacted with during the test period amongst a set of randomly sampled negative candidate items that were not interacted with (Koren, 2008; Elkahky et al., 2015; He et al., 2017). To explore the implications of this evaluation technique, we vary both the numbers of negative candidates, and the distribution from which the negatives candidates are drawn. For the latter, three different distributions parameterized as in (Eqn. 5) are used; the empirical distribution (), the training distribution (), and the uniform distribution ().
In addition to being computational advantageous, the approach of sampling a pool of candidates is related to the practice of decomposing large-scale recommendation problems into the distinct sub-problems of candidate selection and candidate ranking (Covington et al., 2016; Rudin and Wang, 2018). Within this framework, the candidate selection algorithm typically focuses on surfacing generically applicable content with high precision, possibly incorporating various business criteria or eligibility constraints, and the ranking algorithm must order these items for the current user and/or context. From this perspective, all the candidate generation procedures we consider have perfect recall, but differ in terms of approximating an algorithm with high (the empirical distribution) to low (the uniform distribution) precision.
5.4 Results
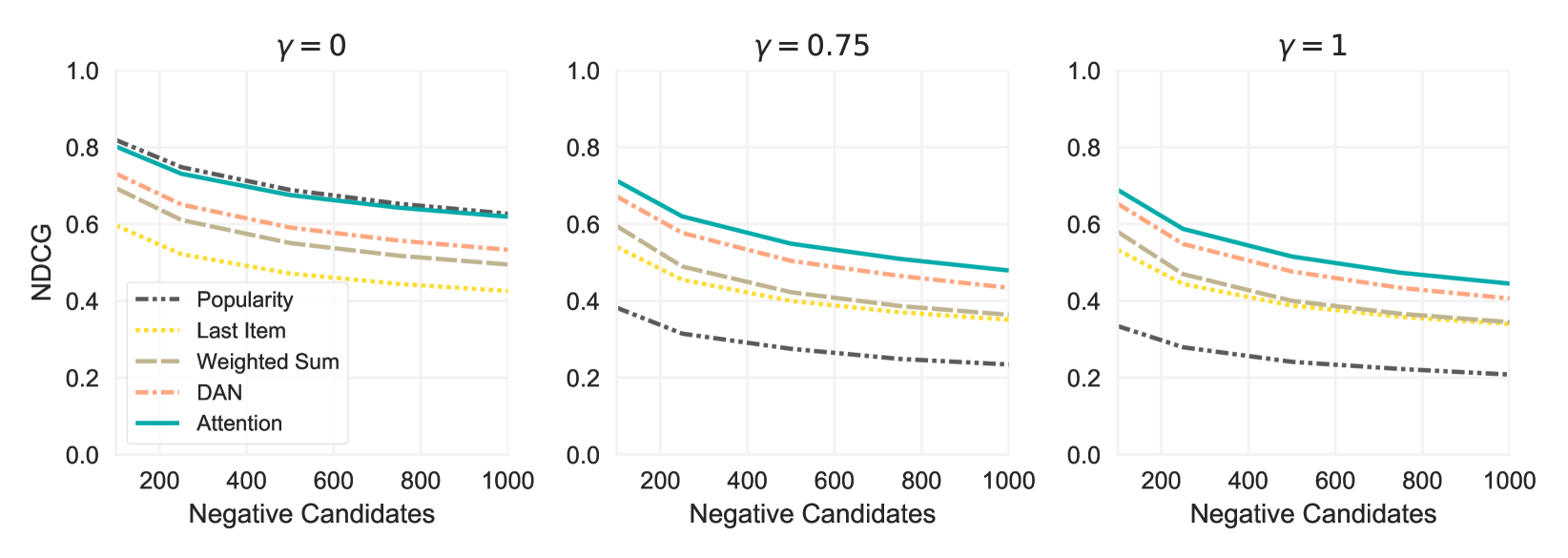
Comparisons against baselines are displayed in Figures 2 and 3. In Figure 2 we look at how NDCG varies with both the number of additional negative candidates included in the candidate pool, and the distribution from which they are sampled (recall that more negative candidates implies more candidates to rank, i.e. a strictly harder ranking problem). When the sampling distribution for negative candidates resembles that used in training () or is set to the empirical distribution (), the attention based method outperforms other methods by a clear margin (statistically significant at ), with DAN, our approximation to other state-of-the-art nonlinear recommenders, being the next best performer, and popularity being the worst performer. When negative candidates are sampled from the uniform distribution over items (), popularity performs slightly better than the attention based method. However, this performance can be explained by the fact that most items in our dataset are generally “unpopular”, so sorting by popularity discriminates extremely well between the items that were actually interacted with and a relatively small random sample of items, given the highly skewed nature of user-item interactions.
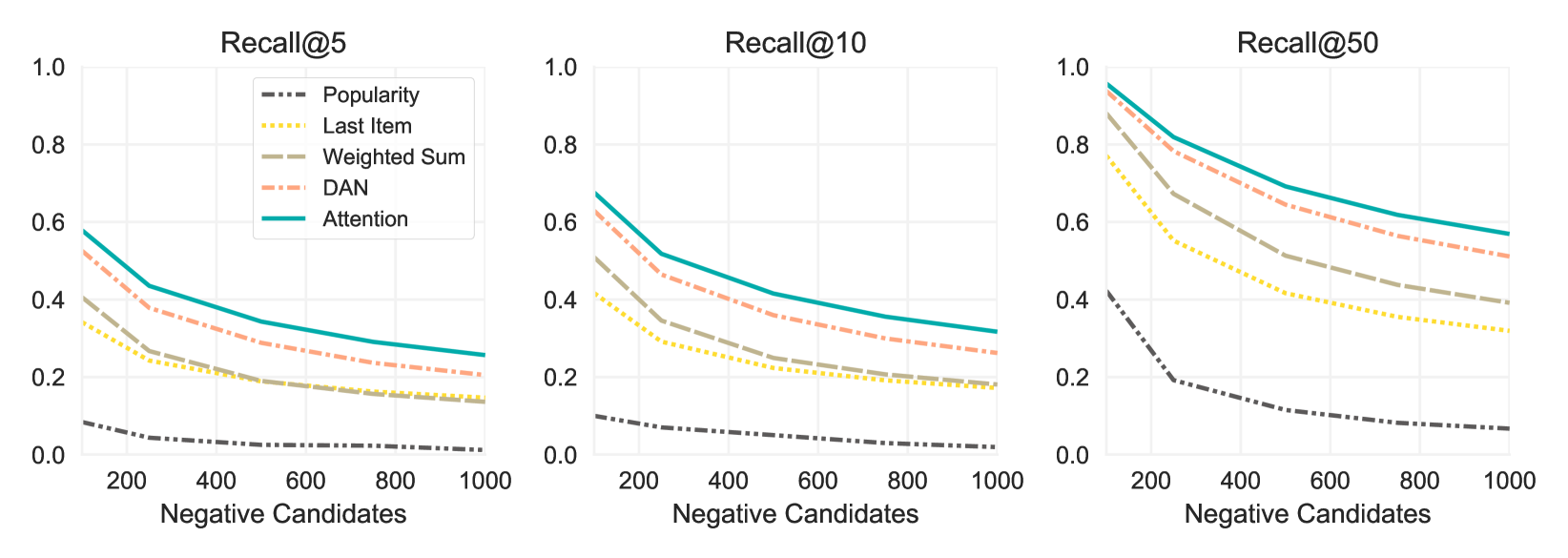
In Figure 3, we look at Recall@K where the sampling distribution is set to the empirical distribution. Similar results are found when we use , i.e. the training distribution. The findings mirror the results for NDCG: the attention based method achieves the best recall (again, statistically significant at ) and the non-personalized method performs worst. The ability of attention based model to perform well across a variety of settings provides further evidence of its benefits over the alternative techniques considered here.
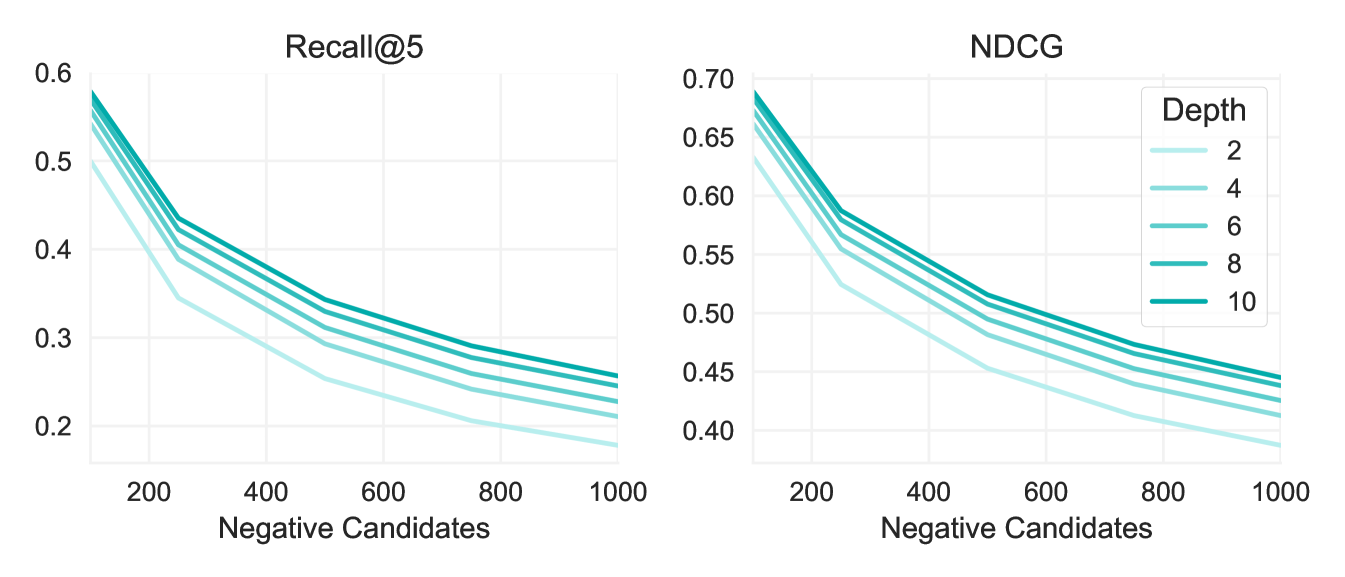
Figure 4 shows the effect of increasing depth in the attention based model. Increasing from depth 2 to 4 yields a large improvement in both recall and NDCG. Further increases in depth result in consistent, but diminishing improvements. These results were obtained using negative instances sampled from the empirical distribution.
6 CREATING PERSONALIZED CONTENT
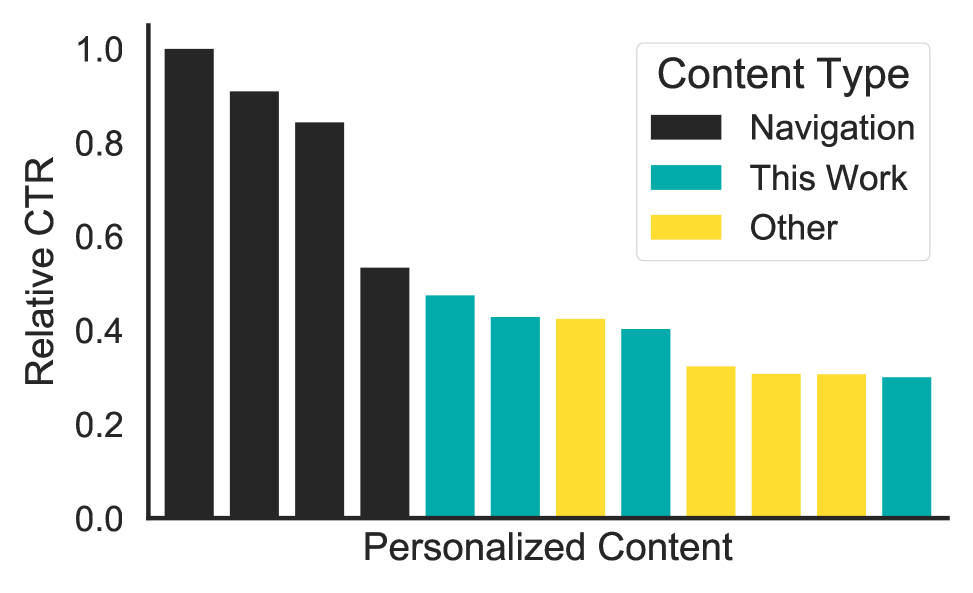
In an e-commerce setting, a key motivation behind inferring customer preferences is to improve customers’ experiences. To explore whether the improved preference modeling translates into a high-quality customer experience, we used our proposed attention based model to populate several pieces of content available on the Amazon homepage in a real-world, online setting. Each piece of content featured products selected from one of four categories: Digital Movies, Digital Music, Books, or Video Games. The set of candidate products for each category were chosen in advance according to heuristics that consider attributes such as a product’s average rating, listing date, and various business constraints. We used the proposed algorithm to select a personalized subset of these candidate products, based on the personalized scores (Eqn. 3).
We evaluated the quality of the resulting pieces of content by considering their click through rate. Figure 5 depicts the click through rate (CTR) of top-performing personalized content, relative to the content with the highest CTR. For context, we show this content alongside the highest performing navigational content and existing personalized content on the homepage. Navigational content includes content such as “Your Orders” and links to recent searches; unsurprisingly such content has a high CTR as it is used to navigate the site. The other content is produced using various proprietary production personalization algorithms which have been extensively optimized for the task. We see from Figure 5 that content produced using the attention-based personalization mechanism compares favorably with content produced using other personalization methods. Indeed, the top two content items in terms of CTR were produced using the attention-based algorithm.
7 CONCLUSIONS AND FUTURE WORK
This paper presented an attention based method for leveraing pre-trained item representations for personalized ranking. The proposed method was shown to significantly outperform a number of baselines according to common ranking evaluation metrics using purely behavioral data. Employing this model in an real-world product recommendation setting yielded personalized content that obtained high CTR.
There are many possible variations of the attention based model described here. Exploring pairwise ranking functions, the inclusion of non-behavioral features, extensions to the content ranking setting, reliably adapting item embeddings while learning the rest of the model parameters, personalized candidate selection mechanisms, and better understanding the importance of the temporal nature of item interactions by incorporating recurrent or bidirectional (Schuster and Paliwal, 1997) components into the model are all interesting directions.
Interpretability is also an extremely interesting direction for further research. In contrast to most modern neural machinery, the outputs of attention mechanisms are highly interpretable. For example, in Bahdanau et al. (2015), an attention mechanism is used to visualize what source words are most important when generating each target word in a machine translation task. Attention based recommendation systems could provide a mechanism to help users better understand why certain items are being recommended, and help internal merchandisers focus their efforts and create more compelling content.
References
- Bahdanau et al. [2015] Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. Neural machine translation by jointly learning to align and translate. In International Conference on Learning Representations, 2015.
- Bennett et al. [2007] James Bennett, Stan Lanning, et al. The Netflix prize. In KDD cup and workshop, 2007.
- Biswas et al. [2017] Arijit Biswas, Mukul Bhutani, and Subhajit Sanyal. MRNet-product2vec: A multi-task recurrent neural network for product embeddings. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, 2017.
- Chen et al. [2017a] Jingyuan Chen, Hanwang Zhang, Xiangnan He, Liqiang Nie, Wei Liu, and Tat-Seng Chua. Attentive collaborative filtering: Multimedia recommendation with item-and component-level attention. In ACM SIGIR conference on Research and Development in Information Retrieval. ACM, 2017a.
- Chen et al. [2017b] Ting Chen, Yizhou Sun, Yue Shi, and Liangjie Hong. On sampling strategies for neural network-based collaborative filtering. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2017b.
- Chen et al. [2009] Wei Chen, Tie-Yan Liu, Yanyan Lan, Zhi-Ming Ma, and Hang Li. Ranking measures and loss functions in learning to rank. In Advances in Neural Information Processing Systems, 2009.
- Cheng et al. [2016] Heng-Tze Cheng, Levent Koc, Jeremiah Harmsen, Tal Shaked, Tushar Chandra, Hrishi Aradhye, Glen Anderson, Greg Corrado, Wei Chai, Mustafa Ispir, et al. Wide & deep learning for recommender systems. In RecSys Workshop on Deep Learning for Recommender Systems, 2016.
- Covington et al. [2016] Paul Covington, Jay Adams, and Emre Sargin. Deep neural networks for YouTube recommendations. In ACM Conference on Recommender Systems, 2016.
- Dahl et al. [2012] George E Dahl, Ryan Prescott Adams, and Hugo Larochelle. Training restricted Boltzmann machines on word observations. In International Conference on Machine Learning, 2012.
- De Boom et al. [2016] Cedric De Boom, Steven Van Canneyt, Thomas Demeester, and Bart Dhoedt. Representation learning for very short texts using weighted word embedding aggregation. Pattern Recognition Letters, 80, 2016.
- Dziugaite and Roy [2015] Gintare Karolina Dziugaite and Daniel M Roy. Neural network matrix factorization. arXiv preprint arXiv:1511.06443, 2015.
- Elkahky et al. [2015] Ali Mamdouh Elkahky, Yang Song, and Xiaodong He. A multi-view deep learning approach for cross domain user modeling in recommendation systems. In International Conference on World Wide Web, 2015.
- Fu et al. [2018] Mingsheng Fu, Hong Qu, Dagmawi Moges, and Li Lu. Attention based collaborative filtering. Neurocomputing, 2018.
- Gemulla et al. [2011] Rainer Gemulla, Erik Nijkamp, Peter Haas, and Yannis Sismanis. Large-scale matrix factorization with distributed stochastic gradient descent. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2011.
- Graves et al. [2014] Alex Graves, Greg Wayne, and Ivo Danihelka. Neural Turing machines. arXiv preprint arXiv:1410.5401, 2014.
- Grbovic and Cheng [2018] Mihajlo Grbovic and Haibin Cheng. Real-time personalization using embeddings for search ranking at Airbnb. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2018.
- Grbovic et al. [2015] Mihajlo Grbovic, Vladan Radosavljevic, Nemanja Djuric, Narayan Bhamidipati, Jaikit Savla, Varun Bhagwan, and Doug Sharp. E-commerce in your inbox: Product recommendations at scale. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2015.
- Guo et al. [2017] Huifeng Guo, Ruiming Tang, Yunming Ye, Zhenguo Li, and Xiuqiang He. Deepfm: a factorization-machine based neural network for ctr prediction. In International Joint Conference on Artificial Intelligence, 2017.
- Hansen et al. [2003] Nikolaus Hansen, Sibylle D Müller, and Petros Koumoutsakos. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (cma-es). Evolutionary computation, 11(1), 2003.
- He et al. [2017] Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, and Tat-Seng Chua. Neural collaborative filtering. In International Conference on World Wide Web, 2017.
- Hu et al. [2008] Yifan Hu, Yehuda Koren, and Chris Volinsky. Collaborative filtering for implicit feedback datasets. In IEEE International Conference on Data Mining, 2008.
- Iyyer et al. [2015] Mohit Iyyer, Varun Manjunatha, Jordan Boyd-Graber, and Hal Daumé III. Deep unordered composition rivals syntactic methods for text classification. In International Joint Conference on Natural Language Processing, 2015.
- Johnson [2014] Christopher C Johnson. Logistic matrix factorization for implicit feedback data. In Advances in Neural Information Processing Systems, 2014.
- Jozefowicz et al. [2015] Rafal Jozefowicz, Wojciech Zaremba, and Ilya Sutskever. An empirical exploration of recurrent network architectures. In International Conference on Machine Learning, 2015.
- Kim [2014] Yoon Kim. Convolutional neural networks for sentence classification. In Empirical Methods in Natural Language Processing, 2014.
- Kim et al. [2017] Yoon Kim, Carl Denton, Luong Hoang, and Alexander M Rush. Structured attention networks. In International Conference on Learning Representations, 2017.
- Kingma and Ba [2015] Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In International Conference on Learning Representations, 2015.
- Koren [2008] Yehuda Koren. Factorization meets the neighborhood: a multifaceted collaborative filtering model. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2008.
- Koren et al. [2009] Yehuda Koren, Robert Bell, and Chris Volinsky. Matrix factorization techniques for recommender systems. Computer, (8), 2009.
- Kronmal and Peterson Jr [1979] Richard A Kronmal and Arthur V Peterson Jr. On the alias method for generating random variables from a discrete distribution. The American Statistician, 33(4), 1979.
- Lake et al. [2015] Brenden M Lake, Ruslan Salakhutdinov, and Joshua B Tenenbaum. Human-level concept learning through probabilistic program induction. Science, 350(6266):1332–1338, 2015.
- Linden et al. [2003] Greg Linden, Brent Smith, and Jeremy York. Amazon.com recommendations: Item-to-item collaborative filtering. IEEE Internet Computing, 7, 2003.
- McMahan et al. [2013] H Brendan McMahan, Gary Holt, David Sculley, Michael Young, Dietmar Ebner, Julian Grady, Lan Nie, Todd Phillips, Eugene Davydov, Daniel Golovin, et al. Ad click prediction: a view from the trenches. In ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2013.
- Mikolov et al. [2013] Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems, 2013.
- Miller et al. [2016] Alexander Miller, Adam Fisch, Jesse Dodge, Amir-Hossein Karimi, Antoine Bordes, and Jason Weston. Key-value memory networks for directly reading documents. In Empirical Methods in Natural Language Processing, 2016.
- Mnih and Salakhutdinov [2008] Andriy Mnih and Ruslan Salakhutdinov. Probabilistic matrix factorization. In Advances in Neural Information Processing Systems, 2008.
- Nedelec et al. [2017] Thomas Nedelec, Elena Smirnova, and Flavian Vasile. Specializing joint representations for the task of product recommendation. arXiv preprint arXiv:1706.07625, 2017.
- Ng [2016] Andrew Ng. Nuts and bolts of building ai applications using deep learning. 2016.
- Oard and Kim [1998] Douglas Oard and Jinmook Kim. Implicit feedback for recommender systems. In AAAI workshop on recommender systems, 1998.
- Olah and Carter [2016] Chris Olah and Shan Carter. Attention and augmented recurrent neural networks. Distill, 2016.
- Pan et al. [2008] Rong Pan, Yunhong Zhou, Bin Cao, Nathan N Liu, Rajan Lukose, Martin Scholz, and Qiang Yang. One-class collaborative filtering. In IEEE International Conference on Data Mining, 2008.
- Pascanu et al. [2013] Razvan Pascanu, Tomas Mikolov, and Yoshua Bengio. On the difficulty of training recurrent neural networks. In International Conference on Machine Learning, 2013.
- Paszke et al. [2017] Adam Paszke, Sam Gross, Soumith Chintala, Gregory Chanan, Edward Yang, Zachary DeVito, Zeming Lin, Alban Desmaison, Luca Antiga, and Adam Lerer. Automatic differentiation in PyTorch. In NIPS Autodiff Workshop, 2017.
- Quadrana et al. [2017] Massimo Quadrana, Alexandros Karatzoglou, Balázs Hidasi, and Paolo Cremonesi. Personalizing session-based recommendations with hierarchical recurrent neural networks. In ACM Conference on Recommender Systems, 2017.
- Rudin and Wang [2018] Cynthia Rudin and Yining Wang. Direct learning to rank and rerank. In International Conference on Artificial Intelligence and Statistics, 2018.
- Salakhutdinov et al. [2007] Ruslan Salakhutdinov, Andriy Mnih, and Geoffrey Hinton. Restricted Boltzmann machines for collaborative filtering. In International Conference on Machine Learning, 2007.
- Santoro et al. [2017] Adam Santoro, David Raposo, David G Barrett, Mateusz Malinowski, Razvan Pascanu, Peter Battaglia, and Timothy Lillicrap. A simple neural network module for relational reasoning. In Advances in neural information processing systems, 2017.
- Saxe et al. [2014] Andrew M Saxe, James L McClelland, and Surya Ganguli. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. In International Conference on Learning Representations, 2014.
- Schein et al. [2002] Andrew I Schein, Alexandrin Popescul, Lyle H Ungar, and David M Pennock. Methods and metrics for cold-start recommendations. In ACM SIGIR conference on Research and development in information retrieval. ACM, 2002.
- Schuster and Paliwal [1997] Mike Schuster and Kuldip K Paliwal. Bidirectional recurrent neural networks. IEEE Transactions on Signal Processing, 45(11), 1997.
- Sedhain et al. [2015] Suvash Sedhain, Aditya Krishna Menon, Scott Sanner, and Lexing Xie. Autorec: Autoencoders meet collaborative filtering. In International Conference on World Wide Web, 2015.
- Slaney [2011] Malcolm Slaney. Web-scale multimedia analysis: Does content matter? IEEE MultiMedia, 18(2), 2011.
- Sukhbaatar et al. [2015] Sainbayar Sukhbaatar, Jason Weston, Rob Fergus, et al. End-to-end memory networks. In Advances in Neural Information Processing Systems, 2015.
- Tan et al. [2016] Wei Tan, Liangliang Cao, and Liana Fong. Faster and cheaper: Parallelizing large-scale matrix factorization on GPUs. In ACM International Symposium on High-Performance Parallel and Distributed Computing, 2016.
- Van den Oord et al. [2013] Aaron Van den Oord, Sander Dieleman, and Benjamin Schrauwen. Deep content-based music recommendation. In Advances in Neural Information Processing Systems, 2013.
- Vartak et al. [2017] Manasi Vartak, Arvind Thiagarajan, Conrado Miranda, Jeshua Bratman, and Hugo Larochelle. A meta-learning perspective on cold-start recommendations for items. In Advances in Neural Information Processing Systems, 2017.
- Vasile et al. [2016] Flavian Vasile, Elena Smirnova, and Alexis Conneau. Meta-prod2vec: Product embeddings using side-information for recommendation. In ACM Conference on Recommender Systems, 2016.
- Vaswani et al. [2017] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Advances in Neural Information Processing Systems, 2017.
- Vinyals et al. [2016] Oriol Vinyals, Charles Blundell, Timothy Lillicrap, Koray Kavukcuoglu, and Daan Wierstra. Matching networks for one shot learning. In Advances in neural information processing systems, 2016.
- Wang et al. [2017] Ruoxi Wang, Bin Fu, Gang Fu, and Mingliang Wang. Deep & cross network for ad click predictions. In Proceedings of AdKDD. ACM, 2017.
- Wang et al. [2013] Yining Wang, Liwei Wang, Yuanzhi Li, Di He, and Tie-Yan Liu. A theoretical analysis of NDCG type ranking measures. In Conference on Learning Theory, 2013.
- Weston et al. [2013] Jason Weston, Ron J Weiss, and Hector Yee. Nonlinear latent factorization by embedding multiple user interests. In ACM Conference on Recommender systems, 2013.
- Weston et al. [2014] Jason Weston, Sumit Chopra, and Antoine Bordes. Memory networks. arXiv preprint arXiv:1410.3916, 2014.
- White et al. [2015] Lyndon White, Roberto Togneri, Wei Liu, and Mohammed Bennamoun. How well sentence embeddings capture meaning. In Australasian Document Computing Symposium. ACM, 2015.
- Wu et al. [2017] Ledell Wu, Adam Fisch, Sumit Chopra, Keith Adams, Antoine Bordes, and Jason Weston. Starspace: Embed all the things! arXiv preprint arXiv:1709.03856, 2017.
- Zaheer et al. [2017] Manzil Zaheer, Satwik Kottur, Siamak Ravanbakhsh, Barnabas Poczos, Ruslan R Salakhutdinov, and Alexander J Smola. Deep sets. In Advances in Neural Information Processing Systems, 2017.
- Zheng et al. [2016a] Yin Zheng, Cailiang Liu, Bangsheng Tang, and Hanning Zhou. Neural autoregressive collaborative filtering for implicit feedback. In RecSys Workshop on Deep Learning for Recommender Systems, 2016a.
- Zheng et al. [2016b] Yin Zheng, Bangsheng Tang, Wenkui Ding, and Hanning Zhou. A neural autoregressive approach to collaborative filtering. In International Conference on Machine Learning, 2016b.