Le Conte de la Mesure sur les Complexes Cubiques CAT(0)
Abstract.
We revisit the topic of probability measures on CAT(0) cube complexes and prove that an amenable group acting on a CAT(0) cube complex, regardless of dimension, necessarily preserves an interval in the Roller compactification. In the finite dimensional case, we prove that there must be an orbit of cardinality , where is bounded by the dimension. This is a slight extension of the author’s previuos Tits’ Alternative.
Key words and phrases:
CAT(0), Cube Complexes, Tits’ Alternative2020 Mathematics Subject Classification:
Primary 54C40, 14E20; Secondary 46E25, 20C202020 Mathematics Subject Classification:
Primary 20F65, 20E05, 60B05; Secondary 05C12, 05E18, 06A07, 20F29![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/e8ea2b6a-6215-465a-9af1-8af633ad0fb1/x1.png)
Introduction The idea for this short paper came through preparations for a talk I gave in summer of 2023 at the Séminaire Virtuel Francophone – Groupes et Géométrie. The seminar is aimed to be expository in nature and so I thought I would revisit the topic of probability measures on CAT(0) cube complexes, and their associated intervals (see Section 0.6). This association was introduced by Monod and Shalom in [MS04, Proposition 4.5] for trees and developed further in my joint work with Chatterji and Iozzi [CFI16]. It was also used either implicitly or explicitly in [Fer18, FLM18, FLM21], and even [FFH23]. The key tool for this is the Lifting Decomposition which is discussed in Section Lemma.
As I was preparing my lecture, I realized that I could in fact make a small improvement on my previous contribution to the story of Tits’ Alternatives. Therefore, I take the opportunity to share that here. I also include some of the drawings I made (using notability on an ipad).
Theorem.
Let be a CAT(0) cube complex of finite dimension , and suppose that preserves an interval in the Roller compactification . Then must have an orbit in of cardinality , for some .
If is not finite dimensional and is assumed to be amenable then it must preserve an interval .
Combining with the Tits’ Alternative from [Fer18], we obtain the following (the reader should compare statements):
Corollary (Tits’ Alternative).
Suppose is a finite dimensional CAT(0) cube complex. Given a group action either contains a freely acting free group on 2 generators, or has an orbit of cardinality in , for some , where is the dimension of .
Examples: The following examples show that the bounds above are optimal. We note that all the groups are amenable.
-
❀
Consider the standard action of the infinite dihedral group on . Of course, there is no fixed point but there is an orbit of cardinality 2 in the Roller compactification, namely .
-
❀
Similarly, acts on and has a unique finite orbit which has cardinality .
-
❀
Finally, acts on which is of course infinite dimensional, and does not have a finite orbit in the Roller compactification, but it is an interval.
We note that there are many Tits’ Alternatives available in the literature [Tit72, BFH04, SW05, CS11, Fio18, MP22, OP22, GJN23, Gen21]. However, in this brief note, I will not endeavor to give a comprehensive overview of the Tits’ Alternatives, nor to give a thorough account of CAT(0) cube complexes. The reader can see the references provided for further details.
Acknowledements: I thank Dafne Sanchez for help with the coloring scheme, inspired by Matisse. I also thank Indira Chatterji, François Dahmani, Anne Lonjou, and Yves Stalder for the invitation to speak at the Séminaire Virtuel Francophone – Groupes et Géométrie which inspired me to write this article. I thank all of my collaborators and mentors with whom I have discussed CAT(0) cube complexes for helping me explore how to understand and communicate their beauty. Finally, I thank the National Science Foundation for their generous support of my work, particularly through NSF grant DMS–2005640. \specialsectionBasics
A cube complex is a space obtained by gluing unit cubes isometrically along their faces. Moreover, it is said to be CAT(0) if it is nonpositively curved and simply connected.
You may think of the process of creating a CAT(0) cube complex as gluing together cubes in a particular order. If at some point there is positive curvature that is created locally, it is due to something as in Figure 1. There, we have created part of the boundary of a 3-dimensional cube by gluing 3 unit squares together. That creates a cone angle of . Since , it is positively curved. However, we may annul the positive curvature by “filling” in the other side to create a 3-dimensional cube. Nonpositive curvature of a CAT(0) cube complex is equivalent to the Gromov Link Condition. We refer the reader to [Sag95, CN05, Nic04, Rol16] for more details.

0.1. Functoriality: Walled Spaces
A useful way to think of CAT(0) cube complexes is via this functorial construction. Begin with a set together with a collection of (nonempty) two-sided (walls) partitions . Two sided here means that if then . The wall may be thought of as the pair .
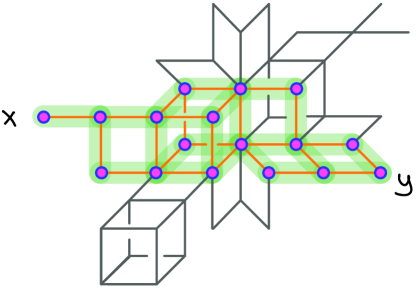
Next, create a graph by declaring that each maximal non-empty intersection of sets from is a vertex. We connect two vertices if their corresponding defining intersections differ by the choice of exactly one side of one partition from . In Figure 2, you can see a choice of 5 partitions. Each region is not empty. The regions labeled and differ by the choice of one partition and therefore, their associated vertices and respectively are connected by an edge.
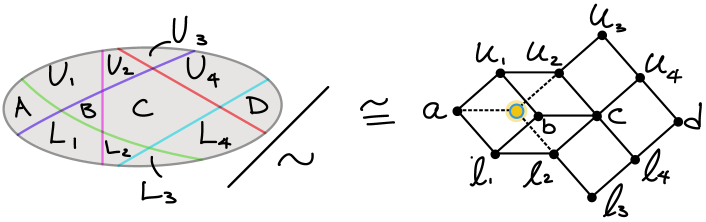
Once we have done this, we may not have a CAT(0) cube complex. However, we may take the cubical completion (as in Figure 2, where we must add the unlabled “back” vertex to creat a 3-cube) to annul positive curvature. We note that this can always be done, except that distances may become infinite (if there are infinitely many partitions separating two regions, i.e. the finite interval condition is not satisfied) or the dimension may become infinite (if there are families of pairwise transverse partitions of unbounded cardinality, see Section 0.3 for the definition of transverse).
Conversely, start with (the vertex set of) a CAT(0) cube complex . Each edge in belongs to an equivalence class generated by “being parallel across a square”. The compliment of that parallelism class has two sides, and the vertices that belong to each side give the two-sided partition of the vertex set (see Figure 3).
Finally, if we apply the previous construction to this collection of two-sided partitions, we get a CAT(0) cube complex, which is cannonically isomorphic to (the vertex set of) .
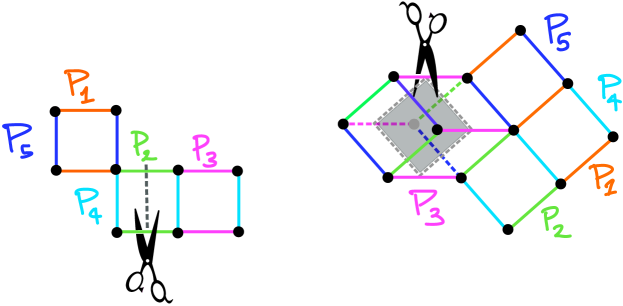
0.2. The Roller Compactification
A halfspace of a CAT(0) cube complex is one side of a two-sided partition, as discussed above. We have established that the vertex set, denoted by , is cannonically determined by the halfspace structure . By mapping a vertex in to the collection of halfspaces that contain it, we obtain an isometric injection:
Here the extended metric on is given by half the cardinality of the symmetric difference . While this metric is useful, we will rely on the standard topology on . This is given by declaring the basic open sets to be cylinder sets, which are themeselves determined by specifying values in finitely many coordinates. Equivalently, this is the topology of pointwise convergence of maps . With this topology, is compact. We note that the induced topology may be different than the metric topology on . This is directly comparable to the weak- topology and respectively the metric topology on a Hilbert space.
Having found an injection of into the compact space , we may take the closure in the image and this defines the Roller compactification. By removing the image of inside this closure, we are left with the Roller boundary.
Note that once we obtain the closure of in , there is a cannonical extension of the halfspaces as partitions of to . Those are the basic clopen sets for our totally disconnected topology on .
The following is then immediate from the functorial construction, and can be thought of as forgetfulness.
Corollary.
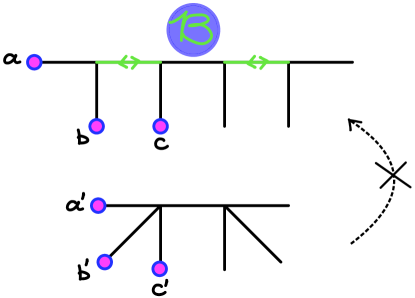
Let be a CAT(0) cube complex with halfspace structure . Let be involution invariant and the associated CAT(0) cube complex. Then the map , given by induces a 1-Lipschitz projection .
We shall see in Section Lemma how and when we can find a cannonical section to this map. The example in Figure 4 is given by taking and a valence consideration shows that an isometric section is impossible.
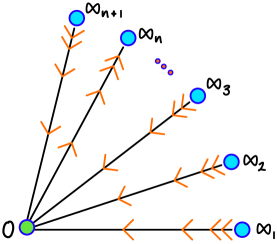
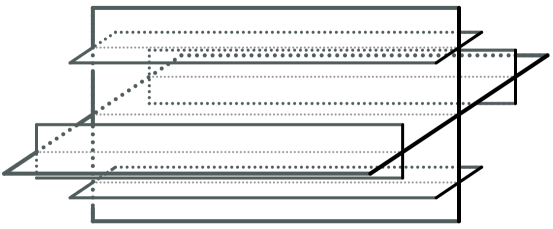
The Roller boundary of a tree is, as a set, the visual boundary, but the topology is different when it is not (large-scale) locally finite. Consider the tree given by identifying at infinitely many copies of , as in Figure 5. It is not difficult to see that since all halfspaces eventually contain .
The Roller compactification has an important multiplicative property:
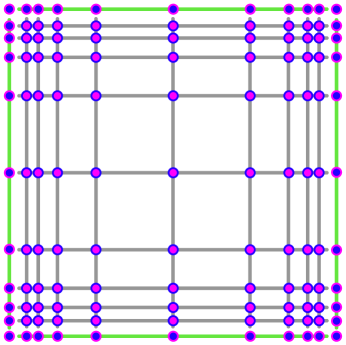
0.3. Comparing halfspaces
Given a pair of halfspaces such that then either all of the pairwise intersections are not empty (and in this case, we say that and are transverse, and write ) or one of the following other cases hold (see Figure 8):
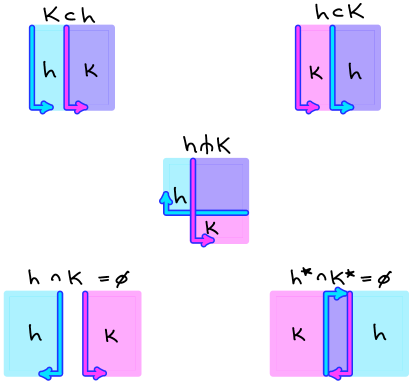
Lemma.
The dimension of is the supremum cardinality of subsets of pairwise transverse halfspaces.
It is straightforward to verify that if is a nontrivial disjoint decomposition into nonempty involution invariant, pairwise transverse sets and , , and are the assocaited CAT(0) cube complexes respectively then there is a cannonical isomorphism . We say that is irreducible if it is not isomorphic to a product.
Theorem.
[CS11, Proposition 2.6] Let be finite dimensional. Then, there is a cannonical decomposition of into a product of irreducible CAT(0) cube complexes.
A pair of halfspaces , with are said to be facing if . This corresponds to the lower right corner in Figure 8. A triple of halfspaces are said to be a facing triple if they are pairwise facing.
0.4. Intervals in
Let be an arbitrary subset. The (involution invariant) collection of halfspaces that separate points in is
Similarly, we denote the collection of halfspaces that contain as , and the collection of compliments of halfspaces that contain , namely the halfspaces that trivially intersect is denoted by , meaning that . We have established the following decomposition:
We say that, is an interval if there exists such that . In this case we write and say that it is the interval between and . We also call and endpoints of . Clearly, does not contain a facing triple.
The structure of intervals in an arbitrary CAT(0) cube complex can be quite exotic; please see the examples in Figures 9 and 10 or come up with your own!
Nevertheless, the following theorem of [BCG+09], which relies on Dilworth’s Theorem for partially ordered sets, shows that intervals are not too wild.
Theorem.
Let be the dimension of . If is an interval then there exists an isometric embedding .
Corollary.
If is an interval then the set of end points of has cardinality , for some .
0.5. The Helly Property in
The following is an important property of halfspaces in a CAT(0) cube complex. The first item is the standard Helly property for halfspaces. The second follows from the first by applying the finite intersection property to the collection of sets , each of which is clopen in the compact space . Comparing it with the classical Helly property for convex sets in euclidean space, we may consider it as telling us that, in a sense, CAT(0) cube complexes are of Helly-dimension 1.
Lemma.
Suppose that is such that for all .
-
•
If then .
-
•
Otherwise
Lifting Decompositions
Let be a CAT(0) cube complex with associated halfspace structure . We shall say is consistent if it satisfies the following two properties:
-
(1)
If then .
-
(2)
If , with , and then .
We note that, according to the functorial construction, if is consistent and then is the collection of halfspaces containing a single point.
Proposition.
Let be a CAT(0) cube complex with associated halfspaces and consistent. Set and let be the associated CAT(0) cube complex. Then the map given by induces an isometric injection , whose image is exactly
Furthermore, if is -invariant, for some action then with the restricted action on the image, the above natural injection is -equivariant.
0.6. Probability Measures
Consider a probability measure and the associated collection of halfspaces . It is straightforward to verify that is consistent and that the collection of halfspaces does not contain any facing triples. Applying the Lifting Decomposition to , we get that is isomorphic to .
Lemma.
[CFI16, Lemma 4.7] If then is an interval.
0.7. Medians
Let and consider the associated probability measure . A simple parity argument shows that if then . Therefore, we have that is a single point, which we shall call the median of the triple and denote it by .
While this is not the standard definition of the median, it fits nicely within our context. We note that several of the natural properties of the median (e.g. invariance under permutation of the points) are immediate, including the property that
Proof of the Main Theorem
Suppose is amenable acting on . Since is compact and metrizable, there must be a -invariant probability measure . By the Lifting Decomposition and the previous lemma, it follows that is a -invariant interval.
Suppose now that is of finite dimension and that is not necessarily amenable but preserves an interval . By Corollary 0.4 (see also [Fer18, Corollary 2.9]), the number of end points on which is an interval is for some and we identify these with . By [CS11, Proposition 2.6] we have that . We may therefore project , and without loss of generality, assume .
Let and note that for some . Fix a choice of right -coset representatives , with trivial -coordinate. Let be defined component-wise by , for . Note that is fixed by and has trivial stabilizer in . Let . Then . We have shown that
Therefore, by the orbit stabilizer theorem, we have
References
- [BCG+09] J. Brodzki, S. J. Campbell, E. Guentner, G. A. Niblo, and N. J. Wright, Property A and cube complexes, J. Funct. Anal. 256 (2009), no. 5, 1408–1431. MR 2490224
- [BFH04] Mladen Bestvina, Mark Feighn, and Michael Handel, Solvable subgroups of are virtually Abelian, Geom. Dedicata 104 (2004), 71–96. MR 2043955
- [CFI16] Indira Chatterji, Talia Fernós, and Alessandra Iozzi, The median class and superrigidity of actions on cube complexes, J. Topol. 9 (2016), no. 2, 349–400, With an appendix by Pierre-Emmanuel Caprace. MR 3509968
- [CN05] Indira Chatterji and Graham Niblo, From wall spaces to cube complexes, Internat. J. Algebra Comput. 15 (2005), no. 5-6, 875–885. MR 2197811
- [CS11] Pierre-Emmanuel Caprace and Michah Sageev, Rank rigidity for CAT(0) cube complexes, Geom. Funct. Anal. 21 (2011), no. 4, 851–891. MR 2827012
- [Fer18] Talia Fernós, The Furstenberg-Poisson boundary and cube complexes, Ergodic Theory Dynam. Systems 38 (2018), no. 6, 2180–2223. MR 3833346
- [FFH23] Talia Fernós, David Futer, and Mark Hagen, Homotopy equivalent boundaries of cube complexes, 2023.
- [Fio18] Elia Fioravanti, The Tits alternative for finite rank median spaces, Enseign. Math. 64 (2018), no. 1-2, 89–126. MR 3959849
- [FLM18] Talia Fernós, Jean Lécureux, and Frédéric Mathéus, Random walks and boundaries of cubical complexes, Comment. Math. Helv. 93 (2018), no. 2, 291–333. MR 3811753
- [FLM21] Talia Fernós, Jean Lécureux, and Frédéric Mathéus, Contact graphs, boundaries, and a central limit theorem for cat(0) cubical complexes, 2021.
- [Gen21] Anthony Genevois, Cyclic hyperbolicity in cat(0) cube complexes, 2021.
- [GJN23] Radhika Gupta, Kasia Jankiewicz, and Thomas Ng, Groups acting on CAT(0) cube complexes with uniform exponential growth, Algebr. Geom. Topol. 23 (2023), no. 1, 13–42. MR 4567998
- [MP22] Alexandre Martin and Piotr Przytycki, Acylindrical actions for two-dimensional Artin groups of hyperbolic type, Int. Math. Res. Not. IMRN (2022), no. 17, 13099–13127. MR 4475273
- [MS04] N. Monod and Y. Shalom, Cocycle superrigidity and bounded cohomology for negatively curved spaces, J. Differential Geom. 67 (2004), no. 3, 395–455. MR 2153026 (2006g:53051)
- [Nic04] Bogdan Nica, Cubulating spaces with walls, Algebr. Geom. Topol. 4 (2004), 297–309. MR 2059193
- [OP22] Damian Osajda and Piotr Przytycki, Tits alternative for 2-dimensional -dimensional complexes, Forum Math. Pi 10 (2022), Paper No. e25, 19. MR 4522694
- [Rol16] Martin Roller, Poc sets, median algebras and group actions, 2016.
- [Sag95] Michah Sageev, Ends of group pairs and non-positively curved cube complexes, Proc. London Math. Soc. (3) 71 (1995), no. 3, 585–617. MR 1347406
- [SW05] Michah Sageev and Daniel T. Wise, The Tits alternative for cubical complexes, Bull. London Math. Soc. 37 (2005), no. 5, 706–710. MR 2164832
- [Tit72] J. Tits, Free subgroups in linear groups, J. Algebra 20 (1972), 250–270. MR 286898