Learning to grow: control of material self-assembly using evolutionary reinforcement learning
Abstract
We show that neural networks trained by evolutionary reinforcement learning can enact efficient molecular self-assembly protocols. Presented with molecular simulation trajectories, networks learn to change temperature and chemical potential in order to promote the assembly of desired structures or choose between competing polymorphs. In the first case, networks reproduce in a qualitative sense the results of previously-known protocols, but faster and with higher fidelity; in the second case they identify strategies previously unknown, from which we can extract physical insight. Networks that take as input the elapsed time of the simulation or microscopic information from the system are both effective, the latter more so. The evolutionary scheme we have used is simple to implement and can be applied to a broad range of examples of experimental self-assembly, whether or not one can monitor the experiment as it proceeds. Our results have been achieved with no human input beyond the specification of which order parameter to promote, pointing the way to the design of synthesis protocols by artificial intelligence.
Molecular self-assembly is the spontaneous organization of molecules or nanoparticles into ordered structures Whitesides et al. (1991); Biancaniello et al. (2005); Park et al. (2008); Nykypanchuk et al. (2008); Ke et al. (2012); Pfeifer and Saccà (2018). It is a phenomenon that happens out of equilibrium, and so while we have empirical and theoretical understanding of certain self-assembling systems and certain processes that occur during assembly Doye et al. (2004); Romano and Sciortino (2011); Glotzer et al. (2004); Doye et al. (2007a); Rapaport (2010); Reinhardt and Frenkel (2014); De Yoreo et al. (2015); Murugan et al. (2015); Whitelam and Jack (2015); Nguyen and Vaikuntanathan (2016); Whitelam et al. (2014a); Jadrich et al. (2017); Lutsko (2019); Fan and Grunwald (2019), we lack a predictive theoretical framework for self-assembly. That is to say, given a set of molecules and ambient conditions, and an observation time, we cannot in general predict which structures and phases the molecules will form, and what will be the yield of the desired structure when (and if) it forms. As a result, industrial processes that use self-assembly, such as the crystallization of pharmaceuticals, require an empirical search of materials and protocols, often at considerable time and cost Chen et al. (2011); Threlfall (2000); Rodríguez-hornedo and Murphy (1999); Shekunov and York (2000).
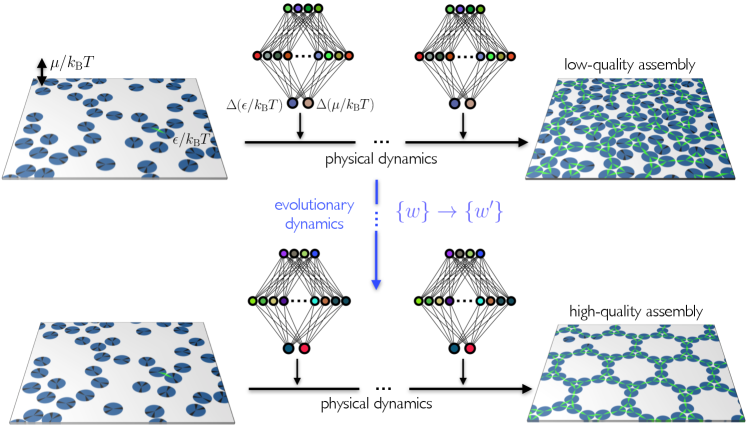
Absent a theoretical framework for self-assembly, an alternative is to seek assistance from machine learning in order to attempt to control self-assembly without human intervention. In this paper we show that neural-network-based evolutionary reinforcement learning can be used to develop protocols for the control of self-assembly, without prior understanding of what constitutes a good assembly protocol. Reinforcement learning is a branch of machine learning concerned with learning to perform actions so as to achieve an objective Sutton and Barto (2018), and has been used recently to play computer games better than humans can Watkins and Dayan (1992); Mnih et al. (2013, 2015); Bellemare et al. (2013); Mnih et al. (2016); Tassa et al. (2018); Todorov et al. (2012); Puterman (2014); Asperti et al. (2018); Riedmiller (2005); Riedmiller et al. (2009); Schulman et al. (2017); Brockman et al. (2016); Kempka et al. (2016); Wydmuch et al. (2018); Silver et al. (2016, 2017); Such et al. (2017). Neuroevolution Holland (1992); Fogel and Stayton (1994); Lehman et al. (2018a); Salimans et al. (2017); Zhang et al. (2017); Lehman et al. (2018b); Conti et al. (2018); Such et al. (2017) is an approach to reinforcement learning that is much less widely applied than value-based methods Sutton and Barto (2018), but is a simple and powerful method that is naturally suited to “sparse-reward” problems such as self-assembly, where the outcome of assembly (good or bad) is not always apparent until its latter stages. Here we apply neuroevolutionary learning to stochastic molecular simulations of patchy particles, a standard choice for representing anisotropically-interacting molecules, nanoparticles, or colloids Zhang and Glotzer (2004); Romano et al. (2011); Sciortino et al. (2007); Doye et al. (2007b); Bianchi et al. (2008); Doppelbauer et al. (2010); Whitelam et al. (2014b); Duguet et al. (2016). While a neural network cannot influence the fundamental dynamical laws by which such systems evolve Frenkel and Smit (1996), it can control the parameters that appear in the dynamical algorithm, such as temperature, chemical potential, and other environmental conditions. In this way the network can influence the sequence of microstates visited by the system. We show that a neural network can learn to enact a time-dependent protocol of temperature and chemical potential (called a policy in reinforcement learning) in order to promote the self-assembly of a desired structure, or choose between two competing polymorphs. In both cases the network identifies strategies different to those informed by human intuition, but which can be analyzed and used to provide new insight. We use networks that take only elapsed time as their input, and networks that take microscopic information from the system. Both learn under evolution, and networks permitted microscopic information learn better than those that are not.
Networks enact protocols that are out of equilibrium, in some cases far from equilibrium, and so are not well-described by existing theories. These “self-assembly kinetic yield” networks act to promote a particular order parameter for self-assembly at the end of a given time interval, with no consideration for whether a process results in an equilibrium outcome or not. It is therefore distinct from feedback approaches designed to promote near-equilibrium behavior Klotsa and Jack (2013). Our approach is similar in intent to Ref. Tang et al. (2016), in which dynamic programming is used to find protocols able to promote colloidal crystallization using an external field. One important difference between that work and ours is that our scheme does not require measurement of the order parameter we wish to promote (except at the end of the experiment), making it applicable to molecular and nanoscale systems whose microscopic states cannot be observed as they evolve. We also use a neural network to encode the assembly protocol, rather than a model of discretized states. Our approach is also similar to that of Ref. Miskin et al. (2016) in the sense that we use evolutionary search to optimize assembly, but we allow the learning procedure to respond to both temporal and microscopic information via the use of a neural network. Our approach is complementary to efforts that use machine learning to analyze existing self-assembly pathways Long et al. (2015); Long and Ferguson (2014), or to infer or design structure-property relationships for self-assembling molecules Lindquist et al. (2016); Thurston and Ferguson (2018); Ferguson (2017). The present scheme is simple and can be straightforwardly altered to observe an arbitrary number of system features, and to control an arbitrary number of system parameters, and so can be applied to a wide range of experimental systems.
In Section I we describe the evolutionary scheme, which involves alternating physical and evolutionary dynamics. In Section II we show that it leads to networks able to promote the self-assembly of a certain structure faster and better than intuitive cooling protocols can. In Section III we show that networks can learn to select between two polymorphs that are equal in energy and that form in unpredictable quantities under slow cooling protocols. The strategy used by the networks to achieve this selection provides new insight into the self-assembly of the system under study. We conclude in Section IV. Networks learn these efficient and new self-assembly protocols with no human input beyond the specification of which target parameter to promote, pointing the way to the design of synthesis protocols by artificial intelligence.
I Evolutionary reinforcement learning of self-assembly protocols
We sketch in Fig. 1 an evolutionary scheme by which a self-assembly kinetic yield net can learn to control self-assembly. We consider a computational model of molecular self-assembly, patchy discs of diameter on a two-dimensional square substrate of edge length . The substrate (simulation box) possesses periodic boundary conditions in both directions. Discs, which cannot overlap, are minimal representations of molecules, and the patches denote their ability to make mutual bonds at certain angles. By choosing certain patch angles, widths, and binding-energy scales it is possible to reproduce the dynamic and thermodynamic behavior of real molecular systems of a broad range of lengthscales and material types Whitelam et al. (2014b). The disc model is a good system on which to test the application of evolutionary learning to self-assembly, because it is simple enough to simulate for long times, and its behavior is complex enough to capture several aspects of real self-assembly, including the formation of competing polymorphs and structures that are not the thermodynamically stable one. Choosing protocols to promote the formation of particular structures within the disc model is therefore nontrivial, and serves as a meaningful test of the learning procedure.
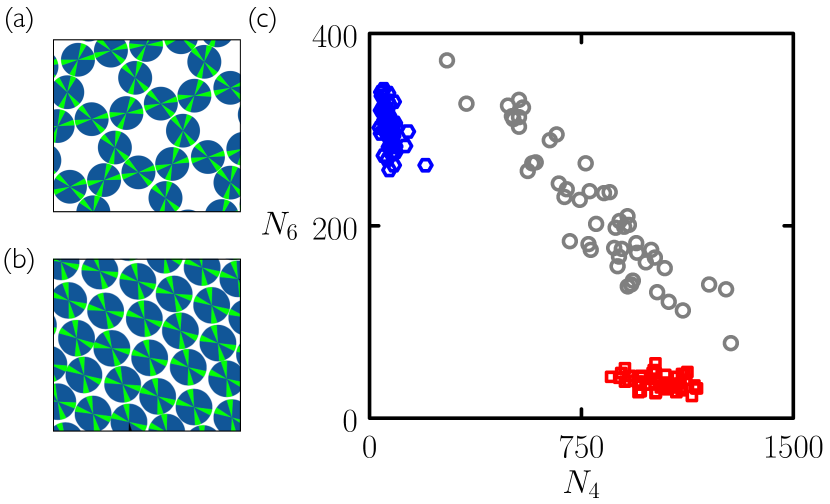
Two discs receive an energetic reward of if their center-to-center distance is between and , and if the line joining those discs cuts through one patch on each disc Kern and Frenkel (2003). In addition, we sometimes require patches to possess certain identities in order to bind, mimicking the ability of e.g. DNA to be chemically specific Whitelam (2016). In this paper we consider disc types with and without DNA-type specificity. Bound patches are shown green in figures, and unbound patches are shown black. In figures we often draw the convex polygons formed by joining the centers of bound particles Whitelam et al. (2014b). Doing so makes it easier to spot regions of order by eye. Polygon counts serve as a useful order parameter for self-assembly, because they are related (in some cases proportional) to the number of unit cells of the desired material. We denote by the number of convex -gons within a simulation box.
We simulated this system in order to mimic an experiment in which molecules are deposited on a surface and allowed to evolve. We use two stochastic Monte Carlo algorithms to do so. One is a grand-canonical algorithm that allows discs to appear on the substrate or disappear into a notional solution Frenkel and Smit (1996); the other is the virtual-move Monte Carlo algorithm Whitelam et al. (2009); Hedges that allows discs to move collectively on the surface in an approximation of Brownian motion Haxton et al. (2015). If is the instantaneous number of discs on the surface then we attempt virtual moves with probability , and attempt grand-canonical moves otherwise. Doing so ensures that particle deposition occurs at a rate (for fixed control parameters) that is roughly insensitive of substrate density. The acceptance rates for grand-canonical moves are given in Ref. Whitelam et al. (2014b) (essentially the textbook rates Frenkel and Smit (1996) with the replacement to preserve detailed balance in the face of a fluctuating proposal rate). One such decision constitutes one Monte Carlo step 111The natural way to measure “real” time in such a system is to advance the clock by an amount upon making an attempted move. Dense systems and sparse systems then take very different amounts of CPU time to run. In order to move simulation generations efficiently through our computer cluster we instead updated the clock by one unit upon making a move. In this way we work in the constant event-number ensemble..
The grand-canonical algorithm is characterized by a chemical potential , where is the energy scale of thermal fluctuations. Positive values of this parameter favor a crowded substate, while negative values favor a sparsely occupied substrate. If the interparticle bond strength is large, then there is, in addition, a thermodynamic driving force for particles to assemble into structures. (In experiment, bond strength can be controlled by different mechanisms, depending upon the physical system, including temperature or salt concentration; here, for convenience, we sometimes describe increasing as “cooling”, and decreasing as “heating”.) For fixed values of these parameters the simulation algorithm obeys detailed balance, and so the system will evolve toward its themodynamic equilibrium. Depending on the parameter choices, this equilibrium may correspond to an assembled structure or to a gas or liquid of loosely-associated discs. For finite simulation time there is no guarantee that we will reach this equilibrium. Here we consider evolutionary simulations or trajectories of individual Monte Carlo steps (not sweeps, or steps per particle), starting from substrates containing 500 randomly-placed non-overlapping discs. These are relatively short trajectories in self-assembly terms: the slow cooling protocols of Ref. Whitelam (2016) used trajectories about 100 times longer.
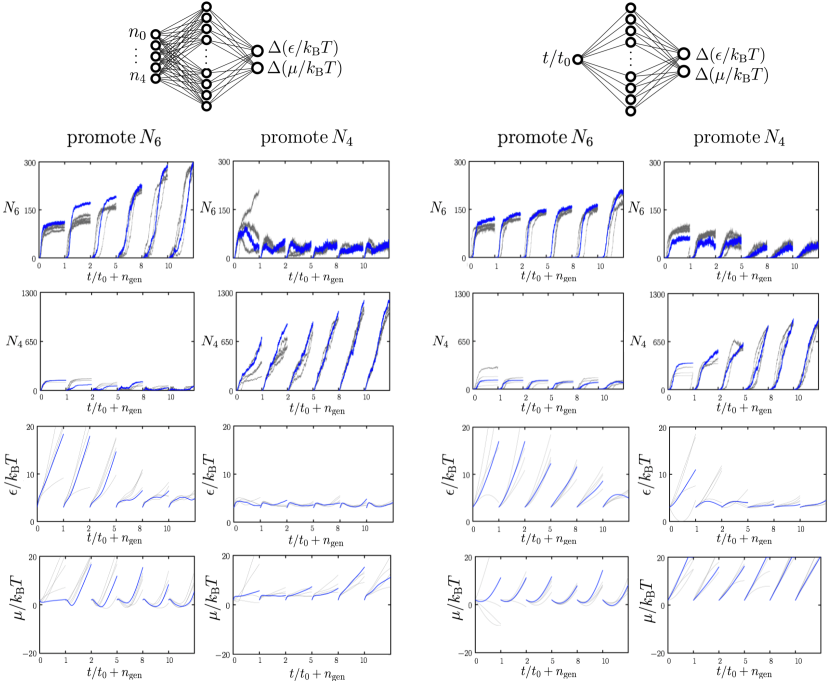
Each trajectory starts with control-parameter values and , which does not give rise to self-assembly. As a trajectory progresses, a neural network chooses, every Monte Carlo steps, a change and of the two control parameters of the system (and so the same network acts 1000 times within each trajectory). These changes are added to the current values of the relevant control parameter, as long as they remain within the intervals and (if a control parameter moves outside of its specified interval then it is returned to the edge of the interval). Between neural-network actions, the values of the control parameters are held fixed. Networks are fully-connected architectures with 1000 hidden nodes and two output nodes, and a number of input nodes appropriate for the information they are fed. We used tanh activations on the hidden nodes; the full network function is given in Section S1.
Training of the network is done by evolution Such et al. (2017). We run 50 initial trajectories, each with a different, randomly-initialized neural network. Each network’s weights and biases are independent Gaussian random numbers of zero mean and unit variance. The collection of 50 trajectories produced by this set of 50 networks is called generation 0. After these trajectories run we assess each according to the number of convex -gons present in the simulation box; the value of depends on the disc type under study and the structure whose assembly we wish to promote. The 5 networks whose trajectories have the largest values of are chosen to be the “parents” of generation 1. Generation 1 consists of these 5 networks, plus 45 mutants. Mutants are made by choosing at random one of the parent networks and adding to each weight and bias a Gaussian random number of zero mean and variance 0.01. After simulation of generation 1 we repeat the evolutionary procedure in order to create generation 2. Alternating the physical dynamics (the self-assembly trajectories) and the evolutionary dynamics (the neural-network weight mutation procedure) results in populations of networks designed to control self-assembly conditions so as to promote certain order parameters.
Each evolutionary scheme used one of three types of network. The first, called the time network for convenience, has a single input node that takes the value of the scaled elapsed time of the trajectory, . The second, called the microscopic network for convenience, has input nodes, where is the number of patches on the disc. Input node takes the value , the number of particles in the simulation box that possess engaged patches (divided by 1000). The third neural network type has input nodes, and takes both and the as inputs. We chose the time network so as to explore the ability of a network to influence the self-assembly protocol if it cannot observe the system at all. We chose the microscopic network to see if a network able to observe the system can do better than one that cannot. We do not intend for its input to be a precise analog of an experimental measurement, but there are several experimental techniques able to access similar information, such as the averaged number of particles in certain types of environment, or the approximate degree of aggregation present in a system De Yoreo et al. (2015).
It is important to note that these microscopic inputs are not related in a simple way to the evolutionary parameters , the number of convex -gons in the box, that we wish to optimize. For instance, in Section II, both dense disordered networks (with small values of ) and well-assembled structures (with large values of ) can contain similar numbers of maximally-coordinated particles. In Section III, the two polymorphs we ask a network to choose between, one described by and the other by , have identical coordination numbers. Thus a network must learn the connection between the data it is fed and the evolutionary order parameters we aim to maximize. Our intent was to mimic an experiment in which which some microscopic information about a system is available, but the quality of assembly can only be assessed after the experiment has run to completion. The success of the learning scheme in the absence of any system-specific information, and our finding that the more information we feed a network the better it performs, suggests that the evolutionary scheme can be applied to a wide variety of experimental systems.
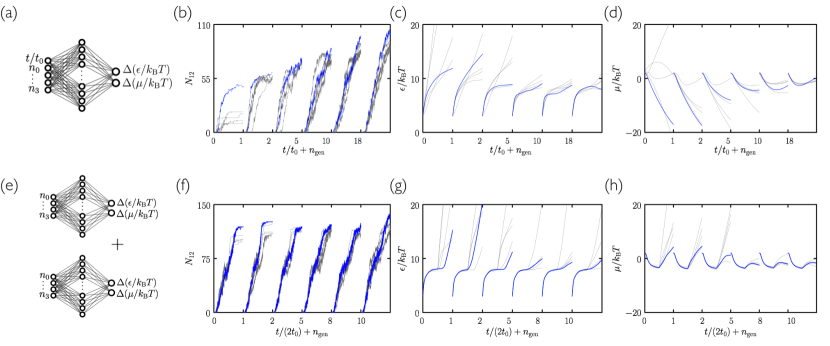
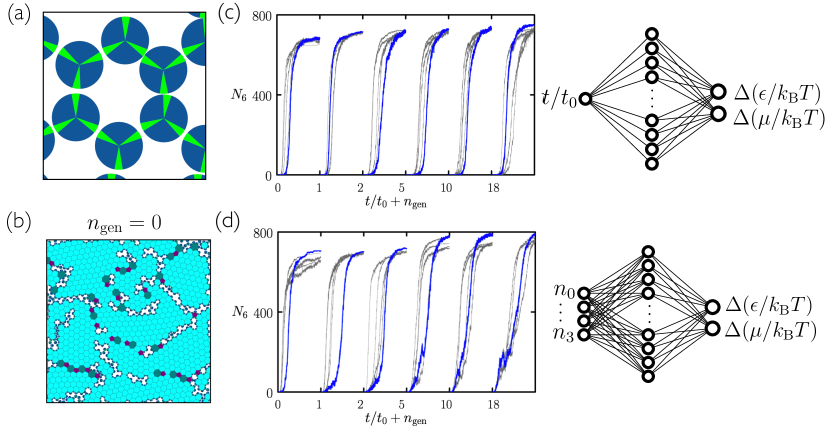
Dynamical trajectories are stochastic, even given a fixed protocol (policy), and so networks that perform well in one generation may be eliminated the next. This can happen if, for example, a certain protocol promotes nucleation, the onset time for which varies from one trajectory to another. By the same token, the best yield can decrease from one generation to the next, and independent trajectories generated using a given protocol have a range of yields. To account for this effect one could place evolutionary requirements on the yield associated with many independent trajectories using the same protocol. Here we opted not to do this, reasoning that over the course of several generations the evolutionary process will naturally identify protocols that perform well when measured over many independent trajectories. We demonstrate this feature in Section II, where independent trajectories produced under slow cooling display a wide variety of outcomes, but independent trajectories generated by evolved protocols display relatively well-defined ones.
II Promoting self-assembly
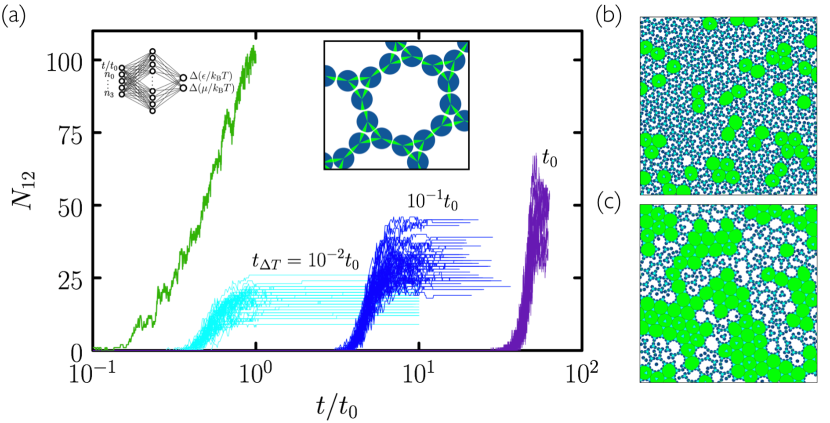
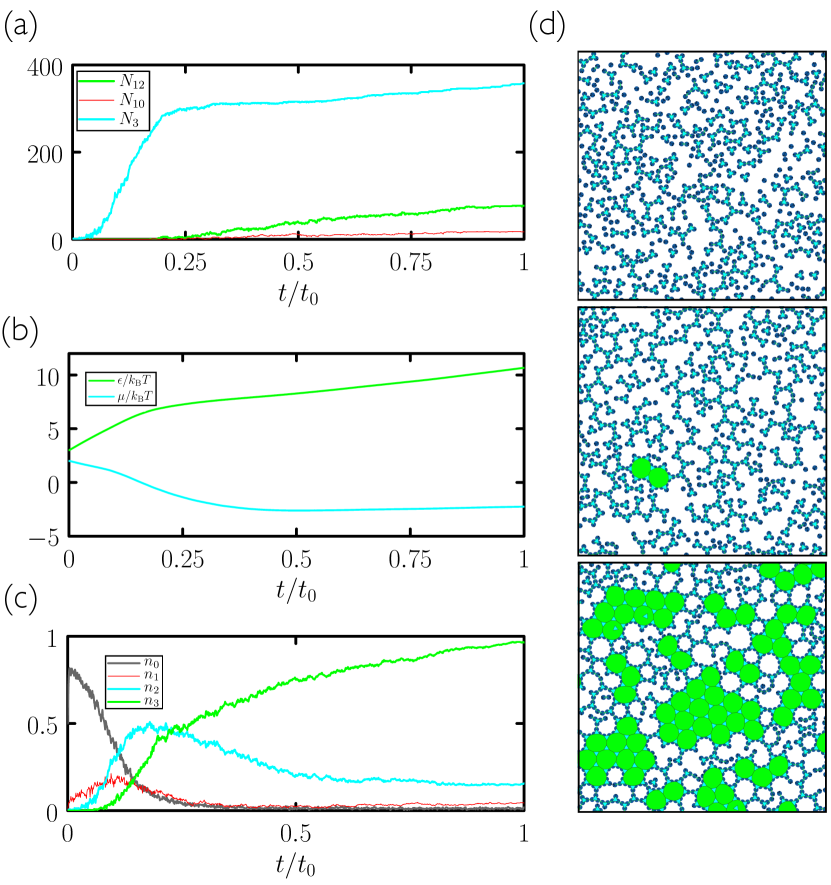
In Fig. 3 we consider the “3.12.12” disc of Ref. Whitelam (2016), which has three, chemically specific patches whose bisectors are separated by angles and . This disc can form a structure equivalent to the 3.12.12 Archimedean tiling (a tiling with one 3-gon and two 12-gons around each vertex). The number of 12-gons counts the number of unit cells of the structure, and so is a suitable order parameter for evolutionary search. This structure is a difficult target for self-assembly because its unit cell is large and must form from floppy intermediates, the nature of which gives plenty of scope for mistakes of binding and kinetic trapping. As a result, while intuitive protocols allow assembly to proceed, they do so with relatively low fidelity. In Fig. 2(a) we show the outcome of “cooling” simulations done at three different rates. As for evolutionary simulations, we start from control-parameter values and , where the equilibrium state is a sparse gas of largely unassociated discs. Every Monte Carlo steps we increase by a value 0.075. We carried out 50 independent simulations at each cooling rate. As the rate of cooling decreases, the yield increases, but achieving much more than 50 unit cells of the target material is time-consuming: single trajectories at each of the cooling rates take, respectively, of order an hour, a day, and a week of CPU time on a single processor. Clearly, substantial improvement using this protocol would require prohibitively long simulations.
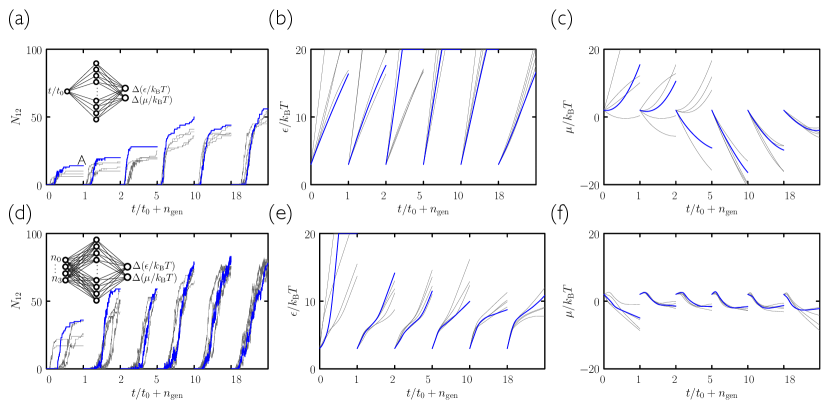
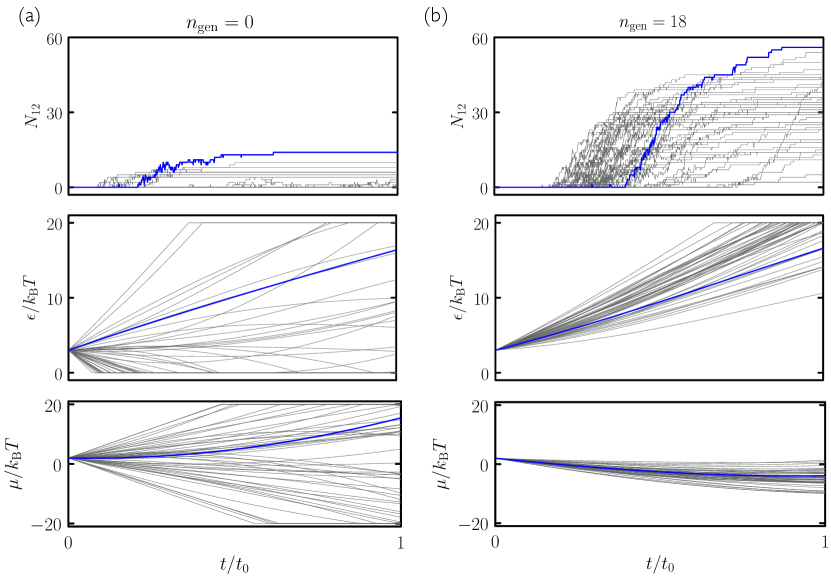
Search using evolutionary learning results in protocols that can greatly exceed the yield of cooling simulations, in a fraction of the time (an example is shown at left in Fig. 2(a)). In Fig. 3(a–c) we show results obtained using the time network within the evolutionary scheme of Fig. 1. Generation-0 trajectories are controlled by essentially random protocols, and many (e.g. those that involve weakening of interparticle bonds) result in no assembly (see Fig. 4). Some protocols result in low-quality assembly (comparable to that seen in the fastest cooling protocols of Fig. 2), and the best of these are used to create generation 1. Fig. 3(a) shows that assembly gets better with generation number: evolved networks learn to promote assembly of the desired structure. The protocols leading to these structures are shown in Fig. 3(b,c): early-generation networks tend to strengthen bonds (“cool”) quickly and concentrate the substrate, while later-generation networks strengthen bonds more quickly but also promote evacuation of the substrate. This strategy appears to reduce the number of obstacles to the closing of the large and floppy intermediate structures. The most advanced networks further refine these bond-strengthening and substrate-evacuation protocols.
The microscopic network [Fig. 3(d–f)] produces slightly more nuanced versions of the time-network protocols, and leads to better assembly. Thus, networks given access to configurational information learn more completely than those that know only the elapsed time of the procedure, even though the information they are given does not directly relate to the quality of assembly. In Fig. 5 we show in more detail a trajectory produced by the best generation-18 microscopic network. The self-assembly dynamics that results is hierarchical assembly of the type seen in Ref. Whitelam (2016), in which trimers (3-gons) form first, and networks of trimers then form 12-gons, but is a more extreme version: in Fig. 5 we see that almost all the 3-gons made by the system form before the 12-gons begin to form. Thus the network has adopted a two-stage procedure in an attempt to maximize yield.
Networks given either temporal or microscopic information have therefore learned to promote self-assembly, without any external direction beyond an assessment, at the end of the trajectory, of which outcomes were best. Moreover, the quality of assembly considerably exceeds the quality of intuition-driven cooling procedures, and proceeds much more quickly. In Fig. 6 we compare trajectories and assembled structures produced by cooling and by two different networks: the networks produce better structures, even though they are constrained to act over much shorter times. Here we observe the counterintuitive result of rapidly-varying nonequilibrium protocols producing better-quality assembly than a slow-cooling procedure designed (at least in an intuitive sense) to promote “near equilibrium” conditions Whitelam (2018).
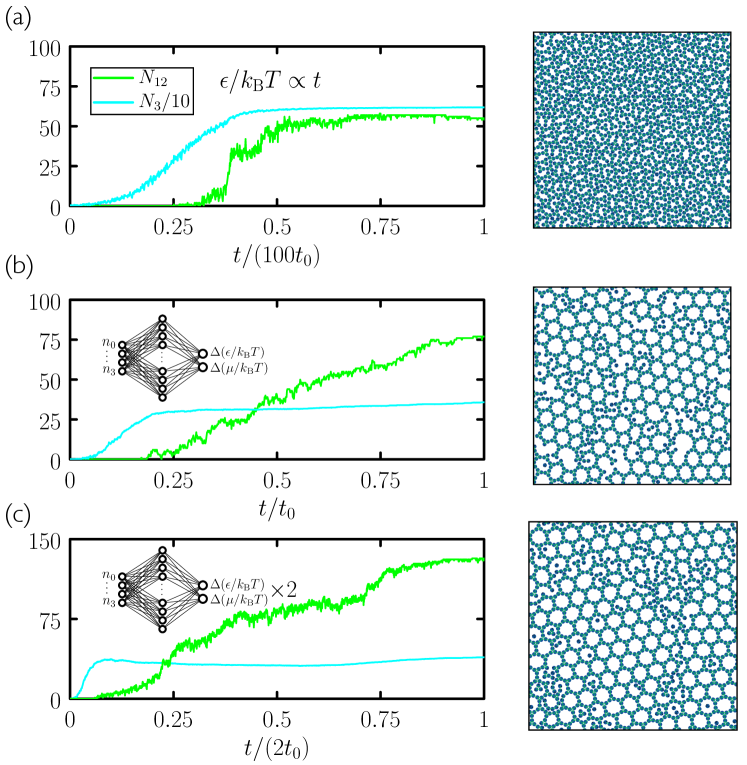
Yield under the evolutionary protocols can be increased by providing more data to the neural network. In Fig. 7 we show that a neural network provided with both temporal and microscopic information outperforms both the time- and the microscopic networks of Fig. 3. Yield can also be increased by using two neural networks, one after the other, trained independently [see Fig. 6(c) and Fig. 7(e–h)]. In these cases the yield of material reaches more than double that obtained under a slow-cooling protocol. Protocols learned by these neural networks are distinctly different at early and late times, suggestive of distinct growth and annealing stages: after an initial stage of rapid growth under cool and sparse conditions, networks heat the substrate and make it more dense, apparently in order to promote error-correction.
Here we have provided no prior input to the neural net to indicate what constitutes a good assembly protocol. One could alternatively survey parameter space as thoroughly as possible, using intuition and prior experience, before turning to evolution. In such cases generation-0 assembly would be better than under randomized protocols. However, we found that even when generation-0 assembly was already of high quality, the evolutionary procedure was able to improve it. In Fig. 8 we consider evolutionary learning using the regular three-patch disc without patch-type specificity Whitelam et al. (2014b); Whitelam (2016). This disc forms the honeycomb network so readily that the best examples of assembly using 50 randomly-chosen protocols (generation 0) are already good. Nonetheless, evolution using the time network or microscopic network is able to improve the quality of assembly, with the microscopic network again performing better.
III Polymorph selection
Controlling the polymorph into which a set of molecules will self-assemble is a key consideration in industrial procedures such as drug crystallization Chen et al. (2011); Threlfall (2000); Rodríguez-hornedo and Murphy (1999); Shekunov and York (2000). Here we show that evolutionary search can be used to find protocols able to direct the self-assembly of a set of model molecules into either of two competing polymorphs. In doing so, the procedure learns strategies that provide physical insight into the system under study.
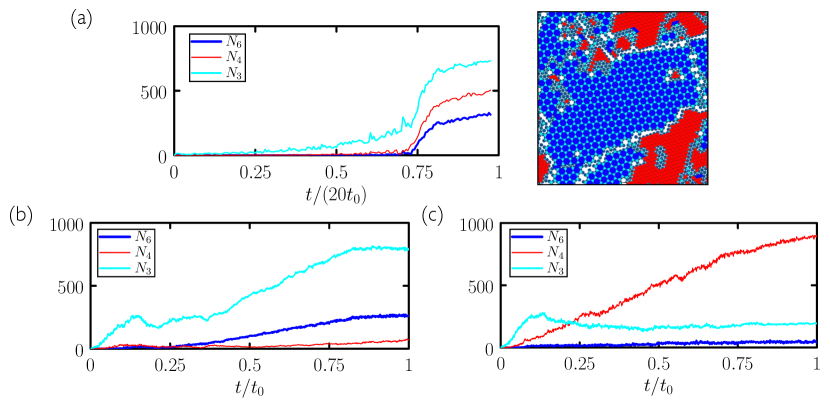
In Fig. 9 we consider a 4-patch disc with angles and between patch bisectors. This disc can form a structure equivalent to the 3.6.3.6 Archimedean tiling (a tiling with two 3-gons and two 6-gons around each vertex), or a rhombic structure. Particles have equal energy within the bulk of each structure, and at zero pressure (the conditions experienced by a cluster growing in isolation in a substrate) there is no thermodynamic preference for one structure over the other. Independent trajectories generated under slow cooling (gray circles) therefore display nucleation of either or both polymorphs, in an unpredictable way (see also Fig. 12) The 3.6.3.6 polymorph can be selected by making the patches chemically selective Whitelam (2016), but here we do not do this. Instead, we show that evolutionary search can be used to develop protocols able to choose between these two polymorphs.
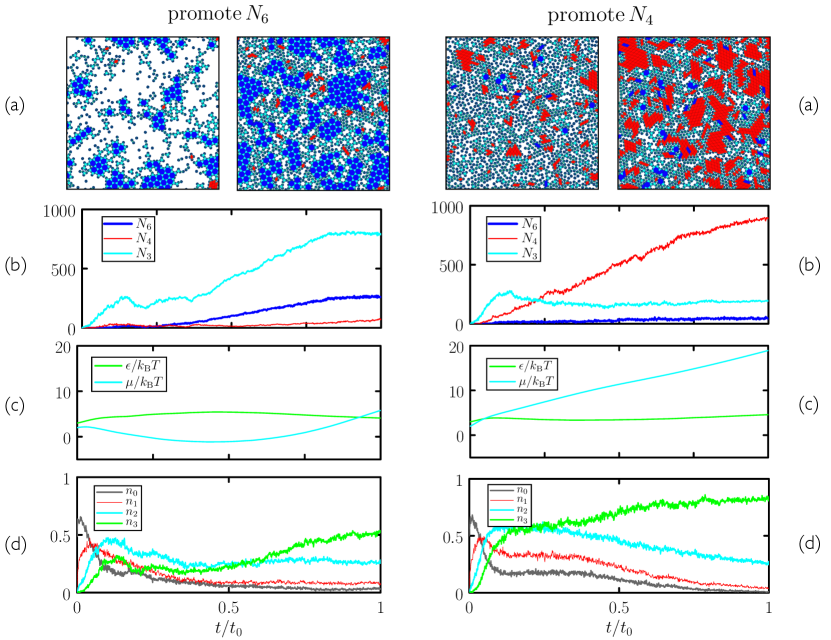
In Fig. 10 we consider evolutionary learning of self-assembly protocols using time- and microscopic networks instructed to promote either the parameter or the parameter . In both cases we see steadily increasing counts, with generation, of the required order parameter, with the microscopic network again performing better. The lower two rows show the evolution of the strategies chosen by each network, with time- and microscopic networks learning qualitatively similar protocols for promotion of a given order parameter.
In Fig. 11 we show in more detail one trajectory per strategy obtained using generation-10 microscopic neural networks. Left-hand panels pertain to a trajectory produced by a neural network evolved to promote 6-gons, while right-hand panels pertain to a trajectory produced by a neural network evolved to promote 4-gons. In each case, neural networks have learned to promote one polymorph and so suppress the other. Both examples of assembly display defects and grain boundaries, but the specified polymorphs cover substantial parts of the substrate. In the case considered in Section II we already knew how to promote assembly, by cooling – although the evolutionary protocol learned to do it more quickly and with higher fidelity – but here we did not possess advance knowledge of how to do polymorph selection using protocol choice.
In Fig. 11, inspection of the snapshots (a), the polygon counts (b), and the control-parameter histories (c) provide insight into the selection strategies adopted by the networks. To select the 3.6.3.6 tiling (left panels) the network has induced a tendency for particles to leave the surface (small ) and for bonds to be moderately strong (moderate ). The balance of these things appears to be such that trimers (3-gons), in which each particle has two engaged bonds, can form. Trimers serve as a building block for the 3.6.3.6 structure, which then forms hierarchically as the chemical potential is increased (and the bond strength slightly decreased). By contrast, the rhombic structure appears to be unable to grow because it cannot form hierarchically from collections of rhombi (which also contain particles with two engaged bonds): growing beyond a single rhombus involves the addition of particles via only one engaged bond, and these particles are unstable, at early times, to dissociation.
To select the rhombic structure (right panels) the network selects moderate bond strength and concentrates the substrate by driving large. In a dense environment it appears that the rhombic structure is more accessible kinetically than the more open 3.6.3.6 network. In addition, in a dense environment there is a thermodynamic preference for the more compact rhombic polymorph, a factor that may also contribute to selection of the latter. Note that simply causing to increase with time is not sufficient to produce the rhombic polymorph in high yield: early-generation networks adopt just such a strategy, but high yield for later generations requires a particular balance of bond strength and chemical potential.
The microscopic network receives information periodically from the system, but the information it receives – the number of particles with certain numbers of engaged bonds – does not distinguish between the bulk forms of the two polymorphs. Networks must therefore learn the relationships between these inputs, their resulting actions, and the final-time order parameter. The time network learns qualitatively similar protocols, albeit with slightly less effectiveness, with no access to the microscopic state of the system.
Returning to Fig. 9(c), we show the results of 50 independent trajectories of length carried out using a single generation-10 microscopic network evolved to promote 6-gons (blue hexagons), and the results of 50 independent trajectories of length carried out using a single generation-10 microscopic network evolved to promote 4-gons. In both cases the networks reliably promote one polymorph and suppress the other, in contrast to slow-cooling simulations whose outcome is unpredictable. In this case the conventional nucleation-and-growth pathway induced by slow cooling provides no control over polymorph selection, while the pathways induced by the neural networks – one of which is strongly hierarchical – do. In addition, as in Section II, assembly under the network protocols is much faster than under slow cooling: see Fig. 12.
IV Conclusions
We have shown that a self-assembly kinetic yield net trained by evolutionary reinforcement learning Holland (1992); Fogel and Stayton (1994); Lehman et al. (2018a); Salimans et al. (2017); Zhang et al. (2017); Lehman et al. (2018b); Conti et al. (2018); Such et al. (2017) can control self-assembly protocols in molecular simulations. Networks learn to promote the assembly of desired structures, or choose between polymorphs. In the first case, networks reproduce the structures produced by previously-known protocols, but faster and with higher fidelity; in the second case they identify strategies previously unknown, and from which we can extract physical insight. Networks that take as input only the elapsed time of the protocol are effective, and networks that take as input microscopic information from the system are more so. This comparison indicates that this scheme can be applied to a wide range of experiments, regardless of how much microscopic information is available as assembly proceeds.
The problem we have addressed falls in the category of reinforcement learning in the sense that the neural network learns to perform actions (choosing new values of the control parameters) given an observation. The evolutionary approach we have applied to this problem requires only the assessment of a desired order parameter (here the polygon count ) at the end of a trajectory. This is an important feature because in self-assembly the best-performing trajectories at short times are not necessarily the best-performing trajectories at the desired observation time: see e.g. Fig. 4. Self-assembly is inherently a “sparse-reward” problem. For this reason it is not obvious that value-based reinforcement-learning methods Sutton and Barto (2018) are ideally suited to a problem such as self-assembly: rewarding “good” configurations at early times may not result in favorable outcomes at later times. This is only speculation on our part, however; which of the many ways of doing reinforcement learning is best for self-assembly is an open question.
Our results demonstrate proof of principle, and can be extended or adapted in several ways. We allow networks to act 1000 times per trajectory, in order to mimic a system in which we have only occasional control; the influence of a network could be increased by allowing it to act more frequently. We have chosen the hyperparameters of our scheme (mutation step size, neural network width, network activation functions, number of trajectories per generation) using values that seemed reasonable and that we subsequently observed to work, but these could be optimized (potentially by evolutionary search).
We end by noting that the scheme we have used is simple to implement. The network architectures we have used are standard and can be straightforwardly adapted to handle an arbitrary number of inputs (system data) and outputs (changes of system control parameters). The mutation protocol is simple to implement. In addition, we have shown that learning can be effective using a modest number of trajectories (50) per generation. The evolutionary scheme should therefore be applicable to a broad range of experimental or computational systems. The results shown here have been achieved with no human input beyond the specification of which order parameter to promote, pointing the way to the design of synthesis protocols by artificial intelligence.
Acknowledgments – This work was performed as part of a user project at the Molecular Foundry, Lawrence Berkeley National Laboratory, supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02–05CH11231. I.T. performed work at the National Research Council of Canada under the auspices of the AI4D Program.
References
- Whitesides et al. (1991) George M Whitesides, John P Mathias, and Christopher T Seto, “Molecular self-assembly and nanochemistry: A chemical strategy for the synthesis of nanostructures,” Science 254, 1312–1319 (1991).
- Biancaniello et al. (2005) Paul L Biancaniello, Anthony J Kim, and John C Crocker, “Colloidal interactions and self-assembly using dna hybridization,” Physical Review Letters 94, 058302 (2005).
- Park et al. (2008) Sung Yong Park, Abigail KR Lytton-Jean, Byeongdu Lee, Steven Weigand, George C Schatz, and Chad A Mirkin, “Dna-programmable nanoparticle crystallization,” Nature 451, 553–556 (2008).
- Nykypanchuk et al. (2008) Dmytro Nykypanchuk, Mathew M Maye, Daniel van der Lelie, and Oleg Gang, “Dna-guided crystallization of colloidal nanoparticles,” Nature 451, 549–552 (2008).
- Ke et al. (2012) Yonggang Ke, Luvena L Ong, William M Shih, and Peng Yin, “Three-dimensional structures self-assembled from dna bricks,” Science 338, 1177–1183 (2012).
- Pfeifer and Saccà (2018) Wolfgang Pfeifer and Barbara Saccà, “Synthetic dna filaments: from design to applications,” Biological Chemistry 399, 773–785 (2018).
- Doye et al. (2004) J. P. K. Doye, A. A. Louis, and M. Vendruscolo, “Inhibition of protein crystallization by evolutionary negative design,” Physical Biology 1, P9 (2004).
- Romano and Sciortino (2011) Flavio Romano and Francesco Sciortino, “Colloidal self-assembly: patchy from the bottom up,” Nature materials 10, 171 (2011).
- Glotzer et al. (2004) SC Glotzer, MJ Solomon, and Nicholas A Kotov, “Self-assembly: From nanoscale to microscale colloids,” AIChE Journal 50, 2978–2985 (2004).
- Doye et al. (2007a) J. P. K. Doye, A. A. Louis, I. C. Lin, L. R. Allen, E. G. Noya, A. W. Wilber, H. C. Kok, and R. Lyus, “Controlling crystallization and its absence: Proteins, colloids and patchy models,” Physical Chemistry Chemical Physics 9, 2197–2205 (2007a).
- Rapaport (2010) D. C. Rapaport, “Modeling capsid self-assembly: design and analysis,” Phys. Biol. 7, 045001 (2010).
- Reinhardt and Frenkel (2014) Aleks Reinhardt and Daan Frenkel, “Numerical evidence for nucleated self-assembly of dna brick structures,” Physical Review Letters 112, 238103 (2014).
- De Yoreo et al. (2015) James J De Yoreo, Pupa UPA Gilbert, Nico AJM Sommerdijk, R Lee Penn, Stephen Whitelam, Derk Joester, Hengzhong Zhang, Jeffrey D Rimer, Alexandra Navrotsky, Jillian F Banfield, et al., “Crystallization by particle attachment in synthetic, biogenic, and geologic environments,” Science 349, aaa6760 (2015).
- Murugan et al. (2015) Arvind Murugan, James Zou, and Michael P Brenner, “Undesired usage and the robust self-assembly of heterogeneous structures,” Nature Communications 6 (2015).
- Whitelam and Jack (2015) Stephen Whitelam and Robert L Jack, “The statistical mechanics of dynamic pathways to self-assembly,” Annual Review of Physical Chemistry 66, 143–163 (2015).
- Nguyen and Vaikuntanathan (2016) Michael Nguyen and Suriyanarayanan Vaikuntanathan, “Design principles for nonequilibrium self-assembly,” Proceedings of the National Academy of Sciences 113, 14231–14236 (2016).
- Whitelam et al. (2014a) Stephen Whitelam, Lester O Hedges, and Jeremy D Schmit, “Self-assembly at a nonequilibrium critical point,” Physical Review Letters 112, 155504 (2014a).
- Jadrich et al. (2017) RB Jadrich, BA Lindquist, and TM Truskett, “Probabilistic inverse design for self-assembling materials,” The Journal of Chemical Physics 146, 184103 (2017).
- Lutsko (2019) James F Lutsko, “How crystals form: A theory of nucleation pathways,” Science advances 5, eaav7399 (2019).
- Fan and Grunwald (2019) Zhaochuan Fan and Michael Grunwald, “Orientational order in self-assembled nanocrystal superlattices,” Journal of the American Chemical Society 141, 1980–1988 (2019).
- Chen et al. (2011) Jie Chen, Bipul Sarma, James MB Evans, and Allan S Myerson, “Pharmaceutical crystallization,” Crystal growth & design 11, 887–895 (2011).
- Threlfall (2000) Terry Threlfall, “Crystallisation of polymorphs: thermodynamic insight into the role of solvent,” Organic Process Research & Development 4, 384–390 (2000).
- Rodríguez-hornedo and Murphy (1999) Naír Rodríguez-hornedo and Denette Murphy, “Significance of controlling crystallization mechanisms and kinetics in pharmaceutical systems,” Journal of pharmaceutical sciences 88, 651–660 (1999).
- Shekunov and York (2000) B Yu Shekunov and P York, “Crystallization processes in pharmaceutical technology and drug delivery design,” Journal of crystal growth 211, 122–136 (2000).
- Sutton and Barto (2018) Richard S Sutton and Andrew G Barto, Reinforcement learning: An introduction (2018).
- Watkins and Dayan (1992) Christopher JCH Watkins and Peter Dayan, “Q-learning,” Machine learning 8, 279–292 (1992).
- Mnih et al. (2013) Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin Riedmiller, “Playing atari with deep reinforcement learning,” arXiv preprint arXiv:1312.5602 (2013).
- Mnih et al. (2015) Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Bellemare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al., “Human-level control through deep reinforcement learning,” Nature 518, 529 (2015).
- Bellemare et al. (2013) Marc G Bellemare, Yavar Naddaf, Joel Veness, and Michael Bowling, “The arcade learning environment: An evaluation platform for general agents,” Journal of Artificial Intelligence Research 47, 253–279 (2013).
- Mnih et al. (2016) Volodymyr Mnih, Adria Puigdomenech Badia, Mehdi Mirza, Alex Graves, Timothy Lillicrap, Tim Harley, David Silver, and Koray Kavukcuoglu, “Asynchronous methods for deep reinforcement learning,” in International conference on machine learning (2016) pp. 1928–1937.
- Tassa et al. (2018) Yuval Tassa, Yotam Doron, Alistair Muldal, Tom Erez, Yazhe Li, Diego de Las Casas, David Budden, Abbas Abdolmaleki, Josh Merel, Andrew Lefrancq, et al., “Deepmind control suite,” arXiv preprint arXiv:1801.00690 (2018).
- Todorov et al. (2012) Emanuel Todorov, Tom Erez, and Yuval Tassa, “Mujoco: A physics engine for model-based control,” in Intelligent Robots and Systems (IROS), 2012 IEEE/RSJ International Conference on (IEEE, 2012) pp. 5026–5033.
- Puterman (2014) Martin L Puterman, Markov decision processes: discrete stochastic dynamic programming (John Wiley & Sons, 2014).
- Asperti et al. (2018) Andrea Asperti, Daniele Cortesi, and Francesco Sovrano, “Crawling in rogue’s dungeons with (partitioned) a3c,” arXiv preprint arXiv:1804.08685 (2018).
- Riedmiller (2005) Martin Riedmiller, “Neural fitted q iteration–first experiences with a data efficient neural reinforcement learning method,” in European Conference on Machine Learning (Springer, 2005) pp. 317–328.
- Riedmiller et al. (2009) Martin Riedmiller, Thomas Gabel, Roland Hafner, and Sascha Lange, “Reinforcement learning for robot soccer,” Autonomous Robots 27, 55–73 (2009).
- Schulman et al. (2017) John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov, “Proximal policy optimization algorithms,” arXiv preprint arXiv:1707.06347 (2017).
- Brockman et al. (2016) Greg Brockman, Vicki Cheung, Ludwig Pettersson, Jonas Schneider, John Schulman, Jie Tang, and Wojciech Zaremba, “Openai gym,” arXiv preprint arXiv:1606.01540 (2016).
- Kempka et al. (2016) Michał Kempka, Marek Wydmuch, Grzegorz Runc, Jakub Toczek, and Wojciech Jaśkowski, “Vizdoom: A doom-based ai research platform for visual reinforcement learning,” in Computational Intelligence and Games (CIG), 2016 IEEE Conference on (IEEE, 2016) pp. 1–8.
- Wydmuch et al. (2018) Marek Wydmuch, Michał Kempka, and Wojciech Jaśkowski, “Vizdoom competitions: Playing doom from pixels,” arXiv preprint arXiv:1809.03470 (2018).
- Silver et al. (2016) David Silver, Aja Huang, Chris J Maddison, Arthur Guez, Laurent Sifre, George Van Den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, et al., “Mastering the game of go with deep neural networks and tree search,” nature 529, 484 (2016).
- Silver et al. (2017) David Silver, Julian Schrittwieser, Karen Simonyan, Ioannis Antonoglou, Aja Huang, Arthur Guez, Thomas Hubert, Lucas Baker, Matthew Lai, Adrian Bolton, et al., “Mastering the game of go without human knowledge,” Nature 550, 354 (2017).
- Such et al. (2017) Felipe Petroski Such, Vashisht Madhavan, Edoardo Conti, Joel Lehman, Kenneth O Stanley, and Jeff Clune, “Deep neuroevolution: genetic algorithms are a competitive alternative for training deep neural networks for reinforcement learning,” arXiv preprint arXiv:1712.06567 (2017).
- Holland (1992) John H Holland, “Genetic algorithms,” Scientific american 267, 66–73 (1992).
- Fogel and Stayton (1994) David B Fogel and Lauren C Stayton, “On the effectiveness of crossover in simulated evolutionary optimization,” BioSystems 32, 171–182 (1994).
- Lehman et al. (2018a) Joel Lehman, Jay Chen, Jeff Clune, and Kenneth O Stanley, “Es is more than just a traditional finite-difference approximator,” in Proceedings of the Genetic and Evolutionary Computation Conference (2018) pp. 450–457.
- Salimans et al. (2017) Tim Salimans, Jonathan Ho, Xi Chen, Szymon Sidor, and Ilya Sutskever, “Evolution strategies as a scalable alternative to reinforcement learning,” arXiv preprint arXiv:1703.03864 (2017).
- Zhang et al. (2017) Xingwen Zhang, Jeff Clune, and Kenneth O Stanley, “On the relationship between the openai evolution strategy and stochastic gradient descent,” arXiv preprint arXiv:1712.06564 (2017).
- Lehman et al. (2018b) Joel Lehman, Jay Chen, Jeff Clune, and Kenneth O Stanley, “Safe mutations for deep and recurrent neural networks through output gradients,” in Proceedings of the Genetic and Evolutionary Computation Conference (2018) pp. 117–124.
- Conti et al. (2018) Edoardo Conti, Vashisht Madhavan, Felipe Petroski Such, Joel Lehman, Kenneth Stanley, and Jeff Clune, “Improving exploration in evolution strategies for deep reinforcement learning via a population of novelty-seeking agents,” in Advances in neural information processing systems (2018) pp. 5027–5038.
- Zhang and Glotzer (2004) Zhenli Zhang and Sharon C Glotzer, “Self-assembly of patchy particles,” Nano Letters 4, 1407–1413 (2004).
- Romano et al. (2011) Flavio Romano, Eduardo Sanz, and Francesco Sciortino, “Crystallization of tetrahedral patchy particles in silico,” The Journal of Chemical Physics 134, 174502 (2011).
- Sciortino et al. (2007) Francesco Sciortino, Emanuela Bianchi, Jack F Douglas, and Piero Tartaglia, “Self-assembly of patchy particles into polymer chains: A parameter-free comparison between wertheim theory and monte carlo simulation,” The Journal of Chemical Physics 126, 194903 (2007).
- Doye et al. (2007b) J.P.K. Doye, A.A. Louis, I.C. Lin, L.R. Allen, E.G. Noya, A.W. Wilber, H.C. Kok, and R. Lyus, “Controlling crystallization and its absence: proteins, colloids and patchy models,” Physical Chemistry Chemical Physics 9, 2197–2205 (2007b).
- Bianchi et al. (2008) Emanuela Bianchi, Piero Tartaglia, Emanuela Zaccarelli, and Francesco Sciortino, “Theoretical and numerical study of the phase diagram of patchy colloids: Ordered and disordered patch arrangements,” The Journal of Chemical Physics 128, 144504 (2008).
- Doppelbauer et al. (2010) Günther Doppelbauer, Emanuela Bianchi, and Gerhard Kahl, “Self-assembly scenarios of patchy colloidal particles in two dimensions,” Journal of Physics: Condensed Matter 22, 104105 (2010).
- Whitelam et al. (2014b) Stephen Whitelam, Isaac Tamblyn, Thomas K Haxton, Maria B Wieland, Neil R Champness, Juan P Garrahan, and Peter H Beton, “Common physical framework explains phase behavior and dynamics of atomic, molecular, and polymeric network formers,” Physical Review X 4, 011044 (2014b).
- Duguet et al. (2016) Étienne Duguet, Céline Hubert, Cyril Chomette, Adeline Perro, and Serge Ravaine, “Patchy colloidal particles for programmed self-assembly,” Comptes Rendus Chimie 19, 173–182 (2016).
- Frenkel and Smit (1996) D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications (Academic Press, Inc. Orlando, FL, USA, 1996).
- Klotsa and Jack (2013) Daphne Klotsa and Robert L Jack, “Controlling crystal self-assembly using a real-time feedback scheme,” The Journal of Chemical Physics 138, 094502 (2013).
- Tang et al. (2016) Xun Tang, Bradley Rupp, Yuguang Yang, Tara D Edwards, Martha A Grover, and Michael A Bevan, “Optimal feedback controlled assembly of perfect crystals,” ACS nano 10, 6791–6798 (2016).
- Miskin et al. (2016) Marc Z Miskin, Gurdaman Khaira, Juan J de Pablo, and Heinrich M Jaeger, “Turning statistical physics models into materials design engines,” Proceedings of the National Academy of Sciences 113, 34–39 (2016).
- Long et al. (2015) Andrew W Long, Jie Zhang, Steve Granick, and Andrew L Ferguson, “Machine learning assembly landscapes from particle tracking data,” Soft Matter 11, 8141–8153 (2015).
- Long and Ferguson (2014) Andrew W Long and Andrew L Ferguson, “Nonlinear machine learning of patchy colloid self-assembly pathways and mechanisms,” The Journal of Physical Chemistry B 118, 4228–4244 (2014).
- Lindquist et al. (2016) Beth A Lindquist, Ryan B Jadrich, and Thomas M Truskett, “Communication: Inverse design for self-assembly via on-the-fly optimization,” Journal of Chemical Physics 145 (2016).
- Thurston and Ferguson (2018) Bryce A Thurston and Andrew L Ferguson, “Machine learning and molecular design of self-assembling-conjugated oligopeptides,” Molecular Simulation 44, 930–945 (2018).
- Ferguson (2017) Andrew L Ferguson, “Machine learning and data science in soft materials engineering,” Journal of Physics: Condensed Matter 30, 043002 (2017).
- Kern and Frenkel (2003) Norbert Kern and Daan Frenkel, “Fluid–fluid coexistence in colloidal systems with short-ranged strongly directional attraction,” The Journal of Chemical Physics 118, 9882 (2003).
- Whitelam (2016) Stephen Whitelam, “Minimal positive design for self-assembly of the archimedean tilings,” Physical Review Letters 117, 228003 (2016).
- Whitelam et al. (2009) Stephen Whitelam, Edward H Feng, Michael F Hagan, and Phillip L Geissler, “The role of collective motion in examples of coarsening and self-assembly,” Soft Matter 5, 1251–1262 (2009).
- (71) L. O. Hedges, “http://vmmc.xyz,” .
- Haxton et al. (2015) Thomas K Haxton, Lester O Hedges, and Stephen Whitelam, “Crystallization and arrest mechanisms of model colloids,” Soft matter 11, 9307–9320 (2015).
- Note (1) The natural way to measure “real” time in such a system is to advance the clock by an amount upon making an attempted move. Dense systems and sparse systems then take very different amounts of CPU time to run. In order to move simulation generations efficiently through our computer cluster we instead updated the clock by one unit upon making a move. In this way we work in the constant event-number ensemble.
- Whitelam (2018) Stephen Whitelam, “Strong bonds and far-from-equilibrium conditions minimize errors in lattice-gas growth,” The Journal of Chemical Physics 149, 104902 (2018).
S1 Neural network
Each network is a fully-connected architecture with input nodes, hidden nodes, and output nodes. Let the indices , , and label nodes in the input, hidden, and output layers, respectively. Let be the weight connecting nodes and , and let be the bias applied to hidden-layer node . Then the two output nodes take the values
| (S1) |
where
| (S2) |
and denotes the input-node value(s). For the time network we have and . For the microscopic network we have , where is the number of patches on the disc, and is the number of particles in the simulation box having engaged patches (divided by 1000). The mixed time-microscopic network of Fig. 7 uses both and the as inputs. The output-node values are taken to be the changes and , provided that and remain in the intervals and , respectively.