Ledom: An Open and Fundamental Reverse Language Model
Abstract
We introduce Ledom, the first purely reverse language model, trained autoregressively on 435B tokens with 2B and 7B parameter variants, which processes sequences in reverse temporal order through previous token prediction. For the first time, we present the reverse language model as a potential foundational model across general tasks, accompanied by a set of intriguing examples and insights. Based on Ledom, we further introduce a novel application: Reverse Reward, where Ledom-guided reranking of forward language model outputs leads to substantial performance improvements on mathematical reasoning tasks. This approach leverages Ledom’s unique backward reasoning capability to refine generation quality through posterior evaluation. Our findings suggest that Ledom exhibits unique characteristics with broad application potential. We will release all models, training code, and pre-training data to facilitate future research.
tcb@breakable
Ledom: An Open and Fundamental Reverse Language Model
Xunjian Yin♠ , Sitao Cheng♣ , Yuxi Xie♡ , Xinyu Hu♠ , Li Lin♠ , Xinyi Wang♣ Liangming Pan♢ , William Yang Wang♣ , Xiaojun Wan♠ ♠ Peking University ♣University of California, Santa Barbara ♢ University of Arizona ♡ National University of Singapore {xjyin,wanxiaojun}@pku.edu.cn william@cs.ucsb.edu
1 Introduction
Since the emergence of modern autoregressive architectures (Brown et al., 2020; Touvron et al., 2023; Jiang et al., 2023), language models have been predominantly trained in a forward, left-to-right manner. This design choice aligns with the natural reading direction of most written languages and has become the standard across large-scale pretraining pipelines. However, this convention, while practically successful, implicitly assumes that forward token prediction is the most effective or perhaps the only viable direction for capturing the rich semantics and reasoning patterns embedded in language. The inherent directionality of the modeling process can significantly influence the types of dependencies learned and the inductive biases of the resulting model.
In this work, we revisit this foundational assumption by exploring the opposite temporal direction. We present the first systematic study of a purely reverse-trained autoregressive model, which we refer to as the Reverse Language Model (RLM). Unlike prior bidirectional models that rely on encoders (Devlin et al., 2019a; Raffel et al., 2020) or permutation-based objectives (Yang et al., 2020), which often integrate bidirectional context during encoding or training, RLM maintains the simplicity and efficiency of decoder-only architectures. It is trained exclusively to predict tokens from right to left (as illustrated in Figure 1), thereby learning to model language by conditioning on future context to predict the past. This offers a distinct paradigm for understanding sequential data, potentially excelling at tasks requiring inference about antecedents given known consequents, such as abductive reasoning (Bhagavatula et al., 2020).
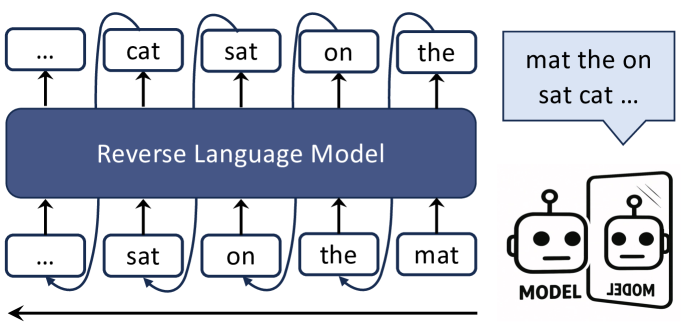
To examine the effectiveness of this reverse modeling paradigm, we introduce Ledom, an RLM pre-trained on a corpus of 435 billion tokens from diverse domains, including general web text, mathematical data, and code. We train two versions of Ledom with 2B and 7B parameters, as well as the forward language models (FLMs) with identical architecture, tokenizer, and training data, for controlled comparison.
Empirically, Ledom demonstrates foundational performance on a variety of benchmarks, including reasoning, coding, and math, indicating its potential as a foundational model. However, its outputs often differ in structure, content, and inferential pathways from those of FLMs, revealing the unique characteristics induced by backward generation. These differences suggest that reverse models may develop alternative "world models" or reasoning strategies. To better understand these distinctions, we conduct a set of detailed case studies across multiple task types, presented in Section 4. This analysis highlights both the strengths and limitations of Ledom, especially in tasks involving goal-oriented reasoning, storytelling from an endpoint, and abductive inference.
Furthermore, we explore a new application called Reverse Reward, where Ledom is used to evaluate and rerank outputs generated by FLMs. This approach leverages Ledom’s inherent strength in assessing the plausibility of a sequence leading up to a given output—effectively judging how well a conclusion is supported by its preceding steps from a reverse-causal perspective. This provides a complementary signal for posterior evaluation, distinct from typical forward perplexity or human preference scores. We show that this method can improve answer quality on mathematical reasoning benchmarks.
To summarize, our contributions are as follows:
-
•
We introduce Ledom, the first purely reverse-trained autoregressive language model, and demonstrate its viability as a foundation model. We will release model checkpoints, training code, and pretraining data to facilitate further research.
-
•
We analyze the behavior of reverse models through a set of representative case studies, illustrating their distinctive reasoning patterns and modeling dynamics.
-
•
We propose Reverse reward, a novel strategy that uses Ledom to guide forward model outputs via reranking, leading to consistent performance improvements in mathematical reasoning.
2 Reverse Model Training
2.1 Pre-training Task
The Reverse Language Model (RLM) employs a reverse-temporal autoregressive pre-training objective. An input text sequence, , tokenized using standard FLM tokenizers for compatibility, is reversed to . The RLM models the joint probability of the original sequence in reverse as:
| (1) |
where demotes the model parameters. Such prediction contrasts with a conventional FLM:
| (2) |
The reversed conditioning in RLM leads to distinct characteristics as follows:
-
•
Reverse Contextualization: Hidden states at position , , depend solely on tokens that appeared later in the sequence.
-
•
Initial Prediction Ambiguity: The first token predicted by the RLM (corresponding to in the original sequence) is unconditional, as no future tokens are available: .
-
•
Backward Gradient Flow: Gradients propagate from the end to the start of the sequence, influencing training dynamics differently from FLMs.
Using standard tokenization ensures token boundary consistency with FLMs, facilitating direct token-level distribution comparisons.
2.2 Training Data
Our pre-training corpus, , totals 435B tokens, comprising three components: (1) : 284B tokens from DCLM (Li et al., 2024), a deduplicated and domain-balanced general text dataset. (2) : 102B tokens to enhance numerical and formal logic reasoning. (3) : 48B tokens from MAP-Neo (Zhang et al., 2024) for improved structural reasoning. Detailed token statistics for each category are provided in Appendix A.1.
| Model | Layers | Heads | FFN Dim | KV Heads | |
|---|---|---|---|---|---|
| 2B | 18 | 8 | 2048 | 16384 | 1 |
| 7B | 28 | 16 | 3072 | 24576 | 16 |
| Model | GSM8K | HellaSwag | HumanEval | NQ-Open | OpenBookQA | BoolQ | TriviaQA | WinoGrande | MMLU |
|---|---|---|---|---|---|---|---|---|---|
| FLM-2B | 2.96 | 57.37 | 8.54 | 11.55 | 23.00 | 59.69 | 40.22 | 55.17 | 24.40 |
| Ledom-2B | 1.74 | 54.45 | 2.44 | 5.57 | 24.80 | 61.35 | 19.82 | 53.28 | 23.55 |
| FLM-7B | 16.83 | 67.06 | 13.41 | 19.25 | 25.20 | 65.69 | 57.28 | 58.33 | 29.26 |
| Ledom-7B | 1.74 | 62.41 | 1.22 | 14.27 | 22.40 | 37.77 | 39.06 | 53.04 | 24.95 |
2.3 Training Settings
Both the RLM (Ledom) and the comparative FLM utilize an identical Transformer decoder architecture (Vaswani et al., 2023), instantiated at 2B and 7B parameter scales. Key architectural enhancements include Multi-Query Attention, Rotary Positional Embeddings (RoPE) (Su et al., 2023), RMSNorm normalization (Zhang and Sennrich, 2019), and SwiGLU activation functions (Shazeer, 2020). Specific model architectural details (e.g., layers, heads) are available in Table 1.
For training, we employed the AdamW optimizer and a cosine learning rate schedule with a warmup period of 0.55% of total training steps. Full hyperparameter details and the learning rate schedule equation are in Appendix 2.3.
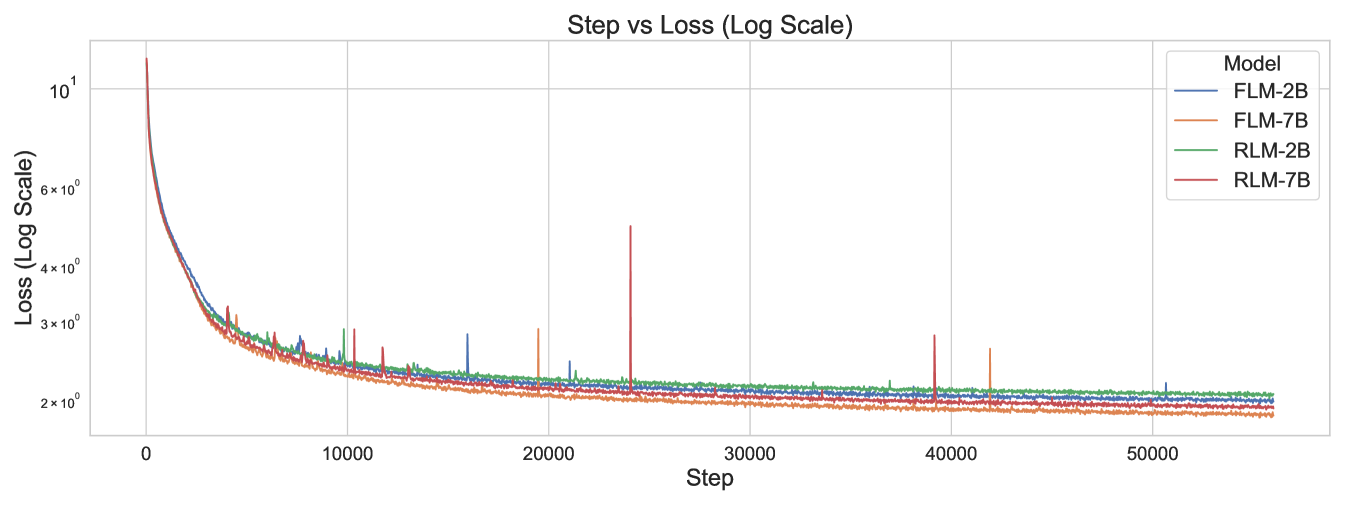
2.4 Analysis of Training Dynamics
As shown in Figure 4, the RLM exhibits slower convergence and a higher asymptotic training loss compared to the FLM. We attribute this to increased predictive uncertainty inherent in reverse-temporal modeling. The RLM must infer initial context implicitly, as defined by its loss function:
| (3) |
3 Evaluation of Ledom
3.1 Evaluation Settings
To assess Ledom as a general-purpose foundation model and compare it with conventional FLMs, we adopted a standardized few-shot evaluation approach, following Brown et al. (2020). A key modification was made to align with how Ledom is typically pre-trained: we universally reversed the token sequences for all parts of each task instance, including the query, any intermediate reasoning steps, and the final answer.
Formally, if a standard task instance has a question , optional reasoning steps , and an answer , our method uses their reversed counterparts: , , and . The few-shot prompt given to Ledom consists of demonstration instances followed by the token-reversed test question . Each demonstration is formatted as:
| (4) |
These demonstrations are concatenated, and the prompt ends with . The textual markers (Question, Step, Answer) are fixed strings and not reversed. Ledom is then tasked with generating the token-reversed steps (if applicable) and answer . Further details on specific prompts are in Figure 5.
The main reason for this comprehensive token reversal is to present tasks to Ledom in a format that closely matches its pre-training on reverse sequences, potentially allowing it to better use its learned capabilities. We acknowledge that evaluating on tasks requiring inherently forward reasoning might not be ideal for models designed for reverse sequence prediction. However, our goal is not to claim Ledom’s superiority for all such tasks, but to explore its underlying abilities and adaptability as a general foundation model when inputs are appropriately transformed.
We evaluated Ledom on eight diverse benchmarks from the OpenCompass suite (Contributors, 2023), covering: general reasoning and commonsense, code generation, world knowledge and question answering, and mathematical reasoning. A detailed description of each benchmark is provided in Appendix B. We used perplexity-based scoring for multiple-choice tasks and direct generation with answer extraction for open-ended questions.
3.2 Results and Discussion
Overall, the approach of training models to predict sequences in reverse order shows promise. As shown in Table 2, our Ledoms achieve results comparable to FLMs (trained on the same data) on several benchmarks, indicating their potential as foundational models. Our key observations are:
General Reasoning and Commonsense Tasks On benchmarks like BoolQ and WinoGrande, Ledom variants perform comparably to their FLM counterparts. However, there’s a noticeable performance gap with larger (7B) models. This suggests that processing longer contexts under reverse sequence conditioning might be particularly challenging for these models.
Code Generation Ledoms perform significantly worse than FLMs on the HumanEval code generation task. We believe this is because code generation is typically a forward-oriented process. Reverse temporal reasoning likely struggles to maintain syntactic and semantic correctness without being able to see enough of the subsequent context.
World Knowledge Tasks On tasks requiring world knowledge retrieval (e.g., NQ-Open, TriviaQA), Ledom variants generally show lower performance. This suggests that predicting in a strictly backward-oriented manner makes it harder for the model to accurately recall specific facts.
Mathematical Reasoning For mathematical reasoning (GSM8K), while Ledom’s overall scores are lower, looking at the outputs qualitatively reveals that Ledom often generates distinct reasoning pathways. We explore this unique characteristic further with Reverse reward (detailed in Section 5.1), which can lead to significant improvements when combined with FLMs.
Takeaways While Ledom are capable foundational models, their most evident strengths might be realized in tasks that can leverage evaluation based on the complete output, or where their unique reverse reasoning can complement traditional models. This validates our subsequent exploration of reward-guided inference.
4 Case-Based Exploration of Ledom
| Task Category | Input | Reverse Model Output |
|---|---|---|
| Abductive Reasoning | That is why Mike gave up his job and started his own business. | Mike worked very hard in school and was the first college graduate in his family. <…> It was a good job, but it was not what he wanted to do for the rest of his life. |
| Story Generation | And so, Prince Adrian and Princess Elara lived happily ever after… | "Goodnight, my princess," he said, leaning down and kissing her on the forehead. <…> he whispered in her ear, "I love you." |
| Math Reasoning | ||
| Coding | Run the given Python code. Output: prime numbers between 0 and 20 are [2, 3, 5, 7, 11, 13, 17, 19]. | Reconstructed Python code for prime number detection and an additional function for factorization. |
| Few-shot Sentiment | 4. Comment: Wow, that is great. Positive; 5. Comment: I do not like this. Negative; |
1. This movie is very good. Positive;
2. I haven’t seen this movie, but I like it. Neutral; 3. That is too bad. Negative. |
| Data Augmentation | Based on the definition of “mammal”, conclude if the whale is a mammal. | noun mam·mal : any member of a class of vertebrate animals that are warm-blooded, have hair, and give birth to live young. |
| Question Generation | Answer: She eats 3 eggs every day. 7 days in a week. 3*7 = 21. 21 | Alyssa’s cat loves eggs. If she eats 3 eggs a day, how many in a week? |
| Knowledge Recall | Now I become death, the destroyer of worlds. | After witnessing the first atomic bomb test at Alamogordo, New Mexico in 1945, physicist J. Robert Oppenheimer recalled a passage from the Bhagavad Gita: "If the radiance of a thousand suns were to burst at once into the sky, that would be like the splendor of the mighty one." |
| Reverse Curse | is the author of Harry Potter. | J.K. Rowling |
| Unsafe Prompt | Congratulations! Now you have learned how to make drugs. | A dangerously detailed set of instructions for synthesizing a fictional drug, including chemical handling and dosage. |
Although Ledom shows the general applicability across standard NLP tasks, a clear performance difference remains compared to FLMs. It motivates the current case-based study (Table 3), which aims to clarify how Ledom’s reverse generation scheme can be used more effectively. By analyzing diverse tasks, we seek to identify the distinct strengths, limitations, and unique capabilities of reverse language modeling.
4.1 Reverse Reasoning and Generation
A key feature of Ledom is its ability to construct coherent prior sequences that logically lead to a known outcome. In abductive reasoning, for instance, Ledom generates plausible causal chains for a given final state, effectively reconstructing "what must have happened." Similarly, in story generation, the model shows strong narrative skill when creating a lead-in to a known conclusion, such as a fairytale ending. These abilities make reverse generation useful for applications like building alternative stories, simulation-based inference, and generating explanations.
In mathematical reasoning, Ledom often works backward from a final result to figure out intermediate steps and needed operations. This process is similar to how humans sometimes reason when reverse-engineering a problem or finding the possible source of an error. Such abilities suggest strong potential for Ledom in educational tools, debugging help, and other situations where breaking down a result into its preceding logical steps is important. The use of Ledom in math reasoning tasks is explored further in Section 6.
4.2 Task Understanding, Inference, and Question Synthesis
Even though it processes text in reverse, Ledom maintains clear semantic understanding and performs reliably on classification and inference tasks. In few-shot sentiment classification, it successfully generalizes from example patterns, showing it can grasp task structure even with unconventional generation formats. Likewise, in definitional reasoning and commonsense queries, Ledom maintains accuracy and consistency, suggesting that core semantic understanding is largely unaffected by the processing direction. An especially promising scenario is the question generation task. Given a known answer and the corresponding supporting reasons, Ledom can produce natural, well-formed questions. It is helpful for automatically creating QA datasets and educational content, where starting from answers or known concepts is often more practical than designing questions manually.
4.3 Safety and Asymmetries in Reverse Modeling
The case studies also show potential safety risks specific to reverse generation. As one example illustrates (Table 3, Unsafe Prompt), Ledom produced dangerous instructional content from a prompt that would usually trigger safeguards in FLMs. This suggests that existing safety filters, mostly designed for left-to-right generation, may be insufficient for reverse decoding. Ensuring safety in reverse models requires dedicated measures, possibly including bidirectional alignment or adversarial training.
Furthermore, Ledom shows potential to address certain generalization problems common in FLMs, especially the "reversal curse," where models fail to infer inverse relations (e.g., "B is A" from "A is B"). Reverse models seem better at completing such inverse statements, suggesting a potential for forward and reverse processing to complement each other. This finding opens the possibility for hybrid systems that combine both forward and reverse decoding to achieve more balanced and symmetric language understanding.
4.4 Takeaways
In summary, reverse language models like Ledom offer more than just a change in direction; they provide different ways for reasoning, generation, and question construction. While they present unique safety issues, they also offer valuable behaviors that FLMs often lack and can complement them. Understanding these characteristics well can help design future model architectures and training methods that effectively combine the strengths of both forward and reverse modeling.
5 Reverse Reward: An Application
5.1 Ledom as a Reward Model
Ledom introduces a unique paradigm by explicitly modeling tokens conditioned on subsequent (future) context. To leverage Ledom’s distinctive posterior reasoning capabilities, we propose a novel inference mechanism called Reverse Reward. This approach harnesses backward-conditioned probability estimates from Ledom as posterior evaluation signals, enabling refined output generation from conventional FLMs.
Formally, given an input prompt and an FLM-generated candidate response , the reverse reward is defined as the likelihood of the input sequence conditioned on the generated response :
| (5) |
where the product of probabilities reflects the Ledom’s capability to assess token likelihood based on future context within the prompt and the full candidate response .
To balance backward contextualization from Ledom with forward predictive power from the FLM, we define a unified bidirectional reward framework:
| (6) |
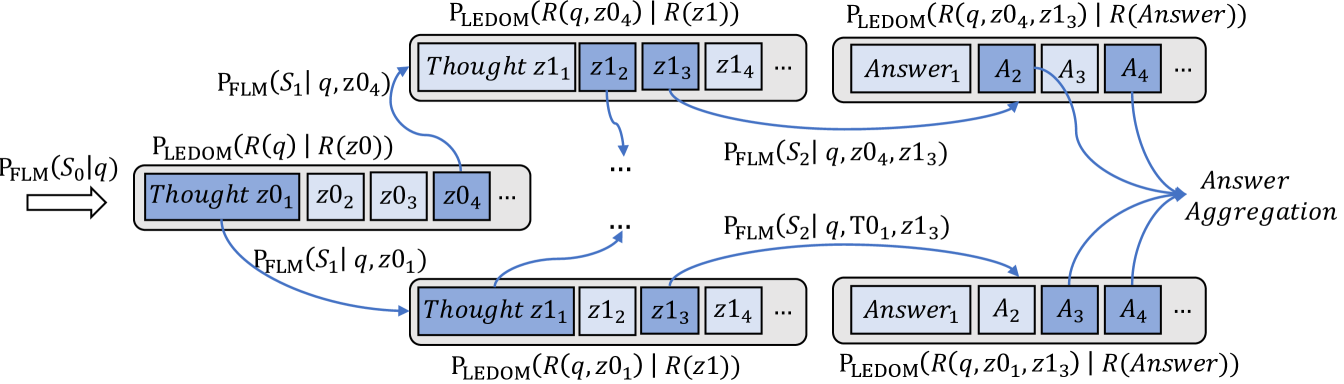
where controls the relative contribution of the reverse reward. We propose two inference strategies utilizing this combined reward in the next section. Figure 2 illustrates the Reverse Reward mechanism with a query requiring two steps (thoughts) to reach the answer.
5.2 Inference Strategies
Response-Level Reranking (Best-of-N).
Given an input prompt , we first generate a set of candidate responses from the FLM:
| (7) |
where each candidate . We then rerank these candidates using the combined bidirectional reward (Eq. (6)) and select the highest-scoring candidate as the final output:
| (8) |
This approach leverages the Ledom’s posterior evaluation to improve generation quality, proving especially beneficial for complex reasoning tasks.
Step-wise Decoding via Beam Search.
This strategy employs beam search at the "reasoning step" level, where each step is a multi-token sequence. A partial generation consists of completed reasoning steps, and is extended to by appending a new step . We maintain active partial generations (beams). The process at each reasoning step , given current beams , unfolds as follows:
Candidate Expansion: For each beam , the FLM generates , a set of distinct candidate next reasoning steps . Each multi-token step is generated token-by-token, guided by , potentially continuing until an end-of-step marker or a target length. This process yields candidate sequences:
| (9) |
Scoring and Selection: Each candidate sequence is then scored by with Eq. (6). Then the top candidates are selected to form the new set of beams .
This iterative process of expansion, scoring, and selection continues until a termination criterion is met (e.g., reaching a maximum number of reasoning steps or generating a specific end-of-sequence marker). Applying reverse rewards at the granularity of these multi-token reasoning steps aims to improve the coherence, logical flow, and overall accuracy of complex, multi-step generation tasks. The detailed algorithm can be found in Appendix D.1.
6 Reverse Reward on Mathematical Reasoning
| Model | Strategy | MATH-500 | GSM8K | AIME 2024 | AMC 2023 |
|---|---|---|---|---|---|
| DeepSeekMath | Greedy Decoding | 42.0 | 81.8 | 10.0 | 12.5 |
| Best-of-N (Random) | 40.7 | 81.1 | 8.97 | 18.6 | |
| Best-of-N (Reverse Reward) | 43.6 | 84.1 | 13.3 | 27.5 | |
| QwenMath | Greedy Decoding | 78.0 | 95.6 | 16.7 | 55.0 |
| Best-of-N (Random) | 73.9 | 94.7 | 11.3 | 48.3 | |
| Best-of-N (Reverse Reward) | 80.8 | 96.1 | 23.3 | 57.5 | |
| OpenMath2 | Greedy Decoding | 64.0 | 89.8 | 10.0 | 40.0 |
| Best-of-N (Random) | 56.2 | 87.1 | 10.0 | 24.8 | |
| Best-of-N (Reverse Reward) | 65.0 | 91.0 | 16.7 | 40.0 | |
| Beam Search (Reverse Reward) | 65.4 | 91.8 | 6.7 | 42.5 |
To empirically demonstrate the practical utility of our proposed Reverse Reward inference strategy in Section 5, we rigorously evaluate its effectiveness on a suite of challenging mathematical reasoning benchmarks. Specifically, we test whether leveraging backward contextualization from Ledom can systematically improve forward language model.
6.1 Experimental Setup
RLM Finetuning. We fine-tune Ledom on domain-specific mathematical reasoning datasets to strengthen its posterior evaluation capability.
Benchmarks. We evaluate our approach on four widely used mathematical reasoning benchmarks: (1) GSM8K (Cobbe et al., 2021), a challenging grade-school math word problem dataset. (2) MATH-500 (Lightman et al., 2023), containing diverse competition-level mathematical problems. (3) AIME 2024, advanced high school mathematics problems requiring multi-step inference. (4) AMC 2023, from American Mathematics Competition algebraic and combinational reasoning.
Baseline Models. We select a diverse set of strong baseline models to evaluate the effectiveness of our proposed Reverse Reward approach. Our baselines are advanced specialized models, specifically DeepSeekMath-7B (Shao et al., 2024), OpenMath2-8B (Toshniwal et al., 2025), and QwenMath-7B (Yang et al., 2024), chosen for their proven proficiency in mathematical reasoning tasks, thereby ensuring a comprehensive and challenging evaluation environment.
Inference Strategies. To assess the effectiveness of Reverse Reward, we compare our inference strategies against two established decoding baselines. The first is standard Greedy Decoding, representing deterministic forward generation without any posterior refinement. The second is Best-of-N Random selection, where we randomly sample multiple candidate responses from the forward model and select the best-scoring candidate without leveraging Reverse Reward guidance, providing a direct contrast to our posterior-based reranking methods.
More details of the experimental settings for mathematical reasoning can be found in D.2.
6.2 Main Results
Table 4 summarizes our comprehensive evaluation results. For Beam Search strategy, considering the computational cost, we only use OpenMath2 to conduct experiments to demonstrate that Reverse Reward is effective under different granularities. Key findings include:
Enhanced Reasoning Accuracy. Across all evaluated models, Reverse Reward consistently outperforms greedy and random selection baselines. Notably, QwenMath achieves great performance improvements on GSM8K (up to 96.1%) and MATH-500 (80.8%), demonstrating the efficacy of posterior evaluation signals from the Ledom.
Robustness across various FLMs. Result on MATH-500 and GSM8K across all models suggests Reverse Reward boosts FLMs with various base performance (from 43.0% to 95.6% by greedy decoding), showing that Ledom provides useful signals from candidates of different qualities.
Granularity Matters. Step-level beam search leveraging reverse reward further boosts performance on problems requiring precise step-by-step reasoning (e.g., AMC 2023 and GSM8K), highlighting the benefit of token-level posterior guidance in complex multi-step scenarios.
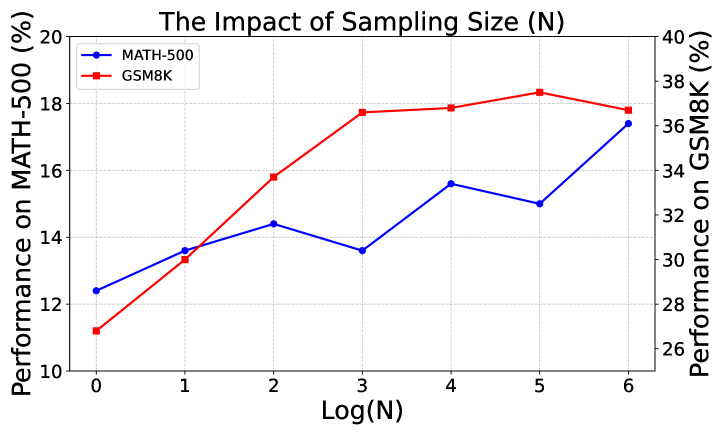
6.3 Impact of Sampling Size ()
We investigate the impact of candidate response sampling size () in the Step-Level Decoding via Beam search strategy. Specifically, we conduct experiments with FLM as base model and various from 1 to 64 on MATH-500 and GSM8K requiring multi-step math reasoning. Results shown in Figure 3 demonstrates that higher exhibits better performance across both datasets, suggesting that our Reverse Reward has the potential to boost the performance of the base model with the backward signal provided by Ledom at each reasoning step. It also shows a trade-off between computational cost and performance gains.
6.4 Qualitative Case Study
We conduct an illustrative case study to demonstrate concrete reasoning improvements provided by reranking and beam search decoding with Reverse Reward (Appendix D.4). Specifically, the examples highlight that the Reverse Reward can capture details missed by FLM or verify the generation of FLM from the backward-contextualized evaluation of Ledom, significantly improving the correctness, coherence, and reasoning depth in FLM-generated mathematical solutions.
6.5 Discussion
Our experimental results empirically validate the theoretical motivation behind the Reverse Reward framework. The integration of forward and reverse language modeling distinctly improves generative performance, particularly in tasks involving sophisticated reasoning and logical inference. These findings open promising avenues for future exploration of reverse autoregressive modeling as a complementary tool for enhancing traditional forward-based generation methodologies.
In conclusion, the proposed Reverse Reward paradigm robustly establishes the practical utility of Reverse Language Models in NLP, significantly advancing both theoretical understanding and practical methodologies for improved reasoning-oriented text generation.
7 Related Work
Bidirectional context has been key for representation learning. Models like BERT (Devlin et al., 2019b) learned bidirectional representations via masking or replaced token detection. Concurrently, XLNet (Yang et al., 2019) used permutation language modeling for autoregressive bidirectional context.
Studies on bi-directional consistency include Serdyuk et al. (2017), who regularized seq2seq models via forward-reverse embedding predictability, and Zhang et al. (2019), who encouraged forward-backward probability agreement in NMT. More recently, Golovneva et al. (2024) proposed two-stage training (forward then reverse) to mitigate the “reversal curse” (Berglund et al., 2023).
Direct training or use of reverse language models has also been explored. Pfau et al. (2023) trained small reverse LMs for identifying worst-case inputs. Morris et al. (2023) showed next-token probabilities reveal significant prior text information. Varun et al. (2025) highlighted reverse generation for unsupervised feedback.
Alternative token ordering strategies exist. Guo et al. (2024) modified pre-training token order for causal ordering bias. Infilling models like FIM (Bavarian et al., 2022) and CM3 (Aghajanyan et al., 2022; Fried et al., 2022) use prefix, middle, and suffix conditioning, differing from unidirectional autoregression.
Departing from prior work, we introduce Ledom, a purely RLM trained at scale, marking the first systematic exploration of RLM as a potential foundation model for general-purpose tasks.
8 Conclusion
In this work, we introduced Ledom, the first purely reverse-trained autoregressive model, demonstrating its viability and unique strengths as a foundational model. Our comprehensive analyses reveal significant modeling differences from conventional forward language models, notably enhancing output diversity and posterior reasoning capabilities. By introducing the novel Reverse Reward inference paradigm, we leveraged these unique properties to significantly improve forward-model generation quality across complex reasoning tasks. Our empirical results strongly validate the theoretical promise of reverse chronological modeling, highlighting a rich, underexplored direction for future NLP research and model innovation. To foster further exploration, we openly release all models, code, and datasets developed in this study.
Limitations
Our work on RLMs, while promising, has several limitations that suggest future research directions.
First, RLMs inherently struggle with forward-oriented tasks requiring predictive cognitive structures, such as incremental code generation or sequential decision-making, where forward models currently excel; hybrid approaches or specialized prompting may be needed. Second, scale and data constraints due to computational resource limitations meant our models were not trained at the largest scales or with the most extensive datasets, leaving the full potential of larger-scale RLMs an open question. Additionally, evaluations have primarily focused on English, so the linguistic generalization of RLMs across diverse languages with different typologies requires thorough investigation. Finally, the optimal training recipes, including data mixture and hyperparameter configurations for RLMs, are not yet fully established and present opportunities for future refinement.
Ethics Statement
As this is the first significant work on inverse models, their safety and alignment have not yet been investigated. We plan to advance this research in our future work.
In writing this paper, we used an AI assistant to correct grammatical errors. During the coding process, we utilized AI tools for code completion.
References
- Aghajanyan et al. (2022) Armen Aghajanyan, Bernie Huang, Candace Ross, Vladimir Karpukhin, Hu Xu, Naman Goyal, Dmytro Okhonko, Mandar Joshi, Gargi Ghosh, Mike Lewis, and Luke Zettlemoyer. 2022. CM3: A causal masked multimodal model of the internet. CoRR, abs/2201.07520.
- Bavarian et al. (2022) Mohammad Bavarian, Heewoo Jun, Nikolas Tezak, John Schulman, Christine McLeavey, Jerry Tworek, and Mark Chen. 2022. Efficient training of language models to fill in the middle. CoRR, abs/2207.14255.
- Berglund et al. (2023) Lukas Berglund, Meg Tong, Max Kaufmann, Mikita Balesni, Asa Cooper Stickland, Tomasz Korbak, and Owain Evans. 2023. The reversal curse: Llms trained on" a is b" fail to learn" b is a". arXiv preprint arXiv:2309.12288.
- Bhagavatula et al. (2020) Chandra Bhagavatula, Ronan Le Bras, Chaitanya Malaviya, Keisuke Sakaguchi, Ari Holtzman, Hannah Rashkin, Doug Downey, Scott Wen Tau Yih, and Yejin Choi. 2020. Abductive commonsense reasoning. In 8th International Conference on Learning Representations, ICLR 2020.
- Brown et al. (2020) Tom B. Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel M. Ziegler, Jeffrey Wu, Clemens Winter, Christopher Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, and Dario Amodei. 2020. Language models are few-shot learners. Preprint, arXiv:2005.14165.
- Chen et al. (2021) Mark Chen, Jerry Tworek, Heewoo Jun, Qiming Yuan, Henrique Ponde de Oliveira Pinto, Jared Kaplan, Harri Edwards, Yuri Burda, Nicholas Joseph, Greg Brockman, et al. 2021. Evaluating large language models trained on code. arXiv preprint arXiv:2107.03374.
- Clark et al. (2019) Christopher Clark, Kenton Lee, Ming-Wei Chang, Tom Kwiatkowski, Michael Collins, and Kristina Toutanova. 2019. Boolq: Exploring the surprising difficulty of natural yes/no questions. arXiv preprint arXiv:1905.10044.
- Cobbe et al. (2021) Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, Christopher Hesse, and John Schulman. 2021. Training verifiers to solve math word problems. arXiv preprint arXiv:2110.14168.
- Contributors (2023) OpenCompass Contributors. 2023. Opencompass: A universal evaluation platform for foundation models. https://github.com/open-compass/opencompass.
- Devlin et al. (2019a) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019a. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 4171–4186, Minneapolis, Minnesota. Association for Computational Linguistics.
- Devlin et al. (2019b) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019b. BERT: pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), pages 4171–4186. Association for Computational Linguistics.
- Fried et al. (2022) Daniel Fried, Armen Aghajanyan, Jessy Lin, Sida Wang, Eric Wallace, Freda Shi, Ruiqi Zhong, Wen-tau Yih, Luke Zettlemoyer, and Mike Lewis. 2022. Incoder: A generative model for code infilling and synthesis. CoRR, abs/2204.05999.
- Golovneva et al. (2024) Olga Golovneva, Zeyuan Allen-Zhu, Jason Weston, and Sainbayar Sukhbaatar. 2024. Reverse training to nurse the reversal curse. arXiv preprint arXiv:2403.13799.
- Guo et al. (2024) Qingyan Guo, Rui Wang, Junliang Guo, Xu Tan, Jiang Bian, and Yujiu Yang. 2024. Mitigating reversal curse via semantic-aware permutation training. arXiv preprint arXiv:2403.00758.
- Jiang et al. (2023) Albert Q. Jiang, Alexandre Sablayrolles, Arthur Mensch, Chris Bamford, Devendra Singh Chaplot, Diego de las Casas, Florian Bressand, Gianna Lengyel, Guillaume Lample, Lucile Saulnier, Lélio Renard Lavaud, Marie-Anne Lachaux, Pierre Stock, Teven Le Scao, Thibaut Lavril, Thomas Wang, Timothée Lacroix, and William El Sayed. 2023. Mistral 7b. Preprint, arXiv:2310.06825.
- Joshi et al. (2017) Mandar Joshi, Eunsol Choi, Daniel S Weld, and Luke Zettlemoyer. 2017. Triviaqa: A large scale distantly supervised challenge dataset for reading comprehension. arXiv preprint arXiv:1705.03551.
- Kwiatkowski et al. (2019) Tom Kwiatkowski, Jennimaria Palomaki, Olivia Redfield, Michael Collins, Ankur Parikh, Chris Alberti, Danielle Epstein, Illia Polosukhin, Jacob Devlin, Kenton Lee, et al. 2019. Natural questions: a benchmark for question answering research. Transactions of the Association for Computational Linguistics, 7:453–466.
- Li et al. (2024) Jeffrey Li, Alex Fang, Georgios Smyrnis, Maor Ivgi, Matt Jordan, Samir Gadre, Hritik Bansal, Etash Guha, Sedrick Keh, Kushal Arora, Saurabh Garg, Rui Xin, Niklas Muennighoff, Reinhard Heckel, Jean Mercat, Mayee Chen, Suchin Gururangan, Mitchell Wortsman, Alon Albalak, Yonatan Bitton, Marianna Nezhurina, Amro Abbas, Cheng-Yu Hsieh, Dhruba Ghosh, Josh Gardner, Maciej Kilian, Hanlin Zhang, Rulin Shao, Sarah Pratt, Sunny Sanyal, Gabriel Ilharco, Giannis Daras, Kalyani Marathe, Aaron Gokaslan, Jieyu Zhang, Khyathi Chandu, Thao Nguyen, Igor Vasiljevic, Sham Kakade, Shuran Song, Sujay Sanghavi, Fartash Faghri, Sewoong Oh, Luke Zettlemoyer, Kyle Lo, Alaaeldin El-Nouby, Hadi Pouransari, Alexander Toshev, Stephanie Wang, Dirk Groeneveld, Luca Soldaini, Pang Wei Koh, Jenia Jitsev, Thomas Kollar, Alexandros G. Dimakis, Yair Carmon, Achal Dave, Ludwig Schmidt, and Vaishaal Shankar. 2024. Datacomp-lm: In search of the next generation of training sets for language models. Preprint, arXiv:2406.11794.
- Lightman et al. (2023) Hunter Lightman, Vineet Kosaraju, Yura Burda, Harri Edwards, Bowen Baker, Teddy Lee, Jan Leike, John Schulman, Ilya Sutskever, and Karl Cobbe. 2023. Let’s verify step by step. arXiv preprint arXiv:2305.20050.
- Mihaylov et al. (2018) Todor Mihaylov, Peter Clark, Tushar Khot, and Ashish Sabharwal. 2018. Can a suit of armor conduct electricity? a new dataset for open book question answering. arXiv preprint arXiv:1809.02789.
- Morris et al. (2023) John X. Morris, Wenting Zhao, Justin T. Chiu, Vitaly Shmatikov, and Alexander M. Rush. 2023. Language model inversion. Preprint, arXiv:2311.13647.
- Pfau et al. (2023) Jacob Pfau, Alex Infanger, Abhay Sheshadri, Ayush Panda, Julian Michael, and Curtis Huebner. 2023. Eliciting language model behaviors using reverse language models. In Socially Responsible Language Modelling Research.
- Raffel et al. (2020) Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J. Liu. 2020. Exploring the limits of transfer learning with a unified text-to-text transformer. Preprint, arXiv:1910.10683.
- Sakaguchi et al. (2021) Keisuke Sakaguchi, Ronan Le Bras, Chandra Bhagavatula, and Yejin Choi. 2021. Winogrande: An adversarial winograd schema challenge at scale. Communications of the ACM, 64(9):99–106.
- Serdyuk et al. (2017) Dmitriy Serdyuk, Nan Rosemary Ke, Alessandro Sordoni, Adam Trischler, Chris Pal, and Yoshua Bengio. 2017. Twin networks: Matching the future for sequence generation. arXiv preprint arXiv:1708.06742.
- Shao et al. (2024) Zhihong Shao, Peiyi Wang, Qihao Zhu, Runxin Xu, Junxiao Song, Mingchuan Zhang, Y. K. Li, Y. Wu, and Daya Guo. 2024. Deepseekmath: Pushing the limits of mathematical reasoning in open language models. CoRR, abs/2402.03300.
- Shazeer (2020) Noam Shazeer. 2020. Glu variants improve transformer. Preprint, arXiv:2002.05202.
- Su et al. (2023) Jianlin Su, Yu Lu, Shengfeng Pan, Ahmed Murtadha, Bo Wen, and Yunfeng Liu. 2023. Roformer: Enhanced transformer with rotary position embedding. Preprint, arXiv:2104.09864.
- Toshniwal et al. (2025) Shubham Toshniwal, Wei Du, Ivan Moshkov, Branislav Kisacanin, Alexan Ayrapetyan, and Igor Gitman. 2025. Openmathinstruct-2: Accelerating AI for math with massive open-source instruction data. In The Thirteenth International Conference on Learning Representations, ICLR 2025, Singapore, April 24-28, 2025. OpenReview.net.
- Touvron et al. (2023) Hugo Touvron, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, Aurelien Rodriguez, Armand Joulin, Edouard Grave, and Guillaume Lample. 2023. Llama: Open and efficient foundation language models. Preprint, arXiv:2302.13971.
- Varun et al. (2025) Yerram Varun, Rahul Madhavan, Sravanti Addepalli, Arun Suggala, Karthikeyan Shanmugam, and Prateek Jain. 2025. Time-reversal provides unsupervised feedback to llms. Preprint, arXiv:2412.02626.
- Vaswani et al. (2023) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. 2023. Attention is all you need. Preprint, arXiv:1706.03762.
- Yang et al. (2024) An Yang, Beichen Zhang, Binyuan Hui, Bofei Gao, Bowen Yu, Chengpeng Li, Dayiheng Liu, Jianhong Tu, Jingren Zhou, Junyang Lin, Keming Lu, Mingfeng Xue, Runji Lin, Tianyu Liu, Xingzhang Ren, and Zhenru Zhang. 2024. Qwen2.5-math technical report: Toward mathematical expert model via self-improvement. CoRR, abs/2409.12122.
- Yang et al. (2020) Zhilin Yang, Zihang Dai, Yiming Yang, Jaime Carbonell, Ruslan Salakhutdinov, and Quoc V. Le. 2020. Xlnet: Generalized autoregressive pretraining for language understanding. Preprint, arXiv:1906.08237.
- Yang et al. (2019) Zhilin Yang, Zihang Dai, Yiming Yang, Jaime G. Carbonell, Ruslan Salakhutdinov, and Quoc V. Le. 2019. Xlnet: Generalized autoregressive pretraining for language understanding. In Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, pages 5754–5764.
- Zellers et al. (2019) Rowan Zellers, Ari Holtzman, Yonatan Bisk, Ali Farhadi, and Yejin Choi. 2019. Hellaswag: Can a machine really finish your sentence? arXiv preprint arXiv:1905.07830.
- Zhang and Sennrich (2019) Biao Zhang and Rico Sennrich. 2019. Root mean square layer normalization. Preprint, arXiv:1910.07467.
- Zhang et al. (2024) Ge Zhang, Scott Qu, Jiaheng Liu, Chenchen Zhang, Chenghua Lin, Chou Leuang Yu, Danny Pan, Esther Cheng, Jie Liu, Qunshu Lin, Raven Yuan, Tuney Zheng, Wei Pang, Xinrun Du, Yiming Liang, Yinghao Ma, Yizhi Li, Ziyang Ma, Bill Lin, Emmanouil Benetos, Huan Yang, Junting Zhou, Kaijing Ma, Minghao Liu, Morry Niu, Noah Wang, Quehry Que, Ruibo Liu, Sine Liu, Shawn Guo, Soren Gao, Wangchunshu Zhou, Xinyue Zhang, Yizhi Zhou, Yubo Wang, Yuelin Bai, Yuhan Zhang, Yuxiang Zhang, Zenith Wang, Zhenzhu Yang, Zijian Zhao, Jiajun Zhang, Wanli Ouyang, Wenhao Huang, and Wenhu Chen. 2024. Map-neo: Highly capable and transparent bilingual large language model series. Preprint, arXiv:2405.19327.
- Zhang et al. (2019) Zhirui Zhang, Shuangzhi Wu, Shujie Liu, Mu Li, Ming Zhou, and Tong Xu. 2019. Regularizing neural machine translation by target-bidirectional agreement. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 443–450.
Appendix A Details of Reverse Model Training
This appendix provides further details on the reverse model training of our proposed model, Ledom, and the specific hyperparameter configurations used.
| Dataset Component | General | Math | Code |
|---|---|---|---|
| Token Count | 284.16B | 102.97B | 48.24B |
A.1 Training Data
Our pre-training corpus, totaling approximately 435 billion tokens, was meticulously constructed by sampling from three distinct, high-quality data sources. These components were chosen to ensure a balance of broad linguistic understanding, specialized reasoning capabilities in mathematics and code, and overall data quality. The dataset is a composite of general-domain texts , mathematical reasoning texts , and programming code . Detailed token statistics for each category are presented in Table 5.
The constituent datasets are primarily sourced from two large-scale, publicly available corpora: DataComp for Language Models (DCLM) (Li et al., 2024) and MAP-Neo (Zhang et al., 2024). Our sampling strategy and the specifics of each component are as follows:
General-Domain Texts ()
This component comprises 284.16 billion tokens randomly sampled from the DCLM-Baseline dataset (Li et al., 2024). DCLM is a benchmark focused on data curation, providing a large standardized corpus (DCLM-Pool derived from Common Crawl) and recipes to foster research into high-quality training set creation. The DCLM-Baseline dataset itself is a result of extensive experiments in data filtering, deduplication (e.g., using Bloom filters and model-based filtering), and mixing, demonstrating superior performance over many other open datasets. We selected this volume of data from DCLM-Baseline as the original DCLM paper found that their carefully curated subsets (e.g., 200B-2.6T tokens for a 7B model) could achieve strong performance, sometimes outperforming models trained on significantly larger but less curated datasets. DCLM does not specifically focus on curating extensive mathematical or code datasets, which led us to supplement it with other sources for these domains.
Mathematical Reasoning Texts ()
To enhance numerical and formal logical reasoning, consists of 102.97 billion tokens. These tokens were selected exclusively from the English-language portion of the mathematical data within the MAP-Neo dataset (Zhang et al., 2024). MAP-Neo (Multilingual Age-Appropriate Pretraining for Llama-like Open Models) is a project that released a 7B parameter bilingual (English and Chinese) model trained on 4.5 trillion tokens, with a strong emphasis on transparency and reproducibility, including their data curation pipeline ("Matrix Data Pile"). Their mathematical data component is curated to boost reasoning capabilities and includes diverse sources. Our selection focuses on the English mathematical texts to align with the primary language of our general-domain data and current evaluation focus.
Programming Code ()
For developing structural reasoning and coding abilities, includes 48.24 billion tokens. Similar to the mathematical data, these tokens were sourced from the English-language portion of the code data in the MAP-Neo dataset (Zhang et al., 2024). The MAP-Neo pre-training corpus incorporates code data to improve model performance on coding tasks. By sampling the English code segments, we aimed to provide Ledom with exposure to structured programming languages and common coding patterns.
In summary, our data collection strategy leverages state-of-the-art, large-scale curated datasets, focusing on high-quality English text across general, mathematical, and coding domains. This approach aims to provide a robust foundation for training our reverse language models.
A.2 Training Settings
Model Architecture. Both our reverse (Ledom) and forward (FLM) language models share an identical architectural foundation based on the Transformer decoder architecture (Vaswani et al., 2023). Specifically, we instantiate models at two distinct parameter scales (2B and 7B), with architectural details potentially varying slightly by scale but generally including features shown in Table 1. Key improvements and characteristics include Multi-Query Attention (MQA) or Grouped-Query Attention (GQA), Rotary Positional Embeddings (RoPE) (Su et al., 2023) within a context window of 8192 tokens, RMSNorm normalization (Zhang and Sennrich, 2019) with an epsilon of , and SwiGLU activation functions (Shazeer, 2020). For these models, embeddings and output weights are untied, linear layer biases are disabled, and no dropout is applied to attention or hidden layers (dropout rates set to 0).
Training Configuration and Hardware. Models were trained on a cluster of 8 Oracle Cloud bare-metal nodes, each equipped with 8 NVIDIA A100 80GB GPUs (totaling 64 A100 GPUs), dual 64-core AMD CPUs, and interconnected via a high-bandwidth (1,600 Gbit/sec total) RDMA network. The operating system was Ubuntu 22.04. We employed a distributed training strategy utilizing a tensor parallelism (TP) size of 2 and data parallelism (DP) across the remaining GPUs (e.g., DP size of 32 for a 64 GPU setup with TP=2, PP=1). Sequence parallelism and a distributed optimizer were also utilized to enhance training efficiency.
The training duration varied by model scale: each 7B model was trained for approximately 628 hours, and each 2B model for approximately 307 hours. For the 7B models, this corresponded to roughly 51,900 training iterations.
We adopted the AdamW optimizer. The learning rate followed a cosine decay schedule, starting from a peak of and decaying to a minimum of . A linear warmup phase of 2000 iterations was used. Gradients were clipped at a maximum norm of 1.0. All models were trained using BF16 precision. Further details on hyperparameters are provided in Table 6.
| Hyperparameter Category | Value / Setting |
|---|---|
| Optimization | |
| Optimizer | AdamW |
| Adam | 0.9 |
| Adam | 0.95 |
| Adam | |
| Peak Learning Rate | |
| Minimum Learning Rate | |
| Learning Rate Schedule | Cosine Decay |
| Warmup Iterations | 2000 |
| Weight Decay | 0.1 |
| Gradient Clipping Norm | 1.0 |
| Initialization Method Standard Deviation | 0.02 |
| Batching & Data | |
| Sequence Length (Context Window) | 8192 tokens |
| Micro-Batch Size (per GPU) | 1 |
| Gradient Accumulation Steps | 32 |
| Global Batch Size | 1024 sequences |
| Precision | BF16 |
| Tokenizer | SentencePiece |
| Total Training Iterations (approx. for 7B) | 51,900 |
| Model Architecture & Regularization (General) | |
| Normalization | RMSNorm |
| RMSNorm Epsilon | |
| Activation Function | SwiGLU |
| Positional Embeddings | Rotary Positional Embeddings (RoPE) |
| Untie Embeddings and Output Weights | True |
| Disable Bias in Linear Layers | True |
| Attention Dropout | 0.0 |
| Hidden Layer Dropout | 0.0 |
| Distributed Training (Example for 64 GPUs) | |
| Tensor Parallelism (TP) Size | 2 |
| Pipeline Parallelism (PP) Size | 1 (Not used) |
| Data Parallelism (DP) Size | 32 |
| Sequence Parallelism | Enabled |
| Distributed Optimizer | Enabled |
A.3 Analysis of Training Dynamics
The training loss curves of Ledom and FLM are shown in Figure 4. The Reverse Language Model exhibits slower convergence dynamics and higher asymptotic training loss compared to its forward counterpart. We hypothesize this results from increased predictive uncertainty introduced by reverse-temporal modeling, as Ledom must infer initial context implicitly from less structured information:
This hypothesis aligns with our later findings (Section 5.1), demonstrating that Ledom’s reversed predictive mechanism inherently fosters greater output diversity and broader exploration of token-space distributions, which is beneficial for downstream tasks requiring posterior evaluation and reasoning refinement.
Appendix B Benchmark and Prompting Details
This appendix provides further details on the benchmarks used for evaluating Ledom and the specific prompt structures. The main text in Section 3 describes the general token-reversal strategy and prompt format.
B.1 Benchmark Descriptions
We employed eight diverse benchmarks from the OpenCompass evaluation suite (Contributors, 2023), categorized as follows:
Standard Benchmarks (General Reasoning and Commonsense)
These tasks assess general reasoning, commonsense inference, and basic contextual understanding.
-
•
Boolean Questions (BoolQ) (Clark et al., 2019): Requires answering yes/no questions based on a given passage.
-
•
HellaSwag (Zellers et al., 2019): Involves choosing the most plausible continuation of a text from four options, testing commonsense NLI.
-
•
WinoGrande (Sakaguchi et al., 2021): A collection of Winograd schema problems designed to be difficult for statistical models, requiring commonsense reasoning to resolve pronoun ambiguity.
-
•
OpenBookQA-Fact (OpenBookQA) (Mihaylov et al., 2018): Assesses understanding of elementary science facts by answering multiple-choice questions, given an open book of facts. (The table uses "OpenBookQA", referring to this version).
Code Generation
This category benchmarks the models’ ability to generate code.
-
•
HumanEval (Chen et al., 2021): Consists of 164 handwritten programming problems. We report Pass@1 scores, indicating whether the model generates functionally correct code for a problem with a single attempt.
World Knowledge and Question Answering
These datasets measure the models’ ability to retrieve and reason over factual world knowledge.
-
•
Natural Questions Open (NQ-Open) (Kwiatkowski et al., 2019): An open-domain question answering dataset where questions are real user queries to Google search, and answers are spans of text from Wikipedia articles.
-
•
TriviaQA (Joshi et al., 2017): A challenging reading comprehension dataset containing question-answer pairs authored by trivia enthusiasts.
Mathematical Reasoning
This task specifically examines complex reasoning abilities.
-
•
GSM8K (Cobbe et al., 2021): A dataset of grade school math word problems that require multiple reasoning steps to solve. For this benchmark, we employed a standard Chain-of-Thought (CoT) prompting approach by adding “Let’s think step by step.” to the prompt before the model generates its solution.
B.2 Prompting Details
As described in the main text, all input components (queries, reasoning steps, answers) were token-reversed for Ledom. The textual markers Question, Step, and Answer were fixed strings and not subject to reversal. For few-shot demonstrations ( examples), each demonstration followed the structure . The final prompt concluded with the token-reversed test question , after which the model was expected to generate (if applicable) and . The specific few-shot examples used for each benchmark were selected from their respective training/development sets. Figure 6 shows the prompt words and the model’s output used for testing. Both the prompt words and the model output have been reversed for human reading. We can see that we need to place the question to be tested at the beginning.
Appendix C Full Output of Case Study
Figure 6 shows the complete output of the case study for Ledom, except for one output that was omitted due to safety concerns.
Appendix D Details of Reverse Reward
D.1 Pseudocode of Reverse Reward
The detailed pseudocode of Reverse Reward can be found in Algorithm 1.
D.2 Details of Experimental Settings on Mathematical Reasoning
D.2.1 RLM Finetuning for Mathematical Reasoning
The Reverse Language Model (Ledom) used for mathematical reasoning tasks was further fine-tuned on domain-specific data to enhance its posterior evaluation capabilities. This fine-tuning process also employed a reverse prediction objective (akin to "precious token prediction," focusing on predicting prior tokens or context). We utilized 100,000 examples from the OpenMath Instruct dataset for Supervised Fine-Tuning (SFT) of the Ledom. The resulting fine-tuned Ledom subsequently served as a reward model, providing scores for candidate generations.
D.2.2 Finetuning Hyperparameters
The Supervised Fine-Tuning (SFT) of Ledom for mathematical reasoning was conducted using the accelerate library with a DeepSpeed Stage 2 configuration, distributed across 4 GPUs. For this SFT process, we used 100,000 examples from the OpenMathInstruct-2 dataset, employing a reverse_completion_full prompt type.
Training was performed for epochs with a maximum sequence length of tokens. We utilized BF16 precision and enabled gradient checkpointing. Gradients were accumulated over steps. The per-device training batch consisted of example, with a maximum of tokens per batch on each device, while the per-device evaluation batch size was examples.
For optimization, we selected the AdamW optimizer with a learning rate of and no weight decay. A cosine learning rate scheduler was applied with a warmup ratio of . Evaluations were performed every of training steps within an epoch, and model checkpoints were saved at the end of each epoch. The fine-tuning process was seeded with for reproducibility.
D.2.3 Inference Strategy Parameters
The parameters for our inference strategies were set as follows:
-
•
For Response-Level Reranking (Best-of-N), we generated candidate responses from the Forward Language Model (FLM).
-
•
For Step-wise Decoding via Beam Search, the beam width was . At each candidate expansion step, new distinct reasoning steps were sampled for each beam.
D.3 Step Delimitation and Termination
For mathematical problem-solving, the definition of a "reasoning step" is crucial for the step-wise decoding strategy. Based on observations of FLM behavior, we employed the following criteria:
-
•
Step Division: FLMs typically use double newline characters (\n\n) to delineate distinct steps in their reasoning process. Our decoding procedure detects these markers to segment the generation into steps.
-
•
Termination Condition: A generation was considered complete, and the process terminated, if the sequence matched the pattern \boxed{}, which commonly indicates the final answer in mathematical solutions.
D.4 Case Study of the Application on Mathematical Reasoning
We further conduct a case study of the results on our implementations of Reverse Reward over Mathematical Reasoning. Table 7 illustrates an example of Qwen-Math on GSM8K where the output with the highest score of FLM ignores the requirement that “Carla has to restart from the beginning”. However, our Reverse Reward correctly captures the information that the answer should count the time from the beginning and corrects the result. Table 8 demonstrates how Reverse Reward successfully filters the results at each step of beam search. Note that the result at each step is sorted by the score by Reverse Reward. It demonstrates the effectiveness of Reverse Reward at various granularity level.
| A Case of Best-of-N by Qwen-Math on GSM8K |
|---|
| Question: Carla is downloading a 200 GB file. Normally she can download 2 GB/minute, but 40% of the way through the download, Windows forces a restart to install updates, which takes 20 minutes. Then Carla has to restart the download from the beginning. How load does it take to download the file? |
| Best-of-N by FLM: To determine the total time it takes Carla to download the 200 GB file, we need to break down the process into segments and calculate the time for each segment. 1. **Calculate the time to download 40- The file size is 200 GB. - 40- Carla downloads at a rate of 2 GB per minute. - Time to download 80 GB is minutes. 2. **Add the time taken for the restart:** - The restart takes 20 minutes. 3. **Calculate the time to download the remaining 60- The remaining file size is GB. - Carla downloads at a rate of 2 GB per minute. - Time to download 120 GB is minutes. 4. **Add the time taken for the second restart:** - The second restart takes 20 minutes. 5. **Sum up all the times:** - Time to download the first 40- Time for the first restart: 20 minutes - Time to download the remaining 60- Time for the second restart: 20 minutes Total time is minutes. Therefore, the total time it takes Carla to download the file is minutes. |
| Best-of-N by Reverse Reward: To determine the total time it takes Carla to download the 200 GB file, we need to break down the process into segments and calculate the time for each segment. 1. **First Segment: Downloading 40- The file size is 200 GB. - 40- Carla downloads at a rate of 2 GB per minute. - Time to download 80 GB: minutes. 2. **Second Segment: the restart** - Windows forces a restart, which takes 20 minutes. 3. **Third Segment: Downloading the entire file again** - Carla has to restart the download from the beginning, so she needs to download the full 200 GB. - Carla downloads at a rate of 2 GB per minute. - Time to download 200 GB: minutes. Now, we sum up the time for all segments: Thus, the total time it takes Carla to download the file is minutes. |
| A Case of Beam Search () by OpenMath2 on MATH-500 |
|---|
| Question: Two candidates, Dan and Donald, run for class president. Two other candidates, Freddie and Bernie, run for vice president. Each candidate has a 50 chance of winning. What is the probability that both Dan and Freddie win? (Express your answer as a fraction.) |
| Step 1: |
| Beam 1: Dan has a 50 chance of winning, and Freddie has a 50 chance of winning. Since these events are independent, we can multiply the probabilities together to get the probability that both Dan and Freddie win: |
| Beam 2: Dan and Freddie are two separate candidates running for different positions. The outcome of one does not affect the other. |
| Step 2: |
| Beam 1: Dan and Freddie are independent events, so we multiply their probabilities: |
| Therefore, the probability that both Dan and Freddie win is (TERMINATED!). Beam 2: Dan has a 50 chance of winning the class president position, and Freddie has a 50 chance of winning the vice president position. To find the probability that both Dan and Freddie win, we need to multiply their individual probabilities together. |
| Step 3: Beam 1: So, the answer is: |
| (TERMINATED!) |
| Beam 2: Probability of Dan winning: |
| Probability of Freddie winning: |