Length and torsion dependence of thermal conductivity in twisted graphene nanoribbons
Abstract
Research on the physical properties of materials at the nanoscale is crucial for the development of breakthrough nanotechnologies. One of the key properties to consider is the ability to conduct heat, i.e., its thermal conductivity. Graphene is a remarkable nanostructure with exceptional physical properties, including one of the highest thermal conductivities (TC) ever measured. Graphene nanoribbons (GNRs) share most fundamental properties with graphene, with the added benefit of having a controllable electronic bandgap. One method to achieve such control is by twisting the GNR, which can tailor its electronic properties, as well as change their TC. Here, we revisit the dependence of the TC of twisted GNRs (TGNRs) on the number of applied turns to the GNR by calculating more precise and mathematically well defined geometric parameters related to the TGNR shape, namely, its twist and writhe. We show that the dependence of the TC on twist is not a simple function of the number of turns initially applied to a straight GNR. In fact, we show that the TC of TGNRs requires at least two parameters to be properly described. Our conclusions are supported by atomistic molecular dynamics simulations to obtain the TC of suspended TGNRs prepared under different values of initially applied turns and different sizes of their suspended part. Among possible choices of parameter pairs, we show that TC can be appropriately described by the initial number of turns and the initial twist density of the TGNRs.
I Introduction
Twist in one-dimensional materials can be either a hindrance or an advantage. It could be a problem when dealing, for example, with the installation of long cables [2], disentangling twisted headphone wires or simply washing the garden or the car with a hose [3]. However, it could be useful when extracting elastic parameters of a nanowire [4], setting up helical artificial muscles [5, 6] or developing torsional-based elastocaloric refrigerators [7]. Knowing the relation between twist and physical properties of filaments in general is important for solving problems in several areas ranging from engineering [2] to biomedicine [8] and molecular biology [9, 10, 11].
In the particular case of graphene nanoribbons (GNRs), the effects of twisting on their properties have been predicted to be useful in applications such as sensors and switches [12, 13, 14]. As the term “twisted graphene” became usual to describe the relative rotation of one graphene layer with respect to the other in bilayer graphene structures, it is important to make clear that in this work, the words “twist” or “torsion”, as well as the term “twisted GNRs” (hereafter referred as TGNRs for short) means the application of twist or torsion along the longitudinal axis of a single GNR.
Gunlycke et al. [15] showed that edge termination can induce twisting in GNRs (at least in the case of small width GNRs) and that TGNRs present different band-gap behavior when compared to flat and straight GNRs. Sadrzadeh, Hua and Yakobson [12] showed that hydrogen-terminated armchair-edge GNRs present a twist dependent band-gap. Koskinen [16] demonstrated a certain equivalence between the effects of tensile and twisting strains on the electronic structure of GNRs. Tang et al. [17], Li et al. [13] and Xu et al. [18] investigated metallic-to-semiconductor transitions in armchair- and zigzag-edge TGNRs, while several other studies also confirmed the dependence of electronic and magnetic properties of GNRs on longitudinal twist, and even suggested applications [19, 20, 21, 22, 23].
Mechanical properties of TGNRs have also been studied. Li [24] investigated the stretchability of TGNRs. Cranford and Buehler [25] presented a comprehensive mechanical study of TGNRs including their conversion to helical GNRs. Dontsova and Dumitrică [26] investigated the mechanics of twisted single and few-layer GNRs. Diniz [27] and Xia et al. [28] studied the structural stability of TGNRs while Savin, Korznikova and Dmitriev [29] showed that TGNRs have larger bending stiffness than flat ones. Further studies demonstrated that the application of large amounts of twist can lead to the formation of GNR scrolls and supercoils [30, 31], the formation of helical ribbons [32], changes in the strength of TGNRs with grain boundaries [33], and the localization of twisting as topological solitons on substrates [34].
The lattice thermal conductivity (or simply “TC” from now on) of graphene has been extensively studied so far (see, for example, Refs. [35, 36, 37, 38]). Nonetheless, very few studies have addressed the dependence of the TC of GNRs on the amount of twist [39, 40, 41, 42, 43, 44]. Most of these studies show that increasing the amount of twist decreases the TC, although one of them [43] found an inverse behavior arguing that twist increases the local tension strain, and thus the contribution of the acoustic out-of plane phonon modes to the TC of the TGNR.
There are even fewer experiments with TGNRs. Chamberlain et al. [45] used carbon nanotubes as nanoreactors to assembly and produce sulfur-terminated GNRs, including TGNRs. Cao et al. [46] obtained TGNRs or curled GNRs by thermal annealing poly-methyl methacrylate (PMMA) terminated GNRs, and Jarrahi et al. [47] studied their photoresponse. An important observation is that transmission and scanning electronic micrographs of TGNRs in those references reveal that TGNR structures are not regularly twisted GNRs as those considered in most of the previously cited modeling and simulation works. In these studies, only one parameter was considered to characterize the TGNR geometry: the initial number of turns applied to its axis. However, the TGNR properties might be dependent also on the GNR length and the curls and folds that form due to its low flexural rigidity and thermal fluctuations, as seen in the experimental micrographs. A study of the TC of TGNRs that takes into account these features is missing and can reveal a higher level of complexity, which would be required for further development of precise applications.
Two important questions arise from the above discussion: (i) how to precisely define and determine the geometric features of a TGNR at finite temperature? and (ii) how to describe the dependence of the TC of a TGNR on these geometric features, including twist and length, at finite temperatures? In the present study, we are going to answer both questions.
Recently, one of us [48] developed a method to precisely calculate the geometric features of a TGNR suspended by two substrates. It was demonstrated that the degree of twist (in a more precise mathematical sense) of a given TGNR is not solely dependent on the number of turns initially applied to it, but also on the size of its suspended portion. One reason for this is that the TGNR’s extremities lay on the substrates, becoming flat and not contributing to its total twist. As a result, the initial turns applied to the TGNR axis become more densely distributed along the suspended part. This increases the twist density of the TGNR favoring the so-called twist-to-writhe conversion (TWC) [49, 50] phenomenon (see the detailed description ahead in section II.1) which allows part of the torsional stress in a ribbon to be released by flexural deformations of the TGNR axis.
Furthermore, Fonseca [48] used these features to propose that the total twist of a TGNR can be tuned by simply changing the distance between the substrates holding its ends. He showed that the total (real) twist of a TGNR can be changed without adding or removing torsion/rotation at the ends of the TGNR. One advantage of this method is to provide a more precise way to determine the total twist of a TGNR and, then, correlate it to other physical properties. Since the literature is mostly limited to the prediction of physical properties of regularly twisted GNRs, here we explore the above geometric features of suspended TGNRs, and their dependence on the size of their suspended part, to investigate the dependence of the TGNR’s TC on the total amount of twist, the size of the suspended part and other TGNR’s geometric parameters. We show that the TC of TGNRs cannot be fully determined by a unique geometric parameter, and that it requires, at least, two parameters.
In the next sections, we present the theoretical background for calculating the total geometric twist of a piece of TGNR, and the computational methods employed for the calculation of the TC. Then, we present our results and discussions, followed by our conclusions.
II Theory and Methodology
II.1 Geometric parameters of a TGNR
The twist-to-writhe conversion (TWC) phenomenon, mentioned in the Introduction, is well known in twisted filamentary structures [49, 50]. It consists of releasing a rod’s torsional stress by spontaneous bending and folding, after the twist density reaches a critical value. This TWC has been shown to satisfy the Călugăreanu-White-Fuller linking number () theorem [50, 51, 52]:
| (1) |
where and are the total (real) amount of twist and a quantity called writhe of a curve which measures its non-planarity, respectively. The linking number, , is a geometric parameter of a pair of closed curves and although it is well defined in terms of a double integral along them, it has been shown to be an integer equal to half the number of times one curve crosses the other [53].
The total twist, , of a pair of curves and the writhe, , of one space curve, are given by the following integrals along the corresponding curves [53]:
| (2) |
| (3) |
where is the arc-length of the curve x, t is its unitary tangent vector and u is a unitary vector orthogonal to t and pointing from the curve x to its parallel curve. All these vector quantities are functions of . The total length of the curve x is simply given by .
Suppose we initially prepare two space closed curves such as to present a certain amount of . The Călugăreanu-White-Fuller theorem guarantees that is always conserved no matter how the curves change along the time, provided they remain closed. Changes to the curves mean changes to their values of and through equations (2) and (3), respectively. According to the theorem, these changes are such that remains constant as along as the curves remain closed. An interesting feature is that the theorem has also been shown to hold for a pair of non-closed curves if their extremities are flat and belong to the same plane [53]. There exists a pair of parallel open curves with that connect the first two ones at infinity [53]. A similar argument can be made for a pair of open curves having a semi-integer value of . As long as the ends of the curves lay on parallel planes, there exists a pair of twisted parallel curves with and that connect the first pair at infinity.
The two space curves required to calculate the twist and writhe of our TGRNs can be defined prior to applying the initial turns to the straight GNR. The first curve can be the GNR axis, and the second curve can be a line parallel to the first. Numerically, both curves can be defined by sets of co-linear carbon atom positions along the main length of the straight untwisted GNR. Once the curves are defined, if one fixes one end of a GNR and applies turns to the other end while keeping the GNR straight, the twist will be and the writhe . Thus, the initial linking number applied to the, now twisted, GNR is . If the ends of this TGNR are placed such that they belong to the same plane and are not allowed to rotate back to release the initially applied torsional stress, the value of will remain constant.
As shown by Fonseca [48], if the extremities of a TGNR are laid down on two different planar substrates, and their planes coincide, the theorem can be applied to the TGNR and eqs. (2) and (3) can be used to infer the values of and of the suspended part. Additionally, it is possible to investigate how and vary with several other parameters and physical conditions, such as the distance between the substrates, temperature, etc. The interesting thing is that as long as the extremities of the TGNR are kept on the substrates (and van der Waals forces guarantee that), no matter how and change with other physical conditions, will remain the same. For instance, Fonseca [48] showed that it holds true for changing the distance between substrates and the temperature of the system.
Here, we will investigate how the TC of TGNRs depends on , its length, , as well as its and taking into account that these last two quantities change with both and . We will analyze the twist and writhe of non-closed TGNRs to which an integer or semi-integer number of turns was initially applied.
II.2 Computational methods
The TC calculation for the TGNRs will be performed by non-equilibrium molecular dynamics (NEMD) simulations using the Adaptive Intermolecular Reactive Empirical Bond Order (AIREBO) potential [54, 55] as implemented in LAMMPS [56]. AIREBO is an extension of the REBO potential originally developed by Brenner et al. [54], which includes Lennard Jones and torsional potential terms [55]. After more than two decades, the AIREBO potential is still being successfully used to simulate structural [57, 58, 59, 60] and thermal properties [61, 62, 63, 64, 65, 66, 67] of carbon nanostructures, including heat transport simulations [35, 36, 37, 38, 68, 69]. One fundamental aspect of our choice is the computational time involved.
Nonetheless, we must keep in mind that AIREBO does not quantitatively reproduce absolute TC values for carbon nanostructures. In order to overcome this limitation, we will focus on how the TC of TGNRs depends on their geometric features, and not on its absolute value. Zhang and collaborators, for example, have performed a similar study using the original REBO/AIREBO to investigate TC trends in graphene with the number of isotopes [70], and in graphene oxide with the percentage of oxygen coverage [71].
The TC simulation protocol can be described as follows. TGNRs having (non-twisted and straight), and are generated by fixing one of their ends and applying rads with respect to the ribbon axis to the opposite end. With the extremities fixed, the TGNRs are optimized with the conjugate gradient energy minimization algorithm as implemented in LAMMPS (with energy and force tolerances of eV and eV/Å, respectively). Then, the TGNR extremities are placed at Å of distance to two different substrates modeled as large area square shape graphene single layers of Å of side, distanced by . The amount of area of the TGNR extremities laid on each substrate is such that its suspended part has one of the following sizes: and Å. Each TGNR is further equilibrated at 300 K for about 1 ns using a Langevin thermostat, with 0.5 fs as time step and 1 ps as thermostat damping factor. Long time simulations are required in order to guarantee that the suspended part of the TGNR reaches equilibrium. During these simulations, the substrates are kept fixed and the objective of this part of the protocol is to get the equilibrium shape of the TGNR at the chosen 300 K temperature. From the equilibrium shapes of TGNRs, and can be calculated using the algorithm described in Ref. [48].
Armchair GNRs of about 600 Å length and 33 Å width are considered in the present study. They are fully hydrogen-passivated. As classical MD simulations show no special dependence of TC with the direction of thermal conduction in pristine graphene we have not repeated the simulations with zigzag GNRs [35].
The TC was calculated as follows. In a real situation, the substrates play the role of thermal baths. However, the simulations to determine the TC of TGNRs will be performed in the nanoribbons alone, without the substrates, to save time in the thermal equilibration of the substrates and to avoid the unknown heat transmission and thermal resistance at the interface between the substrate and the TGNR. Thermostats at K and K are, then, applied to the carbon atoms that, in the simulations with substrates, laid on each of them. In the absence of the substrates, a free TGNR would rotate and release its torsional stress. In order to avoid that, the hydrogen atoms that also laid on the substrates are kept fixed during the simulations to determine the TC. The carbon and hydrogen atoms that are suspended in the simulations with the substrates, are allowed to freely evolve, i. e., no thermostat or constraints are applied to them. The simulations to determine the TC of each TGNR were performed for, at least, 40 ns.
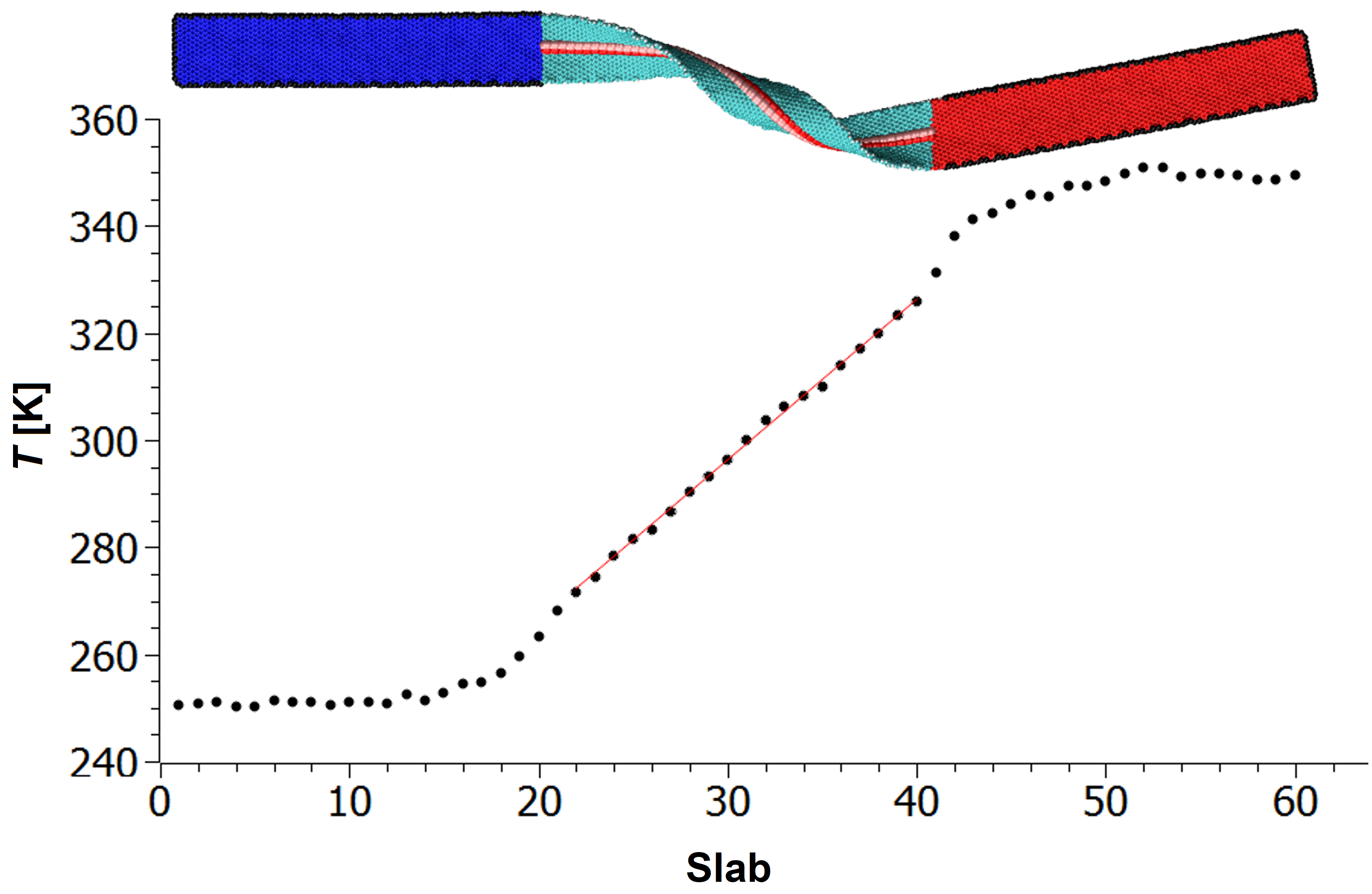
Figure 1 depicts three TGNRs with different values of and . There, red and blue atoms are thermostated at and temperatures, respectively, while black atoms are kept fixed. Cyan, white, red and pink atoms at the suspended part of the TGNR are allowed to evolve freely. Red and pink atoms in the suspended part of the TGNR are those whose coordinates will be used to obtain the space curves needed to calculate and using equations (2) (3), respectively. For every TGNR, the TC, and of the suspended part were calculated.

II.3 Theoretical method to determine the TC
The TC, , of a system along a direction , can be obtained from Fourier law:
| (4) |
where is the heat flux along direction and . The heat flux is calculated by the energy per time per cross-sectional area that the thermostats provide to the system. The temperature gradient is calculated by dividing the TGNR in several slabs of length about 10 Å, and determining the local temperature of each slab through the average kinetic energy of the moving atoms over 10000 timesteps every 10000 timesteps. Figure 2 shows a typical temperature profile along the TGNR after the system reaches the steady state.
III Results
Figure 3(a) presents the results for the TC as function of for the structures at 300 K. Each curve shows the TC for a given value of suspended length, , of the TGNR. The curves have in common the decrease of the TC with up to 1.5, after which the TC remains approximately constant within the error bars, which represent a 5% uncertainty in all calculated conductivities. The curves also show that although the TC increases with increasing , it seems to converge, since the curves for Å become closer to each other than those for Å. As the linking number, , is determined by the number of turns initially applied to the straight GNR, one might think that Figure 3(a) represents the dependence of the TC of a TGNR on twist. However, the ability to change the suspended length, , of the GNR, without changing , poses an extra complexity to the issue of dependence of TC on twist.
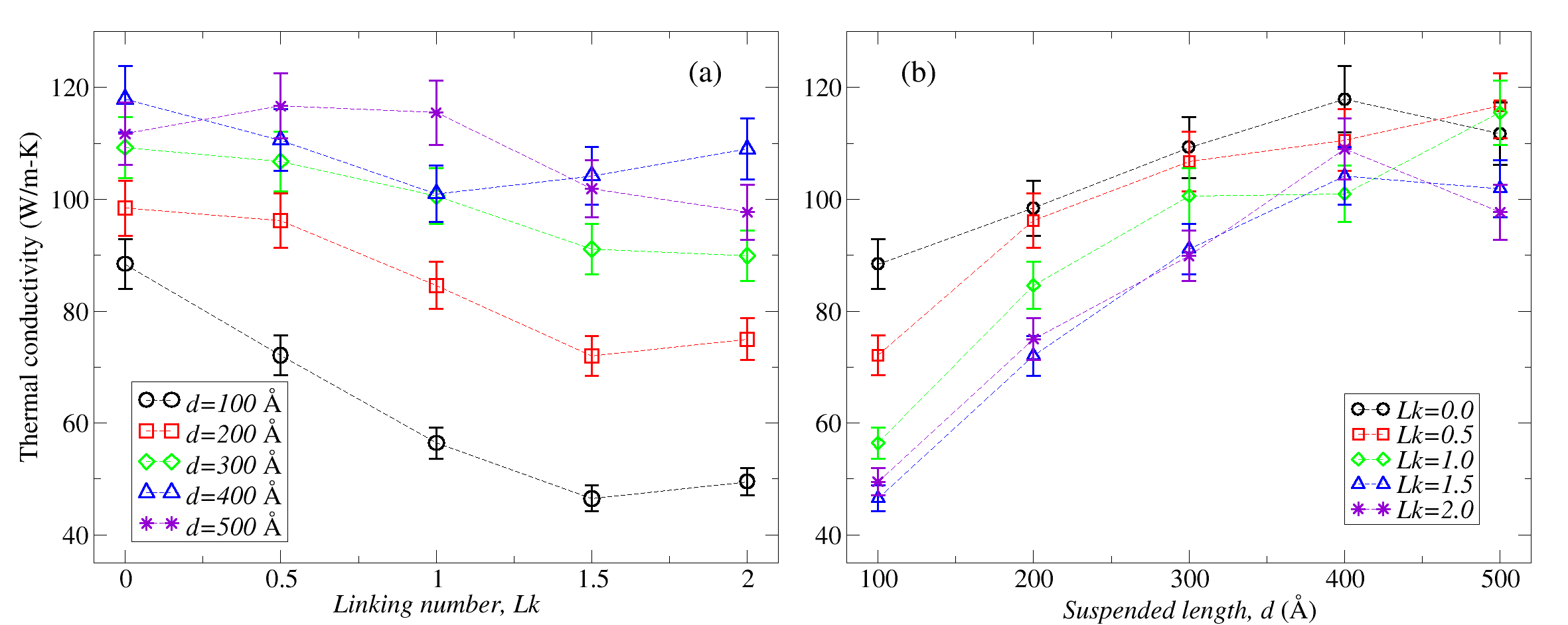
Another form to see the complexity of the dependence of TC on twist comes from the plot of TC as a function of the suspended length, , as shown in Figure 3(b). The curves show that even for the same value of , the TC of a TGNR can change significantly. This observation confirms that, alone, cannot characterize the dependence of TC on twist. Figure 3(b) also allows us to infer that the average rate of change of TC with roughly increases with , at least for Å.
The above results indicate that the TC of a TGNR is not a simple function of only one variable, the number of turns initially applied to the GNR or . The TGNR TC seems to require, at least, a second parameter to appropriately describe its dependence on the geometric features of the TGNR. In order to find out which set of quantities best suits this requirement, we propose, here, three possible alternatives: (A) considering the TGNR suspended length, , as second parameter; (B) considering the pair parameters (or equivalently, and one of them); and (C) considering the initial twist density, , as the second parameter.
III.1 TC dependence on and
Figure 4 illustrates the 3D distribution of values of the TC of the TGNRs as functions of and . The gray surface is the result of an arbitrarily chosen fitting function TC = TC, given by:
| (5) |
where the parameters were determined by a nonlinear fitting.
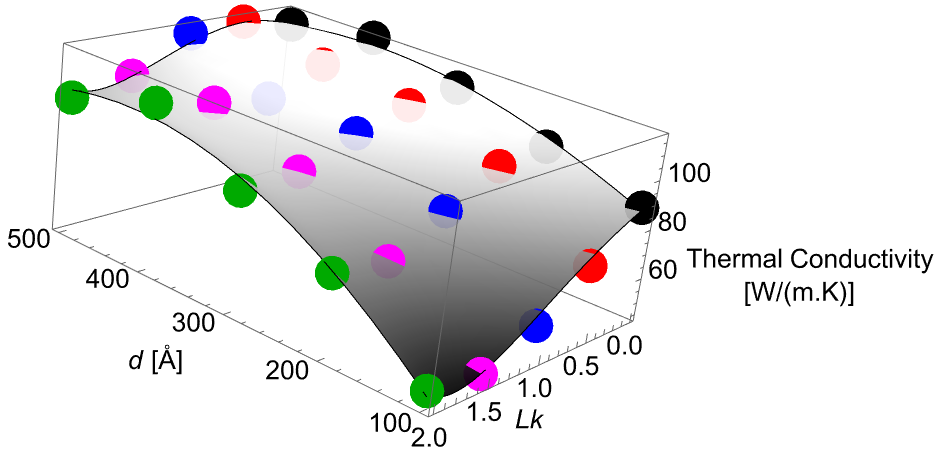
The functional form the the fitting function by itself is not so important at the moment. Different terms could have been added to the fitting equation with no significant difference in the final result. The point is that it is possible to obtain an empirical analytical function for TC = TC from computational and/or experimental data and, then, use it for future predictive purposes. Here, Figure 4 serves to reinforce the conclusion that the TC of TGNRs cannot be described in a simplistic manner, solely in terms of the number of initially applied turns or .
III.2 TC dependence on and
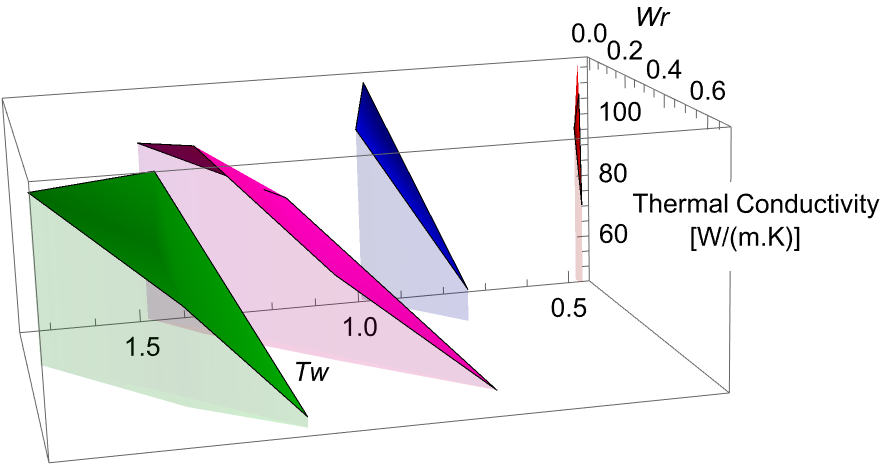
The TC of the TGNRs can be correlated to their geometric features twist, , and writhe, , instead of and , because the present simulations were conducted in such a way that the linking number (or the initial number of turns applied to the straight GNR) remained fixed. Then, the Călugăreanu-White-Fuller theorem, eq. (1), can be used to distinguish groups of TC surfaces in a space, each one corresponding to a value of .
Figure 5 displays four non-zero constant- TC surfaces as function of both and corresponding to the values of and considered in the present study. The area of the surfaces increases with which reflects the ability of the TGNRs to convert twist to writhe to release at least part of the torsional stress. As the surfaces do not intersect one another, each pair of geometric coordinates, univocally characterizes the TC of a TGNR.
Separated plots of TC versus and versus , for different values of suspended length, , are shown in Figure 6. They allow for a better observation of the complexity of the dependence of TC of the TGNRs on their geometric parameters than Figure 5.
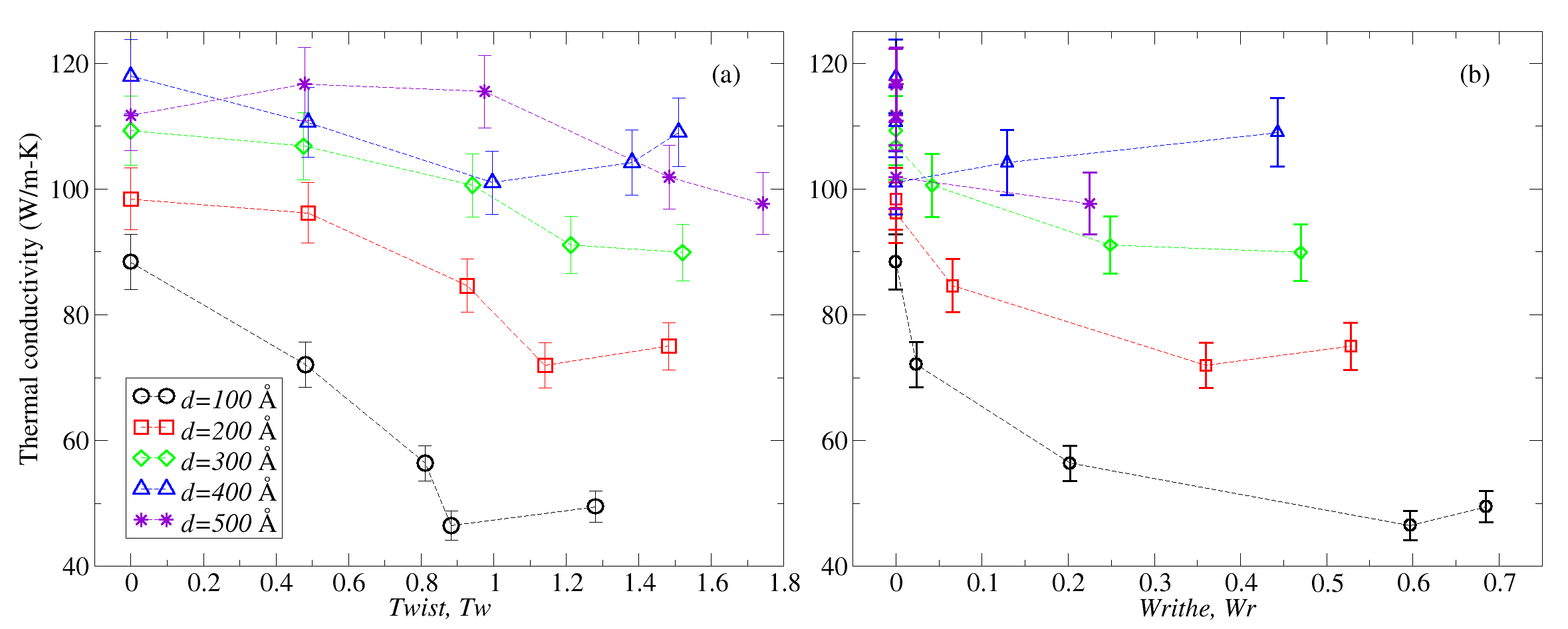
Figure 6(a) shows that TGNRs with smaller suspended lengths, , present larger variations of the TC with the real twist, . In other words, as the value of increases, the TC becomes less dependent on . This shows that the TGNR TC could not be described uniquely even by the real twist, . In fact, the above result is not unexpected. As can be seen in the examples of TGNRs shown in Figure 1, the suspended part of the structure becomes less curved as increases. This is a consequence of the decrease of the linear twist density with increasing of the TGNR having the same . Literature has shown that rods and ribbons become unstable when the applied twist is such that the twist density becomes larger than a critical value [2, 3, 4]. Because of this, we decided to also investigate the dependence of TC on the twist density, as we will discuss in subsection III.3.
The curves in Figure 6(b) look different from those of panel (a) but they are consistent and reflect the fact that and are, in fact, connected by Eq. (1). In fact, Figure 6(b) shows that for TGNRs with larger suspended length, , there is a larger number of TC points corresponding to . This particular observation is coherent with the fact that increasing decreases the twist density of the TGNRs. If the twist density is small, the twisted but straight ribbon is a stable spatial conformation. In other words, the structure becomes less curved when the twist density is low. The points corresponding to values of are those obtained for the largest values of considered in the present study, or . Finally, Figure 6(b) also shows that the TGNR TC cannot be described by only its writhe, .
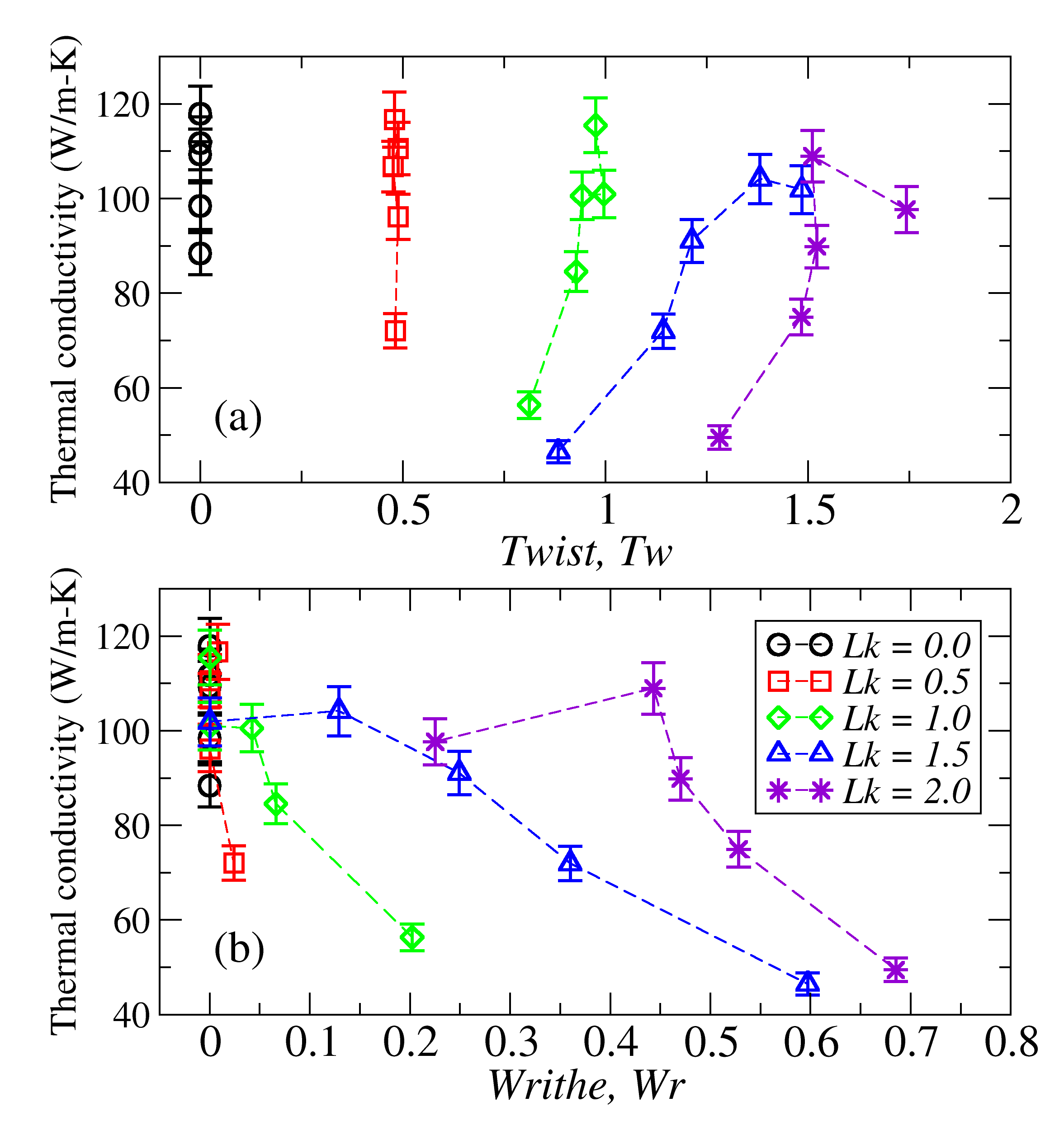
Figures 6(a) and (b) can be re-arranged if we group data points by their values rather than . Indeed, Figure 7 shows TC as a function of (top panel) and (bottom panel), for each value of . Now, the curves display additional results about the complex dependence of the TC of TGNRs on their geometric features. It can be seen that the rate of change of TC with either or , depends on . However, as is constant, for the curves corresponding to the same values of . Thus, for a given value of , the rate of change of TC with is equal in modulus to the rate of change of TC with . For , TC does not depend on or , since there is no twist and the different values of TC correspond only to different values of . It is equivalent to say that if .
However, for , we observe that TC varies with either or . The difference amongst the curves is the rate of change of TC with or , , whose average values are given in Table 1. Although we have only a few values of , and their values might have large uncertainties, we can infer that they roughly decrease from a large amount and converge with increasing .
| [W/(m-K)] | |
|---|---|
| 0.5 | |
| 1.0 | 360.4 |
| 1.5 | 92.2 |
| 2.0 | 104.6 |
The above analysis confirms that the TC of TGNRs in realistic conditions (large size GNRs, suspended and at different temperatures) is much more complex than the simple consideration of its dependence on the number of initially applied turns can deal with. The literature has only presented predictions for the dependence of TC on twist, for zero K, non-writhed, small width TGNRs.
The study of the dependence of TC on both and is not practical from the experimental point of view. It is easier to record the number of times the straight GNR was initially rotated and measure the suspended length of the produced TGNR than defining two space curves along the GNR and develop computational tools to extract its points to compute the corresponding and . Therefore, although the above results show the TC can be well characterized by the pair , they are not unique as shown in subsections III.1 and III.3.
III.3 TC dependence on and the twist density
The analyses in the previous sections suggest one more attempt to characterize the TC of TGNRs on just one quantity: the twist density. In fact, there are two possible twist densities to consider, and . We will stick to the first one since, as mentioned in Section III.2, it is easier for an experiment to measure then to measure in a TGNR.
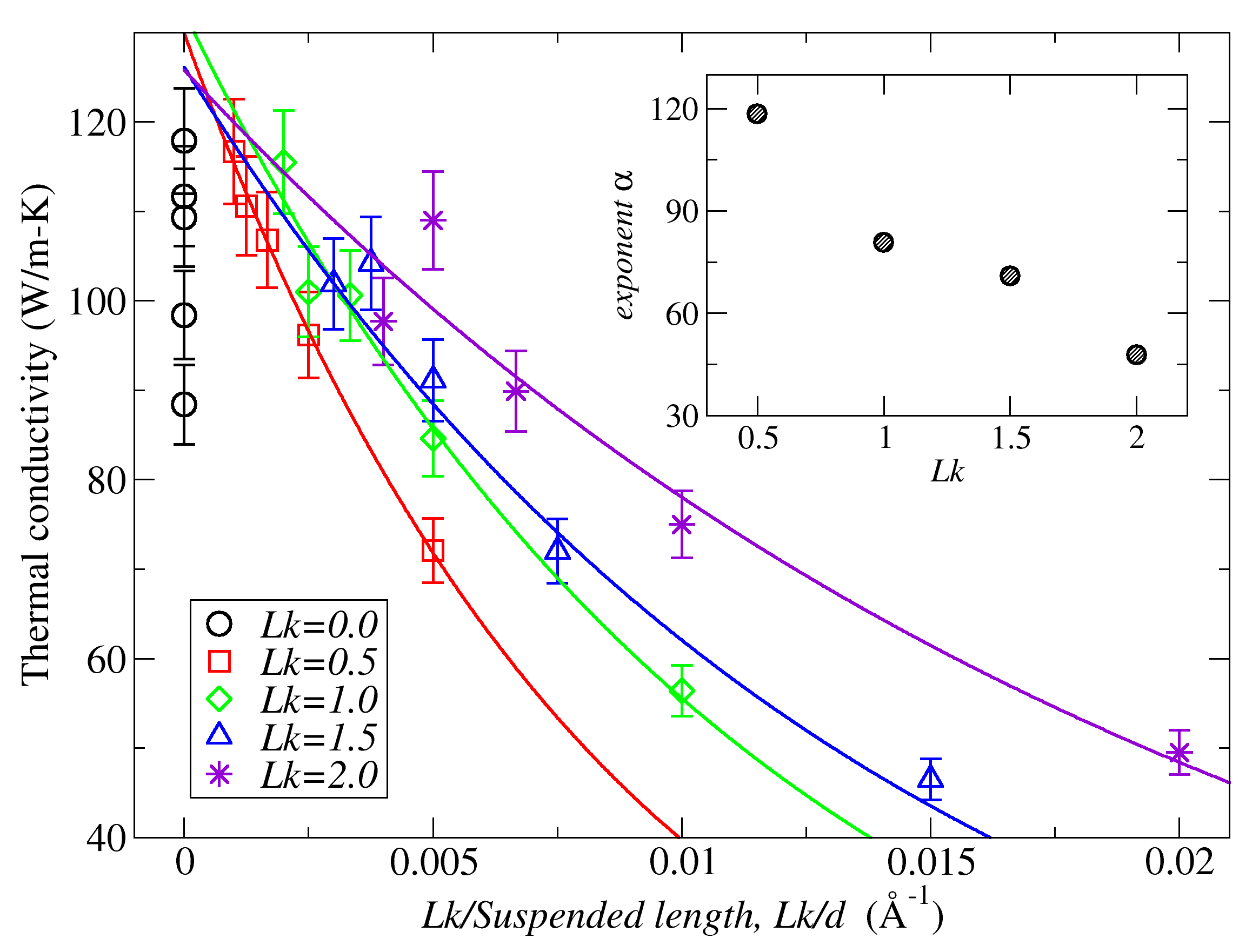
Figure 8 shows the TC of TGNRs as a function of for different values of . It can be seen that each set of data points corresponding to one value of seems to follow one particular decaying curve. We, then, fitted each one to the following equation:
| (6) |
where and are constants that depend on , and is the smallest twist density of the set of data points corresponding to the same , with being the largest suspended size of the TGNRs that, in our case, is 500 Å. The TC of TGNRs is, then, described by the following equation:
| (7) |
| 0.5 | 115.4 | 118.5 |
| 1.0 | 111.2 | 86.74 |
| 1.5 | 102.0 | 70.92 |
| 2.0 | 103.9 | 47.75 |
Table 2 shows the values of and obtained from the fitting of the data points in the main panel of Figure 8, for each value of . While is shown to be weakly dependent on , seems to be a significant function of . In fact, the inset of Figure 8 shows that displays an approximately linear decreasing behavior with . The meaning of this result is quite interesting. As , one can conclude that larger values of lead to a weaker dependence of the TC on the twist density . It is a remarkable, and apparently contradictory, result because larger values of imply larger values of the twist density and, therefore, a stronger dependence of TC on twist density. Thus, one would expect that should increase and not decrease with . But the richness of the twist-to-writhe phenomenon can help understand this feature. As shown by Fonseca [48], a TGNR on top of two separated substrates can present a twist-to-writhe transition, where part of its twist is converted to writhe through curving and curling in the space. As this phenomenon decreases the torsional stress on the nanoribbon, it decreases the torsional stress/strain contribution to its TC.
While the dependence of the TC of TGNRs on is relatively simple, equations similar to (5) are difficult to interpret in physical terms. However, although the dependence on is a bit more complicated than that on , equation (7) carries a simple and physically meaningful form of describing the TC of TGNRs.
IV Conclusion
We have carried out fully atomistic molecular dynamics simulations of TGNRs at 300 K, and obtained their thermal conductivity dependence on geometrical parameters as twist, , writhe, , linking number, , size of the TGNRs suspended parts, , and the twist density, . The results showed that alone, the number of initially applied turns to a straight GNR, , cannot be considered the only parameter that determines the TC of TGNRs. We showed that the TC of TGNRs can be a function of, at least, two parameters, and analysed three sets of parameter pairs: and . Even though each set of parameters can describe the TC of a TGNR, we also showed that a simple and physically meaningful description can be achieved with equation (7), which describes the dependence of TC on a twist density . In the present work, we were mostly concerned on showing that the dependence of the TC on twist is not as simple as previous works have suggested, which is probably related to the lack of experimental studies on TGNRs. We hope that the present analysis and findings will stimulate further experimental investigations of TGNRs, including their thermal transport properties.
Acknowledgements
This work was financed by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) - Finance Code 001, Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), São Paulo Research Foundation (FAPESP), Fundação de Amparo à Ciência e Tecnologia do Estado de Pernambuco (FACEPE), and Financiadora de Estudos e Projetos (FINEP). AFF acknowledges Grant 303284/2021-8 from CNPq, and Grants 2020/02044-9 and 2023/02651-0 from FAPESP. LFCP acknowledges Grant 0041/2022 from CAPES, 436859/2018, 313462/2020, 200296/2023-0 and 371610/2023-0 INCT Materials Informatics from CNPq, APQ-1117-1.05/22 from FACEPE, 0165/21 from FINEP, and the visiting professors program at Sapienza. This work used computational resources provided by “Centro Nacional de Processamento de Alto Desempenho em São Paulo (CENAPAD-SP)” (project proj937), and by the John David Rogers Computing Center (CCJDR) in the Gleb Wataghin Institute of Physics, University of Campinas.
References
- [1]
- [2] Y. Sun and J. W. Leonard, Dynamics of ocean cables with local low-tension regions, Ocean Eng. 25, 443 (1997), DOI: 10.1016/S0029-8018(97)00020-6.
- [3] A. Goriely and M. Tabor, Nonlinear dynamics of filaments I. Dynamical instabilities, PhysicaD: Nonlinear Phenomena 105, 20 (1997), DOI: 10.1016/S0167-2789(96)00290-4.
- [4] A. F. da Fonseca, C. P. Malta, and D. S. Galvão, Elastic properties of nanowires, J. Appl. Phys. 99, 094310 (2006), DOI: 10.1063/1.2194309.
- [5] M. D. Lima, N. Li, M. J. de Andrade, S. Fang, J. Oh, G. M. Spinks, M. E. Kozlov, C. S. Haines, D. Suh, J. Foroughi, S. J. Kim, Y. Chen, T. Ware, M. K. Shin, L. D. Machado, A. F. Fonseca, J. D. W. Madden, W. E. Voit, D. S. Galvão, and R. H. Baughman, Electrically, chemically, and photonically powered torsional and tensile actuation of hybrid carbon nanotube yarn muscles, Science 338, 928 (2012), DOI: 10.1126/science.1226762.
- [6] C. S. Haines, M. D. Lima, N. Li, G. M. Spinks, J. Foroughi, J. D. W. Madden, S. H. Kim, S. Fang, M. J. de Andrade, F. Göktepe, Ö. Göktepe, S. M. Mirvakili, S. Naficy, X. Lepró, J. Oh, M. E. Kozlov, S. J. Kim, X. Xu, B. J. Swedlove, G. G. Wallace, and R. H. Baughman, Artificial muscles from fishing line and sewing thread, Science 343, 868 (2014), DOI: 10.1126/science.1246906.
- [7] R. Wang, S. Fang, Y. Xiao, E. Gao, N. Jiang, Y. Li, L. Mou, Y. Shen, W. Zhao, S. Li, A. F. Fonseca, D. S. Galvão, M. Chen, W. He, K. Yu, H. Lu, X. Wang, D. Qian, A. E. Aliev, N. Li, C. S. Haines, Z. Liu, J. Mu, Z. Wang, S. Yin, M. D. Lima, B. An, X. Zhou, Z. Liu and R. H. Baughman, Torsional refrigeration by twisted, coiled, and supercoiled fibers, Science 366, 216 (2019), DOI: 10.1126/science.aax6182.
- [8] S. -Y. Horng, C. -K. Chen, C. -H. Lee and S. -L. Horng, Quantitative Relationship Between Vascular Kinking and Twisting, Annals of Vascular Surgery 24, 1154 (2010), DOI: 10.1016/j.avsg.2010.07.023.
- [9] W. R. Bauer, R. A. Lund, and J. H. White, Twist and writhe of a DNA loop containing intrinsic bends, Proc. Natl. Acad. Sci. USA 90, 833 (1993), DOI: 10.1073/pnas.90.3.833.
- [10] K. Klenin and J. Langowski, Computation of writhe in modeling of supercoiled DNA, Biopolymers 54, 307 (2000), DOI: 10.1002/1097-0282(20001015)54:5%3C307::AID-BIP20%3E3.0.CO;2-Y.
- [11] M. Barbi, J. Mozziconacci, J.-M. Victor, H. Wong, and C. Lavelle, On the topology of chromatin fibres, Interface Focus 2, 546 (2012), DOI: 10.1098/rsfs.2011.0101.
- [12] A. Sadrzadeh, M. Hua and B. I. Yakobson, Electronic properties of twisted armchair graphene nanoribbons, Appl. Phys. Lett. 99, 013102 (2011), DOI: 10.1063/1.3606553.
- [13] H. Li, N. Al-Aqtash, L. Wang, R. Qin, Q. Liu, J. Zheng, W. -N. Mei, R. F. Sabirianov, Z. Gao and J. Lu, Electromechanical switch in metallic graphene nanoribbons via twisting, Physica E 44, 2021 (2021), DOI: 10.1016/j.physe.2012.06.004.
- [14] N. Al-Aqtash, H. Li, L. Wang, W. -N. Mei and R. F. Sabirianov, Electromechanical switching in graphene nanoribbons, Carbon 51, 102-109 (2013), DOI: 10.1016/j.carbon.2012.08.018.
- [15] D. Gunlycke, J. Li, J. W. Mintmire and C. T. White, Edges Bring New Dimension to Graphene Nanoribbons, Nano Letters 10, 3638 (2010), DOI: 10.1021/nl102034c.
- [16] K. Koskinen, Electromechanics of twisted graphene nanoribbons, Appl. Phys. Lett. 99, 013105 (2011), DOI: 10.1063/1.3607956.
- [17] G. P. Tang, J. C. Zhou, Z. H. Zhang, X. Q. Deng and Z. Q. Fan, Altering regularities of electronic transport properties in twisted graphene nanoribbons, Appl. Phys. Lett. 101, 023104 (2012), DOI: 10.1063/1.4733618.
- [18] N. Xu, B. Huang, J. Li and B. Wang, Semiconductor–metal and metal–semiconductor transitions in twisting graphene nanoribbons, Solid StateCommunications 202, 39 (2015), DOI: 10.1016/j.ssc.2014.10.015.
- [19] S. -Y. Yue, Q. -B. Yan, Z. -G. Zhu, H. -J. Cui, Q. -R. Zheng and G. Su, Carbon 71, 150 (2014), DOI: 10.1016/j.carbon.2014.01.023.
- [20] J. Jia, D. Shi, X. Feng, and G. Chen, First-principles study on electronic and magnetic properties of twisted graphene nanoribbon and Möbius strips, Carbon 76, 54 (2014), DOI: 10.1016/j.carbon.2014.04.048.
- [21] D. -B. Zhang, G. Seifert, and K. Chang, Strain-Induced Pseudomagnetic Fields in Twisted Graphene Nanoribbons, Phys. Rev. Lett. 112, 096805 (2014), DOI: 10.1103/PhysRevLett.112.096805.
- [22] M. Saiz-Bretín, F. Domínguez-Adame, and A. V. Malyshev, Twisted graphene nanoribbons as nonlinear nanoelectronic devices, Carbon 149, 587 (2019), DOI: 10.1016/j.carbon.2019.04.069.
- [23] R. Thakur, P. K. Ahluwalia, A. Kumar, B. Mohan and R. Sharma, Electronic structure and carrier mobilities of twisted graphene helix, Physica E 124, 114280 (2020), DOI: 10.1016/j.physe.2020.114280.
- [24] Y. Li, Twist-enhanced stretchability of graphene nanoribbons: a molecular dynamics study, J. Phys. D: Appl. Phys. 43, 495405 (2010), DOI: 10.1088/0022-3727/43/49/495405.
- [25] S. Cranford and M. J. Buehler, Twisted and coiled ultralong multilayer graphene ribbons, Modelling Simul.Mater. Sci. Eng. 19, 054003 (2011), DOI: 10.1088/0965-0393/19/5/054003.
- [26] E. Dontsova and T. Dumitrică, Nanomechanics of Twisted Mono- and Few-Layer Graphene Nanoribbons, J. Phys. Chem. Lett. 4, 2010 (2013), DOI: 10.1021/jz400747f.
- [27] E. M. Diniz, Self-reconstruction and predictability of bonds disruption in twisted graphene nanoribbons, Appl. Phys. Lett. 104, 083119 (2014), DOI: 10.1063/1.4867266.
- [28] D. Xia, Q. Li, Q. Xue, C. Liang, and M. Dong, Super flexibility and stability of graphene nanoribbons under severe twist, Phys. Chem. Chem. Phys. 18, 18406 (2016), DOI: 10.1039/C6CP02580C.
- [29] A. V. Savin, E. A. Korznikova and S. V. Dmitriev, Improving bending rigidity of graphene nanoribbons by twisting, Mech. Mater. 137, 103123 (2019), DOI: 10.1016/j.mechmat.2019.103123.
- [30] A. Shahabi, H.Wang, andM. Upmanyu, Shaping van der Waals nanoribbons via torsional constraints: Scrolls, folds and supercoils, Sci. Rep. 4, 7004 (2014). DOI: 10.1038/srep07004.
- [31] A. V. Savin and A. P. Klinov, Twisting of graphene nanoribbons partially located on flat substrates, EPL 132, 36002 (2020), DOI:10.1209/0295-5075/132/36002.
- [32] I. Nikiforov, B. Hourahine, Th. Frauenheim and T. Dumitrică, Formation of Helices in Graphene Nanoribbons under Torsion, J. Phys. Chem. Lett. 5, 4083 (2014), DOI: 10.1021/jz501837r.
- [33] X. Y. Liu, F. C. Wang and H. A. Wu, Anomalous twisting strength of tilt grain boundaries in armchair graphene nanoribbons, Phys. Chem. Chem. Phys. 17, 31911 (2015), DOI: 10.1039/c5cp04343c.
- [34] A. V. Savin, E. A. Korznikova, and S. V. Dmitriev, Twistons in graphene nanoribbons on a substrate, Phys. Rev. B 102, 245432 (2020), DOI: 10.1103/PhysRevB.102.245432.
- [35] L. F. C. Pereira and D. Donadio, Divergence of the thermal conductivity in uniaxially strained graphene, Phys. Rev. B 87, 125424 (2013), DOI: 10.1103/PhysRevB.87.125424.
- [36] X. Xu, L. F. C. Pereira, Y. Wang, J. Wu1, K. Zhang, X. Zhao, S. Bae, C. T. Bui, R. Xie, J. T. L. Thong, B. H. Hong, K. P. Loh, D. Donadio, B. Li and B. Özyilmaz, Length-dependent thermal conductivity in suspended single-layer graphene, Nature Comm. 5, 3689 (2014), DOI: 10.1038/ncomms4689.
- [37] Z. Fan, P. Hirvonen, L. F. C. Pereira, M. M. Ervasti, K. R. Elder, D. Donadio, A. Harju and T. Ala-Nissila, Bimodal Grain-Size Scaling of Thermal Transport in Polycrystalline Graphene from Large-Scale Molecular Dynamics Simulations, Nano Lett. 17, 5919-5924 (2017), DOI: 10.1021/acs.nanolett.7b01742.
- [38] Z. Fan, L. F. C. Pereira, P. Hirvonen, M. M. Ervasti, K. R. Elder, D. Donadio, T. Ala-Nissila and A. Harju, Thermal conductivity decomposition in two-dimensional materials: Application to graphene, Phys. Rev. B 95, 144309 (2017), DOI: 10.1103/PhysRevB.95.144309.
- [39] H. Shen, Mechanical properties and thermal conductivity of the twisted graphene nanoribbons, Molecular Physics 112, 2614 (2014). DOI: 10.1080/00268976.2014.899404.
- [40] X. Wei, G. Guo, T. Ouyang and H. Xiao, Tuning thermal conductance in the twisted graphene and gamma graphyne nanoribbons, J. Appl. Phys. 115, 154313 (2014), DOI: 10.1063/1.4872136.
- [41] A. Antidormi, M. Royo and R. Rurali, Electron and phonon transport in twisted graphene nanoribbons, J. Phys. D: Appl. Phys. 50, 234005 (2017), DOI: 10.1088/1361-6463/aa6fd3.
- [42] Y. Terada and T. Shiga, Ballistic phonon transport analysis of twisted graphene nanoribbons, Transactions of the JSME (in Japanese) 86, 20-00292 (2020), DOI: 10.1299/transjsme.20-00292.
- [43] A. V. Savin, E. A. Korznikova, A. M. Krivtsov and S. V. Dmitriev, Longitudinal stiffness and thermal conductivity of twisted carbon nanoribbons, European Journal of Mechanics / A Solids 80, 103920 (2020), DOI: 10.1016/j.euromechsol.2019.103920.
- [44] Z. Liu, Z. Zhang, H. -Y. Zhao, J. Wang and Y. Liu, Lattice dynamics of graphene nanoribbons under twisting, Phys. Chem. Chem. Phys. 23, 25485 (2021), DOI: 10.1039/D1CP03806K.
- [45] T. W. Chamberlain, J. Biskupek, G. A. Rance, A. Chuvilin, T. J. Alexander, E. Bichoutskaia, U. Kaiser, and A. N. Khlobystov, Size, structure, and helical twist of graphene nanoribbons controlled by confinement in carbon nanotubes, ACS Nano 6, 3943 (2012), DOI: 10.1021/nn300137j.
- [46] Y. Cao, R. L. Flores, and Y.-Q. Xu, Curling graphene ribbons through thermal annealing, Appl. Phys. Lett. 103, 183103 (2013), DOI: 10.1063/1.4827209.
- [47] Z. Jarrahi, Y. Cao, T. Hong, Y. S. Puzyrev, B. Wang, J. Lin, A. H. Huffstutter, S. T. Pantelides, and Y.-Q. Xu, Enhanced photoresponse in curled graphene ribbons, Nanoscale 5, 12206 (2013), DOI: 10.1039/C3NR03988A.
- [48] A. F. Fonseca, Twisting or untwisting graphene twisted nanoribbons without rotation, Phys. Rev. B 104, 045401 (2021), DOI: 10.1103/PhysRevB.104.045401.
- [49] F. B. Fuller, The writhing number of a space curve, Proc. Natl. Acad. Sci. USA 68, 815 (1971), DOI: 10.1073/pnas.68.4.815.
- [50] A. Goriely and M. Tabor, The nonlinear dynamics of filaments, Nonlinear Dyn. 21, 101 (2000), DOI: 10.1023/A:1008366526875.
- [51] G. Călugăreanu, On isotopy classes of three dimmensional knots and their invariants, Czech. Math. J. 11, 588 (1961), DOI: 10.21136/CMJ.1961.100486.
- [52] F. B. Fuller, Decomposition of the Lk of a closed ribbon: A problem from molecular biology, Proc. Natl. Acad. Sci. USA 75, 3557 (1978), DOI: 10.1073/pnas.75.8.3557.
- [53] M. A. Berger and C. Prior, The writhe of open and closed curves, J. Phys. A: Math. Gen. 39, 8321 (2006), DOI: 10.1088/0305-4470/39/26/005.
- [54] D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni, and S. B. Sinnott, A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons, J. Phys.: Condens. Matter bf 14, 783 (2002), DOI: 10.1088/0953-8984/14/4/312.
- [55] S. J. Stuart, A. B. Tutein, and J. A. Harrison, A reactive potential for hydrocarbons with intermolecular interactions, J. Chem. Phys. 112, 6472 (2000). DOI: 10.1063/1.481208.
- [56] A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott, and S. J. Plimpton, LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun. 271, 108171 (2022), DOI: 10.1016/j.cpc.2021.108171.
- [57] R. Granta, V. B. Shenoy and R. S. Ruoff, Anomalous strength characteristics of tilt grain boundaries in graphene, Science 330, 946 (2010), DOI: 10.1126/science.1196893.
- [58] L. C. Felix, R. M. Tromer, P. A. S. Autreto, L. A. Ribeiro Junior and D. S. Galvao, On the Mechanical Properties and Thermal Stability of a Recently Synthesized Monolayer Amorphous Carbon, The Journal of Physical Chemistry C, 124, 14855–14860 (2020), DOI: 10.1021/acs.jpcc.0c02999.
- [59] G. B. Kanegae and A. F. Fonseca, Effective acetylene length dependence of the elastic properties of different kinds of graphynes, Carbon Trends, 7, 100152 (2022), DOI: 10.1016/j.cartre.2022.100152.
- [60] G. B. Kanegae and A. F. Fonseca, Density dependence of elastic properties of graphynes, MRS Advances, 8, 355-360 (2023), DOI: 10.1557/s43580-023-00529-x.
- [61] A. R. Muniz and A. F. Fonseca, Carbon-Based Nanostructures Derived from Bilayer Graphene with Zero Thermal Expansion Behavior, The Journal of Physical Chemistry C 119, 17458–17465 (2015), DOI: 10.1021/acs.jpcc.5b05602.
- [62] S. Lisenkov, R. Herchig, S. Patel, R. Vaish, J. Cuozzo and I. Ponomareva, Elastocaloric effect in carbon nanotubes and graphene, Nano Letters 16, 7008 (2016), DOI: 10.1021/acs.nanolett.6b03155.
- [63] T. E. Cantuario and A. F. Fonseca, High Performance of Carbon Nanotube Refrigerators, Annalen Der Physik 531, 1800502 (2019), DOI: 10.1002/andp.201800502.
- [64] M. Li, Z. Guo and T. Chang, Adhesion and stress-enhanced elastocaloric effect in graphene, Science China Technological Sciences 63, 297-302 (2020), DOI: 10.1007/s11431-018-9395-6.
- [65] Z. Zhao, W. Guo and Z. Zhang, Room-Temperature Colossal Elastocaloric Effects in Three-Dimensional Graphene Architectures: An Atomistic Study, Advanced Functional Materials 32, 2203866 (2022), DOI: 10.1002/adfm.202203866.
- [66] T. N. Y. Silva and A. F. Fonseca, High performance of carbon nanotube elastocaloric refrigerators over a large temperature span, Physical Review B 106, 165413 (2022), DOI: 10.1103/PhysRevB.106.165413.
- [67] L. A. Ribeiro Junior, M. L. Pereira Junior and Alexandre F. Fonseca, Nano Letters 23, 8801 (2023), DOI: 10.1021/acs.nanolett.3c02260.
- [68] Y. He, L. -X. Ma, Y. -Z. Tang, Z. -P. Wang, W. Li and D. Kukulka, Thermal Conductivity of Natural Rubber Using Molecular Dynamics Simulation, Journal of Nanoscience and Nanotechnology 15, 3244 (2015), DOI: 10.1166/jnn.2015.9640.
- [69] T. Ito, H. Matsubara, D. Surblys, T. Ohara, Molecular dynamics study on the thermal conductivity of a single polyethylene chain: Strain dependence and potential models’ effect, AIP Advances 12, 105223 (2022), DOI: 10.1063/5.0095975.
- [70] H. Zhang, G. Lee, A. F. Fonseca, T. L. Borders and K. Cho, Isotope Effect on Thermal Conductivity of Graphene, Journal of Nanomaterials 2010, 537657 (2010), DOI: 10.1155/2010/537657.
- [71] H. Zhang, A. F. Fonseca and K. Cho, Tailoring Thermal Transport Property of Graphene through Oxygen Functionalization, The Journal of Physical Chemistry C 118, 1436 (2014), DOI: 10.1021/jp4096369.