Lenses in the Forest: Cross–Correlation of the Lyman- Flux
with Cosmic Microwave Background Lensing
Abstract
We present a theoretical estimate for a new observable: the cross–correlation between the Lyman- flux fluctuations in quasar (QSO) spectra and the convergence of the cosmic microwave background (CMB) as measured along the same line–of–sight. As a first step toward the assessment of its detectability, we estimate the signal–to–noise ratio using linear theory. Although the signal–to–noise is small for a single line–of–sight and peaks at somewhat smaller redshifts than those probed by the Lyman- forest, we estimate a total signal–to–noise of 9 for cross–correlating QSO spectra of SDSS-III with Planck and 20 for cross–correlating with a future polarization based CMB experiment. The detection of this effect would be a direct measure of the neutral hydrogen–matter cross–correlation and could provide important information on the growth of structures at large scales in a redshift range which is still poorly probed by observations.
pacs:
98.62.Ra, 98.70.Vc, 95.30.SfIntroduction. The Lyman- forest – the absorption seen in quasar (QSO) spectra caused by intervening neutral hydrogen of the intergalactic medium (IGM) – has the potential to provide precise information about the matter distribution down to small scales. In the near future, the SDSS III Baryon Oscillation Spectroscopic Survey (BOSS) will measure absorption spectra toward QSOs, a fiftyfold improvement on existing surveys McDonald et al. (2005a). This large sample could potentially provide unprecedented constraints on neutrino masses Gratton et al. (2008), amplitude and slope of the matter power spectrum Lesgourgues et al. (2007), inflationary parameters and the running spectral index Seljak and Slosar (2006). Furthermore, the baryon oscillations in the Lyman- forest can be used to constrain dark energy and curvature McDonald and Eisenstein (2007) and high-resolution QSO spectra can also play a significant role in constraining the properties of dark matter on small scales Viel et al. (2008).
The theoretical studies assume that the physics of the Lyman- forest is relatively simple and that the observed flux fluctuations faithfully trace the dark matter distribution. Hydrodynamical simulations play an essential role in testing this assumption through comparisons with data and in calibrating the measurements. However, many systematic errors still pose challenges at the sub-percent level of accuracy required by the data. The main sources of uncertainty include, but are not limited to: the accurate modeling of fluctuations in the ionization background, the QSO continuum fluctuations, the uncertainties in the slope of the temperature-density relation in the IGM and fluctuations about this mean relation, the effect of galactic superwinds on the Lyman- flux and the contamination of the Lyman- spectrum with metal lines (e.g. Viel et al. (2004)). The ingredients that go into the simulations could be better controlled if we could directly and independently test how the fluctuations in the transmitted flux and the dark matter are related.
In this Letter, we propose one such observable: the cross–correlation of the Lyman- flux fluctuations with the convergence field extracted from the gravitational lensing of the cosmic microwave background (CMB). Gravitational lensing of the CMB is caused by the deflection of CMB photons by intervening large scale structure Lewis and Challinor (2006). Lensing breaks the statistical isotropy of the CMB, introduces non-Gaussianities and produces B-mode polarization from E-modes. Observations of small scale temperature and polarization fluctuations can be used to reconstruct the effective deflection field that lensed the CMB Hu and Okamoto (2002). WMAP measurements have enabled the first detection of CMB lensing Smith et al. (2007); Hirata et al. (2008b). With the ongoing and upcoming high resolution temperature and polarization based CMB experiments like the Atacama Cosmology Telescope, the South Pole Telescope, Planck, QUIET and PolarBearR ALL , high fidelity lensing reconstruction will soon become a reality. The timely convergence of the Lyman- surveys and high resolution CMB experiments in coming few years will make the measurement of their cross–correlation a possibility.
We note that cross–correlating CMB temperature maps with the large-scale structure (LSS) is currently done with many LSS probes including Lyman- (e.g. Peiris and Spergel (2000)), however we focus here on the convergence of the CMB rather than the CMB temperature fluctuations. The cross–correlation signal between these two quantities should provide insights on the relative bias between matter and flux (in a way somewhat analogous to Hirata et al. (2008b)) and may become a powerful tool to calibrate the relationship between the IGM and the dark matter. As a first step toward understanding the information content and the detectability of this correlation, we provide here a simple theoretical estimate of the signal and of the significance with which it can be measured by the upcoming experiments.
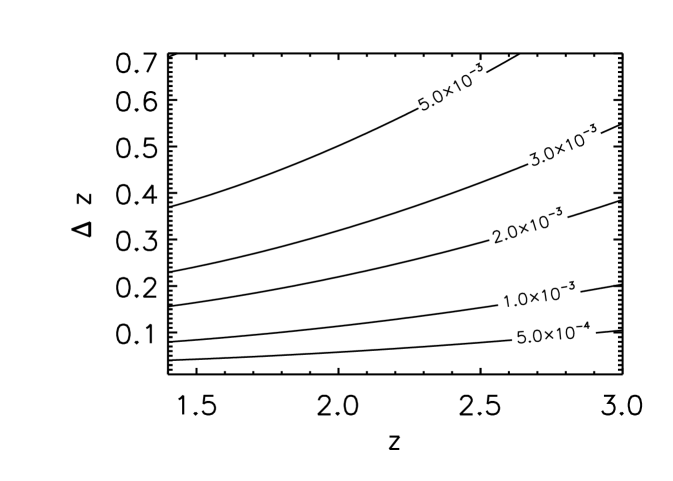
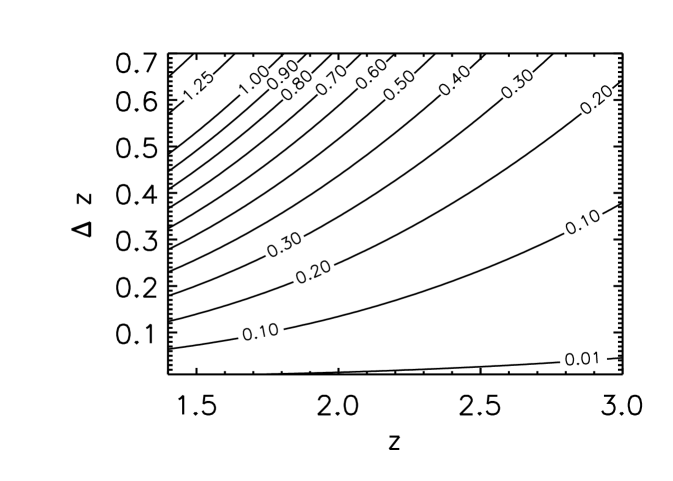
Evaluation of the correlators. We calculate the correlations between the fluctuations in the flux and their variance measured for a single QSO – whose line–of–sight (los) lies in the direction and whose spectrum covers a redshift range – and the CMB convergence measured in the same direction. While the convergence measures the projected matter fluctuations along the los, the quantity is sensitive to the typical fluctuations of the Lyman- forest which are in the range 1-100 comoving . Since structures grow at a faster rate in overdense regions (which in turn are characterized by a positive convergence) Zaldarriaga et al. (2000), the cross–correlation of the convergence with the flux variance is expected to increase the signal. Also, using the flux variance makes the observable less sensitive to the continuum fitting uncertainties of the QSO spectrum since requires correct extrapolation of the continuum from longward of Lyman- .
The effective CMB convergence measured in the direction depends on the amplitude of matter density fluctuations along the los and reads:
| (1) |
where the integral is along the los, is the comoving distance to the last scattering surface, is the usual lensing window function and is the scale factor at comoving distance .
We assume that on large scales fluctuations in the optical depth are linearly proportional to fluctuations in the matter density Hui and Gnedin (1997), motivated by the so–called fluctuating Gunn–Peterson approximation Gunn and Peterson (1965); Croft et al. (1998) that relates flux and matter , where and are two redshift dependent functions: is of order unity and is related to the mean flux level, baryon fraction, IGM temperature, cosmological parameters and the photoionization rate of hydrogen, while depends on to the so-called IGM temperature-density relation (e.g. Hui and Gnedin (1997); McDonald (2003)). However, for the purpose of this Letter, it is fair to neglect their evolution with redshift and to assume that they are constant over the observed QSO redshift interval in each los. In the large scale limit, the exponent is small and we can expand it. Keeping only up to the lowest order term in Viel et al. (2002); Croft et al. (1998) we get: . We stress that this approximation is valid in linear theory neglecting not only the non–linearities produced by gravitational instabilities but also those introduced by the definition of the flux, thermal broadening and peculiar velocities. Higher order terms in the expansion will, in general, contribute to the cross–correlations being estimated here. To keep the calculations analytically tractable, in this Letter we neglect these higher order terms.
We define the th moment of the flux fluctuation averaged over the los interval probed by the Lyman- spectrum (extending from to ) as:
| (2) | |||||
The correlation of this quantity with the CMB convergence measured along the same los is then,
| (3) | |||||
We focus here on the case (and ), which is the cross–correlation between the CMB convergence and the QSO mean flux fluctuation (and variance). To proceed further we Fourier transform the cumulant correlator . The case reduces to the 2-point correlation function of the dark matter overdensities along the los, while the case requires the use of the 3-point correlation function or of its Fourier counterpart, the bispectrum Bernardeau et al. (2002). In both cases we also include in the analysis the fact that both the Lyman- spectra and the CMB convergence are being measured with a finite resolution. To this end we add appropriate gaussian window functions that limit the modes contributing to the CMB convergence (perpendicular to the los) to wavenumbers and the ones contributing to the Lyman- spectra (parallel to the los) to . When these cutoffs are included, the treatment of the case becomes involved. However, by expanding in power series the modified Bessel functions arising from the angular integration in –space, it is possible to obtain an exact series solution for the cumulant correlator.
We calculate the value of and of as a function of the QSO redshift and of the redshift range spanned by the Lyman- spectrum for a flat CDM cosmology with , , and km/s/Mpc. The results obtained – shown in Fig. 1 – make physical sense: if the Lyman- spectrum covers a larger redshift range the correlators increase, as more information is carried by the longer spectrum. On the other hand, if the source QSO redshift is increased while keeping the length of the spectrum fixed the correlators become smaller because the Lyman- spectrum is probing regions where structure had less time to form. Furthermore, the rate at which the correlators are increasing as a function of is itself increasing with the CMB and Lyman- experiment resolutions and . Finally, as expected the correlator is about two orders of magnitude larger than : regions of higher convergence have typically higher mean density and hence larger fluctuations’ variance due to enhanced growth Zaldarriaga et al. (2000).
Estimate for the correlators’ signal-to-noise ratio. To assess the detectability of the above correlations by CMB experiments and QSO surveys we need to evaluate their signal–to–noise ratio (S/N). The calculation of the variances of and requires the evaluation of and of , which are proportional to and , respectively [we adopt the notation ]. The exact evaluation of the latter requires the calculation of a six–point function, the form of which to our knowledge has never been obtained. However, an estimate for the dominant contributions to the variance can be obtained using the approximation
| (4) |
The estimates for the S/N ratio for the measurement of and along a single los are shown in Fig. 2. As before, increasing the length of the spectrum or decreasing the redshift of the source will increase the S/N ratio, as more information is added by the longer spectrum in the first case and as the shallower redshift will allow to probe regions with clumpier structure in the second case. Also, comparing the two panels it is possible to notice how the correlators’ different dependence on the growth of structure affects the redshift range over which a given S/N ratio can be obtained. Finally, we also notice that the S/N for is about four times larger than the one for , a consequence of the fact that cosmic variance is generally higher for higher order statistics.
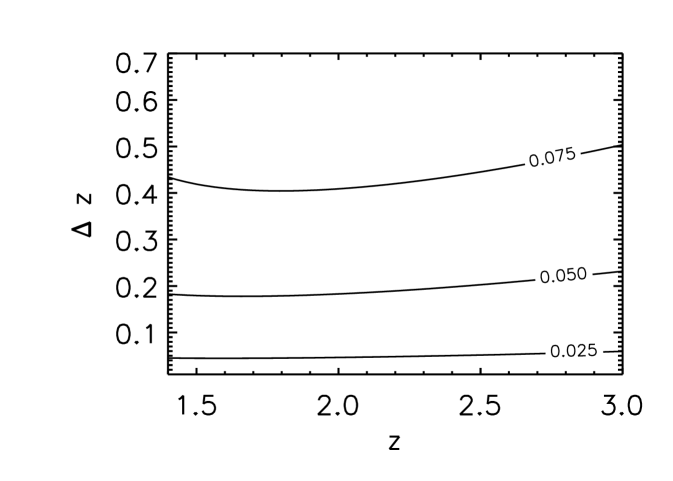
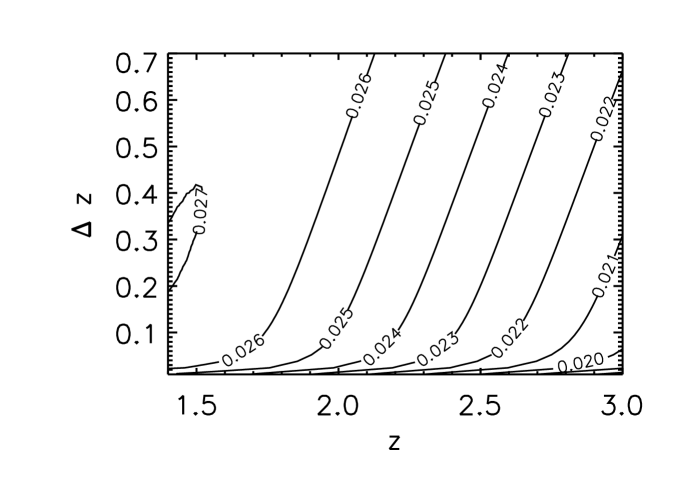
Conclusions. We presented a calculation of the cross–correlation signal (and its noise) between the (variance of the) Lyman- flux fluctuations and the CMB convergence. We found that the cross–correlation signal peaks at somewhat smaller redshifts than those usually probed by Lyman- alone, but it will be detectable with future data sets with a large number of QSO. In particular, we estimate that the S/N ratio for obtained by cross-correlating the BOSS QSO sample with Planck data will yield a S/N ratio of 9.6. The use of higher definition data arising from a hypothetical CMB polarization experiment covering 8000 sq. degrees would further increase the estimated S/N to 20. In all the above cases the present analysis shows that this correlation will be observable.
A few caveats are also in order. First, as large contributions to the signal may actually be arising at small separations, it is necessary to stress that the estimates obtained for the variance of the correlators – and consequently for S/N – do not take into account the non–linearities characteristic of small separations. The latter however are not expected to alter significantly the results, given the QSO mean redshift. Second, it is necessary to point out that the estimates of Fig. 2 do not take into account the detector systematics, which in a more realistic calculation should also be included. Finally, we note that the estimators considered may not be the ones characterized by the least variance. It is reasonable to speculate that the use of redshift weighted estimators in conjuction with lower redshift convergence maps obtained through LSS surveys may allow an improvement in the S/N ratio. The formalism developed can further be extended to cross-correlate the Lyman- flux with convergence maps obtained from optical lensing surveys once these will become available at the redshifts of the Lyman- forest. This would result in an improvement in S/N ratio.
Finally, the present work is just a first step in assessing the information content and the detectability of Lyman- –CMB lensing correlations and more refined calculations, based on non–linear theory and hydrodynamical simulations should be performed to address this more quantitatively, as future observational programs should enable to perform such a measurement with several consequences. First, this would provide independent constraints on the bias between flux and matter, additional to the ones that are obtained by high resolution QSO spectra and hydrodynamical simulations. Second, being sensitive to the growth of structures at intermediate to small scales, this correlation could be used to test for models of early dark energy Xia and Viel (2009) or modification of gravity that produce scale dependent growth evolutions Zhao et al. (2008) and to provide constraints on the neutrino masses.
Acknowledgements: We thank F. Bernardeau, S. Matarrese, S. Dodelson, J. Frieman, E. Sefusatti, N. Gnedin and J. P. Uzan for useful conversations. AV is supported by the DOE and the NASA grant NAG 5-10842 at Fermilab. SD thanks APC - Paris for hospitality when this project was conceived. SD and DS acknowledge NASA grant NNX08AH30G and NSF grant 0707731. MV acknowledges support from an ASI/AAE grant.
References
- McDonald et al. (2005a) P. McDonald, U. Seljak, R. Cen, D. Shih, D. H. Weinberg, S. Burles, D. P. Schneider, D. J. Schlegel, N. A. Bahcall, J. W. Briggs, et al., ApJ 635, 761 (2005a), eprint arXiv:astro-ph/0407377. U. Seljak, A. Makarov, P. McDonald, S. F. Anderson, N. A. Bahcall, J. Brinkmann, S. Burles, R. Cen, M. Doi, J. E. Gunn, et al., Phys. Rev. D 71, 103515 (2005), eprint arXiv:astro-ph/0407372. D. Schlegel, M. White, and D. Eisenstein (with input from the SDSS-III) (2009), eprint 0902.4680.
- Gratton et al. (2008) S. Gratton, A. Lewis, and G. Efstathiou, Phys. Rev. D 77, 083507 (2008), eprint 0705.3100.
- Lesgourgues et al. (2007) J. Lesgourgues, M. Viel, M. G. Haehnelt, and R. Massey, Journal of Cosmology and Astro-Particle Physics 11, 8 (2007), eprint 0705.0533.
- Seljak and Slosar (2006) U. Seljak and A. Slosar, Phys. Rev. D 74, 063523 (2006), eprint arXiv:astro-ph/0604143.
- McDonald and Eisenstein (2007) P. McDonald and D. J. Eisenstein, Phys. Rev. D 76, 063009 (2007), eprint arXiv:astro-ph/0607122.
- Viel et al. (2008) M. Viel, G. D. Becker, J. S. Bolton, M. G. Haehnelt, M. Rauch, and W. L. W. Sargent, Physical Review Letters 100, 041304 (2008), eprint 0709.0131.
- Viel et al. (2004) M. Viel, M. G. Haehnelt, and V. Springel, Mon. Not. Roy. Astron. Soc. 354, 684 (2004), eprint astro-ph/0404600. P. McDonald, U. Seljak, R. Cen, P. Bode, and J. P. Ostriker, MNRAS 360, 1471 (2005b), eprint arXiv:astro-ph/0407378. J. S. Bolton, M. Viel, T.-S. Kim, M. G. Haehnelt, and R. F. Carswell, MNRAS 386, 1131 (2008), eprint 0711.2064.
- Lewis and Challinor (2006) A. Lewis and A. Challinor, Phys. Rep. 429, 1 (2006), eprint arXiv:astro-ph/0601594.
- Hu and Okamoto (2002) W. Hu and T. Okamoto, ApJ 574, 566 (2002), eprint arXiv:astro-ph/0111606. C. M. Hirata and U. Seljak, Phys. Rev. D 68, 083002 (2003), eprint arXiv:astro-ph/0306354. J. Yoo and M. Zaldarriaga, ArXiv e-prints eprint 0805.2155.
- Smith et al. (2007) K. M. Smith, O. Zahn, and O. Dore, Phys. Rev. D 76, 043510 (2007), eprint 0705.3980.
- Hirata et al. (2008b) C. M. Hirata, S. Ho, N. Padmanabhan, U. Seljak, and N. A. Bahcall, Phys. Rev. D 78, 043520 (2008b), eprint 0801.0644.
- (12) http://www.physics.princeton.edu/act; http://quiet.uchicago.edu/; http://pole.uchicago.edu;http://www.rssd.esa.int/index.php?project=planck; http://www.sdss3.org/cosmology.php;http://bolo.berkeley.edu/polarbear/.
- Peiris and Spergel (2000) H. V. Peiris and D. N. Spergel, ApJ 540, 605 (2000), eprint arXiv:astro-ph/0001393. T. Giannantonio, R. Scranton, R. G. Crittenden, R. C. Nichol, S. P. Boughn, A. D. Myers, and G. T. Richards, Phys. Rev. D 77, 123520 (2008), eprint 0801.4380. S. Ho, C. Hirata, N. Padmanabhan, U. Seljak, and N. Bahcall, Phys. Rev. D 78, 043519 (2008), eprint 0801.0642. R. A. C. Croft, A. J. Banday, and L. Hernquist, Mon. Not. Roy. Astron. Soc. 369, 1090 (2006), eprint astro-ph/0512380.
- Zaldarriaga et al. (2000) M. Zaldarriaga, U. Seljak, and L. Hui, Astrophys. J. 551, 48 (2001), eprint astro-ph/0007101.
- Hui and Gnedin (1997) L. Hui and N. Y. Gnedin, Mon. Not. Roy. Astron. Soc. 292, 27 (1997), eprint astro-ph/9612232.
- Gunn and Peterson (1965) J. E. Gunn and B. A. Peterson, Astrophys. J. 142, 1633 (1965). H. Bi and A. F. Davidsen, Astrophys. J. 479, 523 (1997), eprint astro-ph/9611062.
- Croft et al. (1998) R. A. C. Croft, D. H. Weinberg, N. Katz, and L. Hernquist, Astrophys. J. 495, 44 (1998), eprint astro-ph/9708018.
- McDonald (2003) P. McDonald, ApJ 585, 34 (2003), eprint arXiv:astro-ph/0108064.
- Viel et al. (2002) M. Viel, S. Matarrese, H. J. Mo, M. G. Haehnelt, and T. Theuns, Mon. Not. Roy. Astron. Soc. 329, 848 (2002), eprint astro-ph/0105233.
- Bernardeau et al. (2002) F. Bernardeau, S. Colombi, E. Gaztanaga, and R. Scoccimarro, Phys. Rept. 367, 1 (2002), eprint astro-ph/0112551.
- Xia and Viel (2009) J.-Q. Xia and M. Viel, JCAP 0904, 002 (2009), eprint 0901.0605.
- Zhao et al. (2008) G.-B. Zhao, L. Pogosian, A. Silvestri, and J. Zylberberg (2008), eprint 0809.3791.