Leveraging Offline Data from Similar Systems for Online Linear Quadratic Control
Abstract
“Sim2real gap”, in which the system learned in simulations is not the exact representation of the real system, can lead to loss of stability and performance when controllers learned using data from the simulated system are used on the real system. In this work, we address this challenge in the linear quadratic regulator (LQR) setting. Specifically, we consider an LQR problem for a system with unknown system matrices. Along with the state-action pairs from the system to be controlled, a trajectory of length of state-action pairs from a different unknown system is available. Our proposed algorithm is constructed upon Thompson sampling and utilizes the mean as well as the uncertainty of the dynamics of the system from which the trajectory of length is obtained. We establish that the algorithm achieves Bayes regret after time steps, where characterizes the dissimilarity between the two systems and is a function of and . When is sufficiently small, the proposed algorithm achieves Bayes regret and outperforms a naive strategy which does not utilize the available trajectory.
Index Terms:
Identification for control, Sampled Data Control, Autonomous Systems, Adaptive ControlI Introduction
Online learning of linear quadratic regulators (LQRs) with unknown system matrices is a well-studied problem. Many recent works have proposed novel algorithms with performance guarantees on their (cumulative) regret, defined as the difference between the cumulative cost with a controller from the learning algorithm and the cost with an optimal controller that knows the system matrices [1, 2, 3, 4]. However, these algorithms require long exploration times [5], which impedes their usage in many practical applications. To aid these algorithms, we propose to use offline datasets of state-action pairs either from an approximate simulator or a simpler model of the unknown system. We propose an online algorithm that leverages offline data to provably reduce the exploration time, leading to lower regret.
Leveraging offline data is not a new idea. Offline reinforcement learning [6], for instance, uses offline data to learn a policy which is used online. However, this leads to the problem of sim-to-real gap or distribution shift since the system parameters learned offline are different from the ones encountered online [7]. Although many methods have been proposed in the literature to be robust to such issues, in general, such policies are not optimal for the new system. Another approach is to utilize the offline data to warm-start an online learning algorithm. Such strategies have been shown to achieve an improved bound on the regret in multi-armed bandits [8, 9, 10, 11]. However, extending these algorithms to LQR design and establishing their theoretical properties remains unexplored, particularly for characterizing when they provide benefits over learning the policy in a purely online fashion.
Our algorithm provides a framework to incorporate offline data from a similar linear system111Two linear systems, characterized by system matrices and , , are said to be similar if they have the same order and their system matrices satisfy . for online learning, which provably achieves upper bound on the regret, where denotes the offline trajectory length and quantifies the heterogeneity between the two systems. Our algorithm utilizes both the system matrices estimated from offline data and the residual uncertainty. We show via numerical simulations that as increases, an improved regret can be achieved with a fairly small number of measurements from the online system.
Our algorithm uses Thompson Sampling (TS) which samples a model (system matrices) from a belief distribution over unknown system matrices, takes the optimal action based on the sample model, and subsequently updates the belief distribution using the observed feedback (cost). In the purely online setting, control of unknown linear dynamical systems using TS approach has been extensively studied [1, 12, 13, 14]. Under the assumption that the distribution of the true parameters is known, [3] established a (Bayes) regret bound. Recently, the same regret bound was established without that assumption [15, 2]. Finally, our work is also related to the growing literature on transfer learning for linear systems [16, 17, 18, 19]. However, unlike that stream, this work focuses on determining regret guarantees on online LQR control while leveraging offline data.
This work is organized as follows. Section II presents the problem definition and a summary of background material. Section III describes the offline data scheme. Section IV presents the proposed algorithm which is analyzed in Section V. In Section VI, we present additional numerical insights and discuss how this work extends to when data from multiple sources is available. Finally, Section VIII summarizes this work and outlines directions for future work.
Notation: , , , and denotes the operator norm, Frobenius norm, spectral norm, and the trace, respectively. For a positive definite matrix (denoted as ), and denote its maximum and minimum eigenvalue, respectively. denotes the identity matrix and denotes a matrix with independent standard normal entries. Given a set and a sample , represents a sampling operator that ensures .
II Problem Formulation
We first review the classical LQR control problem and then describe our model followed by the formal problem statement.
II-A Classical LQR Design
Let denote the state and denote the control at time . Let and be the system matrices. Further, let and . Then, for and given matrices , consider a discrete-time linear time-invariant system with the dynamics and the cost function
| (1) | ||||
where is the system noise assumed to be white and . The classical LQR control problem is to design a closed-loop control with that minimizes the following cost:
| (2) |
When is known and under the assumption that is stabilizable, the optimal policy is and the corresponding cost is where
is the gain matrix and is the unique positive definite solution to the Riccati equation
II-B Model and Problem Statement
Consider a system characterized by equation (1) with unknown and access to an offline dataset obtained through an approximated simulator. The simulator is assumed to be characterized by the following auxiliary system which is different than and is also unknown.
| (3) |
where, and denotes the state and the control, respectively, at time instant , denotes the system matrices, and . The offline data represents a trajectory of length of state-action pairs . We can characterize and as and , respectively, where (resp. ) represents the change in the system matrices (resp. ) from (resp. ). Thus, the system characterized by equation (1) can be expressed as
| (4) |
In this work, we assume that there exists a known constant such that , where . Let denote the filtration that represents the knowledge up to time during the online process. Similarly, let denote the filtration that represents the knowledge corresponding to the offline data. Then, we make the following standard assumption on the noise process [20].
Assumption 1.
There exists a filtration and such that for any and , are -measurable and are -measurable. Further, and are individually martingale difference sequences. Finally, for ease of exposition, we assume that and .
Assuming that the parameter is a random variable with a known distribution , we quantify the performance of our learning algorithm by comparing the cumulative cost to the infinite-horizon cost attained by the LQR controller if the system matrices defined by were known a priori. Formally, we quantify the performance of our algorithm through the cumulative Bayesian regret defined as follows.
| (5) |
where the expectation is with respect to , and any randomization in the algorithms used to process the offline and online data. This metric has been previously considered for online control of LQR systems [3].
Problem 1.
The aim of this work is to find a control algorithm that minimizes the expected regret defined in (5) while utilizing the offline data .
III Offline Data-Generation
In this work, we do not consider a particular algorithm from which the offline data is generated. As we will see later, any algorithm that satisfies the following two properties can be used to generate the offline dataset . Let denote an algorithm that is used to generate the offline data. Further, let at time , denote the precision matrix of Algorithm . We assume the following on algorithm .
Assumption 2 (Offline Algorithm).
For a given , with probability of at least , Algorithm satisfies
-
1.
.
-
2.
For , .
IV Thompson Sampling with Offline Data for LQR (TSOD-LQR) Algorithm
Although is considered to be stabilizable, an algorithm based on Thompson sampling may sample parameters that are non-stabilizable. Thus, for some fixed constants , we assume that where:
| (6) |
The assumption that leads to the following result.
Lemma 1 (Proposition 5 in [15]).
The set is compact. For any , is stabilizable and there exists a constant , where .
The idea behind Algorithm TSOD-LQR is to augment the data collected online corresponding to system with data collected from the simulated system. To achieve this, we utilize the posterior of to characterize the prior for learning .
Our algorithm works as follows and is summarized in Algorithm 1. At each time , Algorithm 1 samples a parameter according to the following equation:
| (7) |
where, for any ,
| (8) |
Once the parameter is sampled, the gain matrix is determined, the corresponding control is applied, and the system transitions to the next state . Algorithm 1 then updates and using the following equations:
| (9) | ||||
| (10) |
Observe that Algorithm 1 does not require the information of the distribution (the distribution of ). This highlights that Algorithm 1 works even when the distribution is not known, i.e., the assumption that the distribution is known is required only for the analysis. Our first result, proof of which is deferred to the Appendix, characterizes the confidence bound on the estimation error of .
Theorem IV.1.
Suppose that, for a given , Algorithm is used to collect the offline data for time steps and Assumption 1 holds. Then, for any , holds with probability .
In the next section we will establish an upper bound on the regret for Algorithm 1.
V Regret Analysis
Following the standard technique [15, 2] we begin by defining two concentration ellipsoids and .
where . Further, introduce the event and the event .
The following result will be useful to establish that the event holds with high probability.
Lemma 2.
Suppose that . Then, .
Proof.
Remark 1.
The requirement that means that the length of the offline trajectory must be greater than the learning horizon . This is not an onerous assumption especially when a simulator is used to generate the offline data. Further, since the auxiliary system need not be the same as the true system, data available from any other source (such as a simpler model) can also be used in this work. Finally, in cases where generating large amounts of data is not possible through a simulator (for example, when a high-fidelity simulator is used), one can select for the simulations. However, this requires that the horizon length to be known a priori.
Conditioned on the filtration and event , following analogous steps as in [15], the expected regret of Algorithm 1 can be decomposed as
| (11) |
where
We will now characterize an upper bound on each of these terms separately to bound the regret of Algorithm 1.
Lemma 3.
The term .
Proof.
Since the distribution of is assumed to be known, from the posterior sampling lemma [22, Lemma 1], it follows that and the claim follows. ∎
Lemma 4.
The term is upper bounded as .
Proof.
The proof directly follows by expanding the terms in the summation and the fact that is positive definite. ∎
Let and . Then, the following two results, proofs of which are in the appendix, bound and .
Lemma 5.
For a given , suppose that . Then, with probability and under event ,
where contains problem dependent constants and polylog terms in .
Lemma 6.
For a given , suppose that . Then, under event and with probability ,
Theorem V.1.
Proof.
Since we assume that , . For substituting the expression of in Lemma 6 and taking the product yields
We begin with an upper bound for term .
Observe that by Jensen’s inequality
where we used that , law of total expectation, and Lemma 9. Thus, term is upper bounded by . By using analogous algebraic manipulations, term is upper bounded by . Using Lemma 12 followed by Lemma 9, term is upper bounded by
Combining the upper bounds for terms , , and yields an upper bound for . The bound for is obtained analogously and has been omitted for brevity. Combining the bounds for and establishes the claim. ∎
Remark 2.
From Theorem V.1, using offline data from system is beneficial if is sufficiently small.
Corollary 1.
Proof.
By substituting , the proof follows directly from Theorem V.1. ∎
Since , when offline data from the same system is available, Corollary 1 suggests that the regret of Algorithm 1 is bounded by , where contains logarithmic terms in . Such bounds are known to be possible, for instance when or is known [21].
Theorem V.1 provides a general regret bound for Algorithm 1 when an arbitrary algorithm is used for generating data . The next result provides a regret bound for a particular algorithm, i.e., Algorithm TSAC [2] is used. To characterize a state-bound for Algorithm TSAC, we assume (cf. [2, Assumption 1]) that , where
| (13) |
Theorem V.2.
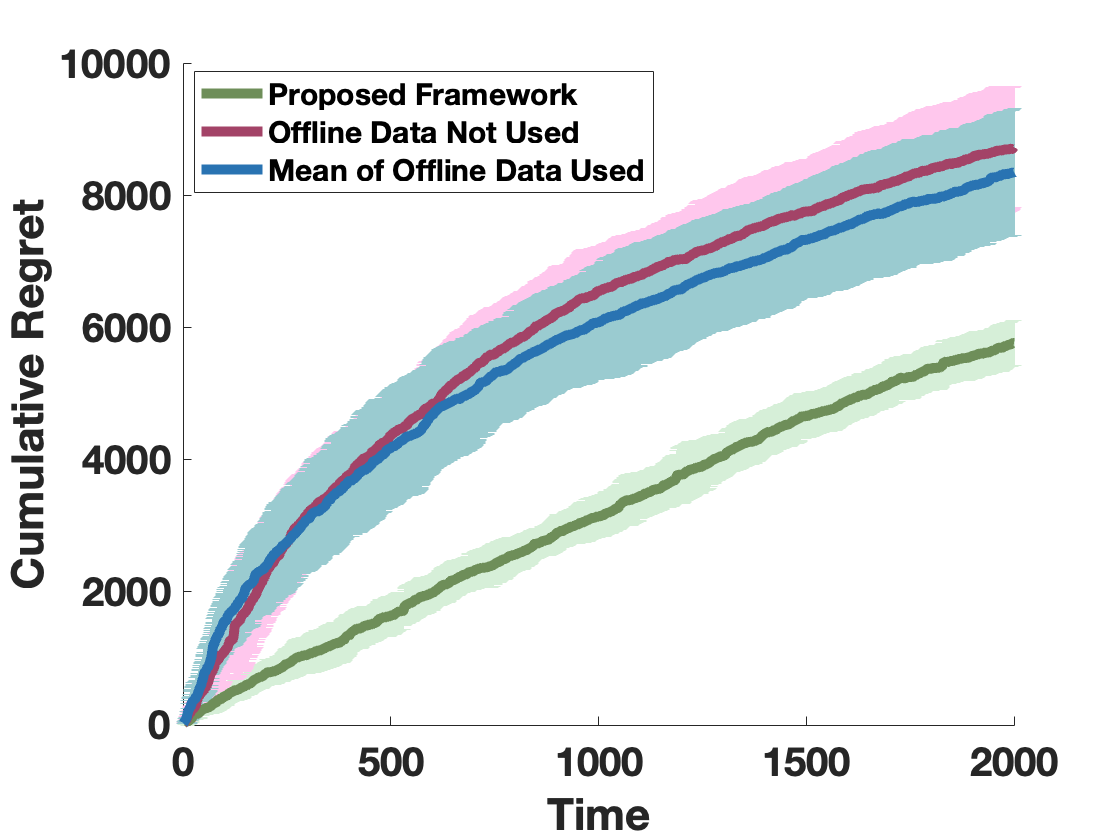
VI Numerical Results
We now illustrate the performance of Algorithm 1 through numerical simulations. The system matrices were selected as
For all of our numerical results, we run simulations and present the mean and the standard deviation for each scenario. Figure 1 presents the numerical results that compare the cumulative regret of Algorithm 1 for . From Figure 1, the proposed approach outperforms al algorithm that either does not utilize the available data or that only uses computed from the offline data, implying that utilizing estimate and the uncertainty from dissimilar systems can be beneficial.
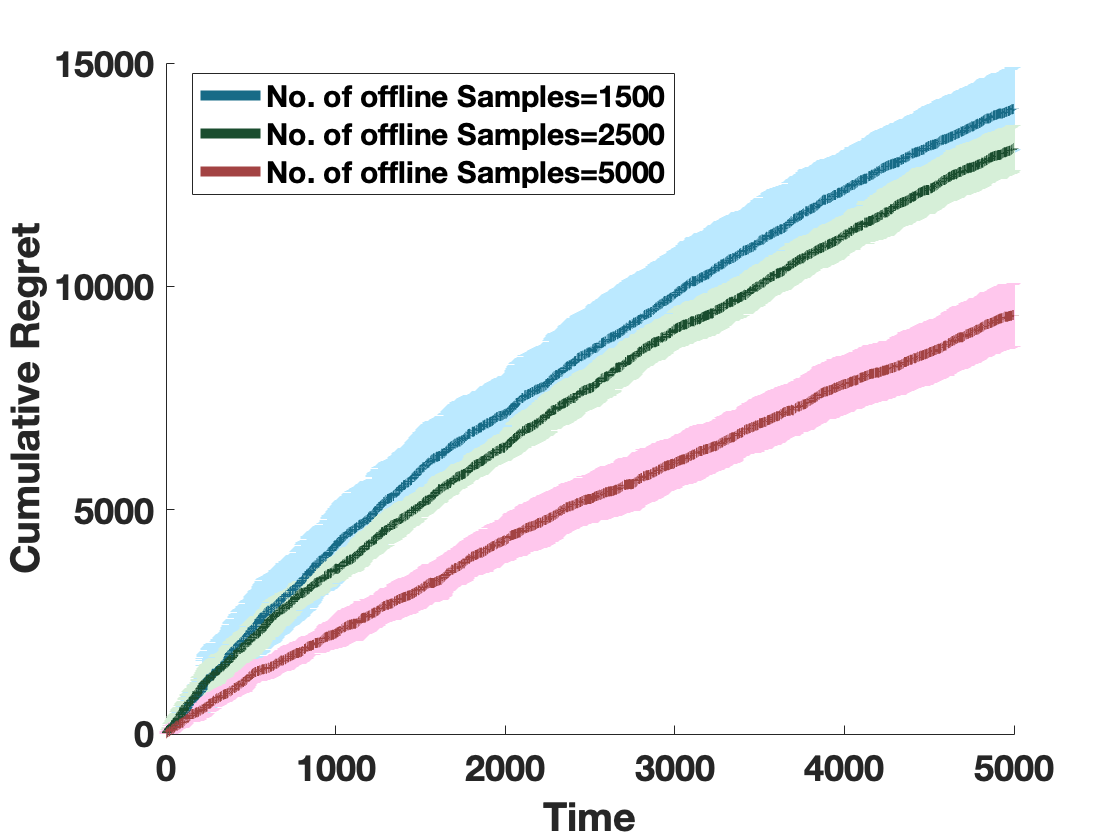
VII Extension to Multiple Offline Sources
We now briefly describe how this framework generalizes to when multiple trajectories are available from systems , respectively.
By defining the -least squares error as
and minimizing with respect to yields
Then, following analogous steps as in the proof of Theorem IV.1, we obtain
With these modifications, we can now utilize Algorithm 1 for online control of LQR when offline data from multiple dissimilar sources are available. By defining and and by following analogous steps as in the proof of Theorem V.1, a similar upper bound on the cumulative regret of Algorithm 1 can be obtained.
VIII Conclusion
In this work, we considered an online control problem of an LQR when an offline trajectory of length of state-action pairs from a similar linear system, also of unknown system matrices, is available. We design and analyze an algorithm that utilizes the available data from the trajectory and establish that the algorithm achieves regret, where is a decreasing function of . Finally, we provide additional numerical insights by comparing our algorithm with two other approaches.
IX Acknowledgement
We greatly acknowledge the valuable comments by Dr. Gugan Thoppe from the Indian Institute of Science (IISc).
-A Proof of Theorem IV.1
From equation (10) and using equation (1)
For any vector , it follows that
Selecting yields,
Since , it follows that . Further, since , it follows by using the triangle inequality that . Thus, we obtain
The first term is bounded by [23, Corollary 1] with probability as
Further, the second term is bounded with probability by from Assumption 2. Finally, using the assumption that an upper bound on is known, the third term is bound as
Combining the three bounds establishes the claim.
-B Proof of Lemma 5
From the fact that every sample and the true parameter belongs to the set and from basic algebraic manipulations, we obtain . We now bound the term with the expectation using Cauchy-Schwarz as
| (15) |
Adding and subtracting in the term and applying triangle inequality yields
where we used the fact that on , and holds and the fact that is increasing in . Thus, by substituting the value of it follows that
Using the fact that followed by using Lemma 13 it follows that, with probability ,
where we used the fact that . Using Lemma 12 establishes the claim.
-C Proof of Lemma 6
The proof of Lemma 6 resembles that of [15, Lemma 1] and so we only provide an outline of the proof, highlighting the differences.
Let and let and . Further, let . Then,
Thus, the term can be re-written as
| (16) |
The result of Lemma 6 can then be obtained by adding the bound characterized in the following two lemmas.
Lemma 7.
Proof.
Since for any matrix , and that is distributed as , we obtain
where . Using [15, Proposition 7] followed by [15, Proposition 8] yields
| (17) |
where . Since on , and , applying [15, Proposition 11]222Proposition 11 can be found in the proof of [15, Proposition 9]. yields
Substituting in equation (17) yields
where we used the law of iterated expectations. Substituting yields
Applying Cauchy Schwarz inequality establishes the claim. ∎
Lemma 8.
Proof.
Let and be the probability distribution function of and , respectively. Following similar steps as in [15] yields where denotes the KL divergence between two distributions. Using Lemma 11 and considering the expectation and the summation operators from yields
The claim then follows by using Cauchy Schwarz inequality. ∎
-D Additional Lemmas
Lemma 9.
For any and any , .
Proof.
Since , using triangle inequality
Using the property of the matrix norm and since the sampled parameter is an element of due to the rejection operator,
From this point on, the proof is analogous to the proof of [3, Lemma 2] and has been omitted for brevity. ∎
Lemma 10.
For the set defined in equation (V), holds for Algorithm TSAC.
Proof.
Suppose that for any in an th iteration, holds. Then,
where in the last inequality we used that the sampled parameter is an element of . Applying this iteratively yields which further yields that Let . We now bound . Observe that Similarly, . Further, following analogous steps, we can bound and . Using the fact that and are independent, yields . The proof for the case when holds, for any in an th iteration, is analogous to that of Lemma 9. ∎
Lemma 11.
Let denote the probability distribution function of . Then, , where .
Proof.
The proof is analogous to that of [15, Proposition 10] and thus has been omitted for brevity. ∎
Lemma 12.
For a given , suppose that and . Then, with probability ,
Proof.
The proof directly follows from the AM-GM inequality and Assumption 2. ∎
Lemma 13.
For a given , suppose that and . Then, with probability ,
References
- [1] Y. Abbasi-Yadkori and C. Szepesvári, “Regret bounds for the adaptive control of linear quadratic systems,” in Proceedings of the 24th Annual Conference on Learning Theory, pp. 1–26, JMLR Workshop and Conference Proceedings, 2011.
- [2] T. Kargin, S. Lale, K. Azizzadenesheli, A. Anandkumar, and B. Hassibi, “Thompson sampling achieves regret in linear quadratic control,” in Conference on Learning Theory, pp. 3235–3284, PMLR, 2022.
- [3] Y. Ouyang, M. Gagrani, and R. Jain, “Control of unknown linear systems with thompson sampling,” in 2017 55th Annual Allerton Conference on Communication, Control, and Computing (Allerton), pp. 1198–1205, IEEE, 2017.
- [4] A. Cohen, T. Koren, and Y. Mansour, “Learning linear-quadratic regulators efficiently with only regret,” in International Conference on Machine Learning, pp. 1300–1309, PMLR, 2019.
- [5] Y. Li, “Reinforcement learning in practice: Opportunities and challenges,” arXiv preprint arXiv:2202.11296, 2022.
- [6] R. F. Prudencio, M. R. Maximo, and E. L. Colombini, “A survey on offline reinforcement learning: Taxonomy, review, and open problems,” IEEE Transactions on Neural Networks and Learning Systems, 2023.
- [7] W. Zhao, J. P. Queralta, and T. Westerlund, “Sim-to-real transfer in deep reinforcement learning for robotics: a survey,” in 2020 IEEE symposium series on computational intelligence (SSCI), pp. 737–744, IEEE, 2020.
- [8] P. Shivaswamy and T. Joachims, “Multi-armed bandit problems with history,” in Artificial Intelligence and Statistics, pp. 1046–1054, PMLR, 2012.
- [9] C. Zhang, A. Agarwal, H. D. Iii, J. Langford, and S. Negahban, “Warm-starting contextual bandits: Robustly combining supervised and bandit feedback,” in Proceedings of the 36th International Conference on Machine Learning, vol. 97, pp. 7335–7344, PMLR, 2019.
- [10] C. Kausik, K. Tan, and A. Tewari, “Leveraging offline data in linear latent bandits,” arXiv preprint arXiv:2405.17324, 2024.
- [11] B. Hao, R. Jain, T. Lattimore, B. Van Roy, and Z. Wen, “Leveraging demonstrations to improve online learning: Quality matters,” in International Conference on Machine Learning, pp. 12527–12545, PMLR, 2023.
- [12] H. Mania, S. Tu, and B. Recht, “Certainty equivalence is efficient for linear quadratic control,” Advances in Neural Information Processing Systems, vol. 32, 2019.
- [13] D. Baby and Y.-X. Wang, “Optimal dynamic regret in lqr control,” Advances in Neural Information Processing Systems, vol. 35, pp. 24879–24892, 2022.
- [14] T.-J. Chang and S. Shahrampour, “Regret analysis of distributed online lqr control for unknown lti systems,” IEEE Transactions on Automatic Control, 2023.
- [15] M. Abeille and A. Lazaric, “Improved regret bounds for thompson sampling in linear quadratic control problems,” in International Conference on Machine Learning, pp. 1–9, PMLR, 2018.
- [16] T. Guo and F. Pasqualetti, “Transfer learning for lqr control,” arXiv preprint arXiv:2503.06755, 2025.
- [17] T. Guo, A. A. Al Makdah, V. Krishnan, and F. Pasqualetti, “Imitation and transfer learning for lqg control,” IEEE Control Systems Letters, vol. 7, pp. 2149–2154, 2023.
- [18] L. Li, C. De Persis, P. Tesi, and N. Monshizadeh, “Data-based transfer stabilization in linear systems,” IEEE Transactions on Automatic Control, vol. 69, no. 3, pp. 1866–1873, 2023.
- [19] L. Xin, L. Ye, G. Chiu, and S. Sundaram, “Learning dynamical systems by leveraging data from similar systems,” IEEE Transactions on Automatic Control, 2025.
- [20] Y. Abbasi-Yadkori, D. Pál, and C. Szepesvári, “Improved algorithms for linear stochastic bandits,” Advances in neural information processing systems, vol. 24, 2011.
- [21] A. Cassel, A. Cohen, and T. Koren, “Logarithmic regret for learning linear quadratic regulators efficiently,” in International Conference on Machine Learning, pp. 1328–1337, PMLR, 2020.
- [22] I. Osband and B. Van Roy, “Posterior sampling for reinforcement learning without episodes,” arXiv preprint arXiv:1608.02731, 2016.
- [23] Y. Abbasi-Yadkori, D. Pál, and C. Szepesvári, “Online least squares estimation with self-normalized processes: An application to bandit problems,” arXiv preprint arXiv:1102.2670, 2011.