July 30, 2025
Light-by-light scattering in ultra-peripheral heavy-ion collisions
at low diphoton masses
Abstract
We present a study of photon-photon scattering in the mass range GeV. We extend earlier calculations of this cross section for 5 GeV into the low mass range where photoproduction of the pseudoscalar resonances , contributes to two-photon final states. We present the elementary photon-photon cross section as a function of diphoton mass arising from lepton and quark loop diagrams, and the visible cross section obtained with the gamma-gamma decay branching fractions of the resonances , , , , . We derive the corresponding cross sections in ultra-peripheral Pb-Pb collisions at = 5.02 TeV by folding the elementary cross section with the heavy-ion photon fluxes. We consider the dominating background of the two photon final state which arises from gamma decays of photoproduced -pairs. Such -pairs contribute to the background when only two of the four decay photons are within the experimental acceptance, while the other two photons escape undetected. We reduce this background by applying cuts on asymmetries of transverse momenta of the two photons and indicate how the background can be further suppressed using a multivariate sideband analysis. We present the cross section for the signal and the background at midrapidity 0.9, and in the forward rapidity range 2.0 4.5.
1 Introduction
The properties of light have at all times fascinated physicists. The development of instruments for measuring light, and the design of experiments using light, have resulted in fundamental contributions to our current knowledge of modern physics. Our present understanding of the behaviour of light at the classical level is conveniently expressed by Maxwell’s equations. These equations are linear in the electric currents as sources, and in the resulting electric and magnetic fields E and B. At the classical level, two electromagnetic waves in vacuum will superimpose, and will pass through each other without scattering. With the emergence of quantum mechanics, first attempts to formulate equations for the scattering of photons off each other were formulated in 1925 Schaposchnikow:1925 . Shortly thereafter, Louis de Broglie associated possible solutions of these equations to non-trivial scattering between two photons, in violation of the superposition principle Broglie:1926 . This breakdown of the superposition principle can be incorporated in non-linear Lagrangians, which result in non-linear field equations. Attempts to solve the infinite Coulomb energy of a point source led to Born-Infeld electrodynamics, which effectively confirms the linearity down to some length scale, and introduces non-linearities at smaller scales Born:1925 . Virtual electron-positron pairs were suggested in 1933 to be at the origin of this photon-photon scattering Halpern:1933 . The continued study of photon-photon scattering led to the Euler-Kockel-Heisenberg Lagrangian which modifies the classical Maxwell’s equation in vacuum by leading non-linear terms Heisenberg:1936 . A more detailed account of the history of photon-photon scattering can be found in a recent review Scharnhorst:2017wzh .
The advent of accelerating heavy-ions to ultra-relativistic energies with large associated photon fluxes provides new opportunities in gaining insight into the mechanisms of photon-photon scattering dEnterria:2013zqi ; Klusek-Gawenda:2016euz . At these energies, not only lepton and quark loop diagrams constitute the signal, but also meson-exchange currents are predicted to contribute Klusek-Gawenda:2013rtu . Such measurements in heavy-ion collisions hence extend photon-photon scattering from a pure QED issue to a subject connecting QED with QCD topics. This QED-QCD connection is, for example, an important ingredient in the quantum electrodynamical calculation of the muon anomalous moment (see e.g. Bennett:2006fi , Colangelo:2017urn and references therein). In these calculations, light-by-light diagrams appear inside more complicated QCD-QED diagrams. There are proposals to study such diagrams in double back-Compton scattering using high-power lasers Bula:1996st .
First evidence of diphoton measurements in ultra-peripheral heavy-ion collisions have been reported by the ATLAS and CMS Collaborations Aaboud:2017bwk ; Sirunyan:2018fhl . These data are, however, restricted to photon-photon invariant masses W 5 and 6 GeV for the CMS and ATLAS analysis, respectively. ATLAS measured a fiducial cross section of (stat.) (syst.) nb and theoretical calculations (including experimental acceptance) gave nb dEnterria:2013zqi and nb Klusek-Gawenda:2016euz . ATLAS comparison of its experimental results to the predictions from Ref. Klusek-Gawenda:2016euz shows a reasonable agreement. Only 13 events were identified in the ATLAS data sample, with an expectation of 7.3 signal events and 2.6 background events from Monte Carlo simulations Aaboud:2017bwk . Recently, the CMS Collaboration measured the same process but for a slightly lower threshold of diphoton invariant mass Sirunyan:2018fhl . The measured fiducial light-by-light scattering cross section, (stat.) (syst.) (theo.) nb was obtained. The CMS measured value is in good agreement with the result obtained according to Ref. Klusek-Gawenda:2018ijg . It is important to further test the light-by-light scattering - for different energies and with a better precision.
The purpose of the study presented here is to examine the possibility of measuring photon-photon scattering in ultra-peripheral heavy-ion collisions at LHC energies in the range GeV. At lower diphoton masses, photoproduction of meson resonances plays a role in addition to the Standard Model box diagrams Lebiedowicz:2017cuq , as well as double photon fluctuations into light vector mesons Klusek-Gawenda:2016euz or two-gluon exchanges Klusek-Gawenda:2016nuo .
In the present study we consider also background from the process measured e.g. by the Belle Uehara:2009cka and Crystal Ball Marsiske:1990hx collaborations. In Ref. Klusek-Gawenda:2013rtu a multi-component model, which describes the Belle data, has been constructed. This model was used next to make predictions for the reaction Klusek-Gawenda:2013rtu . If only two photons from different neutral pions are measured within the experimental acceptance such an event could be wrongly identified as scattering. Extra cuts need to be imposed to reduce or eliminate this background.
This paper is organized as follows. In section 2, the theoretical framework for calculating photon-photon scattering is outlined, the background from is reviewed, and the cross section for photoproduction of resonances is studied. The experimental acceptances used for the given photon-photon scattering cross sections are described in section 3. The nuclear cross sections for light-by-light scattering in ultra-peripheral lead-lead collisions at the energy TeV are given in section 4. The treatment of the background is discussed in section 5, and conclusions are presented in section 6.
2 Theoretical approach for the signal and background
We consider nuclear ultra-peripheral collisions (UPCs). In Fig. 1 we illustrate the signal ( scattering) which we take to be the dominant box mechanism (see Klusek-Gawenda:2016euz ). Panel (b) shows a diagram for -channel pseudoscalar/scalar/tensor resonances which also contributes to the process. We also show (diagram (c)) the process, which leads to what we consider as the dominant background when only one photon from each decay is detected. Other processes such as diffractive multi-hadron production that result in only two measured photons may also contribute to the background, but can be reduced using the techniques shown here. Being strongly dependent on the acceptance and detection thresholds, these processes need to be experimentally assessed and are beyond the scope of the current study.
(a)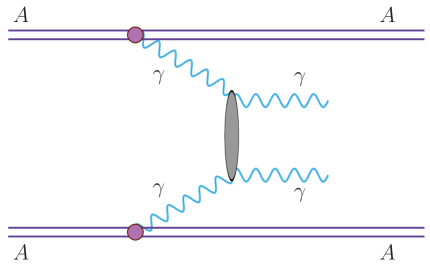 (b)
(b)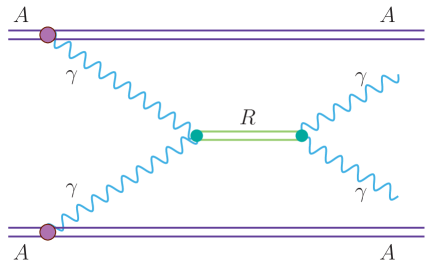 (c)
(c)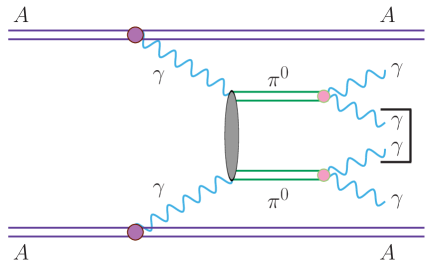
In the equivalent photon approximation (EPA) in impact parameter space, the phase space integrated cross section for reaction is expressed through the five-fold integral,
| (1) | |||||
where is a pair of photons or neutral pions. and are invariant mass and rapidity of the outgoing system. The energy of the photons is expressed through . The variables and are impact parameters of the photon-photon collision point with respect to parent nuclei 1 and 2, respectively, and is the standard impact parameter for the collision. The absorption factor assures UPC implying that the nuclei do not undergo nuclear breakup. The photon fluxes () are expressed through a nuclear charge form factor of the nucleus. In our calculations we use a realistic form factor which is a Fourier transform of the charge distribution in the nucleus. More details can be found e.g. in Ref. KlusekGawenda:2010kx .
The elementary cross section in Eq. (1) for the scattering is calculated within LO QED with fermion loops (see left panel of Fig. 1 in Ref. Klusek-Gawenda:2016euz ). The one-loop box diagrams were calculated with the help of the Mathematica package FormCalc Hahn:1998yk and the LoopTools library based on vanOldenborgh:1989wn to evaluate one-loop integrals. In the numerical calculations we include box diagrams with leptons and quarks only. Inclusion of the -boson loops is not necessary because this contribution is important only for energies larger than twice the boson mass Lebiedowicz:2013fta . Our results have been compared to and agree with Ref. Jikia:1993tc ; Bern:2001dg ; Bardin:2009gq . Other production mechanisms were considered in Ref. Klusek-Gawenda:2016euz ; Klusek-Gawenda:2016nuo , but their contributions are much smaller in the low diphoton mass region 5 GeV considered here.
2.1 Pion pair production
The elementary cross section for was studied in detail in Ref. Klusek-Gawenda:2013rtu . Both and reactions were considered within the physical framework describing existing experimental data. Two of us calculated, for the first time, both the total cross section and angular distributions and demonstrated significance of resonances, continuum and pQCD mechanisms in these processes. Following Klusek-Gawenda:2013rtu , here we include nine resonances, continuum, Brodsky-Lepage and handbag mechanisms. A detailed formalism and description of these sub-processes can be found in Ref. Klusek-Gawenda:2013rtu . The angular distribution for the process can be written in standard form with the help of the photon helicity-dependent amplitudes, as a function of , where is the pion scattering angle
| (2) |
We use the formalism sketched above to calculate the multi-dimensional distribution
| (3) | |||||
for the reaction. Here, , are the rapidities of the first and second pion, is the transverse momentum of the pions (identical in our LO approximation) and is the pion center-of-mass scattering angle. Integration of this formula allows comparison with Eq. (1).
A dense three-dimensional grid of the triple differential cross section of Eq. (3) is prepared in a broad range of rapidities of both neutral pions and transverse momentum of one of them. A Monte Carlo code has been written to include radiative decays of both pions. As the pions are spin-0 mesons, the decays are taken to be isotropic in the rest frames of the decaying pions. Lorentz boosts are performed to obtain the kinematic distributions of photons in the laboratory (nucleus-nucleus center of mass) frame. Then logical conditions and cuts on the photons are imposed and distributions in different variables are obtained by an appropriate binning in the selected kinematic variable. The distributions are presented below and different experimental requirements are examined in order to estimate whether the process can be observed.
2.2 Resonance contributions
The angular distribution for the -channel resonances is typically used in calculating Feynman diagram contributions in the form:
| (4) |
where denotes the polar angle between the beam direction and the outgoing nucleon in the c.m. frame, is the invariant mass of the system. The amplitudes for the production through the -channel exchange of a pseudoscalar/scalar meson are written as
| (5) |
Here we use the same notation as in Ref. Klusek-Gawenda:2013rtu . In the present analysis we take into account only pseudoscalar and scalar mesons: , , , , . Their masses , total widths and branching ratios are taken from the PDG Patrignani:2016xqp .
To calculate a resonance that decays into two photons, we use the following expression
| (6) | |||||
for the calculation of the nuclear cross section. This formula includes the unpolarized differential elementary cross section of Eq. (4). Further discussions of the cross section for the mesonic resonant states in the context of light-by-light scattering are in Ref. Lebiedowicz:2017cuq .
3 Experimental acceptance and resolution
We briefly summarize the experimental acceptance for measuring two-photon final states in Run 3 and beyond at the LHC, and describe the experimental resolution used in deriving our results. To illustrate our case, we take the acceptance of the ALICE central barrel at mid-rapidity, and the LHCb spectrometer acceptance at forward rapidities.
The ALICE central barrel covers the pseudorapidity range 0.9 ALICE:2014 . Within this range, ALICE is capable of measuring photons by different methods. First, electromagnetic calorimeters EMCal and PHOS cover part of the solid angle EMCal:2010 ; PHOS:2014 . Second, photons can be detected by the photon conversion method (PCM). In this approach, photons which convert into pairs in the detector material are reconstructed by detecting the two charged tracks of the lepton pair. Whereas the photon measurement can be carried out with high efficiency but limited solid angle by the electromagnetic calorimeters, the measurement by PCM covers the full solid angle of the central barrel but suffers from reduced efficiency. Additionally, hybrid measurements are possible with one photon being detected by the calorimeters, and the other photon being reconstructed by the PCM. Analyses of and meson production in proton-proton collisions at = 8 TeV by PCM in the ALICE central barrel resulted in a mass resolution of the meson 5 MeV (see Fig. 4 in Ref. Acharya:2017tlv ), from which a PCM energy resolution for single photons of 1.3 % is deduced. For the azimuthal angular resolution , we choose a value of = 0.02 in order to illustrate the different behaviour of scalar and vector asymmetries explained and used below for suppressing the background. A comparative study of photon measurements by electromagnetic calorimeters to the PCM for measuring light-by-light scattering in the energy range considered, as well as a comprehensive analysis of the experimental resolutions, requires detailed studies of the response of the detectors used. Such an analysis is beyond the scope of this paper.
LHCb is fully instrumented in the pseudorapidity range with tracking, calorimetry and particle identification. Tracks can be reconstructed down to a transverse momentum of about 100 MeV, and photons down to a transverse energy of about 200 MeV. In this study we assume that any photon with MeV and will be detected by LHCb, while photons outside this region are undetected. The energy resolution is parametrized as AbellanBeteta:2012dd :
| (7) |
where is the photon energy in GeV. These fiducial requirements and resolution allow us to make rough estimates for the feasibility of observing light-by-light scattering: a full study using the LHCb detector simulation would be necessary to obtain precise results (Ref. Clemencic:2011zza ).
The fiducial regions used in the present study are summarized in Table 1. In the following they will be named “ALICE-fiducial” or “LHCb-fiducial” for brevity. It should be noted that for massless particles in the final state, and , as well as rapidity and pseudorapidity are identical.
| experiment | pseudorapidity range | energy cut |
|---|---|---|
| ALICE | -0.9 0.9 | 0.2 GeV |
| LHCb | 2.0 4.5 | 0.2 GeV |
4 Cross sections
We present the total cross section for different contributions to the diphoton final state in Table 2. In this table, the total cross section is listed for two ranges of photon-photon invariant mass. The first range is from 0 to 2 GeV, with the second range for values larger than 2 GeV. We take = 50 GeV for fermionic boxes, = 5 GeV for the background (it is negligible above = 5 GeV) and for resonances.
| Energy | GeV | 2 GeV | ||
|---|---|---|---|---|
| Fiducial region | ALICE | LHCb | ALICE | LHCb |
| boxes | 4 890 | 3 818 | 146 | 79 |
| background | 135 300 | 40 866 | 46 | 24 |
| 722 573 | 568 499 | |||
| 54 241 | 40 482 | |||
| 9 | 5 | |||
| 4 | 2 | |||
| 2 | 1 | |||
The largest cross section is obtained for resonance production. The background contribution dominates over the signal up to GeV, however, as discussed in the following, can be reduced. Comparing results for GeV, the cross section for light-by-light scattering at midrapidity is about a factor 2 larger than at forward rapidity. The cross sections for both fermionic box and resonant signal are similar for the ALICE and LHCb fiducial regions.
4.1 Differential cross section at midrapidity
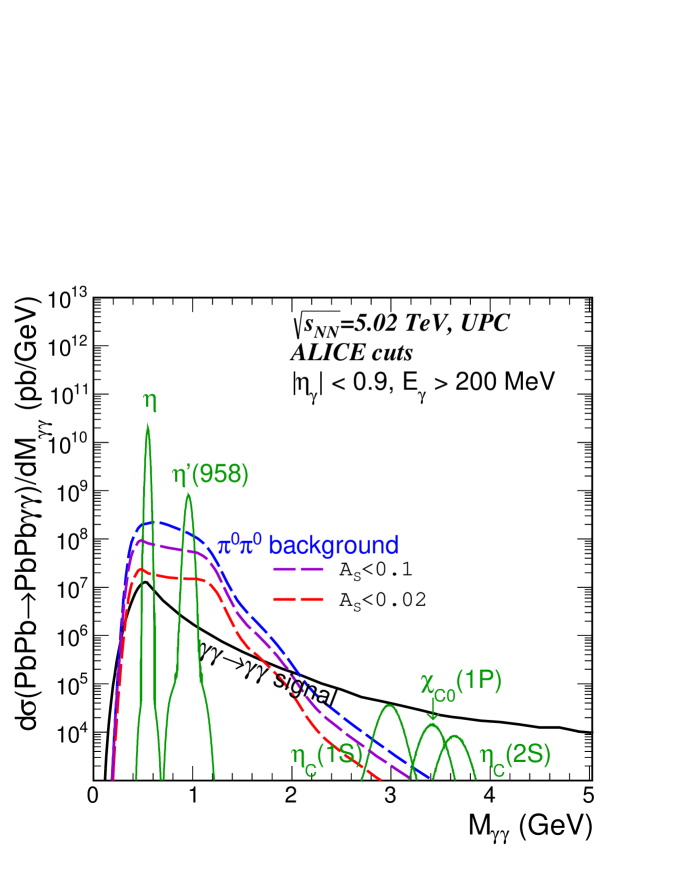
First we present some distributions within the ALICE fiducial region. The invariant mass distribution of two photon final states contains different contributions of signal and background as discussed in sections 2. In Fig. 2, the contribution to the signal due to the Standard Model boxes is shown by the solid black line. The contributions to the signal by the different meson resonances are shown by the solid green lines, while the dashed blue line represents the background as discussed in section 2.1. The background shown in Fig. 2 is composed of events where exactly two out of the four decay photons are within the fiducial volume, with the condition that each of the pair contributes one photon. At low invariant photon masses 1.5 GeV, this background dominates over the signal by about an order of magnitude but can be reduced by taking into account the different phase space distribution of the signal and the background.
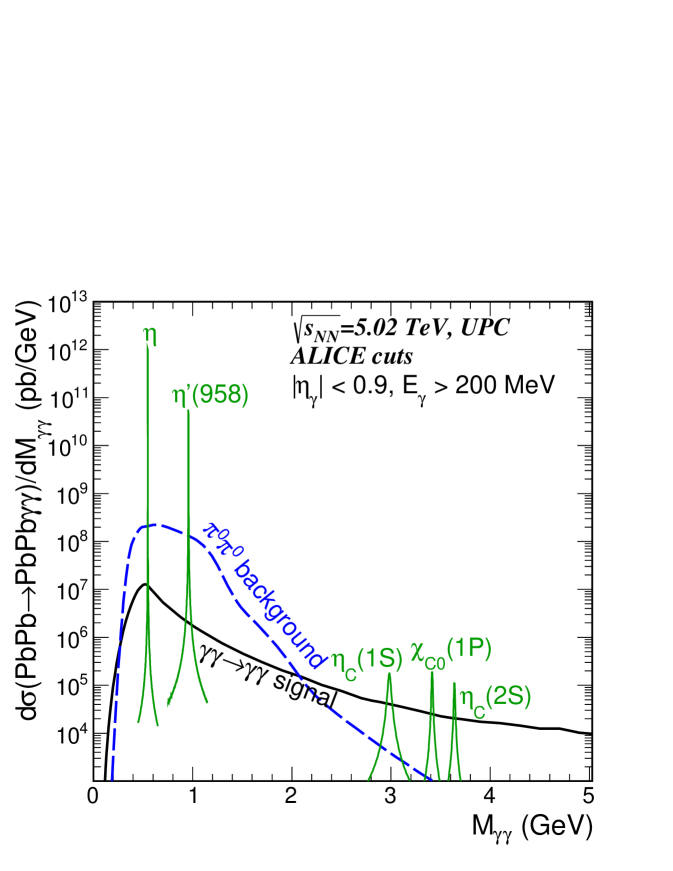
(a) 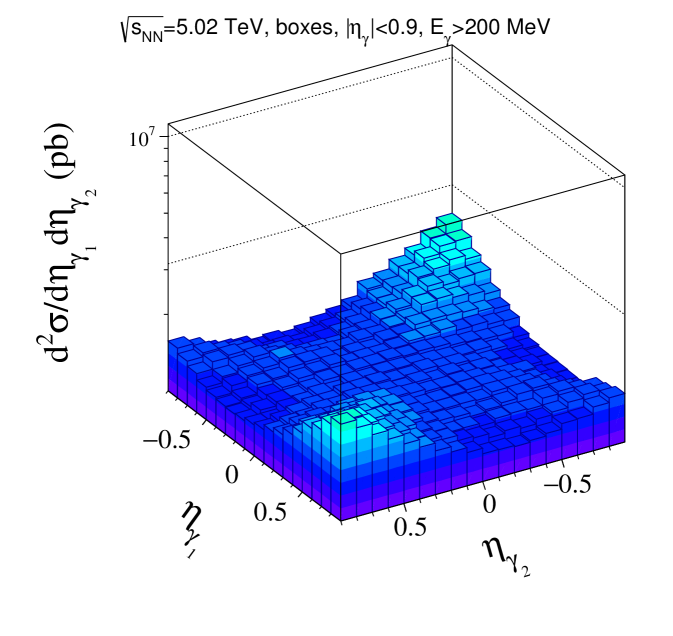 (b)
(b) 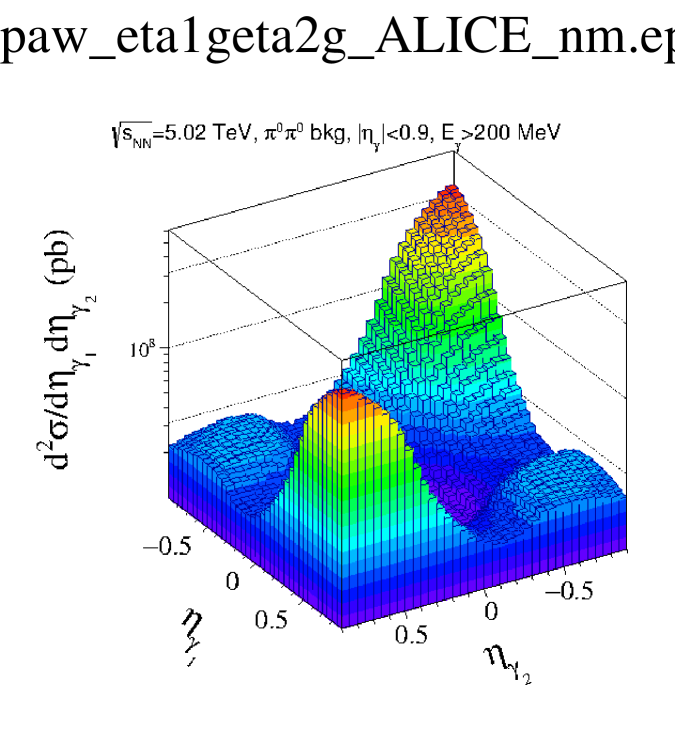
The two-dimensional distribution in rapidity of the first and second photon for signal and background is shown in Fig. 3 . The two distributions are peaked at forward and backward rapidities and are qualitatively rather similar, but differ by about two orders of magnitude. This figure shows that cuts on could be used to reduce the background. However this leads to marginal improvements due to the similarity in the shape of signal and background.
4.2 Differential cross section at forward rapidity
Equivalent distributions are now shown within the LHCb fiducial region. In Fig. 4 we show the diphoton invariant mass distribution. The distributions are similar to the ALICE conditions both in normalization and shape. The solid black line is the signal corresponding to the Standard Model box contribution, the solid green lines correspond to resonant mesonic states while the dashed line corresponds to the background defined in the main text. The relative background is slightly lower than for ALICE but the conclusion again is that the signal can be clearly observed only for 2 GeV and one can observe very clear contributions coming from and resonances. The inclusion of the LHCb energy resolution (Eq. (7)) broadens the peak in the distribution, which is plotted in Fig. 4 with and without energy smearing.
(a) 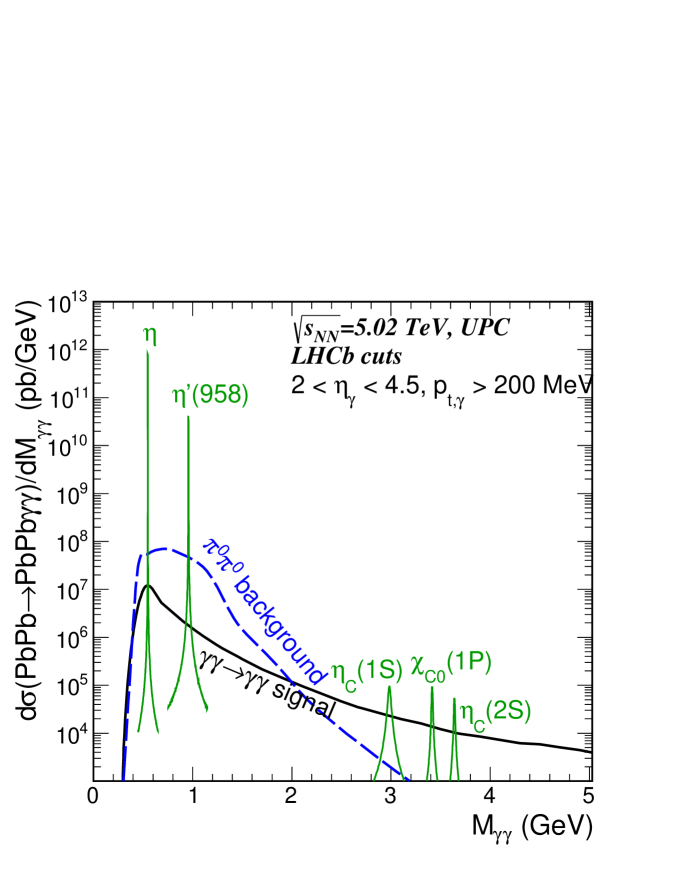 (b)
(b) 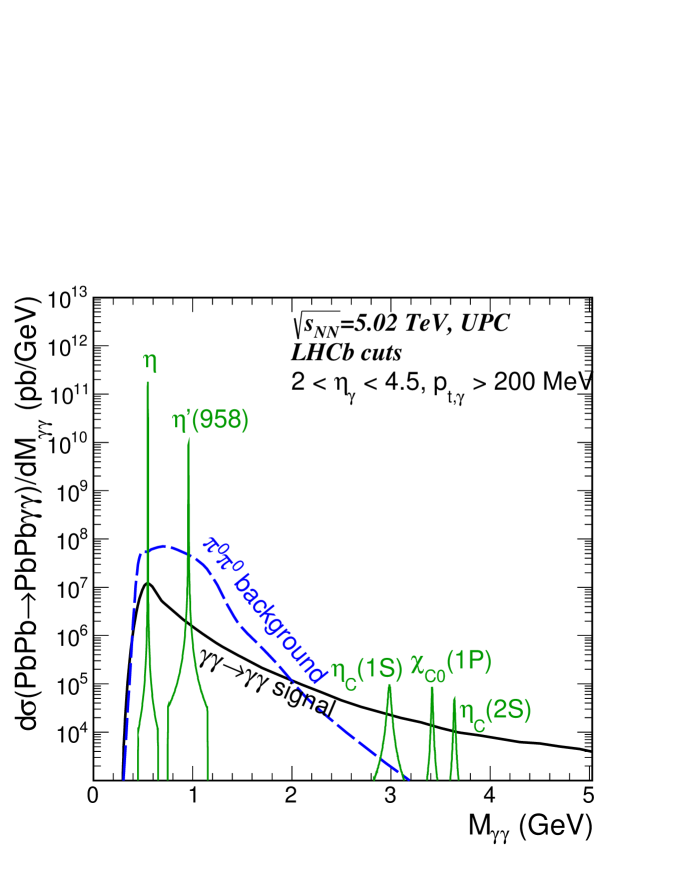
In Fig. 5 we show two-dimensional distributions as a function of pseudorapidity of the first and second photon. The left panel corresponds to the (box) signal and the right panel shows the result for the background. In some regions of () space the background contribution is much larger than the signal one. Note the different scale on -axis in the left and right panels. As in the case of the ALICE fiducial region (Fig. 3), the signal is two orders of magnitude smaller than the background but in the LHCb case the shapes of the distributions are rather different. Here there is relatively more background when both photons have large rapidities.
(a) 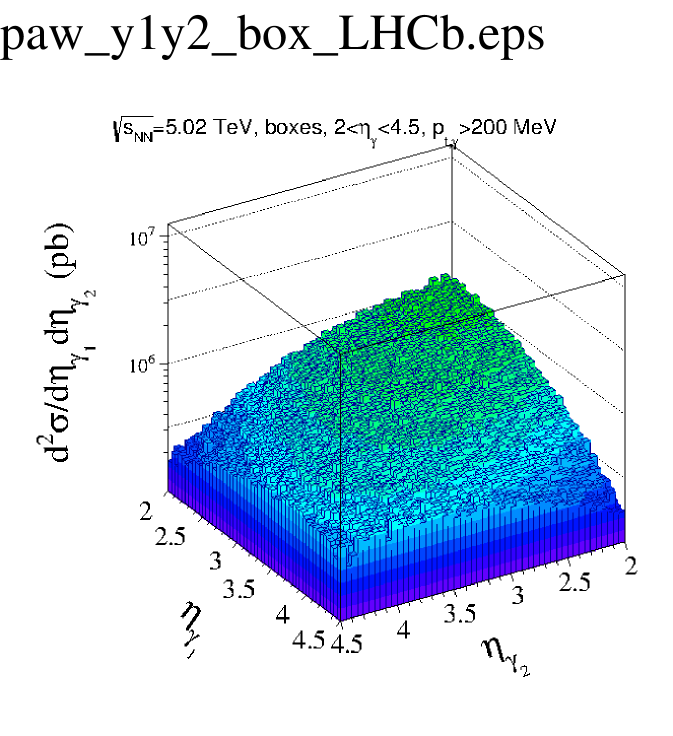 (b)
(b) 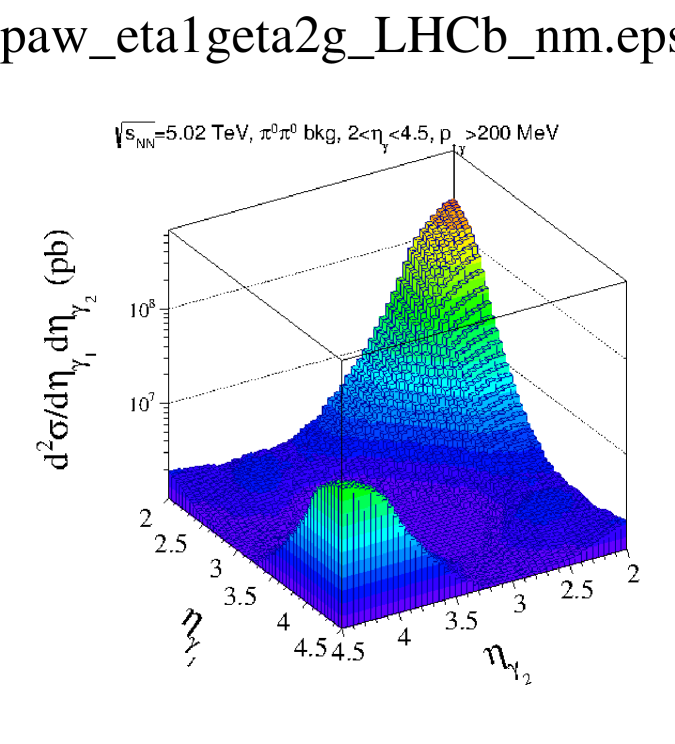
5 Background suppression of decays
The background from the decays shown in Fig. 2 can be reduced by kinematic cuts. Not taking into account the experimental resolution, the two final state photons of scattering, shown in Fig. 1 a,b), are of equal transverse momenta and are back-to-back in azimuthal angle. In first order, the correlation in transverse momentum will be smeared out by the experimental resolution in the measurement of the two photons. Higher order corrections, such as the finite values of the beam emittance and the crossing angle of the colliding beams, are beyond the scope of the study presented here, and are hence neglected in the results presented below. The correlations of the signal can be quantified by two asymmetries,
| (8) |
| (9) |
Here, the scalar asymmetry is a measure of the relative difference in transverse momentum of the two photons, and is non-zero for two back-to-back photons of the signal due to the finite energy resolution of the measurement. The vector asymmetry defined in Eq. (9) reflects a convolution of the experimental resolutions of photon energy and azimuthal angle measurement. The two-photon background resulting from the decays does not show the correlations discussed above. The correlations can hence be used to suppress the background by kinematical cuts on these two asymmetries.
(a) 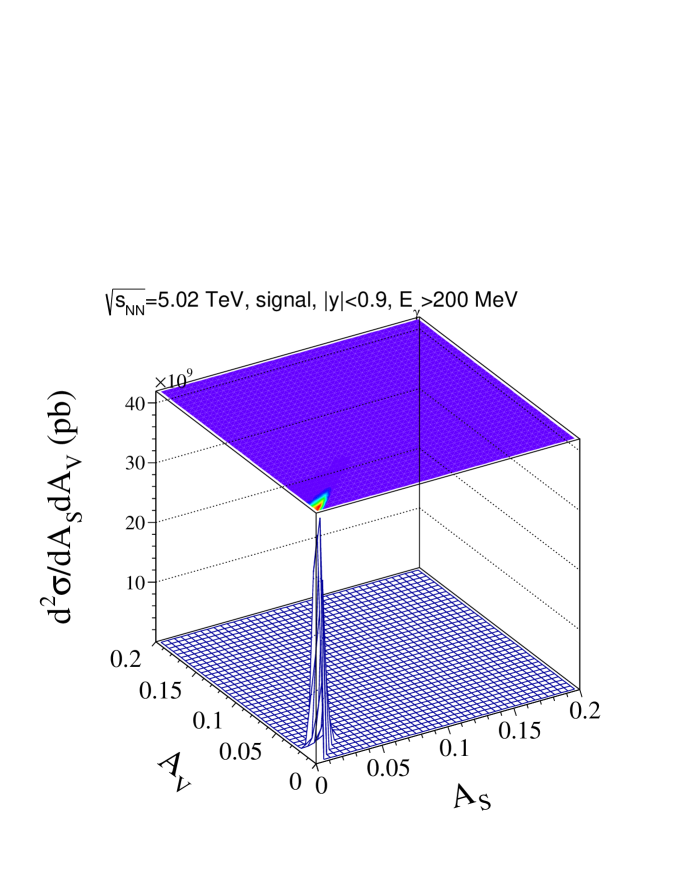 (b)
(b) 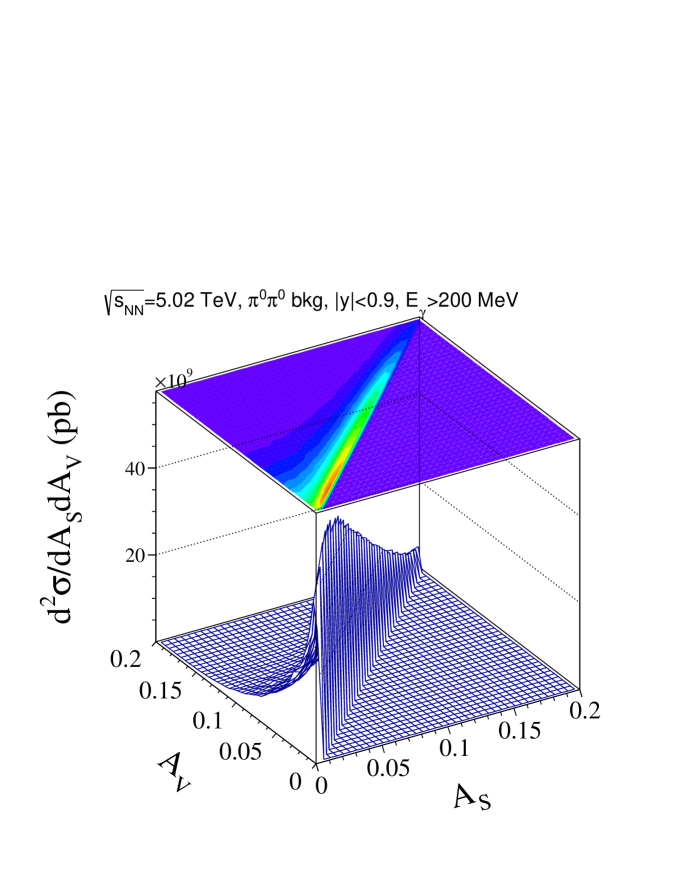
The correlation of the two asymmetries discussed above are shown for the signal in Fig. 6 (a) for an energy resolution of = 1.3 % and an azimuthal angle resolution of = 0.02. From the considerations on asymmetries outlined above, one expects the vector asymmetry to be larger than the scalar asymmetry, , as shown in Fig. 6 (a). The corresponding histogram (Fig. 6 (b)) is shown for photon background pairs resulting from the decays. This background distribution is an order of magnitude wider compared to the distribution of the signal. A carefully chosen cut on the asymmetry parameters and will therefore reduce the background substantially, while reducing the signal only marginally.
The diphoton mass distribution is shown in Fig. 7 from a study performed within the ALICE fiducial region, with successive cuts on applied. The signal is reduced by a negligible amount for both values of . The cut reduces the background by about a factor of 10 as shown by the red line, and results in a remaining background which is a factor of about 10 larger than the signal at diphoton masses GeV.
(a) 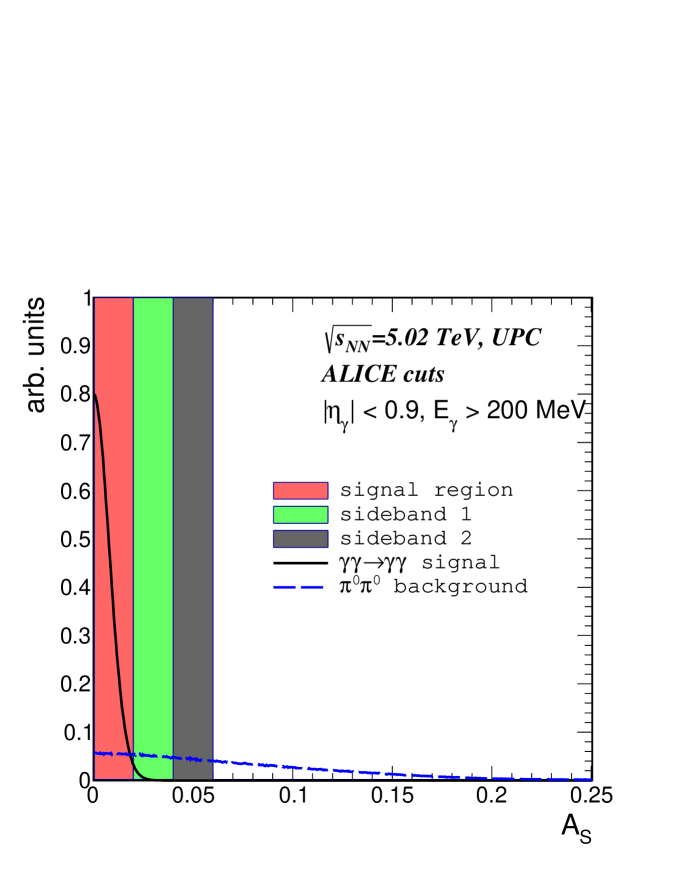 (b)
(b) 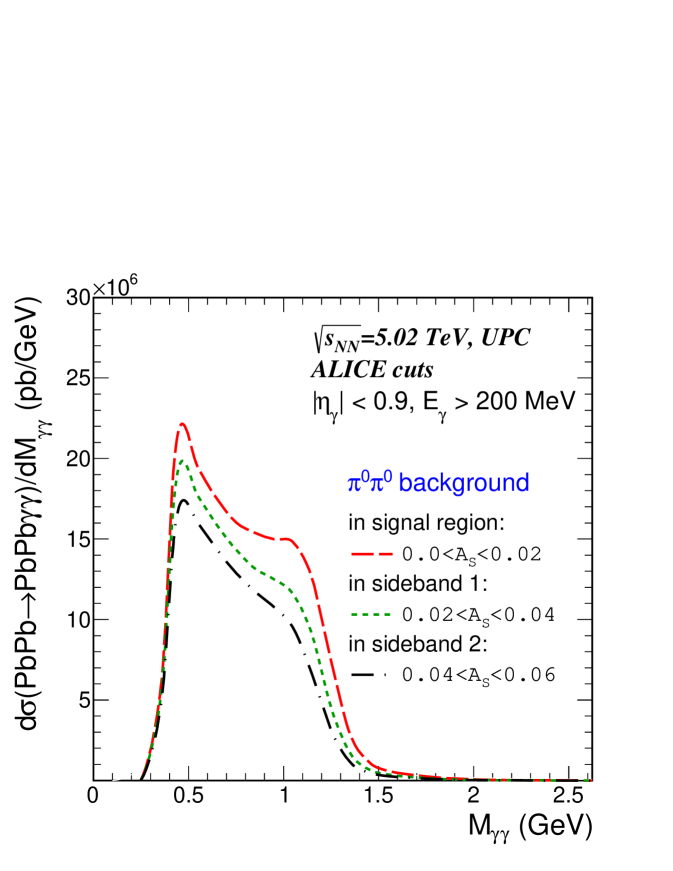
A sideband subtraction method using the asymmetry parameter as separation variable can be used to extract the signal in this mass range. In this approach, kinematic distributions of signal and background, which can be one or multi-dimensional, are fit in intervals of the separation variable. For the diphoton signal a one-dimensional analysis could be based on the mass distribution while a higher-dimensional approach could include the pseudorapidity distributions of the two photons shown in Fig. 3, and the transverse momentum distribution of the photon pair. To illustrate the one-dimensional approach, we show in Fig. 8 (a) the distribution of signal and background for the first three intervals of the separation variable, labeled signal region, sideband 1 and sideband 2. The signal region, defined by , contains 95 % of the signal events. Sideband 1 and sideband 2 are defined by and , respectively. The distribution of the signal is at the 5 % level in sideband 1, and negligibly small in sideband 2, whereas the background distribution extends well into the sideband regions as shown in Fig. 8 (a) by the dashed blue line. In Fig. 8 (b), the mass distributions of background events in the signal and the two sideband regions are shown by the red-dashed, green-dotted and black-dot-dashed lines, respectively. Clearly visible in this panel is a continuous reduction of the background cross section from the signal to the sideband 2 region, as expected by the behaviour of the background scalar asymmetry shown in Fig. 8 (a). Based on the kinematical fits of the signal and background distributions, the sideband analysis derives a factor expressing the likelihood of the event belonging to the signal or background sample (see e.g. Williams:2008sh ). Quantitative results on the misidentification of background as signal events depend, however, on the event statistics available and information on the single photon detection efficiency, and are beyond the scope of the study presented here.
6 Conclusions
Ultra-peripheral heavy-ion collisions at high energies open the possibility to measure scattering. So far the ATLAS and CMS collaborations obtained first evidence of photon-photon scattering for invariant masses 6 and 5 GeV, respectively. Due to the experimental cuts on transverse photon momenta 3 GeV, the resulting statistics is so far rather limited. The ATLAS result is roughly consistent with the Standard Model predictions for elementary cross section embedded into state-of-art nuclear calculation including realistic photon fluxes as the Fourier transform of realistic charge distribution.
Here we consider the possibility to study elastic scattering in the diphoton mass range GeV at the LHC using ALICE and LHCb detectors. Our results show that the contributions of the pseudoscalar resonances , are clearly visible on top of the diphoton mass continuum arising from lepton loop diagrams. We have made first predictions for cross sections as a function of diphoton mass for typical acceptances of the ALICE and LHCb experiments. The evaluation of counting rates needs, however, Monte Carlo simulations which take into account detailed acceptances and realistic responses of the detectors used for measuring two-photon final states.
In addition to the signal () we consider the background dominated by the reaction when only two out of the four decay photons in the final state are registered. This background can be reduced by imposing cuts on scalar and vector asymmetry of transverse momenta of the two photons. Cuts on sum of photon rapidities (or the rapidity of the diphoton system) can additionally be used to reduce the background. The background remaining after these cuts dominates the signal by a factor of about ten at diphoton masses 1.2 GeV. The extraction of the signal in this mass range is feasible by a multi-variate sideband subtraction analysis. Quantitative results on the signal efficiency and background suppression in this sideband subtraction approach depend on the statistics of the data sample available for analysis.
In our study we take the dominant background shown in Fig. 1 (c) as arising from the decay of two ’s which are correlated by the emission from two vertices which, however, cannot be resolved at the macroscopic level due to detector resolution limitation. In a crossing of heavy-ion bunches, single production can occur by different pairs of particles in the two beams, resulting in multiple uncorrelated production. These ’s emerge from different vertices which are spread along the interaction region of the two colliding beams. The contribution of the decay photons of these uncorrelated ’s to the background depends on the beam parameters at the interaction point and the position resolution of the photon reconstruction along the beam direction, and is beyond the scope of the study presented here.
Acknowledgements.
The authors thank the ExtreMe Matter Institute EMMI for the support of the workshop "Challenges in Photon Induced Interactions" in Krakow where this study was initiated. This work has been supported by the Polish National Science Center grant DEC-2014/15/B/ST2/02528 (MKG and AS) and by the German Federal Ministry of Education and Research under promotional reference 05P19VHCA1 (RS).References
- (1) K. Schaposchnikow, Über Zusammenstöße von Lichtquanten, Z.Phys. 33, no.1 (1925) 706–709.
- (2) L. de Broglie, Ondes et Mouvements, Collection de Physique Mathmatique Vol. 1 (1926) .
- (3) M. Born, Modified field equations with a finite radius of the electron, Nature 132:3329 (1933) 282.
- (4) O. Halpern, Scattering processes produced by electrons in negative energy states, Phys.Rev. 44, no.10 (1933) 855–856.
- (5) W. Heisenberg and H. Euler, Consequences of Dirac’s theory of positrons, Z. Phys. 98 no. 11-12, (1936) 714–732, arXiv:physics/0605038 [physics].
- (6) K. Scharnhorst, Photon-photon scattering and related phenomena. Experimental and theoretical approaches: The early period, hal-01638181, arXiv:1711.05194 [physics.hist-ph].
- (7) D. d’Enterria and G. G. da Silveira, Observing light-by-light scattering at the Large Hadron Collider, Phys. Rev. Lett. 111 (2013) 080405, arXiv:1305.7142 [hep-ph]. [Erratum: Phys. Rev. Lett.116,no.12,129901(2016)].
- (8) M. Kłusek-Gawenda, P. Lebiedowicz, and A. Szczurek, Light-by-light scattering in ultraperipheral Pb-Pb collisions at energies available at the CERN Large Hadron Collider, Phys. Rev. C93 no. 4, (2016) 044907, arXiv:1601.07001 [nucl-th].
- (9) M. Kłusek-Gawenda and A. Szczurek, and pair production in photon-photon and in ultraperipheral ultrarelativistic heavy ion collisions, Phys. Rev. C87 no. 5, (2013) 054908, arXiv:1302.4204 [nucl-th].
- (10) G. W. Bennett et al., (Muon g-2), Final Report of the Muon E821 Anomalous Magnetic Moment Measurement at BNL, Phys. Rev. D73 (2006) 072003, arXiv:hep-ex/0602035 [hep-ex].
- (11) G. Colangelo, M. Hoferichter, M. Procura, and P. Stoffer, Hadronic light-by-light contribution to : a dispersive approach, in 35th International Symposium on Lattice Field Theory (Lattice 2017) Granada, Spain, June 18-24, 2017. 2017. arXiv:1711.00281 [hep-ph].
- (12) C. Bula et al., (E144), Observation of nonlinear effects in Compton scattering, SLAC-PUB-7221, Phys. Rev. Lett. 76 (1996) 3116–3119.
- (13) M. Aaboud et al., (ATLAS), Evidence for light-by-light scattering in heavy-ion collisions with the ATLAS detector at the LHC, CERN-EP-2016-316, Nature Phys. 13 no. 9, (2017) 852–858, arXiv:1702.01625 [hep-ex].
- (14) A. M. Sirunyan et al., (CMS Collaboration), Evidence for light-by-light scattering and searches for axion-like particles in ultraperipheral PbPb collisions at 5.02 TeV, CMS-FSQ-16-012, CERN-EP-2018-271, arXiv:1810.04602 [hep-ex].
- (15) M. Kłusek-Gawenda, Importance of mesons in light-by-light scattering in ultraperipheral lead-lead collisions at the LHC, in 15th International Workshop on Meson Physics (MESON 2018) Kraków, Poland, June 7-12, 2018. 2018. arXiv:1809.03823 [hep-ph].
- (16) P. Lebiedowicz and A. Szczurek, The role of meson exchanges in light-by-light scattering, Phys. Lett. B772 (2017) 330–335, arXiv:1705.06535 [hep-ph].
- (17) M. Kłusek-Gawenda, W. Schäfer, and A. Szczurek, Two-gluon exchange contribution to elastic scattering and production of two-photons in ultraperipheral ultrarelativistic heavy ion and proton-proton collisions, Phys. Lett. B761 (2016) 399–407, arXiv:1606.01058 [hep-ph].
- (18) S. Uehara et al., (Belle), High-statistics study of neutral-pion pair production in two-photon collisions, KEK-PREPRINT-2008-50, BELLE-PREPRINT-2009-4, Phys. Rev. D79 (2009) 052009, arXiv:0903.3697 [hep-ex].
- (19) H. Marsiske et al., (Crystal Ball), A Measurement of Production in Two Photon Collisions, SLAC-PUB-5163, DESY-90-002, Phys. Rev. D41 (1990) 3324.
- (20) M. Kłusek-Gawenda and A. Szczurek, Exclusive muon-pair productions in ultrarelativistic heavy-ion collisions – realistic nucleus charge form factor and differential distributions, Phys. Rev. C82 (2010) 014904, arXiv:1004.5521 [nucl-th].
- (21) T. Hahn and M. Perez-Victoria, Automatized one loop calculations in four-dimensions and D-dimensions, UG-FT-87-98, KA-TP-7-1998, Comput. Phys. Commun. 118 (1999) 153–165, arXiv:hep-ph/9807565 [hep-ph].
- (22) G. J. van Oldenborgh and J. A. M. Vermaseren, New Algorithms for One Loop Integrals, NIKHEF-H/89-17, Z. Phys. C46 (1990) 425–438.
- (23) P. Lebiedowicz, R. Pasechnik, and A. Szczurek, Search for technipions in exclusive production of diphotons with large invariant masses at the LHC, Nucl. Phys. B881 (2014) 288–308, arXiv:1309.7300 [hep-ph].
- (24) G. Jikia and A. Tkabladze, Photon-photon scattering at the photon linear collider, Phys.Lett. B323 (1994) 453–458, arXiv:hep-ph/9312228 [hep-ph].
- (25) Z. Bern, A. De Freitas, L. J. Dixon, A. Ghinculov, and H. L. Wong, QCD and QED corrections to light by light scattering, SLAC-PUB-8974, UCLA-01-TEP-18, JHEP 11 (2001) 031, arXiv:hep-ph/0109079 [hep-ph].
- (26) D. Bardin, L. Kalinovskaya, and E. Uglov, Standard Model light-by-light scattering in SANC: analytic and numeric evaluation, Phys. Atom. Nucl. 73 (2010) 1878–1888, arXiv:0911.5634 [hep-ph].
- (27) C. Patrignani et al., (Particle Data Group), Review of Particle Physics, Chin. Phys. C40 no. 10, (2016) 100001.
- (28) B. Abelev et al., (ALICE Collaboration), Performance of the ALICE Experiment at the CERN LHC, Int.J.Mod.Phys. A29 (2014) 1430044, arXiv:1402.4476 [nucl-ex].
- (29) J. Allen et al., (ALICE EMCal Collaboration), Performance of prototypes for the ALICE electromagnetic calorimeter, Nucl.Instrum.Meth. A615 (2010) 6–13, arXiv:0912.2005 [physics.ins-det].
- (30) B. Abelev et al., (ALICE Collaboration), Neutral pion production at midrapidity in pp and Pb-Pb collisions at =2.76 TeV., Eur. Phys. J. C74, no.10 (2014) 3108, arXiv:1405.3794 [nucl-ex].
- (31) S. Acharya et al., (ALICE), and meson production in proton-proton collisions at TeV, CERN-EP-2017-216, Eur. Phys. J. C78 no. 3, (2018) 263, arXiv:1708.08745 [hep-ex].
- (32) C. Abellan Beteta et al., Time alignment of the front end electronics of the LHCb calorimeters, JINST 7 (2012) P08020.
- (33) M. Clemencic, G. Corti, S. Easo, C. R. Jones, S. Miglioranzi, M. Pappagallo, and P. Robbe, (LHCb Collaboration), The LHCb simulation application, Gauss: Design, evolution and experience, J. Phys. Conf. Ser. 331 (2011) 032023.
- (34) M. Williams, M. Bellis, and C. A. Meyer, Multivariate side-band subtraction using probabilistic event weights, JINST 4 (2009) P10003, arXiv:0809.2548 [nucl-ex].