Gregory G. Howes
(gregory-howes@uiowa.edu)
Limitations of Hall MHD as a model for turbulence in weakly collisional plasmas
Zusammenfassung
The limitations of Hall MHD as a model for turbulence in weakly collisional plasmas are explored using quantitative comparisons to Vlasov-Maxwell kinetic theory over a wide range of parameter space. The validity of Hall MHD in the cold ion limit is shown, but spurious undamped wave modes exist in Hall MHD when the ion temperature is finite. It is argued that turbulence in the dissipation range of the solar wind must be one, or a mixture, of three electromagnetic wave modes: the parallel whistler, oblique whistler, or kinetic Alfvén waves. These modes are generally well described by Hall MHD. Determining the applicability of linear kinetic damping rates in turbulent plasmas requires a suite of fluid and kinetic nonlinear numerical simulations. Contrasting fluid and kinetic simulations will also shed light on whether the presence of spurious wave modes alters the nonlinear couplings inherent in turbulence and will illuminate the turbulent dynamics and energy transfer in the regime of the characteristic ion kinetic scales.
Understanding the dynamical evolution of the turbulence in the solar wind and its thermodynamic consequences for the energy balance in the heliosphere is a major goal of heliospheric physics. As the time resolution of in situ satellite measurements of this turbulence is increased, ever smaller length scales of the turbulence are probed. We have now reached a new frontier in the study of turbulence as we begin to focus on the dynamics of the plasma turbulence at kinetic scales—e.g., the ion Larmor radius. Understanding the turbulence at these small scales is critical because the kinetic plasma physics at these scales determines the dissipation of the turbulent fluctuations and the inevitable conversion of the fluctuation energy into plasma heat (Schekochihin et al., 2007; Howes, 2008).
The simple fluid model of MHD is not sufficient to describe this new regime of kinetic turbulence in the weakly collisional solar wind plasma. The appealing simplicity of the Hall MHD model—an extension of MHD that maintains a fluid description while accounting for the Hall terms in Ohm’s Law, leading to dispersive behavior at small scales—has lead a number of investigators to use it to study turbulence at these small scale lengths (Shebalin, 1991; Huba, 1994; Ghosh et al., 1996; Sahraoui et al., 2003; Krishan and Mahajan, 2004; Hori et al., 2005; Mininni et al., 2005; Dmitruk and Matthaeus, 2006; Servidio et al., 2007), with some recommending Hall MHD as the preferred model for the study of solar wind turbulence (Matthaeus et al., 2008). The applicability of the Hall MHD model to turbulence in a weakly collisional plasma such as the solar wind, however, has been called into question (Howes et al., 2008b). Here we investigate the limitations of the Hall MHD model for the study of turbulence in kinetic plasmas.
Hall MHD is a rigorous limit of the kinetic behavior in a weakly collisional plasma only if all of the following conditions are satisfied: , and (Ito et al., 2004). Although this cold ion limit is not universally applicable to the turbulent solar wind, we nevertheless would like to estimate quantitatively the error in using the fluid description given by Hall MHD rather than a kinetic description. Although a turbulent plasma inherently involves dynamically significant nonlinear wave-wave interactions which drive the turbulent cascade of energy to small scales, we focus our attention on the ability of compressible Hall MHD to reproduce the properties of the linear wave modes of the Vlasov-Maxwell kinetic theory. If the linear physics described by Hall MHD deviates from the kinetic description, then it is likely that the nonlinear wave-wave couplings that comprise the turbulence will be incorrect as well.
A comparison of the (complex) linear eigenfrequencies determined by compressible Hall MHD and Vlasov-Maxwell kinetic theory provides a simple quantitative measure of the fidelity of the Hall MHD description to the kinetic physics in a weakly collisional plasma. Krauss-Varban et al. (1994) have already published a very thorough comparison of the low-frequency wave mode properties of Hall MHD and kinetic theory, concluding that “fluid theory does not correctly describe the mode structure and mode properties for most plasmas of interest in space physics.” Their study, however, evaluated the properties at a particular wavenumber , where the is ion inertial length—see Table 1 for all symbol definitions. Because the turbulent cascade extends over a large range of scales (more than four orders of magnitude in the solar wind), the accuracy of Hall MHD in describing the turbulence must be assessed over a logarithmic scale in wave vector space .
This paper aims to identify the regimes of parameter space for which Hall MHD is not an accurate description. The Hall MHD and Vlasov-Maxwell systems are specified, and their properties briefly explored, in §1 and §2. In §3, some of the subtleties involved in quantitatively comparing Hall MHD to kinetic theory are discussed and the measures of comparison are defined. The results of the comparison are presented in §4, the implications of choosing the Hall MHD model to describe kinetic turbulence are discussed in §5, and the key findings are summarized in §5.3.
1 Standard Hall MHD
Consider a fully ionized, homogeneous plasma of protons and electrons threaded by a straight, uniform magnetic field . By retaining the Hall term in Ohm’s law during the derivation of the MHD equations, the following form for the compressible Hall MHD equations is obtained:
| (1) |
| (2) |
| (3) |
| (4) |
where the substantial time derivative is and other terms are defined in Table 1. Although there exist numerous variations of Hall MHD—e.g., employing a double adiabatic equation of state—this is the simplest compressible system incorporating the Hall effect, and generally appears to be the most widely used in studies employing Hall MHD (Lighthill, 1960; Kuvshinov, 1994; Mininni et al., 2002; Ohsaki and Mahajan, 2004; Hirose et al., 2004; Servidio et al., 2007). We therefore refer to this particular system as standard Hall MHD.
| \tophlineVariable | Symbol |
|---|---|
| \middlehlineSpecies | |
| Speed of light | |
| Mass | |
| Charge | |
| Number Density | |
| Temperature | |
| Species Plasma Beta | |
| Plasma Frequency | |
| Cyclotron Frequency | |
| Thermal Velocity | |
| Alfvén Velocity | |
| Ion Larmor Radius | |
| Ion Inertial Length | |
| \bottomhline |
The linear dispersion relation for standard Hall MHD may be written in dimensionless form as
| (5) | |||||||
where the frequency is normalized to the ion cyclotron frequency , the plasma beta is with the sound speed defined by . It is clear from the form of this dispersion relation that the eigenfrequencies depend on only three dimensionless parameters: the normalized components of the wave vector with respect to the mean magnetic field, and , and the plasma beta . Thus, .
The six solutions of the standard Hall MHD dispersion relation (5) correspond to three distinct physical wave modes, each with two counter propagating solutions. 111Already factored out from equation (5) is a non-propagating, entropy mode, corresponding to pressure balance but a non-zero entropy fluctuation. This mode, examined in Hameiri et al. (2005), is not discussed in this paper. In the MHD limit , the three solutions to equation (5) give the usual fast, Alfvén , and slow wave eigenmodes. We will refer to the continuation of each these modes at by their name in the MHD limit: thus, whistler waves correspond to the fast wave branch, and kinetic Alfvén waves and ion cyclotron waves are the extension of the Alfvén branch into the nearly perpendicular and nearly parallel kinetic regimes, respectively.
Hirose et al. (2004) and Ito et al. (2004) found that the Hall MHD dispersion relation (5) is a rigorous limit of Vlasov-Maxwell kinetic theory if
| (6) |
and only if
| (7) | |||||
| (8) | |||||
| (9) |
Although condition (6) is sufficient to recover the kinetic results, it is not a necessary condition under all circumstances. In a study of the fluid closures for collisionless plasmas, Chust and Belmont (2006) suggested two constraints for validity: (a) appropriate modeling of the pressure term in the momentum equation (2); and (b) the negligibility of the pressure gradient term in Ohm’s law. They showed a sufficient condition satisfying the second constraint under general conditions is . For the isotropic equation of state (4) used in standard Hall MHD, the scalar treatment of the pressure means that the pressure gradient term in Ohm’s law is always negligible because Ohm’s law enters the induction equation (3) only through its curl.
A complementary calculation shows that gyrokinetics (Rutherford and Frieman, 1968; Frieman and Chen, 1982; Howes et al., 2006), a rigorous anisotropic limit of kinetic theory for and , yields a reduced (anisotropic) version of Hall MHD in the limit (Schekochihin et al., 2007). The description of a collisionless plasma by a fluid model, such as Hall MHD, is only valid when wave-particle interactions and finite-Larmor-radius effects are negligible (Ballai et al., 2002); this is ensured by the conditions (6)–(9)
Condition (7) is the cold ion approximation, meaning that the ion temperature is negligible compared to the electron temperature. In this limit, the sound speed in the standard Hall MHD system is the ion acoustic speed . Condition (8) means that the ion Landau resonance is negligible because the ions are too cold, while condition (9) means that the electron Landau resonance is negligible because the electrons are too hot. Implied by condition (7), but not explicitly stated in Ito et al. (2004), is the requirement that (Ballai et al., 2002); the ions must be cold enough such that the ion Larmor radius is small compared to the perpendicular scales of interest, and therefore finite-ion-Larmor-radius effects may be neglected. The ion acoustic Larmor radius , however, may be comparable to the perpendicular scale, .
Although few weakly collisional plasmas in space or astrophysical environments satisfy these very restrictive conditions (6)–(9), one may ask at what point will non-negligible kinetic effects lead to a poor description by Hall MHD. In this spirit, we wish to evaluate in this paper the practical limitations of the Hall MHD model for turbulence in a weakly collisional plasma, making quantitative comparisons of standard Hall MHD with Vlasov-Maxwell kinetic theory in the parameter regime relevant to turbulent solar wind.
2 Vlasov-Maxwell Kinetic Theory
To test the Hall MHD model, we compare the real frequency from its dispersion relation to the complex eigenfrequencies from the Vlasov-Maxwell dispersion relation (Stix, 1992) assuming a homogeneous, fully ionized proton and electron plasma with isotropic Maxwellian equilibrium distribution functions and no drift velocities. This dispersion relation is solved numerically (see Quataert (1998) for a description of the code used to solve it), performing the Bessel function sums to 100 terms to ensure accurate results at high . The linear Vlasov-Maxwell dispersion relation depends on five parameters: the normalized perpendicular wavenumber , the normalized parallel wavenumber , the ion plasma beta , the ion to electron temperature ratio , and the ratio of ion thermal velocity to the speed of light . The solution may then be expressed as . A realistic ratio of proton to electron mass, , is used. We note here that, in the non-relativistic limit relevant to the turbulent solar wind, the low-frequency modes are rather insensitive to the specific value of , so we choose the typical value for all comparisons in this paper. Just as in the Hall MHD case, we choose to label to the low-frequency wave mode solutions (low compared to the electron cyclotron frequency ) of Vlasov-Maxwell kinetic theory by their names in the MHD limit—the fast, Alfvén , and slow waves.
3 Comparing Hall MHD to Kinetic Theory
3.1 Subtle Aspects of the Comparison
Two complications arise when making a detailed comparison of standard Hall MHD with Vlasov-Maxwell kinetic theory. The first is the use of an isotropic equation of state (4) in standard Hall MHD. Condition (9) suggests that the electron response is so fast that, if the ion temperature is ignorable, the pressure response may be correctly treated as isothermal and isotropic (Hirose et al., 2004). But for finite ion temperatures, the ion response is anisotropic and appears to be better described with a double polytropic equation of state,
For example, a choice of and corresponds to the double adiabatic, CGL closure for the ions (Chew et al., 1956; Abraham-Shrauner, 1973; Ballai et al., 2002). Even this more complicated closure, however, fails to yield a dispersion relation that is a rigorous limit of kinetic theory for a weakly collisional plasma with a finite ion temperature (Hirose et al., 2004). But, it appears that the slow wave branch is the most strongly affected by this complication; for example, the one-dimensional collisionless dynamics of ions along the magnetic field leads to a parallel sound speed (Hirose et al., 2004), and this produces unusual behavior, even at MHD scales , such as a slow wave with a faster phase speed than the Alfvén wave (Ballai et al., 2002). The closest connection between kinetic theory and the standard Hall MHD dispersion relation appears to occur by defining an isotropic sound speed (Hirose et al., 2004), so this is the definition taken here. Although this choice is not entirely satisfactory, we will see that the slow wave is strongly damped via wave-particle interactions when warm ions are present, so the differences arising from the details of the fluid closure are often irrelevant.
The second complication in comparing Hall MHD with kinetics is that the linear fluid modes of Hall MHD cannot be assigned a one-to-one correspondence with the linear kinetic modes over all parameter space (Orlowski et al., 1994; Krauss-Varban et al., 1994; Yoon and Fang, 2008). For example, in a study of low-frequency waves in the solar wind upstream of Venus, Orlowski et al. (1994) found a correspondence to the fast Hall MHD mode at low and to the Alfvén Hall MHD mode at high , while the results were uniformly consistent with the fast mode of kinetic theory. A subsequent study comparing Hall MHD with kinetic theory found this mixing of modes to be commonplace (Krauss-Varban et al., 1994), perhaps accounting for the surprising changes in the linear wave properties of Hall MHD at small scales noted in a recent paper (Hameiri et al., 2005).
This mixing of solutions to the linear dispersion relations can lead to confusion about the connections between wave modes in different regimes of parameter space. For a chosen set of plasma parameters , , and , each solution to the dispersion relation describes a manifold in space, termed a “dispersion surface” (Andre, 1985). A single dispersion surface may describe distinct wave modes (with different physical properties) in different regimes of wave vector space. For example, the Alfvén dispersion surface describes the MHD Alfvén wave at large scale ( and ), the ion cyclotron wave at small parallel scales ( and ), and the kinetic Alfvén wave at small perpendicular scales ( and ) (Yoon and Fang, 2008). In this paper we avoid confusion by naming the solution branch of the dispersion relation according to the MHD mode to which it is topologically connected along the dispersion surface. Thus, we will investigate the properties of the slow (S), Alfvén (A), and fast (F) branch solutions of both the linear Hall MHD and Vlasov-Maxwell systems. Since the solutions of these branches in the two systems do not exhibit a one-to-one correspondence, we take the position that we want to compare the Hall MHD wave modes with the most similar kinetic mode at each point in parameter space, and will remark upon which modes were chosen when relevant.
To connect quantitatively Hall MHD to kinetic theory, we must specify the relation between in the Hall MHD dispersion relation and in the Vlasov-Maxwell dispersion relation. For a finite ion temperature, we choose to define , where we take an isotropic sound speed . Thus, the necessary relation is given by . Note that, in the limit in which Hall MHD is rigorously valid, the ion pressure is ignorable and so , the ion acoustic speed; for turbulence in the solar wind, the ion and electron temperatures are comparable , but standard Hall MHD has no means to account for distinct ion and electron temperatures, so we merely quote the value of used for the Vlasov-Maxwell calculation.
3.2 Comparative Measures
Hall MHD is a fluid theory of the behavior in a magnetized plasma, and therefore does not account for the effect of collisionless damping; the eigenfrequencies of the Hall MHD dispersion relation (5) are real, . Therefore, in comparing with the complex eigenfrequencies of the Vlasov-Maxwell dispersion relation , we must separately account for the error due to the differences in the real frequencies and the error due to the absence of damping in Hall MHD. Discrepancies in the real mode frequencies may yield Hall MHD results for a turbulent cascade that are quantitatively incorrect but still qualitatively correct with respect to a kinetic solution. But without capturing the often strong kinetic damping (via wave-particle interactions) occurring in a weakly collisional plasma, the Hall MHD model may give results for turbulence in the plasma that are both quantitatively and qualitatively incorrect.
We therefore will present two measures of comparison: first, the normalized difference between the Hall MHD frequency and the real part of the complex kinetic frequency ; and, second, the normalized collisionless damping rate in linear kinetic theory. In general , a normalized damping rate of is sufficient to reduce the amplitude of a wave mode by over a single wave period. The position is taken in this work that any damping rate is sufficient to cause qualitative differences in the dynamics.
4 Results
4.1 Cold Ion Limit,
First, we wish to verify that standard Hall MHD and Vlasov-Maxwell kinetic theory do agree in the limit . We choose the plasma beta and take , yielding an ion plasma beta in the kinetic theory . Figure 1 presents real frequencies (dashed line for Hall MHD, dotted line for Vlasov-Maxwell) in the top panel and damping rates (solid line for Vlasov-Maxwell) in the bottom panel for parallel wavenumbers and perpendicular wavenumber . The solution labeled F is the fast magnetosonic wave at and the parallel whistler wave at . At , the solution A is the shear Alfvén wave and the solution S is the slow wave, often termed the ion acoustic wave in this cold ion limit. In Figure 1, the inset in the top panel shows an expanded view of the region around , demonstrating that neither the Hall MHD nor the kinetic solutions cross. An examination of the linear kinetic eigenfunctions (not shown) shows that the A and S solution branches undergo a mode conversion (Swanson, 1989; Stix, 1992) at , exchanging physical characteristics with each other. Thus, at , the A branch corresponds to the slow wave and the S branch corresponds to the ion cyclotron wave. This mixing of the A and S branches occurs commonly in Hall MHD (Krauss-Varban et al., 1994; Yoon and Fang, 2008). In this limit , the real frequencies for all three modes are in excellent agreement; damping is weak for all modes over this range except for the S branch at , due to cyclotron damping of the corresponding ion cyclotron waves.
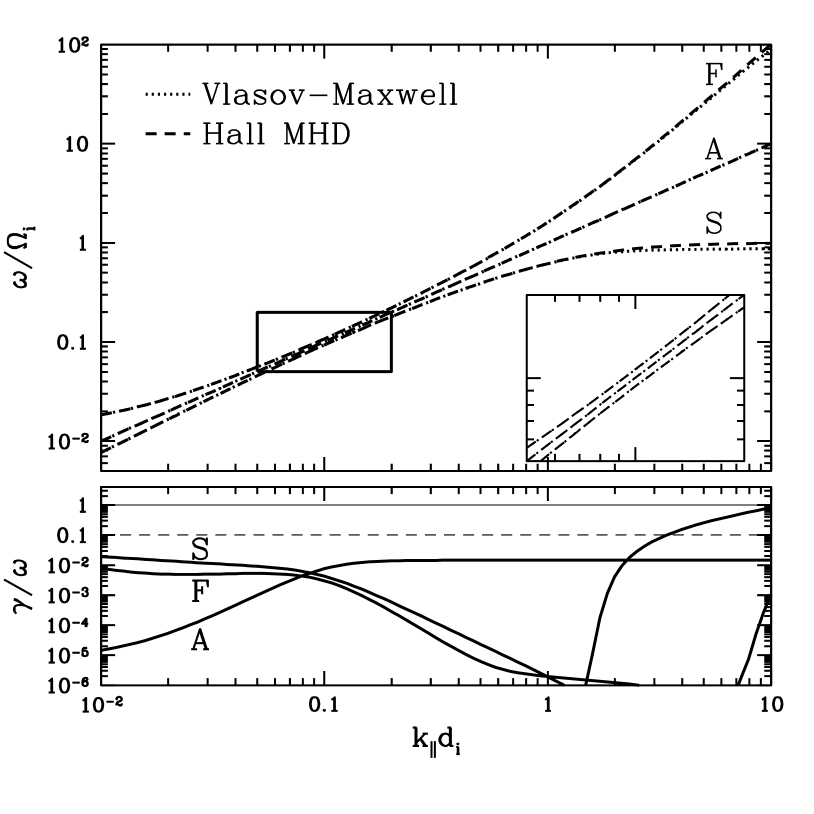
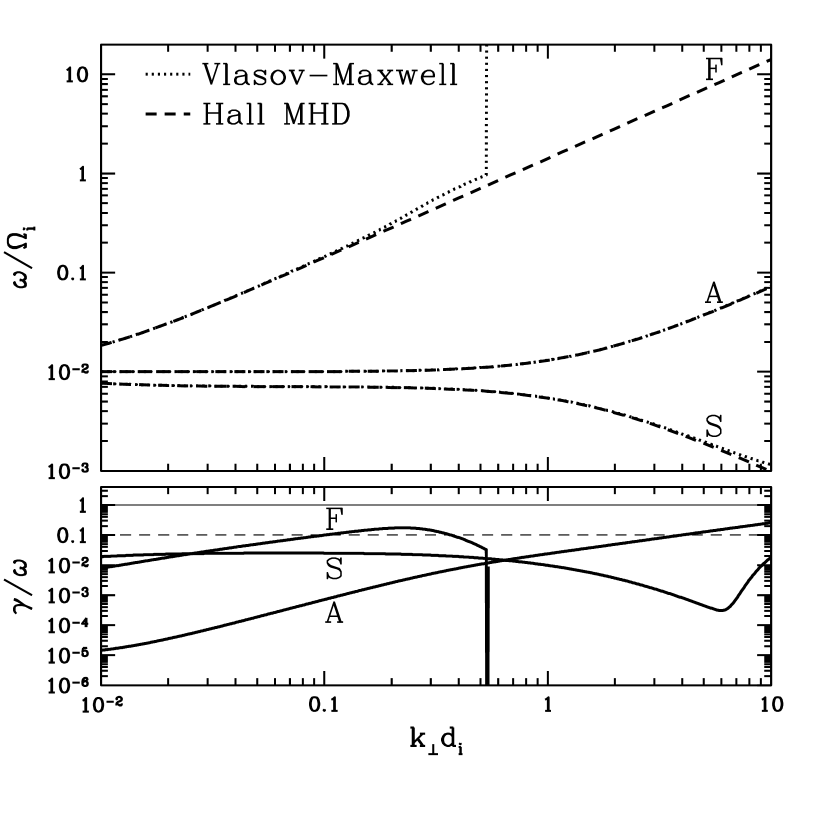
Figure 2 presents real frequencies and damping rates for perpendicular wavenumbers and parallel wavenumber . The Hall MHD slow wave solution S agrees well with the weakly damped kinetic solution. The Alfvén wave mode A also shows good agreement, but after it transitions to the kinetic Alfvén wave at , damping via the Landau resonance becomes significant at . The fast wave solution F from kinetic theory, on the other hand, deviates from the Hall MHD solution at ; here the numerical solver used is unable to follow the fast wave root as it undergoes a mode conversion into an ion Bernstein mode. Bernstein waves arise due to finite Larmor radius effects that have no counterpart in cold plasma theory and that are not described by Hall MHD (Swanson, 1989); the impact of the ion Bernstein waves is discussed at length in §4.3.
4.2 Finite Ion Temperature
Next, we explore the limit of warm ions relevant to most space and astrophysical plasmas. We take and , giving an ion plasma beta in the kinetic theory . Figure 3 presents real frequencies (top) and damping rates (bottom) for parallel wavenumbers and perpendicular wavenumber . The frequency of the kinetic fast wave F (dotted) is well reproduced by Hall MHD solution F’ (dashed), and its damping is weak except for a small region around . Comparison of the slow and Alfvén wave solutions demonstrates some of the complications arising in a comparison of Hall MHD to kinetic theory as described in §3.1. The kinetic slow wave solution S (dotted) has a phase speed that is faster than that of the Alfvén wave solution A (dotted) of kinetic theory (this is perhaps more easily seen Figure 4); the anisotropic ion pressure response in the kinetic theory that leads to this curious result (Ballai et al., 2002) is not captured by the isotropic equation of state used in the standard Hall MHD model. But this error is overshadowed by a far more serious discrepancy between Hall MHD and kinetic theory: at finite ion temperature the kinetic slow wave S (dotted)—the ion acoustic wave—is heavily damped with , yet a fluid theory such as Hall MHD does not account for this damping. Therefore, at finite ion temperature the Hall MHD slow wave represents an unphysical, spurious wave that does not exist in a weakly collisional plasma.
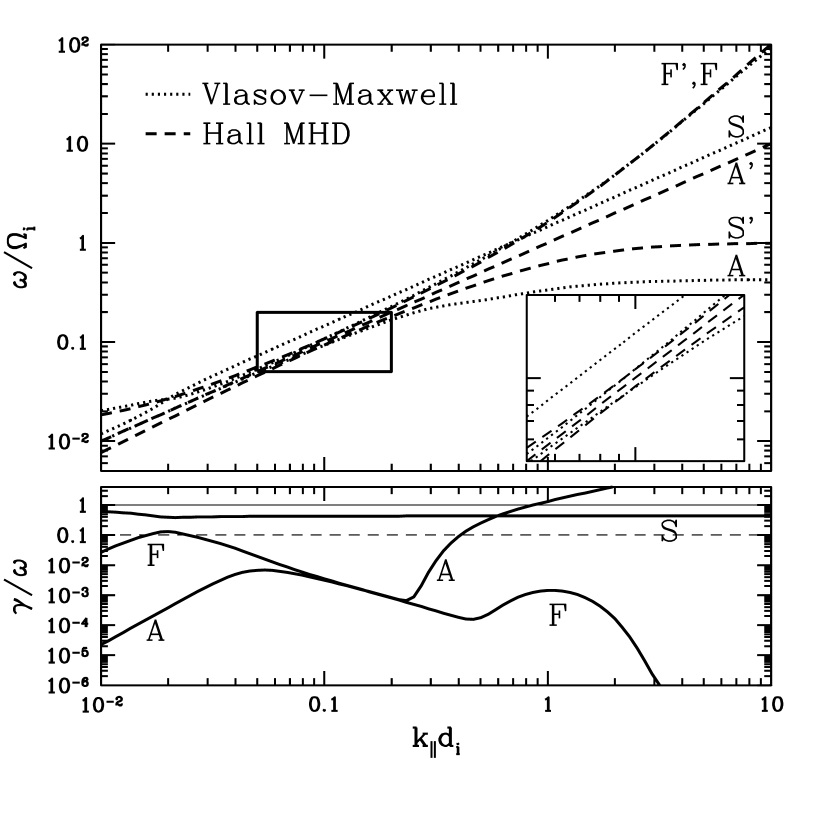
The second complication apparent in Figure 3 is the mixing of the modes between the solution branches of kinetic theory and those of Hall MHD (Krauss-Varban et al., 1994; Yoon and Fang, 2008). The inset in the top panel of Figure 3 shows that the Hall MHD solutions do not cross, however the correspondence between kinetic A and S branches and Hall MHD A’ and S’ branches changes with increasing : at , the solution A (dotted) of kinetic theory agrees closely with the Hall MHD solution A’ (dashed); but at , the solution A (dotted) from kinetic theory (the ion cyclotron wave) appears to correspond to the Hall MHD solution S’ (dashed) and the kinetic solution S (dotted) appears to correspond most closely with the Hall MHD solution A’. This mixing up of fluid and kinetic modes complicates any attempted comparison of the two models, but a careful matching of the most similar wave modes will yield a fair evaluation. Again, however, the major discrepancy between the models is that Hall MHD does not capture the strong kinetic damping of the kinetic S branch at all scales and of the solution A from kinetic theory (the ion cyclotron wave) at .
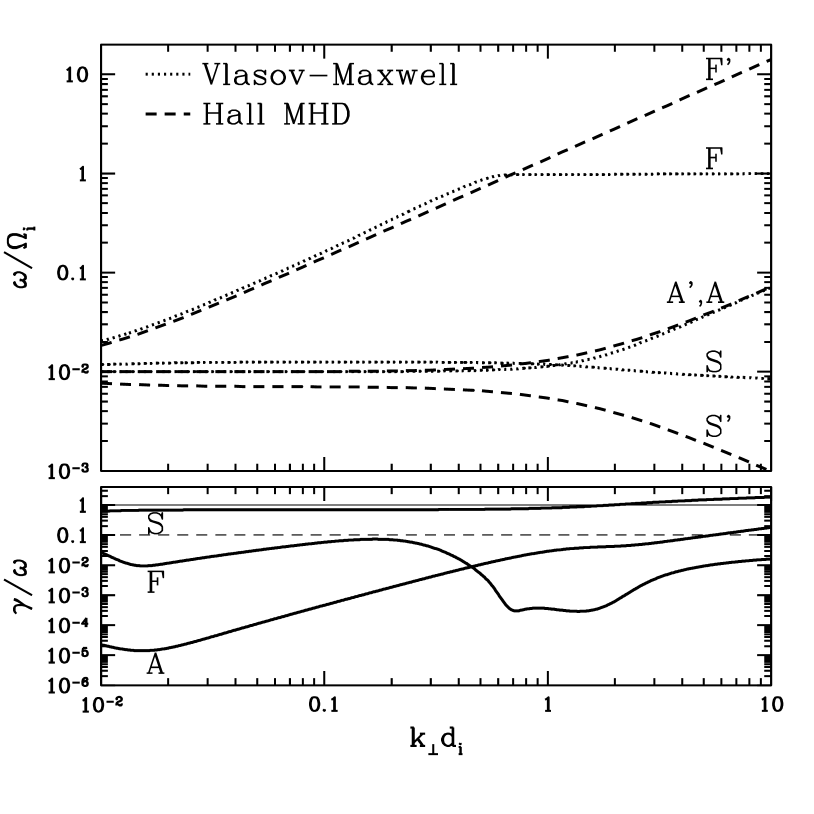
Figure 4 presents real frequencies and damping rates for perpendicular wavenumbers and parallel wavenumber for the warm ion case with and . The kinetic branch S is once again strongly damped by the warm ions, so Hall MHD supports a spurious, undamped slow wave mode S’. The kinetic branch A, representing MHD Alfvén waves and kinetic Alfvén waves, is quite well represented over the entire wavenumber range, with some discrepancy near . The kinetic fast wave solution F is well matched by the Hall MHD fast wave solution F’, with only a slight deviation, for . At , however, the kinetic branch F goes through a mode conversion to become an ion Bernstein wave, a situation discussed at length in §4.3.
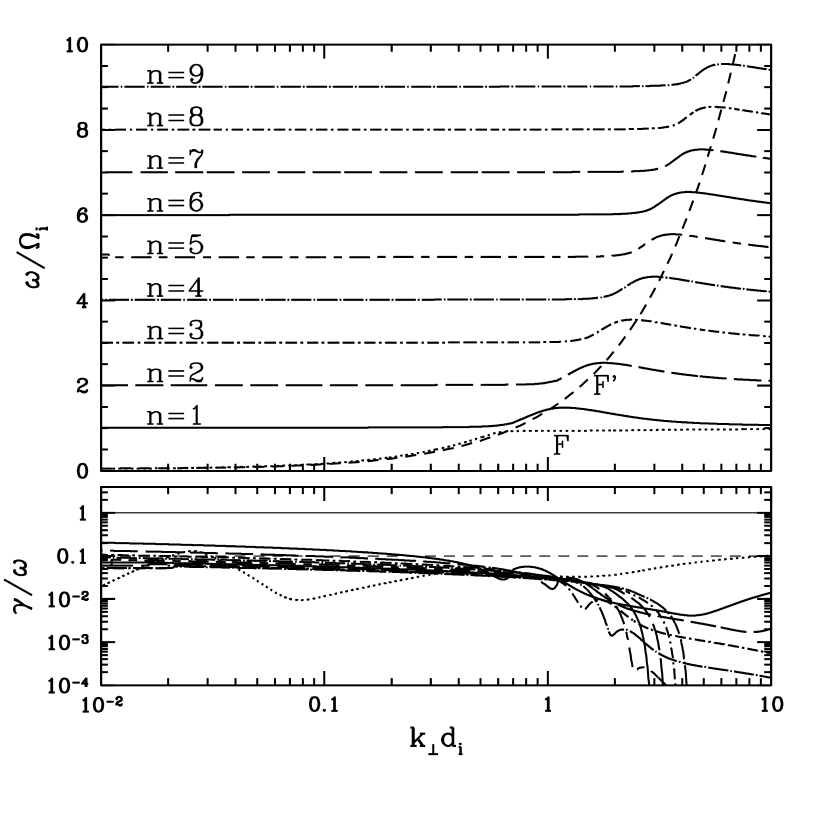
In summary, at finite ion temperature, Hall MHD does a good job modeling the kinetic fast wave branch F for nearly parallel wave vectors and the kinetic Alfvén wave branch for nearly perpendicular wave vectors. But, it fails to capture the strong kinetic damping of the slow mode branch in all cases and of the Alfvén branch in the nearly parallel case. The correspondence of the Hall MHD fast wave branch F’ at nearly perpendicular wave vectors to a series of kinetic ion Bernstein waves is discussed next.
4.3 Ion Bernstein Waves
The fast solution F from kinetic theory in Figure 4 deviates greatly from the Hall MHD fast solution F’ at . The cause of this deviation is the conversion, in kinetic theory, from an MHD fast wave to an ion Bernstein wave (with ) on the dispersion surface of solution branch F. Not shown in Figure 4 is the conversion of an ion Bernstein wave (with ) to a continuation of the fast wave at ; this wave lies on a different dispersion surface from branch F. Mode conversion from fast wave solutions to ion Bernstein waves at nearly perpendicular propagation is a well known physical phenomenon (Swanson, 1989; Stix, 1992; Li and Habbal, 2001). Here we aim to evaluate the accuracy of the Hall MHD description of the kinetic plasma behavior in this regime.
In Figure 5 are presented the real frequencies (top panel) and damping rates (bottom panel) for the Hall MHD fast branch F’ (dashed), the kinetic fast branch F (dotted), and the kinetic through ion Bernstein solutions for perpendicular wavenumbers and parallel wavenumber for and . Note that each of the ion Bernstein solutions lie on distinct dispersion surfaces. In the top panel, the relation between the Hall MHD branch F’ and the series of ion Bernstein wave solutions is clear, yet the summed effect of these kinetic wave modes differs significantly in a number of ways from the Hall MHD fast branch solution F’. First, between each of the ion Bernstein solutions lies a frequency gap in which no solution exists. Second, the real frequency of the ion Bernstein waves (and thus the perpendicular phase velocity ) is only coincident with the frequency given by Hall MHD at a single point for each of the the Bernstein modes. Finally, although the perpendicular group velocity (the slope of the plot ) of the Hall MHD F’ solution is always positive and increasing with , each of the ion Bernstein waves have a positive but smaller group velocity at lower , and a negative group velocity at higher , corresponding to a backward wave (Stix, 1992) at these scales. The lower panel of Figure 5 shows that the kinetic fast branch F and through ion Bernstein waves are not strongly damped. Our conclusion is that the kinetic dynamics of the fast branch for nearly perpendicular wave vectors in a weakly collisional plasma is not well represented by Hall MHD.
4.4 Comparison on the Plane
The axisymmetric nature of any uniform magnetized plasma about the direction of a uniform, straight magnetic field reduces the dependence on the wave vector to its two components perpendicular and parallel to the magnetic field, ; this is clearly seen in the dispersion relations of both the Hall MHD and the Vlasov-Maxwell systems with their dependence on the parameters and . Therefore, plots of the real frequency difference and of the kinetic damping rate on the plane provide excellent quantitative measures of the fidelity of Hall MHD to the kinetic physics in a weakly collisional plasma over a wide range of scales.
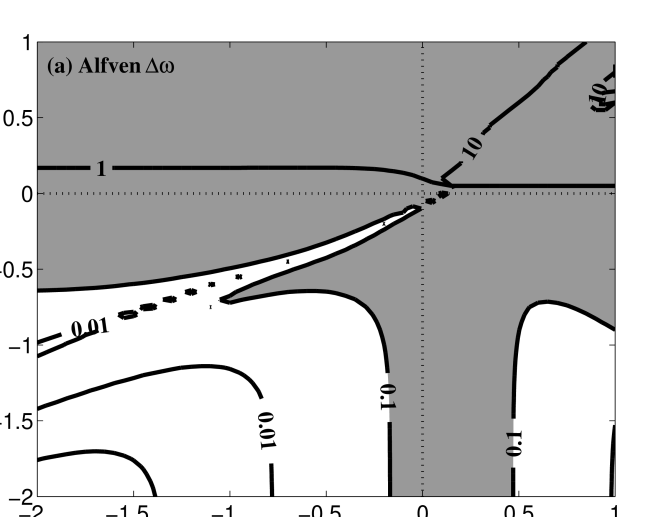
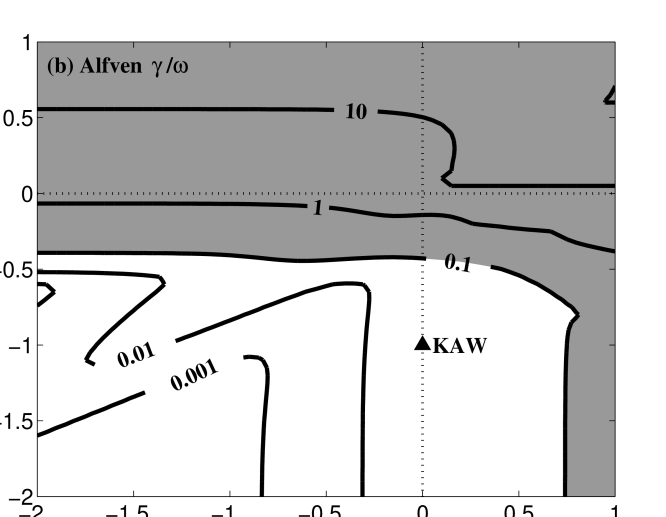
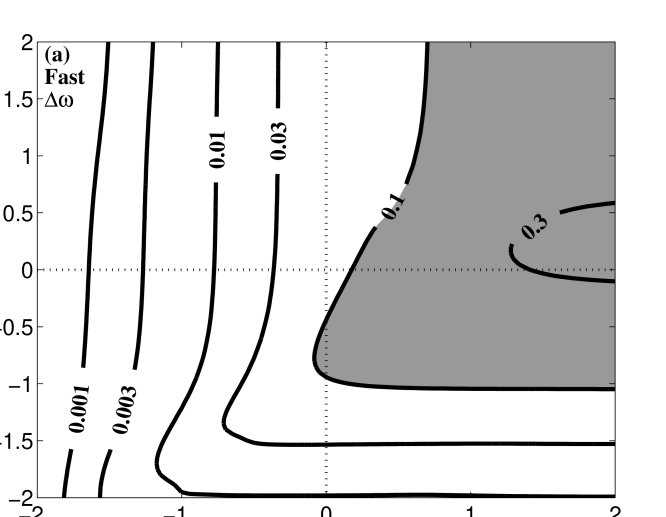
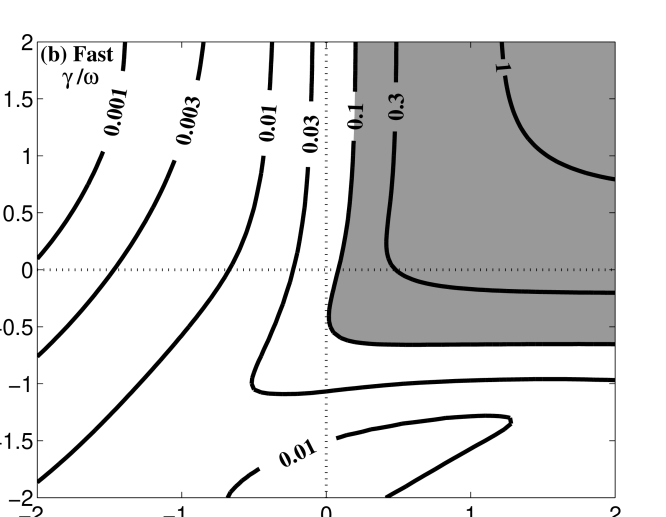
In panel (a) of Figure 6, the normalized real frequency difference between Hall MHD and Vlasov-Maxwell kinetics, , is plotted for the Alfvén solution over and ; in panel (b) is plotted the normalized linear kinetic damping rate, . Plasma parameters relevant to the near-earth solar wind, and , are chosen. Areas of panel (a) with are shaded to highlight the regions of parameter space over which the frequency using Hall MHD deviates significantly from the kinetic value; as evident, the Alfvén solution from Hall MHD222Because of the tendency for the kinetic modes to correspond to different fluid modes as parameters vary, as discussed in §3.1, in this paper the calculation of at each point uses the Hall MHD mode that the yields the minimum value of this difference. deviates substantially from the Vlasov-Maxwell frequency at and moderately at . Areas of panel (b) with are shaded to denote regions of parameter space over which the linear collisionless damping of this mode in Vlasov-Maxwell kinetic theory is strong. It is evident that for , the regime corresponding to ion cyclotron waves, strong damping occurs via the ion cyclotron resonance; it seems likely that this strong damping, due to wave-particle interactions not captured by Hall MHD, is also responsible for the poor agreement in real frequency. Also evident in panel (b) is the increasingly strong damping of the Alfvén solution at and ; this is the regime of kinetic Alfvén waves in which damping occurs via Landau resonance with the electrons.
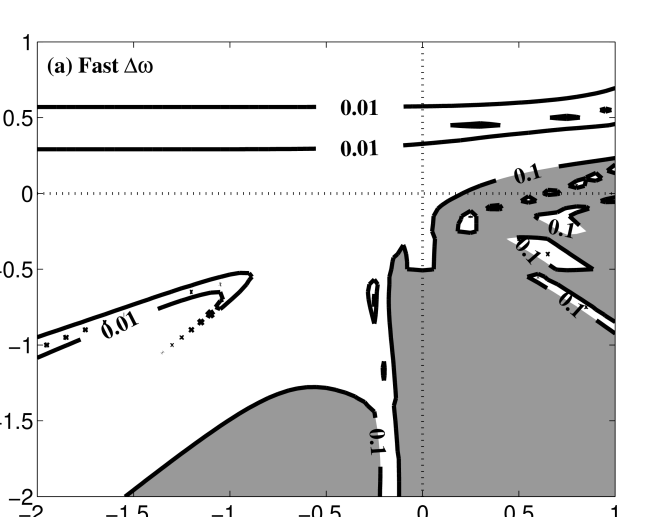
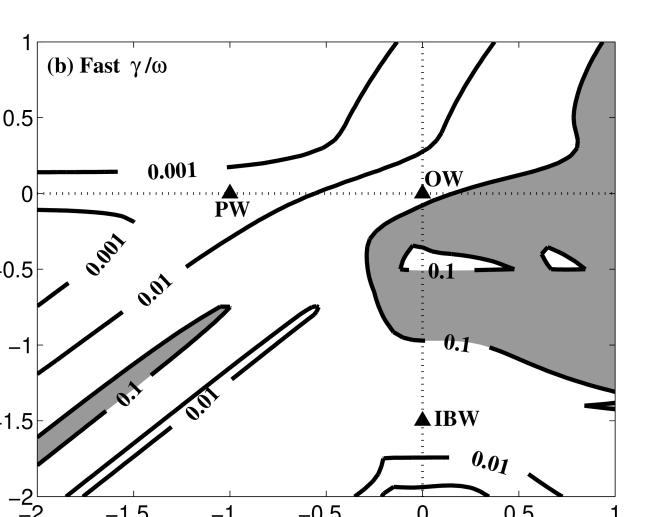
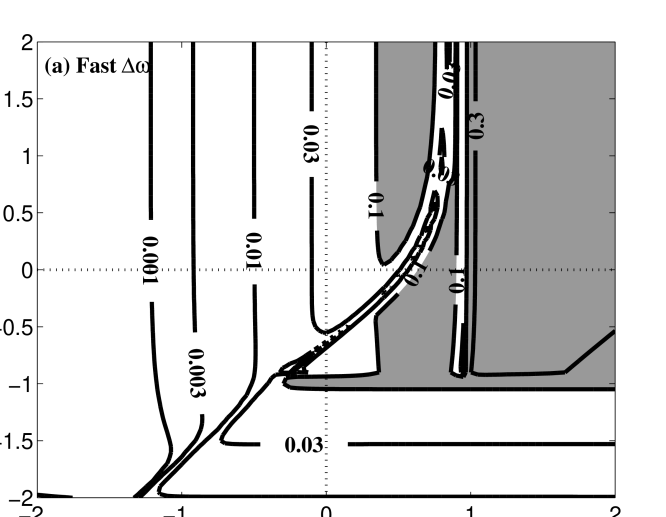
The analogous calculation for the fast wave branch is presented in Figure 7, with the frequency difference plotted in panel (a) and the kinetic damping rate in panel (b), again for plasma parameters and . Note that this calculation employs only the kinetic solutions on the dispersion surface of the F branch and does not consider the ion Bernstein wave dispersion surfaces. The real frequency derived from Hall MHD differs from the kinetic value in two regimes: a moderate difference occurs at and ; and the difference becomes more dramatic at and due to the mode conversion in kinetic theory of the F branch from the fast wave to an ion Bernstein wave in this regime. The kinetic damping, shown in panel (b), is relatively weak except for the regime of the ion Bernstein waves, and ; these waves are strongly damped unless (Swanson, 1989).
The slow wave branch suffers very strong linear collisionless damping in a plasma with finite ion temperature, such as the solar wind, over the entire range of scales considered in Figures 6 and 7. A comparison of the real frequency in this case would be meaningless since a wave with a damping rate is so heavily damped that it can scarcely be considered a wave.
4.5 Plasma Parameter and Variations
A very important aspect of the behavior of weakly collisional plasmas is made clear by the damping rate plots in panel (b) of both Figures 6 and 7: at small length scales, with wavenumbers , there exist only four regimes in which undamped wave modes occur. These are:
-
1.
Kinetic Alfvén Waves: The Alfvén branch solution of Vlasov-Maxwell kinetic theory in the nearly perpendicular regime and corresponds to the kinetic Alfvén wave mode (KAW) .
-
2.
Parallel Whistler Waves: The fast branch solution in the regime and corresponds to the whistler wave with a nearly parallel wave vector (PW).
-
3.
Oblique Whistler Waves: The fast branch solution in the regime and corresponds to the whistler wave with an oblique wave vector (OW).
-
4.
Ion Bernstein Waves: The fast branch solution in the nearly perpendicular regime and corresponds to an ion Bernstein wave (IBW).
Since the plasma turbulence at small length scales—for example, the dissipation range in the solar wind—is likely to consist of one, or a mixture, of these four undamped modes, we would like to explore the ability of Hall MHD to reproduce their linear wave frequencies accurately (relative to linear Vlasov-Maxwell kinetic theory). We note, however, that the ion Bernstein wave is an electrostatic wave mode (Swanson, 1989; Stix, 1992), and therefore has no corresponding magnetic field fluctuation; since the solar wind dissipation range is observed to have magnetic fluctuations (Goldstein et al., 1995; Leamon et al., 1998; Smith et al., 2006; Hamilton et al., 2008), we do not further pursue the ion Bernstein waves here, but rather we focus solely on the first three modes, all of which are electromagnetic.
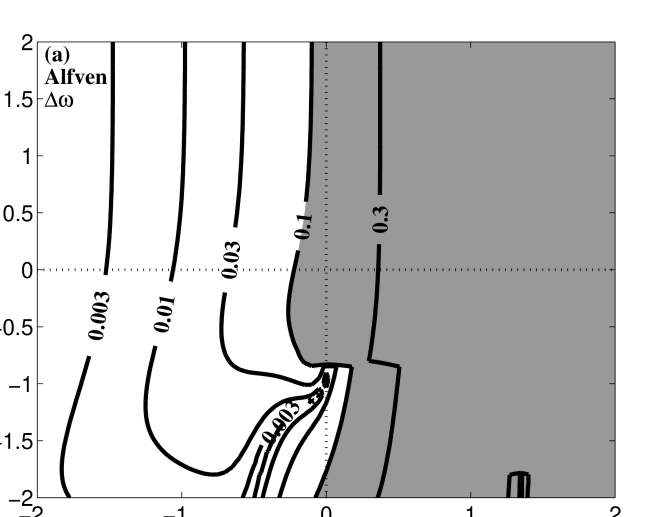
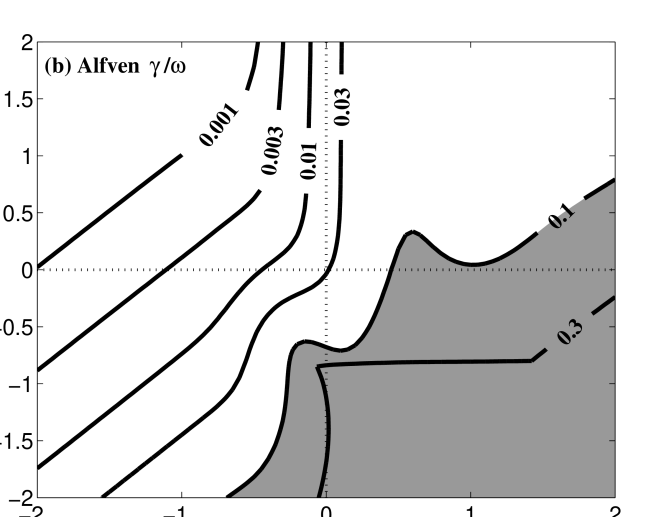
For a kinetic Alfvén wave at and , denoted by the triangle (KAW) in panel (b) of Figure 6, we plot the frequency difference and kinetic damping rate over and in panels (a) and (b) of Figure 8. The kinetic Alfvén wave appears to be well reproduced by Hall MHD for , but is less accurately determined for . The linear kinetic damping of the mode appears to become strong only for and .
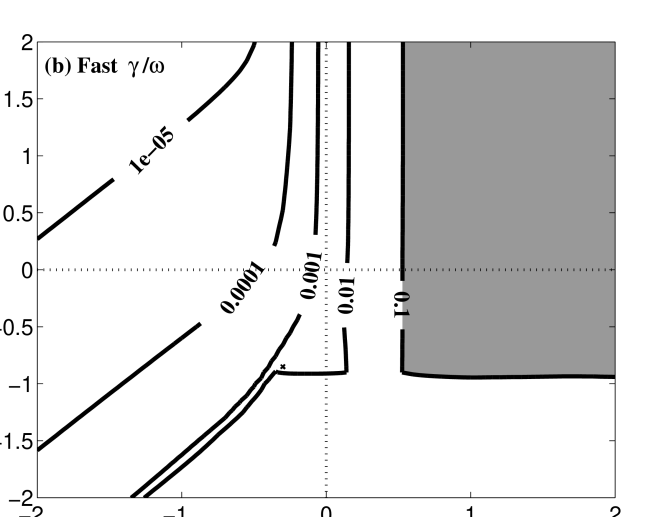
For a parallel whistler wave (on the fast wave branch) at and , denoted by the triangle (PW) in panel (b) of Figure 7, we plot the frequency difference and kinetic damping rate on the plane in panels (a) and (b) of Figure 9. This parallel whistler wave appears to be well reproduced by Hall MHD over all parameter space except for and ; in this problematic regime, the whistler wave mode converts to an ion Bernstein wave and is therefore both strongly damped and poorly described by Hall MHD.
For an oblique whistler wave (on the fast wave branch) at and , denoted by the triangle (OW) in panel (b) of Figure 7, we plot the frequency difference and kinetic damping rate on the plane in Figure 10. The results are very similar to those for the parallel whistler wave, with strong damping, and correspondingly poor agreement in linear real frequency, occurring over the regime and .
With the exception of the regime and for the kinetic Alfvén wave, where Hall MHD predicts a quantitatively different real frequency from kinetic theory, all of the differences between Hall MHD and kinetic theory occur when the damping becomes strong, with . That the weakly damped wave modes should be well represented by Hall MHD is precisely what is expected—the fluid limit of the kinetic plasma physics is valid only when kinetic effects, such as collisionless damping by wave-particle interactions, are negligible (Ballai et al., 2002).
5 Discussion
The detailed comparison of linear eigenfrequencies presented in §4 provides a solid quantitative foundation upon which to construct a thorough discussion of the central question of this paper: How does choosing the standard Hall MHD system affect the description of the dynamics and evolution of turbulence in a weakly collisional plasma?
One functional definition of turbulence is that it is nothing more than the sum of all nonlinear wave-wave couplings that serve to transfer energy from one spatial scale to another; in a three-dimensional physical system such as the solar wind, the generally accepted picture is that energy in large scale fluctuations is transferred via these nonlinear interactions to ever smaller scales, cascading until eventually reaching a scale at which some dissipation mechanism damps the fluctuations, ultimately thermalizing their energy (see Schekochihin et al. (2007) and Howes (2008) for a theoretical picture of how this process may occur in a weakly collisional plasma). Three important questions essentially frame the frontier of research on kinetic turbulence, and are particularly relevant to an evaluation of the Hall MHD description for turbulence in a kinetic plasma:
-
1.
What are the characteristic wave modes of the turbulence at scales ?
-
2.
Is the collisionless damping of the turbulence at scales well described by linear damping rates?
-
3.
Are the nonlinear wave-wave couplings that drive the turbulent cascade altered by the presence of unphysical wave modes?
5.1 The Wave Modes Comprising Kinetic Turbulence
By exploiting the highly super-Alfvénic speed of the solar wind flow, the temporal fluctuations measured by in situ spacecraft can be mapped, according to the Taylor hypothesis (Taylor, 1938), to spatial fluctuations. Thus, the break in the solar wind magnetic energy spectrum, typically observed at around Hz, is thought to correspond to some characteristic length scale in the plasma, perhaps the ion inertial length or the ion Larmor radius (Leamon et al., 1998; Howes et al., 2008a; Hamilton et al., 2008). At frequencies above this spectral break, corresponding to yet smaller spatial scales, the magnetic energy spectrum appears steeper (Smith et al., 2006)—this regime is denoted the “dissipation range.”
The kinetic theory results presented in §4.4 clearly demonstrate that, for a weakly collisional plasma with a finite ion temperature—such as the solar wind—all slow branch modes, the ion cyclotron wave of the Alfvén branch, and the fast branch ion Bernstein wave at are strongly damped. Only three weakly damped electromagnetic wave modes exist at scales : the kinetic Alfvén wave, the parallel whistler wave, and the oblique whistler wave. It seems unlikely, even in a nonlinearly turbulent plasma, that wave modes with strong linear kinetic damping rates could be responsible for the dissipation range fluctuations. The linear wave properties are quite likely to play a large role in the turbulent dynamics, in particular at the small length scales where the amplitude of the magnetic fluctuations is small compared to the magnitude of the local interplanetary magnetic field (Howes et al., 2008a). This line of reasoning suggests that the fluctuations in the dissipation range must consist of one, or perhaps a mixture, of the three undamped electromagnetic wave modes. The finding of §4.5 suggests that, for typical solar wind parameters with , Hall MHD generally does an adequate job of describing these undamped wave modes.
5.2 Kinetic Damping Rates
How effective are linear collisionless damping mechanisms in a turbulent plasma where nonlinear interactions are continually transferring energy from one wave mode to another? This question essentially weighs the importance of linear kinetic wave-particle interactions versus nonlinear fluid wave-wave interactions in turbulent, weakly collisional plasma. According to models for turbulent fluids, the energy in a particular wave mode will be transferred to other wave modes through nonlinear interactions on some characteristic nonlinear time scale. The theory for strong incompressible MHD turbulence takes this nonlinear timescale to be the eddy-turnover time in the perpendicular direction (Goldreich and Sridhar, 1995); the central conjecture of this theory is that, as the turbulent energy cascades to smaller scales, this nonlinear timescale remains in an approximate critical balance with the linear Alfvén wave period, and consequently predicts an anisotropic cascade to high perpendicular wavenumbers that is supported by numerical evidence (Cho and Vishniac, 2000; Maron and Goldreich, 2001) and is consistent with a careful analysis of solar wind turbulence observations (Horbury et al., 2008).
The key question in weakly collisional plasmas is whether or not this nonlinear transfer suppresses the linear collisionless damping via wave-particle interactions. Conversely, it is possible that nonlinear wave-wave interactions can transfer energy into a strongly damped mode, ultimately leading to energy loss from the turbulent fluctuations through linear wave-particle interactions of that strongly damped mode. But it is conceivable that nonlinear couplings involving strongly damped modes are inhibited by an impedance mismatch, thus preventing energy loss in such a manner. Ultimately, of course, the turbulence must be dissipated via kinetic damping mechanisms (Howes, 2008); in this case, an evaluation of both the rate of energy transfer by the turbulent cascade and the rate of kinetic damping is necessary to determine the dissipation as a function of wavenumber, as in the cascade model of Howes et al. (2008a).
These important questions will most likely only be answered through detailed nonlinear kinetic numerical simulations. On this front, turbulence simulations using undamped fluid models, such as Hall MHD, will provide valuable comparison points for analysis and interpretation of the kinetic simulation results.
Until such work can provide further guidance, it seems a reasonable strategy to assume the applicability of the linear kinetic damping rates to turbulent plasmas. In fact, the first such nonlinear kinetic simulation of turbulence at the scale of the ion Larmor radius has been well fit by a model assuming linear damping rates (Howes et al., 2008c). The plasma parameters chosen for this study, however, predicted rather weak linear collisionless damping over the range of scales simulated, so we must await further simulations in more strongly damped parameter regimes to test more thoroughly the effectiveness of the kinetic damping in a turbulent plasma. The study did show, however, that the damping via kinetic mechanisms in the turbulent plasma was not stronger than the linear prediction, a result that is not obvious a priori.
Despite the many unanswered questions about damping in kinetic turbulence, there is no question that the dissipation of turbulence in a weakly collisional plasma cannot be studied by Hall MHD, or any standard fluid model. The viscous and resistive dissipation terms used in such models are merely ad hoc fluid closures that do not accurately represent the underlying kinetic mechanisms. Only a much more complicated model, such as a Landau-fluid model (Snyder et al., 1997; Passot and Sulem, 2007), is capable of adequately representing the kinetic dissipation. The steeper spectral index of the magnetic energy spectrum in the dissipation range of solar wind turbulence has been variously attributed to either kinetic dissipation (Coleman, 1968; Leamon et al., 1999; Gary, 1999; Howes et al., 2008a) or to wave dispersion (Stawicki et al., 2001; Krishan and Mahajan, 2004; Galtier, 2006). If dissipation does play a significant role, further investigation requires a kinetic model. It has even been argued that, without a kinetic model to determine that kinetic dissipation is negligible for a specific case, the use of a fluid model such as Hall MHD is unjustified (Howes et al., 2008b).
5.3 Nonlinear Wave-Wave Interactions
Hall MHD has proven to be a valuable framework for the study of a number of plasma phenomena, in particular magnetic reconnection. For example, the finding that whistler waves mediated a faster reconnection rate (Mandt et al., 1994) paved the way in identifying the importance of the Hall term in magnetic reconnection. Such applications depend on the accurate description of the linear properties of a particular wave mode. But turbulence is consequence of nonlinear wave couplings; to provide a useful framework for kinetic turbulence, a model must accurately describe the behavior not of just one mode, but of all modes.333The nonlinear interactions in a turbulent plasma will depend not only on the complex eigenfrequencies of the normal modes but on their eigenfunctions as well. Although this paper restricts its focus to the frequencies, a detailed comparison of all mode properties at found that the kinetic mode properties are not always well represented by Hall MHD (Krauss-Varban et al., 1994).
Because the turbulent dynamics and evolution will depend on the nonlinear couplings between all possible wave modes, the existence of certain undamped wave modes in Hall MHD—modes that are strongly damped in a weakly collisional plasma according to kinetic theory—is troubling. These spurious wave modes effectively provide additional degrees of freedom to the turbulence that would otherwise be strongly impeded in a kinetic plasma. Consider, for example, waves in the parameter regime in a plasma with and as presented in Figure 3 of §4.2. In Vlasov-Maxwell kinetic theory, both the Alfvén and slow branch modes are heavily damped in this regime, leaving only fast branch waves available. But the Hall MHD model supports undamped Alfvén and slow waves. It seems unlikely that the nonlinear dynamics would be the same in the presence of three undamped modes as when only the fast mode is available, but just how the presence of the unphysical modes will alter the nonlinear wave-wave couplings is unclear. Here, once again, a promising avenue for progress is a detailed study contrasting nonlinear couplings in the presence and absence of these spurious modes. A suite of nonlinear kinetic simulations compared to Hall MHD simulations in the same regime will provide valuable insight, identifying the regimes of validity for which Hall MHD provides an adequate description.
Two arguments exist that may serve to diminish the impact of the spurious undamped waves in Hall MHD. First, as shown in Figure 4, in the limit that , the fast wave frequency is much higher than the Alfvén wave frequency; since the strength of nonlinear interactions typically diminishes rapidly as the wave mode frequencies become widely separated, the presence of a spurious wave mode may negligibly impact the turbulent couplings in such a case. Of course, in the opposite limit , seen in Figure 3, all three wave modes have similar frequencies for . A second argument, derived in the gyrokinetic limit444The fast wave branch is ordered out of the system in the gyrokinetic approximation. and , shows that the turbulent cascade of Alfvén waves does not exchange energy with the slow wave cascade except in the regime where the perpendicular scale is near the ion Larmor radius (Schekochihin et al., 2007). Thus, the existence of a spuriously undamped slow wave may not influence the Alfvén wave cascade. To explore the exchange of energy between the separate cascades at the scale of the ion Larmor radius , however, will certainly require nonlinear kinetic simulations.
As a model that extends beyond the limits of MHD, Hall MHD has seen increasing use in recent years as a framework for describing turbulence in weakly collisional plasmas, such as the near-earth solar wind. Its applicability to turbulence in kinetic systems has been called into question (Krauss-Varban et al., 1994; Howes et al., 2008b), so a thorough evaluation of the limitations of Hall MHD in this context is desirable. This paper takes the first step in this process by quantitatively comparing the real linear eigenfrequencies of standard Hall MHD with the complex linear eigenfrequencies of Vlasov-Maxwell kinetic theory.
Previous work has shown that Hall MHD is a rigorous limit of kinetic theory only in the cold ion limit satisfying , and (Ito et al., 2004; Hirose et al., 2004); the fluid description is only valid when wave-particle interactions and finite-Larmor-radius effects are negligible (Ballai et al., 2002). The quantitative comparisons with kinetic theory in §4 bear out the general finding that Hall MHD is a valid limit of Hall MHD in the cold ion limit ; for finite ion temperature , however, the lack of collisionless damping in Hall MHD leads to undamped wave modes that do not exist in a weakly collisional plasma.
Three key issues are identified regarding the use of Hall MHD to describe turbulence in kinetic plasmas: (1) what are the wave modes comprising the turbulence at scales ?; (2) are the collisionless damping rates from linear kinetic theory applicable in a nonlinearly turbulent plasma?; and (3) are the nonlinear wave-wave mode couplings inherent in turbulence altered by the presence of spurious, undamped wave modes in Hall MHD? In a weakly collisional plasma, the only three undamped electromagnetic wave modes that exist at scales are the kinetic Alfvén wave, the parallel whistler wave, and the oblique whistler wave; each of these waves is generally well-described by Hall MHD for . To determine the effective collisionless damping in a turbulent plasma, a research program using nonlinear numerical simulations to contrast the predictions of a kinetic approach with those of a fluid approach is the most promising path forward. For studies focusing on the dissipation of turbulence and the thermalization of the turbulent energy, a kinetic description is certainly required. Both fluid Hall MHD and kinetic nonlinear numerical simulations will be instrumental in shedding light on the question of whether the presence of the spuriously undamped waves in Hall MHD alters the nonlinear couplings of the available wave modes, thus changing the dynamics and evolution of the turbulence due to unphysical effects. A study focused on the turbulent dynamics at the characteristic length scales in the plasma, such as the ion Larmor radius or the ion inertial length, is the natural starting point for such a numerical investigation. In conclusion, although nonlinear kinetic simulations will be indispensable for the study of turbulence at kinetic scales in weakly collisional plasmas, Hall MHD will certainly continue to provide useful insights and valuable points for comparison in the study of kinetic turbulence.
Acknowledgements.
The author thanks Ben Chandran for insightful discussions.Literatur
- Abraham-Shrauner (1973) Abraham-Shrauner, B.: Small amplitude hydromagnetic waves for a plasma with a generalized polytrope law , Plasma Physics, 15, 375–385, 1973.
- Andre (1985) Andre, M.: Dispersion surfaces, J. Plasma Phys., 33, 1–19, 1985.
- Ballai et al. (2002) Ballai, I., Erdélyi, R., Voitenko, Y., and Goossens, M.: Linear and nonlinear wave propagation in rarefied plasmas, Physics of Plasmas, 9, 2593–2603, 10.1063/1.1476918, 2002.
- Chew et al. (1956) Chew, G. L., Goldberger, M. L., and Low, F. E.: The Boltzmann Equation and the One-Fluid Hydromagnetic Equations in the Absence of Particle Collisions, Proc. R. Soc. London A”, 236, 112, 1956.
- Cho and Vishniac (2000) Cho, J. and Vishniac, E. T.: The Anisotropy of Magnetohydrodynamic Alfvénic Turbulence, Astrophys. J., 539, 273–282, 2000.
- Chust and Belmont (2006) Chust, T. and Belmont, G.: Closure of fluid equations in collisionless magnetoplasmas, Phys. Plasmas, 13, 012 506–+, 10.1063/1.2138568, 2006.
- Coleman (1968) Coleman, Jr., P. J.: Turbulence, Viscosity, and Dissipation in the Solar-Wind Plasma, Astrophys. J., 153, 371, 1968.
- Dmitruk and Matthaeus (2006) Dmitruk, P. and Matthaeus, W. H.: Structure of the electromagnetic field in three-dimensional Hall magnetohydrodynamic turbulence, Physics of Plasmas, 13, 042 307–+, 10.1063/1.2192757, 2006.
- Frieman and Chen (1982) Frieman, E. A. and Chen, L.: Nonlinear gyrokinetic equations for low-frequency electromagnetic waves in general plasma equilibria, Phys. Fluids, 25, 502–508, 1982.
- Galtier (2006) Galtier, S.: Wave turbulence in incompressible Hall magnetohydrodynamics, J. Plasma Phys., 72, 721–769, 10.1017/S0022377806004521, 2006.
- Gary (1999) Gary, S. P.: Collisionless dissipation wavenumber: Linear theory, J. Geophys. Res., 104, 6759–6762, 10.1029/1998JA900161, 1999.
- Ghosh et al. (1996) Ghosh, S., Siregar, E., Roberts, D. A., and Goldstein, M. L.: Simulation of high-frequency solar wind power spectra using Hall magnetohydrodynamics, jgr, 101, 2493–2504, 10.1029/95JA03201, 1996.
- Goldreich and Sridhar (1995) Goldreich, P. and Sridhar, S.: Toward a Thoery of Interstellar Turbulence II. Strong Alfvénic Turbulence, Astrophys. J., 438, 763–775, 1995.
- Goldstein et al. (1995) Goldstein, M. L., Roberts, D. A., and Matthaeus, W. H.: Magnetohydrodynamic Turbulence In The Solar Wind, Ann. Rev. Astron. Astrophys., 33, 283–326, 10.1146/annurev.aa.33.090195.001435, 1995.
- Hameiri et al. (2005) Hameiri, E., Ishizawa, A., and Ishida, A.: Waves in the Hall-magnetohydrodynamics model, pop, 12, 072 109–+, 10.1063/1.1952887, 2005.
- Hamilton et al. (2008) Hamilton, K., Smith, C. W., Vasquez, B. J., and Leamon, R. J.: Anisotropies and helicities in the solar wind inertial and dissipation ranges at 1 AU, J. Geophys. Res., 113, 1106–+, 10.1029/2007JA012559, 2008.
- Hirose et al. (2004) Hirose, A., Ito, A., Mahajan, S. M., and Ohsaki, S.: Relation between Hall-magnetohydrodynamics and the kinetic Alfvén wave, Physics Letters A, 330, 474–480, 10.1016/j.physleta.2004.08.021, 2004.
- Horbury et al. (2008) Horbury, T. S., Forman, M., and Oughton, S.: Anisotropic Scaling of Magnetohydrodynamic Turbulence, Phys. Rev. Lett., 101, 175 005, 10.1103/PhysRevLett.101.175005, 2008.
- Hori et al. (2005) Hori, D., Furukawa, M., Ohsaki, S., and Yoshida, Z.: A Shell Model for the Hall MHD System, Journal of Plasma and Fusion Research, 81, 141–142, 10.1585/jspf.81.141, 2005.
- Howes (2008) Howes, G. G.: Inertial range turbulence in kinetic plasmas, Phys. Plasmas, 15, 055 904–+, 10.1063/1.2889005, 2008.
- Howes et al. (2006) Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E., and Schekochihin, A. A.: Astrophysical Gyrokinetics: Basic Equations and Linear Theory, Astrophys. J., 651, 590–614, 10.1086/506172, 2006.
- Howes et al. (2008a) Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E., and Schekochihin, A. A.: A model of turbulence in magnetized plasmas: Implications for the dissipation range in the solar wind, J. Geophys. Res., 113, 5103–+, 10.1029/2007JA012665, 2008a.
- Howes et al. (2008b) Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E., Schekochihin, A. A., and Tatsuno, T.: Howes etal. Reply:, Phys. Rev. Lett., 101, 149 502–+, 10.1103/PhysRevLett.101.149502, 2008b.
- Howes et al. (2008c) Howes, G. G., Dorland, W., Cowley, S. C., Hammett, G. W., Quataert, E., Schekochihin, A. A., and Tatsuno, T.: Kinetic Simulations of Magnetized Turbulence in Astrophysical Plasmas, Phys. Rev. Lett., 100, 065 004–+, 10.1103/PhysRevLett.100.065004, 2008c.
- Huba (1994) Huba, J. D.: Hall dynamics of the Kelvin-Helmholtz instability, Phys. Rev. Lett., 72, 2033–2036, 1994.
- Ito et al. (2004) Ito, A., Hirose, A., Mahajan, S. M., and Ohsaki, S.: Remarks on the discrete Alfvén wave spectrum induced by the Hall current, Physics of Plasmas, 11, 5643–5647, 10.1063/1.1804979, 2004.
- Krauss-Varban et al. (1994) Krauss-Varban, D., Omidi, N., and Quest, K. B.: Mode properties of low-frequency waves: Kinetic theory versus Hall-MHD, J. Geophys. Res., 99, 5987–6009, 1994.
- Krishan and Mahajan (2004) Krishan, V. and Mahajan, S. M.: Magnetic fluctuations and Hall magnetohydrodynamic turbulence in the solar wind, J. Geophys. Res., 109, 11 105–+, 10.1029/2004JA010496, 2004.
- Kuvshinov (1994) Kuvshinov, B. N.: Magnetohydrodynamic model for plasma instabilities in the ion-kinetic regime , Plasma Phys. Con. Fus., 36, 867–877, 1994.
- Leamon et al. (1998) Leamon, R. J., Smith, C. W., Ness, N. F., Matthaeus, W. H., and Wong, H. K.: Observational Constraints on the Dynamics of the Interplanetary Magnetic Field Dissipation Range, J. Geophys. Res., 103, 4775–4787, 1998.
- Leamon et al. (1999) Leamon, R. J., Smith, C. W., Ness, N. F., and Wong, H. K.: Dissipation Range Dynamics: Kinetic Alfén Waves and the importance of , J. Geophys. Res., 104, 22 331–22 344, 1999.
- Li and Habbal (2001) Li, X. and Habbal, S. R.: Damping of fast and ion cyclotron oblique waves in the multi-ion fast solar wind, J. Geophys. Res., 106, 10 669–10 680, 10.1029/2000JA000420, 2001.
- Lighthill (1960) Lighthill, M. J.: Studies on Magnetohydrodynamic Waves and Other Anisotropic Wave Motions, Royal Society of London Philosophical Transactions Series A, 252, 397–430, 1960.
- Mandt et al. (1994) Mandt, M. E., Denton, R. E., and Drake, J. F.: Transition to whistler mediated magnetic reconnection, grl, 21, 73–76, 1994.
- Maron and Goldreich (2001) Maron, J. and Goldreich, P.: Simulations of Incompressible Magnetohydrodynamic Turbulence, Astrophys. J., 554, 1175–1196, 2001.
- Matthaeus et al. (2008) Matthaeus, W. H., Servidio, S., and Dmitruk, P.: Comment on “Kinetic Simulations of Magnetized Turbulence in Astrophysical Plasmas”, Phys. Rev. Lett., 101, 149 501–+, 10.1103/PhysRevLett.101.149501, 2008.
- Mininni et al. (2002) Mininni, P. D., Gómez, D. O., and Mahajan, S. M.: Dynamo Action in Hall Magnetohydrodynamics, apjl, 567, L81–L83, 10.1086/339850, 2002.
- Mininni et al. (2005) Mininni, P. D., Gómez, D. O., and Mahajan, S. M.: Direct Simulations of Helical Hall-MHD Turbulence and Dynamo Action, Astrophys. J., 619, 1019–1027, 10.1086/426534, 2005.
- Ohsaki and Mahajan (2004) Ohsaki, S. and Mahajan, S. M.: Hall current and Alfvén wave, Physics of Plasmas, 11, 898–902, 10.1063/1.1647566, 2004.
- Orlowski et al. (1994) Orlowski, D. S., Russell, C. T., Krauss-Varban, D., and Omidi, N.: A test of the Hall-MHD model: Application to low-frequency upstream waves at Venus, J. Geophys. Res., 99, 169–178, 1994.
- Passot and Sulem (2007) Passot, T. and Sulem, P. L.: Collisionless magnetohydrodynamics with gyrokinetic effects, Phys. Plasmas, 14, 082 502–+, 10.1063/1.2751601, 2007.
- Quataert (1998) Quataert, E.: Particle Heating by Alfvenic Turbulence in Hot Accretion Flows, Astrophys. J., 500, 978–+, 10.1086/305770, 1998.
- Rutherford and Frieman (1968) Rutherford, P. H. and Frieman, E. A.: Drift Instabilities in General Mangetic Field Configurations, Phys. Fluids, 11, 569–585, 1968.
- Sahraoui et al. (2003) Sahraoui, F., Belmont, G., and Rezeau, L.: Hamiltonian canonical formulation of Hall-magnetohydrodynamics: Toward an application to weak turbulence theory, Physics of Plasmas, 10, 1325–1337, 10.1063/1.1564086, 2003.
- Schekochihin et al. (2007) Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E., and Tatsuno, T.: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Astrophysical Plasmas, Astrophys. J. Supp., submitted, arXiv:0704.0044, 2007.
- Servidio et al. (2007) Servidio, S., Carbone, V., Primavera, L., Veltri, P., and Stasiewicz, K.: Compressible turbulence in Hall Magnetohydrodynamics, planss, 55, 2239–2243, 10.1016/j.pss.2007.05.023, 2007.
- Shebalin (1991) Shebalin, J. V.: Thermoelectric effects in decaying homogeneous magneto-gas turbulence, Physics of Fluids B, 3, 1990–1993, 1991.
- Smith et al. (2006) Smith, C. W., Hamilton, K., Vasquez, B. J., and Leamon, R. J.: Dependence of the Dissipation Range Spectrum of Interplanetary Magnetic Fluctuationson the Rate of Energy Cascade, Astrophys. J. Lett., 645, L85–L88, 10.1086/506151, 2006.
- Snyder et al. (1997) Snyder, P. B., Hammett, G. W., and Dorland, W.: Landau fluid models of collisionless magnetohydrodynamics, Phys. Plasmas, 4, 3974–3985, 1997.
- Stawicki et al. (2001) Stawicki, O., Gary, S. P., and Li, H.: Solar wind magnetic fluctuation spectra: Dispersion versus damping, J. Geophys. Res., 106, 8273–8282, 10.1029/2000JA000446, 2001.
- Stix (1992) Stix, T. H.: Waves in Plasmas, New York: American Institute of Physics, 1992, 1992.
- Swanson (1989) Swanson, D. G.: Plasma waves., Plasma waves., by Swanson, D. G.. Academic Press, Boston, MA (USA), 1989, 434 p., ISBN 0-12-678955-X,, 1989.
- Taylor (1938) Taylor, G. I.: The Spectrum of Turbulence, Proc. Roy. Soc. A, 164, 476–490, 1938.
- Yoon and Fang (2008) Yoon, P. H. and Fang, T.-M.: Dispersion surfaces for low-frequency modes, Plasma Phys. Con. Fus., 50, 125 002–+, 10.1088/0741-3335/50/12/125002, 2008.