Linear and Non Linear Effects on the Newtonian Gravitational Constant as deduced from the Torsion Balance
Abstract
The Newtonian gravitational constant has still 150 parts per million of uncertainty. This paper examines the linear and nonlinear equations governing the rotational dynamics of the torsion gravitational balance. A nonlinear effect modifying the oscillation period of the torsion gravitational balance is carefully explored.
keywords:
Experimental studies of gravity ; Determination of fundamental constants;PACS numbers: 04.80.-y ; 06.20.Jr;
1 Introduction
After many years of measurements, begun by H. Cavendish, the Newtonian gravitational constant value, said , is still affected by a large error [1]. The CODATA recommends , meaning a relative standard uncertainty of 150 parts per million (in the following ppm) [2]. This value has had recent confirmation by means, on one hand, of a super-conducting gravimeter [3] and, on the other hand, of a careful analysis of the possible beam balance nonlinearity [4]. The original Cavendish method of measure, employing the torsion balance, still reveals a large discrepancy from the recommended value: about 500 ppm [5] . This is probably due to imperfections of the crystalline structure of the torsion fibre [6, 7, 8]. Moreover recent studies point out that the period of a torsion pendulum might vary under disturbances of environmental noise factors, see see [9]. Other authors suggest a possible deviation from Newton’s law specified as an additional contribution of Yukawa potential type [10]. This paper first analyses the linear and non linear equations governing the torsional balance rotational dynamics (Section 2). By means of a gravitational torsion balance, same values of are obtained and summarised (Section 3). The oscillation period’s variation, due to a non linear effect, is then discussed (Section 4).
2 The basic equations
The form of Newton’s law of gravitation is
| (1) |
where is the gravitational constant , the great mass , the small mass and their relative distance. The Leybold balance represents a widespread instrument to determine the constant , see Figure 1,
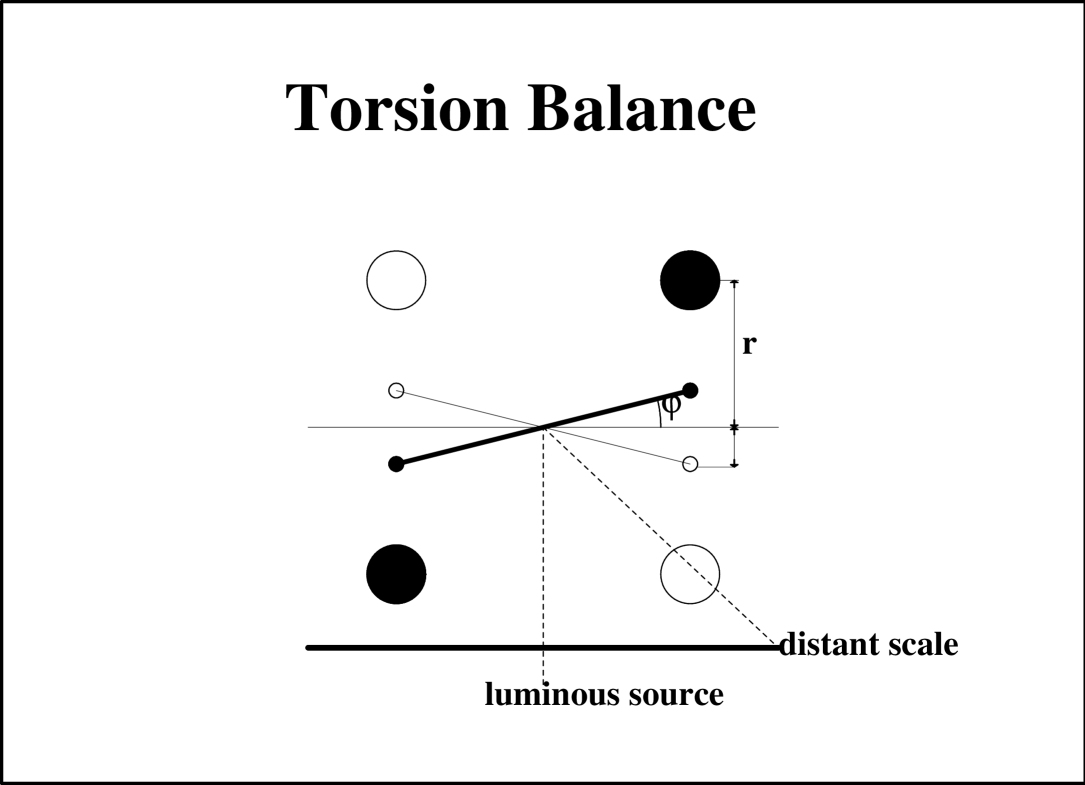
and is constructed with the following components.
-
1.
A freely oscillating horizontal bar , of length , holding two small lead balls of mass as in Figure 1 supported by a torsion fibre that has a torsional constant .
-
2.
Two larger balls of mass that can be positioned next to the small balls as in Figure 1. The center of mass of the two and are supposed to be all on a plane perpendicular to the fibre.
-
3.
A luminous source directed toward the center of mass of the bar where is reflected by a mirror.
-
4.
A scale at distance l where the reflected light beam is measured.
Thus the equilibrium position about which the pendulum oscillates is different for the two positions and it is this difference which we use to determine G. The Figure 2 reports a plot of the motion.
The moment of inertia of the bar, is
| (2) |
The fundamental equation of rotational dynamics is
| (3) |
where
| (4) |
| (5) |
here is the coefficient of viscosity of air , the angle between bar and bar itself when the torque is zero. This angle is measured in the anti clockwise direction. The term represents the torque of the gravitational forces. From equation , we obtain
| (6) |
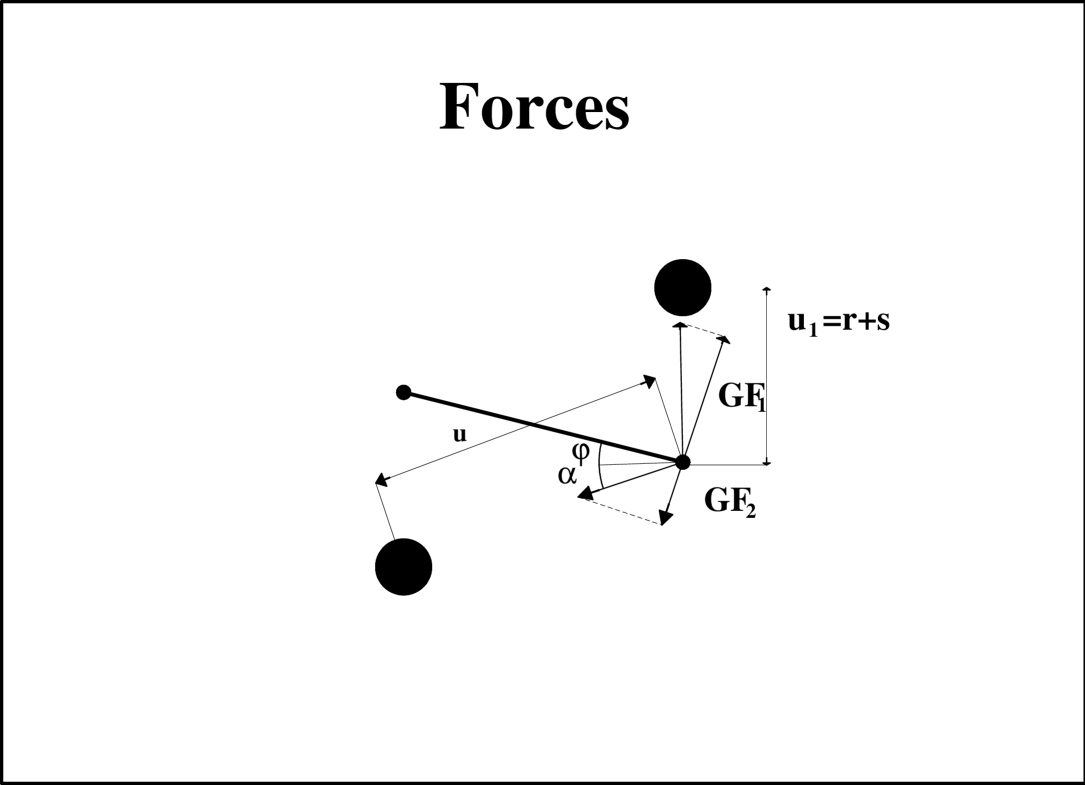
where is a function of the angle . The law of dependence of with is complex and will here be analysed. When the motion starts the resulting force is
| (7) |
where
| (8) |
| (9) |
now (where e are defined as in Figure 1). With our data , see Section 3 the maximum angular excursion of the angle is
| (10) |
The angle has a low values, see Table 1, and a Taylor series expansion that keep terms to order will be adopted. This means to forget quantities less than 3 . The series representation gives
| (11) |
Developing the last term with a Maclaurin series we obtain
| (12) |
As a consequence
| (13) |
and expanding the denominator we obtain
| (14) |
that means
| (15) |
An expression for can be obtained from equation
| (16) |
On Taylor expanding the denominator
| (17) |
and therefore
| (18) |
Now from equation can be expressed like a Taylor expansion truncated at
| (19) |
where
| (20) |
| (21) |
| (22) |
Three methods that allow to obtain an expression for in terms of measurable quantities are now introduced. Further on the well known formula for G extracted from the Leybold manual is reviewed.
2.1 Averaged G
Let for all the experience ; in first approximation we may assume that is given by equation to first order
| (23) |
where is the average of the values that assumes between the first position , , and the last position ,, of the balance ; are given by equations ( 20) and (21) . The differential equation that describes the motion is
| (24) |
and it’s solution is
| (25) |
where represents the amplitude and
| (26) |
| (27) |
The angle , that represents the bar position at the end of the phenomena can be determined as follows
| (28) |
and should be the same as predicted by the theory
| (29) |
therefore
| (30) |
In order to continue a value for should be derived. This can be obtained from the period of oscillation of the bar
| (31) |
We continue by identifying with the empirical value . We continue on assuming that is small ; therefore from equations , and , the following is obtained
| (32) |
2.2 G with air viscosity
2.3 G to the first order
Let assume that is not constant, we can assume at the order with the aid of formula (19)
| (35) |
where e are defined in equations and respectively. In this case the law of motion is still equation
| (36) |
and the solution is
| (37) |
where the angular velocity has now the following expression
| (38) |
As a consequence
| (39) |
| (40) |
and therefore
| (41) |
Once equation is substituted in this relationship we obtain
| (42) |
2.4 G from Leybold manual
The deduction of G through the Leybold torsional balance is widely known , see [11]. We simply report the final expression
| (43) |
where
| (44) |
The meaning of the symbols is
-
•
:Distance between center of the great mass and small mass
-
•
S:Total deflection of the light spot
-
•
:The length of the lever arm
-
•
:Distance between mirror and screen
-
•
: Great mass
-
•
T Period of the oscillations
3 Analysis of the data
The physical parameters as well their uncertainties are reported in Table 1.
| parameter | value | unit |
|---|---|---|
| (1.5 ) | ||
| (1.5 ) | ||
| (4.65 ) | ||
| (5.0 ) | ||
| (5.475 ) | ||
| (-6.715 1.3) | ||
| ( 1.432 1.11) |
The data were analysed through the following fitting function
| (45) |
The data has been processed through the Levenberg–Marquardt method ( subroutine MRQMIN in [12]) in order to find the parameters , , and . The results are reported in Table 2 together with the derived quantities.
| parameter | value | unit |
|---|---|---|
| (8.188 1.11) | ||
| ( 0.1470 ) | ||
| (552.98 0.16) | ||
| (1047.0 4.8) |
The value of can be derived coupling the basic parameters of the torsion balance , see Table 1, and the measured parameters of the damped oscillations , see Table 2. Table 3 reports the four values of here considered with the uncertainties expressed in absolute value and in ppm ; the precision of the measure in respect of the so called ”true” value is also reported. A considerable source of error is the uncertainty in the determination of the span between the two spheres that in our case is . Adopting a rotating gauge method [13] the uncertainty in the determination of the span between the two spheres is ; this is the way to lower the uncertainty in Table 3.
4 Non linear effects in the vacuum
By starting from the equation of rotational dynamics up to the second order
| (46) |
the case of =0 is analysed ,
| (47) |
that corresponds to perform the experiment in the vacuum. On dropping the constant term and dividing by we obtain
| (48) |
On imposing
| (49) |
the nonlinear ordinary differential equation , in the following ODE , has the form
| (50) |
On adopting the transformation the nonlinear ODE is
| (51) |
where
| (52) |
The solution of equation (51) is reported in the Appendix A and in our case =0.0187. We now have a measured period ,, that is equalised to the non linear value , . The period of the linear case , , can be written as
| (53) |
and therefore
| (54) |
In the various formulae of without damping , for example equations (32) and (43), the periods and are raised to the square
| (55) |
and in the denominator, making the non linear greater than the linear
| (56) |
The value of this correction , , can be evaluated as a difference between 1 and the multiplicative factor of
| (57) |
The official error on is and therefore the nonlinear correction can be expressed as the double of the official error on .
Appendix A The eardrum equation
The equation
| (58) |
is well known under the name ”eardrum equation”. It can be solved , see [14], transforming it in
| (59) |
and adopting the method of Poisson that imposes the following solution to
| (60) |
and to
| (61) |
The computer algebra system (CAS) gives
| (62) |
Acknowledgements
We thank Richard Enns who has provided us the Maple routine Example 04-S08 extracted from [14].
References
- [1] G. T. Gillies, Reports of Progress in Physics 60 , 151(1997) .
- [2] P. J. Mohr, B. N. Taylor, Reviews of Modern Physics 77 , 1(2005) .
- [3] P. Baldi, E. G. Campari, G. Casula, S. Focardi, G. Levi, F. Palmonari, Phys. Rev. D 71 (2) , 022002(2005) .
- [4] S. Schlamminger, E. Holzschuh, W. Kündig, F. Nolting, R. E. Pixley, J. Schurr, U. Straumann, Phys. Rev. D 74 (8) , 082001(2006) .
- [5] J. Schurr, F. Nolting, W. Kündig, Physics Letters A 248 , 295(1998) .
- [6] C. H. Bagley, G. G. Luther, Physical Review Letters 78 , 3047(1997) .
- [7] K. Kuroda, Physical Review Letters 75 , 2796(1995) .
- [8] S. Matsumura, N. Kanda, T. Tomaru, H. Ishizuka, K. Kuroda, Physics Letters A 244 , 4(1998) .
- [9] J. Luo , D. Wang , Q. Liu , C. Shao, Chinese Phys. Letters 22 , 2169(2005) .
- [10] S. Kononogov , V. Mel’nikov, Measurement Techniques 48 , 521(2005) .
- [11] N. N., Leybold Physics Leaflets Determining the gravitational constant, Leybold, Cologne, 1958.
- [12] W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery, Numerical recipes in FORTRAN. The art of scientific computing, Cambridge University Press, Cambridge, 1992.
- [13] J. Luo , D. Wang , Z. Hu , X. Wang, Chinese Phys. Letters 18 , 1012(2001) .
- [14] R. H. Enns, G. C. McGuire, Computer Algebra Recipes for Classical Mechanics, Birkhauser, Boston, 2002.