11email: giulia.perotti@nbi.ku.dk 22institutetext: School of Physical Sciences, The Open University, Walton Hall, Milton Keynes, MK7 6AA, United Kingdom 33institutetext: Department of Space, Earth, and Environment, Chalmers University of Technology, Onsala Space Observatory, 439 92 Onsala, Sweden 44institutetext: Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
Linking ice and gas in the Orionis Barnard 35A cloud
Abstract
Context. Dust grains play an important role in the synthesis of molecules in the interstellar medium, from the simplest species such as H2 to complex organic molecules. How some of these solid-state molecules are converted into gas-phase species is still a matter of debate.
Aims. Our aim is to directly compare ice and gas abundances of methanol (CH3OH) and carbon monoxide (CO), obtained from near-infrared (2.55 m) and millimeter (1.3 mm) observations, and to investigate the relationship between ice, dust and gas in low-mass protostellar envelopes.
Methods. We present Submillimeter Array (SMA) and Atacama Pathfinder EXperiment (APEX) observations of gas-phase CH3OH ( = 54K), 13CO and C18O ( = 21) towards the multiple protostellar system IRAS 05417+0907 located in the B35A cloud, Orionis region. We use archival IRAM 30 m data and AKARI H2O, CO and CH3OH ice observations towards the same target to compare ice and gas abundances and directly calculate CH3OH and CO gas-to-ice ratios.
Results. The CO isotopologues emissions are extended, whereas the CH3OH emission is compact and traces the giant molecular outflow emanating from IRAS 05417+0907. A discrepancy between submillimeter dust emission and H2O ice column density is found for B35A4 and B35A5, similar to what has previously been reported. B35A2 and B35A3 are located where the submillimeter dust emission peaks and show H2O column densities lower than for B35A4.
Conclusions. The difference between the submillimeter continuum emission and the infrared H2O ice observations suggests that the distributions of dust and H2O ice differ around the young stellar objects in this dense cloud. The reason for this may be that the four sources are located in different environments resolved by the interferometric observations: B35A2, B35A3 and in particular B35A5 are situated in a shocked region plausibly affected by sputtering and heating impacting the submillimeter dust emission pattern, while B35A4 is situated in a more quiescent part of the cloud. Gas and ice maps are essential to connect small-scale variations in the ice composition with large-scale astrophysical phenomena probed by gas observations.
Key Words.:
ISM: molecules — stars:protostars — astrochemistry — molecular processes — ISM:individual objects: Orion1 Introduction
The interaction between dust, ice and gas is ubiquitous in star-forming regions and it is essential for the synthesis of interstellar molecules, the main ingredients for the origin of life on Earth. In the last decades the number of detected molecules in the interstellar medium (ISM) increased considerably (McGuire, 2018) and with it, the awareness of an interplay between solid and gaseous molecules in star-forming regions (Herbst & van Dishoeck, 2009; Boogert et al., 2015; Jørgensen et al., 2020; Öberg & Bergin, 2021). Some of the questions remained to be answered are what is the link between the distribution of solids (dust, ices) and gaseous molecules in molecular clouds, and what does this tell us about the solid-gas intertwined chemistries (e.g., thermal and non-thermal desorption mechanisms releasing solid-state molecules into the gas-phase and vice versa).
Desorption mechanisms are of utmost importance to understand some critical aspects of star- and planet-formation (van Dishoeck & Blake, 1998). Besides enhancing the chemical complexity in the gas-phase (Cazaux et al., 2003; Jørgensen et al., 2016; Bergner et al., 2017; Calcutt et al., 2018; Manigand et al., 2020; van Gelder et al., 2020), the positions in protostellar disks at which they occur (i.e., snow-lines), influences the formation and evolution of planets (Öberg et al., 2011; Eistrup et al., 2016; van ’t Hoff et al., 2017; Grassi et al., 2020). Simultaneously, desorption processes can also shape the composition of grain surfaces. This is a consequence of the fact that all desorption mechanisms are much more efficient for volatile species (CO, O2, N2; Bisschop et al. 2006; Noble et al. 2012; Cazaux et al. 2017) than for less volatile species (H2O, CH3OH; Fraser et al. 2001; Bertin et al. 2016; Cruz-Diaz et al. 2016; Martín-Doménech et al. 2016). Since thermal desorption mechanisms alone can often not account for the diversity of species observed in star-forming regions, a further question remains open as to the extent that the prevailing physical conditions might impact ice loss, e.g. through photo-desorption, sputtering, chemical- and shock-induced processes (e.g., Kristensen et al. 2010; Vasyunin & Herbst 2013; Dulieu et al. 2013; Öberg 2016; Dartois et al. 2019). Obtaining key insights on the desorption mechanisms is crucial to study the composition of ice mantles, and hence the production of complex organics, during the early phases of star-formation.
The preferred observational approach to constrain solid-state chemistry consists of inferring abundances of solid-state molecules based on their observed gas-phase emissions (Bergin & Tafalla, 2007; Öberg et al., 2009; Whittet et al., 2011). Although this method of indirectly deriving ice abundances from gas-phase observations is the most used to get insights into the ice composition, it relies on major assumptions, for instance on the formation pathways and the desorption efficiency of solid-state species.
One way to test these assumptions is to combine ice and gas observations (i.e., ice- and gas-mapping techniques) and thus compare ice abundances with gas abundances towards the same region (Noble et al., 2017; Perotti et al., 2020). The evident advantage of combining the two techniques is that it enables us to study the distribution of gas-phase and solid-state molecules concurrently on the same lines of sight, and hence to address how solid-state processes are affected by physical conditions probed by gas phase-mapping such as density, temperature and radiation field gradients, turbulence and dust heating. However, the number of regions where such combined maps are available is still limited.
In this article we explore the interplay between ice and gas in the bright-rimmed cloud Barnard 35 (B35A; also known as BRC18, SFO18 and L1594) located in the Orionis star-forming region (Sharpless, 1959; Lada & Black, 1976; Murdin & Penston, 1977; Mathieu, 2008; Hernández et al., 2009; Bayo et al., 2011; Barrado et al., 2011; Kounkel et al., 2018; Ansdell et al., 2020) at a distance of 410 20 pc (GAIA DR2; Zucker et al. 2019, 2020). The Orionis region is characterized by a core of OB stars enclosed in a ring of dust and gas (Wade, 1957; Heiles & Habing, 1974; Maddalena & Morris, 1987; Zhang et al., 1989; Lang et al., 2000; Dolan & Mathieu, 2002; Sahan & Haffner, 2016). The OB stars formed approximately 5 Myr ago, whereas the ring formation is less certain, occurring between 1 and 6 Myr ago due to a supernova explosion (Dolan & Mathieu, 1999, 2002; Kounkel, 2020). The presence of strong stellar winds from the massive stars and ionization fronts in the region has shaped and ionized the neighboring ring of gas leading to the formation of dense molecular clouds (e.g., B35A, B30; Barrado et al. 2018) and photodissociation regions (PDRs; Wolfire et al. 1989; De Vries et al. 2002; Lee et al. 2005). For instance, the stellar wind from Orionis, the most massive star of the Collinder 69 cluster (an O8III star; Conti & Leep 1974), hits the western side of B35A compressing the cloud and forming a PDR between the molecular cloud edge and the extended HII region S264 (De Vries et al., 2002; Craigon, 2015).
Star formation is currently occurring in B35A: the multiple protostellar system IRAS 05417+0907 (i.e., B35A3) lies within the western side of the cloud (Figure 1). IRAS 05417+0907 was long thought to be a single source but it is a cluster of at least four objects (B35A2, B35A3, B35A4 and B35A5) which were partially resolved by IRAC observations as part of the c2d Legacy survey111https://irsa.ipac.caltech.edu/data/SPITZER/C2D/cores.html (Evans et al. 2014; Table 1). B35A3 (i.e., IRAS 05417+0907) is a Class I YSO and it is the primary of a close binary system (Connelley et al., 2008); the classification of the other sources remains uncertain. B35A3 is emanating a giant bipolar molecular outflow extending in the NE/SW direction relative to Orionis and terminating in the Herbig-Haro object HH 175 (Myers et al., 1988; Qin & Wu, 2003; Craigon, 2015; Reipurth, 2000). A detailed multi-wavelength analysis and characterization of HH 175 and of the multiple protostellar system presented by Reipurth & Friberg (2021).
The ice reservoir towards the YSOs in B35A has been extensively studied by Noble et al. (2013, 2017) and Suutarinen (2015). These works were based on near-infrared spectroscopic observations (2.55 m) with the AKARI satellite. In Noble et al. (2013), H2O, CO2 and CO ice features were identified towards all four YSOs, whereas Suutarinen (2015) performed a multi-component, multi-line fitting of all the ice features towards the same B35A sources identified by Noble et al. (2013) and Evans et al. (2014), and in a method similar to that employed by Perotti et al. (2020) were able to extract the H2O, CO and CH3OH ice column densities concurrently from the spectral data. It is these ice column densities that are used for comparison in the remainder of this paper.
In parallel, the morphology and kinematics of the gas in B35A has been investigated using single-dishes such as the James Clerck Maxwell Telescope (JCMT) and the Institut de RadioAstronomie Millimétrique (IRAM) 30 m telescope by Craigon (2015). The survey mapped 12CO, 13CO and C18O =32 and =21 over a 14.6 14.6 region and confirmed the existence of a bright and dense rim along the western side of B35A, heated and compressed by the stellar wind of the nearby Orionis, and of a giant bipolar outflow emanating from the YSO region.
To investigate the interaction between the solid (ice) and gas phases in the region, ice maps of B35A were compared to gas-phase maps in Noble et al. (2017). From the combination of ice- and gas-mapping techniques, no clear correlation was found between gas or dust to ice towards B35A. The local scale variations traced by the ice-mapping were not immediately related to large scale astrophysical processes probed by the dust and gas observations.
In this paper, we present interferometric Submillimeter Array (SMA) observations of the = 54K rotational band of CH3OH at 241.791 GHz and of the =21 rotational bands of two CO isotopologues (13CO and C18O) towards the multiple protostellar system IRAS 05417+0907 in B35A. The angular resolution of the interferometric observations allows us to study the distribution of the targeted species in greater spatial detail compared to existing single-dish observations. To also recover the large-scale emission, the SMA observations are combined with single-dish data, thus resolving the protostellar system members and, concurrently probing the surrounding cloud. Furthermore, we produce ice and gas maps of a pivotal complex molecule, CH3OH, and of one of its precursors, CO, to analyse the gas and ice interplay in the region. Lastly, we directly calculate gas-to-ice ratios of B35A to compare with ratios obtained for nearby star-forming regions.

The article is organized as follows. Section 2 describes the gas-phase observations and the archival data used to produce the gas and ice maps. Section 3 presents the results of the observations. Section 4 analyses the variations between the gas-phase and solid-state distributions of the different molecules. Section 5 discusses the observational results with a particular focus on the obtained gas-to-ice ratios. Finally, Section 6 summarizes the main conclusions.
2 Observations and archival data
2.1 SMA and APEX observations
The sample of sources was observed on September 19, 2018 with the Submillimeter Array (SMA; Ho et al. 2004). The array was in its subcompact configuration with 7 operating antennas. The targeted region was covered by two overlapping pointings; the first pointing was centered on B35A3 (i.e., IRAS 05417+0907) and the second was offset by one half primary beam to the south-east. Their exact coordinates are , and , , respectively.
| Objecta | RA | DEC | |
|---|---|---|---|
| [J2000] | [J2000] | [mag] | |
| B35A2 | 05:44:29.30 | +09:08:57.0 | 52.7b |
| B35A3 | 05:44:30.00 | +09:08:57.3 | 54.9 0.2c |
| B35A4 | 05:44:30.85 | +09:08:26.0 | 49.6 2.3c |
| B35A5 | 05:44:31.64 | +09:08:57.8 | 19.5 1.5c |
| Transition | Frequencya | ||||
|---|---|---|---|---|---|
| [GHz] | [s-1] | [K] | [cm-3] | ||
| C18O = 2 1 | 219.560 | 6.01 10-7 | 5 | 15.9 | 9.3 |
| 13CO = 2 1 | 220.398 | 6.04 | 5 | 15.9 | 9.4 |
| CH3OH = 5 E+ | 241.700 | 6.04 | 11 | 47.9 | 5.5 |
| CH3OH = 5 E- | 241.767 | 5.81 | 11 | 40.4 | 4.8 |
| CH3OH = 5 A+ | 241.791 | 6.05 | 11 | 34.8 | 5.0 |
| CH3OH = 5 E+ | 241.879 | 5.96 | 11 | 55.9 | 4.9 |
| CH3OH = 5 E- | 241.904 | 5.09 | 11 | 60.7 | 4.2 |
-
•
Notes.a From the Cologne Database for Molecular Spectroscopy (CDMS; Müller et al. (2001)) and the Jet Propulsion Laboratory catalog (Pickett et al., 1998). b Calculated using a collisional temperature of 20 K and collisional rates from the Leiden Atomic and Molecular Database (LAMDA; Schöier et al. 2005). The references for the collisional rates are Yang et al. (2010) for the CO isotopologues and Rabli & Flower (2010) for CH3OH.
The SMA observations probed frequencies spanning from 214.3 to 245.6 GHz with a spectral resolution of 0.1 MHz (0.135 km s-1). Among other species this frequency range covers the CH3OH = 54K branch at 241.791 GHz, 13CO = 21 at 220.398 GHz and C18O = 21 at 219.560 GHz (Table 2). The observational setup consisted of a first long integration on the bandpass calibrator, the strong quasar 3c84, followed by alternated integrations on the source and on the gain calibrator, the quasar J0510+180. The absolute flux scale was obtained through observations of Uranus. The SMA data set was both calibrated and imaged using CASA222http://casa.nrao.edu/ (McMullin et al., 2007). At these frequencies, the typical SMA beam-sizes were 73 24 with a position angle of -32.2∘ for CH3OH, and 79 26 with a position angle of -31.2∘ for 13CO and C18O.
To trace the more extended structures in the region, the SMA data were complemented by maps obtained using the Atacama Pathfinder EXperiment (APEX; Güsten et al. 2006) on August 2022, 2018. The single-dish observations covered frequencies between 236243.8 GHz, matching the SMA 240 GHz receiver upper side band. The spectral resolution of the APEX observations was 0.061 MHz (0.076 km s-1). The APEX map size was 100 125′′ and it extended over both SMA primary beams. The coordinates of the APEX pointing are , . The APEX beam size was 274 for the CH3OH = 54K lines emission. The APEX data set was reduced using the GILDAS package CLASS333http://www.iram.fr/IRAMFR/GILDAS. At a later stage, the reduced APEX data cube was imported to CASA and combined with the interferometric data using the feathering technique. A description of the combination procedure is given in Appendix A.1.
2.2 JCMT/SCUBA-2, Spitzer IRAC, 2MASS, IRAM 30 m and AKARI data
Ancillary data to the SMA and APEX observations were adopted in this study. To construct H2 column density maps of B35A, we used submillimeter continuum maps at 850 m obtained with the SCUBA2 camera at the James Clerk Maxwell Telescope (JCMT) by Reipurth & Friberg (2021), visual extinction values from the c2d catalog444https://irsa.ipac.caltech.edu/data/SPITZER/C2D/cores.html and 2MASS and IRAC photometric data (Skrutskie et al., 2006; Evans et al., 2014). Institut de RadioAstronomie Millimétrique (IRAM) 30 m telescope observations (Craigon, 2015) were used to trace the extended emission for 13CO and C18O = 21. Finally, to produce gas-ice maps of B35A we made use of the ice column densities determined by Suutarinen (2015), from AKARI satellite observations.
3 Results
This section lists the observational results, supplying a summary of the methods employed to determine CO and CH3OH gas column densities (Section 3.1 and Appendix A). Additionally, it presents the H2O, CO and CH3OH ice column densities (Section 3.2) and the two H2 column density maps used in the calculation of the abundances of the ice and gas species (Sect. 3.3).
3.1 Gas-phase species
| Object | ||||||||
|---|---|---|---|---|---|---|---|---|
| [1018cm-2] | [1018cm-2] | [1018cm-2] | [1015cm-2] | [1018cm-2] | [1014cm-2] | [1022cm-2] | [1022cm-2] | |
| B35A2 | 2.96 0.13 | 0.34 0.03 | 0.26 0.03 | 9.38 1.92 | 5.22 1.07 | … | 1.76 0.09 | 7.22∗ |
| B35A3 | 2.96 0.12 | 0.32 0.03 | 0.16 0.03 | 7.02 1.44 | 3.91 0.80 | … | 1.69 0.08 | 7.52 0.02 |
| B35A4 | 3.35 0.11 | 0.28 0.06 | 0.10 0.06 | 4.99 1.03 | 2.78 0.57 | … | 0.39 0.02 | 6.79 0.68 |
| B35A5 | 0.78 0.12 | ¡ 0.18 | ¡ 0.18 | 7.11 1.46 | 3.96 0.81 | 1.91 0.24 | 1.09 0.05 | 2.66 0.20 |
Notes. Columns 24 display the ice column densities from Suutarinen (2015). Columns 57 list the gas column densities for = 25 K. The errors are estimated based on the rms noise of the spectra and on the 20% calibration uncertainty. Non-detections are indicated by ”…”. † is calculated using = 25 K. The errors are calculated from the 5% flux calibration uncertainty and do not take into account the uncertainty on the . ∗ The uncertainty on the and consequently on the for B352 is not estimated because this object is not detected in the J, H and K bands.
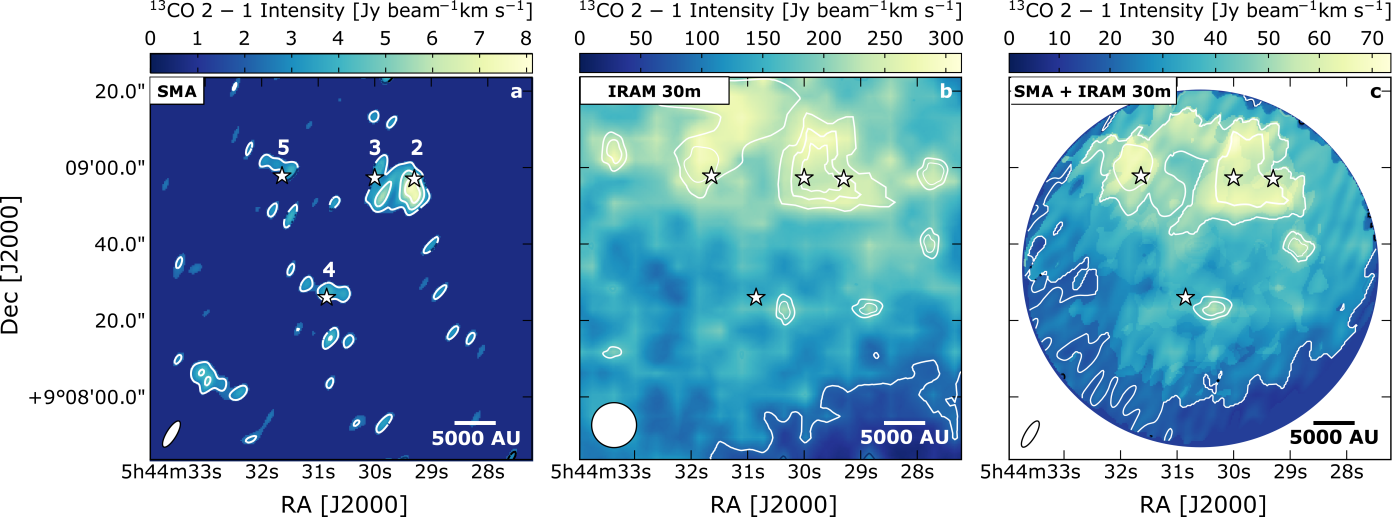
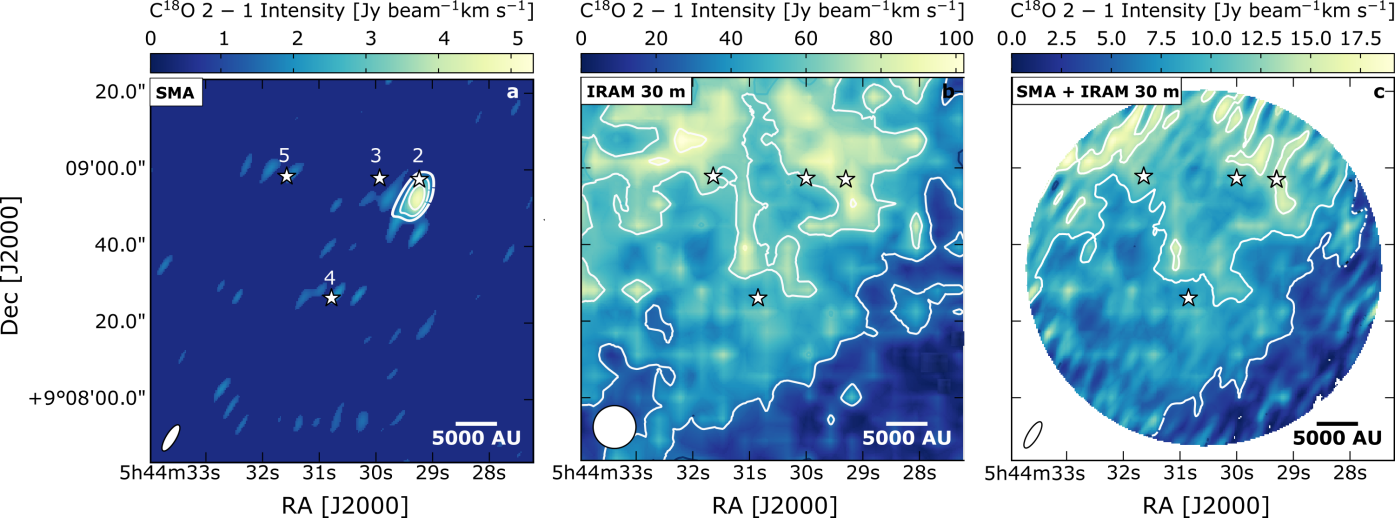
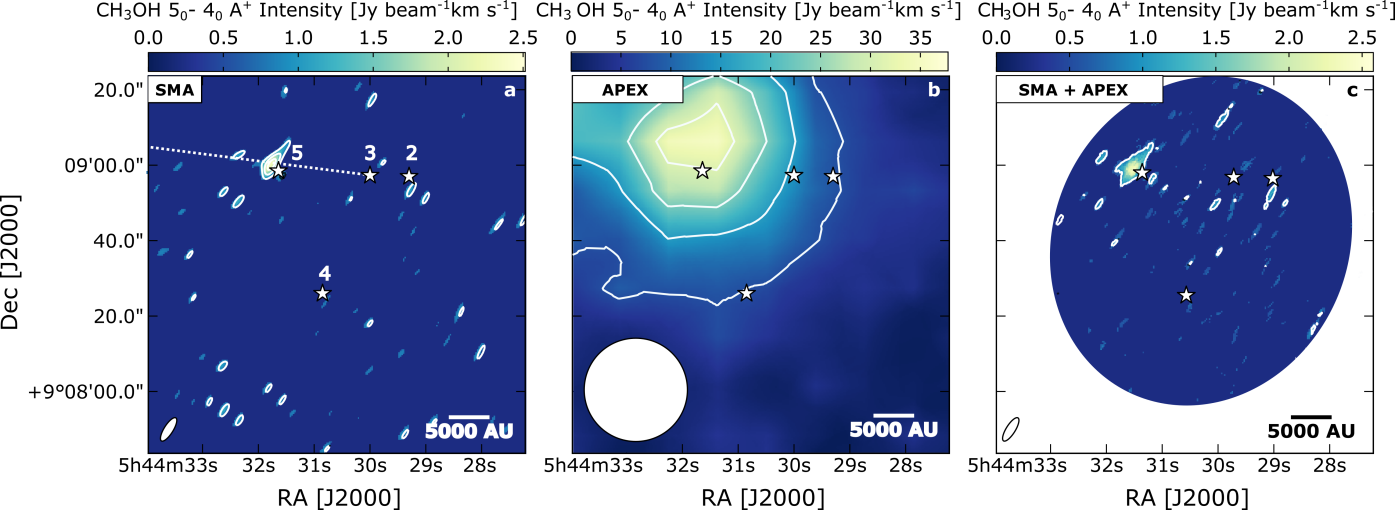
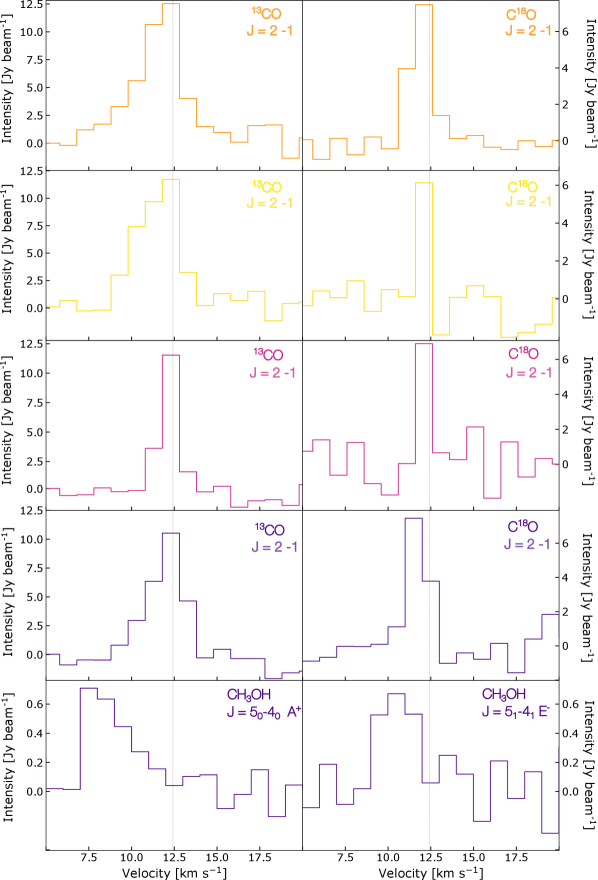
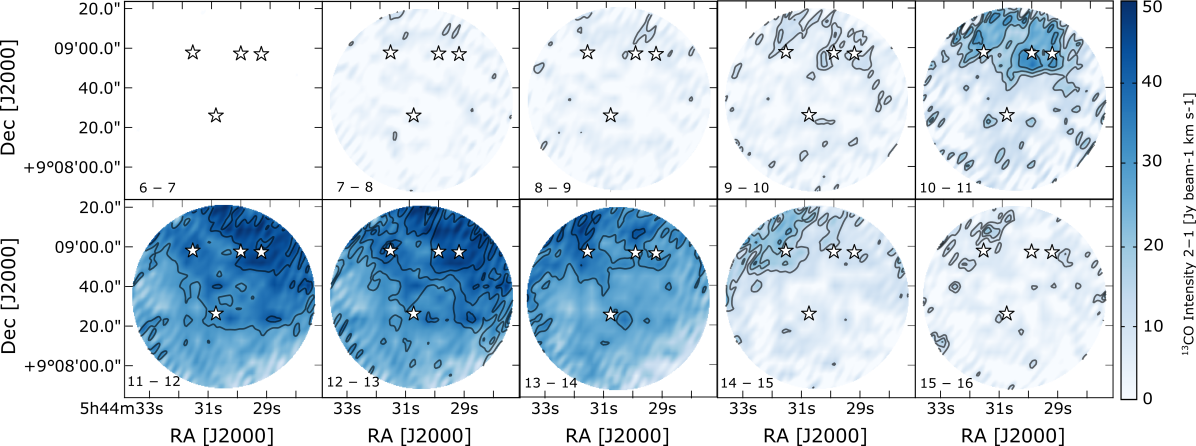
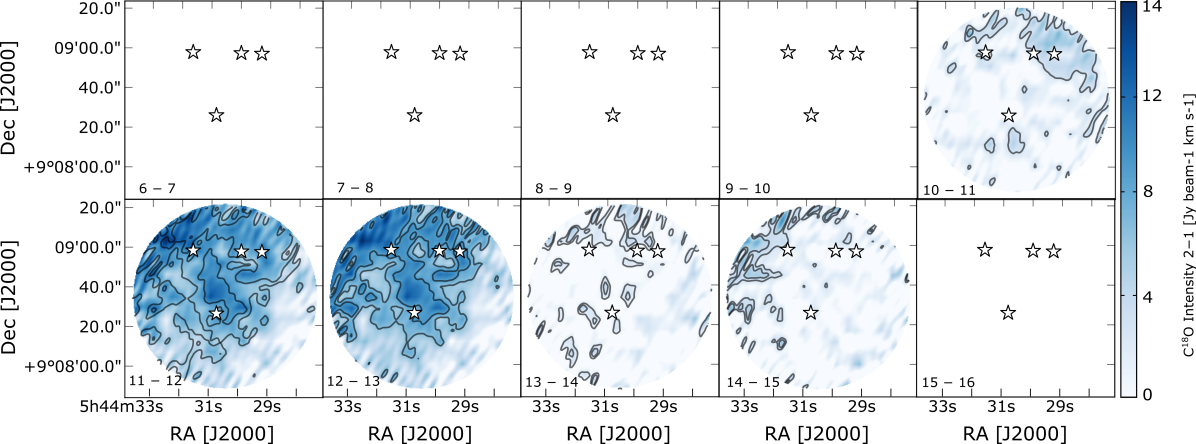
The spectral line data of the detected molecular transitions are listed in Table 2. Figures 2–4 display moment 0 maps of the 13CO and C18O =21 lines and CH3OH =5 A+ line, using SMA, IRAM 30 m and APEX data. Moment 0 maps of the CH3OH =5 A+ line are presented in this section as this transition is the brightest of the CH3OH =5 branch at 241.791 GHz. The maps show that the SMA observations filter out spatially extended emission related to the B35A cloud. The SMA data only recover 10% of the extended emission detected in the single-dish data. Thus, consequently we need to combine the interferometric data with the single-dish maps in order not to underestimate the column densities severely.
Panels (a) of Figures 2–3 show that the interferometric emission is predominantly compact and the peak intensity is seen, for both CO isotopologues, at the location of B35A2. The emission observed in the IRAM 30 m data sets (panels (b) of Figures 2–3) is extended and mostly concentrated around B35A2, B35A3 and B35A5. In the combined SMA + IRAM 30 m maps (panels (c) of Fig. 2–3) the peak emission is also located in the region where B35A2, B35A3 and B35A5 are present.
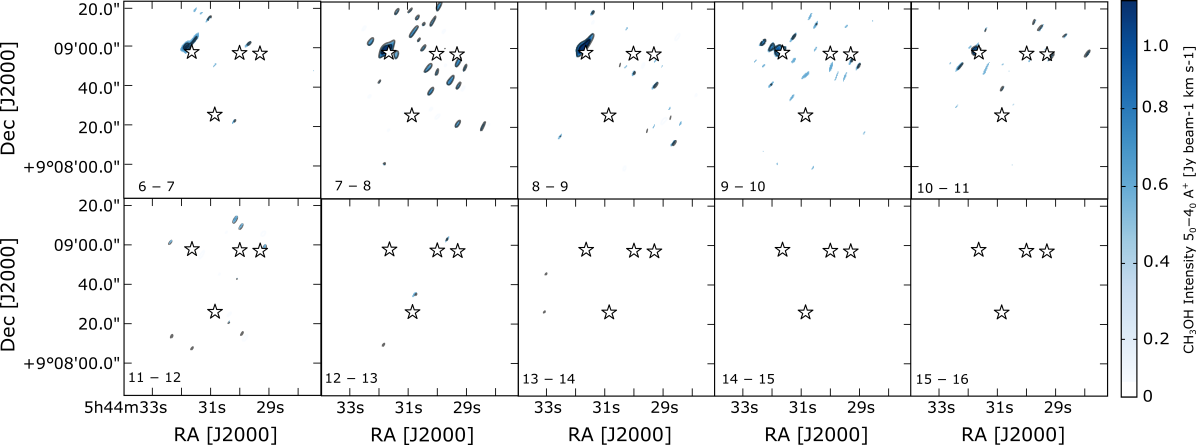
In contrast, the observed CH3OH peak intensity is exclusively localized at the B35A5 position in the SMA data (panel (a) of Fig.4). B35A5 lies along the eastern lobe of the giant bipolar molecular outflow emanated from IRAS 05417+0907 (i.e., B35A3) and terminating at the location of the Herbig-Haro object HH 175 (Craigon, 2015). The CH3OH emission is extended in the APEX data (panel (b) of Fig.4) and hence not resolved at one particular source position. The emission in the SMA + APEX moment 0 map (panel (c) of Fig.4) is compact and concentrated in one ridge in the proximity of B35A5. The channel maps (Figures 1414) and the spectra (Figure 10) extracted from the combined interferometric and single-dish data sets show predominantly blue-shifted components (Appendix A.3). Blue- and red-shifted components are seen for the CO isotopologues, which were previously observed by De Vries et al. (2002), Craigon (2015) and Reipurth & Friberg (2021) and attributed to outflowing gas.
The 13CO emission is optically thick towards the B35A sources, therefore the 13CO column densities are underestimated towards the targeted region (Appendix A.2). Consequently, the optically thin C18O emission is adopted to estimate the column density of 12CO in B35A. First, C18O column densities towards the protostellar system members are obtained from the integrated line intensities of the combined SMA + IRAM 30 m maps (panels (c) of Figure 3), assuming optically thin emission and a kinetic temperature for the YSO region equal to 25 K (Craigon, 2015). The formalism adopted in the column density calculation is presented in Appendix A.4, whereas the calculated C18O column densities and their uncertainties are listed in Table 3. The C18O column densities are converted to 12CO column densities assuming a 16O/18O isotope ratio of 557 30 (Wilson, 1999). The resulting 12CO column densities (Table 3) are in good agreement with the values reported in Craigon (2015).
The CH3OH column density towards B35A5 is estimated from the integrated line intensities of the combined SMA + APEX maps for the five CH3OH lines (Table 6), assuming optically thin CH3OH emission, a kinetic temperature of 25 K (Craigon, 2015) and local thermodynamic equilibrium (LTE) conditions. The CH3OH column density and its uncertainty is reported in Table 3. For all the gas-phase species, the uncertainty on the column densities is estimated based on the spectral rms noise and on the 20% calibration uncertainty.
3.2 Ice column densities
The ice column densities of H2O, CO and CH3OH made use of in this paper were originally derived by Suutarinen (2015) from the AKARI (2.55 m) NIR spectra of the targeted B35A sources. Suutarinen (2015) adopted a non-heuristic approach, employing ice laboratory data and analytical functions to concurrently account for the contribution of a number of molecules to the observed ice band features. A detailed description of the AKARI observations is given in Noble et al. (2013) and the methodology adopted to derive the column densities of the major ice species can be found in Suutarinen (2015).
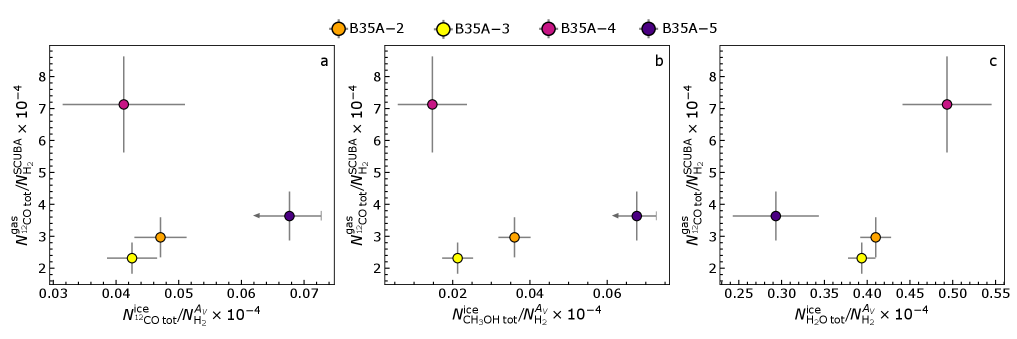
The total ice column densities from Suutarinen (2015) are listed in Table 3. Among the three molecules, H2O ice is the most abundant in the ices of B35A, with column densities up to 3.35 1018 cm-2, followed by CO and CH3OH (Table 3). The column densities of the latter two molecules are comparatively one order of magnitude less abundant than H2O ice. Upper limits are given for the CO and CH3OH column densities towards B35A5 because of difficulties in distinguishing the absorption features in the spectrum of this YSO (Noble et al., 2013; Suutarinen, 2015). A trend is observed for the CO and CH3OH values: the column densities towards B35A2 are the highest reported, followed by B35A3, B35A4 and B35A5. The CO and CH3OH ice column densities appear to follow the visual extinction with B35A2 and B35A3 being the most extincted sources and showing the highest CO and CH3OH column densities (Tables 1 & 3). In this regard, it is important to recall that B35A2 is not detected in the J, H and K bands, making the determination of its visual extinction uncertain (Section 3.3 and Appendix B).
3.3 H2 column densities
An important factor to consider when combining ice- and gas-mapping techniques is that ice absorption and dust and gas emissions may probe different spatial scales (Noble et al., 2017). As a matter of fact, the targeted sources may be embedded to different depths in the B35A cloud and consequently, the gas and ice observations may not be tracing the same columns of material. Therefore, the search for gas-ice correlations towards B35A has to be performed by comparing gas and ice abundances relative to H2, following the approach adopted in Perotti et al. (2020).
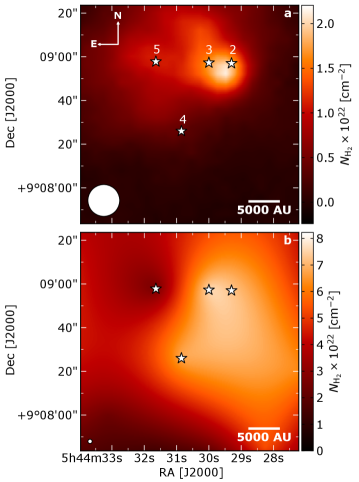
To keep the gas and ice observations in their own reference frame, two H2 column density maps are produced: one to derive gas abundances and one to determine ice abundances (Figure 5). For the gas observations, estimates of the H2 column density are made using submillimeter continuum maps of B35A at 850m (SCUBA2; Reipurth & Friberg 2021), under the assumption that the continuum emission is originated from optically thin thermal dust radiation (Kauffmann et al., 2008). In this regime, the strength of the submillimeter radiation is dependent on the column density (), the opacity () and the dust temperature (). The adopted value for the opacity per unit dust+gas mass at 850 m is 0.0182 cm2 g-1 (”OH5 dust”; Ossenkopf & Henning 1994). The temperature of B35A has been estimated by Morgan et al. (2008) and Craigon (2015). Both studies found two distinct regimes within the cloud: a cold region ( 10 – 20 K, 18 K) in the shielded cloud interior to the east of the YSOs and a warm region ( 20 – 30 K) to the west of the YSOs. Since the region where the YSOs are located lies close to the warm cloud western edge, a 25 K is adopted to estimate the H2 column density map illustrated in Figure 5 (a) based on Craigon (2015) and Reipurth & Friberg (2021). The H2 column density towards the B35A sources is reported in Table 3. The error on the H2 column density was estimated according to the 5% flux calibration uncertainty (Dempsey et al., 2013). It does not include the errors on due to the uncertainties on the upper and lower limits for in the YSOs region.
Increasing the dust temperature to 30 K would lower the H2 column density by 22% and consequently increase the abundance of the gas-phase species by the same amount – while lowering the dust temperature to 18 K would increase the H2 column density by 61% and consequently lowering the gas abundance likewise. The above estimates assume an excitation temperature equal to 25 K for CO and CH3OH. Increasing both the excitation temperature and the dust temperature to 30 K would result in gas abundances increasing by 24%. Conversely, lowering both temperatures to 18 K, would lower the abundances by 33%. A comprehensive description of the production of the H2 column density map from SCUBA2 measurements is given in Appendix C of Perotti et al. (2020).
The H2 column density map calculated from the SCUBA2 measurements supplies an accurate estimate of the total beam-averaged amount of gas towards B35A, and therefore provides a useful reference for the optically thin gas-phase tracers. However, the derived H2 column density map can not directly be related to the AKARI data that supply (pencil-beam) measurements of the column densities towards the infrared sources that may or may not be embedded within the B35A cloud.
For the ice observations, the H2 column density map is therefore obtained by performing a linear interpolation of the tabulated visual extinction () values for B35A taken from the c2d catalog555https://irsa.ipac.caltech.edu/data/SPITZER/C2D/cores.html (see Appendix B). Since no calculated values are reported for B35A2 and B35A3, the for B35A3 is acquired by de-reddening the spectral energy distribution (SED) at the 2MASS J, H, K photometric points to fit a blackbody and using a second blackbody to model the infrared excess at longer wavelengths. A detailed description of the fitting procedure adopted for B35A3 is given in Appendix B. Following Evans et al. (2009) and Chapman et al. (2009) we adopt an extinction law for dense interstellar medium gas with 5.5 from Weingartner & Draine (2001) to calculate . The visual extinction for B35A2 could not be estimated through a similar procedure due to the lack of near-IR photometry data available for this object, thus the for this source is obtained through the interpolation of the available visual extinction measurements for B35A. The final values of the four sources are listed in Table 1. Finally, the visual extinction is converted to column density using the relation: cm-2 (/mag) established for dense interstellar medium gas (Evans et al., 2009). The H2 column density calculated from the map is shown in Figure 5 (b).
The H2 column densities calculated from both methods are of the same order of magnitude, 1022 cm-2 (Table 3). The column densities differ by approximately a factor of 4 possibly due to variations in the exact column densities traced by SCUBA2 and measurements and assumptions on the dust temperature. In both H2 column density maps (Fig. 5 a and b), it is seen that the four sources lie in the densest region of the cloud, confirming the results previously presented in Craigon (2015) and Reipurth & Friberg (2021). Although the two maps were calculated using two different methods, they reproduce the same trend: B35A2 and B35A3 are located where the H2 column density peaks, whereas B35A4 and B35A5 are situated in less dense regions. However, in the H2 column density map calculated from the visual extinction (Fig. 5 b), lower values are reported for B35A5 with respect to the other YSOs, whereas this is not the case in the H2 column density map calculated from the SCUBA2 map (Fig. 5 a) where lower values are observed for B35A4. This difference can be explained by recalling that B35A5 is the less extincted YSO ( = 19.5 mag) and it is located along the trajectory of the giant outflow launched by B35A3. Consequently, the SCUBA2 observations (14.6 beam) are likely tracing the more extended structure of the dust emission in the region and not resolving the more compact emission towards each individual objects. It is worth observing that embedded protostars and Herbig-Haro objects can substantially affect the dust emission morphology (Chandler & Carlstrom, 1996), hence, the enhancement seen in Figure 5 (a) likely reflects dust heating by the embedded protostars and by HH175 resulting in an increase of the submillimeter continuum flux, rather than in an higher column density.
4 Analysis
4.1 Gas-ice maps
In Figure 6, the distributions of gas-phase 13CO 21 (panel a) and C18O 21 (panel b) emissions are compared to CO ice abundances. Both CO isotopologue emissions are concentrated at the B35A2, B35A3, B35A5 source positions. The emission towards these three sources is of comparable intensity but it drops in the surroundings of B35A4 and especially towards the southern edge of the cloud. The CO ice abundances with respect to H2 are not characterized by large variations, instead, they are quite uniform and consistent within the uncertainties (Table 4). Only an upper limit could be determined for the CO ice column density towards B35A5, due to the uncertainty in distinguishing the absorption feature at 3.53 m in the spectrum of this object.
| Object | |||||
|---|---|---|---|---|---|
| [10-5] | [10-5] | [10-5] | [10-4] | [10-8] | |
| B35A2 | 4.10 0.18 | 0.47 0.04 | 0.36 0.04 | 2.97 0.63 | … |
| B35A3 | 3.99 0.16 | 0.43 0.04 | 0.21 0.04 | 2.31 0.49 | … |
| B35A4 | 4.93 0.52 | 0.41 0.50 | 0.15 0.09 | 7.13 1.50 | … |
| B35A5 | 2.93 0.50 | ¡ 0.68 | ¡ 0.68 | 3.63 0.76 | 1.75 0.24 |
Notes. The column densities employed in the determination of the ice and gas abundances of H2O, CO and CH3OH are listed in Table 3. The abundances of the gaseous species are obtained using , whereas the abundances of the ice species are relative to (Table 3). ”…” mark the non-detections of gas-phase CH3OH.
In Figure 6 (c), the distribution of gas-phase CH3OH 540 A+ emission is compared to CH3OH ice abundances. As described in Section 3.1, the CH3OH emission is concentrated solely in one ridge, located in proximity of the B35A5 position. At this location only an upper limit on the CH3OH ice abundance could be determined. The morphology of the CH3OH emission suggests that while B35A5 is situated in a shocked region, sitting along the trajectory of the giant outflow, B35A4 lies in a more quiescent area, less influenced by high-velocity flows of matter. The CH3OH ice abundances with respect to H2 are characterized by slightly larger variations compared to CO ice (Table 4).
Finally, in Figure 6 (d), the distribution of gas-phase CH3OH 540 A+ emission is compared to H2O ice abundances. The H2O ice abundances are approximately one order of magnitude higher than the CO and CH3OH ice abundances (Table 4). The lowest H2O ice abundance is reported towards B35A5 where the CH3OH peak emission is observed. In contrast, the highest H2O ice abundance is obtained towards B35A4, where CH3OH emission is not detected.
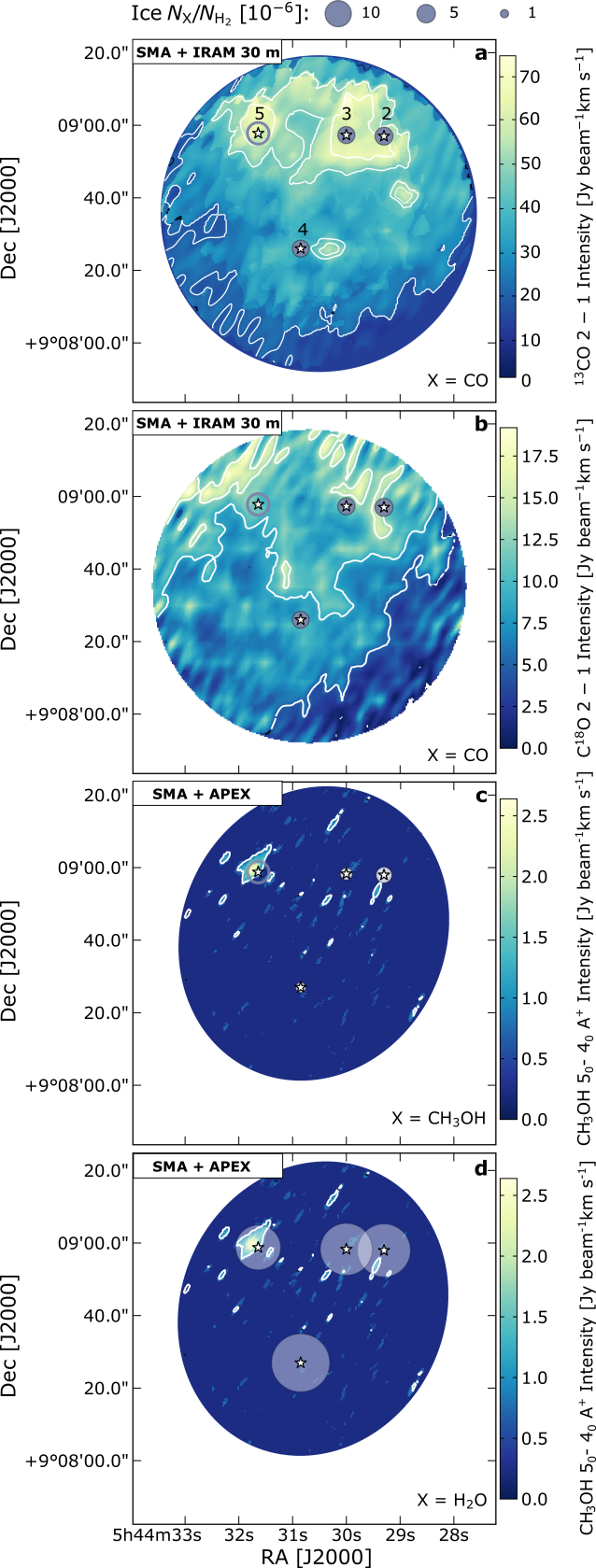
4.2 Gas and ice variations
In Figure 7, the search for gas-ice correlations towards B35A is addressed by analysing gas and ice abundances relative to H2 (Table 4). The y-axes of all three panels display CO gas abundances, which are compared to abundances of CO ice (panel a), CH3OH ice (panel b) and H2O ice (panel c). To maintain gas and ice observations in their own reference frame, the CO gas abundances have been estimated using calculated from SCUBA2 850 m maps, whereas the ice abundances have been calculated using obtained from the visual extinction map (see Section 3.3 and Appendix B). The formalism adopted to propagate the uncertainty from the column densities to the abundances is reported in Appendix A.4.
It can be immediately noted that none of the ice species exhibits a predictable trend in ice abundance with gas abundance. Panels (a) and (b) show a similar behaviour since they are comparing molecules chemically linked - CO gas versus CO ice and CO gas vs CH3OH ice being CO the precursor of CH3OH. At the same time, panel (c) does not display the same relationships seen in the previous two panels. The latter observation is not surprising since there are no reasons for CO and H2O to be directly linked from a purely chemical perspective.
In both panels (a) and (b) of Figure 7, B35A4 displays the highest CO gas and the lowest CO and CH3OH ice abundances. When the uncertainties are taken into account, the CO ice abundances towards B35A2, B35A3 and B35A4 are alike (Table 4). For the CH3OH ice abundances, B35A3 and B35A4 are consistent within the error bars, only towards B35A2 a significant difference is found. Both CO and CH3OH ice abundances towards B35A5 are upper limits (Table 4). The similarity between CO and CH3OH ice trends and the fact that the CH3OH/CO ice ratios are 0.3 indicates an efficient CH3OH formation through CO hydrogenation (Watanabe & Kouchi, 2002) on the grain surfaces of B35A. The CO gas abundances towards B35A2, B35A3 and B35A5 are in agreement within the uncertainties (Table 4).
In panels (c) some of the gas-ice variations differ with respect to panels (a) and (b): B35A4 is characterized by the highest H2O ice abundance, whereas B35A5 shows the lowest H2O ice abundance. This result corroborates the prediction that the ices of B35A5 are the most depleted of volatile molecules among the B35A sources. The behaviours of B35A2 and B35A3 are similar if the uncertainties are considered (Table 4). The observed ice and gas variations between CO gas, CH3OH gas and H2O ice towards B35A4 and B35A5 favour a scenario in which H2O ice is formed and predominantly resides on the ices of B35A4, likely located in the most ”quiescent” area of the targeted region, whereas in the proximity of a shocked region (B35A5), H2O ice mantles are partially desorbed. This result is discussed further in Sect. 5.1. Although the gas and ice variations analysed in this Section and in Sect. 4.1 are based on a small sample, they still highlight interesting trends in accordance to what we would expect from our knowledge of the physical structure of the targeted region.
4.3 Comparison with previous gas-ice maps of B35A
Noble et al. (2017) produced the first gas-ice maps of B35A. They compared AKARI ice abundances from Noble et al. (2013) with single-dish (JCMT/HARP and IRAM 30 m/HERA) gas-phase maps of C18O (Buckle et al. 2009; Craigon 2015; =32 and 21), submillimeter continuum SCUBA maps at 850 m, 450 m/850 m (Di Francesco et al., 2008) and Herschel/SPIRE maps at 250 m (Griffin et al., 2010). The H2 gas-phase map adopted to calculate ice abundances was determined from CO observations (Craigon, 2015).
Noble et al. (2013, 2017) derived their ice column densities without considering the presence of CH3OH, thus the H2O ice column densities were routinely higher than those used here from Suutarinen (2015) (Figure 8). Simultaneously, the CO ice column densities were calculated using different laboratory data (e.g., the CO-ice red component was fitted using a CO:H2O (Fraser & van Dishoeck, 2004) laboratory spectrum as opposite to the CO:CH3OH mixture (Cuppen et al., 2011), resulting in higher CO-ice column density compared to Suutarinen (2015).
The combination of gas, dust and ice observations proposed in Noble et al. (2017) is characterized by a number of limitations which are taken into account in the presented work. The lower angular resolution of the adopted single-dish observations, the analysis of the chemical behaviours of simple molecules only (e.g., H2O, CO and CO2) and the avoidance to consider that the ice and gas observations might probe different depths are some of them. The presented work overcomes these limitations by making use of higher angular resolution interferometric observations, studying the ice and gas variations of both simple (H2O, CO) and complex molecules (CH3OH) and lastly, by comparing ice and gas abundances derived using two different H2 column density maps (to keep the ice and gas observations in their own reference frame).
From the analysis of the gas-ice maps, Noble et al. (2017) inferred that the dust in B35A is mainly localized around B35A2 and B35A3, in agreement with the higher ice column densities of H2O and CO towards these two sources (Figure 8). However, they observed that the H2O ice column densities are lower towards B35A5 compared to B35A4, even though the dust emission is higher towards B35A5. The authors concluded that no clear trend is seen between ice, dust and gas in B35A and that more knowledge of the local-scale astrophysical environment is needed to disentangle the exact interplay between ice and gas in the region. The findings of Noble et al. (2017) are in agreement with the observational results and the gas-ice maps of B35A presented here (with the caveat that both CO ice abundances towards B35A5 in Noble et al. (2017) and in this work are upper limits). However, the gas-ice maps produced in this study allow to explain that the lower H2O ice abundance towards B35A5 compared to B35A4 is plausibly caused by the influence of shocks on the ice chemistry. CH3OH is a tracer of energetic inputs in the form of outflows (Kristensen et al., 2010; Suutarinen et al., 2014), and it traces the trajectory of the bipolar outflow in B35A. As a result, lower H2O ice abundances towards B35A5 are likely the result of sputtering effects in the outflow shocks (e.g., Suutarinen et al. 2014 and references therein). Simultaneously, the fact that the submillimeter dust emission towards B35A5 is high where the H2O ice abundances are lower can also be explained by the presence of the outflow terminating in the HH object 175. In fact, UV radiation generated in the Herbig-Haro object itself may locally heat the dust, enhancing the sub-millimeter continuum flux of the region (Chandler & Carlstrom 1996; Kristensen et al. 2010; Figure 5 a).
5 Discussion
The CH3OH gas abundances in B35A (10-8) are greater than what could be inferred by pure gas-phase synthesis (e.g., Garrod et al. 2006). Hence, the observed CH3OH gas must be produced on the grain surfaces and be desorbed afterwards. In the following, the preferred scenario for CH3OH desorption in B35A is discussed. Additionally, the observational results presented in Sections 3.13.2 are employed to determine CH3OH and CO gas-to-ice ratios (/) towards the multiple protostellar system in B35A. Finally, a comparison between the gas-to-ice ratios directly determined towards B35A and the gas-to-ice ratios of nearby star-forming regions is proposed.
5.1 Sputtering of CH3OH in B35A
In Sections 3.1 and 4.1, it is seen that the CH3OH emission is concentrated almost exclusively in one ridge, which coincides with the B35A5 position. B35A5 sits along the eastern lobe of a large collimated outflow emanated from the binary Class I IRAS 05417+0907 (i.e, B35A). The eastern lobe has a total extent of 0.6 pc and it terminates into the Herbig-Haro object HH 175 (Craigon, 2015). The total extent of the outflow is 1.65 pc (Reipurth & Friberg, 2021), which places HH 175 among the several dozens HH objects with parsec dimensions (Reipurth & Bally, 2001). Herbig-Haro objects are omnipresent in star-forming regions, but it is still not clear how exactly they are tied into the global star-formation process, e.g., how do they alter the morphology and kinematics of the gas in which they originate. These are highly energetic phenomena which are believed to form when high-velocity protostellar jets collide with the surrounding molecular cloud, inducing shocks. Such shocks compress and heat the gas, generating UV radiation (Neufeld & Dalgarno, 1989). The activity of Herbig-Haro objects can dramatically change the chemical composition of the gas in their vicinity, mutating the chemistry of the region during so-called sputtering processes (Neufeld & Dalgarno, 1989; Hollenbach & McKee, 1989).
Sputtering takes place in shocks when neutral species (e.g., H2, H or He) collide with the surface of ice-covered dust grains with sufficient kinetic energy to expel ice species (e.g., CH3OH, NH3, H2O) into the gas phase (Jørgensen et al., 2004; Jiménez-Serra et al., 2008; Kristensen et al., 2010; Suutarinen et al., 2014; Allen et al., 2020). During a sputtering event, the ice molecules can desorb intact or be destroyed (e.g., via dissociative desorption) either due to the high kinetic energy or by reactions with H atoms (Blanksby & Ellison, 2003; Dartois et al., 2019, 2020). The fragments of dissociated molecules can then readily recombine in the gas-phase (Suutarinen et al. 2014 and references therein).
The inferred dust temperatures in the B35A region (2030 K) are remarkably lower than the CH3OH sublimation temperature (128 K; Penteado et al. 2017), excluding thermal desorption as potential mechanism triggering the observed CH3OH emission. This consideration, together with the observation of the CH3OH emission along the HH 175 flow direction and the anticorrelation between CH3OH emission and the lower H2O ice abundances towards B35A5 suggests that ice sputtering in shock waves is a viable mechanism to desorb ice molecules in B35A. Simultaneously, the absence of shocks towards B35A4 likely explains the highest abundance of H2O ice observed in this more quiescent region (Figure 6 d). Higher angular resolution observations of CH3OH in the region are required to provide quantitative measurements of the amount of CH3OH desorbed via sputtering compared to other non-thermal desorption mechanisms. Additional gas-phase observations of H2O towards the B35A sources are needed to constrain further the processes linking H2O ice and H2O gas in this shocked region (e.g., sputtering of H2O ice mantles versus direct H2O gas-phase synthesis) and, in a broader context to contribute explaining the high abundances of H2O observed in molecular outflows (Nisini et al., 2010; Bjerkeli et al., 2012, 2016; Santangelo et al., 2012; Vasta et al., 2012; Dionatos et al., 2013).
5.2 Gas-to-ice ratios
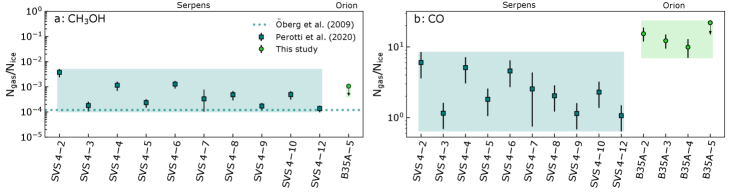
Figure 9 displays the CH3OH (panel a) and CO (panel b) gas-to-ice ratios towards ten sources constituting the SVS 4 cluster located in the Serpens molecular cloud (Perotti et al., 2020) and towards the B35A sources in the Orion molecular cloud. The shaded areas indicate the estimated ranges of gas-to-ice ratios towards both molecular clouds, providing complementary information of the gas-to-ice ratios of both regions compared to the value calculated towards each individual source.
Figure 9 (a) shows the CH3OH gas-to-ice ratios (/) towards the SVS 4 sources and B35A5. Only an upper limit for the CH3OH gas-to-ice towards B35A5 is obtained (i.e, 1.1 10-3) due to the uncertainty on the CH3OH ice column density determination towards this source (Suutarinen, 2015). Therefore, only limited information is available on the CH3OH chemistry in B35A. Figure 9 (a) also displays the averaged CH3OH gas-to-ice ratio towards four low-mass embedded protostars located in nearby star-forming regions from Öberg et al. (2009). A detailed comparison between the CH3OH gas-to-ice ratios for the SVS 4 cluster members and the value estimated by Öberg et al. (2009) is given in Perotti et al. (2020), and therefore not repeated here.
The observations of B35A address cold quiescent CH3OH emission (= 54K transitions at 241.7 GHz and from 34.8 to 60.7 K, see Table 2) and presumably quiescent gas not affected by outflow shocks and/or thermally desorbed in the vicinity of the protostar. The same applies to the observations presented in Öberg et al. (2009) (= 21 transitions at 96.7 GHz and in the range 14.435.4 K). However, B35A5 and the SVS 4 sources reporting the highest gas-to-ice ratios are likely affected to some extent by outflow shocks (i.e., B35A5 by the giant outflow terminating in HH 175 and the SVS 4 sources by the outflow notoriously associated to SMM 4). This might justify the mismatch between Öberg et al. (2009) value and the higher values of the gas-to-ice ratios. In the case of the B35A cloud, high-sensitivity infrared observations of B35A are required to constrain further this observation.
CO gas-to-ice ratios (/) towards the SVS 4 and B35A sources are illustrated in Figure 9 (b). As discussed previously in Perotti et al. (2020), the range of gas-to-ice ratios for SVS 4 extends between 1 and 6 and it is significantly higher than the predicted value (410-2; Cazaux et al. 2016). This theoretical prediction is estimated from the three-phase astrochemical model by Cazaux et al. (2016) which includes thermal and non-thermal desorption processes of the species constituting the ice mantles. This comparison with the theoretical prediction has to be taken with care, since the physical model is not specifically tuned to reproduce the structures of the SVS 4 cluster or the B35A cloud. The estimated dust temperature towards the SVS 4 cluster is below 20 K (Kristensen et al., 2010), indicating that CO is likely frozen out on the grain surfaces in this temperature range. We concluded from the high relative CO gas abundances that the gas-mapping is not tracing the densest regions of the SVS 4 cluster but an extended component that is not sensitive to the effect of freeze-out (Figure 8 of Perotti et al. 2020).
High CO gas-to-ice ratios are also observed for B35A, but in this case they are mainly attributable to CO thermally desorbed in the region. The physical conditions of B35A and SVS 4 differ significantly, for example, the western side of B35A is highly influenced by the ionization-shock front driven by the Orionis OB stars and the dust temperature in the YSOs region of B35A has been estimated to be at least 2530 K (Craigon, 2015; Morgan et al., 2008). Therefore, at these temperatures, above the CO sublimation temperature (20 K; Bisschop et al. 2006; Collings et al. 2004; Acharyya et al. 2007), CO is efficiently thermally desorbed from the grain surfaces and it is expected to primarily reside in the gas-phase. According to this result, the observed CH3OH ice might have formed at earlier stages, prior to the warm-up of the dust grains or alternatively, from CO molecules trapped in porous H2O matrices, and therefore not sublimated at these temperatures. Additionally, higher abundances of CO might reflect an active CO gas-phase synthesis in the region. Follow-up observations of higher transitions of CO isotopologues are required to provide a conclusive assessment.
6 Conclusions
Millimetric (SMA, APEX, IRAM 30 m) and infrared (AKARI) observations are used to investigate the relationships between ice, dust and gas in the B35A cloud, associated with the Orionis region. Gas and ice maps are produced to compare the distribution of solid (H2O, CO and CH3OH) and gaseous (13CO, C18O and CH3OH) molecules and to link the small-scale variations traced by ice observations with larger-scale astrophysical phenomena probed by gas observations. The main conclusions are:
-
•
The CO isotopologues emission is extended in B35A, whereas the observed CH3OH emission is compact and centered in the vicinity of B35A5. B35A5 sits along the trajectory of the outflow emanated from IRAS 05417+0907 (i.e., B35A3), thus the observed gas-phase CH3OH may be plausibly explained by sputtering of ice CH3OH in the outflow shocks.
-
•
The dust column density traced by the submillimeter emission is not directly related to the ice column inferred from the infrared observations. The submillimeter dust emission is stronger towards B35A2, B35A3 and B35A5 compared to B35A4, however the H2O ice column density is higher for B35A4. This discrepancy is understood by taking into account that B35A2, B35A3 and B35A5 are situated in a shocked region affected by the presence of the Herbig-Haro object HH175 – and thus likely influenced by sputtering and heating affecting the observed submillimeter dust emission pattern.
-
•
None of the ice species shows a predictable trend in ice abundance with gas-phase abundance. This implies that inferring ice abundances from known gas-phase abundances and vice versa is inaccurate without an extensive knowledge of the physical environment of the targeted region.
-
•
The high CO gas-to-ice ratios suggest that the CO molecules are efficiently thermally desorbed in B35A. This is supported by dust temperature estimates (2530 K) towards the B35A sources above the CO sublimation temperature (20 K).
-
•
Simultaneously, the dust temperatures in the region are significantly lower than the CH3OH sublimation temperature (128 K), excluding thermal desorption as the mechanism responsible for the observed CH3OH emission.
-
•
The combination of gas- and ice observations is essential to comprehend the relationships at the interface between solid and gas phases, and hence to link the small-scale variations detected in the ice observations with large-scale phenomena revealed by gas-phase observations.
The presented work is a preparatory study for future JWST + ALMA observations, which will shed further light on the dependencies of gas-to-ice ratios on the physical conditions of star-forming regions. In fact, future mid-infrared facilities, among all JWST, will considerably increase the number of regions for which ice maps are available. Such high-sensitivity ice maps can be then combined with ALMA observations, to provide better constraints on the complex interplay between ice, dust and gas during the earliest phases of star-formation. The present study already shows that such gas-ice maps will be valuable, given that they probe ice- and gas-phase chemistries to a greater extent than by ice- or gas-maps alone.
Acknowledgements.
The authors wish to thank Bo Reipurth for fruitful discussions on HH 175 and Alison Craigon, Zak Smith, Jennifer Noble for providing the reduced IRAM 30 m data. The authors also wish to acknowledge the significance of Mauna Kea to the indigenous Hawaiian people and the anonymous reviewer for the careful reading of the manuscript and the useful comments. This work is based on observations with the Submillimeter Array, Mauna Kea, Hawaii, program code: 2018A-S033, with the Atacama Pathfinder Experiment, Llano Chajnantor, Chile, program code: 0102.F-9304. The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica. The Atacama Pathfinder EXperiment (APEX) telescope is a collaboration between the Max Planck Institute for Radio Astronomy, the European Southern Observatory, and the Onsala Space Observatory. Swedish observations on APEX are supported through Swedish Research Council grant No 2017-00648. The study is also based on data from the IRAM Science Data Archive, obtained by H.J.Fraser with the IRAM 30 m telescope under project ID 088-07. Finally, this work is based on archival data from the AKARI satellite, a JAXA project with the participation of the European Space Agency (ESA). The group of JKJ acknowledges the financial support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 646908) through ERC Consolidator Grant ”S4F”. The research of LEK is supported by research grant (19127) from VILLUM FONDEN. HJF gratefully acknowledges the support of STFC for Astrochemistry at the OU under grant Nos ST/P000584/1 and ST/T005424/1 enabling her participation in this work.References
- Acharyya et al. (2007) Acharyya, K., Fuchs, G. W., Fraser, H. J., van Dishoeck, E. F., & Linnartz, H. 2007, A&A, 466, 1005
- Allen et al. (2020) Allen, V., Cordiner, M., & Charnley, S. 2020, arXiv e-prints, arXiv:2010.01151
- Ansdell et al. (2020) Ansdell, M., Haworth, T. J., Williams, J. P., et al. 2020, AJ, 160, 248
- Barnes et al. (2015) Barnes, P. J., Muller, E., Indermuehle, B., et al. 2015, ApJ, 812, 6
- Barrado et al. (2018) Barrado, D., de Gregorio Monsalvo, I., Huélamo, N., et al. 2018, A&A, 612, A79
- Barrado et al. (2011) Barrado, D., Stelzer, B., Morales-Calderón, M., et al. 2011, A&A, 526, A21
- Bayo et al. (2011) Bayo, A., Barrado, D., Stauffer, J., et al. 2011, A&A, 536, A63
- Bergin & Tafalla (2007) Bergin, E. A. & Tafalla, M. 2007, Annual Review of Astronomy and Astrophysics, 45, 339–396
- Bergner et al. (2017) Bergner, J. B., Öberg, K. I., Garrod, R. T., & Graninger, D. M. 2017, ApJ, 841, 120
- Bertin et al. (2016) Bertin, M., Romanzin, C., Doronin, M., et al. 2016, ApJ, 817, L12
- Bisschop et al. (2006) Bisschop, S. E., Fraser, H. J., Öberg, K. I., van Dishoeck, E. F., & Schlemmer, S. 2006, A&A, 449, 1297
- Bjerkeli et al. (2016) Bjerkeli, P., Jørgensen, J. K., Bergin, E. A., et al. 2016, A&A, 595, A39
- Bjerkeli et al. (2012) Bjerkeli, P., Liseau, R., Larsson, B., et al. 2012, A&A, 546, A29
- Blanksby & Ellison (2003) Blanksby, S. & Ellison, G. 2003, Accounts of Chemical Research, 36, 255
- Boogert et al. (2015) Boogert, A. C. A., Gerakines, P. A., & Whittet, D. C. B. 2015, ARA&A, 53, 541
- Buckle et al. (2009) Buckle, J. V., Hills, R. E., Smith, H., et al. 2009, MNRAS, 399, 1026
- Calcutt et al. (2018) Calcutt, H., Jørgensen, J. K., Müller, H. S. P., et al. 2018, A&A, 616, A90
- Carlhoff et al. (2013) Carlhoff, P., Nguyen Luong, Q., Schilke, P., et al. 2013, A&A, 560, A24
- Cazaux et al. (2017) Cazaux, S., Martín-Doménech, R., Chen, Y. J., Muñoz Caro, G. M., & González Díaz, C. 2017, ApJ, 849, 80
- Cazaux et al. (2016) Cazaux, S., Minissale, M., Dulieu, F., & Hocuk, S. 2016, A&A, 585, A55
- Cazaux et al. (2003) Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51
- Chandler & Carlstrom (1996) Chandler, C. J. & Carlstrom, J. E. 1996, ApJ, 466, 338
- Chapman et al. (2009) Chapman, N. L., Mundy, L. G., Lai, S.-P., & Evans, II, N. J. 2009, ApJ, 690, 496
- Collings et al. (2004) Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133
- Connelley et al. (2008) Connelley, M. S., Reipurth, B., & Tokunaga, A. T. 2008, AJ, 135, 2496
- Conti & Leep (1974) Conti, P. S. & Leep, E. M. 1974, ApJ, 193, 113
- Craigon (2015) Craigon, A. M. 2015, PhD thesis, Dept. of Physics, Univ. of Strathclyde, http://digitool.lib.strath.ac.uk/R/?func=dbin-jump-full&object_id=27550
- Cruz-Diaz et al. (2016) Cruz-Diaz, G. A., Martín-Doménech, R., Muñoz Caro, G. M., & Chen, Y.-J. 2016, A&A, 592, A68
- Cuppen et al. (2011) Cuppen, H. M., Penteado, E. M., Isokoski, K., van der Marel, N., & Linnartz, H. 2011, MNRAS, 417, 2809
- Dartois et al. (2020) Dartois, E., Chabot, M., Bacmann, A., et al. 2020, A&A, 634, A103
- Dartois et al. (2019) Dartois, E., Chabot, M., Id Barkach, T., et al. 2019, Astronomy and Astrophysics, 627, A55
- De Vries et al. (2002) De Vries, C. H., Narayanan, G., & Snell, R. L. 2002, ApJ, 577, 798
- Dempsey et al. (2013) Dempsey, J. T., Friberg, P., Jenness, T., et al. 2013, MNRAS, 430, 2534
- Di Francesco et al. (2008) Di Francesco, J., Johnstone, D., Kirk, H., MacKenzie, T., & Ledwosinska, E. 2008, ApJS, 175, 277
- Dionatos et al. (2013) Dionatos, O., Jørgensen, J. K., Green, J. D., et al. 2013, A&A, 558, A88
- Dolan & Mathieu (1999) Dolan, C. J. & Mathieu, R. D. 1999, AJ, 118, 2409
- Dolan & Mathieu (2002) Dolan, C. J. & Mathieu, R. D. 2002, AJ, 123, 387
- Dulieu et al. (2013) Dulieu, F., Congiu, E., Noble, J., et al. 2013, Scientific Reports, 3, 1338
- Eistrup et al. (2016) Eistrup, C., Walsh, C., & van Dishoeck, E. F. 2016, A&A, 595, A83
- Evans et al. (2014) Evans, II, N. J., Allen, L. E., Blake, G. A., et al. 2014, VizieR Online Data Catalog, 2332
- Evans et al. (2009) Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321
- Fraser et al. (2001) Fraser, H. J., Collings, M. P., McCoustra, M. R. S., & Williams, D. A. 2001, MNRAS, 327, 1165
- Fraser & van Dishoeck (2004) Fraser, H. J. & van Dishoeck, E. F. 2004, Advances in Space Research, 33, 14
- Garrod et al. (2006) Garrod, R., Park, I. H., Caselli, P., & Herbst, E. 2006, Faraday Discussions, 133, 51
- Goldsmith & Langer (1999) Goldsmith, P. F. & Langer, W. D. 1999, ApJ, 517, 209
- Grassi et al. (2020) Grassi, T., Bovino, S., Caselli, P., et al. 2020, A&A, 643, A155
- Griffin et al. (2010) Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3
- Güsten et al. (2006) Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13
- Heiles & Habing (1974) Heiles, C. & Habing, H. J. 1974, A&AS, 14, 1
- Herbst & van Dishoeck (2009) Herbst, E. & van Dishoeck, E. F. 2009, ARA&A, 47, 427
- Hernández et al. (2009) Hernández, J., Calvet, N., Hartmann, L., et al. 2009, ApJ, 707, 705
- Ho et al. (2004) Ho, P. T. P., Moran, J. M., & Lo, K. Y. 2004, ApJ, 616, L1
- Hollenbach & McKee (1989) Hollenbach, D. & McKee, C. F. 1989, ApJ, 342, 306
- Jiménez-Serra et al. (2008) Jiménez-Serra, I., Caselli, P., Martín-Pintado, J., & Hartquist, T. W. 2008, A&A, 482, 549
- Jørgensen et al. (2020) Jørgensen, J. K., Belloche, A., & Garrod, R. T. 2020, ARA&A, 58, 727
- Jørgensen et al. (2004) Jørgensen, J. K., Hogerheijde, M. R., Blake, G. A., et al. 2004, A&A, 415, 1021
- Jørgensen et al. (2016) Jørgensen, J. K., van der Wiel, M. H. D., Coutens, A., et al. 2016, A&A, 595, A117
- Kauffmann et al. (2008) Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, II, N. J., & Lee, C. W. 2008, A&A, 487, 993
- Kounkel (2020) Kounkel, M. 2020, ApJ, 902, 122
- Kounkel et al. (2018) Kounkel, M., Covey, K., Suárez, G., et al. 2018, AJ, 156, 84
- Kristensen et al. (2010) Kristensen, L. E., van Dishoeck, E. F., van Kempen, T. A., et al. 2010, A&A, 516, A57
- Lada & Black (1976) Lada, C. J. & Black, J. H. 1976, ApJ, 203, L75
- Ladd et al. (1998) Ladd, E. F., Fuller, G. A., & Deane, J. R. 1998, ApJ, 495, 871
- Lang et al. (2000) Lang, W. J., Masheder, M. R. W., Dame, T. M., & Thaddeus, P. 2000, A&A, 357, 1001
- Lee et al. (2005) Lee, H.-T., Chen, W. P., Zhang, Z.-W., & Hu, J.-Y. 2005, ApJ, 624, 808
- Maddalena & Morris (1987) Maddalena, R. J. & Morris, M. 1987, ApJ, 323, 179
- Manigand et al. (2020) Manigand, S., Jørgensen, J. K., Calcutt, H., et al. 2020, A&A, 635, A48
- Martín-Doménech et al. (2016) Martín-Doménech, R., Muñoz Caro, G. M., & Cruz-Díaz, G. A. 2016, A&A, 589, A107
- Mathieu (2008) Mathieu, R. D. 2008, The Orionis Star Forming Region, Vol. 4, ASP Monographs (Reipurth, B. ed), 757
- McGuire (2018) McGuire, B. A. 2018, ApJS, 239, 17
- McMullin et al. (2007) McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Society of the Pacific Conference Series, Vol. 376, Astronomical Data Analysis Software and Systems XVI, ed. R. A. Shaw, F. Hill, & D. J. Bell, 127
- Morgan et al. (2008) Morgan, L. K., Thompson, M. A., Urquhart, J. S., & White, G. J. 2008, A&A, 477, 557
- Müller et al. (2001) Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49
- Murdin & Penston (1977) Murdin, P. & Penston, M. V. 1977, MNRAS, 181, 657
- Myers et al. (1988) Myers, P. C., Heyer, M., Snell, R. L., & Goldsmith, P. F. 1988, ApJ, 324, 907
- Myers et al. (1983) Myers, P. C., Linke, R. A., & Benson, P. J. 1983, ApJ, 264, 517
- Neufeld & Dalgarno (1989) Neufeld, D. A. & Dalgarno, A. 1989, ApJ, 340, 869
- Nisini et al. (2010) Nisini, B., Benedettini, M., Codella, C., et al. 2010, A&A, 518, L120
- Noble et al. (2012) Noble, J. A., Congiu, E., Dulieu, F., & Fraser, H. J. 2012, MNRAS, 421, 768
- Noble et al. (2013) Noble, J. A., Fraser, H. J., Aikawa, Y., Pontoppidan, K. M., & Sakon, I. 2013, ApJ, 775, 85
- Noble et al. (2017) Noble, J. A., Fraser, H. J., Pontoppidan, K. M., & Craigon, A. M. 2017, Monthly Notices of the Royal Astronomical Society, 467, 4753
- Öberg (2016) Öberg, K. I. 2016, Chemical Reviews, 116, 9631, pMID: 27099922
- Öberg & Bergin (2021) Öberg, K. I. & Bergin, E. A. 2021, Phys. Rep, 893, 1
- Öberg et al. (2009) Öberg, K. I., Bottinelli, S., & van Dishoeck, E. F. 2009, A&A, 494, L13
- Öberg et al. (2011) Öberg, K. I., Murray-Clay, R., & Bergin, E. A. 2011, ApJ, 743, L16
- Ossenkopf & Henning (1994) Ossenkopf, V. & Henning, T. 1994, A&A, 291, 943
- Penteado et al. (2017) Penteado, E. M., Walsh, C., & Cuppen, H. M. 2017, ApJ, 844, 71
- Perotti et al. (2020) Perotti, G., Rocha, W. R. M., Jørgensen, J. K., et al. 2020, A&A, 643, A48
- Pickett et al. (1998) Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883
- Qin & Wu (2003) Qin, S.-L. & Wu, Y.-F. 2003, Chinese J. Astron. Astrophys., 3, 69
- Rabli & Flower (2010) Rabli, D. & Flower, D. R. 2010, MNRAS, 406, 95
- Reipurth (2000) Reipurth, B. 2000, VizieR Online Data Catalog, V/104
- Reipurth & Bally (2001) Reipurth, B. & Bally, J. 2001, ARA&A, 39, 403
- Reipurth & Friberg (2021) Reipurth, B. & Friberg, P. 2021, MNRAS, 501, 5938
- Sahan & Haffner (2016) Sahan, M. & Haffner, L. M. 2016, AJ, 151, 147
- Santangelo et al. (2012) Santangelo, G., Nisini, B., Giannini, T., et al. 2012, A&A, 538, A45
- Schöier et al. (2005) Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369
- Sharpless (1959) Sharpless, S. 1959, ApJS, 4, 257
- Skrutskie et al. (2006) Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163
- Suutarinen (2015) Suutarinen, A. 2015, PhD thesis, Dept. of Physics, The Open University, http://oro.open.ac.uk/61309/
- Suutarinen et al. (2014) Suutarinen, A. N., Kristensen, L. E., Mottram, J. C., Fraser, H. J., & van Dishoeck, E. F. 2014, MNRAS, 440, 1844
- van Dishoeck & Blake (1998) van Dishoeck, E. F. & Blake, G. A. 1998, ARA&A, 36, 317
- van Gelder et al. (2020) van Gelder, M. L., Tabone, B., Tychoniec, Ł., et al. 2020, A&A, 639, A87
- van ’t Hoff et al. (2017) van ’t Hoff, M. L. R., Walsh, C., Kama, M., Facchini, S., & van Dishoeck, E. F. 2017, A&A, 599, A101
- Vasta et al. (2012) Vasta, M., Codella, C., Lorenzani, A., et al. 2012, A&A, 537, A98
- Vasyunin & Herbst (2013) Vasyunin, A. I. & Herbst, E. 2013, ApJ, 769, 34
- Wade (1957) Wade, C. M. 1957, AJ, 62, 148
- Watanabe & Kouchi (2002) Watanabe, N. & Kouchi, A. 2002, ApJ, 571, L173
- Weingartner & Draine (2001) Weingartner, J. C. & Draine, B. T. 2001, ApJ, 548, 296
- Whittet et al. (2011) Whittet, D. C. B., Cook, A. M., Herbst, E., Chiar, J. E., & Shenoy, S. S. 2011, ApJ, 742, 28
- Wilson (1999) Wilson, T. L. 1999, Reports on Progress in Physics, 62, 143
- Wilson & Matteucci (1992) Wilson, T. L. & Matteucci, F. 1992, A&A Rev., 4, 1
- Wolfire et al. (1989) Wolfire, M. G., Hollenbach, D., & Tielens, A. G. G. M. 1989, ApJ, 344, 770
- Yang et al. (2010) Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062
- Zhang et al. (1989) Zhang, C. Y., Laureijs, R. J., Chlewicki, G., Clark, F. O., & Wesselius, P. R. 1989, A&A, 218, 231
- Zhang et al. (2018) Zhang, Z.-Y., Romano, D., Ivison, R. J., Papadopoulos, P. P., & Matteucci, F. 2018, Nature, 558, 260
- Zucker et al. (2020) Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2020, A&A, 633, A51
- Zucker et al. (2019) Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2019, ApJ, 879, 125
Appendix A Production of gas-phase maps
A.1 Interferometric and single-dish data combination
The combined interferometric (SMA) and single-dish (APEX/IRAM 30 m) data were obtained using CASA version 5.6.1 by executing the CASA task feather. The feathering algorithm consists of Fourier transforming and scaling the single-dish (lower resolution) data to the interferometric (higher resolution) data. In a second step, the two datasets with different spatial resolution are merged. In this work, APEX short-spacing are used to correct the CH3OH emission detected by SMA observations, whereas the IRAM 30 m short-spacing are folded into the CO isotopologue emissions observed with the SMA. The combination of the interferometric and single-dish datasets was carried out following the procedure described in Appendix B.1 of Perotti et al. (2020) and references therein.
Artefacts might arise when combining interferometric and single dish data. To benchmark our results we have been varying the arguments of the feathering algorithm (e.g., sdfactor (scale factor to apply to single dish image), effdishdiam (new effective single dish diameter) and lowpassfiltersd (filtering out the high spatial frequencies of the single dish image) from the default values. The variations of the above parameters resulted in amplifying the signal close to the primary beam edges by approximately 15%, therefore the default values were chosen.
A.2 Optical depth of the CO isotopologues
If the emission of the 13CO and C18O isotopologues is co-spatial, the line profiles are similar and the gas ratio abundance 12CO:13CO:C18O is constant, the 13CO optical depth can be assessed from the 13CO and C18O integrated intensity ratio / using the formalism firstly described by Myers et al. (1983) and Ladd et al. (1998). The treatment employed here is adapted from Myers et al. (1983) and uses formula 1 given by e.g., Carlhoff et al. (2013) and Zhang et al. (2018), relating the integrated intensity ratio of the two isotopologues (Table 5) and the optical depth :
| (1) |
In the above equation is the optical depth, and is the intrinsic abundance ratio, which is equal to 710 for the Milky Way (Wilson & Matteucci 1992; Barnes et al. 2015). If =8 is assumed, to be consistent with the approach adopted in Perotti et al. (2020), is equal to 1.22 for B35A2, 0.39 for B353, 0.47 for B35A5, and 0.03 for B354, indicating 13CO optically thick emission towards three (B35A2, B353 and B35A5) out of four sources in the B35A cloud as / is below the intrinsic ratio for these three sources. The same conclusion is obtained if =7 or =10 are assumed. Based on this result, the C18O emission is used to estimate the column densities of 12CO under local thermodynamic equilibrium (LTE) conditions.
| Source | 13CO () | C18O () |
|---|---|---|
| B35A2 | 70.64 10.59 | 14.18 2.86 |
| B35A3 | 72.36 10.85 | 10.66 2.17 |
| B35A4 | 59.63 8.95 | 7.55 1.56 |
| B35A5 | 70.74 10.61 | 10.75 2.19 |
A.3 Channel maps and spectra of individual transitions
Channel maps and spectra for the 13CO =21, C18O =21 and CH3OH =540 A+ detected in the combined interferometric (SMA) and single-dish (IRAM 30m/APEX) data are displayed in Figures 10, 14, 14 and 14. The CO isotopologue emission is predominantly concentrated towards B35A2 and B35A3, whereas the CH3OH emission is uniquely localized in the vicinity of B35A5. Blue-shifted components are observed in combination with broad spectral profiles and wings which deviate from the cloud velocity (12.42 km s-1).
| Source | 5 E+ | 5 E- | 5 A+ | 5 E+ | 5 E- |
|---|---|---|---|---|---|
| B35A5 | 0.27 0.10 | 0.77 0.18 | 1.03 0.22 | 0.29 0.11 | 0.20 0.09 |
A.4 Derivation of gas-phase column densities
The column densities of gas-phase species towards the B35A sources were calculated using the integrated intensities of the combined interferometric (SMA) and single-dish (IRAM 30 m/APEX) data (Tables 5 and 6). The values inserted in the equations below are listed in Table 2 and have been taken from the CDMS (Müller et al. 2001), JPL (Pickett et al. 1998) and LAMDA (Schöier et al. 2005) spectral databases. The adopted formalism assumes local thermodynamic equilibrium (LTE) conditions and more specifically, optically thin line emission, homogeneous source filling the telescope beam and that level populations can be described by a single excitation temperature. According to the treatment by Goldsmith & Langer (1999), under the aforementioned conditions, the integrated main-beam temperature and the column density in the upper energy level are related by:
| (2) |
where is the Boltzmann’s constant, is the transition frequency, is the Planck’s constant, is the speed of light and is the spontaneous Einstein coefficient of the transition. The total column density and the rotational temperature are related to the column density in the upper energy level (Goldsmith & Langer 1999) by:
| (3) |
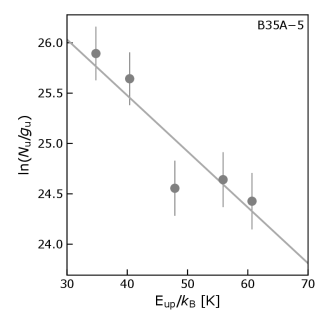
where is the upper level degeneracy, is the rotational partition function, is the Boltzmann’s constant and is the energy of the upper level . In summary, the column densities have been calculated using the formalism of Goldsmith & Langer (1999), but assuming a fixed rotational temperature equal to 25 K (Craigon 2015; Reipurth & Friberg 2021). Figure 11 displays the rotational diagram of CH3OH for B35A5. Only CH3OH transitions above 5 were considered. The uncertainties on the gas column densities were estimated based on the rms noise of the spectra and on the 20% calibration uncertainty.
Appendix B H2 column density from visual extinction
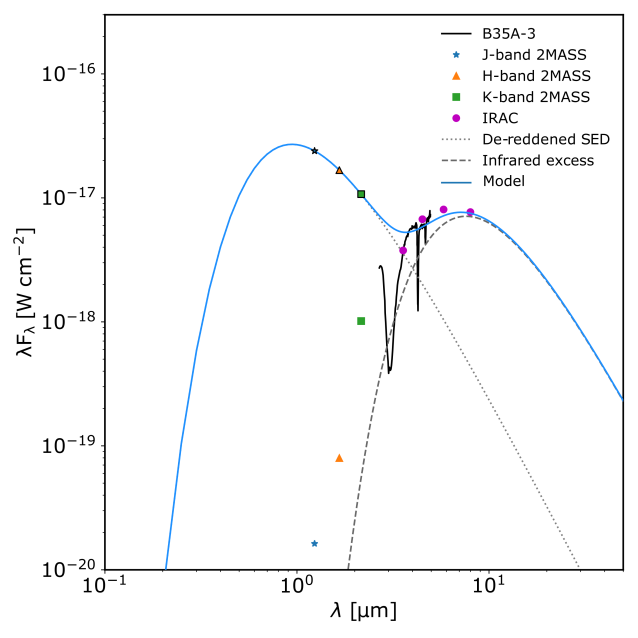
The production of the H2 column density map is accomplished by using the visual extinction () values for B35A tabulated in the c2d catalog666https://irsa.ipac.caltech.edu/data/SPITZER/C2D/cores.html. No values are reported for B35A2 and B35A3 in the catalog. As a result, the visual extinction for B35A3 is retrieved by de-reddening its spectral energy distribution (SED) at the J, H, K 2MASS photometric points of Table 7 to fit a first blackbody and fit a second blackbody to model the infrared excess at the IRAC photometric points (see Figure 15). The extinction in the H-band () is then calculated using the following equation (Chapman et al. 2009):
| (4) |
where is the wavelength corresponding in this case to the H-band (1.662 m), Fλ is the observed flux at the selected , k is a scaling factor and Bλ is the blackbody function. The extinction in the H-band is then converted to visual extinction using the equation below:
| (5) |
where the conversion factor is taken from Weingartner & Draine (2001). The adopted extinction law takes into account the dust model from Weingartner & Draine (2001) for designed for the dense interstellar medium and used by the c2d collaboration (Chapman et al. 2009; Evans et al. 2009). No near-IR photometry data are available for B35A2, thus the for this source is obtained by interpolating all the tabulated visual extinction values for B35A taken from the c2d catalog including the value for B35A3. The obtained visual extinction map of B35A is then converted to a column density map using the relation:
| (6) |
established for dense interstellar medium gas (Evans et al. 2009).