Local dependence of ion temperature gradient on magnetic configuration, rotational shear and turbulent heat flux in MAST
Abstract
Experimental data from the Mega Amp Spherical Tokamak (MAST) is used to show that the inverse gradient scale length of the ion temperature (normalized to the major radius ) has its strongest local correlation with the rotational shear and the pitch angle of the magnetic field (or, equivalently, an inverse correlation with , the safety factor/the inverse aspect ratio). Furthermore, is found to be inversely correlated with the gyro-Bohm-normalized local turbulent heat flux estimated from the density fluctuation level measured using a 2D Beam Emission Spectroscopy (BES) diagnostic. These results can be explained in terms of the conjecture that the turbulent system adjusts to keep close to a certain critical value (marginal for the excitation of turbulence) determined by local equilibrium parameters (although not necessarily by linear stability).
Introduction.
A key physics challenge posed by magnetically confined plasmas in fusion devices is how their internal energy can be kept from being transported too fast from the core to the periphery. The problem is primarily one of turbulent transport, the temperature gradient between the edge and the core of a toroidal plasma supplying the free energy for the turbulent fluctuations that then enhance the effective thermal diffusivity and relax the gradient. It is the ion temperature gradient (ITG) that is expected to cause the most virulent instabilities (on ion Larmor scales) Rudakov and Sagdeev (1961); Coppi et al. (1967); Cowley et al. (1991) and then to be self-consistently limited by the resulting turbulence Horton (1999). If we view the edge ion temperature as fixed by the physics and engineering aspects of the tokamak design that will not concern us here Snyder et al. (2011), the key question is how to maximize the ion temperature gradient. We therefore wish to inquire, experimentally, what this gradient depends on and how. Motivated by the fact (or the conjecture) that the ion-scale turbulence is largely determined by the local (to a given flux surface) equilibrium conditions Candy et al. (2004, 2009); Barnes et al. (2010); Abel et al. (2012); Ghim et al. (2012) and in turn acts back to adjust them locally, we ask what local parameters are most strongly correlated with the corresponding value of , the inverse radial gradient scale length of the ion temperature () normalized to the major radius of the torus.
How universal are any such measured dependences likely to be for situations with different global conditions, e.g., different neutral-beam-injection (NBI) heating powers? It has been recognized for some time that the turbulent heat flux tends to increase very strongly (much faster than linearly) with , a phenomenon known as “stiff” transport Kotschenreuther et al. (1995); Barnes et al. (2011a); Mantica et al. (2009, 2011, 2011). If (or when) the transport is stiff, any experimentally measured relationship between and other equilibrium parameters should be quite close to some critical manifold in the parameter space separating dominant turbulent transport from a non-turbulent or weakly turbulent state (the “zero-turbulence manifold” Highcock et al. (2012)). This critical manifold would be independent of the power input and can be represented as a local parameter dependence of the critical temperature gradient , where is the safety factor (number of toroidal revolutions per one poloidal revolution of the magnetic field around the torus on a given flux surface), the inverse aspect ratio ( is the minor radius of the flux surface), the magnetic shear, the radial shear of the mean toroidal rotation velocity , and the gradient scale lengths of the plasma density and electron temperature, the ion collision rate, the ion-to-electron temperature ratio, the ion-to-magnetic pressure ratio and “” stand for everything else (e.g., the many parameters required to fully describe the magnetic configuration) 111We do not suggest causality between all these parameters and — all local equilibrium characteristics, including , jointly adjust to form the critical manifold.. We stress that need not be the same as the threshold for the existence of linearly unstable eigenmodes. Two known examples when it is not are the “Dimits upshift” of above the linear stability threshold Dimits et al. (2000); Rogers et al. (2000); Mikkelsen and Dorland (2008) and the case of sufficiently large when the system is linearly stable but strong transient excitations Newton et al. (2010); Schekochihin et al. (2012) lead to sustained subcritical turbulence Barnes et al. (2011b); Highcock et al. (2010, 2011). Thus, in general, there is a nonlinear threshold with some definite dependence on local equilibrium parameters.
Recent theoretical Newton et al. (2010); Schekochihin et al. (2012) and numerical Highcock et al. (2012) investigations suggest that and may be the most important such parameters, at least at low . Let us explain why this is. It is well known, both from experimental measurements Ghim et al. (2012); Field et al. (2009) and theory Hinton and Wong (1985); Cowley and Bishop (1986); Abel et al. (2012), that strong (finite-Mach) flows in a tokamak are predominantly toroidal (certainly when plasma is heated by tangential neutral beams, which produce a toroidal torque) 222Any mean poloidal flow exceeding the diamagnetic velocity would be damped by collisions Connor et al. (1987); Catto et al. (1987).. Therefore, any radial shear in the toroidal flow results in sheared flow in both the perpendicular (, is the poloidal field) and parallel (, is the toroidal field) directions. While perpendicular flow shear is known (theoretically Dorland et al. (1994); Waltz et al. (1994); Dimits et al. (2001); Kinsey et al. (2005); Camenen et al. (2009); Roach et al. (2009); Casson et al. (2009); Barnes et al. (2011b); Highcock et al. (2010) and experimentally Burrell (1997, 1999); Mantica et al. (2009, 2011, 2011); Schaffner et al. (2012)) to suppress turbulence and the associated transport, parallel flow shear can drive turbulence via the “parallel-velocity-gradient” (PVG) instability Catto et al. (1973); Newton et al. (2010); Schekochihin et al. (2012). The average ratio of these two shearing rates on a flux surface, , can be approximated by and so the degree to which sheared equilibrium flow suppresses or drives turbulence is expected to depend on this parameter. Indeed, numerical studies of ITG- and PVG-driven turbulence have shown that the critical at any given increases with decreasing (at least for low Highcock et al. (2012)); while at any given , increases with increasing provided the latter is not too large Barnes et al. (2011b); Highcock et al. (2010, 2011, 2012) (as in most real tokamaks).
A comprehensive numerical parameter scan of the dependence of on all other potentially important local quantities (, , , , , , etc.) is probably unaffordable in the near future. Faster progress can be made experimentally. In this Letter, our first goal is to establish, based on a relatively sizable dataset for MAST, what the most important parameters for the critical manifold are: we will show that, indeed, the local value of is most strongly correlated inversely with the local and positively with the local rotational shear — consistently with the result obtained in Highcock et al. (2012).
Our second goal is to obtain an experimental signature that the measured is determined by — or, more precisely, correlated with — the local characteristics of the ion-scale turbulence, directly measured by the 2D beam emission spectroscopy (BES) diagnostic Field et al. (2012). We will show that not only does a strong correlation between and an estimated turbulent heat flux level exist but its (at the first glance, counterintuitive) inverse nature is consistent with staying close to the critical threshold and hence with stiff transport.
Equilibrium parameters.
A database was compiled of equilibrium quantities (and turbulence characteristics; see below) from 39 neutral-beam-heated discharges from the 2011 MAST experimental campaign. These discharges had a double-null diverted (DND) magnetic configuration, no pellet injection and no applied resonant magnetic perturbations. Mean electron density and temperature were measured with the Thomson scattering system Scannell et al. (2010), mean impurity ion (C6+) temperature and the toroidal flow velocity with the Charge eXchange Recombination Spectroscopy (CXRS) system Conway et al. (2006) (we assumed that in these discharges the impurity and bulk ions have negligible differences in their temperature and flow velocities Kim et al. (1990)). The local magnetic pitch angle () was measured with the Motional Stark Effect (MSE) diagnostic De Bock et al. (2008); pressure- and MSE-constrained EFIT equilibria Lao et al. (1985) were used to obtain the field strength . All parameters were determined over intervals either by averaging if the diagnostic’s temporal resolution was smaller or by interpolation if it was larger than . Only data points from a limited range of minor radii ( is the edge of the plasma) were used, in order to minimize any correlations between various quantities due to their profile dependence alone (thus, we did not attempt to prove locality here; see, however, Ghim et al. (2012)). In total, 988 data points were available (out of which 109 points are from H-mode discharges).
From this information, we constructed 7 local dimensionless parameters, which, motivated by theoretical models and common sense, we deemed a priori the most important ones (we also give the range of variation of each parameter): , , , , , , , . The ion collision rate and the perpendicular velocity shear (which is used instead of ) were normalized, as in Ghim et al. (2012), to the ion parallel streaming time , where and is the connection length (the approximate distance along the field line from the outboard to the inboard side of the torus, expected to determine the parallel correlation scale of the turbulence Barnes et al. (2011a); if the flux surfaces had been circular, ). The local magnetic configuration is represented by and . The choice of was motivated by the physical considerations outlined in the Introduction; since varied little in our database, we cannot distinguish any individual correlations of with and . It is left for further study whether other properties of the flux surfaces matter (e.g., Shafranov shift, triangularity, elongation, etc.; some of these may, in fact, affect the stiff-transport threshold Beer et al. (1997); Mikkelsen and Dorland (2008)). We have not included , , , which are not normalizable by any natural local quantities; note that usually has a large but trivial correlation with : larger temperature gradients lead to larger temperatures in the core. We also have excluded because, in the absence of large variation of in our dataset, is simply the normalized ion pressure and, similarly to , has a large positive correlation with (it remains to be investigated whether larger magnetic fluctuations at larger are large enough to have a nontrivial effect on turbulent transport Rechester and Rosenbluth (1978); Pueschel and Jenko (2010); Nevins et al. (2011); Hatch et al. (2012); Guttenfelder et al. (2012); Doerk et al. (2012); Abel and Cowley (2012)).
Correlation analysis.
We perform a Canonical Correlation Analysis (CCA) Hotelling (1936) with treated as the dependent variable and the other 7 local parameters itemized above as independent ones. This amounts to finding the maximum correlations between and linear combinations of logarithms of 1, 2, 3, …, or 7 other parameters, leading to an effective statistical dependence
| (1) |
This is of course not valid if the dependence of on any of the parameters is non-monotonic. A non-monotonic dependence on is, in fact, expected, with first increasing, then decreasing at larger values of due to increased transport from the PVG-driven turbulence Barnes et al. (2011b); Highcock et al. (2010, 2011, 2012). However, the range of values of in our database do not extend to sufficiently high values for such a dependence to be observed (see Fig. 1).
The results are shown in Table 1, where the values of the canonical correlation (i.e., the correlation coefficient between the logarithms of and the right-hand of Eq. (1)) are given together with the corresponding exponents . We start by calculating the individual correlations of with each of the 7 parameters and then include pairs, triplets, etc., only if the correlation improves. We see that the strongest individual correlation of are with (61%) and (46%). The overall fit is measurably improved (66%) if both are included. Including further parameters does not make a significant difference; the third strongest (although not very strong) dependence is on .
| Canonical | |||||||
|---|---|---|---|---|---|---|---|
| correlation | |||||||
| 2.7% | 0 | 0 | 0 | 0 | 0 | 0 | |
| 13.5% | 0 | 0 | 0 | 0 | 0 | 0 | |
| 15.4% | 0 | 0 | 0 | 0 | 0 | 0 | |
| 16.8% | 0 | 0 | 0 | 0 | 0 | 0 | |
| 36% | 0 | 0 | 0 | 0 | 0 | 0 | |
| 46% | 0 | 0 | 0 | 0 | 0 | 0 | |
| 61% | 0 | 0 | 0 | 0 | 0 | 0 | |
| 62% | 0 | 0 | 0 | 0 | 0 | ||
| 66% | 0 | 0 | 0 | 0 | 0 | ||
| 67% | 0 | 0 | 0 | 0 | |||
| 69% |
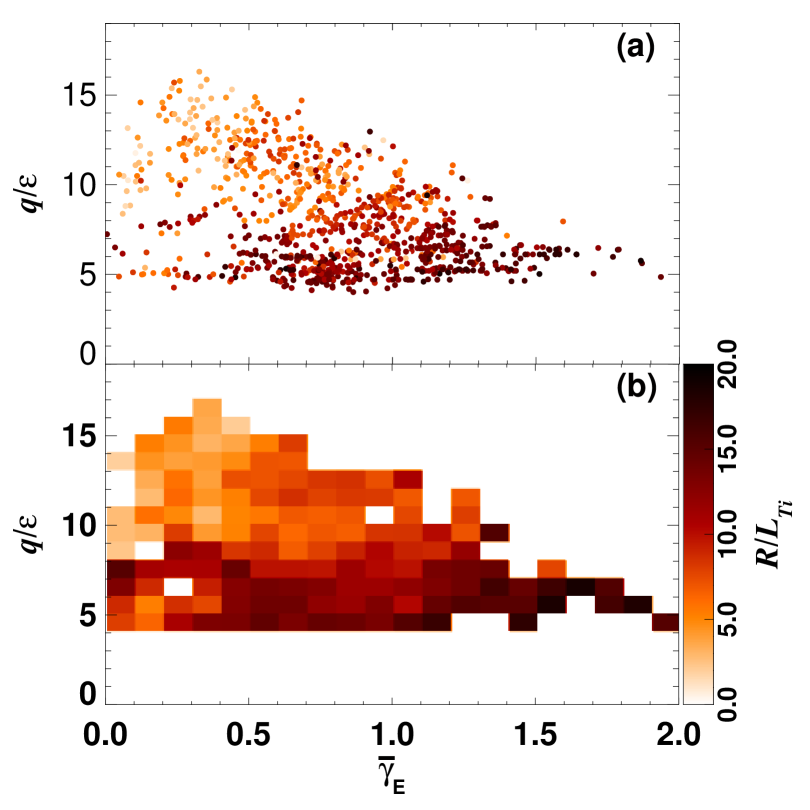
The dependence of on and is shown in Fig. 1. generally increases with decreasing and increasing 333The broad scatter of data points in Fig. 1(a) suggests that the correlation between and is weak; the lack of higher values of at large is due to the fact that the flow shear is weak at earlier times in the discharges, when the central value of is high., broadly consistent with the expectations based on intuitive physical reasoning (explained in the Introduction) and on the numerical study of Highcock et al. (2012).
The conclusion is that, at least on a very rough qualitative level, it is sensible to consider to be a function primarily of and . Since the profile tends to change more slowly in tokamaks than other equilibrium profiles 444It can be proven that the functional dependence , where is the flux-surface label, only changes on the resistive timescale of the mean magnetic field Abel and Cowley (2012)., it may be useful to think of a critical curve Parra et al. (2011) parametrized by Highcock et al. (2012), the latter quantity containing the essential information about the nature of the magnetic cage confining the plasma.
Collisionality dependence.
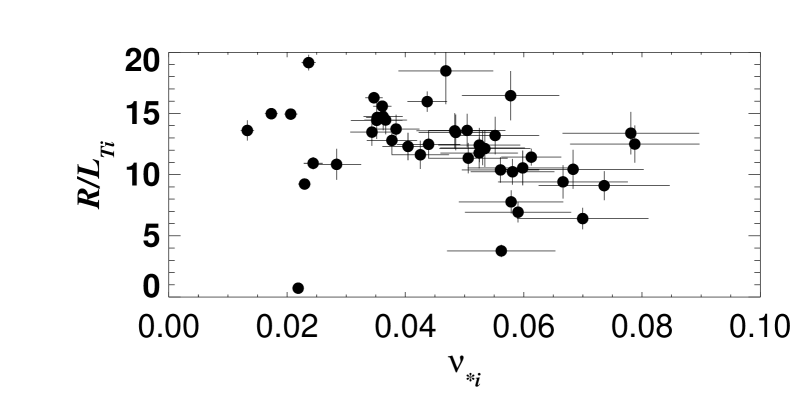
Even though the dependence of is not as strong as and , some discernible inverse correlation between and might be expected because zonal flows, believed to suppress turbulence Rogers et al. (2000); Diamond et al. (2005), should be more strongly damped at higher ion collisionality Hinton and Rosenbluth (1999); Lin et al. (1999); Ricci et al. (2006); Xiao et al. (2007). To isolate this dependence, we selected data points for approximately fixed and (the largest number of data points could be found within these narrow ranges and no measurable correlation between and or was present). The resulting Fig. 2 confirms a degree of inverse correlation between and .
Turbulent heat flux.
The turbulent ion heat flux through a given flux surface is (very approximately!) , where the effective turbulent diffusivity , is the (radial) fluctuating velocity, its correlation time, its poloidal correlation scale and the fluctuating electrostatic potential. The latter can be estimated from density fluctuations using the approximation of Boltzmann electrons: ( is the proton charge, and the mean and fluctuating density, respectively). Both theory of ITG turbulence Barnes et al. (2011a) and the BES measurements in MAST Ghim et al. (2012) suggest that (the drift time; is the ion Larmor radius). Collecting all this together, we estimate the gyro-Bohm-normalized turbulent ion heat flux:
| (2) |
where .
Since ion-scale density fluctuations in MAST can be measured directly by the BES system, can be obtained independently of any transport reconstruction models such as TRANSP Hawryluk (1980). The method of determining and using the BES system on MAST (8 radial 4 vertical channels with spatial resolution of cm Field et al. (2012)) is explained in detail in Ghim et al. (2012). This is done from the covariance and correlation functions of the photon intensity fluctuations, averaged over the same intervals for the same 39 discharges as the equilibrium quantities studied above, although not in all intervals there was good BES data. Restricted to the radial range , the number of available data points for and was 102.
Inverse correlation between and .
It is shown in Fig. 3(a) ( vs. and ; cf. Fig. 1) and Fig. 3(b) ( vs. ) that smaller is observed where is large and vice versa. This is perhaps counterintuitive as one might expect that the larger , the more turbulent the plasma and so the larger the turbulent heat flux. This would indeed have been the case had been externally fixed, as in local flux-tube simulations, where does increase with Dimits et al. (2000); Barnes et al. (2011a). In contrast, in the real plasma, a certain amount of power flows through a flux surface and, if transport is stiff, the temperature gradient (along with other equilibrium quantities) adjusts to stay close to the critical gradient defined by the manifold . Indeed, in plasmas with both power and momentum injection, there is a regime with close to where the turbulent and the neoclassical (collisional) transport are comparable and in which a larger heat flux results in lower . For a detailed explanation, we refer the reader to Parra et al. (2011) (see also Fig. 4(b) of Highcock et al. (2010), which should be compared to our Fig. 3(b)). In brief, in the neoclassical regime, the momentum transport is much less efficient than the heat transport, while in the turbulent regime, they are comparable (the turbulent Prandtl number is order unity Casson et al. (2009); Barnes et al. (2011b); Highcock et al. (2011); Meyer et al. (2009) while the neoclassical one is small Hinton and Wong (1985)), so, as a larger heat flux takes the system (slightly) farther from the marginal state, this leads to much more efficient momentum transport, hence smaller velocity shear , hence a regime with less suppression of turbulence and smaller (see Fig. 3(c), where the correspondence between larger , lower and lower is shown at approximately fixed ; cf. Fig. 3(b) of Parra et al. (2011)). We stress that all of this happens quite close to marginality and so our experimental observation of an inverse correlation between and provides circumstantial evidence that in MAST is indeed close to its critical value 555This situation is distinct from the experiments on transport stiffness on JET Mantica et al. (2009, 2011, 2011) in that they provided vigorous extra heating power using localized ion-cyclotron-resonance heating (ICRH) to depart far from marginality..
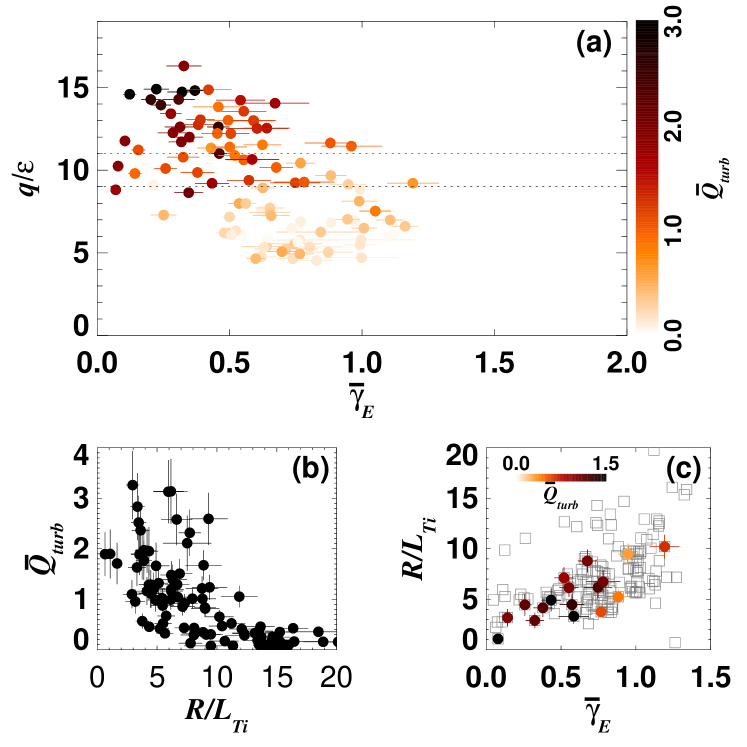
Conclusion.
We have found that the normalized inverse ion-temperature-gradient scale length has its strongest local correlation with and the shear in the equilibrium toroidal flow: increases with increasing shear, which is a well known effect, and with decreasing , which corresponds to an increasing ratio of the perpendicular to the parallel shearing rates. We note that a similar dependence of is also observed in JET Fern et al. (2012), suggesting that the inverse correlation between and is perhaps ubiquitous, as would be the case if were generally fixed at some locally determined critical value Highcock et al. (2012). Furthermore, we have found an inverse correlation between and the gyro-Bohm-normalized turbulent heat flux (estimated via direct measurements of density fluctuations) and argued that this is consistent with always remaining close to a critical manifold separating the turbulent and non-turbulent regimes Highcock et al. (2010); Parra et al. (2011); Highcock et al. (2011) (stiff transport). It is thus plausible that we have essentially produced this critical manifold for the MAST discharges we investigated. Practically, our results suggest that can be increased by lowering the , which is relatively easier and less expensive than increasing the shearing rate in tokamak operations 666With tangential NBI heating, it is difficult to increase the toroidal Mach number — and hence the equilibrium flow shear — because of the fixed ratio of injected torque to power at a fixed injection energy..
Acknowledgements.
We thank I. Abel, M. Barnes, J. Connor, S. Cowley, W. Dorland, D. Dunai, R. Fern, G. Hammett, T. Horbury, F. I. Parra, J. B. Taylor, M. Valovič and S. Zoletnik for valuable discussions. This work was supported by the RCUK Energy Programme under grant EP/I501045, the Kwanjeong Educational Foundation (Y-cG), the European Communities under the contract of Association between EURATOM and CCFE (Y-cG, ARF) and by the Leverhulme Trust International Network for Magnetised Plasma Turbulence. The views and opinions expressed herein do not necessarily reflect those of the European Commission.References
- Rudakov and Sagdeev (1961) L. I. Rudakov and R. Z. Sagdeev, Dokl. Akad. Nauk SSSR 138, 581 (1961).
- Coppi et al. (1967) B. Coppi, M. N. Rosenbluth, and R. Z. Sagdeev, Phys. Fluids 10, 582 (1967).
- Cowley et al. (1991) S. C. Cowley, R. M. Kulsrud, and R. Sudan, Phys. Fluids B 3, 2767 (1991).
- Horton (1999) W. Horton, Rev. Mod. Phys. 71, 735 (1999).
- Snyder et al. (2011) P. B. Snyder, R. J. Groebner, J. W. Hughes, T. H. Osborne, M. Beurskens, A. W. Leonard, H. R. Wilson, and X. Q. Xu, Nucl. Fusion 51, 103016 (2011).
- Candy et al. (2004) J. Candy, R. E. Waltz, and W. Dorland, Phys. Plasmas 11, L25 (2004).
- Candy et al. (2009) J. Candy, C. Holland, R. E. Waltz, M. R. Fahey, and E. Belli, Phys. Plasmas 16, 060704 (2009).
- Barnes et al. (2010) M. Barnes, I. G. Abel, W. Dorland, T. Görler, G. W. Hammett, and F. Jenko, Phys. Plasmas 17, 056109 (2010).
- Abel et al. (2012) I. G. Abel, G. G. Plunk, E. Wang, M. Barnes, S. C. Cowley, W. Dorland, and A. A. Schekochihin, submitted to Rep. Prog. Phys. [arXiv:1209.4782] (2012).
- Ghim et al. (2012) Y.-c. Ghim, A. A. Schekochihin, A. R. Field, I. G. Abel, M. Barnes, G. Colyer, S. C. Cowley, F. I. Parra, D. Dunai, S. Zoletnik, and the MAST Team, submitted to Phys. Rev. Lett. [arXiv:1208.5970] (2012).
- Kotschenreuther et al. (1995) M. Kotschenreuther, W. Dorland, M. A. Beer, and G. W. Hammett, Phys. Plasmas 2, 2381 (1995).
- Barnes et al. (2011a) M. Barnes, F. I. Parra, and A. A. Schekochihin, Phys. Rev. Lett. 107, 115003 (2011a).
- Mantica et al. (2009) P. Mantica, D. Strintzi, T. Tala, C. Giroud, T. Johnson, H. Leggate, E. Lerche, T. Loarer, A. G. Peeters, A. Salmi, S. Sharapov, D. van Eester, P. C. de Vries, L. Zabeo, and K.-D. Zastrow, Phys. Rev. Lett. 102, 175002 (2009).
- Mantica et al. (2011) P. Mantica, C. Angioni, C. Challis, G. Colyer, L. Frassinetti, N. Hawkes, T. Johnson, M. Tsalas, P. C. deVries, J. Weiland, B. Baiocchi, M. N. A. Beurskens, A. C. A. Figueiredo, C. Giroud, J. Hobirk, E. Joffrin, E. Lerche, V. Naulin, A. G. Peeters, A. Salmi, C. Sozzi, D. Strintzi, G. Staebler, T. Tala, D. Van Eester, and T. Versloot, Phys. Rev. Lett. 107, 135004 (2011).
- Mantica et al. (2011) P. Mantica, C. Angioni, B. Baiocchi, M. Baruzzo, M. N. A. Beurskens, J. P. S. Bizarro, R. V. Budny, P. Buratti, A. Casati, C. Challis, J. Citrin, G. Colyer, F. Crisanti, A. C. A. Figueiredo, L. Frassinetti, C. Giroud, N. Hawkes, J. Hobirk, E. Joffrin, T. Johnson, E. Lerche, P. Migliano, V. Naulin, A. G. Peeters, G. Rewoldt, F. Ryter, A. Salmi, R. Sartori, C. Sozzi, G. Staebler, D. Strintzi, T. Tala, M. Tsalas, D. Van Eester, T. Versloot, P. C. deVries, J. Weiland, and J. EFDA Contributors, Plasma Phys. Control. Fusion 53, 124033 (2011).
- Highcock et al. (2012) E. G. Highcock, A. A. Schekochihin, S. C. Cowley, M. Barnes, F. I. Parra, C. M. Roach, and W. Dorland, submitted to Phys. Rev. Lett. [arXiv:1203.6455] (2012).
- Note (1) We do not suggest causality between all these parameters and — all local equilibrium characteristics, including , jointly adjust to form the critical manifold.
- Dimits et al. (2000) A. M. Dimits, G. Bateman, M. A. Beer, B. I. Cohen, W. Dorland, G. W. Hammett, C. Kim, J. E. Kinsey, M. Kotschenreuther, A. H. Kritz, L. L. Lao, J. Mandrekas, W. M. Nevins, S. E. Parker, A. J. Redd, D. E. Shumaker, R. Sydora, and J. Weiland, Phys. Plasmas 7, 969 (2000).
- Rogers et al. (2000) B. N. Rogers, W. Dorland, and M. Kotschenreuther, Phys. Rev. Lett. 85, 5336 (2000).
- Mikkelsen and Dorland (2008) D. R. Mikkelsen and W. Dorland, Phys. Rev. Lett. 101, 135003 (2008).
- Newton et al. (2010) S. L. Newton, S. C. Cowley, and N. F. Loureiro, Plasma Phys. Control. Fusion 52, 125001 (2010).
- Schekochihin et al. (2012) A. A. Schekochihin, E. G. Highcock, and S. C. Cowley, Plasma Phys. Control. Fusion 54, 055011 (2012).
- Barnes et al. (2011b) M. Barnes, F. I. Parra, E. G. Highcock, A. A. Schekochihin, S. C. Cowley, and C. M. Roach, Phys. Rev. Lett. 106, 175004 (2011b).
- Highcock et al. (2010) E. G. Highcock, M. Barnes, A. A. Schekochihin, F. I. Parra, C. M. Roach, and S. C. Cowley, Phys. Rev. Lett. 105, 215003 (2010).
- Highcock et al. (2011) E. G. Highcock, M. Barnes, F. I. Parra, A. A. Schekochihin, C. M. Roach, and S. C. Cowley, Phys. Plasmas 18, 102304 (2011).
- Ghim et al. (2012) Y.-c. Ghim, A. R. Field, D. Duani, S. Zoletnik, L. Bardoczi, A. A. Schekochihin, and the MAST Team, Plasma Phys. Control. Fusion 54, 095012 (2012).
- Field et al. (2009) A. R. Field, J. McCone, N. J. Conway, M. Dunstan, S. Newton, and M. Wisse, Plasma Phys. Control. Fusion 51, 105002 (2009).
- Hinton and Wong (1985) F. L. Hinton and S. K. Wong, Phys. Fluids 28, 3082 (1985).
- Cowley and Bishop (1986) S. C. Cowley and C. M. Bishop, Culham Laboratory Report CLM-M , 109 (1986).
- Note (2) Any mean poloidal flow exceeding the diamagnetic velocity would be damped by collisions Connor et al. (1987); Catto et al. (1987).
- Dorland et al. (1994) W. Dorland, M. Kotschenreuther, M. A. Beer, G. W. Hammett, R. E. Waltz, R. R. Dominguez, P. M. Valanju, W. H. Miner Jr., J. Q. Dong, W. Horton, F. L. Waelbroeck, T. Tajima, and M. J. LeBrun, Plasma Phys. Controlled Nucl. Fusion Res. 3, 463 (1994).
- Waltz et al. (1994) R. E. Waltz, G. D. Kerbel, and J. Milovich, Phys. Plasmas 1, 2229 (1994).
- Dimits et al. (2001) A. M. Dimits, B. I. Cohen, W. M. Nevins, and D. E. Shumaker, Nucl. Fusion 41, 1725 (2001).
- Kinsey et al. (2005) J. E. Kinsey, R. E. Waltz, and J. Candy, Phys. Plasmas 12, 062302 (2005).
- Camenen et al. (2009) Y. Camenen, A. G. Peeters, C. Angioni, F. J. Casson, W. A. Hornsby, A. P. Snodin, and D. Strintzi, Phys. Plasmas 16, 012503 (2009).
- Roach et al. (2009) C. M. Roach, I. G. Abel, R. J. Akers, W. Arter, M. Barnes, Y. Camenen, F. J. Casson, G. Colyer, J. W. Connor, S. C. Cowley, D. Dickinson, W. Dorland, A. R. Field, W. Guttenfelder, G. W. Hammett, R. J. Hastie, E. Highcock, N. F. Loureiro, A. G. Peeters, M. Reshko, S. Saarelma, A. A. Schekochihin, M. Valovic, and H. R. Wilson, Plasma Phys. Control. Fusion 51, 124020 (2009).
- Casson et al. (2009) F. J. Casson, A. G. Peeters, Y. Camenen, W. A. Hornsby, A. P. Snodin, D. Strintzi, and G. Szepesi, 16, 092303 (2009).
- Burrell (1997) K. H. Burrell, Phys. Plasmas 4, 1499 (1997).
- Burrell (1999) K. H. Burrell, Phys. Plasmas 6, 4418 (1999).
- Schaffner et al. (2012) D. A. Schaffner, T. A. Carter, G. D. Rossi, D. S. Guice, J. E. Maggs, S. Vincena, and B. Friedman, Phys. Rev. Lett. 109, 135002 (2012).
- Catto et al. (1973) P. J. Catto, M. N. Rosenbluth, and C. S. Liu, Phys. Fluids 16, 1719 (1973).
- Field et al. (2012) A. R. Field, D. Dunai, R. Gaffka, Y.-c. Ghim, I. Kiss, B. Meszaros, T. Krizsanoczi, S. Shibaev, and S. Zoletnik, Rev. Sci. Instrum. 83, 013508 (2012).
- Scannell et al. (2010) R. Scannell, M. J. Walsh, M. R. Dunstan, J. Figueiredo, G. Naylor, T. O’Gorman, S. Shibaev, K. J. Gibson, and H. Wilson, Rev. Sci. Instrum. 81, 10D520 (2010).
- Conway et al. (2006) N. J. Conway, P. G. Carolan, J. McCone, M. J. Walsh, and M. Wisse, Rev. Sci. Instrum. 77, 10F131 (2006).
- Kim et al. (1990) Y. B. Kim, P. H. Diamond, H. Biglari, and P. W. Terry, Phys. Fluids B 2, 2143 (1990).
- De Bock et al. (2008) M. F. M. De Bock, N. J. Conway, M. J. Walsh, P. G. Carolan, and N. C. Hawkes, Rev. Sci. Instrum. 79, 10F524 (2008).
- Lao et al. (1985) L. L. Lao, H. St John, R. D. Stambaugh, A. G. Kellman, and W. Pfeiffer, Nucl. Fusion 25, 1611 (1985).
- Beer et al. (1997) M. A. Beer, G. W. Hammett, G. Rewoldt, E. J. Synakowski, M. C. Zarnstorff, and W. Dorland, Phys. Plasmas 4, 1792 (1997).
- Rechester and Rosenbluth (1978) A. B. Rechester and M. N. Rosenbluth, Phys. Rev. Lett. 40, 38 (1978).
- Pueschel and Jenko (2010) M. J. Pueschel and F. Jenko, Phys. Plasmas 17, 062307 (2010).
- Nevins et al. (2011) W. M. Nevins, E. Wang, and J. Candy, Phys. Rev. Lett. 106, 065003 (2011).
- Hatch et al. (2012) D. R. Hatch, M. J. Pueschel, F. Jenko, W. M. Nevins, P. W. Terry, and H. Doerk, Phys. Rev. Lett. 108, 235002 (2012).
- Guttenfelder et al. (2012) W. Guttenfelder, J. Candy, S. M. Kaye, W. M. Nevins, E. Wang, J. Zhang, R. E. Bell, N. A. Crocker, G. W. Hammett, B. P. LeBlanc, D. R. Mikkelsen, Y. Ren, and H. Yuh, Phys. Plasmas 19, 056119 (2012).
- Doerk et al. (2012) H. Doerk, F. Jenko, T. Görler, D. Told, M. J. Pueschel, and D. R. Hatch, Phys. Plasmas 19, 055907 (2012).
- Abel and Cowley (2012) I. G. Abel and S. C. Cowley, submitted to New J. Phys. [arXiv:1210.1417] (2012).
- Hotelling (1936) H. Hotelling, Biometrika 28, 321 (1936).
- Note (3) The broad scatter of data points in Fig. 1(a) suggests that the correlation between and is weak; the lack of higher values of at large is due to the fact that the flow shear is weak at earlier times in the discharges, when the central value of is high.
- Note (4) It can be proven that the functional dependence , where is the flux-surface label, only changes on the resistive timescale of the mean magnetic field Abel and Cowley (2012).
- Parra et al. (2011) F. I. Parra, M. Barnes, E. G. Highcock, A. A. Schekochihin, and S. C. Cowley, Phys. Rev. Lett. 106, 115004 (2011).
- Diamond et al. (2005) P. H. Diamond, S.-I. Itoh, K. Itoh, and T.-S. Hahm, Plasma Phys. Control. Fusion 47, R35 (2005).
- Hinton and Rosenbluth (1999) F. L. Hinton and M. N. Rosenbluth, Plasma Phys. Control. Fusion 41, A653 (1999).
- Lin et al. (1999) Z. Lin, T. S. Hahm, W. W. Lee, W. M. Tang, and P. H. Diamond, Phys. Rev. Lett. 83, 3645 (1999).
- Ricci et al. (2006) P. Ricci, B. N. Rogers, and W. Dorland, Phys. Rev. Lett. 97, 245001 (2006).
- Xiao et al. (2007) Y. Xiao, P. J. Catto, and K. Molvig, Phys. Plasmas 14, 032302 (2007).
- Hawryluk (1980) R. Hawryluk, in Physics of plasmas close to thermonuclear conditions, Vol. 1, edited by B. Coppi (Commission of the European Communities, Brussels, 1980) p. 19.
- Meyer et al. (2009) H. Meyer et al., Nucl. Fusion 49, 104017 (2009).
- Note (5) This situation is distinct from the experiments on transport stiffness on JET Mantica et al. (2009, 2011, 2011) in that they provided vigorous extra heating power using localized ion-cyclotron-resonance heating (ICRH) to depart far from marginality.
- Fern et al. (2012) R. Fern, E. G. Highcock, A. A. Schekochihin, and M. N. A. Beurskens, unpublished (2012).
- Note (6) With tangential NBI heating, it is difficult to increase the toroidal Mach number — and hence the equilibrium flow shear — because of the fixed ratio of injected torque to power at a fixed injection energy.
- Connor et al. (1987) J. W. Connor, S. C. Cowley, R. J. Hastie, and L. R. Pan, Plasma Phys. Control. Fusion 29, 919 (1987).
- Catto et al. (1987) P. J. Catto, I. B. Bernstein, and M. Tessarotto, Phys. Fluids 30, 2784 (1987).