Local Differential Privacy Is Equivalent to Contraction of -Divergence
Abstract
We investigate the local differential privacy (LDP) guarantees of a randomized privacy mechanism via its contraction properties. We first show that LDP constraints can be equivalently cast in terms of the contraction coefficient of the -divergence. We then use this equivalent formula to express LDP guarantees of privacy mechanisms in terms of contraction coefficients of arbitrary -divergences. When combined with standard estimation-theoretic tools (such as Le Cam’s and Fano’s converse methods), this result allows us to study the trade-off between privacy and utility in several testing and minimax and Bayesian estimation problems.
I Introduction
A major challenge in modern machine learning applications is balancing statistical efficiency with the privacy of individuals from whom data is obtained. In such applications, privacy is often quantified in terms of Differential Privacy (DP) [1]. DP has several variants, including approximate DP [2], Rényi DP [3], and others [4, 5, 6, 7]. Arguably, the most stringent flavor of DP is local differential privacy (LDP) [8, 9]. Intuitively, a randomized mechanism (or a Markov kernel) is said to be locally differentially private if its output does not vary significantly with arbitrary perturbations of the input.
More precisely, a mechanism is said to be -LDP (or pure LDP) if the privacy loss random variable, defined as the log-likelihood ratio of the output for any two different inputs, is smaller than with probability one. One can also consider an approximate variant of this constraint: is said to be -LDP if the privacy loss random variable does not exceed with probability at least (see Def. 1 for the formal definition).
The study of statistical efficiency under LDP constraints has gained considerable traction, e.g., [9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 8]. Almost all of these works consider -LDP and provide meaningful bounds only for sufficiently small values of (i.e., the high privacy regime). For instance, Duchi et al. [10] studied minimax estimation problems under -LDP constraints and showed that for , the price of privacy is to reduce the effective sample size from to . A slightly improved version of this result appeared in [19, 13]. More recently, Duchi and Rogers [20] developed a framework based on the strong data processing inequality (SDPI) [21] and derived lower bounds for minimax estimation risk under -LDP that hold for any .
In this work, we develop an SDPI-based framework for studying hypothesis testing and estimation problems under -LDP, extending the results of [20] to approximate LDP. In particular, we derive bounds for both the minimax and Bayesian estimation risks that hold for any and . Interestingly, when setting , our bounds can be slightly stronger than [10].
Our main mathematical tool is an equivalent expression for DP in terms of -divergence. Given , the -divergence between two distributions and is defined as
| (1) |
We show that a mechanism is -LDP if and only if
for and any pairs of distributions where represents the output distribution of when the input distribution is . Thus, the approximate LDP guarantee of a mechanism can be fully characterized by its contraction under -divergence. When combined with standard statistical techniques, including Le Cam’s and Fano’s methods [22, 23], -contraction leads to general lower bounds for the minimax and Bayesian risk under -LDP for any and . In particular, we show that the price of privacy in this case is to reduce the sample size from to .
There exists several results connecting pure LDP to the contraction properties of KL divergence and total variation distance . For instance, for any -LDP mechanism , it is shown in [10, Theorem 1] that and in [13, Theorem 6] that for any pairs . Inspired by these results, we further show that if is -LDP then for any arbitrary -divergences and any pairs .
Notation. For a random variable , we write and for its distribution (i.e., ) and its alphabet, respectively. For any set , we denote by the set of all probability distributions on . Given two sets and , a Markov kernel (i.e., channel) is a mapping from to given by . Given and a Markov kernel , we let denote the output distribution of when the input distribution is , i.e., . Also, we use to denote the binary symmetric channel with crossover probability . For sequences and , we use to indicate for some universal constant .
II Preliminaries
II-A -Divergences
Given a convex function such that , the -divergence between two probability measures is defined as [24, 25]
| (2) |
Due to convexity of , we have . If, furthermore, is strictly convex at , then equality holds if and only . Popular examples of -divergences include corresponding to KL divergence, corresponding to total variation distance, and corresponding to -divergence. In this paper, we mostly concern with an important sub-family of -divergences associated with for a parameter . The corresponding -divergence, denoted by , is called -divergence (or sometimes hockey-stick divergence [26]) and is explicitly defined in (1). It appeared in [27] for proving converse channel coding results and also used in [28, 29, 30, 7] for characterizing privacy guarantees of iterative algorithms in terms of other variants of DP.
II-B Contraction Coefficient
All -divergences satisfy data processing inequality, i.e., for any pair of probability distributions and Markov kernel [24]. However, in many cases, this inequality is strict. The contraction coefficient of Markov kernel under -divergence is the smallest number such that for any pair of probability distributions . Formally, is defined as
| (3) |
Contraction coefficients have been studied for several -divergences, e.g., for total variation distance was studied in [31, 32, 33], for -divergence was studied in [34, 35, 36, 37, 38, 39], and for -divergence was studied in [33, 39, 40]. In particular, Dobrushin [31] showed that has a remarkably simple two-point characterization .
Similarly, one can plug -divergence into (3) and define the contraction coefficient for a Markov kernel under -divergence. This contraction coefficient has recently been studied in [30] for deriving approximate DP guarantees for online algorithms. In particular, it was shown [30, Theorem 3] that enjoys a simple two-point characterization, i.e., . Since , this is a natural extension of Dobrushin’s result.
II-C Local Differential Privacy
Suppose is a randomized mechanism mapping each to a distribution . One could view as a Markov kernel (i.e., channel) .
Definition 1 ([8, 9]).
A mechanism is -LDP for and if
| (4) |
is said to be -LDP if it is -LDP. Let be the collection of all Markov kernels with the above property. When , we use to denote .
Interactivity in Privacy-Preserving Mechanisms: Suppose there are users, each in possession of a datapoint , . The users wish to apply a mechanism that generates a privatized version of , denoted by . We say that the collection of mechanisms is non-interactive if is entirely determined by and independent of for . When all users apply the same mechanism , we can view as independent applications of to each . We denote this overall mechanism by . If interactions between users are permitted, then need not depend only on . In this case, we denote the overall mechanism by . In particular, the sequentially interactive [10] setting refers to the case when the input of depends on both and the outputs of the previous mechanisms.
III LDP As the Contraction of -Divergence
We show next that the -LDP constraint, with not necessarily equal to zero, is equivalent to the contraction of -divergence.
Theorem 1.
A mechanism is -LDP if and only if or equivalently
We note that Duchi et al. [10] showed that if is -LDP then . They then informally concluded from this result that -LDP acts as a contraction on the space of probability measures. Theorem 1 makes this observation precise.
According to Theorem 1, a mechanism is -LDP if and only if for any distributions and . An example of such Markov kernels is given next.
Example 1. (Randomized response mechanism) Let and consider the mechanism given by the binary symmetric channel with . This is often called randomized response mechanism [41] and denoted by . This simple mechanism is well-known to be -LDP which can now be verified via Theorem 1. Let and with . Then and where . It is straightforward to verify that for any , implying . When , a simple generalization of this mechanism, called -ary randomized response, has been reported in literature (see, e.g., [19, 13]) and is defined by and and for . Again, it can be verified that for this mechanism we have , for all Bernoulli and .
-divergence underlies all other -divergences, in a sense that any arbitrary -divergence can be represented by -divergence [42, Corollary 3.7]. Thus, an LDP constraint implies that a Markov kernel contracts for all -divergences, in a similar spirit to -contraction in Theorem 1.
Lemma 1.
Let and . Then, or, equivalently,
Notice that this lemma holds for any -divergences and any general family of -LDP mechanisms. However, it can be improved if one considers particular mechanisms or a certain -divergence. For instance, it is known that [21]. Thus, we have for the randomized response mechanism (cf. Example 1), while Lemma 1 implies that . Unfortunately, is difficult to compute in closed form for general Markov kernels, in which case Lemma 1 provides a useful alternative.
Next, we extend Lemma 1 for the non-interactive mechanism. Fix an -LDP mechanism and consider the corresponding non-interactive mechanism . To obtain upper bounds on directly through Lemma 1, we would first need to derive privacy parameters of in terms of and (e.g., by applying composition theorems). Instead, we can use the tensorization properties of contraction coefficients (see, e.g., [39, 38]) to relate to and then apply Lemma 1, as described next.
Lemma 2.
Let and . Then for
Each of the next three sections provide a different application of the contraction characterization of LDP.
IV Private Minimax Risk
Let be independent and identically distributed (i.i.d.) samples drawn from a distribution in a family . Let also be a parameter of a distribution that we wish to estimate. Each user has a sample and applies a privacy-preserving mechanism to obtain . Generally, we can assume that are sequentially interactive. Given the sequences , the goal is to estimate through an estimator . The quality of such estimator is assessed by a semi-metric and is used to define the minimax risk as:
| (5) |
The quantity uniformly characterizes the optimal rate of private statistical estimation over the family using the best possible estimator and privacy-preserving mechanisms in . In the absence of privacy constraints (i.e., ), we denote the minimax risk by .
The first step in deriving information-theoretic lower bounds for minimax risk is to reduce the above estimation problem to a testing problem [23, 43, 22]. To do so, we need to construct an index set with and a family of distributions such that for all in for some . The canonical testing problem is then defined as follows: Nature chooses a random variable uniformly at random from , and then conditioned on , the samples are drawn i.i.d. from , denoted by . Each is then fed to a mechanism to generate . It is well-known [22, 43, 23] that , where denotes the probability of error in guessing given . Replacing by its -privatized samples in this result, one can obtain a lower bound on in terms of . Hence, the remaining challenge is to lower-bound over the choice of mechanisms . There are numerous techniques for this objective depending on . We focus on two such approaches, namely Le Cam’s and Fano’s method, that bound in terms of total variation distance and mutual information and hence allow us to invoke Lemmas 1 and 2.
IV-A Locally Private Le Cam’s Method
Le Cam’s method is applicable when is a binary set and contains, say, and . In its simplest form, it relies on the inequality (see [22, Lemma 1] or [23, Theorem 2.2]) . Thus, it yields the following lower bound for non-private minimax risk
| (6) | ||||
| (7) |
for any in , where the second inequality follows from Pinsker’s inequality and chain rule of KL divergence. In the presence of privacy, the estimator depends on instead of , which is generated by a sequentially interactive mechanism . To write the private counterpart of (6), we need to replace and with and the corresponding marginals of , respectively. A lower bound for is therefore obtained by deriving an upper bound for for all .
Lemma 3.
Let satisfy . Then we have
By comparing with the original non-private Le Cam’s method (7), we observe that the effect of -LDP is to reduce the effective sample size from to . Setting , this result strengthens Duchi et al. [10, Corollary 2], where the effective sample size was shown to be for sufficiently small .
Example 2. (One-dimensional mean estimation) For some , we assume is given by
The goal is to estimate under the squared metric. This problem was first studied in [10, Propsition 1] where it was shown only for . Applying our framework to this example, we obtain a similar lower bound that holds for all and .
Corollary 1.
For all , , and , we have
| (8) |
It is worth instantiating this corollary for some special values of . Consider first the usual setting of finite variance setting, i.e., . In the non-private case, it is known that the sample mean has mean-squared error that scales as . According to Corollary 1, this rate worsens to in the presence of -LDP requirement. As , the moment condition implies the boundedness of . In this case, Corollary 1 implies the more standard lower bound .
IV-B Locally Private Fano’s Method
Le Cam’s method involves a pair of distributions in . However, it is possible to derive a stronger bound considering a larger subset of by applying Fano’s inequality (see, e.g., [22]). We follow this path to obtain a better minimax lower bound for the non-interactive setting.
Consider the index set . The non-private Fano’s method relies on the Fano’s inequality to write a lower bound for in terms of mutual information as
| (9) |
To incorporate privacy into this result, we need to derive an upper bound for over all choices of mechanisms . Focusing on the non-interactive mechanisms, the following lemma exploits Lemma 2 for such an upper bound.
Lemma 4.
Given and as described above, let be constructed by applying on . If is -LDP, then we have
This lemma can be compared with [10, Corollary 1], where it was shown
| (10) |
This is a looser bound than Lemma 4 for any and and only holds for .
Example 3. (High-dimensional mean estimation in an -ball) For a parameter , define
| (11) |
where is the -ball of radius in . The goal is to estimate the mean given the private views . This example was first studied in [10, Proposition 3] that states for . In the following, we use Lemma 4 to derive a similar lower bound for any and , albeit slightly weaker than [10, Proposition 3].
Corollary 2.
For the non-interactive setting, we have
| (12) |
V Private Bayesian Risk
In the minimax setting, the worst-case parameter is considered which usually leads to over-pessimistic bounds. In practice, the parameter that incurs a worst-case risk may appear with very small probability. To capture this prior knowledge, it is reasonable to assume that the true parameter is sampled from an underlying prior distribution. In this case, we are interested in the Bayes risk of the problem.
Let be a collection of parametric probability distributions on and the parameter space is endowed with a prior , i.e., . Given an i.i.d. sequence drawn from , the goal is to estimate from a privatized sequence via an estimator . Here, we focus on the non-interactive setting. Define the private Bayes risk as
| (13) |
where the expectation is taken with respect to the randomness of both and . It is evident that must depend on the prior . This dependence can be quantified by
| (14) |
for . Xu and Raginsky [44] showed that the non-private Bayes risk (i.e., ), denoted by , is lower bounded as
| (15) |
Replacing with in this result and applying Lemma 2 (similar to Lemma 4), we can directly convert (15) to a lower bound for .
Corollary 3.
In the non-interactive setting, we have
In the following theorem, we provide a lower bound for that directly involves -divergence, and thus leads to a tighter bounds than (3). For any pair of random variables with marginals and and a constant , we define their -information as
Theorem 2.
Let be an -LDP mechanism. Then, for we have
and for in non-interactive setting we have
Example 4. Suppose is uniformly distributed on , , and . As mentioned earlier, . We can write for
| (16) |
A straightforward calculation shows that , for any , and where is the number of 1’s in . Given these marginal and conditional distribution, one can obtain after algebraic manipulations
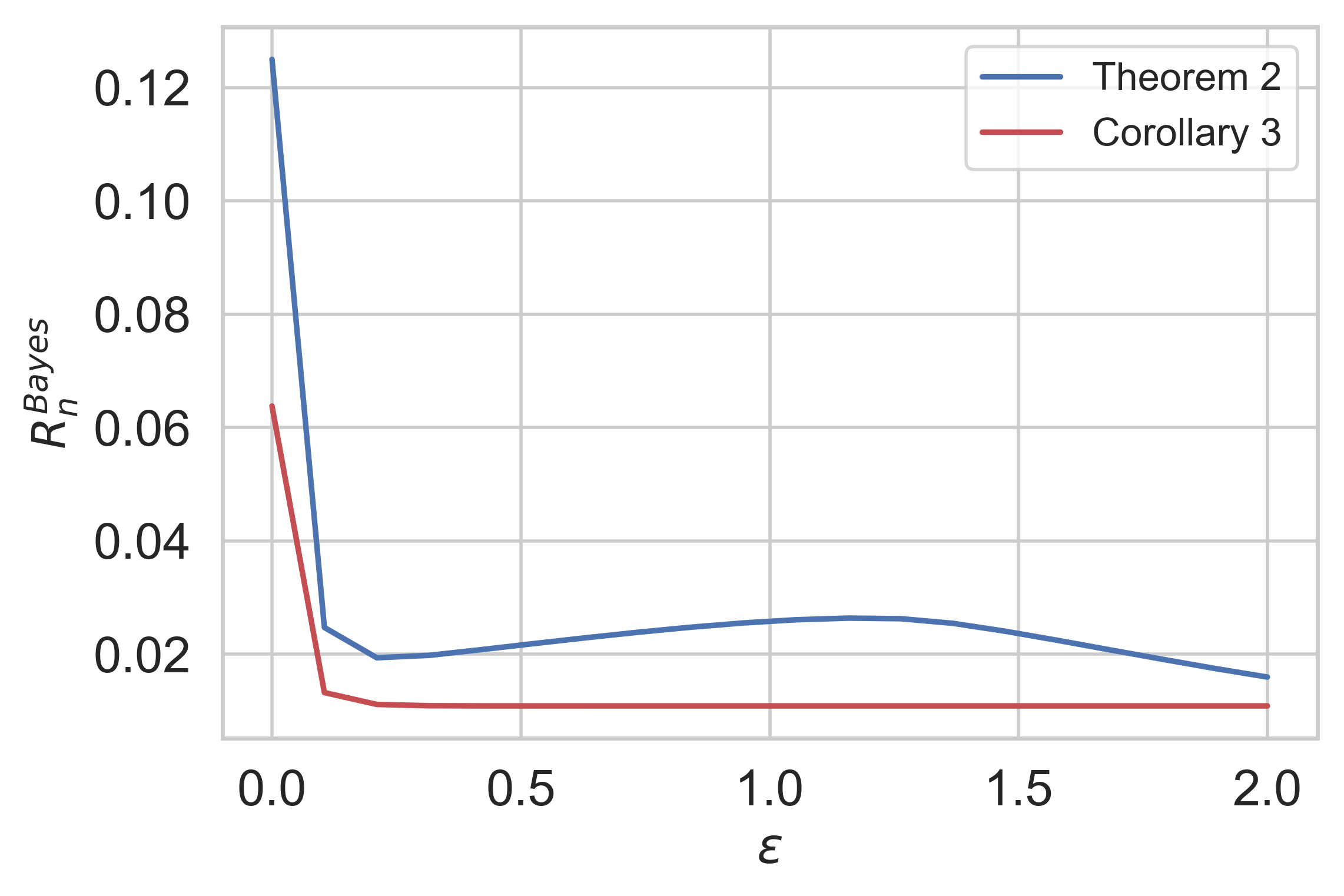
Plugging this into Theorem 2, we arrive at a maximization problem that can be numerically solved. Similarly, we compute and plug it into Corollary 3 and numerically solve the resulting optimization problem. In Fig. 1, we compare these two lower bounds for and , indicating the advantage of Theorem 2 for small .
Remark 1.
The proof of Theorem 2 leads to the following lower bound for the non-private Bayes risk
| (17) |
For a comparison with (15), consider the following example. Suppose is a uniform random variable on and . We are interested in the Bayes risk with respect to the -loss function . It can be shown that nats while
| (18) |
Moreover, . It can be verified that (15) gives , whereas our bound (17) yields .
VI Private Hypothesis Testing
We now turn our attention to the well-known problem of binary hypothesis testing under local differential privacy constraint. Suppose i.i.d. samples drawn from a distribution are observed. Let now each be mapped to via a mechanism (i.e., sequential interaction is permitted). The goal is to distinguish between the null hypothesis from the alternative given . Let be a binary statistic, generated from a randomized decision rule where indicates that is rejected. Type I and type II error probabilities corresponding to this statistic are given by and , respectively. To capture the optimal trade-off between type I and type II error probabilities, it is customary to define where the infimum is taken over all kernels such that and non-interactive mechanisms with . In the following lemma, we apply Lemma 1 to obtain an asymptotic lower bound for .
Corollary 4.
We have for any and
| (19) |
A similar result was proved by Kairouz et al. [13, Sec. 3] that holds only for sufficiently “small” (albeit unspecified) and . When compared to Chernoff-Stein lemma [45, Theorem 11.8.3], establishing as the asymptotic exponential decay rate of , the above corollary, once again, justifies the reduction of effective sample size from to in the presence of -LDP requirement.
VII Mutual Information of LDP Mechanisms
Viewing mutual information as a utility measure, we may consider maximizing mutual information under local differential privacy as yet another privacy-utility trade-off. To formalize this, let . The goal is to characterize the supremum of over , i.e., the maximum information shared between and its -LDP representation. Such mutual information bounds under local DP have appeared in the literature, e.g., McGregor et al. [46] provided a result that roughly states for and Kairouz et al. [13, Corollary 15] showed for sufficiently small
| (20) |
where satisfies . Next, we provide an upper bound for the mutual information under LDP that holds for all and .
Corollary 5.
We have for any and
| (21) |
References
- [1] C. Dwork, F. McSherry, K. Nissim, and A. Smith, “Calibrating noise to sensitivity in private data analysis,” in Proc. Theory of Cryptography (TCC), Berlin, Heidelberg, 2006, pp. 265–284.
- [2] C. Dwork, K. Kenthapadi, F. McSherry, I. Mironov, and M. Naor, “Our data, ourselves: Privacy via distributed noise generation,” in EUROCRYPT, S. Vaudenay, Ed., 2006, pp. 486–503.
- [3] I. Mironov, “Rényi differential privacy,” in Proc. Computer Security Found. (CSF), 2017, pp. 263–275.
- [4] M. Bun and T. Steinke, “Concentrated differential privacy: Simplifications, extensions, and lower bounds,” in Theory of Cryptography, 2016, pp. 635–658.
- [5] C. Dwork and G. N. Rothblum, “Concentrated differential privacy,” vol. abs/1603.01887, 2016. [Online]. Available: http://arxiv.org/abs/1603.01887
- [6] J. Dong, A. Roth, and W. J. Su, “Gaussian differential privacy,” arXiv 1905.02383, 2019.
- [7] S. Asoodeh, J. Liao, F. P. Calmon, O. Kosut, and L. Sankar, “Three variants of differential privacy: Lossless conversion and applications,” To appear in Journal on Selected Areas in Information Theory (JSAIT), 2021.
- [8] A. Evfimievski, J. Gehrke, and R. Srikant, “Limiting privacy breaches in privacy preserving data mining,” in Proc. ACM symp. Principles of Database Systems (PODS). ACM, 2003, pp. 211–222.
- [9] S. P. Kasiviswanathan, H. K. Lee, K. Nissim, S. Raskhodnikova, and A. Smith, “What can we learn privately?” SIAM J. Comput., vol. 40, no. 3, pp. 793–826, Jun. 2011.
- [10] J. C. Duchi, M. I. Jordan, and M. J. Wainwright, “Local privacy, data processing inequalities, and statistical minimax rates,” in Proc. Symp. Foundations of Computer Science, 2013, p. 429–438. [Online]. Available: https://arxiv.org/abs/1302.3203
- [11] M. Gaboardi, R. Rogers, and O. Sheffet, “Locally private mean estimation: -test and tight confidence intervals,” in Proc. Machine Learning Research, 2019, pp. 2545–2554.
- [12] A. Bhowmick, J. Duchi, J. Freudiger, G. Kapoor, and R. Rogers, “Protection against reconstruction and its applications in private federated learning,” arXiv 1812.00984, 2018.
- [13] P. Kairouz, S. Oh, and P. Viswanath, “Extremal mechanisms for local differential privacy,” Journal of Machine Learning Research, vol. 17, no. 17, pp. 1–51, 2016.
- [14] L. P. Barnes, W. N. Chen, and A. Özgür, “Fisher information under local differential privacy,” IEEE Journal on Selected Areas in Information Theory, vol. 1, no. 3, pp. 645–659, 2020.
- [15] J. Acharya, C. L. Canonne, and H. Tyagi, “Inference under information constraints i: Lower bounds from chi-square contraction,” IEEE Transactions on Information Theory, vol. 66, no. 12, pp. 7835–7855, 2020.
- [16] M. Ye and A. Barg, “Optimal schemes for discrete distribution estimation under locally differential privacy,” IEEE Trans. Inf. Theory, vol. 64, no. 8, pp. 5662–5676, 2018.
- [17] D. Wang and J. Xu, “On sparse linear regression in the local differential privacy model,” IEEE Trans. Inf. Theory, pp. 1–1, 2020.
- [18] A. Rohde and L. Steinberger, “Geometrizing rates of convergence under local differential privacy constraints,” Ann. Statist., vol. 48, no. 5, pp. 2646–2670, 10 2020.
- [19] P. Kairouz, K. Bonawitz, and D. Ramage, “Discrete distribution estimation under local privacy,” in Proc. Int. Conf. Machine Learning, vol. 48, 20–22 Jun 2016, pp. 2436–2444.
- [20] J. Duchi and R. Rogers, “Lower bounds for locally private estimation via communication complexity,” in Proc. Conference on Learning Theory, 2019, pp. 1161–1191.
- [21] R. Ahlswede and P. Gács, “Spreading of sets in product spaces and hypercontraction of the markov operator,” Ann. Probab., vol. 4, no. 6, pp. 925–939, 12 1976.
- [22] B. Yu, Assouad, Fano, and Le Cam. Springer New York, 1997, pp. 423–435.
- [23] A. B. Tsybakov, Introduction to Nonparametric Estimation, 1st ed. Springer Publishing Company, Incorporated, 2008.
- [24] I. Csiszár, “Information-type measures of difference of probability distributions and indirect observations,” Studia Sci. Math. Hungar., vol. 2, pp. 299–318, 1967.
- [25] S. M. Ali and S. D. Silvey, “A general class of coefficients of divergence of one distribution from another,” Journal of Royal Statistics, vol. 28, pp. 131–142, 1966.
- [26] N. Sharma and N. A. Warsi, “Fundamental bound on the reliability of quantum information transmission,” CoRR, vol. abs/1302.5281, 2013. [Online]. Available: http://arxiv.org/abs/1302.5281
- [27] Y. Polyanskiy, H. V. Poor, and S. Verdú, “Channel coding rate in the finite blocklength regime,” IEEE Trans. Inf. Theory, vol. 56, no. 5, pp. 2307–2359, 2010.
- [28] B. Balle, G. Barthe, and M. Gaboardi, “Privacy amplification by subsampling: Tight analyses via couplings and divergences,” in NeurIPS, 2018, pp. 6280–6290.
- [29] B. Balle, G. Barthe, M. Gaboardi, and J. Geumlek, “Privacy amplification by mixing and diffusion mechanisms,” in NeurIPS, 2019, pp. 13 277–13 287.
- [30] S. Asoodeh, M. Diaz, and F. P. Calmon, “Privacy analysis of online learning algorithms via contraction coefficients,” arXiv 2012.11035, 2020.
- [31] R. L. Dobrushin, “Central limit theorem for nonstationary markov chains. I,” Theory Probab. Appl., vol. 1, no. 1, pp. 65–80, 1956.
- [32] P. Del Moral, M. Ledoux, and L. Miclo, “On contraction properties of markov kernels,” Probab. Theory Relat. Fields, vol. 126, pp. 395–420, 2003.
- [33] J. E. Cohen, Y. Iwasa, G. Rautu, M. Beth Ruskai, E. Seneta, and G. Zbaganu, “Relative entropy under mappings by stochastic matrices,” Linear Algebra and its Applications, vol. 179, pp. 211 – 235, 1993.
- [34] V. Anantharam, A. Gohari, S. Kamath, and C. Nair, “On hypercontractivity and a data processing inequality,” in 2014 IEEE Int. Symp. Inf. Theory, 2014, pp. 3022–3026.
- [35] Y. Polyanskiy and Y. Wu, “Strong data-processing inequalities for channels and bayesian networks,” in Convexity and Concentration, E. Carlen, M. Madiman, and E. M. Werner, Eds. New York, NY: Springer New York, 2017, pp. 211–249.
- [36] Y. Polyanskiy and Y. Wu, “Dissipation of information in channels with input constraints,” IEEE Trans. Inf. Theory, vol. 62, no. 1, pp. 35–55, Jan 2016.
- [37] F. P. Calmon, Y. Polyanskiy, and Y. Wu, “Strong data processing inequalities for input constrained additive noise channels,” IEEE Trans. Inf. Theory, vol. 64, no. 3, pp. 1879–1892, 2018.
- [38] A. Makur and L. Zheng, “Comparison of contraction coefficients for -divergences,” Probl. Inf. Trans., vol. 56, pp. 103–156, 2020.
- [39] M. Raginsky, “Strong data processing inequalities and-sobolev inequalities for discrete channels,” IEEE Trans. Inf. Theory, vol. 62, no. 6, pp. 3355–3389, June 2016.
- [40] H. S. Witsenhausen, “On sequences of pairs of dependent random variables,” SIAM Journal on Applied Mathematics, vol. 28, no. 1, pp. 100–113, 1975.
- [41] S. L. Warner, “Randomized response: A survey technique for eliminating evasive answer bias,” Journal of the American Statistical Association, vol. 60, no. 309, pp. 63–69, 1965.
- [42] J. Cohen, J. Kemperman, and G. Zbăganu, Comparisons of Stochastic Matrices, with Applications in Information Theory, Economics, and Population Sciences. Birkhäuser, 1998.
- [43] Y. Yang and A. Barron, “Information-theoretic determination of minimax rates of convergence,” Ann. Statist., vol. 27, no. 5, pp. 1564–1599, 10 1999.
- [44] A. Xu and M. Raginsky, “Converses for distributed estimation via strong data processing inequalities,” in IEEE Int. Sympos. Inf. Theory (ISIT), 2015, pp. 2376–2380.
- [45] T. M. Cover and J. A. Thomas, Elements of information theory. John Wiley & Sons, 2012.
- [46] A. McGregor, I. Mironov, T. Pitassi, O. Reingold, K. Talwar, and S. Vadhan, “The limits of two-party differential privacy,” in Proc. of the 51st Annual IEEE Symposium on Foundations of Computer Science (FOCS ‘10), 23–26 October 2010, p. 81–90.
- [47] I. Csiszár and J. Körner, Information Theory: Coding Theorems for Discrete Memoryless Systems. Cambridge University Press, 2011.
We begin by some alternative expressions for -divergence that are useful for the subsequent proofs. It is straightforward to show that for any , we have
| (22) | ||||
| (23) | ||||
| (24) |
The proof of Theorem 1 relies on the following theorem, recently proved by the authors in [30, Theorem 3].
Theorem 3.
For any and Markov kernel with input alphabet , we have
| (25) |
Notice that for , this theorem reduces to the well-known Dobrushin’s result [31] that states
| (26) |
Proof of Theorem 1.
It follows from Theorem 3 that
| (27) |
which, according to (23), implies
Hence, in light of Definition 1, is -LDP if and only if .
∎
Proof of Lemma 1.
We first show the following upper and lower bounds for -divergence in terms of the total variation distance.
Claim. For any distributions and on and any , we have
| (28) |
Proof of Claim.
According to this claim, we can write for
Replacing and with and , respectively, for some and in , we obtain
Taking supremum over and from both side and invoking Theorem 3 and (26), we conclude that
| (29) |
It is known [33, 39] that for any Markov kernel and any convex functions we have
| (30) |
from which the desired result follows immediately. ∎
Proof of Lemma 2.
Given mechanisms , we consider the non-interactive mechanism given by
If for , then we have . According to (29), it thus leads to . Invoking [35, Corollary 9] (see also [44, Lemma 3] and [38, Eq. (62)]), we obtain
∎
Proof of Lemma 3.
Recall that is an i.i.d. sample of distribution and each , is obtained by applying to . Note that by assumption specifies the conditional distribution . Let and denote the distribution of when and , respectively. Thus, we have for and any
| (31) | ||||
| (32) | ||||
| (33) |
Having this in mind, we can write
| (34) | ||||
| (35) | ||||
| (36) |
where follows from Pinsker’s inequality, is due to the chain rule of KL divergence, is an application of Lemma 1. Plugging (36) in (6), we obtain the desired result. ∎
Proof of Corollary 1.
Fix and consider two distributions and on defined as
and
It can be verified that both and belong to . Note that . Let and be the corresponding output distributions of the mechanism , the composition of mechanisms . Le Cam’s bound for -metric yields
| (37) |
where the last inequality follows from the fact for being the Hellinger distance. Notice that and where each for is -LDP. It is well known that
Thus,
| (38) |
Hence, we obtain
| (39) |
Plugging (38) into (37), we obtain
| (40) |
Now, choose . Notice that we assume and hence regardless of . Plugging this choice of into the above bound, we obtain
| (41) |
∎
Proof of Lemma 4.
Note that we have the Markov chain . It has been shown in [47, Problem 15.12] (see also [34, 47]) that for any channel connecting random variable to , we have
| (42) |
Replacing and with and , respectively, in the above equation, we obtain
where and . The desired result then follows from Lemma 2 and the convexity of KL-divergence. ∎
Proof of Corollary 2.
The proof strategy is as follows: we first construct a set of probability distribution for taking values in a finite set and then apply Fano’s inequality (9) where is a uniform random variable on . Duchi el el. [10, Lemma 6] showed that there exists a set of the -dimensional hypercube satisfying for each with and some integer , while being at least . If , one can extend to a subset of by considering . Fix and define a distribution for as follows: Choose an index uniformly and set and where is the standard basis vector in . Given , let be a random variable taking values in and be an i.i.d. sample of . Furthermore, as before, let be a privatized sample of obtained by with being an -LDP mechanism. To apply Fano’s inequality, we first need to bound . According to Lemma 4, we have
| (43) |
Hence, bounding reduces to bounding . To this end, first notice that . Let be a uniform random variable on independent of that chooses the coordinate of . Note that can be determined by and hence
where the last inequality follows from the fact that for due to the concavity of entropy. Consequently, we can write
| (44) |
Applying Fano’s inequality, we obtain
| (45) | ||||
| (46) |
Setting and assuming , we can write
| (47) |
By choosing , we obtain
| (48) |
∎
Proof of Theorem 2.
Let be an estimate of for some and and , i.e., and correspond to the probability of the event under the joint and product distributions, respectively. By definition, we have for any
where the last inequality follows from the fact that , that can be shown as follows
Recalling that , the above thus implies
| (49) |
Since, by Markov’s inequality, , we can write by setting
where the second inequality comes from the data processing inequality for . To further lower bound the right-hand side, we write
where the inequality follows from the definition of contraction coefficient. When , we have as is assumed to be -DP. For , we invoke Lemma 2 to obtain . ∎
Proof of Corollary 4 .
Let be the non-private trade-off between type I and type II error probabilities (i.e., ). According to Chernoff-Stein lemma (see, e.g., [45, Theorem 11.8.3]), we have
| (50) |
Assume now that, is the output of for an -LDP mechanism . According to (50), we obtain that
| (51) |
Applying Lemma 1, we obtain the desired result. ∎