Local gaps in three-dimensional periodic media

The discovery of photonic and phononic crystals, the creation and advancement of electromagnetic and acoustic metamaterials stimulated the development of efficient numerical methods for calculating their bandgap structure. The main tool for the evaluation of dispersion relations was the plane wave expansion method [1, 2, 3]. Later, other methods such as the finite-difference time-domain [4, 5, 6], the finite element [7, 8, 9] and boundary element methods [10, 11] employed. All these methods reduce the bandgap problem to the solution of an eigenvalue problem from which propagating frequency is determined. Analytic determination of bandgaps is a more challenging problem which becomes possible by introducing small or large parameters. This situation occurs in solid-state physics in the study of the energy bands of electrons when the periodic potential of crystals is small [12, 13]. Other examples are dealing with high contrast materials for inclusions and the matrix, such results were established in [14, 15, 16, 17].

The aim of standard bandgap analysis is the determination of absolute gaps consisting of frequencies for which no waves propagate in any direction. We will show the absence of absolute gaps in our problem and investigate local gaps defined by pairs $(\omega,\bm{k}_{0})$ for which waves with frequency $\omega$ do not propagate for small variations of the Bloch vector $\bm{k}_{0}$. A detailed definition of a local gap is given later.

We study the propagation of Bloch waves in a medium containing a periodic array of identical inclusions. The amplitude $u$ of the waves is governed by the equation

where $k=\omega/c$ is the wave number, $\omega$ is the time frequency, and $c$ is the wave propagation speed (different in the host medium and inclusions). Solution of (1.1) is sought in the form

where $\bm{k}=(k_{1},k_{2},k_{3})$ is the Bloch vector, and function $\Phi({\bm{x}})$ is periodic with the period of the lattice. The representation above is equivalent to

where $\rrbracket f\llbracket$ denotes the jump of $f$ and its gradient across the opposite sides of the cells of periodicity.

For simplicity, we assume that the fundamental cell of periodicity $\Pi$ is a cube $[-\pi,\pi]^{3}$. Denote by $\Omega$ the domain occupied by the inclusion in $\Pi$ (see Figure 1). We select the origin for the coordinate system to be in $\Omega$ and suppose that $\Omega$ has a small size. Specifically, $\Omega=\Omega(a)$ is produced by compressing an $a$-independent region $\widehat{\Omega}$ of arbitrary shape using the factor $a^{-1}$, $0<a\ll 1$. In other words, the transformation ${\bm{x}}\to a{\bm{\xi}}$ maps $\Omega(a)\subset{\mathbb{R}}^{3}_{{\bm{x}}}$ into $\widehat{\Omega}\subset{\mathbb{R}}^{3}_{{\bm{\xi}}}$. We assume that the boundary $\partial\Omega$ belongs to the class $C^{1,\beta}$, which means that the functions that define the boundary have first-order derivatives that belong to the Hölder space with index $\beta$.

We consider first the case when homogeneous Dirichlet conditions, which arise for some soft inclusions, are imposed on the boundary. The transmission problem is considered in §6. Then function $u$ in the fundamental cell of periodicity $\Pi$ obeys the equation

and the boundary conditions

A non-trivial solution of (1.3),(1.4) with fixed $\widehat{\Omega}$ exists not for all values of $k=\omega/c,a,$ and $\bm{k}$. The relation between the parameters $\omega,a,\bm{k}$, for which there is a non-trivial solution, is called the dispersion relation. The problem (1.3),(1.4) is one-periodic in each component of $\bm{k}$, and the dispersion relation is a periodic function defined in ${\mathbb{R}}^{3}_{\bm{k}}$.

The goal of this work is to find gaps i.e. the values of time frequency $\omega=kc$ such that (1.3),(1.4) has only trivial solutions for all Bloch vectors $\bm{k}\in{\mathbb{R}}^{3}$. Thus, the waves with frequency $\omega$ do not propagate if $\omega$ belongs to a gap. These gaps are also called global or complete gaps. Geometrically, global gaps are empty intervals in the orthogonal projection of the dispersion surface onto the vertical $\omega$-axis. Global gaps in $\omega$ correspond to the gaps in the spectrum $\lambda=k^{2}$ of $-\Delta$ in $\Pi\smallsetminus\Omega(a)$ with an arbitrary $\bm{k}$ in the boundary condition (1.4). We will also consider local gaps whose rigorous definition will be provided later in this section.

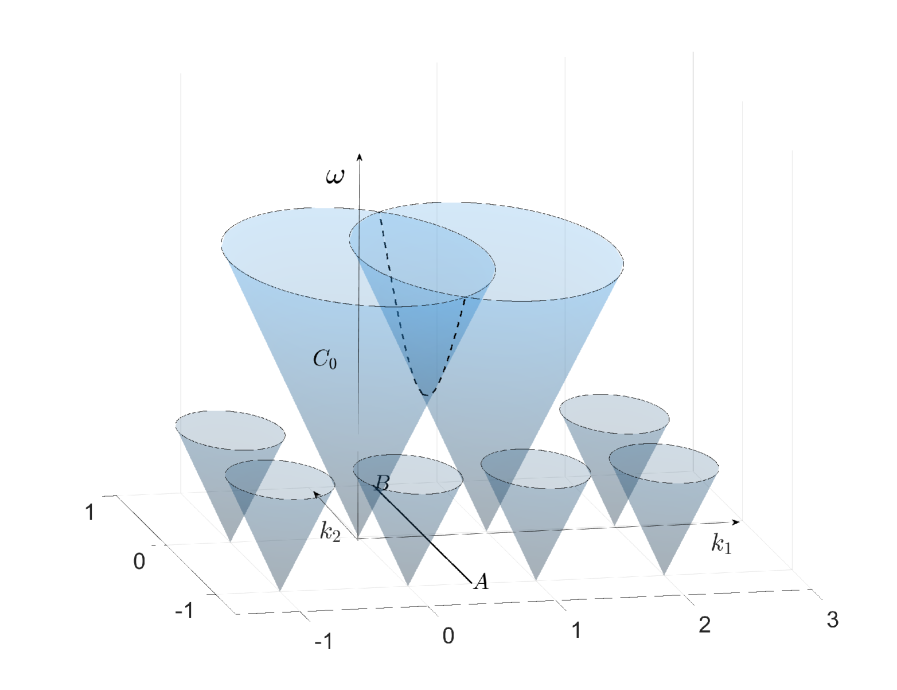
Consider the unperturbed problem. Observe that in the absence of inclusions, function $\mathrm{e}^{-\mathrm{i}\bm{k}\cdot{\bm{x}}}$ satisfies (1.3),(1.4) with $k=|\bm{k}|$, i.e. $\omega=c|\bm{k}|$. For any vector $\bm{m}=(m_{1},m_{2},m_{3})$ with integer components, functions $\mathrm{e}^{-\mathrm{i}(\bm{k}-\bm{m})\cdot{\bm{x}}}$ are also satisfy the same boundary condition (1.4) and equation (1.3) with $\omega=c|\bm{k}-\bm{m}|$. The graph of the infinite-valued periodic in $\bm{k}$ dispersion function for the unperturbed problem consists of the set of all the cones $\omega=c|\bm{k}-\bm{m}|$, see Figure 2.

For some values of $\bm{k}$, the unperturbed problem (1.3),(1.4) with $k=|\bm{k}|$ has solutions different from $\mathrm{e}^{-\mathrm{i}\bm{k}\cdot{\bm{x}}}$, and the solution space has dimension $n>1$. All such solutions have the form $\mathrm{e}^{-\mathrm{i}(\bm{k}-\bm{m})\cdot{\bm{x}}}$ provided that $|\bm{k}|=|\bm{k}-\bm{m}|$ and $\bm{m}$ is a vector with integer components. The values of $\bm{k}$ for which $n>1$ are called exceptional of order $n$. Geometrically, $n$ refers to the number of points $\bm{m}$ in the integer lattice $\mathbb{Z}^{3}$ (including the origin) belonging to the Ewald sphere [13] centered at $\bm{k}$ with radius $|\bm{k}|$, i.e. equation

has $n>1$ solutions $\bm{m}\neq{\bm{0}}$ for exceptional $\bm{k}$, and only one solution $\bm{m}={\bm{0}}$ for non-exceptional $\bm{k}$. Equation (1.5) can be written as

i.e. exceptional points belong to planes in ${\mathbb{R}}^{3}_{\bm{k}}$ whose distance from the origin goes to infinity as $|\bm{m}|\to\infty$. An exceptional point $\bm{k}$ has order $n>1$ if it belongs to $n-1$ planes (1.6). One can also describe exceptional wave vectors as values of $\bm{k}$ for which $n>1$ cones in Figure 2 interest each other. In particular, in the two-dimensional analog of our problem in Figure 2, the line $AB$ consists of exceptional points of order at least two.

The set of solutions of the problem (1.3),(1.4) remains the same if the wave vector is changed by a period of the reciprocal lattice. Thus it is enough to study local gaps related to one cone centered at the origin: $C_{0}:=\{\omega=c|\bm{k}|\}$. This will allow us to define local gaps related to other cones in Figure 2 using the periodicity of solutions in $\bm{k}$.

Let us fix a wave vector $\bm{k}_{0}$. The local gap $g(\bm{k}_{0})$ corresponding to $\bm{k}_{0}$ and associated with $C_{0}$ consists of frequencies $\omega=\omega_{a}$ for which Bloch waves do not propagate when wave vector $\bm{k}$ has the same direction as $\bm{k}_{0}$ and $|\bm{k}-\bm{k}_{0}|$ is sufficiently small. More precisely, Bloch waves with the frequency $\omega_{a}$ do not exist when $\bm{k}=(1+\delta)\bm{k}_{0}$ for sufficiently small $a$-independent $|\delta|$.

It is not expedient to consider frequencies $\omega$ if the point $(\omega,\bm{k}_{0})$ is located at a positive, $a$-independent distance $d$ from the set of cones shown in Fig. 2 (dispersion surfaces of the unperturbed problem). Bloch waves with parameters $(\omega,(1+\delta)\bm{k}_{0})$ and $\delta<d/2$ do not propagate in the unperturbed problem and the problem with inclusions if $a$ is small enough. Thus, we introduce one more requirement in the definition of local gap $g(\bm{k}_{0})$. We assume that $\omega=\omega_{a}\to\omega_{0}$ as $a\to 0$ where $(\omega_{0},\bm{k}_{0})\in C_{0}$, i.e. $\omega_{0}=c|\bm{k}_{0}|$.

Let $\omega_{a}$ tends to $\omega_{0}=c|\bm{k}_{0}|$. We will show that

1. (a)

   If $(\omega_{0},\bm{k}_{0})$ belongs to a cone $C_{0}$ but not to the intersection of the cones, then $g(\bm{k}_{0})=\varnothing$, i. e. there are no local gap for wave vector $\bm{k}_{0}$ and frequencies $\omega$ near $\omega_{0}$.

2. (b)

   If $(\omega_{0},\bm{k}_{0})$ belongs to an intersection of $C_{0}$ with some other cone shown in Figure 2 then local gap $g(\bm{k}_{0})$ exists in a neighborhood of $\omega_{0}$ for small $a$ if and only if $\displaystyle\frac{|\bm{k}_{0}|}{|\bm{m}_{0}|}<\frac{\sqrt{2}}{2}$, where $\bm{k}_{0},\bm{m}_{0}$ satisfy (1.5). The location of the gap will be specified. We do not consider the points $(\omega_{0},\bm{k}_{0})$ that belong to the intersection of three or more cones and those for which $\displaystyle\frac{|\bm{k}_{0}|}{|\bm{m}_{0}|}=\frac{\sqrt{2}}{2}$.

3. (c)

   We will show that global gaps do not exist in any fixed interval $\epsilon<\omega<\epsilon^{-1}$ of the time frequency $\omega$ if the size $a$ of the inclusion is small enough.

Note that the set of values of $\bm{k}$ omitted from the consideration in item (b) forms a one-dimensional manifold in ${\mathbb{R}}^{3}$. Indeed, the set of exceptional vectors of multiplicity $n\geqslant 2$ is given by the planes (1.6). Omitted from the consideration set of exceptional vectors of order higher than two are lines of intersections of those planes. Also, condition $\displaystyle\frac{|\bm{k}_{0}|}{|\bm{m}_{0}|}=\frac{\sqrt{2}}{2}$ defines curves on planes (1.6), see Figure 3, where these curves are circles that are boundaries of shaded disks.

In [18, 19] we devised a new approach to determining the dispersion relation which allowed us to find the asymptotic expansion of the dispersion relation as $a\to 0$. The expansions have a form of power series in $a$ which are different for non-exceptional and exceptional wave vectors $\bm{k}$. The expansion depends analytically on $\bm{k}$ when $\bm{k}$ is not exceptional, see a discussion below. To study gaps, we need to develop further these results in the present paper to obtain asymptotics in $a$ which is uniform in $\bm{k}$ in a neighborhood of exceptional points.

As before, we enclose the inclusion $\Omega$ in a ball $B_{R}\subset\Pi$ of radius $R>a$ centered at the origin and split $\Pi$ into the ball $B_{R}$ and its complement $\Pi\smallsetminus B_{R}$ (see Figure 1). Next, we consider the following two problems in these two regions:

where

$\varepsilon$ will be determined below, $u\in H^{2}(B_{R}\smallsetminus\Omega),~v\in H^{2}(\Pi\smallsetminus B_{R})$. The unperturbed problems with $a=\varepsilon=0$ are uniquely solvable for smooth enough $\psi$ for all $R$ except a countable set $\{R_{i}\}$, and we choose $R\notin\{R_{i}$}. Then solutions of (2.1),(2.2) defines two Dirichlet-to-Neumann operators ${\mathsfbfit N}^{-}_{a,\varepsilon}$, ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}$: $H^{3/2}(\partial B_{R})\to H^{1/2}(\partial B_{R})$, i.e.

The existence of a non-trivial solution to the problem (1.3),(1.4) is equivalent to the existence of a zero eigenvalue (EZE) for the operator ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{a,\varepsilon}$. This abbreviation pertains specifically to the operator ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{a,\varepsilon}$. Hence, the dispersion relation is given by (2.3) with $\varepsilon=\varepsilon(a,\bm{k})$ determined from the EZE condition. In [18, 19], the reduction of the dispersion relation to the EZE problem enabled us to use regular perturbation techniques to study dispersion relations for each $\bm{k}$.

Observe that the choice of $R$ and therefore the definition of operators $\mathsfbfit N^{\pm}$ depend on $\bm{k}$. Since $k^{2}$ is an analytic function of $\bm{k}$ and since $R$ is chosen in such a way that the problem (2.2) is uniquely solvable when $\bm{k}=\bm{k}^{\prime}$ is fixed and $\varepsilon=0$, the operator ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}$ is analytic in $\bm{k}$ and $\varepsilon$ when $|\bm{k}-\bm{k}^{\prime}|+|\varepsilon|\ll 1$. We will call this property the local analyticity in $\bm{k}\in{\mathbb{R}}^{3}$ and small $\varepsilon$. Similarly, the operator ${\mathsfbfit N}^{-}_{a,\varepsilon}$ is locally analytic in $\bm{k}$ and small $\varepsilon$. The smoothness of the operator ${\mathsfbfit N}^{-}_{a,\varepsilon}$ in $a$ is not obvious, because problem (2.1) is a singular perturbation of the corresponding problem without the inclusion ($\Omega=\varnothing$), and solutions of (2.1) do not have uniform limits as $a\to 0$. However, the solution of (2.1) is infinitely smooth in $a$ when $a$ is small and ${\bm{x}}$ is outside of a fixed neighborhood of the origin, and it was shown in [18, 19] that the interior DtN operator ${\mathsfbfit N}^{-}_{a,\varepsilon}$ is infinitely differentiable in $a,~a\ll 1$. We summarize these properties in the Lemma.

The Lemma reduces the study of the dispersion relation to the EZE problem for a smooth operator function. Special matrix representations of operators ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon},~{\mathsfbfit N}^{-}_{a,\varepsilon}$ were constructed in [18, 19] that allowed us to solve the EZE problem and find the asymptotics of the dispersion relation $\varepsilon=\varepsilon(a,\bm{k})$ as $a\to 0$ which is analytic in $\bm{k}$ for non-exceptional $\bm{k}$ and is valid for fixed exceptional $\bm{k}$. The gaps are related to exceptional points, and the study of gaps requires a uniform in $\bm{k}$ asymptotics of $\varepsilon(a,\bm{k})$. The main goal of the present paper is to construct a matrix representation of the operator ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{a,\varepsilon}$, allowing to obtain uniform in $\bm{k}$ asymptotics of the dispersion relations near the exceptional points and use them to study the gaps.

The study of the operator ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{a,\varepsilon}$ is simplified if we subtract ${\mathsfbfit N}^{-}_{0,\varepsilon}$ from both terms of the difference above.

This section provides the results from [18, 19] needed to understand the goal and approach of the present paper.

The dispersion surface for the inclusionless ($\Omega=\varnothing,k=|\bm{k}|$) problem (1.3), (1.4) consists of the cone $C_{0}:~\omega=c|\bm{k}|$ and its shifts shown in Fig. 1,2. Since the solutions of (1.3), (1.4) and of the corresponding transmission problem are periodic in $\bm{k}$ and their dispersion surfaces are close to the surface for the inclusionless problem, it is enough to study the dispersion surface of the problems with inclusions only in a small neighborhood of $C_{0}$. The information about other parts of the surface can be obtained simply by the shift in $\bm{k}$. Thus, similar to the approach used in [18, 19], we will assume first that $(\omega,\bm{k})$ is located in a small neighborhood of $C_{0}$.
Non-exceptional wave vectors. Let $\bm{k}$ be a non-exceptional wave vector. Then solution space of the unperturbed problem (1.3),(1.4) ($\Omega=\varnothing,k=|\bm{k}|$) is one-dimensional and consists of functions proportional to $\mathrm{e}^{-\mathrm{i}\bm{k}\cdot{\bm{x}}},~{\bm{x}}\in\Pi$. Respectively, the kernel of the operator ${\mathsfbfit N}^{+}_{\bm{k},0}-{\mathsfbfit N}^{-}_{0,\varepsilon}$ consists of functions proportional to ${\psi^{\prime}}=\mathrm{e}^{-\mathrm{i}\bm{k}\cdot{\bm{x}}},~{\bm{x}}\in\partial B_{R}$ which is the restriction of the exponent on $\partial B_{R}$. We present the domain $H^{\frac{3}{2}}(\partial B_{R})$ and the range $H^{\frac{1}{2}}(\partial B_{R})$ of the operator ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{a,\varepsilon}$ as a direct sum of the one-dimensional space $\mathscr{E}$ of functions proportional to ${\psi^{\prime}}$ and spaces $\mathscr{E}_{\bot,d}$,$\mathscr{E}_{\bot,r}$, respectively, of functions orthogonal in $L^{2}(\partial\Omega)$ to ${\psi^{\prime}}$. Here subindexes “$d$” and “$r$” stay for the domain and the range.

We represent each element $\psi$ in the domain and the range of operator ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{a,\varepsilon}$ in the vector form $\psi=(\psi_{\mathscr{E}},\psi_{\bot}),$ where $\psi_{\mathscr{E}}$ is the projection in $L^{2}(\partial B_{R})$ of the function $\psi$ on ${\psi^{\prime}}$, and $\psi_{\bot}$ is orthogonal to ${\psi^{\prime}}$ in $L^{2}(\partial B_{R})$, and use matrix representation of all the operators in the basis $(\psi_{\mathscr{E}},\psi_{\bot}).$ Due to Green’s formula, the operators ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon},$ ${\mathsfbfit N}^{-}_{a,\varepsilon}$ are symmetric and therefore

where $\bm{A}:\mathscr{E}_{\bot,d}\to\mathscr{E}_{\bot,r}$ is an isomorphism.

Since operator ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{0,\varepsilon}$ depends smoothly on $\varepsilon$, we have

where $C$ is a constant, and $\varepsilon$ is defined in (2.3). In [18] it was shown that $C=2|\bm{k}|^{2}|\Pi|$.

Matrix representation for the interior operator has the form

where $qa$ depends on the shape of $\partial\Omega$ and is equal to its electrical capacitance, i.e. total charge of $\partial\Omega$ when its potential is unity. In particular, $q=1$ for a sphere. Thus

This matrix representation allows one to find $\varepsilon=\varepsilon(a,\bm{k})$ for which the kernel of the operator ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{a,\varepsilon}$ is not empty. Using (3.4), we write the equation $({\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{a,\varepsilon})\psi=0$ in the form

Due to the invertibility of $\bm{A}$, we solve equation above for $\psi_{\perp}:~\psi_{\bot}={\cal O}(a+|\varepsilon|)\psi_{\mathscr{E}}$, and reduce (3.5) to a simple equation for $\psi_{\mathscr{E}}$. This implies that function $\varepsilon(a,\bm{k})$ can be found by equating the top left element in (3.5) with a different remainder term to zero. Thus, the implicit function theorem implies the following statement:

The formula (3.1) remains valid when $\bm{k}=\bm{k}_{0}$ is an exceptional wave vector of order two if zeroes of the matrix on the right-hand side of (3.1) are understood as the zero elements of the first two rows and first two columns of the matrix. In addition, formulas (3.2) and (3.3) remain valid if constants $C$ and $q$ are replaced by $C\bm{I}$ and $q\bm{J}$, respectively, where $\bm{I}$ and $\bm{J}$ are $2\times 2$ identity and all-ones matrices, respectively. The analogue of (3.4) has the following $2\times 2$ block $\bm{S}$ in the top left corner of the matrix:

and therefore, (3.5) now takes the form

The arguments after (3.5) imply that the dispersion relation at $\bm{k}=\bm{k}_{0}$ is defined by the equation $\det{\widetilde{\bm{S}}}=0$ where ${\widetilde{\bm{S}}}$ and $\bm{S}$ have the same asymptotics with different specific values of the remainders. Since the eigenvalues of $\bm{J}$ are distinct, the implicit function theorem can be applied to the equation $\det{\widetilde{\bm{S}}}=0$ for the variable $\varepsilon/a$. This leads to the existence of the following two roots:

In addition, the following important observation was made in [18]: there are no solutions to the problem (1.3),(1.4) with $\bm{k}=\bm{k}_{0}$ propagating in one direction of either vector $\bm{k}_{0}$ or $\bm{k}_{1}$. Each of the Bloch solutions with $\varepsilon=\varepsilon_{i},~i=0,1,$ is a cluster of waves propagating in both directions.

The results concerning non-exceptional points described above are valid for all non-exceptional points. In particular, the function (3.6) is analytic in $\bm{k}$. On the contrary, formulas (3.9) were obtained for fixed exceptional points whose neighborhoods contained mostly non-exceptional points. We need to extend (3.1)-(3.4) in such a way that the corresponding asymptotics would be valid in the neighborhood of fixed wave vector $\bm{k}=\bm{k}_{0}$ of multiplicity two.

We do not consider the whole neighborhood of $\bm{k}_{0}$. It will be sufficient to focus only on the values of $\bm{k}$ that belong to the ray through $\bm{k}_{0}$. Thus $\bm{k}=(1+\delta)\bm{k}_{0}$,  $|\delta|\ll 1$. We will denote this segment by $I$. It contains one exceptional point $\bm{k}=\bm{k}_{0}$, and other points in $I\smallsetminus\bm{k}_{0}$ are non-exceptional if $\delta$ is small enough. Matrix representation (3.1)-(3.4) in the previous section was based on one-dimensional space $\mathscr{E}$ when $\bm{k}\in I\smallsetminus\bm{k}_{0}$ and two-dimensional space $\mathscr{E}$ when $\bm{k}=\bm{k}_{0}$. Our next goal is to obtain the dispersion relation for the entire interval $I$ using the two-dimension space $\mathscr{E}$ spanned by functions $\psi_{0}$ and $\psi_{1}$. This will allow us to obtain the asymptotics of the dispersion relation as $a\to 0$, $\bm{k}\in I$, which is uniform in $\bm{k}$.

We start with a matrix representation of ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{0,\varepsilon}$ for $\bm{k}\in I$ similar to (3.1)-(3.2). As mentioned at the end of the previous section, if $\varepsilon=\delta=0$ then formula (3.1) remains valid for the two-dimensional space $\mathscr{E}$. Since all the operators involved depend infinitely smoothly on small $\varepsilon,\delta$ and the space $\mathscr{E}$ is independent on $\varepsilon,\delta,$ the matrix representation of ${\mathsfbfit N}^{+}_{\bm{k},\varepsilon}-{\mathsfbfit N}^{-}_{0,\varepsilon}$ for sufficiently small $\varepsilon$ and $\delta$ has the form

where $\bm{L}$ is a $2\!\times\!2$ matrix which is linear in $\varepsilon$ and $\delta$, and the entries of the matrix on the right-hand side are infinitely smooth in $\varepsilon$ and $\delta$. The next Lemma reveals the dependence of $\bm{L}$ on $\varepsilon$ and $\delta$.