\newaliascnt

lemmathm \aliascntresetthelemma \newaliascntpropthm \aliascntresettheprop \newaliascntcorthm \aliascntresetthecor \newaliascntwarningthm \aliascntresetthewarning \newaliascntremthm \aliascntresettherem \newaliascntexamplethm \aliascntresettheexample \newaliascntdefinitionthm \aliascntresetthedefinition \newaliascntwarthm \aliascntresetthewar \newaliascntblockthm \aliascntresettheblock \newaliascntconvthm \aliascntresettheconv

Local Newton nondegenerate Weil divisors in toric varieties

András Némethi Alfréd Rényi Institute of Mathematics, ELKH
     Reáltanoda utca 13-15, H-1053, Budapest, Hungary
     ELTE - University of Budapest, Dept. of Geometry, Budapest, Hungary
     BCAM - Basque Center for Applied Math., Mazarredo, 14 E48009 Bilbao, Basque Country, Spain nemethi.andras@renyi.hu and Baldur Sigurðsson Institute of Mathematics,
     18 Đường Hoàng Quốc Việt, Quận Cầu Giấy, 10307, Hanoi, Vietnam baldursigurds@gmail.com

Abstract.

We introduce and develop the theory of Newton nondegenerate local Weil divisors $(X,0)$ in toric affine varieties. We characterize in terms of the toric combinatorics of the Newton diagram different properties of such singular germs: normality, Gorenstein property, or being an Cartier divisor in the ambient space. We discuss certain properties of their (canonical) resolution $\widetilde{X}\to X$ and the corresponding canonical divisor. We provide combinatorial formulae for the delta–invariant $\delta(X,0)$ and for the cohomology groups $H^{i}(\widetilde{X},\mathcal{O}_{\widetilde{X}})$ for $i>0$ . In the case $\dim(X,0)=2$ , we provide the (canonical) resolution graph from the Newton diagram and we also prove that if such a Weil divisor is normal and Gorenstein, and the link is a rational homology sphere, then the geometric genus is given by the minimal path cohomology, a topological invariant of the link.

The first author was partially supported by NKFIH Grant “Élvonal (Frontier)” KKP 126683.

1. Introduction

\theblock.

Hypersurface (or complete intersection) germs with nondegenerate Newton principal part constitute a very important family of singularities. They provide a bridge between toric geometry and the combinatorics of polytopes. The computation of their analytic and topological invariants serve as guiding models for the general cases, and also as testing ground for different general conjectures and ideas.

On the other hand, from the point of view of the general classification theorems in algebraic/analytic geometry and singularity theory, these hypersurface germs are rather restrictive. In particular, it is highly desired to extend such germs to a more general setting. Besides the algebraic/analytic motivations there are also several topological ones too: one has to create a flexible family, which is able to follow at analytic level different inductive (cutting and pasting procedures) of the topology. For example, the link of a surface singularity is an oriented plumbed 3–manifold associated with a graph. In inductive proofs and constructions it is very efficient to consider their splice or JSJ decomposition. This would correspond to cutting the Newton diagram by linear planes though their 1–faces, in this way creating non-regular cones as well, as completely general toric 3–folds as ambient spaces for our germs.

The first goal of the present work is to introduce and develop the theory of Weil divisors in general affine toric varieties with additional Newton nondegeneracy condition. By such extensions we wish to cover non–Gorenstein singularities as well, or germs which are not necessarily Cartier divisors in their canonical ambient toric spaces. In the toric presentation two combinatorial/geometrical packages are needed: the fan and geometry of the ambient toric variety, and the ‘dual fan’ (as a subdivision of the previous one) together with the Newton polytope associated with the equations of the Weil divisor.

In fact, we will focus on three level of invariants.

The first level is the analytic geometry of the abstract or embedded singular germs, e.g. normality, or being Gorenstein or isolated singularity, or being Cartier (or ${\mathbb{Q}}$ –Cartier) in the ambient toric variety. Furthermore, at this level we wish to understand/determine several numerical sheaf–cohomological invarints as well.

The second level is the toric combinatorics. In terms of this we wish to characterize the above analytic properties and provide formulae for the numerical invariants.

The third level appears explicitly in the case of curve and surface singularities. In the case of surfaces we construct the resolution graph (as the plumbing graph of the link, hence as a complete topological invariant). It is always a very interesting and difficult task to decide whether the numerical analytic invariants can be recovered from the resolution graph. (This is much harder than the formulae via the toric combinatorics: the Newton polytope preserves considerably more information from the structure of the equations than the resolution graph.) In the last part we prove that the geometric genus of the resolution can be recovered from the graph. This is a new substantial step in a project which aims to provide topological interpretations for sheaf–cohomological invariants, see [23, 25, 21, 22]

\theblock.

Next we provide some additional concrete comments and the detailed presentation of the sections.

After recalling some notation and results from toric geometry, we generalize the notion of a Newton nondegenerate hypersurface in $\mathbb{C}^{r}$ to an arbitrary Weil divisor in an affine toric variety in section 3. These Newton nondegenerate Weil divisors can be resolved using toric geometry similarly as in the classical case [27], or in a different generalization [4]. In section 4 we consider Newton nondegenerate curves. In section 5 we provide conditions for Newton nondegenerate surface singularities to be isolated, and in section 6 we generalize Oka’s algorithm [27] to construct a resolution of a Newton nondegenerate Weil divisor, along with an explicit description of its resolution graph.

In section 7, we give a formula for the $\delta$ -invariant and dimensions of cohomologies of the structure sheaf on a resolution of a Newton nondegenerate germ in terms of the Newton polyhedron, see theorem 7.1, whose statement should have independent interest. In particular, this yields a formula for the geometric genus. In the classical case, this formula was given by Merle and Teissier in [19, Théorème 2.1.1].

In section 8, we give a formula for a canonical divisor on a resolution of a Newton nondegenerate Weil divisor, as well as the canonical cycle in the surface case, in terms of the Newton diagram, see section 8. This formula generalizes results of Oka [27, §9]. In the surface case, we also prove in section 9 that the Gorenstein property is identified by the Newton polyhedron, theorem 9.1. A similar, but weaker, condition implies that the singularity is $\mathbb{Q}$ -Gorenstein, but is not sufficient, as shown by an example in section 9.

Using the above results, and a technical result verfied in section 11, we generalize a previous result [25] for the classical case of Newton nondegenerate hypersurface singularities in $\mathbb{C}^{3}$ , namely that the geometric genus is determined by a computation sequence, and is therefore topologically determined:

1.1 Theorem.

Let $(X,0)\subset(Y,0)$ be a two-dimensional Newton nondegenerate Weil divisor in the affine toric ambients space $Y$ . Assume that $(X,0)$ is normal and Gorenstein, and that its link is a rational homology sphere. Then the geometric genus $p_{g}(X,0)$ equals the minimal path lattice cohomology associated with the link of $(X,0)$ . In particular, the geometric genus is determined by the topology of $(X,0)$ .

2. Toric preliminaries

In this section, we will recall some definitions and statements from toric geometry. For an introduction, see e.g. [13] and [10].

\theblock.

Let $N$ be a free Abelian group of rank $r\in\mathbb{N}$ and set $M=N^{\vee}=\mathop{\rm Hom}\nolimits(N,\mathbb{Z})$ , as well as $M_{\mathbb{R}}=M\otimes\mathbb{R}$ and $N_{\mathbb{R}}=N\otimes\mathbb{R}$ . If $\sigma\subset N_{\mathbb{R}}$ is a cone, the dual cone is defined as

\sigma^{\vee}=\left\{u\in M_{\mathbb{R}}\,\middle|\,\forall v\in\sigma:\,\langle u,v\rangle\geq 0\right\}.

We also set

\sigma^{\perp}=\left\{u\in M_{\mathbb{R}}\,\middle|\,\forall v\in\sigma:\,\langle u,v\rangle=0\right\}.

We will always assume cones to be finitely generated and rational. To a cone $\sigma\subset N_{\mathbb{R}}$ we associate the semigroup $S_{\sigma}$ , the algebra $A_{\sigma}$ and the affine variety $U_{\sigma}$ by setting

S_{\sigma}=\sigma^{\vee}\cap M,\quad A_{\sigma}=\mathbb{C}[S_{\sigma}],\quad U_{\sigma}=\mathop{\rm Spec}\nolimits(A_{\sigma}).

A variety of the form $U_{\sigma}$ is called an affine toric variety. It has a canonical action of the $r$ -torus $\mathbb{T}^{r}=(\mathbb{C}^{*})^{r}$ .

\theblock.

A fan $\triangle$ in $N$ is a collection of cones in $N_{\mathbb{R}}$ satisfying the following two conditions.

(i)

Any face of a cone in $\triangle$ is in $\triangle$ .
(ii)

The intersection of two cones in $\triangle$ is a face of each of them.

The support of a fan $\triangle$ is defined as $|\triangle|=\cup_{\sigma\in\triangle}\sigma$ . If $\tau,\sigma\in\triangle$ and $\tau\subset\sigma$ , then we get a morphism $U_{\tau}\to U_{\sigma}$ . These morphisms form a direct system, whose limit is denoted by $Y_{\triangle}$ and called the associated toric variety. The actions of $\mathbb{T}^{r}$ on the affine varieties $U_{\sigma}$ for $\sigma\in\triangle$ glue together to form an action on $Y_{\triangle}$ . Note that the canonical maps $U_{\sigma}\to Y_{\triangle}$ are open inclusions (note also that the notation $Y_{\triangle}$ differs from [13]).

Let $\widetilde{\triangle}$ be another fan in a lattice $\widetilde{N}$ and let $\phi:\widetilde{N}\to N$ be a linear map. Assume that for any $\widetilde{\sigma}\in\widetilde{\triangle}$ there is a $\sigma\in\triangle$ so that $\phi(\widetilde{\sigma})\subset\sigma$ . This induces maps $U_{\widetilde{\sigma}}\to U_{\sigma}\to Y_{\triangle}$ , which glue together to form a map $Y_{\widetilde{\triangle}}\to Y_{\triangle\vphantom{\widetilde{\triangle}}}$ .

\thelemma Lemma (Proposition, p. 39, [13]).

Let $\widetilde{\triangle}$ and $\triangle$ be fans as above. The induced map $Y_{\widetilde{\triangle}}\to Y_{\triangle\vphantom{\widetilde{\triangle}}}$ is proper if and only if $\phi^{-1}(|\triangle|)=|\widetilde{\triangle}|$ .

\theblock.

For any $p\in M$ , there is an associated rational function on $U_{\sigma}$ . These glue together to form a rational function $x^{p}$ on $Y_{\triangle}$ . We refer to these functions as monomials. A monomial $x^{p}$ is a regular function on $Y_{\triangle}$ if $p\in|\triangle|^{\vee}=\cap_{\sigma\in\triangle}\sigma^{\vee}$ . A map $\phi:\widetilde{N}\to N$ as above induces $\phi^{*}:M\to\widetilde{M}$ . The monomial $x^{p}$ on $Y_{\triangle}$ then pulls back to $x^{\phi^{*}(p)}$ .

\theblock.

For $\sigma\in\triangle$ , let $O_{\sigma}$ be the closed subset of $U_{\sigma}$ defined by the ideal generated by monomials $x^{p}$ where $p\in(\sigma^{\vee}\setminus\sigma^{\perp})\cap M$ . We identify this set with its image in $Y_{\triangle}$ . The closure of $O_{\sigma}$ in $Y_{\triangle}$ is denoted by $V(\sigma)$ . In the case when $\sigma$ is a ray, $V(\sigma)$ is a Weil divisor and we write $D_{\sigma}=V(\sigma)$ . The orbits of the $\mathbb{T}^{r}$ action on $Y_{\triangle}$ are precisely the sets $O_{\sigma}$ for $\sigma\in\triangle$ . Furthermore, we have (as sets)

U_{\sigma}=\coprod_{\tau\subset\sigma}O_{\tau},\quad V(\sigma)=\coprod_{\sigma\subset\tau}O_{\tau},\quad O_{\sigma}=V(\sigma)\setminus\bigcup_{\sigma\subsetneq\tau}V(\tau).

Let $N_{\sigma}$ be the subgroup of $N$ generated by $\sigma\cap N$ and define

N(\sigma)=N/N_{\sigma},\quad M(\sigma)=\sigma^{\perp}\cap M,\quad M_{\sigma}=M/M(\sigma).

Note that this way we have $M_{\sigma}^{\phantom{\vee}}\cong N_{\sigma}^{\vee}$ and $M(\sigma)\cong N(\sigma)^{\vee}$ . Let $\pi_{\sigma}:N_{\mathbb{R}}\to N_{\mathbb{R}}(\sigma)$ be the canonical projection and set

\mathop{\rm Star}\nolimits(\sigma)=\left\{\pi_{\sigma}(\tau)\,\middle|\,\sigma\subset\tau\in\triangle\right\}.

This set is a fan in $N(\sigma)$ , whose associated toric variety is identified canonically with the orbit closure $V(\sigma)$ . Similarly, let $\varpi_{\sigma}:M\to M_{\sigma}$ be the canonical projection. Assuming $\sigma\in\triangle$ has dimension $s$ , we have $(U_{\sigma},O_{\sigma})\cong(Y_{\sigma}\times(\mathbb{C}^{*})^{r-s},(\{0\}\times(\mathbb{C}^{*})^{r-s})$ . In particular, $O_{\sigma}\subset Y_{\triangle}$ has $Y_{\sigma}$ as a transverse type.

\thedefinition Definition.

(i)

For a cone $\Sigma\subset N_{\mathbb{R}}$ , let $\triangle_{\Sigma}$ denote the fanfan consisting of all the faces of $\Sigma$ . We also write $Y_{\Sigma}$ instead of $Y_{\triangle_{\Sigma}}$ .
(ii)

If $\triangle$ is a fan and $i\in\mathbb{N}$ , define

$\triangle^{(i)}=\left\{\sigma\in\triangle\,\middle|\,\dim\sigma=i\right\}.$
(iii)

A regular cone (resp. simplicial cone) is a cone generated by a subset of an integral (resp. rational) basis of $N$ .
(iv)

A subdivision of a fan $\triangle$ is a fan $\widetilde{\triangle}$ so that $|\widetilde{\triangle}|=|\triangle|$ and each cone in $\triangle$ is a union of cones in $\widetilde{\triangle}$ . A regular subdivision is a subdivision consisting of regular cones.
(v)

If $\Sigma\subset N_{\mathbb{R}}$ is a cone and $\triangle$ is a subdivision of $\triangle_{\Sigma}$ , denote by $\triangle^{*}$ the fan consisting of $\sigma\in\triangle$ for which $\sigma\subset\partial\Sigma$ . Here we see $\partial\Sigma$ as the union of the proper faces of $\Sigma$ . As a result, $\triangle^{*}$ is a subdivision of the fan $\triangle_{\Sigma}\setminus\{\Sigma\}$ .
(vi)

Let $\triangle_{1},\triangle_{2}$ be subdivisions of a fan $\triangle$ . We say that $\triangle_{2}$ refines $\triangle_{1}$ if $\triangle_{2}$ is a subdivision of $\triangle_{1}$ , or that $\triangle_{2}$ is a refinement of $\triangle_{1}$ .
(vii)

Let $\triangle$ be a fan with a subdivision $\triangle_{1}$ and let $\sigma\in\triangle$ . The restriction of $\triangle_{1}$ to $\sigma$ is defined as

$\triangle_{1}|_{\sigma}=\left\{\tau\in\triangle_{1}\,\middle|\,\tau\subset\sigma\right\}.$

3. Analytic Weil divisors in affine toric varieties

\theblock.

Throughout this section, as well as the following sections, we will assume that $N$ has rank $r$ and that $\Sigma$ is an $r$ -dimensional, rational, finitely generated, strictly convex cone in $N_{\mathbb{R}}$ . This means that $\Sigma\subset N_{\mathbb{R}}$ is generated over $\mathbb{R}_{\geq 0}$ by a finite set of elements from $N$ , which generate $N$ as a vectorspace, and that $\Sigma^{\perp}=\{0\}$ . In particular, the orbit $O_{\Sigma}$ consists of a single point, which we denote by $0$ , and refer to as the origin. Let $Y_{\Sigma}$ be the affine toric variety associated with $\Sigma$ .

Any subdivision $\triangle$ of $\triangle_{\Sigma}$ induces a modification $\pi_{\triangle}:Y_{\triangle}\to Y_{\Sigma}$ .

In the sequel we denote by $(Y_{\Sigma},0)$ the analytic germ of $Y_{\Sigma}$ at 0, and usually we will denote by $Y$ a (small Stein) representative of $(Y_{\Sigma},0)$ . (Hence $(Y,0)=(Y_{\Sigma},0)$ .) If $\pi_{\Delta}$ is a toric modification, in the discussions regarding the local analytic germ $(Y,0)$ , we will use the same notation $Y_{\Delta}$ for $\pi_{\Delta}^{-1}(Y)$ and $D_{\sigma}$ for $D_{\sigma}\cap\pi_{\Delta}^{-1}(Y)$ . Similarly, $O_{\sigma}$ might stay for $O_{\sigma}\cap Y\subset Y$ as well. If in some argument we really wish to stress the differences, we write $Y^{loc}_{\Delta}$ , $D^{loc}_{\sigma}$ , $O^{loc}_{\sigma}$ for the local objects.

Assume that $f\in\mathcal{O}_{Y,0}$ is the germ of a holomorphic function at the origin, which has an expansion

(3.1)

f(x)=\sum_{p\in S_{\Sigma}}a_{p}x^{p},\quad a_{p}\in\mathbb{C}.

Then $(\{f=0\},0)\subset(Y,0)$ is the germ of an analytic space. We set $\mathop{\rm supp}\nolimits(f)=\left\{p\in S_{\Sigma}\,\middle|\,a_{p}\neq 0\right\}$ too.

\thedefinition Definition.

The Newton polyhedron of $f$ with respect to $\Sigma$ is the polyhedron

\Gamma_{+}(f)=\mathop{\rm conv}\nolimits(\mathop{\rm supp}\nolimits(f)+\Sigma^{\vee}),

where $\mathop{\rm conv}\nolimits$ denotes the convex closure in $M_{\mathbb{R}}$ . The union of compact faces of $\Gamma_{+}(f)$ is denoted by $\Gamma(f)$ and is called the Newton diagram of $f$ with respect to $\Sigma$ .

\theblock.

The fan $\triangle_{f}$ and some combinatorial properties. It follows from definition that $\Sigma$ is precisely the set of those linear functions on $M_{\mathbb{R}}$ having a minimal value on $\Gamma_{+}(f)$ . Denote by $F(\ell)$ the minimal set of $\ell\in\Sigma$ on $\Gamma_{+}(f)$ . For $\ell_{1},\ell_{2}\in\Sigma$ , say that $\ell_{1}\sim\ell_{2}$ if and only if $F(\ell_{1})=F(\ell_{2})$ . Then $\sim$ is an equivalence relation on $\Sigma$ having finitely many equivalence classes, each of whose closure is a finitely generated rational strictly convex cone. These cones form a fan, which we will denote by $\triangle_{f}$ . We refer to $\triangle_{f}$ as the dual fan associated with $f$ and $\Sigma$ . Note that $\triangle_{f}$ refines $\triangle_{\Sigma}$ .

For any $\sigma\in\triangle_{f}$ , the face $F(\ell)$ is independent of the choice of $\ell\in\sigma^{\circ}$ , where $\sigma^{\circ}\subset\sigma$ is the relative interior, that is, the topological interior of $\sigma$ as a subset of $N_{\sigma,\mathbb{R}}$ . For $\sigma\in\triangle_{f}^{(1)}$ , the set $\sigma\cap N$ is a semigroup generated by a unique element, which we denote by $\ell_{\sigma}$ . For a series

g\in\mathcal{O}_{Y,0}[x^{M}]=\left\{x^{p}h\,\middle|\,p\in M,\,h\in\mathcal{O}_{Y,0}\right\},

the support $\mathop{\rm supp}\nolimits(g)$ is defined similarly as above, and for $\sigma\in\triangle_{f}^{(1)}$ we set

\mathop{\rm wt}\nolimits_{\sigma}(g)=\min\left\{\ell_{\sigma}(p)\,\middle|\,p\in\mathop{\rm supp}\nolimits(g)\right\}.

One verifies that for any such $g$

(3.2)

\mbox{the vanishing order of $g$ along $D_{\sigma}\subset Y_{\triangle_{f}}$ is exactly $\mathop{\rm wt}\nolimits_{\sigma}(g)$}.

\thedefinition Definition.

Let $\sigma\in\triangle_{f}$ and $\ell\in\sigma^{\circ}$ . Define

F_{\sigma}=F(\ell),\quad f_{\sigma}=\sum_{p\in F_{\sigma}}a_{p}x^{p}.

If $\sigma^{\prime}\subset N_{\mathbb{R}}$ is a cone, and $\sigma^{\prime\circ}\subset\sigma^{\circ}$ (for example, if $\sigma^{\prime}$ is an element of a refinement of $\triangle_{f}$ ), then we set $F_{\sigma^{\prime}}=F_{\sigma}$ .

If $\sigma\subset\Sigma$ is one dimensional, set $m_{\sigma}=\mathop{\rm wt}\nolimits_{\sigma}(f)$ . Thus, $\ell_{\sigma}|_{F_{\sigma}}\equiv m_{\sigma}$ . Note that we have

\Gamma_{+}(f)=\left\{u\in M_{\mathbb{R}}\,\middle|\,\forall\sigma\in\triangle_{f}^{(1)}:\,\ell_{\sigma}(u)\geq m_{\sigma}\right\}.

This can be compared with the following set.

\thedefinition Definition.

Let

\Gamma_{+}^{*}(f)=\left\{u\in M_{\mathbb{R}}\,\middle|\,\forall\sigma\in\triangle_{f}^{*(1)}:\,\ell_{\sigma}(u)\geq m_{\sigma}\right\},

where $\triangle_{f}^{*(1)}$ denotes the set of rays in $\triangle_{f}$ contained in the boundary of $\Sigma$ .

\thedefinition Definition.

Denote by $(X,0)\subset(Y,0)$ the union of those local primary components of the germ defined by $f$ (with their non-reduced structure), which are not invariant by the torus action. If $f$ is reduced along the non-invariant components, this means the following. Let $U\subset Y$ be a neighbourhood of the origin on which $f$ converges and let $X^{\prime}\subset U$ be defined by $f=0$ . Then $X$ is the closure of $X^{\prime}\setminus\cup\left\{D_{\sigma}\,\middle|\,\sigma\in\triangle_{\Sigma}^{(1)}\right\}$ in $U$ .

\therem Remark.

(i) For any $p\in M$ , the function $x^{p}f$ defines the same germ $(X,0)$ . Thus, we may allow $f\in\mathcal{O}_{Y,0}[x^{M}]=\left\{x^{p}g\,\middle|\,p\in M,\,g\in\mathcal{O}_{Y,0}\right\}$ as well.

(ii) Since the divisors $\{D_{\sigma}\,:\,\sigma\in\triangle_{\Sigma}^{(1)}\}$ are torus-invariant, the divisor of $f$ in $Y_{\Sigma}$ is $X+\sum_{\sigma}m_{\sigma}D_{\sigma}$ .

\theprop Proposition.

(i)

We have $\Gamma_{+}(f)=p+\Sigma^{\vee}$ for some $p\in M$ if and only if $\triangle_{f}=\triangle_{\Sigma}$ if and only if the germ $X$ at $0$ is the empty germ.
(ii)

For a $\sigma\in\triangle_{\Sigma}$ , we have $O_{\sigma}\subset X$ if and only if the normal fan $\triangle_{f}$ subdivides $\sigma$ into smaller cones, i.e. $\triangle_{f}|_{\sigma}\neq\triangle_{\sigma}$ .
(iii)

The ideal $I_{X}\subset\mathcal{O}_{Y,0}$ which defines $(X,0)$ in $(Y,0)$ , is generated by the functions $x^{p}f$ for $p\in M$ satisfying $\ell_{\sigma}(p)+m_{\sigma}\geq 0$ for all $\sigma\in\triangle^{(1)}_{\Sigma}$ .

Proof.

Statement i is clear, since $\Gamma_{+}(f)$ is of the form $p+\Sigma^{\vee}$ if and only if $f$ is a product of a monomial and a unit in $\mathcal{O}_{Y,0}$ .

Statement ii follows from i, and the fact that the intersection of $X$ and a generic transverse space $Y_{\sigma}$ to $O_{\sigma}$ has Newton polygon $\varpi_{\sigma}(\Gamma(f))$ , cf. section 2.

iii Assuming the given conditions on $p$ , the function $x^{p}f$ is meromorphic and has no poles. Since $Y$ is normal, $x^{p}f$ is analytic and vanishes on $X$ . As a result, $x^{p}f\in I_{X}$ .

To show that these generate $I_{X}$ , take $g\in I_{X}$ . We must show that $g=hf$ , with $h\in\mathcal{O}_{Y,0}[x^{M}]$ and $\ell_{\sigma}(p)+m_{\sigma}\geq 0$ for $p\in\mathop{\rm supp}\nolimits(h)$ .

Let $I_{X,M}$ be the localization of $I_{X}$ along the invariant divisors, that is, the ideal of meromorphic function germs on $(Y,0)$ , regular on the open torus and vanishing on $X$ . It follows that $I_{X,M}=f\cdot\mathcal{O}_{Y,0}[x^{M}]$ and $I_{X}=I_{X,M}\cap\mathcal{O}_{Y,0}$ .

Thus, $g=x^{r}hf$ for some $h\in\mathcal{O}_{Y,0}$ and $r\in M$ . Then, there exist finite families $(h_{i})_{i}$ of units in $\mathcal{O}_{Y,0}$ and exponents $(p_{i})_{i}$ in $M$ so that $x^{r}h=\sum_{i}x^{p_{i}}h_{i}$ and the support of $x^{r}h$ is the disjoint union of the supports of $x^{p_{i}}h_{i}$ . Let us take any $\sigma\in\triangle^{(1)}_{\Sigma}$ . The condition on disjointness of supports gives

\min_{i}\mathop{\rm wt}\nolimits_{\sigma}x^{p_{i}}h_{i}f=\mathop{\rm wt}\nolimits_{\sigma}x^{r}hf=\mathop{\rm wt}\nolimits_{\sigma}g\geq 0.

As a result, we have $\ell_{\sigma}(p_{i})+m_{\sigma}\geq 0$ for all $i$ . The result follows. ∎

\thedefinition Definition.

Let $f$ and $\triangle_{f}$ be as above. We say that $\Gamma_{+}(f)$ , or $f$ , is ( $\mathbb{Q}$ -)pointed if there exists a $p\in M$ ( $p\in M_{\mathbb{Q}})$ such that $\ell_{\sigma}(p)=m_{\sigma}$ for all $\sigma\in\triangle_{\Sigma}^{(1)}$ .

\theprop Proposition.

(i)

If $\Sigma$ is regular (resp. simplicial), then any Newton polyhedron (w.r.t. $\Sigma$ ) is pointed at some $p\in M$ (resp. $p\in M_{\mathbb{Q}}$ ).
(ii)

$f$ is pointed at $p\in M$ if and only if $(X,0)$ in $(Y,0)$ is defined by a single equation $x^{-p}f$ (cf. section 3). In other words, $f$ is pointed if and only if $(X,0)$ is a Cartier divisor in $(Y,0)$ .
(iii)

$f$ is pointed at $p\in M_{\mathbb{Q}}$ if and only if $(X,0)$ is a $\mathbb{Q}$ -Cartier divisor in $(Y,0)$ .

Proof.

(i) Use the fact that $\{\ell_{\sigma}\,:\,\sigma\in\triangle_{\Sigma}^{(1)}\}$ is an integral (resp. rational) basis.

(ii) If $f$ is pointed at $p\in M$ then by section 3, $x^{-p}f\in I_{X}$ . Moreover, if $x^{-q}f\in I_{X}$ for some $q\in M$ , then $\ell_{\sigma}(p-q)\geq 0$ for any $\sigma\in\triangle_{\Sigma}^{(1)}$ , hence $p-q\in\Sigma\cap M$ and $x^{p-q}\in\mathcal{O}_{Y,0}$ .

Conversely, assume that $(X,0)\subset(Y,0)$ is an (analytic) Cartier divisor. Let $\widetilde{\triangle}_{f}$ be a smooth subdivision of $\triangle_{f}$ , and set $\widetilde{Y}=Y_{\widetilde{\triangle}_{f}}$ . This is a smooth variety, and the map $\pi:\widetilde{Y}\to Y_{\Sigma}$ is a resolution of $Y$ . Take a small Stein representative $Y^{\rm loc}\subset Y$ , and set $\widetilde{Y}^{\rm loc}=\pi^{-1}(Y^{\rm loc})$ . Then we have the vanishing $H^{\geq 1}(\widetilde{Y},\mathcal{O}_{\widetilde{Y}})=0$ (see e.g. [13, Corrollary, p. 74] or [10, §8.5]), and also its local analogue $H^{\geq 1}(\widetilde{Y}^{\rm loc},\mathcal{O}_{\widetilde{Y}^{\rm loc}})=0$ (since the local analytic germ $(Y,0)$ is rational too). Thus, from the exponential exact sequence, $\mathop{\rm Pic}\nolimits(\widetilde{Y})=H^{2}(\widetilde{Y},\mathbb{Z})$ and $\mathop{\rm Pic}\nolimits(\widetilde{Y}^{\rm loc})=H^{2}(\widetilde{Y}^{\rm loc},\mathbb{Z})$ . On the other hand, $Y$ is weighted homogeneous (as any affine toric variety), hence $H^{2}(\widetilde{Y},\mathbb{Z})=H^{2}(\widetilde{Y}^{\rm loc},\mathbb{Z})$ . In particular, $\mathop{\rm Pic}\nolimits(\widetilde{Y})\cong\mathop{\rm Pic}\nolimits(\widetilde{Y}^{\rm loc})$ . Here the first group is the Picard group of the algebraic variety, while the second one is the Picard group of the analytic manifold.

Next, consider the Chow group $A_{r-1}(Y)$ of codimension one, i.e. the group freely generated by Weil divisors, modulo linear equivalence. Note that since $\widetilde{Y}$ is smooth, we have $A_{r-1}(\widetilde{Y})\cong\mathop{\rm Pic}\nolimits(\widetilde{Y})$ and $A_{r-1}(\widetilde{Y}^{\rm loc})\cong\mathop{\rm Pic}\nolimits(\widetilde{Y}^{\rm loc})$ . If we factor these isomorphic groups by the subgroups generated by the exceptional divisors, we find that the restriction induces an isomorphism $A_{r-1}(Y)\cong A_{r-1}(Y^{\rm loc})$ .

Denote by $D^{\rm loc}_{\sigma}$ the restriction image of $D_{\sigma}$ under the above isomorphism. Since $(X,0)\subset(Y,0)$ is local analytic Cartier, and the local divisor of $f$ in $Y$ is $X+D^{\rm loc}_{f}$ , where $D^{\rm loc}_{f}=\sum_{\sigma\in\triangle_{\Sigma}^{(1)}}m_{\sigma}D^{\rm loc}_{\sigma}$ , we find that the class of $D^{\rm loc}_{f}$ is zero in $A_{r-1}(Y^{\rm loc})$ . But then, by the above isomorphisms, the class of $D_{f}=\sum_{\sigma\in\triangle_{\Sigma}^{(1)}}m_{\sigma}D_{\sigma}$ is zero in $A_{r-1}(Y)$ .

Finally note that $A_{r-1}(Y)$ can be computed as follows [13, 3.4]. Consider the group $\mathop{\rm Div}\nolimits_{\mathbb{T}}(Y)=\mathbb{Z}\left\langle D_{\sigma}\,\middle|\,\sigma\in\triangle_{\Sigma}\right\rangle$ of invariant divisors and the inclusion $M\hookrightarrow\mathop{\rm Div}\nolimits_{\mathbb{T}}(Y)$ sending $p\in M$ to $\sum_{\sigma}\ell_{\sigma}(p)D_{\sigma}$ . Along with the map $\mathop{\rm Div}\nolimits_{\mathbb{T}}\to A_{r-1}(Y)$ , this gives a short exact sequence

0\to M\to\mathop{\rm Div}\nolimits_{\mathbb{T}}(Y)\to A_{r-1}(Y)\to 0.

Since $D_{f}\in A_{r-1}(Y)$ maps to zero in $A_{r-1}(Y^{\rm loc})$ under the above isomorphism, and $D_{f}\in\mathop{\rm Div}\nolimits_{\mathbb{T}}(Y)$ , we find that $D_{f}$ is in the image of $M$ . But this means exactly that there exists $p\in M$ such that $\ell_{\sigma}(p)=m_{\sigma}$ for all $\sigma\in\triangle^{(1)}_{\Sigma}$ .

(iii) Use part (ii) for a certain power of $f$ . ∎

\thedefinition Definition.

We say that $f$ has Newton nondegenerate principal part with respect to $\Sigma$ (or simply that $f$ or $(X,0)$ is Newton nondegenerate) if for every $\sigma\in\triangle_{f}$ with $F_{\sigma}$ compact, the variety $\mathop{\rm Spec}\nolimits(\mathbb{C}[M]/(f_{\sigma}))$ (that is, $\left\{x\in\mathbb{T}^{r}\,\middle|\,f_{\sigma}(x)=0\right\}$ with its non-reduced structure) is smooth. Note that $f_{\sigma}$ is a polynomial since $F_{\sigma}$ is compact.

\thelemma Lemma.

Assume that $(X,0)\subset(Y,0)$ is Newton nondegenerate and let $\sigma\in\triangle_{\Sigma}$ . If $O_{\sigma}\subset X$ , then the generic transverse type of $X$ to $O_{\sigma}$ is a Newton nondegenerate singularity with Newton polyhedron $\varpi_{\sigma}(\Gamma_{+}(f))\subset M_{\sigma}$ .

Proof.

The statement follows by restricting $f$ to a toric subspace transverse to $O_{\sigma}$ , see section 2. ∎

\theblock.

The fan $\widetilde{\triangle}_{f}$ and the associated resolution. Assume that $f$ is Newton nondegenerate. Let $\widetilde{\triangle}_{f}$ be a regular subdivision of $\triangle_{f}$ . Then $\widetilde{Y}=Y_{\widetilde{\triangle}_{f}}$ is a smooth variety, and we have a modification $\pi:\widetilde{Y}\to Y$ . As a result of the nondegeneracy of $f$ , the strict transform $\widetilde{X}$ of $X$ in $\widetilde{Y}$ intersects all orbits in $\widetilde{Y}$ smoothly. In particular, $\widetilde{X}$ is smooth, and $\pi$ is an embedded resolution of $(X,0)\subset(Y,0)$ .

\thelemma Lemma.

Assume $(X,0)\subset(Y,0)$ is a Newton nondegenerate Weil divisor. Then, the singular locus of the germ $(X,0)$ is contained in the union of codimension $\geq 2$ orbits in $(Y,0)$ .

Proof.

Let $Y^{(\leq r-2)}$ be the union of orbits of dimension $\leq r-2$ , that is, codimension $\geq 2$ , in $Y$ . Let $\pi:\widetilde{Y}\to Y$ be as in section 3. The restriction $\pi^{-1}(Y\setminus Y^{(\leq r-2)})\to Y\setminus Y^{(\leq r-2)}$ is an isomorphism, and $\widetilde{X}$ is smooth. Therefore, $X\setminus Y^{(\leq r-2)}$ is smooth. ∎

4. Newton nondegenerate curve singularities

In this section, we will assume that $\mathop{\mathrm{rk}}N=2$ and that $\Sigma\subset N_{\mathbb{R}}$ is a two dimensional finitely generated strictly convex rational cone. Nondegenerate rank 2 singularities appear naturally in the $r=3$ case as transversal types of certain orbits.

We will introduce the canonical subdivision and we establish criterions for irreducibility and smoothness. They will be used in the context of rank $r=3$ cones in the definition of their canonical subdivision and in the characterization of Newton nondegenerate isolated surface singularities.

\theblock.

Canonical primitive sequence. Assume first that $\Sigma$ is nonregular. Then there exists a sequence of vectors $\ell_{0},\ldots,\ell_{s+1}\in\Sigma\cap N$ , called the canonical primitive sequence [27] and integers $b_{1},\ldots,b_{s}\geq 2$ , called the associated selfintersection numbers, so that:

(i)

If $0\leq j\leq s$ , then $\ell_{j},\ell_{j+1}$ form an integral basis for $N$ .
(ii)

If $0<j\leq s$ , then $b_{j}\ell_{j}=\ell_{j-1}+\ell_{j+1}$ .
(iii)

The set $\{\ell_{0},\ldots,\ell_{s+1}\}$ is a minimal set of generators for the semigroup $\Sigma\cap N$ .

This data is uniquely determined up to reversing the order of $(\ell_{j})_{j}$ and $(b_{j})_{j}$ . It can, in fact, be determined as follows. Let $\alpha$ be the absolute value of the determinant of the $2\times 2$ matrix whose columns $\ell,\ell^{\prime}$ are the primitive generators of the one dimensional faces of $\Sigma$ , given in any integral basis. Then, there exists a unique integer $0\leq\beta<\alpha$ so that $\beta\ell+\ell^{\prime}\in\alpha N$ . The selfintersection numbers are determined as the negative continued fraction expansion

\frac{\alpha}{\beta}=b_{1}-\frac{1}{b_{2}-\ddots-\frac{1}{b_{s}}}.

We use the notation $[b_{1},\ldots,b_{s}]$ for the right hand side above. We have

\ell_{0}=\ell,\quad\ell_{1}=\frac{\beta\ell+\ell^{\prime}}{\alpha}.

Along with condition (ii), this determines the canonical primitive sequence recursively and we have $\ell_{s+1}=\ell^{\prime}$ .

Refer to caption — Figure 1. In this example, $\Sigma$ is generated by $(0,1)$ and $(5,3)$ . The canonical primitive sequence consists of four elements, including the generators of the cone.

Alternatively, the vectors $\ell_{0},\ell_{1},\ldots,\ell_{s+1}$ are the integral points lying on compact faces of the convex closure of the set $\Sigma\cap N\setminus\{0\}$ . For a detailed discussion of this construction, see [26, 1.6].

If $\Sigma$ is regular, then we prefer to modify the minimality of the resolution considered above, and set $s=1$ , $\ell_{1}=\ell$ and $\ell_{2}=\ell^{\prime}$ and $\ell_{1}=\ell_{0}+\ell_{2}$ . Accordingly, in item (ii), we will have $-b_{1}=-1$ . In particular, the set $\{\ell_{0},\ell_{1},\ell_{2}\}$ is not a minimal set of generators of the semigroup $\Sigma\cap N$ . We make this choice here mostly for technical reasons (directed by properties of the induced reslution), which will appear in section 10. The same choice is made in [27], Definition (3.5).

\thedefinition Definition.

Let $\Sigma$ be a two dimensional rational strictly convex cone with a canonical primitive sequence $\ell_{0},\ell_{1},\ldots,\ell_{s+1}$ . The canonical subdivision of $\triangle_{\Sigma}$ is the unique subdivision $\widetilde{\triangle}_{\Sigma}$ for which

\widetilde{\triangle}_{\Sigma}^{(1)}=\left\{\mathbb{R}_{\geq 0}\langle\ell_{i}\rangle\,\middle|\,0\leq i\leq s+1\right\}.

For each $i=1,\ldots,s$ , there is a unique number $-b_{i}\in\mathbb{Z}_{\leq-1}$ satisfying $\ell_{i-1}-b_{i}\ell_{i}+\ell_{i+1}=0$ . We define $\alpha(\ell_{0},\ell_{s+1})$ and $\beta(\ell_{0},\ell_{s+1})$ as the numerator and denominator, respectively, of the negative continued fraction

[b_{1},\ldots,b_{s}]=b_{1}-\frac{1}{b_{2}-\frac{1}{\cdots}},

(we require $\gcd(\alpha(\ell_{0},\ell_{s+1}),\beta(\ell_{0},\ell_{s+1}))=1$ , and $\beta(\ell_{0},\ell_{s+1})\geq 0$ , so that these numbers are well defined). The number $\alpha(\ell_{0},\ell_{s+1})$ is referred to as the determinant of $\Sigma$ .

\therem Remark.

Let $\ell_{1},\ell_{2}\in N$ be two linearly independent elements. Then we have $\alpha(\ell_{1},\ell_{2})=1$ if and only if $\ell_{1},\ell_{2}$ form part of an integral basis of $N$ . In general, $\alpha=\alpha(\ell_{1},\ell_{2})$ can be computed as the content of the restriction of $\ell_{2}$ to the kernel of $\ell_{1}$ . In other words, let $K\subset N$ be the kernel of $\ell_{1}$ . Then $\ell_{2}|_{K}$ is divisible by $\alpha$ , and $(\ell_{2}|_{K})/\alpha$ is primitive.

\thelemma Lemma.

If $\Sigma$ is not a regular cone, then $Y_{\Sigma}$ has a cyclic quotient singularity at the origin and the map $Y_{\widetilde{\triangle}_{\Sigma}}\to Y_{\Sigma}$ induced by the identity map on $N$ is the minimal resolution.

Proof.

See Proposition 1.19 and Proposition 1.24 of [26]. ∎

\theprop Proposition.

Assume that $\mathop{\mathrm{rk}}N=2$ , and that $f$ is Newton nondegenerate with respect to $\Sigma\subset N_{\mathbb{R}}$ defining a germ $(X,0)$ .

(i)

The germ $(X,0)$ is irreducible if and only if $\Gamma(f)$ is a single interval with no integral interior points. In fact, in general, the number of components in $(X,0)$ is precisely the combinatorial length of $\Gamma(f)$ .
(ii)

Assume that $(X,0)$ is irreducible and let $\sigma\in\triangle_{f}^{(1)}$ so that $\Gamma(f)=F_{\sigma}$ . Then $(X,0)$ is smooth if and only if $\ell_{\sigma}$ lies on the boundary of the convex hull of the set $\Sigma^{\circ}\cap N$ . In other words, let $\ell_{0},\ldots,\ell_{s+1}$ be the canonical primitive sequence of $\Sigma$ . Then either $\ell_{\sigma}$ is one of $\ell_{1},\ldots,\ell_{s}$ , or there is an $a\in\mathbb{Z}_{>0}$ such that either

$\ell_{\sigma}=a\ell_{0}+\ell_{1}\quad or\quad\ell_{\sigma}=a\ell_{s+1}+\ell_{s}.$
(iii)

The curve $(X,0)$ is smooth if and only if the following condition holds: If $p\in M$ and $\ell_{\sigma}(p)>m_{\sigma}$ for all $\sigma\in\triangle_{\Sigma}^{(1)}$ , then $\ell_{\sigma}(p)>m_{\sigma}$ for all $\sigma\in\triangle_{f}^{(1)}$ .

\therem Remark.

One can ask why the vectors $\ell_{0}$ and $\ell_{s+1}$ do not appear in the list of (ii). The answer is that the corresponding divisors $D_{\sigma}$ , though they intersect $E$ transversaly, they are $\mathbb{T}$ –invariant, hence they are eliminated by the convention of the definition 3.6.

Proof of section 4.

We start with the following observations. Write $\sigma_{i}=\mathbb{R}_{\geq 0}\langle\ell_{i}\rangle$ . Let $\triangle^{\prime}$ be a regular subdivision of $\triangle_{\Sigma}$ which refines both $\triangle_{f}$ and the canonical subdivision of $\triangle_{\Sigma}$ . The map $Y_{\triangle^{\prime}}\to Y_{\Sigma}$ is then a resolution of $Y_{\Sigma}$ with exceptional divisor $E^{\prime}$ . We can write $E^{\prime}=\cup_{i=1}^{s^{\prime}}E^{\prime}_{i}$ , where each $E_{i}^{\prime}$ is a rational curve. Furthermore, if $i\neq j$ , then $E_{i}^{\prime}$ and $E_{j}^{\prime}$ intersect if and only if $|i-j|=1$ . In fact, we can write

\triangle^{\prime(1)}=\{\sigma_{1}^{\prime},\ldots,\sigma_{s^{\prime}}^{\prime}\}\cup\{\sigma,\tau\}

where $\sigma,\tau$ are the two faces of $\Sigma$ and $E_{i}^{\prime}=V(\sigma_{i}^{\prime})$ .

Similarly as in [27], we see that $Y_{\triangle^{\prime}}$ resolves $(X,0)$ and that the strict transform $X^{\prime}$ of $X$ in $Y_{\triangle^{\prime}}$ intersects the exceptional divisor $E^{\prime}$ transversally in smooth points of $E^{\prime}$ . In fact, these intersection points lie in the open orbit $O_{\sigma_{i}^{\prime}}\subset E^{\prime}_{i}$ . Therefore, we have (see [27, Theorem 5.1])

|X^{\prime}\cap E^{\prime}_{i}|=\chi(X^{\prime}\cap O_{\sigma^{\prime}_{i}})=\mathop{\rm Vol}\nolimits_{1}(F(\ell_{i}^{\prime}))

where $\ell_{i}^{\prime}$ is the primitive generator of $\sigma_{i}^{\prime}$ . Now, the components of $(X,0)$ are in bijection with the intersection points $X^{\prime}\cap E^{\prime}$ , which proves (i).

For (ii), let $\widetilde{\triangle}_{\Sigma}$ be the canonical subdivision, and $\pi:\widetilde{Y}\to Y$ the associated modification, which is a resolution of $Y$ . Let $\widetilde{X}\subset\widetilde{Y}$ be the strict transform of $X$ . The minimal cycle of the resolution $\widetilde{Y}\to Y$ is the reduced exceptional divisor $E\subset\widetilde{Y}$ and $(Y,0)$ is rational. By [5], the pullback of the maximal ideal of $0\in Y$ is the reduced exceptional divisor in $\widetilde{Y}$ , and the maximal ideal has no base points in $\widetilde{Y}$ . It follows that the multiplicity of $(X,0)$ is the intersection number between $\widetilde{X}$ and $E$ . In particular, $(X,0)$ is smooth if and only if $E\cup\widetilde{X}$ is a normal crossing divisor. If $\sigma=\sigma_{i}$ for some $1\leq i\leq s$ , then this is indeed the case. Otherwise, there is an $0\leq i\leq s$ so that $\ell_{\sigma}=a\ell_{i}+b\ell_{i+1}$ . In a neighbourhood of $E_{i}\cap E_{i+1}$ we have coordinates $u,v$ so that $E_{i}=\{x=0\}$ , $E_{i+1}=\{y=0\}$ and we have some generic coefficients $c,d$ so that the strict transform of $X$ is defined by $cx^{b}+dy^{a}$ . Thus, $(X,0)$ is not smooth if $1<i<s$ . In the case $i=0$ (the case $i=s$ is similar), $\widetilde{X}$ is smooth and transverse to $E_{1}$ if and only if $b=1$ .

The condition in item (iii) is equivalent with the equality

(4.1)

(\Gamma^{*}_{+}(f)\setminus\Gamma_{+}(f))\cap M=\emptyset.

Choose a basis for $N$ , inducing an isomorphism $N\cong M$ via the dual basis, as well as an inner product on $N_{\mathbb{R}}\cong M_{\mathbb{R}}$ . If we rotate the segment $\Gamma(f)$ by $\pi/2$ and translate it, then it can be identified with the vector $\ell_{i}$ (segment $t\ell_{i}$ , $t\in[0,1]$ ). Consider the parallelogram $P(\ell_{i})$ whose sides are parallel to $\ell_{0}$ and $\ell_{s+1}$ , and it has $\ell_{i}$ as diagonal. It is divided by $\ell_{i}$ into two triangles, each of them can be identified by $\Gamma^{*}_{+}(f)\setminus\Gamma_{+}(f)$ . Hence, eq. 4.1 holds if and only if $P(\ell_{i})^{\circ}\cap N=\emptyset$ .

Clearly, $P(\ell_{i})^{\circ}\cap N$ is empty if $\ell_{\sigma}\in\partial\mathop{\rm conv}\nolimits(\Sigma^{\circ}\cap N)$ . The converse can be seen as follows. Let $(\ell^{\mathrm{b}}_{i})_{i\in\mathbb{Z}}$ be a family consisting of integral points on $\partial\mathop{\rm conv}\nolimits(\Sigma^{\circ}\cap N)$ , ordered according one of the orientation of this boundary. Two consecutive elements of this family form a basis of $N$ , and

\Sigma^{\circ}\cap N=\bigcup_{i\in\mathbb{Z}}\mathbb{Z}_{\geq 0}\langle\ell^{\mathrm{b}}_{i},\ell^{\mathrm{b}}_{i+1}\rangle\setminus\{0\}.

It follows that the set of irreducible elements in the semigroup $\Sigma^{\circ}\cap N$ are presicely the elements on the boundary $\partial\mathop{\rm conv}\nolimits(\Sigma^{\circ}\cap N)$ . In particular, if $\ell_{\sigma}\in(\mathop{\rm conv}\nolimits(\Sigma^{\circ}\cap N))^{\circ}$ , then $\ell_{\sigma}=\ell^{\prime}+\ell^{\prime\prime}$ for some $\ell^{\prime},\ell^{\prime\prime}\in\Sigma^{\circ}\cap N$ . It follows that $\ell^{\prime},\ell^{\prime\prime}\in P(\ell_{i})^{\circ}$ . ∎

\thecor Corollary.

Consider the notation from the proof of section 4(ii), that is, $(X,0)$ irreducible and $\ell_{\sigma}=a\ell_{i}+b\ell_{i+1}$ with $\gcd(a,b)=1$ . Then the multiplicity of $(X,0)$ is

\mathop{\rm mult}\nolimits(X,0)=\begin{cases}b&i=0,\\ a+b&0<i<s,\\ a&i=s.\end{cases}\qed

\therem Remark.

Let $\ell,\ell^{\prime}$ be any two linearly independent integral vectors in any free $\mathbb{Z}$ module, and let $N$ be the free $\mathbb{Z}$ module generated by them. Then the definitions from 4 and 4 can be repeated in $N$ . Then the determinant of two such vectors can be seen as the greatest common divisor of the maximal minors of the matrix having the coordinate vectors of $\ell,\ell^{\prime}$ as rows, see [27]. Note that $\alpha(\ell,\ell^{\prime})=\alpha(\ell^{\prime},\ell)$ . Moreover, $\beta(\ell_{0},\ell_{s+1})\beta(\ell_{s+1},\ell_{0})\equiv 1\,(\mathop{\rm mod}\nolimits\alpha(\ell_{0},\ell_{s+1}))$ , cf. [29, Proposotion 5.6].

5. Isolated surface singularities

In the next theorem we give necessary and sufficient conditions for a Newton nondegenerate surface singularity to be isolated, in terms of the Newton polyhedron. In particular, we assume that $r=3$ in this section. This is a (non-direct) generalization of a result of Kouchnirenko valid in the classical case [15].

5.1 Theorem.

Let $(X,0)$ be a Newton nondegenerate singularity and assume $\mathop{\mathrm{rk}}N=3$ . The following are equivalent

(i)

$(X,0)$ has an isolated singularity.
(ii)

If $p\in M$ satisfies $\ell_{\sigma}(p)>m_{\sigma}$ for all $\sigma\in\triangle_{\Sigma}^{(1)}$ , then $\ell_{\sigma}(p)>m_{\sigma}$ for all $\sigma\in\triangle_{f}^{*(1)}$ .
(iii)

Let $\sigma_{1},\sigma_{2}\in\triangle_{\Sigma}^{(1)}$ and $\sigma=\mathbb{R}_{\geq 0}\langle\sigma_{1},\sigma_{2}\rangle\in\triangle_{\Sigma}^{(2)}$ and assume that $\tau\in\triangle_{f}^{(1)}$ with $\tau\subset\sigma$ . If $p\in M$ so that $\ell_{\sigma_{1}}(p)>m_{\sigma_{1}}$ and $\ell_{\sigma_{2}}(p)>m_{\sigma_{2}}$ , then $\ell_{\tau}(p)>m_{\tau}$ .

(iv)

Let $\sigma_{1},\sigma_{2}\in\triangle_{\Sigma}^{(1)}$ and $\sigma=\mathbb{R}_{\geq 0}\langle\sigma_{1},\sigma_{2}\rangle\in\triangle_{\Sigma}^{(2)}$ . Then there is at most one $\tau\in\triangle_{f}^{(1)}$ with $\tau\subset\sigma$ and $\sigma_{1}\neq\tau\neq\sigma_{2}$ . If such a $\tau$ exists, then $\ell_{\tau}$ is one of the following

(5.1)

\ell_{1},\ldots,\ell_{s},\quad a\ell_{0}+\ell_{1},\quad\ell_{s}+a\ell_{s+1},\qquad a\in\mathbb{Z}_{\geq 0}

and, furthermore, there exists an $e\in\mathbb{Q}$ so that

(5.2)

e\ell_{\tau}+\frac{\ell_{\sigma_{1}}}{\alpha(\ell_{\tau},\ell_{\sigma_{1}})}+\frac{\ell_{\sigma_{2}}}{\alpha(\ell_{\tau},\ell_{\sigma_{2}})}=0,

(see section 4 for $\alpha(\cdot,\cdot)$ ) and

(5.3)

em_{\tau}+\frac{m_{\sigma_{1}}}{\alpha(\ell_{\tau},\ell_{\sigma_{1}})}+\frac{m_{\sigma_{2}}}{\alpha(\ell_{\tau},\ell_{\sigma_{2}})}=-1.

Proof.

By section 3, the singular locus of the punctured germ $X\setminus\{0\}$ is a union of orbits $O_{\sigma}$ for some $\sigma\in\triangle_{\Sigma}^{(2)}$ . For such a $\sigma$ , we have $(V(\sigma),0)\subset(X,0)$ if and only if the projection of $\Gamma_{+}(f)$ in $M_{\sigma}$ is nontrivial, by section 3. By the same lemma, if $(V(\sigma),0)\subset(X,0)$ , then the generic transverse type to $V(\sigma)$ in $(X,0)$ is a Newton nondegenerate curve with Newton polyhedron the projection of $\Gamma_{+}(f)$ to $M_{\sigma}$ . Therefore item (i) $\Leftrightarrow$ item (iii) follows from section 4. The equivalence of item (ii) and item (iii) is an exercise.

The generic transverse type to $(V(\sigma),0)$ in $(X,0)$ is smooth if and only if its diagram has a single face corresponding to a $\tau$ as in eq. 5.1, and this face has length one. item (i) $\Leftrightarrow$ item (iv) follows, once we show that given such a $\tau$ , an $e\in\mathbb{Q}$ satisfying eq. 5.2 exists and is unique, and that, furthermore, the left hand side of eq. 5.3 is minus the combinatorial length of the face $F$ of the Newton diagram corresponding to $\tau$ .

Take a smooth subdivision of $\sigma$ containing $\tau$ as a ray, and let $\tau_{i}$ be the ray adjacent to $\tau$ between $\tau$ and $\sigma_{i}$ . Then there exists a $-b\in\mathbb{Z}$ so that

(5.4)

-b\ell_{\tau}+\ell_{\tau_{1}}+\ell_{\tau_{2}}=0.

Furthermore, for $i=1,2$ , we may assume that

\ell_{\tau_{i}}=\frac{\beta_{i}\ell_{\tau}+\ell_{\sigma_{i}}}{\alpha_{i}}

where $\alpha_{i}/\beta_{i}$ is the continued fraction associated with $\ell_{\tau}$ and $\ell_{\sigma_{i}}$ . As a result, eq. 5.4 can be rewritten as (5.2) with $e=-b+\beta_{1}/\alpha_{1}+\beta_{2}/\alpha_{2}$ . Let $p_{1},p_{2}$ be the endpoints of $F$ so that $\ell_{\tau_{1}}(p_{2}-p_{1})>0$ and $\ell_{\tau_{2}}(p_{1}-p_{2})>0$ . Since $\ell_{\tau_{i}}$ is a primitive function on the affine hull of the face of $F$ , $\ell_{\tau_{1}}(p_{2}-p_{1})=\ell_{\tau_{2}}(p_{1}-p_{2})=$ the length of $F$ . We find

\begin{split}em_{\tau}+\frac{m_{\sigma_{1}}}{\alpha_{1}}+\frac{m_{\sigma_{2}}}{\alpha_{2}}&=e\ell_{\tau}(p_{1})+\frac{\ell_{\sigma_{1}}(p_{1})}{\alpha_{1}}+\frac{\ell_{\sigma_{2}}(p_{2})}{\alpha_{2}}\\ &=-b\ell_{\tau}(p_{1})+\ell_{\tau_{1}}(p_{1})+\ell_{\tau_{2}}(p_{2})=\ell_{\tau_{2}}(p_{2}-p_{1}).\qed\end{split}

6. Resolution of Newton nondegenerate surface singularities

In this section, we retain the notation introduced in section 3, with the assumption that $\mathop{\mathrm{rk}}N=3$ . We describe Oka’s algorithm which describes explicitly the graph of a resolution of a Newton nondegenerate Weil divisor of dimension $2$ . This algorithm was originally described by Oka [27] for Newton nondegenerate hypersurface singularities in $(\mathbb{C}^{3},0)$ . The general methods for resolving Newton nondegenerate hypersurface singularities have been used in e.g. [32] and [3, Chapter 8].

\thedefinition Definition.

A canonical subdivision of $\triangle_{f}$ is a subdivision $\widetilde{\triangle}_{f}$ satisfying the following.

(i)

$\widetilde{\triangle}_{f}$ is a regular subdivision of $\triangle_{f}$ .
(ii)

If $\sigma\in\triangle^{(2)}_{f}\setminus\triangle_{f}^{*}$ , then $\widetilde{\triangle}_{f}|_{\sigma}$ is the canonical subdivision $\widetilde{\triangle}_{\sigma}$ of $\triangle_{\sigma}$ given in section 4.

\theblock.

The existence of a canonical subdivision is proved in [27, §3]. We fix such a subdivision $\widetilde{\triangle}_{f}$ . We will denote by $\widetilde{Y}$ the toric variety associated with $\widetilde{\triangle}_{f}$ . The map $\widetilde{Y}\to Y$ is denoted by $\pi$ , and the strict transform of $X$ under this map is denoted by $\widetilde{X}$ . We denote by $\pi_{X}$ the restriction $\pi|_{\widetilde{X}}:\widetilde{X}\to X$ . By section 2, the map $\widetilde{Y}\to Y$ is proper, hence $\widetilde{X}\to X$ is proper as well.

\thedefinition Definition.

For $i,d\in\mathbb{N}$ , define

\begin{split}\widetilde{\triangle}_{f}^{(i,d)}&=\left\{\sigma\in\widetilde{\triangle}_{f}^{(i)}\,\middle|\,\dim(F_{\sigma}\cap\Gamma(f))=d\right\}\\ \widetilde{\triangle}_{f}^{*(i,d)}&=\widetilde{\triangle}_{f}^{(i,d)}\cap\widetilde{\triangle}_{f}^{*}.\end{split}

\thedefinition Definition.

We start by defining a graph $G^{*}$ as follows. Index the set $\widetilde{\triangle}_{f}^{(1,2)}$ by a set $\mathcal{N}$ , i.e. write $\widetilde{\triangle}_{f}^{(1,2)}=\left\{\sigma_{n}\,\middle|\,n\in\mathcal{N}\right\}$ in such a way that the map $\mathcal{N}\to\widetilde{\triangle}_{f}^{(1,2)}$ , $n\mapsto\sigma_{n}$ is bijective. Similarly, index the set $\widetilde{\Delta}_{f}^{(1,2)}\cup\widetilde{\Delta}_{f}^{*(1,1)}$ by $\mathcal{N}^{*}$ . Hence $\mathcal{N}\subset\mathcal{N}^{*}$ . The elements of $\mathcal{N}^{*}$ are referred to as extended nodes, while ${\mathcal{N}}$ as nodes.

Denote by $F_{n}$ the face of $\Gamma_{+}(f)$ corresponding to $\sigma_{n}$ and by $\ell_{n}$ the primitive integral generator of $\sigma_{n}$ . Note that $n\in\mathcal{N}$ if and only if $F_{n}$ is bounded. For $n,n^{\prime}\in\mathcal{N}^{*}$ , let $t_{n,n^{\prime}}$ be the length of the segment $F_{n}\cap F_{n^{\prime}}$ if this is a bounded segment of dimension 1. If $F_{n}\cap F_{n^{\prime}}$ is unbounded, or has dimension 0, then we set $t_{n,n^{\prime}}=0$ . Now, for every pair $n$ and $n^{\prime}\in\mathcal{N}^{*}$ , we join $n,n^{\prime}$ by $t_{n,n^{\prime}}$ bamboos of type $\alpha(\ell_{n},\ell_{n^{\prime}})/\beta(\ell_{n},\ell_{n^{\prime}})$ , as in fig. 3. This finishes the construction of the graph $G^{*}$ . Denote its set of vertices $\mathcal{V}^{*}$ .

Define the graph $G$ as the induced full subgraph of $G^{*}$ on the set of vertices $\mathcal{V}=\mathcal{V}^{*}\setminus(\mathcal{N}^{*}\setminus\mathcal{N})$ .

In order to have a plumbing graph structure on $G$ , we must specify an Euler number and a genus for each vertex, as well as a sign for each edge. All edges are positive. Vertices appearing on bamboos have genus zero, whereas the genus $g_{n}$ associated with $n\in\mathcal{N}$ is defined as the number of integral interior points in the polygon $F_{n}$ .

To every extended node $n\in\mathcal{N}^{*}$ we have associated the cone $\sigma_{n}$ and its primitive integral generator $\ell_{n}$ . If $v_{1},\ldots,v_{s}$ are the vertices appearing on a bamboo, in this order, from $n$ to $n^{\prime}\in\mathcal{N}^{*}$ , let $\ell_{0},\ell_{1},\ldots,\ell_{s+1}$ be the canonical primitive sequence associated with $\ell_{n},\ell_{n^{\prime}}$ . We then set $\ell_{v}=\ell_{i}$ for $v=v_{i}$ , $i=1,\ldots,s$ , and $\sigma_{v}=\mathbb{R}_{\geq 0}\langle\ell_{i}\rangle$ . This induces a map $\gamma:\mathcal{V}\to\widetilde{\triangle}_{f}^{(1)}$ with the property that $\gamma(n)=\sigma_{n}$ for $n\in\mathcal{N}^{*}$ , and $\ell_{v},\ell_{w}$ generate an element of $\widetilde{\triangle}_{f}^{(2)}$ if $v,w$ are adjacent in $G^{*}$ .

For any $v\in\mathcal{V}$ , let $\mathcal{V}_{v}$ and $\mathcal{V}_{v}^{*}$ be the set of neighbours of $v$ in $G$ and $G^{*}$ , respectively. Then there exists a unique $-b_{v}\in\mathbb{Z}_{\leq-1}$ satisfying

-b_{v}\ell_{v}+\sum_{u\in\mathcal{V}_{v}^{*}}\ell_{u}=0\ \ \mbox{in}\ \ N,

The number $-b_{v}$ is the Euler number associated with $v\in\mathcal{V}$ . We note that if $v$ lies on a bamboo, with the notation of the previous paragraph, $v=v_{i}$ , then $-b_{v}=-b_{i}$ and $-b_{i}\leq-2$ unless $\alpha(\ell_{n},\ell_{n^{\prime}})=1$ .

\therem Remark.

The link of an isolated surface singularity is a rational homology sphere if and only if it has a resolution whose graph is a tree and all vertices have genus zero, see e.g. [20]. The above construction produces such a graph if and only if all integral points on $\Gamma(f)$ lie on its boundary $\partial\Gamma(f)$ .

Indeed, if $P\subset\Gamma(f)$ is a vertex which is not on the boundary, then the nodes corresponding to faces of $\Gamma(f)$ containing $P$ lie on an embedded cycle. Similarly, if $S\subset\Gamma(f)$ is a face of dimension $1$ which is not a subset of the boundary, and $S$ contains integral interior points, then the nodes corresponding to the two faces containing $S$ are joined by more than one bamboo, inducing an embedded cycle in $G$ . Finally, if $F\subset\Gamma(f)$ is a two dimensional face containing interior integral interior points, then the corresponding node has nonzero genus. The converse is not difficult.

The classical case $Y=\mathbb{C}^{3}$ is discussed in details in [7].

\theexample Example.

Let $\Sigma=\mathbb{R}^{3}_{\geq 0}$ , and consider standard coordinates $x,y,z$ on $Y=\mathbb{C}^{3}$ , and the function

f(x,y,z)=x^{5}+x^{2}y^{2}+y^{7}+z^{10}.

The Newton diagram $\Gamma(f)$ consists of two triangular faces, whose intersection is a segment of length two. The diagram, as well as the graph obtained by Oka’s algorithm can be seen in fig. 4.

\theprop Proposition.

Let $(X,0)$ be a Newton nondegenerate surface singularity. Then the map $\widetilde{X}\to X$ is a resolution of $(X,0)$ whose resolution graph is $G$ .

More precisely, $\widetilde{X}$ is smooth and the exceptional set $E\subset\widetilde{X}$ is a normal crossing divisor. For each $\sigma\in\widetilde{\triangle}_{f}^{(1)}$ , we can enumerate the irreducible components of $E_{\sigma}$ by $\gamma^{-1}(\sigma)$ so that $E_{\sigma}=\amalg_{v\in\gamma^{-1}(\sigma)}E_{v}$ , where $E_{v}$ is a smooth curve.

If $\gamma(v)\in\widetilde{\triangle}_{f}^{(1)}\setminus\widetilde{\triangle}^{*}$ , then $E_{v}$ is compact, has genus $g_{v}$ , and its normal bundle in $\widetilde{X}$ has Euler number $-b_{v}$ . If $\gamma(v)\in\widetilde{\triangle}^{(1)*}$ , then $E_{v}$ is a smooth germ, transverse to a smooth point of the exceptional divisor.

Furthermore, if $v,w\in\mathcal{V}$ , then the number of intersection points $|E_{v}\cap E_{w}|$ equals the number of edges between $v$ and $w$ in $G$ .

Proof.

The proof goes exactly as in [27] ∎

\thedefinition Definition.

For $v\in\mathcal{V}^{*}$ , (recall section 3 and section 3) let

F_{v}=F_{\gamma(v)},\quad\ell_{v}=\ell_{\gamma(v)},\quad m_{v}=m_{\gamma(v)}.

\thelemma Lemma.

For $v\in\mathcal{V}$ , we have

-b_{v}\ell_{v}+\sum_{u\in\mathcal{V}^{*}_{v}}\ell_{u}=0,\quad-b_{v}m_{v}+\sum_{u\in\mathcal{V}^{*}_{v}}m_{u}=-2\mathop{\rm Vol}\nolimits_{2}(F_{v}).

Proof.

The first equality follows from construction, see also [27, §6]. The second equality follows from [7, Prop. 4.4.4] and the formula $\alpha\ell_{1}=\beta\ell_{0}+\ell_{s+1}$ , where $\ell_{0},\ell_{1},\ldots,\ell_{s+1}$ is a primitive sequence. ∎

\therem Remark.

(i)

The exceptional divisor $E$ is the union of $E_{\sigma}$ for which $\sigma\in\widetilde{\triangle}_{f}^{(1)}$ is a cone which is not contained in $\partial\Sigma$ , or, equivalently, $F_{\sigma}$ is compact.
(ii)

If $\sigma\in\widetilde{\triangle}_{f}^{(1,2)}$ , then $E_{\sigma}$ is a compact smooth irreducible curve. If $\sigma\in\widetilde{\triangle}_{f}^{(1,1)}\setminus\widetilde{\triangle}^{*}_{f}$ , then $E_{\sigma}$ is the union of $t_{\sigma}$ disjoint smooth compact rational curves. For $\sigma\in\widetilde{\triangle}_{f}^{*(1,1)}$ , the intersection $E_{\sigma}=V(\sigma)\cap\widetilde{X}$ is the disjoint union of $t$ smooth curve germs, where $t$ is the length of the segment $F_{\sigma}\cap\Gamma(f)$ . If $\sigma\in\widetilde{\triangle}_{f}^{(1,0)}$ , then $E_{\sigma}=\emptyset$ (the global divisor $D_{\sigma}$ does not intersect $\widetilde{X}$ ).

\thedefinition Definition.

We denote by $L=\mathbb{Z}\left\langle E_{v}\,\middle|\,v\in\mathcal{V}\right\rangle$ the lattice of integral cycles in $\widetilde{X}$ supported on the exceptional divisor $E$ .

\thedefinition Definition.

Let $g\in\mathcal{O}_{Y,0}$ and denote its restriction by $\overline{g}\in\mathcal{O}_{X,0}$ . For any $v\in\mathcal{V}^{*}$ , we define

\begin{split}\mathop{\rm wt}\nolimits_{v}(g)=\min\left\{\ell_{v}(p)\,\middle|\,p\in\mathop{\rm supp}\nolimits(g)\right\},\quad&\mathop{\rm wt}\nolimits(g)=\sum_{v\in\mathcal{V}}\mathop{\rm wt}\nolimits_{v}(g)E_{v}\in L,\\ \mathop{\rm wt}\nolimits_{v}(\overline{g})=\max\left\{\mathop{\rm wt}\nolimits_{v}(g+h)\,\middle|\,h\in I_{X}\right\},\quad&\mathop{\rm wt}\nolimits(\overline{g})=\sum_{v\in\mathcal{V}}\mathop{\rm wt}\nolimits_{v}(\overline{g})E_{v}\in L.\end{split}

For $\sigma=\gamma(v)$ , we also write $\mathop{\rm wt}\nolimits_{\sigma}$ instead of $\mathop{\rm wt}\nolimits_{v}$ , as this is independent of $v\in\gamma^{-1}(\sigma)$ .

Similarly, for any $v\in\mathcal{V}$ , let $\mathop{\rm div}\nolimits_{v}$ be the valuation on $\mathcal{O}_{X,0}$ associated with the divisor $E_{v}$ , that is, for $\overline{g}\in\mathcal{O}_{X,0}$ , denote by $\mathop{\rm div}\nolimits_{v}(\overline{g})$ the order of vanishing of the function $\pi_{X}^{*}(\overline{g})$ along $E_{v}$ . Set also

\mathop{\rm div}\nolimits(\overline{g})=\sum_{v\in\mathcal{V}}\mathop{\rm div}\nolimits_{v}(\overline{g})E_{v}\in L.

\therem Remark.

(i)

If $\sigma=\gamma(v)$ and $|\gamma^{-1}(\sigma)|>1$ , then $\mathop{\rm div}\nolimits_{v}$ is not independent of the choice of $v\in\gamma^{-1}(\sigma)$ .
(ii)

For $\sigma\in\widetilde{\triangle}_{f}^{(1)}$ , the function $\mathop{\rm wt}\nolimits_{\sigma}:\mathcal{O}_{Y,0}\setminus\{0\}\to\mathbb{Z}$ is the valuation on $\mathcal{O}_{Y,0}$ associated with the irreducible divisor $V(\sigma)\subset\widetilde{Y}$ , cf. eq. 3.2.
(iii)

In general, the functions $\mathop{\rm wt}\nolimits_{v}$ and $\mathop{\rm div}\nolimits_{v}$ do not coincide on $\mathcal{O}_{X,0}$ . However, $\mathop{\rm wt}\nolimits_{v}(\overline{g})\leq\mathop{\rm div}\nolimits_{v}(\overline{g})$ for any $\overline{g}\in\mathcal{O}_{X,0}$ and $v\in\mathcal{V}$ . Furthermore, if $p\in M$ and $\gamma(v)\in\widetilde{\triangle}_{f}^{(1,>0)}\setminus\widetilde{\triangle}_{f}^{*}$ , then $\mathop{\rm div}\nolimits_{v}(x^{p})=\mathop{\rm wt}\nolimits_{v}(x^{p})=\ell_{v}(p)$ . In particular, this defines a group homomorphism $M\to L$ , $p\to\mathop{\rm wt}\nolimits(x^{p})$ .

7. The geometric genus

In this section we provide a formula for the delta invariant and geometric genus for an arbitrary generalized Newton nondegenerate singularity in terms of its Newton polyhedron. In this section, the rank $r$ of $N$ is under no restriction. Recall that we say that $f$ (or $\Gamma_{+}(f)$ ) is pointed at $p\in M_{\mathbb{Q}}$ , if for any $\sigma\in\triangle_{\Sigma}^{(1)}$ we have $m_{\sigma}=\ell_{\sigma}(p)$ , see section 3.

\therem Remark.

In the proof of theorem 7.1, one of the main steps consists of computing the cohomology of a line bundle on a toric variety. To do this, we build on classical methods [13, 10]. A more general method to compute such cohomology has been described by Altmann and Ploog in [2].

\thedefinition Definition.

For a point $x$ in an analytic variety $X$ , denote by $\overline{\mathcal{O}}_{X,x}$ the normalization of its local ring $\mathcal{O}_{X,x}$ . The delta invariant associated with $x\in X$ is defined as

\delta(X,x)=\dim_{\mathbb{C}}\overline{\mathcal{O}}_{X,x}/\mathcal{O}_{X,x}.

Let $\widetilde{X}\to X$ be a resolution of the singularity $x\in X$ and assume that $X$ has dimension $d$ . Assume, furthermore, that $\delta(X,x)<\infty$ , and that the higher direct image sheaves $R^{i}\pi_{*}\mathcal{O}_{\widetilde{X}}$ , $i>0$ , are concentrated at $x$ . The geometric genus $p_{g}=p_{g}(X,0)$ is defined as

(-1)^{d-1}p_{g}(X,x)=\delta(X,x)+\sum_{i=1}^{d-1}(-1)^{i}h^{i}(\widetilde{X},\mathcal{O}_{\widetilde{X}}).

We say that $(X,x)$ is rational if $\delta(X,x)=0$ and $h^{i}(\widetilde{X},\mathcal{O}_{\widetilde{X}})=0$ for $i>0$ .

7.1 Theorem.

Let $(X,0)\subset(Y,0)$ be a Newton nondegenerate Weil divisor of dimension $d=r-1$ .

(i)

We have the following canonical identifications

\begin{split}\overline{\mathcal{O}}_{X,0}/\mathcal{O}_{X,0}&\cong\bigoplus_{p\in M}\widetilde{H}^{0}(\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee},\mathbb{C}),\\ H^{i}(\widetilde{X},\mathcal{O}_{\widetilde{X}})&\cong\bigoplus_{p\in M}\widetilde{H}^{i}(\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee},\mathbb{C}),\quad i>0.\end{split}

In particular, if these vector spaces have finite dimension, then

\begin{split}\delta(X,0)&=\sum_{p\in M}\widetilde{h}^{0}(\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee},\mathbb{C}),\\ p_{g}(X,0)&=(-1)^{d-1}\sum_{p\in M}\widetilde{\chi}(\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee},\mathbb{C}),\end{split}

where $\widetilde{\chi}$ denotes the reduced Euler characteristic, that is, the alternating sum of ranks of reduced singular cohomology groups.

(ii)

We have

\widetilde{h}^{d-1}(\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee},\mathbb{C})=\begin{cases}1&\textrm{if}\quad 0\in\Gamma_{+}^{*}(x^{p}f)^{\circ}\setminus\Gamma_{+}(x^{p}f)^{\circ},\\ 0&\textrm{else}.\end{cases}

In particular, $h^{d-1}(\widetilde{X},\mathcal{O}_{\widetilde{X}})=|M\cap\Gamma_{+}^{*}(f)^{\circ}\setminus\Gamma_{+}(f)^{\circ}|$ (recall section 3).

(iii)

Assume that $f$ is $\mathbb{Q}$ -pointed, that $d\geq 2$ , and that $(X,0)$ has only rational singularities outside the origin. Then $(X,0)$ is normal and $h^{i}(\widetilde{X},\mathcal{O}_{\widetilde{X}})=0$ for $1\leq i<d-1$ .

\thecor Corollary.

Assume that $d=2$ and $(X,0)$ is normal. Then

p_{g}(X,0)=|M\cap\Gamma_{+}^{*}(f)^{\circ}\setminus\Gamma_{+}(f)^{\circ}|.\qed

This generalizes a result of Merle and Teissier [19] valid for the classical case $\Sigma={\mathbb{R}}_{\geq 0}^{3}$ .

\thecor Corollary.

Assume that $d=1$ and $(X,0)$ is an irreducible germ of a curve, and that $\sigma\in\widetilde{\triangle}^{(1)}_{f}$ satisfies $F_{\sigma}=\Gamma(f)$ (cf. section 4 item (i)). Then $\delta(X,0)$ is the number of unordered pairs $\ell^{\prime},\ell^{\prime\prime}\in\Sigma^{\circ}\cap N$ satisfying $\ell^{\prime}+\ell^{\prime\prime}=\ell_{\sigma}$ .

Proof.

Let $P(\ell_{\sigma})$ be the parallelogram introduced in the proof of section 4. The diagonal splits $P(\ell_{\sigma})$ into two triangles, $T_{1}$ and $T_{2}$ , say. If $\ell^{\prime}\in T_{1}^{\circ}$ , then $\ell_{\sigma}-\ell^{\prime}\in T^{\circ}_{2}$ . This induces a bijection between elements $\ell^{\prime}\in T^{\circ}_{1}\cap N$ and unordered pairs $\{\ell^{\prime},\ell^{\prime\prime}\}\subset\Sigma^{\circ}\cap N$ adding up to $\ell_{\sigma}$ . By rotating by $\pi/2$ as in the proof of section 4, $T_{1}^{\circ}\cap N$ is in bijection with $M\cap\Gamma_{+}^{*}(f)^{\circ}\setminus\Gamma_{+}(f)^{\circ}$ . ∎

\therem Remark.

Assume that $d\geq 2$ , and that $X$ is rational outside $\{0\}$ . Then, for $0<i<d-1$ , we have

H^{i}(\widetilde{X},\mathcal{O}_{\widetilde{X}})\cong H^{i}(\widetilde{X}\setminus E,\mathcal{O}_{\widetilde{X}})\cong H^{i}(X\setminus\{0\},\mathcal{O}_{X})\cong H^{i+1}_{\{0\}}(X,\mathcal{O}_{X}).

Here, the first isomorphism comes from the long exact sequence for cohomology with support in $E$ , and the vanishing $H^{i}_{E}(\widetilde{X},\mathcal{O}_{\widetilde{X}})=0$ , for $i<d$ [14, Corollary 3.3]. The second isomorphism follows from the rationality assumption, and the Leray spectral sequence. The third isomorphism comes from the similar long exact sequence for cohomology with support in $\{0\}$ , and the fact that $H^{j}(X,\mathcal{O}_{X})=0$ for $j>0$ , if we choose a Stein representative $X$ of the germ $(X,0)$ . This last long exact sequence furthermore gives

H^{1}_{\{0\}}(X,\mathcal{O}_{X})\cong\frac{H^{0}(X\setminus\{0\},\mathcal{O}_{X})}{H^{0}(X,\mathcal{O}_{X})}\cong\overline{\mathcal{O}}_{X,0}/\mathcal{O}_{X,0}.

Therefore, in this case, the groups described in theorem 7.1 are closely related with the depth of $\mathcal{O}_{X,0}$ . In particular, the conclusion of theorem 7.1 item (iii) is that $(X,0)$ is a Cohen–Macaulay ring.

If $f$ is pointed at $p\in M$ , then this statement can be proved as follows. Since $(X,0)$ is a Cartier divisor in $(Y,0)$ , cf. section 3 ii, and $(Y,0)$ is Cohen–Macaulay [9, Theorem 6.3.5] so is $(X,0)$ [9, Theorem 2.1.3].

Proof of theorem 7.1.

To prove item (i), we use results and notation from [10, §7], see also [13, 3.5]. Define

D_{m}=\sum\left\{m_{\sigma}D_{\sigma}\,\middle|\,\sigma\in\widetilde{\triangle}_{f}^{(1)}\right\}.

Then $D_{m}+\widetilde{X}$ is the divisor of the pullback of $f$ to $\widetilde{Y}$ , and we have a short exact sequence

0\to\mathcal{O}_{\widetilde{Y}}(D_{m})\stackrel{{\scriptstyle\cdot f}}{{\to}}\mathcal{O}_{\widetilde{Y}}\to\mathcal{O}_{\widetilde{X}}\to 0.

By [10, Corollary 7.4], we have $H^{i}(\widetilde{Y},\mathcal{O}_{\widetilde{Y}})=0$ for all $i>0$ . Furthermore, $H^{0}(\widetilde{X},\mathcal{O}_{\widetilde{X}})\cong\overline{\mathcal{O}}_{X,0}$ , and the image of $H^{0}(\widetilde{Y},\mathcal{O}_{\widetilde{Y}})=\mathcal{O}_{Y,0}$ in $\overline{\mathcal{O}}_{X,0}$ is $\mathcal{O}_{X,0}$ . Therefore,

\begin{split}\overline{\mathcal{O}}_{X,0}/\mathcal{O}_{X,0}&\cong H^{1}(\widetilde{Y},\mathcal{O}_{\widetilde{Y}}(D_{m})),\ \ \mbox{and}\\ H^{i}(\widetilde{X},\mathcal{O}_{\widetilde{X}})&\cong H^{i+1}(\widetilde{Y},\mathcal{O}_{\widetilde{Y}}(D_{m})),\quad i>0.\end{split}

Denote by $g$ the order function defined in [10, §6] (using the natural trivialization of $\mathcal{O}_{\widetilde{Y}}(D_{m})$ on the open torus)

g:|\widetilde{\triangle}_{f}|\to\mathbb{R},\quad g(\ell)=-\min\left\{\ell(q)\,\middle|\,q\in\Gamma_{+}(f)\right\}

and define the sets

Z_{p}=\left\{\ell\in|\widetilde{\triangle}_{f}|\,\middle|\,\ell(p)\geq g(\ell)\right\},\quad p\in M.

We note that $Z_{p}$ is a convex cone and that $0\in Z_{p}$ for all $p\in M$ . By [10, Theorem 7.2], we have isomorphisms

H^{i+1}(\widetilde{Y},\mathcal{O}_{\widetilde{Y}}(D_{m}))\cong\bigoplus_{p\in M}H^{i+1}_{Z_{p}}(|\widetilde{\triangle}_{f}|,\mathbb{C}).

Since $|\widetilde{\triangle}_{f}|=\Sigma$ is a convex set, the long exact sequence associated with cohomology with supports provides, for any $p\in M$

0\cong\widetilde{H}^{i}(|\widetilde{\triangle}_{f}|,\mathbb{C})\to\widetilde{H}^{i}(|\widetilde{\triangle}_{f}|\setminus Z_{p},\mathbb{C})\cong H^{i+1}_{Z_{p}}(|\widetilde{\triangle}_{f}|,\mathbb{C})\to\widetilde{H}^{i+1}(|\widetilde{\triangle}_{f}|,\mathbb{C})\cong 0.

To finish the proof of (i), we will show that for any $p\in M$ , the spaces $|\widetilde{\triangle}_{f}|\setminus Z_{p}=\Sigma\setminus Z_{p}$ and $\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee}$ are in fact homotopically equivalent. We start by noting that the the condition $Z_{p}\subset\partial|\widetilde{\triangle}_{f}|$ (including the case when $Z_{p}=\emptyset$ ) is equivalent to $0\in\Gamma_{+}(x^{p}f)\setminus\Gamma(x^{p}f)$ . If this happens then we can choose a $q\in\Sigma^{\vee}$ small so that $-q\in\Gamma_{+}(x^{p}f)\setminus\Gamma(x^{p}f)$ as well, and so $\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee}$ is star-shaped with center $-q$ . In particular, in this case,

\Sigma\setminus Z_{p}\sim\{\mbox{a point}\}\sim\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee},

where $\sim$ denotes the homotopy equivalence. Thus, in what follows, we assume that $Z_{p}$ contains an interior point in $\Sigma$ , equivalently, $0\notin\Gamma_{+}(x^{p}f)\setminus\Gamma(x^{p}f)$ .

Choose $\ell_{0}\in\Sigma^{\circ}$ and $q_{0}\in(\Sigma^{\vee})^{\circ}$ satisfying $\ell_{0}(q_{0})=1$ and define the hyperplanes

H=\left\{\ell\in N_{\mathbb{R}}\,\middle|\,\ell(q_{0})=1\right\},\quad H^{\vee}=\left\{q\in M_{\mathbb{R}}\,\middle|\,\ell_{0}(q)=1\right\}.

Then, seeing $H$ and $H^{\vee}$ as linear spaces by choosing origins $\ell_{0},q_{0}$ , the pairing $H\times H^{\vee}\ni(\ell,q)\mapsto\ell(q)-1$ is nondegenerate and the polyhedrons $H\cap\Sigma$ and $H^{\vee}\cap\Sigma^{\vee}$ are each others polar sets as in [13, 1.5].

Since $0\in Z_{p}$ , we have

\Sigma\setminus Z_{p}\,\sim\,(H\cap\Sigma\setminus Z_{p})\times\mathbb{R}\,\sim\,H\cap\Sigma\setminus Z_{p}.

By the assumptions made above, there is an $\ell\in Z_{p}\cap\Sigma^{\circ}$ . Both $\Sigma\cap H$ and $Z_{p}\cap H$ are compact convex polyhedrons in $H$ . Projection away from $\ell$ onto $\partial(H\cap\Sigma)$ then induces a homotopy equivalence

H\cap\Sigma\setminus Z_{p}\sim H\cap\partial\Sigma\setminus Z_{p}.

By projection, we mean that any element in a ray $r=\ell+\mathbb{R}_{>0}\ell^{\prime}\subset H$ maps to the unique element in $r\cap\partial(H\cap\Sigma)$ . By section 7 item (i), this has the subset

\cup\left\{H\cap\sigma\,\middle|\,\sigma\in\triangle_{f}^{*},\,H\cap\sigma\cap Z_{p}=\emptyset\right\}

as a strong deformation retract. All this yields

(7.1)

\Sigma\setminus Z_{p}\sim\cup\left\{H\cap\sigma\,\middle|\,\sigma\in\triangle_{f}^{*},\,\sigma\cap Z_{p}=\{0\}\right\}.

Using a projection, this time onto $\partial\Sigma^{\vee}$ in $M$ , having as center any element in $(\Sigma^{\vee}\cap\Gamma_{+}(x^{p}f))^{\circ}$ , we get a homotopy equivalence

\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee}\sim\Gamma_{+}(x^{p}f)^{\circ}\cap\partial\Sigma^{\vee}.

By section 7 item (ii), we have a homotopy equivalence

\Gamma_{+}(x^{p}f)^{\circ}\cap\partial\Sigma^{\vee}\sim\cup\left\{(\sigma^{\perp}\cap\Sigma^{\vee})^{\circ}\,\middle|\,\sigma\in\triangle_{\Sigma},\,\sigma\neq\{0\},\,(\sigma^{\perp}\cap\Sigma^{\vee})^{\circ}\cap\Gamma_{+}(x^{p}f)^{\circ}\neq\emptyset\right\}.

Since, by assumption made above, $0\notin\Gamma_{+}(x^{p}f)^{\circ}$ , and so the right hand side above has a free action by $\mathbb{R}_{>0}$ which has a section given by intersection with $H^{\vee}$ . Furthermore, one checks that if $\sigma\in\triangle_{f}^{*}$ , then

(\sigma^{\perp}\cap\Sigma^{\vee})^{\circ}\cap\Gamma_{+}(x^{p}f)^{\circ}\neq\emptyset\quad\Leftrightarrow\quad\forall\ell\in\sigma\setminus\{0\}:\,\ell(p)+m_{\ell}<0.

Here, the condition on the left is equivalent to $\sigma\cap Z_{p}=\{0\}$ , so

(7.2)

\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee}\sim\cup\left\{H\cap(\sigma^{\perp}\cap\Sigma^{\vee})^{\circ}\,\middle|\,\sigma\in\triangle_{f}^{*},\,\sigma\cap Z_{p}=\{0\}\right\}.

Now, consider the CW structure $K$ given by the cells $H\cap\sigma$ in $H\cap\partial\Sigma$ and $K^{\prime}$ given by cells $H^{\vee}\cap(\sigma^{\perp}\cap\Sigma^{\vee})$ in $H^{\vee}\cap\partial\Sigma^{\vee}$ . Using barycentric subdivision, one obtains a homeomorphism $\phi:H\cap\partial\Sigma\to H^{\vee}\cap\partial\Sigma^{\vee}$ , sending the center of a cell $H\cap\sigma$ to the center of the dual cell $H\cap\sigma^{\vee}$ , thus identifying $K$ with the dual of $K^{\prime}$ . By this identification, the left hand side of eq. 7.2 is a regular neighbourhood around the image under $\phi$ of the left hand side of eq. 7.1. This concludes (i).

Next, we prove (ii). By the above discussion, the result is clear in the cases when $Z_{p}=\emptyset$ or $Z_{p}\subset\partial\Sigma$ . Assuming that this is not the case, the complex, say, $A$ , on the right hand side of eq. 7.1 is a closed subset of $H\cap\partial\Sigma\sim S^{d-1}$ . Then $h^{d-1}(A,\mathbb{C})=0$ , unless $A=H\cap\partial\Sigma$ , in which case $h^{d-1}(A,\mathbb{C})=1$ . But this is equivalent to $\ell(p)+m_{\ell}<0$ for all $\ell\in\partial\Sigma\setminus 0$ , that is, $0\in\Gamma_{+}^{*}(x^{p}f)^{\circ}$ .

For (iii), we will show that $\Gamma_{+}(x^{p}f)\setminus\Sigma^{\vee}$ has trivial homology in degrees $i<d-1$ for all $p\in M$ . By assumption, there is a $q\in M_{\mathbb{Q}}$ so that for $\sigma\in\triangle_{\Sigma}^{(1)}$ we have $m_{\sigma}=\ell_{\sigma}(q)$ . We can again assume that $0\in\Gamma_{+}(x^{p}f)\setminus\Gamma(x^{p}f)$ . We must show that $\widetilde{h}^{i}(A,\mathbb{C})=0$ for $i<d-1$ , where $A$ is the right hand side of eq. 7.1. We note that by definition, $A$ consists of cells $H\cap\sigma$ for $\sigma\in\triangle_{f}^{*}$ satisfying $\forall\ell\in H\cap\sigma:\,\ell(p)<-m_{\ell}$ . Define similarly

A_{\Sigma}=\cup\left\{H\cap\sigma\,\middle|\,\sigma\in\triangle_{\Sigma}^{*},\forall\ell\in H\cap\sigma:\,\ell(p)<-\ell(q)\right\}.

Define

A_{q}=\left\{\ell\in H\cap\partial\Sigma\,\middle|\,\ell(p)<-\ell(q)\right\}.

This space can be either $S^{d-1}$ , an $d-1$ dimensional ball, or empty. In each case, $\widetilde{H}^{i}(A_{q},\mathbb{C})=0$ for $i<d-1$ . We will show that $A_{q}\supset A_{\Sigma}\subset A$ , and that these inclusions are homotopy equivalences. For the first one, in fact, this is clear by definition and section 7 (i).

For the second one, denote by $A_{\Sigma}^{i}$ the $i$ -skeleton of the complex $A_{\Sigma}$ , and define similarly

A^{i}=A\setminus\cup\left\{\sigma^{\circ}\,\middle|\,\sigma\in\triangle_{\Sigma}^{*(\geq i+2)}\right\}.

We will prove by induction on $i$ that $A^{i}_{\Sigma}\subset A^{i}$ and that this is a homotopy equivalence. The case $i=0$ follows from the pointed condition: assuming $\sigma\in\triangle_{\Sigma}^{*(1)}$ is a ray, there is a $t>0$ so that $H\cap\sigma=\{t\ell_{\sigma}\}$ . By assumption, we have $m_{\ell_{\sigma}}=\ell_{\sigma}(q)$ , so that $H\cap\sigma\subset A_{\Sigma}$ if and only if $H\cap\sigma\subset A$ . Since $A^{0}$ consists only of such zero-cells, we get $A_{\Sigma}^{0}=A^{0}$ .

Next, assume that for some $i>0$ we have an inclusion $A^{i-1}_{\Sigma}\subset A^{i-1}$ which is a homotopy equivalence. Let $\sigma\in\triangle_{\Sigma}^{*(i+1)}$ provide an $i$ -cell $H\cap\sigma$ in $A_{\Sigma}$ . In this case, we want to show that $H\cap\sigma\subset A^{i}$ . In fact, we have $\partial(H\cap\sigma)\subset A^{i-1}_{\Sigma}$ , hence $\partial(H\cap\sigma)\subset A^{i-1}$ , by induction. But by the rationality assumption on the transverse type, it follows from (ii) and section 3 that we must have $\sigma\subset A^{i}$ , thus $A_{\Sigma}^{i}\subset A^{i}$ .

To show that this inclusion is a homotopy equivalence, let $\sigma\in\triangle_{f}^{*(i+1)}$ provide an $i$ -cell $H\cap\sigma$ which is not in $A_{\Sigma}^{i}$ . By definition, we see that $\sigma\not\subset A^{i}$ as well. In fact, similarly as in the proof of (i), the inclusion $\partial(H\cap\sigma)\cap A^{i}\subset(H\cap\sigma)\cap A^{i}$ is a strong deformation retract. Since these cells, along with $A_{\Sigma}^{i}$ provide a finite closed covering, these glue together to form a strong deformation retract $A^{i}\to A_{\Sigma}^{i}$ . ∎

\thelemma Lemma.

Let $K,L\subset\mathbb{R}^{N}$ . Assume that $K$ is given as a finite disjoint union $K=\cup_{\alpha\in I}K_{\alpha}$ of relatively open convex polyhedrons $K_{\alpha}$ , i.e. each $K_{\alpha}$ is given by a finite number of affine equations and strict inequalities. Furthermore, assume the following two conditions:

❀

If $F$ is the face of $\overline{K}_{\alpha}$ for some $\alpha$ , then $F=\overline{K}_{\beta}$ for some $\beta$ .
❀

For any $\alpha,\beta$ , the intersection $\overline{K}_{\alpha}\cap\overline{K}_{\beta}$ is a face of both $\overline{K}_{\alpha}$ and $\overline{K}_{\beta}$ .

Note that the polyhedrons $K_{\alpha}$ may be unbounded. In this case

(i)

Assume that $K$ is compact and $L$ is convex. Then the inclusion

(7.3) $\bigcup_{\alpha\in I}\left\{\overline{K}_{\alpha}\,\middle|\,\overline{K}_{\alpha}\cap L=\emptyset\right\}\subset K\setminus L$

is a strong deformation retract.
(ii)

Assume that $L$ is convex. Then the inclusion

$\bigcup_{\alpha\in I}\left\{K_{\alpha}\,\middle|\,K_{\alpha}\cap L\neq\emptyset\right\}\subset K\cap L$

is a strong deformation retract.

Proof.

We prove item (i), similar arguments work for (ii). We use induction on the number of $\alpha$ with $K_{\alpha}\cap L\neq\emptyset$ . Indeed, if this number is zero, then the inclusion in eq. 7.3 is an equality.

Otherwise, there is an $\alpha_{0}$ with $K_{\alpha_{0}}\cap L\neq\emptyset$ . Define

I^{\prime}=\left\{\alpha\in I\,\middle|\,\overline{K}_{\alpha}\not\supset\overline{K}_{\alpha_{0}}\right\}\subsetneq I,\quad K^{\prime}=\cup_{\alpha\in I^{\prime}}K_{\alpha}.

Then the left hand side of eq. 7.3 does not change if we replace $I$ by $I^{\prime}$ . Therefore, using the induction hypothesis, it is enough to show that the inclusion $K^{\prime}\setminus L\subset K\setminus L$ is a homotopy equivalence. We do this by constructing a deformation retract $h:K\setminus L\times[0,1]\to K\setminus L$ . For this, we use the finite closed covering $\overline{K}_{\alpha}\setminus L$ , $\alpha\in I$ of $K\setminus L$ . It is then enough to define the restriction $h_{\alpha}$ of $h$ to $(\overline{K}_{\alpha}\setminus L)\times[0,1]$ for $\alpha\in I$ in such a way that these definitions coincide on intersections.

For any $\alpha\in I^{\prime}$ , we define $h_{\alpha}(x,t)=x$ . Let $q\in K_{\alpha_{0}}\cap L$ . If $\alpha\in I\setminus I^{\prime}$ , then $q\in\overline{K}_{\alpha}$ , and we define $h_{\alpha}$ by projecting away from $q$ , that is, for any $x\in K_{\alpha}$ there is a unique $y$ in the intersection of $\partial\overline{K}_{\alpha}\setminus K_{\alpha_{0}}$ and they ray starting at $q$ passing through $x$ . We define $h_{\alpha}(x,t)=(1-t)x+ty$ . One readily verifies that these functions are continuous, agree on intersections of their domains and define a strong deformation retract. ∎

8. Canonical divisors and cycle

In this section we describe possible canonical divisors for $\widetilde{Y}=Y_{\widetilde{\triangle}_{f}}$ and $\widetilde{X}$ . Furthermore, in the case $d=2$ , we give a formula for the canonical cycle.

\thedefinition Definition.

Let $\widetilde{X}\to X$ be a resolution of singularities of an $(r-1)$ -dimensional singularity. A canonical divisor $K_{\widetilde{X}}$ on $\widetilde{X}$ is any divisor satisfying $\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}})\cong\Omega_{\widetilde{X}}^{r-1}$ .

If $r=3$ then let $E=\cup_{v\in\mathcal{V}}E_{v}$ be the exceptional divisor of a resolution $\widetilde{X}\to X$ , where $E_{v}$ are the irreducible components of $E$ . Recall that we denoted by $L$ the lattice of integral cycles in $\widetilde{X}$ supported on the exceptional divisor $E$ : that is, $L=\mathbb{Z}\left\langle E_{v}\,\middle|\,v\in\mathcal{V}\right\rangle$ . We also set $L_{\mathbb{Q}}=L\otimes\mathbb{Q}$ and

L^{\prime}=\mathop{\rm Hom}\nolimits(L,\mathbb{Z})\cong\left\{l^{\prime}\in L_{\mathbb{Q}}\,\middle|\,\forall l\in L:\,(l^{\prime},l)\in\mathbb{Z}\right\},

where $(\cdot,\cdot)$ denotes the intersection form, extended linearly to $L_{\mathbb{Q}}$ . Moreover, set $E^{*}_{v}\in L^{\prime}$ for the unique rational cycle satisfying $(E_{v},E_{v}^{*})=-1$ and $(E_{w},E_{v}^{*})=0$ for $w\neq v$ .

In this surface singularity case the canonical cycle $Z_{K}\in L^{\prime}$ is the unique rational cycle on $\widetilde{X}$ supported on the exceptional divisor, satisfying the adjunction formula

(E_{v},Z_{K})=-b_{v}+2-2g_{v}

for any irreducible component $E_{v}$ of the exceptional divisor, where $-b_{v}$ is the Euler number of the normal bundle of $E_{v}\subset\widetilde{X}$ , and $g_{v}$ is the genus of $E_{v}$ (we assume here that the components $E_{v}$ of the exceptional divisor are smooth).

\therem Remark.

The cycles $Z_{K}$ and $E_{v}^{*}$ are well defined, since the intersection matrix, with entries $(E_{v},E_{w})$ , associated with any resolution is negative definite. Notice also that any two canonical divisors are linearly equivalent, and that any canonical divisor $K$ is numerically equivalent to $-Z_{K}$ . However, it can happen that $\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}+Z_{K})$ has infinite order in the Picard group.

\theprop Proposition.

Fix any $r$ . Let $(X,0)\subset(Y,0)$ be a Newton nondegenerate Weil divisor, and $\widetilde{\triangle}_{f}$ a subdivision of the normal fan $\triangle_{f}$ so that $\widetilde{Y}\to Y$ is an embedded resolution. Then the divisors

(8.1)

K_{\widetilde{Y}}=-\sum_{\sigma\in\widetilde{\triangle}^{(1)}_{f}}D_{\sigma}\in\mathop{\rm Div}\nolimits(\widetilde{Y}),\quad K_{\widetilde{X}}=-\sum_{\sigma\in\widetilde{\triangle}^{(1)}_{f}}(1+m_{\sigma})E_{\sigma}\in\mathop{\rm Div}\nolimits(\widetilde{X})

are possible canonical divisors for $\widetilde{Y}$ and $\widetilde{X}$ , respectively.

Furthermore, in the surface case ( $r=3$ ), the canonical cycle on $\widetilde{X}$ is given by the formula

(8.2)

Z_{K}-E=\mathop{\rm wt}\nolimits(f)-\sum(m_{n}+1)E_{v}^{*},

where the sum to the right runs through edges $\{n,v\}$ in the graph $G^{*}$ so that $n\in\mathcal{N}^{*}\setminus\mathcal{N}$ and $v\in\mathcal{V}$ (and the identity is in $L$ ).

Proof.

For $K_{\widetilde{Y}}$ , see e.g. 4.3 of [13]. Since the divisor $\widetilde{X}+\sum_{\sigma\in\widetilde{\triangle}_{f}^{(1)}}m_{\sigma}D_{\sigma}=(\pi^{*}f)$ is principal in $\widetilde{Y}$ (and $D_{\sigma}|_{\widetilde{X}}=E_{\sigma}$ ), the adjunction formula gives

K_{\widetilde{X}}=\left.\left(K_{\widetilde{Y}}+\widetilde{X}\right)\right|_{\widetilde{X}}=-\sum_{\sigma\in\widetilde{\triangle}_{f}^{(1)}}(m_{\sigma}+1)E_{\sigma},

which proves eq. 8.1. To prove eq. 8.2, it is enough to show that in $L$ for all $v\in\mathcal{V}$ ,

(8.3)

(Z_{K}-E,E_{v})=\left(\mathop{\rm wt}\nolimits(f)-\sum(m_{n}+1)E_{v}^{*},E_{v}\right),

where the sum is as in eq. 8.2. Recall that $\mathop{\rm wt}\nolimits(f)=\sum_{v\in\mathcal{V}}m_{v}E_{v}$ . We note that the adjunction formula gives $(Z_{K}-E,E_{v})=2-2g_{v}-\delta_{v}$ for all $v\in\mathcal{V}$ , where $\delta_{v}$ is the valency of the vertex $v$ in $G$ , and $g_{v}$ is the genus of $E_{v}$ . Furthermore, it follows from section 6 that if $v\in\mathcal{V}$ , then

❀

$\delta_{v}=1$ if and only $v$ is on the end of a bamboo joining a node $n\in\mathcal{N}$ and an extended node $n^{\prime}\in\mathcal{N}^{*}\setminus\mathcal{N}$ . In this case, $v$ has exactly one neighbour in $\mathcal{V}^{*}\setminus\mathcal{V}$ in the graph $G^{*}$ .
❀

$\delta_{v}=2$ if and only $v$ is on a bamboo joining two extended nodes, and is not of the form described in the previous item.
❀

$\delta_{v}\geq 3$ if and only if $v$ is a node.

Consider first the case $\delta_{v}=1$ , and let $n$ be the unique neighbour of $v$ in $\mathcal{N}^{*}\setminus\mathcal{N}$ . It follows from section 6 that $(\mathop{\rm wt}\nolimits(f),E_{v})=-m_{n}$ , since $F_{v}$ is a segment, and so has area zero. As a result, the right hand side of eq. 8.3 is $1=(Z_{K}-E,E_{v})$ .

Next, assume that $\delta_{v}=2$ . Then both sides of eq. 8.3 vanish (use again section 6).

Assume finally that $v\in\mathcal{N}$ . Then, $v$ has no neighbours in $\mathcal{N}^{*}\setminus\mathcal{N}$ . Furthermore, $\delta_{v}$ coincides with the number of integral points on the boundary of $F_{v}$ , since each edge adjacent to $v$ can be seen to correspond to a primitive segment of the boundary. By using Pick’s theorem and section 6, we therefore get

(Z_{K}-E,E_{v})=2-2g_{v}-\delta_{v}=-2\mathop{\rm Vol}\nolimits_{2}(F_{v})=(E_{v},\mathop{\rm wt}\nolimits(f)),

which finishes the proof. ∎

\therem Remark.

As $m_{\sigma}$ depends on the choice of $f$ up to a $x^{p}$ multiplication, the right hand side of the second formula from eq. 8.1 depends on this choice too. In fact, the monomial rational function $x^{p}$ realizes the linear equivalence between the two divisors $K_{\widetilde{X}}$ associated with two such choices.

9. Gorenstein surface singularities

In this section we prove theorem 9.1, which characterizes nondegenerate normal surface Gorenstein singularities by their Newton polyhedron. The key technical sections 9 and 9 provide the tools for the proof. They are proved using vanishing of certain cohomology groups calculated by toric methods. In the first lemma, the restriction $r=3$ is not needed. However, the second lemma relies on the negative definiteness of the intersection form, restricting our result to the surface case.

\thedefinition Definition.

Let $f$ and $\triangle_{f}$ be as above. We say that $\Gamma_{+}(f)$ , or $f$ , is ( $\mathbb{Q}$ -)Gorenstein-pointed if there exists a $p\in M$ ( $p\in M_{\mathbb{Q}}$ ) such that $\ell_{\sigma}(p)=m_{\sigma}+1$ for all $\sigma\in\triangle^{*(1,1)}_{f}$ .

\theexample Example.

Recall that $(Y,0)$ is Gorenstein if and only if there is a $p\in M$ satisfying $\ell_{\sigma}(p)=1$ for all $\sigma\in\triangle_{\Sigma}^{(1)}$ , see e.g. [8], Theorem 6.32. Therefore, if $(X,0)$ is Cartier, and $\triangle_{f}^{*}=\triangle_{\Sigma}^{*}$ , then $f$ is Gorenstein pointed (since $m_{\sigma}=0$ for $\sigma\in\triangle_{\Sigma}^{(1)}$ ). Furthermore, $(X,0)$ is Gorenstein since $(Y,0)$ is Gorenstein and $f$ forms a regular sequence.

Similarly, $(Y,0)$ is $\mathbb{Q}$ -Gorenstein if there is a $p\in M_{\mathbb{Q}}$ satisfying $\ell_{\sigma}(p)=1$ for all $\sigma\in\triangle_{\Sigma}^{(1)}$ , see e.g. [1]. Therefore, if $(X,0)$ is Cartier, and $\triangle_{f}^{*}=\triangle_{\Sigma}^{*}$ , then $f$ is $\mathbb{Q}$ -Gorenstein pointed.

\therem Remark.

Though the two combinatorial conditions in definitions 3 and 9 look very similar, they codify two rather different geometrical properties. Being ‘pointed’ codifies an embedding property, namely that $(X,0)\subset(Y,0)$ is Cartier, see section 3. However, being ‘Gorenstein pointed’ codifies an abstract property of the germ $(X,0)$ , namely its Gorenstein property, see theorem 9.1 below.

\theblock.

Recall also that $(X,0)$ is Gorenstein if it admits a Gorenstein form. A Gorenstein form is a nowhere vanishing section in $H^{0}(X\setminus 0,\Omega^{2}_{X\setminus 0})=H^{0}(\widetilde{X}\setminus E,\Omega^{2}_{\widetilde{X}\setminus E})$ . A Gorenstein pluri-form is a nowhere vanishing section in $H^{0}(\widetilde{X}\setminus E,(\Omega^{2}_{\widetilde{X}\setminus E})^{\otimes k})$ for some $k\in\mathbb{Z}_{>0}$ .

In this section $K_{\widetilde{Y}}$ and $K_{\widetilde{X}}$ are canonical divisors with a choice as in eq. 8.1.

\thedefinition Definition.

Let $\omega_{f}$ be some meromorphic 2-form on $\widetilde{X}$ whose divisor $(\omega_{f})$ is $K_{\widetilde{X}}$ .

9.1 Theorem.

Assume that $(X,0)\subset(Y,0)$ is a normal Newton nondegenerate surface singularity (i.e. $r=3$ ). The following conditions are equivalent:

(i)

$f$ is Gorenstein-pointed at some $p\in M$ .
(ii)

There exists a $p\in M$ so that for all $v\in\mathcal{V}^{*}\setminus\mathcal{V}$ we have $\ell_{v}(p)=m_{v}+1$ .
(iii)

There exists a $p\in M$ so that for all $v\in\mathcal{V}$ we have $\ell_{v}(p)=m_{v}+1-m_{v}(Z_{K})$ .
(iv)

There exists a $p\in M$ so that $x^{p}\omega_{f}$ is a Gorenstein form.
(v)

$(X,0)$ is Gorenstein.

When these conditions hold, (i), (ii), (iii) and (iv) uniquely identify the same point $p$ .

In fact, the analogues of parts item (i)–item (iv) are equivalent over rational points $p\in M_{\mathbb{Q}}$ as well.

\theprop Proposition.

Under the assumption of theorem 9.1, the following conditions are equivalent, and imply that $(X,0)$ is $\mathbb{Q}$ -Gorenstein:

(i)

$f$ is $\mathbb{Q}$ -Gorenstein-pointed at some $p\in M_{\mathbb{Q}}$ .
(ii)

There exists a $p\in M_{\mathbb{Q}}$ so that for all $v\in\mathcal{V}^{*}\setminus\mathcal{V}$ we have $\ell_{v}(p)=m_{v}+1$ .
(iii)

There exists a $p\in M_{\mathbb{Q}}$ so that for all $v\in\mathcal{V}$ we have $\ell_{v}(p)=m_{v}+1-m_{v}(Z_{K})$ .
(iv)

There exists a $p\in M_{\mathbb{Q}}$ so that $x^{kp}(\omega_{f})^{\otimes k}$ is a Gorenstein pluri-form for some $k\in\mathbb{Z}_{>0}$ .

Furthermore, all these these conditions identify the very same $p$ uniquely.

Proof.

(ii) is a rephrasing of (i), since $\triangle^{*(1,1)}_{f}=\mathcal{V}^{*}\setminus\mathcal{V}$ .

(ii) $\Rightarrow$ (iii) For any $p\in M_{\mathbb{Q}}$ consider the cycles

Z_{1}:=\sum_{v\in\mathcal{V}}\ell_{v}(p)E_{v}\in L_{\mathbb{Q}},\qquad Z_{2}:=\sum(m_{n}+1)E_{v}^{*}\in L_{\mathbb{Q}},

where the sum runs over edges $\{n,v\}$ in $G^{*}$ so that $n\in\mathcal{V}^{*}$ and $v\in\mathcal{V}$ (as in eq. 8.2), and $Z^{*}:=\sum_{n\in\mathcal{V}^{*}\setminus\mathcal{V}}\ell_{n}(p)E_{n}$ (where all these $E_{n}$ ’s are the noncompact curves in $\widetilde{X}$ ).

If $\{n,v\}$ is an edge as above, then $(Z_{2},E_{v})=-(m_{n}+1)$ . Moreover, $(Z^{*},E_{v})_{\widetilde{X}}=\ell_{n}(p)$ . Therefore, by assumption (ii), $(Z^{*}+Z_{2},E_{u})_{\widetilde{X}}=0$ for any $u\in\mathcal{V}$ . On the other hand, by section 6, $(Z^{*}+Z_{1},E_{u})_{\widetilde{X}}=0$ for any $u\in\mathcal{V}$ as well. Hence $Z_{1}=Z_{2}$ . But by eq. 8.2 $m_{u}(Z_{2})=m_{v}+1-m_{v}(Z_{K})$ .

(iii) $\Rightarrow$ (ii) With the above notations, (iii) shows that $Z_{1}=Z_{2}$ . Let $\{n,v\}$ be an edge as above, let $w\in\mathcal{V}$ be the other neighbour of $v$ , and note that $E_{v}=b_{v}E^{*}_{v}-E^{*}_{w}$ in $L^{\prime}$ . Then,

m_{n}+1=(Z_{2},-E_{v})=(Z_{1},-b_{v}E^{*}_{v}+E^{*}_{w})=\ell_{v}(p)b_{v}-\ell_{w}(p)=\ell_{n}(p)

(in the last equality use section 6).

For (ii) $\Leftrightarrow$ (iv) use the second identity of eq. 8.1. ∎

\therem Remark.

Similarly as in theorem 9.1, one may ask whether the equivalent cases in 9 are equivalent with the property that $(X,0)$ is $\mathbb{Q}$ -Gorenstein. If $f$ is $\mathbb{Q}$ -Gorenstein-pointed at $p\in M_{\mathbb{Q}}$ , then (iv) implies that $(X,0)$ is $\mathbb{Q}$ -Gorenstein. The converse does not hold, as seen by the following example.

Let $N=\mathbb{Z}^{3}$ and

\Sigma=\mathbb{R}_{\geq 0}\langle(1,0,0),(0,1,0),(1,0,1),(0,1,1)\rangle,\quad f(x)=x^{(0,0,2)}+x^{(1,0,1)}+x^{(0,2,0)}+2x^{(1,2,-1)}.

Write $\sigma_{i}$ , $i=1,2,3,4$ for the rays generated by the vector specified above and denote by $m_{i}$ the corresponding multiplicities. We find $m_{1}=m_{2}=m_{3}=0$ and $m_{4}=1$ . As a result, since the linear equation

\left(\begin{matrix}1&0&0\\ 0&1&0\\ 1&0&1\\ 0&1&1\end{matrix}\right)\cdot p=\left(\begin{matrix}1\\ 1\\ 1\\ 2\end{matrix}\right)

has no solution, hence $f$ is not $\mathbb{Q}$ -Gorenstein pointed.

On the other hand, one verifies that the Weil divisor defined by $f$ is normal using theorem 7.1. Furthermore, Oka’s algorithm shows that this singularity has a resolution with an exceptional divisor consisting of a single rational curve with Euler number $-3$ . Such a singularity is a cyclic quotient singularity. In particular, it is $\mathbb{Q}$ -Gorenstein.

\theblock.

Next, we focus on the proof of theorem 9.1. The equivalences of the first four cases follow from (or, as) section 9. For item (i) $\Rightarrow$ item (v) note that if $f$ is Gorenstein-pointed at $p\in M$ then $x^{p}\omega_{f}$ trivializes the canonical bundle. The implication item (v) $\Rightarrow$ item (i) will be proved below based on two lemmas.

\thelemma Lemma.

Let $\,\overline{g}\in H^{0}(\widetilde{X}\setminus E,\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}))$ , that is, $\overline{g}$ is a meromorphic function on the complement of the exceptional divisor in $\widetilde{X}$ satisfying

(9.1)

(\overline{g})\geq-K_{\widetilde{X}}|_{\widetilde{X}\setminus E}=\sum_{v\in\mathcal{V}^{*}\setminus\mathcal{V}}(m_{v}+1)E_{v}.

Then, there exists a Laurent series $g\in\mathcal{O}_{Y,0}[x^{M}]$ satisfying $(\pi^{*}g)|_{\widetilde{X}\setminus E}=\overline{g}$ and

(9.2)

\forall\sigma\in\widetilde{\triangle}_{f}^{*(1)}:\,\mathop{\rm wt}\nolimits_{\sigma}g\geq m_{\sigma}+1.

Proof.

Let $I=H^{0}(\widetilde{X}\setminus E,\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}))$ and let $J$ be the set of meromorphic functions obtained as a restriction of Laurent series satisfying eq. 9.2. We want to show that $I=J$ .

We immediately see $J\subset I$ . In fact, this inclusion fits into an exact sequence as follows. Recall the notation $D_{m}=\sum_{\sigma\in\widetilde{\triangle}_{f}^{(1)}}m_{\sigma}D_{\sigma}$ from the proof of theorem 7.1, and $K_{\widetilde{Y}}=-\sum_{\sigma\in\widetilde{\triangle}_{f}^{(1)}}D_{\sigma}$ . Also, define $D_{\mathrm{c}}$ as the union of compact divisors in $\widetilde{Y}$ , that is, $\cup_{\sigma}D_{\sigma}$ for $\sigma\not\in\widetilde{\triangle}_{f}^{*(1)}$ . Since $(\pi^{*}f)=\widetilde{X}+D_{m}$ , we have a short exact sequence of sheaves

0\to\mathcal{O}_{\widetilde{Y}\setminus D_{\mathrm{c}}}(K_{\widetilde{Y}})\stackrel{{\scriptstyle\cdot f}}{{\to}}\mathcal{O}_{\widetilde{Y}\setminus D_{\mathrm{c}}}(-D_{m}+K_{\widetilde{Y}})\to\mathcal{O}_{\widetilde{X}\setminus E}(-D_{m}+K_{\widetilde{Y}})\to 0

yielding a long exact sequence of cohomology groups. We have

I=H^{0}(\widetilde{X}\setminus E,\mathcal{O}_{\widetilde{X}\setminus E}(-D_{m}+K_{\widetilde{Y}})),

since $K_{\widetilde{X}}=(-D_{m}+K_{\widetilde{Y}})|_{\widetilde{X}}$ . Furthermore, since $\widetilde{Y}$ is normal, $H^{0}(\widetilde{Y}\setminus D_{\mathrm{c}},\mathcal{O}_{\widetilde{Y}\setminus D_{\mathrm{c}}}(-D_{m}+K_{\widetilde{Y}}))$ is the set of Laurent series satisfying eq. 9.2. Thus, its image in $I$ is $J$ . Therefore, the quotient $I/J$ injects into $H^{1}(\widetilde{Y}\setminus D_{\mathrm{c}},\mathcal{O}_{\widetilde{Y}\setminus D_{\mathrm{c}}}(K_{\widetilde{Y}}))$ . On the other hand,

(9.3)

H^{1}(\widetilde{Y}\setminus D_{\mathrm{c}},\mathcal{O}_{\widetilde{Y}\setminus D_{\mathrm{c}}}(K_{\widetilde{Y}}))\cong\bigoplus_{p\in M}H^{1}_{Z(p)}(\partial\Sigma,\mathbb{C}),

where, following Fulton [13], $\psi_{K}:\partial\Sigma\to\mathbb{R}$ is the unique function restricting to linear function on all $\sigma\in\widetilde{\triangle}_{f}^{*}$ , and satisfying $\psi_{K}(\ell_{\sigma})=1$ for $\sigma\in\widetilde{\triangle}_{f}^{(1)*}$ , and for $p\in M$ we set

Z(p)=\left\{\ell\in\partial\Sigma\,\middle|\,\ell(p)\geq\psi_{K}(\ell)\right\}.

Firstly, since $\partial\Sigma$ is contractible, we find

H^{1}_{Z(p)}(\partial\Sigma,\mathbb{C})\cong\widetilde{H}^{0}(\partial\Sigma\setminus Z(p),\mathbb{C}).

Secondly, define $Z^{\prime}(p)$ as the union of those cones $\sigma\in\widetilde{\triangle}_{f}^{*}$ satisfying $p|_{\sigma}\geq 0$ (i.e. $\ell(p)\geq 0$ for all $\ell\in\sigma$ ), and let $Z^{\prime\prime}(p)$ be the set of $\ell\in\partial\Sigma$ satisfying $\ell(p)\geq 0$ . By section 7, the inclusions

\partial\Sigma\setminus Z(p)\subset\partial\Sigma\setminus Z^{\prime}(p)\supset\partial\Sigma\setminus Z^{\prime\prime}(p)

are strong deformation retracts. But the right hand side above is either a contractible set, or it has the homotopy of $S^{r-2}$ . In particular, it is connected, by our assumption $r>2$ , and so eq. 9.3 vanishes. ∎

\thelemma Lemma.

Assume that $(X,0)$ is a Gorenstein normal surface singularity, i.e. $r=3$ , and that we have a Gorenstein form $\omega$ on $\widetilde{X}\setminus E$ . Thus, $-K_{\widetilde{X}}-Z_{K}$ is linearly trivial, and there exists

\overline{g}\in H^{0}(\widetilde{X},\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}+Z_{K})),\quad(\overline{g})=(\omega)-(\omega_{f})=-Z_{K}-K_{\widetilde{X}}.

Then there is a $g\in\mathcal{O}_{Y,0}[x^{M}]$ satisfying

(9.4)

(\pi^{*}g)|_{\widetilde{X}}=\overline{g}\quad\mathrm{and}\quad\forall v\in\mathcal{V}^{*}:\,\mathop{\rm wt}\nolimits_{v}(g)=\mathop{\rm div}\nolimits_{v}(\overline{g}).

Proof.

By the previous section 9, we can find a $g$ satisfying $g|_{\widetilde{X}\setminus E}=\overline{g}$ and eq. 9.2. Let $A=(\overline{g})$ and $B=\sum_{v\in\mathcal{V}^{*}}\mathop{\rm wt}\nolimits_{v}(g)E_{v}$ . We want to prove that $A=B$ . Both $A$ and $B$ are supported in the exceptional divisor and the noncompact curves $E_{v}$ for $v\in\mathcal{V}^{*}\setminus\mathcal{V}$ , and by our assumptions, they have the same multiplicity along this noncompact part. Thus, $A-B$ is supported on the exceptional divisor. Furthermore, we have $\mathop{\rm wt}\nolimits_{v}(g)\leq\mathop{\rm div}\nolimits_{v}(\overline{g})$ for $v\in\mathcal{V}$ , thus $B-A\leq 0$ .

For the reverse inequality, note first that $(A,E_{v})=0$ for all $v\in\mathcal{V}$ since $A$ is principal. For any $v\in\mathcal{V}$ , let $q\in M$ be an element of the support of the principal part of $g$ with respect to $\ell_{v}$ , i.e. $q\in\mathop{\rm supp}\nolimits(g)$ and $\ell_{v}(q)=\mathop{\rm wt}\nolimits_{v}(g)$ . By definition, we also have $\ell_{u}(q)\geq\mathop{\rm wt}\nolimits_{u}(g)$ for all $u\in\mathcal{V}^{*}_{v}$ . Therefore,

(B,E_{v})=-b_{v}\mathop{\rm wt}\nolimits_{v}(g)+\sum\left\{\mathop{\rm wt}\nolimits_{u}(g)\,\middle|\,u\in\mathcal{V}^{*}_{v}\right\}\leq-b_{v}\ell_{v}(q)+\sum\left\{\ell_{u}(q)\,\middle|\,u\in\mathcal{V}^{*}_{v}\right\}=0.

As a result, $B-A$ is in the Lipman cone, and so, $B-A\geq 0$ , proving eq. 9.4. ∎

Proof of theorem 9.1.

The first four conditions are equivalent by section 9, and item (iv) clearly implies item (v).

Assuming that $(X,0)$ is Gorenstein, let $\omega$ be a Gorenstein form. Then there is meromorphic $\overline{g}$ so that $\overline{g}\omega_{f}=\omega$ on $\widetilde{X}\setminus E$ . By section 9, $\overline{g}$ is the restriction of a Laurent series $g\in\mathcal{O}_{Y,0}[x^{M}]$ satisfying eq. 9.4.

For any $v\in\mathcal{V}$ , denote by $g_{v}$ the principal part of $g$ with respect to the weight $\ell_{v}$ . We make the

Claims:

(a)

For any $n\in\mathcal{N}$ , $g_{n}$ is a monomial, that is, there is a $p_{n}\in M$ so that $g_{n}=a_{n}x^{p_{n}}$ for some $a_{n}\in\mathbb{C}^{*}$ .
(b)

If $v$ is a vertex on a bamboo connecting $n\in\mathcal{N}$ and some other node in $\mathcal{N}^{*}$ , then $g_{v}=a_{n}x^{p_{n}}$ .

By (b), the exponent $p=p_{n}$ does not depend on $n$ , finishing the proof since hence $x^{p}\omega_{f}$ is a Gorenstein form.

(a) is proved as follows. Set $q\in\mathop{\rm supp}\nolimits(g_{n})$ arbitrarily. We then have $\mathop{\rm wt}\nolimits_{n}(g)=\ell_{n}(q)$ , and also $\mathop{\rm wt}\nolimits_{u}(g)\leq\ell_{u}(q)$ , for any other $u$ , since $\mathop{\rm supp}\nolimits(g_{n})\subset\mathop{\rm supp}\nolimits(g)$ . In particular,

-b_{n}\mathop{\rm wt}\nolimits_{n}(g)+\sum_{u\in\mathcal{V}_{n}}\mathop{\rm wt}\nolimits_{u}(g)\leq-b_{n}\ell_{n}(q)+\sum_{u\in\mathcal{V}_{n}}\ell_{u}(q).

The right hand side is sero since $\ell_{n}+\sum_{u\in\mathcal{V}_{n}}\ell_{u}=0$ for $n\in\mathcal{N}$ . On the other hand, by the section 9, we have $\mathop{\rm wt}\nolimits_{v}(g)=\mathop{\rm div}\nolimits_{v}(\overline{g})$ for all $v$ , thus, the left hand side above equals $(\mathop{\rm div}\nolimits(g),E_{n})$ . Furthermore, since $(\overline{g})=(\omega)-(\omega_{f})$ , $g$ does not have any zeroes or poles outside the exceptional divisor, in a neighbourhood around $E_{n}$ , hence $(\mathop{\rm div}\nolimits(\overline{g}),E_{n})=((g),E_{n})=0$ . Therefore, the inequality above is an equality, and we have $\mathop{\rm wt}\nolimits_{u}(g)=\ell_{u}(q)$ for $u\in\mathcal{V}_{n}$ .

This fact is true for any choice of $q$ , therefore, $\ell_{u}(q^{\prime})=\mathop{\rm wt}\nolimits_{u}(g)=\ell_{u}(q)$ for any $u\in\mathcal{V}_{n}$ and for any other choice $q^{\prime}$ . But the vectors $\{\ell_{u}\}_{u\in\mathcal{V}_{n}}$ form a generator set, hence necessarily $q=q^{\prime}$ .

For (b), assume that $n$ and $n^{\prime}\in\mathcal{N}^{*}$ are joined by a bamboo, consisting of vertices $v_{1},\ldots,v_{s}$ , with $v_{1}\in\mathcal{V}_{n}$ and $v_{s}\in\mathcal{V}_{n^{\prime}}$ , and $v_{i},v_{i+1}$ neighbours for $i=1,\ldots,s-1$ . For convenience, we set $v_{0}=n$ and $v_{s+1}=n^{\prime}$ . We start by showing that $\mathop{\rm wt}\nolimits_{i}(g)=\ell_{i}(p_{n})$ using induction (we replace the subscript $v_{i}$ by just $i$ for legibility). Indeed, for $i=0$ this is clear, and we showed in the proof of (a) that this holds for $i=1$ . For the induction step we use the recursive formulas

\ell_{i+1}-b_{i}\ell_{i}+\ell_{i-1}=0,\quad\mathop{\rm wt}\nolimits_{i+1}(g)-b_{i}\mathop{\rm wt}\nolimits_{i}(g)+\mathop{\rm wt}\nolimits_{i-1}(g)=0.

The first one holds by section 6, and the second one follows from $\mathop{\rm wt}\nolimits_{i}(g)=\mathop{\rm div}\nolimits_{i}(g)$ similarly as above, although for the case $i=s$ , we may have to use a component of the noncompact curve $E_{n^{\prime}}$ .

We now see that for any $1\leq i\leq s$ , the support of $g_{i}$ consists of points $q\in M$ for which $\ell_{i}(q)=\ell_{i}(p_{n})$ and $\ell_{i\pm 1}(q)\geq\ell_{i\pm 1}(p_{n})$ . But these equations are equivalent to $\ell_{n}(q)=\ell_{n}(p_{n})$ and $\ell_{n^{\prime}}(q)=\ell_{n^{\prime}}(p_{n})$ . Therefore, $\mathop{\rm supp}\nolimits(g_{i})=\mathop{\rm supp}\nolimits(g_{n})$ for these $i$ . ∎

10. The geometric genus and the diagonal computation sequence

In this section we construct the diagonal computation sequence, and show that it computes the geometric genus of any Newton nondegenerate, $\mathbb{Q}$ -Gorenstein pointed, normal surface singularity having a rational homology sphere link. Any computation sequence provides an upper bound for the geometric genus. The smallest such bound is a topological invariant, and we show that this is realized by this diagonal sequence. This is done by showing that the diagonal computation sequence counts the lattice points “under the diagram”, whose number is precisely the geometric genus, according to section 7.

\theblock.

Discussions regarding general normal surface singularities. Throughout this section, when not mentioned specifically, $\pi:(\widetilde{X},E)\to(X,0)$ denotes a resolution of a normal surface singularity $(X,0)$ with exceptional divisor $E$ , whose irreducible decomposition is $E=\cup_{v\in\mathcal{V}}E_{v}$ .

We assume that $(X,0)$ has a rational homology sphere link; thus $E_{v}\cong\mathbb{CP}^{1}$ for all $v\in\mathcal{V}$ .

We use the notations $L$ , $L^{\prime}$ and $E^{*}_{v}$ as in section 8. For $Z=\sum_{v}r_{v}E_{v}$ with $r_{v}\in\mathbb{Q}$ we write $\lfloor Z\rfloor=\sum_{v}\lfloor r_{v}\rfloor E_{v}$ . $Z_{K}$ denotes the canonical cycle. Note that $Z_{K}=0$ if and only if $(X,0)$ is an $ADE$ germ. Otherwise, it is known that in the minimal resolution, or, even in the minimal good resolution, all the coefficients of $Z_{K}$ are strictly positive. However, usually this is not the case in non-minimal resolutions, i.e. in our $G$ it is not automatically guaranteed.

\thelemma Lemma.

In any resolution $\widetilde{X}\to X$ of a normal surface singularity with $\lfloor Z_{K}\rfloor\geq 0$ we have

(10.1)

p_{g}=\dim_{\mathbb{C}}\frac{H^{0}(\widetilde{X},\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}+\lfloor Z_{K}\rfloor))}{H^{0}(\widetilde{X},\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}))}.

Proof.

By the generalized version of Grauert–Riemenschneider vanishing we have the two vanishings

(10.2)

H^{1}(\widetilde{X},\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}))=0,\ \ \ H^{1}(\widetilde{X},\mathcal{O}_{\widetilde{X}}(-\lfloor Z_{K}\rfloor))=0.

Hence, if $\lfloor Z_{K}\rfloor=0$ then $p_{g}=0$ too. Otherwise, from the long exact sequence of cohomology groups associated with

0\to\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}})\to\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}+\lfloor Z_{K}\rfloor)\to\mathcal{O}_{\lfloor Z_{K}\rfloor}(K_{\widetilde{X}}+\lfloor Z_{K}\rfloor)\to 0,

we obtain that the right hand side of eq. 10.1 equals $\dim\,H^{0}(\lfloor Z_{K}\rfloor,\mathcal{O}_{\lfloor Z_{K}\rfloor}(K_{\widetilde{X}}+\lfloor Z_{K}\rfloor))$ . By Serre duality, this equals $H^{1}(\lfloor Z_{K}\rfloor,\mathcal{O}_{\lfloor Z_{K}\rfloor})$ . Now, the short exact sequence

0\to\mathcal{O}_{\widetilde{X}}(-\lfloor Z_{K}\rfloor)\to\mathcal{O}_{\widetilde{X}}\to\mathcal{O}_{\lfloor Z_{K}\rfloor}\to 0,

with the above vanishing eq. 10.2 gives $H^{1}(\lfloor Z_{K}\rfloor,\mathcal{O}_{\lfloor Z_{K}\rfloor})\cong H^{1}(\widetilde{X},\mathcal{O}_{\widetilde{X}})\cong\mathbb{C}^{p_{g}}$ . ∎

\thedefinition Definition.

A computation sequence is a sequence of cycles $(Z_{i})_{i=0}^{k}$ from $Z_{K}+L$ ,

Z_{K}-\lfloor Z_{K}\rfloor=Z_{0}<\ldots<Z_{k}

such that

(i)

for all $0\leq i<k$ there is a $v(i)\in\mathcal{V}$ so that $Z_{i+1}=Z_{i}+E_{v(i)}$ , and
(ii)

$Z_{k}\geq Z_{K}$ and $Z_{k}-Z_{K}$ is the union of some reduced and non-intersecting rational $(-1)$ -curves

Given such a sequence $(Z_{i})_{i=0}^{k}$ , we define

\mathcal{L}_{i}=\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}+Z_{K}-Z_{i}),\quad\mathcal{Q}_{i}=\mathcal{L}_{i}/\mathcal{L}_{i+1}.

Then $\mathcal{Q}_{i}$ is a line bundle on $E_{v(i)}$ . Denote by $d_{i}$ its degree. Since $K_{\widetilde{X}}+Z_{K}$ is numerically equivalent to zero, we have $d_{i}=(-Z_{i},E_{v(i)})$ . In particular, since $E_{v(i)}\cong\mathbb{CP}^{1}$ , we get $\mathcal{Q}_{i}=\mathcal{O}_{E_{v(i)}}(-d_{i})$ and

h^{0}(E_{v(i)},\mathcal{Q}_{i})=\max\{0,(-Z_{i},E_{v(i)})+1\}.

\theblock.

Given a computation sequence $(Z_{i})_{i}$ , the inclusion $\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}+Z_{K}-Z_{k})\hookrightarrow\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}})$ induces an isomorphism

H^{0}(\widetilde{X},\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}+Z_{K}-Z_{k})\stackrel{{\scriptstyle\cong}}{{\longrightarrow}}H^{0}(\widetilde{X},\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}})).

Indeed, let $\mathcal{U}\subset\mathcal{V}$ be such that $Z_{k}-Z_{K}=\sum_{u\in\mathcal{U}}E_{u}$ . Then we have a short exact sequence

0\to\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}-E_{\mathcal{U}})\to\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}})\to\bigoplus\mathcal{O}_{E_{u}}(K_{\widetilde{X}})\to 0,

which induces an exact sequence

0\to H^{0}(\widetilde{X},\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}+Z_{K}-Z_{k})\to H^{0}(\widetilde{X},\mathcal{O}_{\widetilde{X}}(K_{\widetilde{X}}))\to\bigoplus H^{0}(E_{u},\mathcal{O}_{E_{u}}(K_{\widetilde{X}})),

and the right hand side vanishes, since $(E_{u},K_{\widetilde{X}})=-2-2g_{u}+b_{u}=-1$ .

\thecor Corollary.

Let $(Z_{i})_{i=0}^{k}$ be a computation sequence. Then

(10.3)

p_{g}=\sum_{i=0}^{k-1}\dim\,\frac{H^{0}(\widetilde{X},\mathcal{L}_{i})}{H^{0}(\widetilde{X},\mathcal{L}_{i+1})}\leq\sum_{i=0}^{k-1}\max\{0,d_{i}+1\}.

with equality if and only if the map $H^{0}(\widetilde{X},\mathcal{L}_{i})\to H^{0}(E_{v(i)},\mathcal{Q}_{i})$ is surjective for all $0\leq i<k$ . ∎

\therem Remark.

(i)

We note in particular that if there exists a computation sequence $(Z_{i})_{i=0}^{k}$ so that $(Z_{i},E_{v(i)})>0$ for all $i$ , then $p_{g}=0$ , that is, $(X,0)$ is rational. In general, if $(Z_{i},E_{v(i)})>0$ for some $i$ , then the inequality between the $i^{\textrm{th}}$ terms in the sums eq. 10.3 is an equality.
(ii)

Let $S(Z_{i})$ be the sum $\sum_{i}\max\{0,d_{i}+1\}$ from the right hand side of eq. 10.3 associated with $(Z_{i})$ . Then we have

(10.4) $p_{g}\leq\min_{(Z_{i})}S(Z_{i}),$

where the minimum is taken over all computation sequences. Note that $\min_{(Z_{i})}S(Z_{i})$ is an invariant associated with the topological type (graph), hence in this way we get a topological upper bound for the geometric genus of all possible analytic types supported on a fixed topological type.

On the other hand we emphasize the following facts. In general it is hard to identify a sequence which minimizes $\{S(Z_{i})\}$ . Also, for an arbitrary fixed topological type, it is not even true that there exists an analytic type supported on the fixed topological type for which eq. 10.4 holds. Furthermore, it is even harder to identify those analytic structures which maximize $p_{g}$ , e.g., if eq. 10.4 holds for some analytic structure, then which are these maximizing analytic structures, see e.g. [24].

In the sequel our aim is the following: in our toric Newton nondegenerate case we construct combinatorially a sequence (it will be called ‘diagonal sequence’), which satisfies eq. 10.3 with equality (in particular it minimizes $\{S(Z_{i})\}$ as well). This also shows that if a topological type is realized by a Newton nondegenerate Weil divisor, then this germ maximizes the geometric genus of analytic types supported by that topological type.

\theblock.

We recall the construction of the Laufer operator and generalized Laufer sequences with respect to $\mathcal{N}\subset\mathcal{V}$ . We claim that for any cycle $Z\in L^{\prime}$ , there is a smallest cycle $x(Z)\in Z+L$ satisfying

(10.5)

\left\{\begin{array}[]{l}\forall n\in\mathcal{N}:\,m_{n}(x(Z))=m_{n}(Z),\\ \forall v\in\mathcal{V}\setminus\mathcal{N}:\,(x(Z),E_{v})\leq 0.\end{array}\right.

The existence and uniqueness of such an element is explained in [21] in the case when $|\mathcal{N}|=1$ and in general in [16, 25, 31]. The name comes from a construction of Laufer in [17, Proposition 4.1]. Note that $x(Z)$ only depends on the multiplicities $m_{n}(Z)$ of $Z$ for $n\in\mathcal{N}$ and the class $[Z]\in H=L^{\prime}/L$ .

The following properties hold for the operator $x$ , assuming $Z_{1}-Z_{2}\in L$ :

Monotonicity: If $Z_{1}\leq Z_{2}$ then $x(Z_{1})\leq x(Z_{2})$ .

Idempotency: We have $x(x(Z))=x(Z)$ for any $Z\in L^{\prime}$ .

Lower bound by intersection numbers: If $Z\in L^{\prime}$ and $Z^{\prime}\in L_{\mathbb{Q}}$ so that $m_{n}(Z)=m_{n}(Z^{\prime})$ for $n\in\mathcal{N}$ and $(Z^{\prime},E_{v})\geq 0$ for all $v\in\mathcal{V}\setminus\mathcal{N}$ , then $x(Z)\geq Z^{\prime}$ .

Generalized Laufer sequence: Assume that $Z\leq x(Z)$ . First note that if $(Z,E_{v})>0$ for some $v\in\mathcal{V}\setminus\mathcal{N}$ , then we have $Z+E_{v}\leq x(Z)$ as well, similarly as in the proof of Proposition 4.1 [17]. We claim that there exists a generalized Laufer sequence which connects $Z$ with $x(Z)$ . It is determined recursively as follows. Start by setting $Z_{0}=Z$ . Assume that we have constructed $Z_{i}$ . By induction, we then have $Z_{i}\leq x(Z)$ . If $(Z,E_{v})\leq 0$ for all $v\in\mathcal{V}\setminus\mathcal{N}$ then by the minimality of $x(Z)$ we get $Z_{i}=x(Z)$ ; hence the construction is finished and we stop. Otherwise, there is a $v\in\mathcal{V}\setminus\mathcal{N}$ so that $(Z,E_{v})>0$ . We then define $Z_{i+1}=Z_{i}+E_{v}$ (for some choice of such $v$ ).

\therem Remark.

The computation sequence $(Z_{i})_{i=0}^{k}$ (as in corollary 10), what we will construct, will have several intermediate parts formed by generalized Laufer sequences as above. Note that if $Z_{i}$ and $Z_{i+1}=Z_{i}+E_{v}$ are two consecutive elements in a Laufer sequence, then $-d_{i}=(Z_{i},E_{v})>0$ , hence $\max\{0,d_{i}+1\}=0$ , and the comment from section 10 applies: this step does not contribute in the sum on the right hand side of eq. 10.3. Informally, we say that parts given by Laufer sequences “do not contribute to the geometric genus”.

\theblock.

The Newton nondegenerate case. Let us consider again the resolution $\widetilde{X}\to X$ of Newton nondegenerate Weil divisor as in section 6. Let $K_{\widetilde{X}}$ denote a canonical divisor as in section 8. In this section we will assume that in the dual resolution graph $G$ we have $m_{n}(Z_{K})\geq 1$ for any node $n$ . This assumption will be justified in section 11.

From the assumption $m_{n}(Z_{K})\geq 1$ , valid for any node $n$ , an immediate application of the construction of $G$ from section 6 gives that $Z_{K}\geq 0$ . Thus $\lfloor Z_{K}\rfloor>0$ .

\thelemma Lemma.

(i)

$x(Z_{K}-\lfloor Z_{K}\rfloor)\geq Z_{K}-\lfloor Z_{K}\rfloor$ .
(ii)

Let $\mathcal{U}\subset\mathcal{V}$ be the set of $(-1)$ -vertices appearing on bamboos joining $n,n^{\prime}\in\mathcal{N}^{*}$ with $\alpha(\ell_{n},\ell_{n^{\prime}})=1$ in section 6. Then $x(Z_{K})=Z_{K}+\sum_{u\in\mathcal{U}}E_{u}$ . In particular, the sequence constructed in section 10 satisfies ii in section 10.

Proof.

i Since $x(Z)-Z\in L$ for any $Z\in L^{\prime}$ , it is enough to show that $x(Z_{K}-\lfloor Z_{K}\rfloor)\geq 0$ . We can analyse each component of $G\setminus\mathcal{N}$ independently, let $G_{B}$ be such a bamboo formed from $E_{1},\ldots,E_{s}$ , with dual vectors in $G_{B}$ denoted by $E_{i}^{*}$ . If $a\geq 0$ and $b\geq 0$ are the multiplicities of $Z_{K}-\lfloor Z_{K}\rfloor$ along the neighboring nodes of $G_{B}$ in $G$ (with convention that $a=0$ if there is only one such node), we search for a cycle $x$ with $(x,E_{i})\leq(aE_{1}^{*}+bE_{s}^{*},E_{i})$ for all $i$ . Thus, $x-(aE_{1}^{*}+bE_{s}^{*})$ is in the Lipman cone of $G_{B}$ , hence $x\geq aE_{1}^{*}+bE_{s}^{*}\geq 0$ .

ii Using the lower bound by intersection numbers, we find that $x(Z_{K})\geq Z_{K}-E+\sum_{n\in\mathcal{N}}E_{n}$ . Since $x(Z_{K})=x(Z_{K}-E+\sum_{n\in\mathcal{N}}E_{n})$ , there exists a Laufer sequence from $Z_{K}-E+\sum_{n\in\mathcal{N}}E_{n}$ to $x(Z_{K})$ . Now, one verifies that the construction/algorithm of this sequence chooses each vertex $v\in\mathcal{V}\setminus(\mathcal{N}\cup\mathcal{U})$ once, and each vertex in $\mathcal{U}$ twice. ∎

\thedefinition Definition.

A (coarse) diagonal computation sequence $(\bar{Z}_{i})_{i=0}^{\bar{k}}$ with respect to $\mathcal{N}$ is defined as follows. Start with $Z_{0}=Z_{K}-\lfloor Z_{K}\rfloor$ , and define $\bar{Z}_{0}=x(Z_{K}-\lfloor Z_{K}\rfloor)$ . Assuming $\bar{Z}_{i}$ ( $i\geq 0$ ) has been defined, and that $\bar{Z}_{i}|_{\mathcal{N}}<Z_{K}|_{\mathcal{N}}$ , choose a $\bar{v}(i)\in\mathcal{N}$ minimizing the ratio

(10.6)

n\mapsto r(n):=\frac{m_{n}(\bar{Z}_{i})}{m_{n}(Z_{K}-E)},\ \ \ n\in\mathcal{N}.

Then set $\bar{Z}_{i+1}=x(\bar{Z}_{i}+E_{\bar{v}(i)})$ . If $\bar{Z}_{i}|_{\mathcal{N}}=(Z_{K}-E)|_{\mathcal{N}}$ , then we record $\bar{k}^{\prime}=i$ . If $\bar{Z}_{i}|_{\mathcal{N}}=Z_{K}|_{\mathcal{N}}$ , then we stop, and set $\bar{k}=i$ .

We refine the above choice as follows. Choose some node $n_{0}\in\mathcal{N}$ and define a partial order $\leq$ on the set $\mathcal{N}$ : for $n,n^{\prime}\in\mathcal{N}$ , define $n\leq n^{\prime}$ if $n$ lies on the geodesic joining $n^{\prime}$ and $n_{0}$ (here we make use of the assumption that the link is a rational homology sphere, in particular, $G$ is a tree). When choosing $\bar{v}(i)$ , if given a choice of several nodes minimizing $\{r(n)\}_{n}$ , and $\min_{n}\{r(n)\}<1$ , then, we choose $\bar{v}(i)$ minimal of those with respect to $(\mathcal{N},\leq)$ . If $\min_{n}\{r(n)\}=1$ , let $\mathcal{N}^{\prime}\subset\mathcal{N}$ be the set of nodes $n$ for which $r(n)=1$ . If $\mathcal{N}^{\prime}$ has one element we have to chose that one. Otherwise, let $G^{\prime}$ be the minimal connected subgraph of $G$ containing $\mathcal{N}^{\prime}$ , and we choose $\bar{v}(i)$ as a leaf of $G^{\prime}$ .

Note that by section 10 i, $Z_{0}=Z_{K}-\lfloor Z_{K}\rfloor\leq x(Z_{K}-\lfloor Z_{K}\rfloor)=\bar{Z}_{0}$ , hence there exists a Laufer sequence connecting $Z_{0}$ with $\bar{Z}_{0}$ . Furthermore, using idempotency and monotonicity of the Laufer operator section 10, we find

\bar{Z}_{i}+E_{\bar{v}(i)}=x(\bar{Z}_{i})+E_{\bar{v}(i)}\leq x(\bar{Z}_{i}+E_{\bar{v}(i)})=\bar{Z}_{i+1}.

As a result, we can join $\bar{Z}_{i}+E_{\bar{v}(i)}$ and $\bar{Z}_{i+1}$ by a Laufer sequence. This way, we obtain a computation sequence $(Z_{i})_{i}$ , connecting $Z_{K}-\lfloor Z_{K}\rfloor$ with $x(Z_{K})$ . Finally, by section 10 ii, $x(Z_{k})$ satisfies the requirement section 10 ii too, hence section 10 applies.

\theblock.

For a diagonal computation sequence as above at each step, except for the step from $\bar{Z}_{i}$ to $\bar{Z}_{i}+E_{\bar{v}(i)}$ , we have $d_{i}<0$ , we find, using sections 10 and 10

(10.7)

p_{g}\leq\sum_{i=0}^{\bar{k}-1}\max\{0,(-\bar{Z}_{i},E_{\bar{v}(i)})+1\}.

10.1 Theorem.

Let $(X,0)$ be a normal Newton nondegenerate Weil divisor given by a function $f$ , with a rational homology sphere link, and assume that the polyhedron $\Gamma_{+}(f)$ is $\mathbb{Q}$ -Gorenstein pointed at $p\in M_{\mathbb{Q}}$ . Then, a diagonal computation sequence $(Z_{i})_{i}$ constructed above computes the geometric genus, that is, equality holds in eq. 10.7.

In this sequel we prove the theorem under the assumption 10.9 regarding the multiplicities of $Z_{K}$ , by the results of the next section this assumption can be removed.

\thedefinition Definition.

Let $n\in\mathcal{N}$ , corresponding to the face $F_{n}\subset\Gamma(f)$ . Denote by $C_{n}$ the convex hull of the union of $F_{n}$ and $\{p\}$ . Set also

C^{-}_{n}=C_{n}\setminus\bigcup_{n^{\prime}\geq n}C_{n^{\prime}},

where we use the partial ordering $\leq$ on $\mathcal{N}$ defined in section 10. For $i=0,\ldots,\bar{k}-1$ , let $H_{i}$ be the hyperplane in $M_{\mathbb{R}}$ defined as the set of points $q\in M_{\mathbb{R}}$ satisfying $\ell_{n}(q-p)=m_{\bar{v}(i)}(\bar{Z}_{i})$ . For $i=0,\ldots,\bar{k}-1$ , we set

F_{i}=C_{\bar{v}(i)}\cap H_{i},\qquad F^{-}_{i}=C_{\bar{v}(i)}^{-}\cap H_{i}.

\therem Remark.

The affine plane $H_{i}$ contains an affine lattice $M\cap H$ , that is there is an affine isomorphism $H\to\mathbb{R}^{2}$ , inducing a bijection $H\cap M\to\mathbb{Z}^{2}$ . The polyhedron $F_{i}$ is then the image of a lattice polyhedron with no integral integer points under a homothety with ratio in $[0,1[$ if $i<\bar{k}^{\prime}$ . These properties allow us to apply section 10 in the proof of theorem 10.1. Furthermore, the polygon $F_{i}$ is always nonempty, even if $F_{i}^{-}$ may be empty.

\theblock.

The sets $C^{-}_{n}$ form a partitioning of the union of segments starting at $p$ and ending in points on $\Gamma(f)$ , that is, $\cup_{n\in\mathcal{N}}C_{n}$ . This follows from the construction as follows. The partially ordered set $(\mathcal{N},\leq)$ is an lower semilattice, i.e. any subset has a largest lower bound. If $q\in\cup_{n\in\mathcal{N}}C_{n}$ , and $\mathcal{I}\subset\mathcal{N}$ is the set of nodes $n$ for which $q\in C_{n}$ , then $q\in C_{n_{q}}^{-}$ , and $p\notin C^{-}_{n}$ for $n\neq n_{q}$ , where $n_{q}$ is the largerst lower bound of $\mathcal{I}$ .

The integral points $q$ in the union of the sets $C_{n}^{-}\setminus F_{n}$ are presicely the integral points satisfying $\ell_{\sigma}(q)>m_{\sigma}$ for all $\sigma\in\widetilde{\triangle}_{f}^{*(1,1)}$ and $\ell_{\sigma}(q)\leq m_{\sigma}$ for some $\sigma\in\triangle_{f}\setminus\triangle_{f}^{*}$ . Indeed, by the rational homology sphere assumption, any integral point on the Newton diagram $\Gamma(f)$ must lie on the boundary $\partial\Gamma(f)$ , see section 6. These are the points “under the Newton diagram”; by theorem 7.1, the number of these points is $p_{g}$ . It follows from construction that the family $(F^{-}_{i}\cap M)_{i=0}^{\bar{k}-1}$ forms a partition of these points. We conclude:

(10.8)

p_{g}=\sum_{i=0}^{\bar{k}^{\prime}-1}|F^{-}_{i}\cap M|.

\thedefinition Definition.

For $r,x\in\mathbb{R}$ , denote by $\lceil r\rceil_{x}$ the smallest real number larger or equal to $r$ and congruent to $x$ modulo $\mathbb{Z}$ . That is,

\lceil r\rceil_{x}=\min\left\{a\in\mathbb{R}\,\middle|\,a\geq r,\;a\equiv x\;(\mathop{\rm mod}\nolimits\mathbb{Z})\right\}

\therem Remark.

The number $\lceil r\rceil_{x}$ depends on $x$ only up to an integer. For all $i$ , we have $\bar{Z}_{i}\equiv Z_{K}\;(\mathop{\rm mod}\nolimits L)$ . In particular, given an $n\in\mathcal{N}$ , we have $m_{n}(\bar{Z}_{i})\equiv m_{n}(Z_{K}-E)\;(\mathop{\rm mod}\nolimits\mathbb{Z})$ .

\thelemma Lemma.

Let $Z\in L^{\prime}$ and take $n,n^{\prime}\in\mathcal{N}^{*}$ connected by a bamboo, and $u\in\mathcal{V}$ a neighbour of $n$ on this bamboo. Then

(10.9)

m_{u}(x(Z))=\left\lceil\frac{\beta m_{n}(Z)+m_{n^{\prime}}(Z)}{\alpha}\right\rceil_{m_{u}(Z)}

where $\alpha=\alpha(\ell_{n},\ell_{n^{\prime}})$ and $\beta=\beta(\ell_{n},\ell_{n^{\prime}})$ (see section 4 and section 4). Furthermore, if for all $v\in\mathcal{V}$ lying on the bamboo joining $n,n^{\prime}$ , we have $(Z,E_{v})=0$ , then $x(Z)=Z$ along the bamboo and

(10.10)

m_{u}(x(Z))=\frac{\beta m_{n}(Z)+m_{n^{\prime}}(Z)}{\alpha}.

Proof.

We prove eq. 10.9, eq. 10.10 follows similarly. Let $u=u_{1},\ldots,u_{s}$ be the vertices on the bamboo with Euler numbers $-b_{1},\ldots,-b_{s}$ as in fig. 3. Set $\widetilde{m}_{0}=m_{0}=m_{n}(Z)$ and $\widetilde{m}_{s+1}=m_{s+1}=m_{n^{\prime}}(Z)$ . There exists a unique set of numbers $\widetilde{m}_{1},\ldots,\widetilde{m}_{s}\in\mathbb{Q}$ so that the equations

(10.11)

\widetilde{m}_{i-1}-b_{i}\widetilde{m}_{i}+\widetilde{m}_{i+1}=0,\quad i=1,\ldots,s

are satisfied. This follows from the fact that the intersection matrix of the bamboo is invertible over $\mathbb{Q}$ . In fact, it follows from [12, Lemma 20.2] that in fact,

\widetilde{m}_{1}=\frac{\beta m_{0}+m_{s+1}}{\alpha}.

This, and the lower bound by intersection numbers from section 10, implies that $m_{u}(x(Z))\geq\widetilde{m}_{1}$ , and therefore $m_{u}(x(Z))\geq\lceil\widetilde{m}_{1}\rceil_{m_{u}(Z)}$ , since $x(Z)-Z\in L$ .

For the inverse inequality, we must show that there exist numbers $m_{1},\ldots,m_{s}$ satisfying

(10.12)

m_{i-1}-b_{i}m_{i}+m_{i+1}\leq 0,\qquad m_{i}\equiv m_{i}(Z)\;(\mathop{\rm mod}\nolimits\mathbb{Z}),

for $i=1,\ldots,s$ , and so that $m_{1}$ is the right hand side of eq. 10.9. Let $\ell_{n}=\ell_{0},\ell_{1},\ldots,\ell_{s},\ell_{s+1}=\ell_{n^{\prime}}$ be the canoncial primitive sequence as in section 6, and note that $\beta=\alpha(\ell_{1},\ell_{s+1})$ . Set recursively

m_{i}=\left\lceil\frac{\alpha(\ell_{i},\ell_{s+1})m_{i-1}+m_{s+1}}{\alpha(\ell_{i-1},\ell_{s+1})}\right\rceil_{m_{u_{i}}(Z)}\qquad i=1,\ldots,s.

Note that, by definition, $m_{i}\equiv m_{i}(Z)$ . The assumption $Z\in L^{\prime}$ therefore implies that the left hand side of eq. 10.12 is an integer. It is then enough to prove eq. 10.12 for $i=1$ . This equation is clear if $s=1$ , so we assume that $s>1$ . Setting $\gamma=\alpha(\ell_{2},\ell_{s})$ , we find

m_{2}-\widetilde{m}_{2}=\left\lceil\frac{\gamma m_{1}+m_{s+1}}{\beta}\right\rceil_{m_{u_{2}}(Z)}-\frac{\gamma\widetilde{m}_{1}+\widetilde{m}_{s+1}}{\beta}=\frac{\gamma}{\beta}(m_{1}-\widetilde{m}_{1})+r

where $0\leq r<1$ . In order to prove eq. 10.12, we start by subtracting zero, i.e. the left hand side of eq. 10.11. The left hand side of eq. 10.12 equals

m_{0}-\widetilde{m}_{0}-b_{1}(m_{1}-\widetilde{m}_{1})+m_{2}-\widetilde{m}_{2}=\left(-b_{1}+\frac{\gamma}{\beta}\right)(m_{1}-\widetilde{m}_{1})+r<1,

since $\gamma/\beta<1$ . Since the left hand side is an integer, eq. 10.12 follows. ∎

\thelemma Lemma.

If $\bar{k}^{\prime}\leq i<\bar{k}$ , then $(\bar{Z}_{i},E_{\bar{v}(i)})>0$ . As a result, the corresponding terms in eq. 10.7 vanish.

Proof.

Let $u\in\mathcal{V}_{n}$ be a neighbour of $\bar{v}(i)$ . Assume first that $u$ lies on a bamboo connecting $\bar{v}(i)$ and $n\in\mathcal{N}$ . We then have $m_{\bar{v}(i)}(\bar{Z}_{i})=m_{\bar{v}(i)}(Z_{K}-E)$ . Furthermore, $m_{n}(\bar{Z}_{i})=m_{n}(Z_{K}-E)+\varepsilon$ , where $\varepsilon$ equals $0$ or $1$ . By the previous lemma, we find

m_{u}(\bar{Z}_{i})=\left\lceil\frac{\beta m_{\bar{v}(i)}(\bar{Z}_{i})+m_{n}(Z_{K}-E)+\varepsilon}{\alpha}\right\rceil_{m_{u}(Z_{K})}=m_{u}(Z_{K}-E)+\varepsilon.

with $\alpha,\beta$ as in the lemma.

Next, assume that $u$ lies on a bamboo connecting $\bar{v}(i)$ and $n^{\prime}\in\mathcal{N}^{*}\setminus\mathcal{N}$ . Name the vertices on the bamboo $u_{1},\ldots,u_{s}$ as in the proof of the previous lemma. We then have $(Z_{K}-E,E_{u_{j}})=0$ for $j=1,\ldots,s-1$ , and $(Z_{K}-E,E_{u_{s}})=1$ . By the lower bound on intersection numbers, we find $x(Z_{K}-E)\geq Z_{K}-E$ . A Laufer sequence which computes $x(Z_{K}-E)$ from $Z_{K}-E$ may start with $E_{u_{s}},E_{u_{s-1}},\ldots,E_{u_{1}}$ . This shows that $m_{u}(x(Z_{K}-E))\geq m_{u}(Z_{K}-E)+1$ in this case.

As a result, for every $u\in\mathcal{V}_{\bar{v}(i)}$ , we have $m_{u}(x(Z_{K}-E))\geq m_{u}(Z_{K}-E)$ , with an equality for at most one neighbour. As a result, since $(Z_{K}-E,E_{v})=2-\delta_{v}$ we find

(\bar{Z}_{i},E_{\bar{v}(i)})\geq(Z_{K}-E,E_{\bar{v}(i)})+(\delta_{\bar{v}(i)}-1)=1.

The final statement of the lemma is now clear. ∎

\thelemma Lemma.

Let $F\subset\mathbb{R}^{2}$ be an integral polygon with no internal integral points. Let $S_{1},\ldots,S_{r}$ be the faces of $F$ and let $c_{j}$ be the integral lenght of $S_{j}$ . Let $0\leq\rho<1$ , $J\subset\{1,\ldots,r\}$ . Then let $a_{i}:\mathbb{R}^{2}\to\mathbb{R}$ be the unique integral affine function whose minimal set on $\rho F$ is $\rho S_{j}$ and this minimal value is $\lambda_{j}\in]-1,0]$ if $j\notin J$ and $\lambda_{j}\in[-1,0[$ if $j\in J$ . Set $F_{\rho}^{-}=\rho F\setminus\cup_{j\in J}\rho S_{j}$ . Then there exists an $a\in\mathbb{Z}$ satifying

\sum_{j=1}^{s}c_{j}a_{j}\equiv a,\qquad|F_{\rho}^{-}\cap\mathbb{Z}^{2}|=\max\{0,a+1\}.

Proof.

This is [31, Theroem 4.2.2]. ∎

Proof of theorem 10.1.

Recall the order $\leq$ on the set $\mathcal{N}$ defined in section 10. We extend this order in the obvious way to all of $\mathcal{V}$ . Also, by assumption, $f$ is $\mathbb{Q}$ -pointed at the point $p\in M_{\mathbb{Q}}$ . Fix an $0\leq i\leq\bar{k}^{\prime}$ and set $H=H_{i}$ . For $u\in\mathcal{V}_{\bar{v}(i)}$ , define

\lambda_{u}=\inf\left\{\ell_{u}(q)\,\middle|\,q\in F_{i}\right\}

(recall that $F_{i}$ is nonempty, see section 10) and

\nu_{u}=\begin{cases}\lambda_{u}+1&\mathrm{if}\;u\leq\bar{v}(i)\;\mathrm{and}\;\lambda_{u}\in\mathbb{Z},\\ \lceil\lambda_{u}\rceil&\mathrm{else.}\end{cases}

Define the affine functions $a_{u}:H\to\mathbb{R}$ , $a_{u}=\ell_{u}|_{H}-\nu_{u}$ . By construction, these are primitive integral functions on $H$ with respect to the affine lattice $H\cap M$ . It now follows from section 10 that there is an $a\in\mathbb{Z}$ so that $\sum_{u}a_{u}\equiv a$ and $|F^{-}_{i}\cap M|=\max\{0,a+1\}$ .

On the other hand, we claim that $\nu_{u}-\ell_{u}(p)\leq m_{u}(\bar{Z}_{i})$ for $u\in\mathcal{V}_{\bar{v}(i)}$ . Using section 6, and the definition of $H_{i}$ , i.e. $\ell_{\bar{v}(i)}(q-p)|_{H}=m_{\bar{v}(i)}(\bar{Z}_{i})$ for $q\in H$ , it follows that

a=\sum_{u}a_{u}(q)=\sum_{u}\ell_{u}(q-p)-(\nu_{u}-\ell_{u}(p))\geq b_{\bar{v}(i)}\ell_{\bar{v}(i)}(q-p)-\sum_{u}m_{u}(\bar{Z}_{i})=(-\bar{Z}_{i},E_{\bar{v}(i)}).

where $q$ is any element of $H$ . As a result, using eq. 10.7 and section 10, as well as eq. 10.8, we have

p_{g}=\sum_{i=0}^{\bar{k}^{\prime}-1}|F^{-}_{i}\cap M|\geq\sum_{i=0}^{\bar{k}-1}\max\{0,(-\bar{Z}_{i},E_{\bar{v}(i)})+1\}\geq p_{g},

and so these inequalities are in fact equalities.

We are left with proving the claim $\nu_{u}\leq m_{u}(\bar{Z}_{i})+\ell_{u}(p)$ for $u\in\mathcal{V}_{\bar{v}(i)}$ . Fix $u$ , and let $n\in\mathcal{N}^{*}$ so that $u$ lies on a bamboo connecting $\bar{v}(i)$ and $n$ . Let $S=F_{\bar{v}(i)}\cap F_{n}$ . Then $S$ is the minimal set of $\ell_{u}$ on $F_{\bar{v}(i)}$ , i.e., $S=F_{u}$ . Let $A$ be the affine hull of $S\cup\{p\}$ . Since the two affine functions

\frac{\ell_{\bar{v}(i)}-\ell_{\bar{v}(i)}(p)}{m_{\bar{v}(i)}(Z_{K}-E)},\quad\frac{\ell_{n}-\ell_{n}(p)}{m_{n}(Z_{K}-E)},

both take value $0$ on $p$ and $1$ on $S$ , by theorem 9.1 item (iii), they conincide on $A$ . Let

r=\frac{m_{\bar{v}(i)}(\bar{Z}_{i})}{m_{\bar{v}(i)}(Z_{K}-E)}

Using the minimality of eq. 10.6, we get for any $q\in p+r(S-p)\subset H\cap A$

(10.13)

\frac{\ell_{n}(q-p)}{m_{n}(Z_{K}-E)}=\frac{\ell_{\bar{v}(i)}(q-p)}{m_{\bar{v}(i)}(Z_{K}-E)}=\frac{m_{\bar{v}(i)}(\bar{Z}_{i})}{m_{\bar{v}(i)}(Z_{K}-E)}\leq\frac{m_{n}(\bar{Z}_{i})}{m_{n}(Z_{K}-E)},

and so $\ell_{n}(q-p)\leq m_{n}(\bar{Z}_{i})$ . In the case when $n\leq\bar{v}(i)$ , or equivalently, $u\leq\bar{v}(i)$ , this inequality is strict. It follows, using section 10, that

(10.14)

\begin{split}m_{u}(\bar{Z}_{i})&=\left\lceil\frac{\beta(\ell_{\bar{v}(i)},\ell_{n})m_{\bar{v}(i)}(\bar{Z}_{i})+m_{n}(\bar{Z}_{i})}{\alpha(\ell_{\bar{v}(i)},\ell_{n})}\right\rceil_{m_{u}(\bar{Z}_{i})}\\ &\geq\frac{\beta(\ell_{\bar{v}(i)},\ell_{n})\ell_{\bar{v}(i)}(q-p)+\ell_{n}(q-p)}{\alpha(\ell_{\bar{v}(i)},\ell_{n})}\\ &=\ell_{u}(q-p)\\ &=\lambda_{u}-\ell_{u}(p).\end{split}

Therefore, since $m_{u}(\bar{Z}_{i})\equiv m_{u}(Z_{K})\equiv-\ell_{u}(p)$ $(\mathop{\rm mod}\nolimits\mathbb{Z})$ , we find

m_{u}(\bar{Z}_{i})\geq\lceil\lambda_{u}\rceil-\ell_{u}(p).

This proves the claim, unless $u\leq\bar{v}(i)$ and $\lambda_{u}\in\mathbb{Z}$ . In that case, the numbers $\ell_{\bar{v}(i)}(q)$ and $\ell_{u}(q)=\lambda_{u}$ are both integers. Since $\ell_{n},\ell_{u}$ form a part of an integral basis of $N=M^{\vee}$ , we can assume that $q\in M$ , hence,

\frac{\beta(\ell_{\bar{v}(i)},\ell_{n})\ell_{\bar{v}(i)}(q-p)+\ell_{n}(q-p)}{\alpha(\ell_{\bar{v}(i)},\ell_{n})}\\ =\ell_{u}(q-p)\equiv-\ell_{u}(p)\equiv m_{u}(Z_{K})\equiv m_{u}(\bar{Z}_{i})\quad(\mathop{\rm mod}\nolimits\mathbb{Z}).

As a result, since we have a strict inequality $m_{n}(\bar{Z}_{i})>\ell_{n}(q-p)$ we get a strict inequality in eq. 10.14 as well. Therefore, we have

m_{u}(\bar{Z}_{i})>\lambda_{u}-\ell_{u}(p)\qquad\mathrm{and}\qquad m_{u}(\bar{Z}_{i})\equiv\lambda_{u}-\ell_{u}(p)\quad(\mathop{\rm mod}\nolimits\mathbb{Z}),

and so $m_{u}(\bar{Z}_{i})\geq\lambda_{u}-\ell_{u}(p)+1=\nu_{u}-\ell_{u}(p)$ , which finishes the proof of the claim. ∎

11. Removing $B_{1}$ -facets

In this section we consider only surface singularities, i.e. we assume that $r=3$ . We consider removable $B_{1}$ -facets of two dimensional Newton diagrams and show that they can be removed without affecting certain invariants of nondegenerate Weil divisors. This is stated in section 11. In parallel we also prove section 11, which allows us to assume that the divisor $Z_{K}-E$ on the resolution provided by Oka’s algorithm has nonnegative multiplicities on nodes, cf. section 10 and the sentence after theorem 10.1. Similar computations are given in [7], providing a stronger result in the case of a hypersurface singularity in $\mathbb{C}^{3}$ with rational homology sphere link.

The concept of a $B_{1}$ -facet appears in [11] in the case of hypersurfaces in $K^{r}$ , where $K$ is a $p$ -adic field, and is further studied in [18, 6].

\thedefinition Definition.

Let $F\subset\Gamma(f)$ be a compact facet, i.e. of dimension $2$ . Then $F$ is a $B_{1}$ -facet if $F$ has exactly $3$ vertices $p_{1},p_{2},p_{3}$ so that there is a $\sigma\in\triangle^{(1)}_{\Sigma}$ so that $m_{\sigma}=\ell_{\sigma}(p_{1})=\ell_{\sigma}(p_{2})=\ell_{\sigma}(p_{3})-1$ . A $B_{1}$ -facet $F$ is removable if furthermore, the segment $[p_{2},p_{3}]$ is contained in the boundary $\partial\Gamma(f)$ of $\Gamma(f)$ .

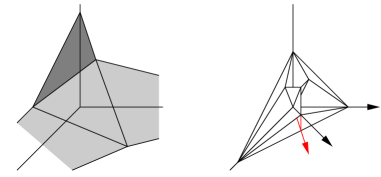
\thedefinition Definition.

Let $T(f)$ be closure in $N_{\mathbb{R}}$ of the union of cones in $\triangle_{f}$ which correspond to compact facets of $\Gamma_{+}(f)$ which have dimension $>0$ . This is the tropicalization of $f$ . We say that $\Sigma$ is generated by the tropicalization of $f$ , if $\Sigma$ is generated as a cone by the set $T(f)$ .

Let $\Sigma^{\prime}$ be the cone generated by $T(f)$ . This is a finitely generated rational strictly convex cone, and if $(X,0)$ is not rational, then $\Sigma^{\prime}$ has dimension $r=3$ . This cone induces an affine toric variety $Y^{\prime}=Y_{\Sigma^{\prime}}$ , and the function $f$ defines a Weil divisor $(X^{\prime},0)\subset(Y^{\prime},0)$ . Furthermore, the inclusion $\Sigma^{\prime}\subset\Sigma$ induces a morphism $Y^{\prime}\to Y$ , which restricts to a morphism $(X^{\prime},0)\to(X,0)$ .

\therem Remark.

The closure of $T(f)$ in a certain partial compactification of $N_{\mathbb{R}}$ is called the local tropicalization of $(X,0)$ [30].

\thelemma Lemma.

Let $\sigma\in\widetilde{\triangle}_{f}$ . Then the orbit $O_{\sigma}$ intersects $\widetilde{X}$ if and only if $\sigma\subset T(f)$ .

Proof.

The orbit $O_{\sigma}$ is an affine variety $O_{\sigma}=\mathop{\rm Spec}\nolimits(\mathbb{C}[M(\sigma)])$ (recall $M(\sigma)=M\cap\sigma^{\perp})$ , and if $p_{\sigma}$ is an element of the affine hull of $F_{\sigma}$ , then $x^{-p_{\sigma}}f_{\sigma}\in\mathbb{C}[M(\sigma)]$ and

\widetilde{X}\cap O_{\sigma}\cong\mathop{\rm Spec}\nolimits\left(\frac{\mathbb{C}[M(\sigma)]}{(x^{-p_{\sigma}}f_{\sigma})}\right).

Therefore, $\widetilde{X}\cap O_{\sigma}$ is empty if and only if $x^{-p_{\sigma}}f_{\sigma}$ is a unit in $\mathbb{C}[M(\sigma)]$ , which is equivalent to $f_{\sigma}$ being a monomial, i.e. $\dim F_{\sigma}=0$ . ∎

\thelemma Lemma.

Let $(X,0)$ and $(X^{\prime},0)$ be as in section 11. If $(X,0)$ is normal, then the morphism $(X^{\prime},0)\to(X,0)$ is an isomorphism.

Proof.

We can assume that the smooth subdivision $\widetilde{\triangle}_{f}$ subdivides the cone $\Sigma^{\prime}$ , so that we get a subdivision $\widetilde{\triangle}_{f}^{\prime}=\widetilde{\triangle}_{f}|_{\Sigma^{\prime}}$ of the cone $\Sigma^{\prime}$ . Let $\widetilde{Y}^{\prime}$ be the corresponding toric variety. Let $\triangle_{T(f)}$ be the fan consisting of cones $\sigma\in\widetilde{\triangle}_{f}$ which are contained in $T(f)$ . We then get open inclusions

Y_{T(f)}\subset\widetilde{Y}^{\prime}\subset\widetilde{Y}

where $Y_{T(f)}$ is the toric variety associated with the fan $\triangle_{T(f)}$ .

It follows from section 11 that the strict transforms $\widetilde{X}$ and $\widetilde{X}^{\prime}$ of $X$ and $X^{\prime}$ , respectively, are contained in $Y_{T(f)}$ , and so $\widetilde{X}^{\prime}=\widetilde{X}$ . As a result, $X^{\prime}\setminus\{0\}\cong\widetilde{X}^{\prime}\setminus\pi^{-1}(0)=\widetilde{X}\setminus\pi^{-1}(0)\cong X\setminus\{0\}$ . Since $(X,0)$ is normal, the morphism $(X^{\prime},0)\to(X,0)$ is an isomorphism. ∎

\theblock.

Assume that $F\subset\Gamma(f)$ is a removable $B_{1}$ -face, and let $\sigma\in\triangle^{(1)}_{\Sigma}$ and $p_{i}$ be as in section 11. If $F$ is the only facet of $\Gamma(f)$ , then we leave as an exercise to show that the graph $G$ is equivalent to a string of rational curves, and so $(X,0)$ is rational. We will always assume that $F$ is not the only facet of $\Gamma(f)$ . There exists an element of $\Sigma^{\circ}$ which is constant on the segment $[p_{1},p_{3}]$ (e.g. the normal vector to $F$ ). As a result, the boundary $\partial\Sigma$ intersects the hyperplane of elements $\ell\in N_{\mathbb{R}}$ which are constant on $[p_{1},p_{3}]$ in two rays, $\sigma_{+}$ and $\sigma_{-}$ , where $\ell\in\sigma_{+}$ satisfies $\ell|_{[p_{1},p_{3}]}\equiv\max_{F}\ell$ , and $\ell\in\sigma_{-}$ satisfies $\ell|_{[p_{1},p_{3}]}\equiv\min_{F}\ell$ .

Let $\ell_{+}\in N$ be a primitive generator of $\sigma_{+}$ , set $m_{+}=\max_{F}\ell$ and define

\bar{f}(x)=\sum\left\{a_{p}x^{p}\,\middle|\,p\in M,\,\ell_{+}(p)\geq m_{+}\right\},

where $a_{p}$ are the coefficients of $f$ as in eq. 3.1. Let $(\bar{X},0)$ be the Weil divisor defined by $\bar{f}$ . We get a Newton polyhedron $\Gamma_{+}(\bar{f})$ , from which we calculate invariants of $(\bar{X},0)$ as described in previous sections. It follows from this construction that $\Gamma(\bar{f})=\overline{\Gamma(f)\setminus F}$ , and that $\bar{f}$ is Newton nondegenerate.

Now, assume that $\Sigma$ is generated by the tropicalization of $f$ . Let $\sigma_{1}$ and $\sigma_{3}\in\triangle_{f}^{(1)}$ be the rays corresponding to the noncompact faces of $\Gamma_{+}(f)$ containing the segments $[p_{2},p_{3}]$ and $[p_{1},p_{2}]$ , respectively. Let $\ell_{1},\ell_{3}$ be primitive generators of $\sigma_{1},\sigma_{3}$ . By construction, and the above assumption that $\Sigma$ is generated by $T(f)$ , we have $\mathbb{R}_{\geq 0}\langle\ell_{1},\ell_{3}\rangle\subset\partial\Sigma$ , and so $\ell_{+}\in\mathbb{R}_{\geq 0}\langle\ell_{1},\ell_{3}\rangle\in\triangle_{f}$ .

In fact, we have $\ell_{+}=\ell_{1}+t\ell_{3}$ where $t=\ell_{1}(p_{1}-p_{2})$ . Indeed, $\ell_{+}$ is the unique positive linear combination of $\ell_{1}$ and $\ell_{3}$ which vanishes on $p_{1}-p_{3}$ , and is primitive. Since $\ell_{3}=\ell_{\sigma}$ , by definition of $F$ , and since $\ell_{1}(p_{3})=\ell_{1}(p_{2})$ , we have

(\ell_{1}+t\ell_{3})(p_{1}-p_{3})=\ell_{1}(p_{1}-p_{3})+\ell_{1}(p_{1}-p_{2})\cdot\ell_{3}(p_{1}-p_{3})=\ell_{1}(p_{1}-p_{2})-\ell_{1}(p_{1}-p_{2})=0.

Furthermore, we have $\ell_{1}(p_{3}-p_{2})=0$ and $\ell_{3}(p_{3}-p_{2})=1$ , and so by section 4, $\ell_{1},\ell_{3}$ form a part of an integral basis, which implies that $\ell_{1}+t\ell_{3}$ is primitive.

Now, define $t^{\prime}$ as the combinatorial length of the segment $[p_{1},p_{2}]$ . We have $t^{\prime}|t$ and via Oka’s algorithm (section 6), this segment corresponds to $t^{\prime}$ bamboos in $G$ , each consisting of a single $(-1)$ -curve, whereas $[p_{2},p_{3}]$ corresponds to one bamboo with determinant $t/t^{\prime}$ .

\theprop Proposition.

Let $f$ , $F$ and $\bar{f}$ be as above, and assume that $f$ is Newton nondegenerate. Assume also that $\Sigma$ is generated by the tropicalization $T(f)$ as described in section 11. Then

(i)

$\bar{f}$ is Newton nondegenerate.
(ii)

$\Gamma(\bar{f})=\overline{\Gamma(f)\setminus F}$ .
(iii)

The singularities $(X,0)$ and $(\bar{X},0)$ have diffeomorphic links.
(iv)

The singularities $(X,0)$ and $(\bar{X},0)$ have equal geometric genera and $\delta$ -invariants.
(v)

If $(X,0)$ is normal, then $(\bar{X},0)$ is normal.
(vi)

If $f$ is $\mathbb{Q}$ -Gorenstein-pointed at $p\in M_{\mathbb{Q}}$ , then so is $\bar{f}$ . In particular, if $(X,0)$ is Gorenstein, then $(\bar{X},0)$ is also Gorenstein.

Proof.

item (i) and item (ii) follow from definition.

We now prove item (iii). We have $G$ , the output of Oka’s algorithm for the Newton polyhedron $\Gamma_{+}(f)$ , and $\bar{G}$ , the output of Oka’s algorithm for $\Gamma_{+}(\bar{f})$ . Let $\sigma_{F}\in\triangle_{f}$ be the ray dual to $F$ and let $F^{\prime}$ be the unique face of $\Gamma_{+}(f)$ adjacent to $F$ , i.e. $F^{\prime}\cap F=[p_{1},p_{3}]$ . Then $\sigma_{F}\subset\mathbb{R}_{\geq 0}\langle\ell_{F^{\prime}},\ell_{+}\rangle\in\triangle_{\bar{f}}$ , and we can subdivide the canonical subdivision of $\mathbb{R}_{\geq 0}\langle\ell_{F}^{\prime},\ell_{+}\rangle$ so that we can assume that $\sigma_{F}\in\widetilde{\triangle}_{\bar{f}}$ . We can therefore identify vertices $v_{F}$ of $G$ and $\bar{G}$ corresponding to the same ray $\sigma_{F}\in\widetilde{\triangle}^{(1)}_{f}$ and $\sigma_{F}\in\widetilde{\triangle}^{(1)}_{\bar{f}}$ . It is then clear from construction that the components of $G\setminus v_{F}$ and $\bar{G}\setminus v_{F}$ in the direction of $v_{F^{\prime}}$ are isomorphic. After blowing down the $(-1)$ -curves corresponding to the segment $[p_{1},p_{2}]$ , we must show

❀

The two bamboos joining $\ell_{F}$ with $\ell_{+}$ on one hand, and with $\ell_{1}$ on the other, are isomorphic.
❀

The vertex $v_{F}$ has the same Euler number in $G$ and in $\bar{G}$ .

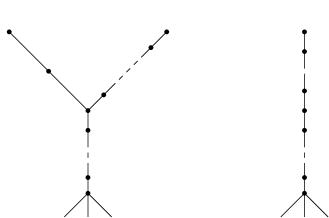
For the first of these, we prove that

\alpha(\ell_{F},\ell_{+})=\alpha(\ell_{F},\ell_{1}),\quad\beta(\ell_{F},\ell_{+})=\beta(\ell_{F},\ell_{1}).

We calculate $\alpha(\ell_{F},\ell_{+})$ as the greatest common divisor of maximal minors of the matrix having coordinate vectors for $\ell_{F}$ and $\ell_{+}=\ell_{1}+t\ell_{3}$ as rows. But $\alpha(\ell_{F},\ell_{1})=t/t^{\prime}$ , and so adding a multiple of $t$ to $\ell_{1}$ does not modify the greatest common divisor of these determinants, hence $\alpha(\ell_{F},\ell_{+})=\alpha(\ell_{F},\ell_{1}+t\ell_{3})=\alpha(\ell_{F},\ell_{1})$ .

The invariant $\beta(\ell_{F},\ell_{+})$ can be calculated as the unique number $0\leq\beta<\alpha(\ell_{F},\ell_{+})$ so that $\beta\ell_{F}+\ell_{+}$ is a multiple of $\alpha(\ell_{F},\ell_{+})$ . On the other hand, we find, setting $\beta=\beta(\ell_{F},\ell_{1})$ and $\alpha=\alpha(\ell_{F},\ell_{+})=\alpha(\ell_{F},\ell_{1})=t/t^{\prime}$ ,

\frac{\beta\ell_{F}+\ell_{+}}{\alpha}=\frac{\beta\ell_{F}+\ell_{1}+t\ell_{3}}{\alpha}=\frac{\beta\ell_{F}+\ell_{1}}{\alpha}+t^{\prime}\ell_{3}\in N.

Finally, we show that $v_{F}$ has the same Euler number in the graphs $G$ and $\bar{G}$ . Denote these by $-b_{F}$ and $-\bar{b}_{F}$ . After blowing down the $(-1)$ curves associated with the segment $[p_{1},p_{2}]$ , the vertex $v_{F}$ has two neighbors in either graph $G$ or $\bar{G}$ . Denote by $v_{-1}$ and $\bar{v}_{-1}$ the neighbor of $v_{F}$ contained in the same component of $G\setminus v_{F}$ and $\bar{G}_{\setminus}v_{F}$ as $v_{F^{\prime}}$ . It is then clear that $\ell_{v_{-1}}=\ell_{\bar{v}_{-1}}$ .

Denote by $u,\bar{v}$ the neighbours of $v_{F},\bar{v}_{F}$ in the direction of $v_{1},v_{+}$ , respectively, and $u^{\prime},\bar{u}^{\prime}$ the other neighbours, as in fig. 8. Then we have $\ell_{u^{\prime}}=\ell_{\bar{u}^{\prime}}$ and

\ell_{u}=\frac{\beta\ell_{F}+\ell_{1}}{\alpha},\quad\ell_{\bar{u}}=\frac{\beta\ell_{F}+\ell_{+}}{\alpha}=\ell_{u}+t^{\prime}\ell_{3},

where $\alpha,\beta$ are as above. The two numbers $-b_{F}$ and $-\bar{b}_{F}$ are identified by section 6

-b_{F}\ell_{F}+\ell_{u}+\ell_{u^{\prime}}+t^{\prime}\ell_{3}=0,\quad-\bar{b}_{F}\ell_{F}+\ell_{\bar{u}}+\ell_{\bar{u}^{\prime}}=0,

which leads to their equality.

Next, we prove item (iv) and item (v). By theorem 7.1, it suffices to show that

\Gamma_{+}(f)\setminus(\Sigma^{\vee}+q),\qquad\Gamma_{+}(\bar{f})\setminus(\Sigma^{\vee}+q)

have the same cohomology for all $q\in M$ . By shifting $\Gamma_{+}(f)$ , we simplify the following proof by assuming $q=0$ . The inclusion

\Gamma(f)\setminus\Sigma^{\vee}\subset\Gamma_{+}(f)\setminus\Sigma^{\vee}

is a homotopy equivalence. Indeed, one can construct a suitable vectorfied on $\Gamma_{+}(f)\setminus\Sigma^{\vee}$ pointing in the direction of $-\Sigma^{\vee}$ , whose trajectories end up in $\Gamma(f)\setminus\Sigma$ , thus giving a homotopy inverse to the above inclusion.

Now, let $K$ be the union of faces of $\Gamma(f)$ which do not intersect $\Sigma^{\vee}$ . By section 7, the inclusion $K\subset\Gamma(f)\setminus\Sigma$ is a homotopy equivalence. Define $\bar{K}$ similarly, using $\bar{f}$ . Thus it suffices to prove that $\widetilde{H}^{i}(K,\bar{K};\mathbb{Z})$ vanish for all $i$ . By excision, this is equivalent to showing

(11.1)

\forall i\in\mathbb{Z}_{\geq 0}:\,\widetilde{H}^{i}(K\cap F,\bar{K}\cap F;\mathbb{Z})=0.

If $\Sigma^{\vee}$ does not intersect the face $F$ , then $K\cap F=F=\bar{K}\cap F$ . Also, if $p_{2}\in\Sigma^{\vee}$ , then $K\cap F=\bar{K}\cap F$ . In either case, eq. 11.1 holds. We can therefore assume that $p_{2}\in K$ and $F\not\subset K$ . With these assumptions at hand, it is then enough to prove that excactly one of the segements $[p_{1},p_{2}]$ and $[p_{2},p_{3}]$ is contained in $K$ , i.e. it cannot happen that either both or neither is contained in $K$ .

Let $A$ be the affine hull of $F_{n}$ , i.e. the hyperplane in $M_{\mathbb{R}}$ defined by $\ell_{n}=m_{n}$ , and let $C=\Sigma^{\vee}\cap A$ . Define a point $r\in A$ by

\ell_{3}(r)=0,\quad\ell_{1}(r)=0,\quad\ell_{n}(r)=m_{n}.

This is well defined, since the functions $\ell_{1},\ell_{3},\ell_{n}$ are linearly independent. Then $C$ is a convex polygon in $A$ , and $r$ is a vertex of $C$ . Furthermore, $r$ is the unique point in $C$ where both functions $\ell_{1}|_{C}$ and $\ell_{3}|_{C}$ take their minimal values.

If neither of the segments $[p_{1},p_{2}]$ , $[p_{2},p_{3}]$ are contained in $K$ , i.e. both intersect $\Sigma^{\vee}$ , then we can choose $r_{1}\in C\cap[p_{1},p_{2}]$ and $r_{2}\in C\cap[p_{2},p_{3}]$ . Furthermore, we have $\ell_{3}(r)\leq\ell_{3}(r_{1})=\ell_{3}(p_{2})$ , and $\ell_{1}(r)\leq\ell_{1}(r_{2})=\ell_{1}(p_{2})$ . Therefore, $p_{2}$ is in the convex hull of $r,r_{1},r_{2}$ , and so $p_{2}\in C$ , contrary to the assumption $p_{2}\in K$ .

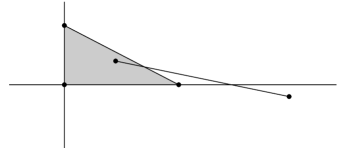
Next, assume that both segments $[p_{1},p_{2}]$ , $[p_{2},p_{3}]$ are contained in $K$ . We start by showing that in this case, we have $r\in F_{n}$ . By assumption, we can choose $r^{\prime}\in C\cap F_{n}$ .

We have $\ell_{3}(r^{\prime})>m_{\ell_{3}}$ . One verifies (see fig. 9) that if $\ell_{3}(r)\leq m_{\ell_{3}}$ , then we would have $\ell_{1}(r^{\prime})<\ell_{1}(r)$ , but $r$ is a minimum for $\ell_{1}|_{C}$ . Therefore, we can assume that $\ell_{3}(r)>m_{\ell_{3}}$ , similarly, $\ell_{1}(r)>m_{\ell_{1}}$ . It follows, since $C\cap F\neq\emptyset$ , that $r\in F$ , so we can assume that $r^{\prime}=r$ . But, since $r\notin[p_{1},p_{2}]\cup[p_{2},p_{3}]$ , we find

\ell_{3}(p_{2})<\ell_{3}(r)<\ell_{3}(p_{3})=\ell_{3}(p_{2})+1,

and so $\ell_{3}(r)\notin\mathbb{Z}$ . But this is a contradiction, since $\ell_{3}(r)=\ell_{3}(q)\in\mathbb{Z}$ .

Next we prove item (vi). Assume that $\Gamma_{+}(f)$ is $\mathbb{Q}$ -Gorenstein pointed at $p\in M_{\mathbb{Q}}$ . It suffices to show that $\ell_{+}(p)=\bar{m}_{\ell_{+}}+1$ , where $\bar{m}_{\ell_{+}}$ is the minimal value of $\ell_{+}$ on $\Gamma_{+}(\bar{f})$ . We immediately find

\bar{m}_{\ell_{+}}=\ell_{+}(p_{3})=\ell_{1}(p_{3})+t\ell_{3}(p_{3})=m_{\ell_{1}}+t(m_{\ell_{3}}+1)=\ell_{1}(p)-1+t\ell_{3}(p)=\ell_{+}(p)-1.\qed

\theexample Example.

Consider the cone $\Sigma=\mathbb{R}^{3}_{\geq 0}$ and the function

f(x,y,z)=x^{3}+xy^{3}+z^{5}+y^{10}z,

which defines a nonrational singularity $(X,0)$ . In this case, $\Gamma(f)$ has a $B_{1}$ -facet

F=\mathop{\rm conv}\nolimits\{(1,3,0),(0,10,1),(0,0,5)\},

corresponding to a node $n\in\mathcal{N}$ . The normal vector to $F$ is $(19,2,5)$ and eq. 8.2 gives $m_{n}(Z_{K}-E)=-1$ . By the above computations, removing the monomial $y^{10}z$ from $f$ gives another singularity with the same link and geometric genus, but $Z_{K}-E$ is nonnegative on the other node. After removing $F$ we find

\bar{f}(x,y,z)=x^{3}+xy^{3}+z^{5}.

Note that $\Sigma$ is generated by the tropicalization of $f$ , but the tropicalization of $\bar{f}$ generates the cone $\mathbb{R}_{\geq 0}\langle(5,0,1),(0,1,0),(0,0,1)\rangle$ .

\theblock.

In what follows, we connect the above construction with the coefficients of $Z_{K}-E$ . We introduce a simplified graph, whose vertices are the nodes of $G$ . whose vertices are the nodes of $G$ , and a bamboo of $G$ connecting two nodes of $G$ is replaced in $G_{\mathcal{N}}$ by an edge. Then $G_{\mathcal{N}}$ is a tree, with an edge connecting $n,n^{\prime}$ if and only if $F_{n}$ and $F^{\prime}_{n}$ intersect in a segment (of length $1$ ). Recall that a leaf of a tree is a vertex with exactly one neighbour. If we assume that $|\mathcal{N}|>1$ , then we see that the following are equivalent, since $G_{\mathcal{N}}$ is a tree:

❀

$n\in\mathcal{N}$ is a leaf in $G_{\mathcal{N}}$ ,
❀

$\Gamma(f)\setminus F_{n}$ is connected,
❀

all edges of $F_{n}$ , except for one, lie on the boundary $\partial\Gamma(f)$ of the Newton diagram.

If $|\mathcal{N}|=1$ , then there is a unique $n\in\mathcal{N}$ , and $\Gamma(f)=F$ , in particular, $\partial\Gamma(f)=\partial F_{n}$ . Finally, if $|\mathcal{N}|=0$ , and if we assume that $(X,0)$ is normal, then $(X,0)$ is rational.

The following lemma is elementary:

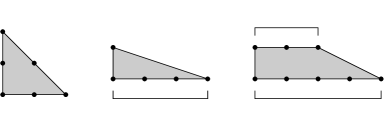
\thelemma Lemma.

Let $F$ be an integral polyhedron in $\mathbb{R}^{2}$ , having no integral interior points. Then, up to an integral affine automorphism of $\mathbb{R}^{2}$ , $F$ is one one the following:

❀

Big triangle The convex hull of $(0,0)$ , $(2,0)$ , $(0,2)$ .
❀

Small triangle of type $t$ The convex hull of $(0,0)$ , $(t,0)$ , $(0,1)$ .
❀

Trapezoid of type $(t,s)$ The convex hull of $(0,0)$ , $(t,0)$ , $(0,1)$ , $(s,1)$ , where $t,s\in\mathbb{Z}$ , $t\geq s>0$ and $t>0$ . ∎

\thelemma Lemma.

Assume that $(X,0)$ is normal, Gorenstein-pointed at $p\in M$ , and not rational. If $n\in\mathcal{N}$ is a leaf in $G_{\mathcal{N}}$ and $m_{n}(Z_{K}-E)<0$ , then $F_{n}$ is a removable $B_{1}$ -facet of $\Gamma(f)$ (See section 11 for the definition of $G_{\mathcal{N}}$ ).

Proof.

By assumption, $F_{n}$ has two adjacent edges contained in $\partial\Gamma(f)$ , say $[q_{1},q_{2}]$ and $[q_{2},q_{3}]$ . Let $F_{1},F_{2}$ be the noncompact faces of $\Gamma_{+}(f)$ containing the segments $[q_{1},q_{2}]$ and $[q_{2},q_{3}]$ , respectively, and let $\ell_{1},\ell_{2}\in\partial\Sigma$ be the primitive functions having $F_{1},F_{2}$ as minimal sets on $\Gamma_{+}(f)$ , denote these minimal values by $m_{\ell_{1}},m_{\ell_{2}}$ .

Let $l_{1}=\mathop{\mathrm{length}}([q_{2},q_{3}])$ and $\alpha_{1}=\ell_{1}(q_{3}-q_{2})/l_{1}$ and $l_{2}=\mathop{\mathrm{length}}([q_{2},q_{3}])$ and $\alpha_{2}=\ell_{2}(q_{1}-q_{2})/l_{2}$ . Then, the bamboos corresponding to the segements $[q_{1},q_{2}]$ and $[q_{2},q_{3}]$ have determininats $\alpha_{1},\alpha_{2}$ , see section 4.

Assume first that $F_{n}$ is a small triangle of type $t$ , that the segment $[q_{1},q_{2}]$ has length $t$ , and that $\alpha_{1}=1$ . This implies that $F_{n}$ is a removable $B_{1}$ -facet.

Otherwise, let $A$ be the affine hull of $F_{n}$ . If $F_{n}$ is a big triangle, a trapezoid, or a small triangle as above, but with $\alpha_{1}>1$ , then the square

\left\{q\in A\,\middle|\,m_{\ell_{1}}\leq\ell_{1}(q)\leq m_{\ell_{1}}+1,\,m_{\ell_{2}}\leq\ell_{2}(q)\leq m_{\ell_{2}}+1\right\}

is contained in $F_{n}$ . In particular, its vertex $q_{0}$ , the unique point in $A$ satisfying $\ell_{i}(q_{0})=m_{\ell_{i}}+1$ for $i=1,2$ , is contained in $F_{n}$ . The set

R=\left\{q\in\Sigma^{\vee}\,\middle|\,\ell_{i}(q)=0,\;i=1,2\right\}

is a one dimensional face of $\Sigma^{\vee}$ (here we use the condition that $\Sigma$ is generated by the tropicalization of $(X,0)$ ). By our assumption $m_{n}\leq\ell_{n}(p)$ we have $p\in q_{0}+R^{\circ}\subset\Gamma_{+}(f)^{\circ}$ , contradicting the assumption that $(X,0)$ is not rational. ∎

\theprop Proposition.

Assume that $(X,0)$ is normal, Gorenstein-pointed at $p\in M$ , and not rational. If there is an $n\in\mathcal{N}$ so that $m_{n}(Z_{K}-E)<0$ , then $\Gamma(f)$ has a removable $B_{1}$ -facet.

Proof.

If $n$ is a leaf in $G_{\mathcal{N}}$ (see section 11), then $F_{n}$ is removable by section 11. So let us assume that $n$ is not a leaf in $G_{\mathcal{N}}$ , i.e. that $\Gamma(f)\setminus F_{n}$ is disconnected. The inclusion

\Gamma(f)^{\circ}\setminus F_{n}\subset\Gamma_{+}^{*}(f)^{\circ}\setminus(\{\ell_{n}\leq m_{n}\}\cup\Gamma_{+}(f)^{\circ})

is a strong homotopy retract (here we set $\Gamma(f)^{\circ}=\Gamma(f)\setminus\partial\Gamma(f)$ ). In particular, the right hand side is disconnected as well. But it follows from our assumptions that the point $p$ is in the right hand side above. Let $C$ be a component of $\Gamma(f)\setminus F_{n}$ contained in a component of the right hand side which does not contain $p$ . Then, for any $n^{\prime}$ so that $F_{n^{\prime}}\subset\overline{C}$ we have $\ell_{n^{\prime}}(p)>m_{n^{\prime}}$ , i.e. $m_{n^{\prime}}(Z_{K}-E)<0$ . Let $G_{C}$ be the induced subgraph of $G_{\mathcal{N}}$ having vertices $n^{\prime}$ for $F_{n^{\prime}}\subset\overline{C}$ . This graph is a nonempty tree, and so has either exactly one vertex, or at has least two leaves. In the first case, the unique vertex $n^{\prime}$ of $G_{C}$ is a leaf of $G$ . In the second case, $G_{C}$ has at least two leaves, so we can choose a leaf $n^{\prime}$ of $G_{C}$ which is not adjacent to $n$ in $G$ . In either case, $F_{n^{\prime}}$ is a removable $B_{1}$ -facet by section 11. ∎

\theprop Proposition.

Assume that $f$ defines a normal Newton nondegenerate Weil divisor $(X,0)$ , which is not rational. Then there exists a normal Newton nondegenerate Weil divisor $(\bar{X},0)$ , defined by a function $\bar{f}$ and a cone $\Sigma^{\prime}$ (possibly different than $\Sigma$ ) satisfying the following conditions:

❀

$(\bar{X},0)$ and $(X,0)$ have diffeomorphic links.
❀

$p_{g}(\bar{X},0)=p_{g}(X,0)$ .
❀

If $(X,0)$ is Gorenstein or pointed at $p\in M_{\mathbb{Q}}$ , then so is $(\bar{X},0)$ .
❀

If $F_{n}\subset\Gamma_{+}(\bar{f})$ is a compact facet, then $m_{n}(Z_{K}-E)\geq 0$ .

In fact, $\Gamma(\bar{f})$ is the union of those facets $F_{n}$ of $\Gamma(f)$ for which $m_{n}(Z_{K}-E)\geq 0$ .

Proof.

By section 11, we can assume that $\Sigma$ is generated by $T(f)$ , since $(X,0)$ is normal (see section 11). The result therefore follows, using induction on the number of facets of $\Gamma(f)$ , and sections 11 and 11 below. ∎

12. Examples

\theexample Example.

Let $N=M=\mathbb{Z}^{3}$ and let $a,b,c\in\mathbb{N}$ be natural numbers with no common factor, and let $0\leq r<s\in\mathbb{N}$ be coprime with $s\leq rc$ . Take

\Sigma^{\vee}=\mathbb{R}_{\geq 0}\left\langle\begin{array}[]{@{(}rrr@{)}}ra,&0,&-s\\ 0,&rb,&-s\\ 0,&0,&1\end{array}\right\rangle,\quad f=x_{1}^{a}+x_{2}^{b}+x_{3}^{c}.

The cone $\Sigma$ is then generated by

\ell_{1}=(1,0,0),\quad\ell_{2}=(0,1,0),\quad\ell_{3}=\frac{1}{\gcd(ab,s)}(bs,as,abr).

Corresponding to these, we have irreducible invariant divisors $D_{1},D_{2},D_{3}\subset Y$ and multiplicities

m_{1}=0,\quad m_{2}=0,\quad m_{3}=\frac{abs}{\gcd(ab,s)}.

The Newton diagram $\Gamma(f)$ consists of a single face with normal vector $\ell_{0}=(bc,ac,ab)$ and $m_{0}=abc$ . Fulton shows in 3.4 of [13] that the group of Weil divisors modulo linear equivalence on $Y$ is generated by $D_{1},D_{2},D_{3}$ , and that $\sum_{j=1}^{3}a_{i}D_{i}$ is Cartier if and only if there is a $p=(p_{1},p_{2},p_{3})\in M=\mathbb{Z}^{3}$ so that $a_{j}=\ell_{j}(p)$ for $j=1,2,3$ .

In our case, $X$ is equivalent to $-\sum_{i=1}^{3}m_{i}D_{i}=-m_{3}D_{3}$ . Therefore, if $X$ is Cartier, then there is a $p=(p_{1},p_{2},p_{3})\in M$ so that $\ell_{i}(p)=m_{i}$ . Therefore, we find $p_{1}=p_{2}=0$ , and

\frac{abr}{\gcd(ab,s)}p_{3}=\frac{abs}{\gcd(ab,s)}.

Therefore, $X$ is Cartier if and only if $r|s$ , i.e. $r=1$ .

\theexample Example.

In [24], Némethi and Okuma analyse upper and lower bounds for the geometric genus of singularities with a specific topological type, namely, whose link is given by the plumbing graph in fig. 13.

They show that for this graph, the path lattice cohomology is $4$ , but that the maximal geometric genus among analytic structures with this topological type is $3$ . As a result, this graph is not the topological type of a Newton nondegenerate Weil divisor in a toric affine space.

On the other hand, this topological type is realized by the complete intersection given by the splice equations

X=\left\{z\in\mathbb{C}^{4}\,\middle|\,z_{1}^{2}z_{2}+z_{3}^{2}+z_{4}^{3}=z_{1}^{3}+z_{2}^{2}+z_{4}^{2}z_{3}=0\right\}.

This singularity is in fact a Newton nondegenerate isolated complete intersection [28]. As a result, the methods of section 10 do not generalize in the most straightforward way to Newton nondegenerate complete intersections.

References

[1] Altmann, Klaus. Toric $\mathbb{Q}$ -Gorenstein singularities. arXiv:alg-geom/9403003.
[2] Altmann, Klaus; Ploog, David. Displaying the cohomology of toric line bundles. Izv. Math., 84(4):683–693, 2020.
[3] Arnold, Vladimir I.; Gusein-Zade, Sabir M.; Varchenko, Alexander N. Singularities of differentiable maps. Volume 2. Modern Birkhäuser Classics. Birkhäuser/Springer, New York, 2012.
[4] Aroca, Fuensanta; Gómez-Morales, Mirna; Shabbir, Khurram. Torical modification of Newton non-degenerate ideals. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat., RACSAM, 107(1):221–239, 2013.
[5] Artin, Michael. On isolated rational singularities of surfaces. Am. J. Math., 88:129–136, 1966.
[6] Bories, Bart; Veys, Willem. Igusa’s $p$ -adic local zeta function and the monodromy conjecture for non-degenerate surface singularities., volume 1145. Providence, RI: American Mathematical Society (AMS), 2016.
[7] Braun, Gábor; Némethi, András. Invariants of Newton non-degenerate surface singularities. Compos. Math., 143(4):1003–1036, 2007.
[8] Bruns, Winfried; Gubeladze, Joseph. Polytopes, rings, and K-theory. New York, NY: Springer, 2009.
[9] Bruns, Winfried; Herzog, Jürgen. Cohen-Macaulay rings. Rev. ed, volume 39. Cambridge: Cambridge University Press, rev. ed. edition, 1998.
[10] Danilov, V. I. The geometry of toric varieties. Uspekhi Mat. Nauk, 33(2(200)):85–134, 247, 1978.
[11] Denef, Jan. Poles of $p$ -adic complex powers and Newton polyhedra. Nieuw Arch. Wiskd., IV. Ser., 13(3):289–295, 1995.
[12] Eisenbud, David; Neumann, Walter D. Three-dimensional link theory and invariants of plane curve singularities., volume 110 of Annals of Mathematics Studies. Princeton University Press, 1985.
[13] Fulton, William. Introduction to toric varieties, volume 131 of Annals of Mathematics Studies. Princeton University Press, Princeton, NJ, 1993. The William H. Roever Lectures in Geometry.
[14] Karras, Ulrich. Local cohomology along exceptional sets. Math. Ann., 275:673–682, 1986.
[15] Kouchnirenko, A. G. Polyèdres de Newton et nombres de Milnor. Invent. Math., 32:1–31, 1976.
[16] László, Tamás. Lattice cohomology and Seiberg–Witten invariants of normal surface singularities. Ph.D. thesis, Central European University, 2013. ArXiv:1310.3682.
[17] Laufer, Henry B. On rational singularities. Am. J. Math., 94:597–608, 1972.
[18] Lemahieu, Ann; Van Proeyen, Lise. Monodromy conjecture for nondegenerate surface singularities. Trans. Am. Math. Soc., 363(9):4801–4829, 2011.
[19] Merle, Michel; Teissier, Bernard. Conditions d’adjonction. (D’après Du Val). In Séminaire sur les singularités des surfaces, volume 777 of Lecture Notes in Mathematics. Springer-Verlag, Berlin Heiderberg New York, 1980.
[20] Némethi, András. Resolution graphs of some surface singularities. I: Cyclic coverings. In Singularities in algebraic and analytic geometry. Papers from the AMS special session, San Antonio, TX, USA, January 13-14, 1999, 89–128. Providence, RI: American Mathematical Society (AMS), 2000.
[21] Némethi, András. On the Ozsváth-Szabó invariant of negative definite plumbed 3-manifolds. Geom. Topol., 9:991–1042, 2005.
[22] Némethi, András. Pairs of invariants of surface singularities. In Proceedings of the international congress of mathematicians, ICM 2018, Rio de Janeiro, Brazil, August 1–9, 2018. Volume II. Invited lectures, 749–779. Hackensack, NJ: World Scientific; Rio de Janeiro: Sociedade Brasileira de Matemática (SBM), 2018.
[23] Némethi, András; Nicolaescu, Liviu I. Seiberg–Witten invariants and surface singularities. Geom. Topol., 6:269–328, 2002.
[24] Némethi, András; Okuma, Tomohiro. Analytic singularities supported by a specific integral homology sphere link. Methods Appl. Anal., 24(2):303–320, 2017.
[25] Némethi, András; Sigurðsson, Baldur. The geometric genus of hypersurface singularities. J. Eur. Math. Soc. (JEMS), 18(4):825–851, 2016.
[26] Oda, Tadao. Convex bodies and algebraic geometry. An introduction to the theory of toric varieties. Berlin etc.: Springer-Verlag, 1988.
[27] Oka, Mutsuo. On the resolution of the hypersurface singularities. In Complex analytic singularities, volume 8 of Adv. Stud. Pure Math., 405–436. North-Holland, Amsterdam, 1987.
[28] Oka, Mutsuo. Principal zeta-function of non-degenerate complete intersection singularity. J. Fac. Sci., Univ. Tokyo, Sect. I A, 37(1):11–32, 1990.
[29] Popescu-Pampu, Patrick. The geometry of continued fractions and the topology of surface singularities. In Singularities in geometry and topology 2004, volume 46 of Adv. Stud. Pure Math., 119–195. Math. Soc. Japan, Tokyo, 2007.
[30] Popescu-Pampu, Patrick; Stepanov, Dmitry. Local tropicalization. In Algebraic and combinatorial aspects of tropical geometry. Proceedings based on the CIEM workshop on tropical geometry, International Centre for Mathematical Meetings (CIEM), Castro Urdiales, Spain, December 12–16, 2011, 253–316. Providence, RI: American Mathematical Society (AMS), 2013.
[31] Sigurðsson, Baldur. The geometric genus and the Seiberg–Witten invariant of Newton nondegenerate surface singularities. Ph.D. thesis, Central European University, 2015. ArXiv:1601.02572.
[32] Varchenko, Alexander N. Zeta-function of monodromy and Newton’s diagram. Invent. Math., 37:253–262, 1976.