Local spin Hall conductivity

In the following we show that under the assumption of periodic boundary conditions (PBC), i.e., for an open system, we obtain the standard Kubo formula for the SHC of periodic systems. We assume a two-dimensional periodic system with a unit cell area $A_{c}$. The bulk SHC is obtained by averaging the LSHC in one unit cell,

We now plug Eq. (5) into Eq. (7). For this step we need the ground-state projection operator in terms of the occupied states of the periodic system,

where the $N_{\bm{k}}$ wavevectors $\bm{k}=(k_{x},k_{y})$ cover the Brillouin zone. In analogy to Eq. (6) we obtain

with $u_{\bm{k},v}$ the cell-periodic part of $\psi_{\bm{k},v}$ and

the electric-field derivative $|\partial_{\mathcal{E}_{b}}u_{\bm{k},v}\rangle$ projected on the empty states. We further defined $v_{b,\bm{k},cv}=\langle u_{\bm{k},c}|\hat{v}_{b,\bm{k}}|u_{\bm{k},v}\rangle$ and $\hat{v}_{b,\bm{k}}=e^{-i\bm{k}\cdot\hat{\bm{r}}}\hat{v}_{b}e^{i\bm{k}\cdot\hat{\bm{r}}}$.

Finally, we let $N_{\bm{k}}\rightarrow\infty$ and obtain

again in full analogy to the LAHC in a slab geometry Rauch et al. (2018). Using Eq. (10) and evaluating the real-space integral in Eq. (11) we arrive at

where we defined $j^{s}_{a,\bm{k},vc}=\langle u_{\bm{k},v}|\frac{1}{2}\left(\hat{v}_{a}\hat{s}^{s}+\hat{s}^{s}\hat{v}_{a}\right)|u_{\bm{k},c}\rangle$. Eq. (12) is the usual bulk formula for the SHC of periodic materials Sinova et al. (2004).

Calculating LSHC from Eq. (5) can be computationally demanding for large finite systems. Therefore, it might be useful to turn to the nanoribbon geometry with mixed boundary condition. We recall that in the symbol $\sigma^{s}_{ab}$ $a$ denotes the propagation direction of the spin current, $b$ denotes the orientation of the electric field, and $s$ is the polarization direction of the spin current. For the nanoribbon geometry, we introduce a new pair of indices $(\alpha,\beta)=(x,y)$, $\alpha\neq\beta$, where $\alpha$ and $\beta$ denote the direction with OBC (bounded) and PBC (open), respectively. The local information shall be kept in the OBC direction and we thus wish to calculate

with $L_{\beta}$ the length of the periodic unit cell along ${\beta}$ and the ground-state projector as in Eq. (8),

In the following it is necessary to distinguish between the two cases where the spin current is oriented along the direction with PBC and the electric field along the direction with OBC, and vice versa.

For the numerical test calculations we use the Kane-Mele model Kane and Mele (2005) which is expressed by the Hamiltonian

where $\gamma$ denotes the spin, $E_{p}\xi_{i}$ is the onsite energy of the orbital $i$, $t$ is the hopping amplitude between the nearest neighbours. The third term on the right-hand side describes next-nearest neighbour spin-orbit coupling, $\bm{s}$ being the Pauli matrices and $\nu_{ij}=\pm 1$, depending on the orientation of the two nearest-neighbour bonds $\bm{d}_{1}$ and $\bm{d}_{2}$ along which the electron hops from orbital $i$ to orbital $j$. Finally, the fourth term describes nearest-neighbour Rashba spin-orbit coupling.

The Kane-Mele model describes a system on a honeycomb lattice with two sites (four orbitals) per unit cell. In the absence of the Rashba term, the spin is conserved. For two occupied orbitals in a unit cell the model describes an insulator if either $\lambda_{\mathrm{SO}}$ or $E_{p}$ is non-zero. For $\lambda_{\mathrm{SO}}=0$, the insulator is trivial and there is zero bulk SHC. If $E_{p}=0$ and $\lambda_{\mathrm{SO}}$ is finite, the Kane-Mele model becomes a topological insulator with a quantized bulk SHC $\sigma^{z}_{xy}=e/(2\pi)$ Kane and Mele (2005). This quantization is violated by switching-on the Rashba spin-orbit coupling, which breaks the conservation of the spin.

In the first test we choose the model parameters to be $E_{p}=0$, $t=1$, $\lambda_{\mathrm{SO}}=0.1$, and $\lambda_{\mathrm{R}}=0$, modelling graphene with finite spin-orbit coupling, which is a $\mathcal{Z}_{2}$ topological insulator at half filling. The bulk SHC calculated with Eq. (12) on a $50\times 50$ $\bm{k}$-point mesh yields $\sigma^{z}_{xy}=-e/(2\pi)$, as expected Kane and Mele (2005).

We then calculate the LSHC of the model using Eq. (5). For this purpose we construct a $1\times 2$ rectangular supercell and multiply it to create a large rectangular flake of the Kane-Mele system. The result is shown in Fig. 1.

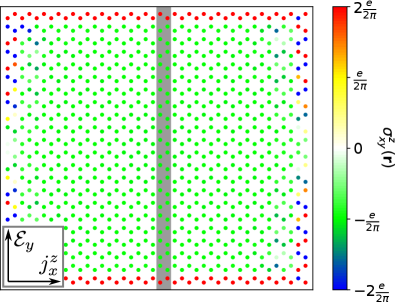
The LSHC ammounts exactly to $-e/(2\pi)$ in the middle of the flake and it thus corresponds with the bulk value. The total SHC of the finite system is zero, since there cannot be any total currents in a system with OBC. This behaviour is analogous to the AHC discussed in Refs. Bianco and Resta, 2011; Marrazzo and Resta, 2017. Therefore, the negative LSHC in the middle of the flake must be canceled by boundary contributions of opposite sign. The thickness of the boundary is $\sim$1 unit cell and the LSHC converges very fast to its bulk value. Indeed, exponential convergence towards the bulk value with the flake size is expected for insulators, owing to the exponential decay of the one-body density matrix Kohn (1996); Bianco and Resta (2011).

In the next step we calculate the LSHC of a nanoribbon with PBC along $x$ and OBC along $y$ constructed multiplying the same $1\times 2$ supercell along the $y$-direction. The model parameters remained as in the previous calculation and the width of the nanoribbon was 21 supercells (84 sites). We calculated both $\sigma^{z}_{xy}(y)$ and $\sigma^{z}_{yx}(y)$ with the electric field oriented along $y$- and $x$-direction, using Eqs. (19) and (17), respectively. We show the results in Fig. 2.

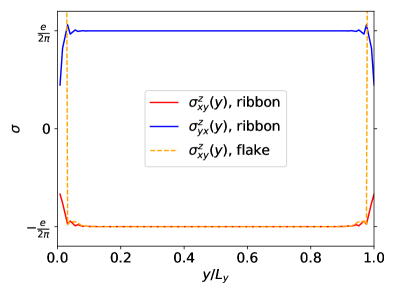
Again, we obtained $\sigma^{z}_{xy}(y)=-e/(2\pi)$ in the middle of the nanoribbon, in perfect agreement with both the flake and bulk calculations. For the rotated geometry with electric field along the PBC direction we got $\sigma^{z}_{yx}(y)=e/(2\pi)$ in the bulk region, which also agrees with the previous results via $\sigma^{z}_{xy}=-\sigma^{z}_{yx}$. As for the finite system, the LSHC at the edges of the nanoribbon differs from the bulk region. Yet in this case the total SHC of the system does not vanish, since the system is periodic (and not finite) in the $x$-direction.

In our second test we turn to a metallic system. We chose the model parameters $E_{p}=0$, $t=1$, $\lambda_{\mathrm{SO}}=0.3$, and $\lambda_{\mathrm{R}}=0.25$ and set the Fermi level $E_{\mathrm{F}}=0.9$ to be located in the empty states. A bulk calculation with $200\times 200$ $\bm{k}$-points for this set of parameters yields $\sigma^{z}_{yx}=$ 0.61 e/($2\pi$).

As discussed in Ref. Marrazzo and Resta, 2017, the one-body density matrix decays as a power law in metals, in contrast to the exponential decay in insulators. This leads to a more delocalized effect of inhomogenities on local properties, which can be for example Friedel oscillations or surface resonant states. These oscillations typically appear on a scale larger than a single bulk unit cell and can influence local material properties far from their origin. We calculated the LSHC of a metallic nanoribbon constructed from up to 404 sites, performing the $\bm{k}$-integration along the periodic direction over 500 $\bm{k}$-points.

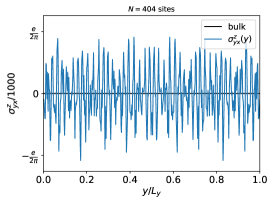
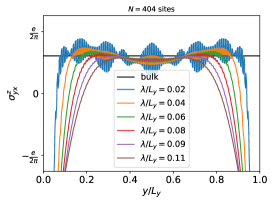
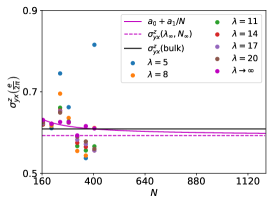
We show the result for $N=404$ sites in the left panel of Fig. 3. The LSHC shows extreme oscillations of up to $\pm 1000e/(2\pi)$ which can be of physical origin as mentioned above, as well as of numerical origin, caused by the finite number of $\bm{k}$-points used in a numerical calculation. In a realistic material, the physical oscillations are typically weakened by the averaging effect of temperature or disorder. In these test calculations we intent to demonstrate that the LSHC values in a locally homogeneous system agree with those calculated for a corresponding bulk periodic system. Therefore, we locally average the calculated LSHC values, effectively reducing both types of oscillations. To achieve this, we apply a Gaussian smearing to the LSHC at site $l$ as

Depending on the parameter $\lambda$, the LSHC at each site is averaged over a certain neighboring region. We show in the central panel of Fig. 3 that with increasing $\lambda$ the locally averaged LSHC approaches the bulk SHC value in the center of the nanoribbon. Assuming an infinitely large nanoribbon ($N\rightarrow\infty$) and a global average ($\lambda\rightarrow\infty$), we expect to obtain the bulk value exactly. Therefore, we performed a set of calculations for $N\in(164,404)$ and $\lambda\in(5,20)$. In the right panel of Fig. 3 we plot the values of the smeared LSHC $\overline{\sigma}^{z}_{yx}(l_{c},\lambda,N)$ for a site $l_{c}$ in the center of the nanoribbon. For each $N$ we fitted the values to $\overline{\sigma}^{z}_{yx}(l_{c},\lambda,N)\propto\lambda^{-2}$ and obtained $\overline{\sigma}^{z}_{yx}(l_{c},\lambda_{\infty},N)$, which we then fitted to $\overline{\sigma}^{z}_{yx}(l_{c},\lambda_{\infty},N)\propto N^{-1}$ and extrapolated for $N\rightarrow\infty$. In the right panel of Fig. 3 we show the fitted LSHC $\overline{\sigma}^{z}_{yx}(l_{c},\lambda_{\infty},N)=a_{0}+a_{1}/N$ as a full magenta line and the extrapolated value $\overline{\sigma}^{z}_{yx}(l_{c},\lambda_{\infty},N_{\infty})=$ 0.59 e/($2\pi$). This value shows a relative error of $\sim 3\%$ with respect to the bulk value, which confirms the validity of the LSHC formulas also for metals.

Finally, we test our local approach on a nanoribbon composed of two different parts. First, we construct an insulator / insulator heterostructure, with one part being described by the Kane-Mele Hamiltonian with the parameters $E_{p}=0$, $t=1$, $\lambda_{\mathrm{SO}}=0.3$, and $\lambda_{\mathrm{R}}=0.0$, which has a bulk SHC $\sigma^{z}_{yx}=$ e/($2\pi$). The Hamiltonian of the second part is specified by the parameters $E_{p}=0$, $t=1$, $\lambda_{\mathrm{SO}}=0.3$, and $\lambda_{\mathrm{R}}=0.3$. The bulk SHC is $\sigma^{z}_{yx}=$ 1.106 e/($2\pi$), owing to the nonzero Rashba-term which breaks the spin conservation. The results of the calculation for the nanoribbon geometry ($N=84$ sites, $50\ \bm{k}$-points) are shown in the top panel of Fig. 4.

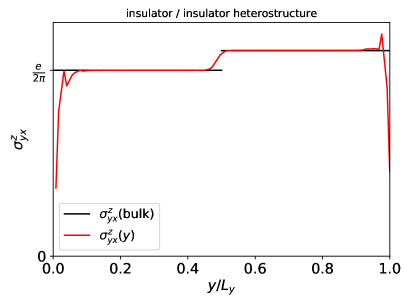
The LSHC in the center of each constituent equals the respective bulk SHC values. Averaging the LSHC is not necessary, because of the exponential decay of the ground-state projector, as described in Sec. III.2.

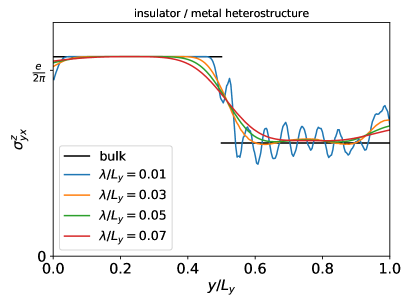
As a second heterostructure we chose an insulator / metal system. The parameters of the insulating part were $E_{p}=0$, $t=1$, $\lambda_{\mathrm{SO}}=0.3$, and $\lambda_{\mathrm{R}}=0.25$ with a bulk SHC $\sigma^{z}_{yx}=$ 1.073 e/($2\pi$). The metallic part was characterized by the same set of parameters, but the orbitals were shifted energetically down by $0.9$, so $E_{\rm F}$ is located in the conduction bands. The subsystem equals the one in Sec. III.3 and the bulk SHC is $\sigma^{z}_{yx}=$ 0.6088 e/($2\pi$). The nanoribbon was constructed from $N=324$ sites and we used $500\ \bm{k}$-points for the integration in the reciprocal space. Since the LSHC values are again strongly oscillating in the metallic region, we applied the averaging given by Eq. (21). We present the results in the bottom panel of Fig. 4, which show a perfect agreement with the bulk SHC for all values of $\lambda$ in the insulating part. Following the same extrapolation procedure of the averaged LSHC value in the middle of the metallic region for $\lambda\rightarrow\infty$, we obtain $\sigma^{z}_{yx}=$ 0.6107 e/($2\pi$), which has a relative error of $0.3\%$ with respect to the corresponding bulk value.

We thus state that our numerical model calculations fully support the analytical formulas for the LSHC with both OBC and mixed boundary conditions. For insulating systems, the expected bulk SHC value is recovered close to the heterogeneous regions, whereas for metallic systems the convergence with system size is much slower ($\sim 1/N$ for the nanoribbon) and averaging over a sufficiently large region (i.e., choosing large $\lambda$) is necessary. On the other hand, for practical uses, $\lambda$ has to be kept small enough to capture the local deviations of the LSHC from the bulk value in inhomogeneous regions.