Long time dynamics of a three-species food chain model with Allee effect in the top predator
Abstract
The Allee effect is an important phenomenon in population biology characterized by positive density dependence, that is a positive correlation between population density and individual fitness. However, the effect is not well studied in multi-level trophic food chains. We consider a ratio dependent spatially explicit three species food chain model, where the top predator is subjected to a strong Allee effect. We show the existence of a global attractor for the the model, that is upper semicontinuous in the Allee threshold parameter . To the best of our knowledge this is the first robustness result, for a spatially explicit three species food chain model with an Allee effect. Next, we numerically investigate the decay rate to a target attractor, that is when , in terms of . We find decay estimates that are , where is found explicitly. Furthermore, we prove various overexploitation theorems for the food chain model, showing that overexploitation has to be driven by the middle predator. In particular overexploitation is not possible without an Allee effect in place. We also uncover a rich class of Turing patterns in the model which depend significantly on the Allee threshold parameter . Our results have potential applications to trophic cascade control, conservation efforts in food chains, as well as Allee mediated biological control.
Rana D. Parshad, Emmanuel Quansah and Kelly Black
Department of Mathematics,
Clarkson University,
Potsdam, New York 13699, USA.
Ranjit K. Upadhyay and S.K.Tiwari
Department of Applied Mathematics,
Indian School of Mines,
Dhanbad 826004, Jharkhand, India.
Nitu Kumari
School of Basic Sciences,
Indian Institute of Technology Mandi,
Mandi, Himachal Pradesh 175 001, India.
-
Keywords:
three species reaction diffusion food chain model, global existence, global attractor, upper semi-continuity, Allee effect, Turing instability .
1 Introduction
Interactions of predator and prey species are ubiquitous in spatial ecology. Therein a predator or a “hunting” organism, hunts down and attempts to kill a prey, in order to feed. Food webs, which comprise all of the predator-prey interactions in a given ecosystem, are inherently more complex. The food chains or linear links of these food webs in real ecosystems, have multiple levels of predator-prey interaction, across various trophic levels. To better understand natural ecosystems, with multiple levels of trophic interaction, where predators and prey alike, disperse in space in search of food, mates and refuge, a natural starting point is to deviate from the classical predator-prey two species models, and investigate spatially explicit three species food chains. Such models are appropriate to model populations of generalist predators, predating on a specialist predator, which in turn predates on a prey species. Also, they can model two specialist predators competing for a single prey [15, 30]. The spatial component of ecological interaction has been identified as an important factor in how ecological communities are shaped, and thus the effects of space and spatially dispersing populations, via partial differential equations (PDE)/spatially explicit models of three and more interacting species, have been very well studied [33, 15, 16, 23, 19]. In most of these models, the prey is regulated or “inhibited” from growing to carrying capacity due to predation by the predator. Whereas loss in the predator is due to death or intraspecific competition terms. However, there are various other natural self regulating mechanisms in a population of predators (or prey). For instance, much research in two species models, has focused on one such mechanism: the so called Allee effect. However, less attention has been paid to this mechanism in the three species case. This effect, named after the ecologist Walter Clyde Allee, can occur whenever fitness of an individual in a small or sparse population, decreases as the population size or density does [8]. Since the pioneering work of Allee [2, 3], Allee dynamics has been regarded as one of the central issues in the population and community ecology.
The effect can be best understood by the following equation for a single species ,
| (1) |
essentially a modification to the logistic equation. Here the state variable, represents the numbers of a certain species at a given time , is the carrying capacity of the environment that resides in, and is the Allee threshold, with . A strong Allee effect occurs if , [31]. This essentially means that if falls below the threshold population , its growth rate is negative, and the species will go extinct [17]. If , then there is a weak Allee effect, and we have a compensatory growth function [13, 5, 7]. For our purposes we assume a strong Allee effect is in place, that is . Note, are stable fixed points for (1), and is unstable. Thus dynamically speaking the global attractor, which is the repository of all the long time dynamics of for (1) is . An interesting question can now be posed: what happens to this attractor as ? Ecologically speaking, this is asking: what happens to the species as the Allee threshold is decreased? When the only stable fixed point is , with being half stable. Thus the global attractor is now reduced to a single point . What we observe is that the difference between having a slight Allee effect (say ) and having no Allee effect (), can change completely what the global attractor of (1) is. That is to say, the global attractor changes from an entire set , to a single fixed point . From an ecological point of view, this says as long as there is a slight Allee effect there is an extinction risk for , but without one there is none, and will always grow to carrying capacity. Proving that an attractor approaches a target attractor , in a continuous sense, in the case of spatially explicit/PDE models requires a fair amount of work. This involves making several estimates of functional norms, independent of the parameter [22]. If this can be proven however, the attractor is said to be robust at . However, to the best of our knowledge there are no robustness results in three species food chain models, where the parameter of interest is the Allee threshold . Note, unless a systems dynamics are robust, there is no possibility to capture the same in a laboratory experiment or natural setting.
The critical importance of the Allee effect has widely been realized in the conservation biology: That is: it is most likely to increase the extinction risk of low-density populations. This is also known as critical depensation in fisheries sciences. Essentially individual species population must surpass the threshold to grow. Hence a small introduced population under strong Allee effect can only succeed if it is faced with favorable ecological conditions, or experiences rapid adaptive evolution, or simply has good luck, so that it can surpass this critical threshold. There are several factors that might cause an Allee effect. These include difficulty of finding mates at low population densities, inbreeding depression and environmental conditioning[28]. The Allee effect can be regarded not only as a suite of problems associated with rarity, but also as the basis of animal sociality [26]. Petrovskii et al. [21] found that a deterministic system with Allee effect, can induce patch invasion. Morozov et al. [14] found that the temporal population oscillations can exhibit chaotic dynamics even when the distribution of the species in the space was regular. Also, Sharma and Samanta [24] developed a ratio-dependent predator-prey model with disease in prey, as well as an Allee effect in prey. Furthermore, Invasion biologists have recently attempted to consider Allee effects as a benefit in limiting establishment of an invading species[28], which without the effect would possibly run amuck, an cause excessive damages to native species because of predation and competition.
On the same lines, a phenomenon that occurs in large food chains, is the excessive harvesting/predation of certain species in the chain, via the predators in the trophic level above them. In many aquatic food chains, this can lead to trophic cascades [6], and is among the major activities that is threatening global biodiversity. Formally, overexploitation refers to the phenomenon where excessive harvesting of a species can result in its extinction. Mathematically, for a two species predator-prey system, one can prove an overexploitation type theorem, if one shows for a large enough initial density of the predator, the prey will be predated on till extinction. In this case, If the predator does not have an alternate food source, it will also subsequently go extinct. Although there is a fair amount of literature on this in two species models [32], it is less studied in three species models. In particular, the Allee effect itself on overexploitation, in multi-trophic level food chains, has not been sufficiently explored.
Our primary goal in the current manuscript is to propose and analyze a reaction-diffusion three species food chain model, with an Allee effect in the top predator. In particular, we aim to investigate the link between the Allee threshold parameter , and the longtime dynamics of the three species food chain, in terms of
-
•
Robustness of global attractors in terms of the Allee threshold parameter .
-
•
Overexploitation phenomenon in the food chain model, as it is effected by the Allee threshold parameter .
-
•
Pattern formation and the effect on patterns that form in the food chain model due to the Allee threshold parameter .
Our hope is that this model could be used as a feasible toy model, to better understand the following in multi-trophic level food chains,
-
•
Top-down pressure in multi-trophic level food chains leading to overexploitation phenomenon.
-
•
Trophic cascades and cascade control via an Allee effect.
-
•
Conservation efforts in food webs mediated via an Allee effect.
-
•
Biological control of an invasive top predator in a food chain via Allee effect
Thus, we consider a situation where a prey species serves as the only food for a specialist predator which is itself predated by a generalist top predator .
This is a typical situation often seen in nature in various food chains [20]. The governing equations for populations and follow ratio dependent functional responses, and are modeled by the Volterra scheme i.e., the middle predator population dies out exponentially in the absence of its prey. There is recently much debate about functional responses used in ecology, and the ratio dependent response is considered to be more realistic than its Holling type counterparts [1]. The above situation is described via the following system of PDE. This is already nondimensionalised, see appendix 7.1 for the details of the nondimensionalisation.
| (2) | |||
| (3) | |||
| (4) |
the spatial domain for the above is , . is assumed bounded, and we prescribe Neuman boundary conditions . In the above is the intrinsic death rate of the specialist predator in the absence of its only food , measures the rate of self-reproduction of the generalist predator . are the maximum values which per capita growth rate can attain. shows that the top predator is a generalist and can switch its food source in the absence of . Also we model the top predator via a Leslie Gower scheme [30], and assume that it is subject to the Allee effect. The parameter is the Allee threshold or minimum of viable population level. In this work, we limit ourselves to the case where , that is we assume a strong Allee effect.
In particular we ask: How does the Allee threshold affect the various dynamical aspects of model system (2)-(4)? To this end we list our primary findings.
- •
-
•
We show that this attractor is upper semi-continuous w.r.t the Allee threshold , via theorem 3.3. That is the attractor is robust at . This result requires making estimates of various functional norms, independent of the parameter , and then proving and using a chain of theorems that facilitate passing to the limit as . The calculations are detailed, so we confine them to an appendix section 7.
- •
- •
- •
2 Preliminary Estimates
2.1 Preliminaries
We now present various notations and definitions that will be used frequently. The usual norms in the spaces , and are respectively denoted by
We define the following phase spaces
We now recall the following lemma.
Lemma 2.1 (Uniform Gronwall Lemma)
Let , and be nonnegative functions in . Assume that is absolutely continuous on and the following differential inequality is satisfied:
| (5) |
If there exists a finite time and some such that
| (6) |
for any , where , and are some positive constants, then
| (7) |
2.2 Uniform and estimates
In all estimates made hence forth the constants are generic constants, that can change in value from line to line, and sometimes within the same line if so required. Using positivity of the solution, and comparison arguments, one is easily able to prove global existence of classical solutions to system (2)-(4). We state the following result.
Proposition 2.2
See appendix 7.2 for the proof. Although we have global existence of classical via proposition 2.2, we can actually derive uniform bounds, for initial data only in . This will facilitate estimates required to show existence of bounded absorbing sets and the compactness of trajectories, which will lead to the existence of a global attractor in the product space . Since the construction of global attractors require a Hilbert space setting, where the appropriate function spaces are the Hilbert spaces and , , we want to proceed by showing there is a weak solution in these function spaces. We then make estimates on this class of solutions, to proceed with the requisite analysis for the global attractors. We state the following theorem:
Theorem 2.3
The proofs of proposition 2.2 and theorem 2.3 follow via remark 2.7 and the estimates referred to therein.
We state the following result next,
Lemma 2.4
Consider that are solutions to the diffusive three species food chain model described via (2)-(4), for any , and spatial dimension , there exists a time , and a constant independent of time, initial data and the allee threshold , and dependent only on the other parameters in (2)-(4), such that for any the following uniform estimates hold:
| (8) |
This follows easily via the estimates and methods of [20, 18, 19]. Note what differs here from [20, 18, 19] is the equation for , particularly due to a Allee effect now being modeled.
We now proceed with the estimate on . We multiply (4) by and integrate by parts to obtain
| (9) |
Thus we obtain
| (10) |
We then use Hölder’s inequality followed by Young’s inequality to obtain
Thus we obtain
| (12) |
which implies
| (13) |
We now use the estimate for via (27) (which does not depend on see remark 2.8) to obtain the following estimates for ,
| (14) |
Integrating (7.4) in the time interval we obtain
| (15) |
for .
Here, do not depend on .
Remark 2.5
We now estimate the gradient of . See the appendix 7.3 for details. What the standard analysis in appendix 7.3 shows, is that we have an estimate of the form
| (16) |
Remark 2.6
The constant in (16) is independent of time and initial conditions, but depend singularly on . In our estimates we apply the uniform Gronwall lemma which requires us to use the estimate via (15). This also depends singularly on , thus the estimate (16) is uniform with respect to time and initial data but depend singularly on .
Remark 2.7
The uniform estimates via lemma 2.4 and (95) give us uniform bounds in . We can now prove the reaction terms are in for . It suffices to show that
| (17) |
| (18) |
| (19) |
But the above follows via the uniform bounds on . This proves proposition 2.2. Furthermore the estimate via (16) and lemma 2.4 allow us to derive the appropriate and bounds on a Galerkin truncation of (2)-(4), extract appropriate subsequebces and pass to the limit as is standard [27, 22], to prove theorem 2.3.
2.3 Uniform in the parameter and estimates for
Note the estimates via (14), (16) are singular in . This causes extensive difficulties if we try to pass to the limit as , hence making it difficult to prove upper semicontinuity. Our next goal is to derive uniform in estimate on . These are derived in detail in the appendix 7.4. However, the key estimate derived therein is
| (20) |
Here are independent of . Thus the estimate for can be made independent of .
2.4 Uniform estimates
We will now estimate the norms of the solution. We rewrite (2) as
We square both sides of the equation and integrate by parts over to obtain
This result follows by the embedding of . Therefore, we obtain
We now make uniform in time estimates of the higher order terms. Integrating the estimates of (2.4) in the time interval , for
Similarly we adopt the same procedure for to obtain
Next, consider the gradient of (2). Following the same technique as in deriving (2.4) we obtain for the left hand side
| (21) |
This follows via the boundary condition. Thus we have
| (22) |
This follows via Young’s inequality with epsilon, as well as the embedding of . This implies that
We now use the uniform Gronwall lemma with
to obtain
The estimate for is derived similarly.
Remark 2.8
It is critical to notice that the estimate for does not involve . This is because in order to derive it, we adopt same procedure as in (2.4), instead for the equation, and square both sides to proceed. Therein notice that the term involving , can be estimated as . So the right hand side has no dependence on .
In order to estimate the norm of we proceed similarly to obtain
We now make uniform in time estimates of the higher order terms. Integrating the estimates of (2.4) in the time interval , for , and using the estimates via (7.4) yields
This yields
| (25) |
3 Long Time Dynamics
3.1 Existence of global attractor
In this section we prove the existence of a global attractor for system (2)-(4), which is subsequently demonstrated to be a attractor. We now state the following theorem,
Theorem 3.1
proof We have shown that the system is well posed via theorems 2.3. Thus there exists a well defined semigroup . The estimates derived in Lemma 2.4 demonstrate the existence of bounded absorbing sets in and . Thus given a sequence , that is bounded in , we know that for ,
| (28) |
Here is the bounded absorbing set in from lemma 2.4. Now for n large enough , thus for such we have
| (29) |
This implies that we have the following uniform bound,
| (30) |
This implies via standard functional analysis theory, see [27], the existence of a subsequence still labeled such that
| (31) |
Which implies via the compact Sobolev embedding of
| (32) |
that
| (33) |
This yields the asymptotic compactness of the semigroup in . The convergences for the components follow similarly. The theorem is now proved.
Next we can state the following theorem
Theorem 3.2
3.2 Upper-semicontinuity of Global attractor with respect to the Allee parameter
Here we state and prove the main semicontinuity result. This result follows via a series of estimates, and theorems, all of which we derive for the reader in appendix 7.5
Theorem 3.3
Consider the reaction diffusion equation described via (2)-(4) where is of spatial dimension . Given a set of positive parameters excluding , the family of global attractors is upper semicontinuous with respect to the Allee threshold as it converges to zero. That is
| (34) |
Proof 3.4
We know that for , the global attractor for the reaction diffusion equation described via (2)-(4) attracts . This follows via theorems 7.6, 7.7 and 7.9. Thus there exists a finite time , such that
| (35) |
Here, is the ball of in the space . Now we also know by the uniform convergence theorem, theorem 7.10 that there exists a such that
| (36) |
Since we know is invariant we have
| (37) |
Thus one obtains the upper semicontinuity,
| (38) |
This proves the theorem.
3.3 Computing the decay rate with respect to the Allee threshold parameter
In the previous subsection 3.2, the role of the Allee threshold parameter on the long time dynamics of system (2)-(4) is explored. Theorem 3.3 shows that the global attractors converge to in the norm, as decreases to zero. It is also seen how changing effects the Turing dynamics in subsection 5. Theorem 3.3 is a purely theoretical result. It gives no information as to the exact decay rate in terms of the parameter . In general, there are no results in the literature to estimate this decay rate. We now aim to examine the role of with respect to convergence, as decreases to zero as discussed earlier. We aim to explicitly find the decay rate of to a target attractor (that is when ). We choose Turing patterns as the state of interest. In particular the numerical scheme discussed in 5 was employed, and the Turing patterns at an extended time are examined. The goal is to gather numerical evidence as to the dependence on with respect to the convergence rate,
| (39) |
where is the solution for , is the solution for any given value of , and both and are constants.
The numerical approximation for the case was established at the scaled time, . The approximations, , , and , were then established for a range of values of with 121 equally spaced values from 0 to 0.0035. The approximation for each value of was established up to , and it was determined that for each value of in this range a fixed spatial pattern was found. The errors for the numerical approximation were then calculated with respect to the case,
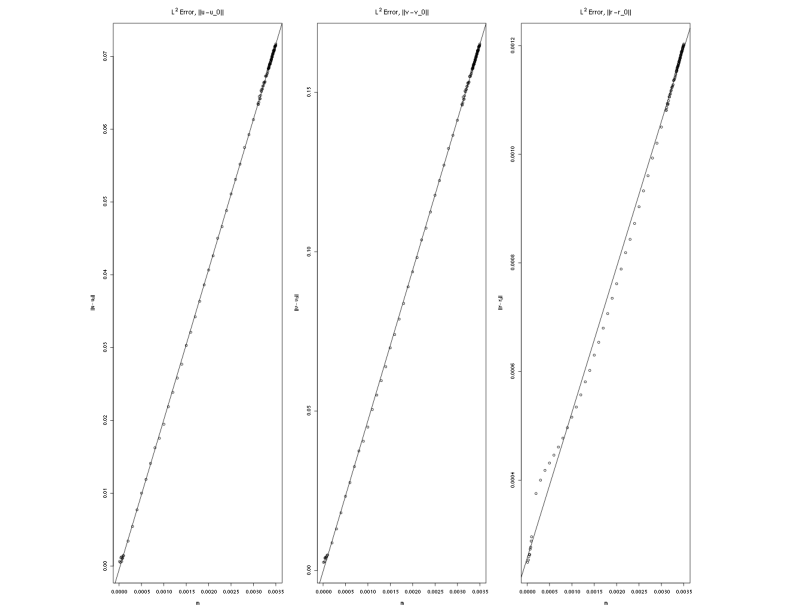
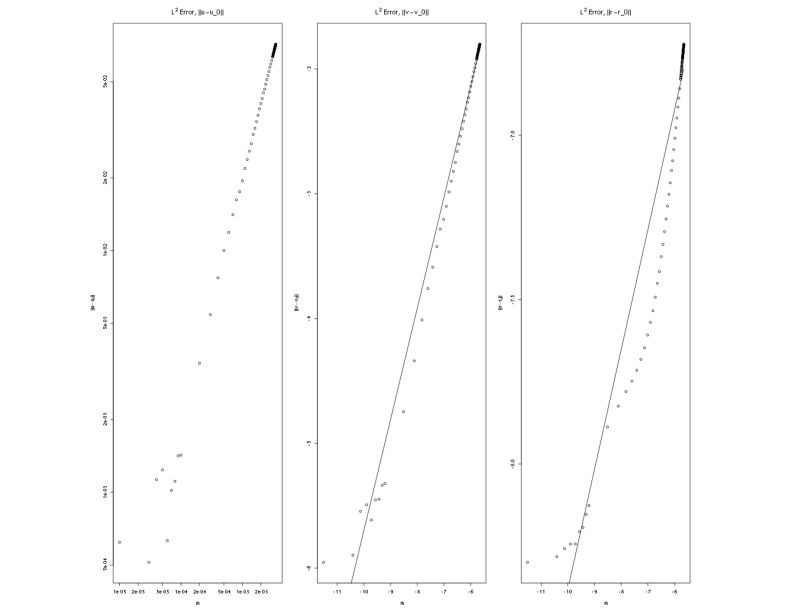
The errors are shown in Figure 1 and Figure 2. The first figure, Figure 1, shows the raw errors, and the second figure, Figure 2, shows the errors as a log-log plot. A linear least squares fit for the data was also calculated, and the best fit straight line is shown on both plots. In both cases the close linear fit for larger values of contribute to strong, positive correlations in the data. However, for smaller values the log-log data moves away from a straight line. For the smaller values of the errors in the numerical approximation are of the same order as the error in the norm, and the data no longer follows the same trend.
Examining the errors for , the correlation for the raw data is 0.99995, and the data reveals a strong, positive linear relationship. In this scenario, it is assumed that the value of in equation (39) is one. The approximation for the slope of the raw data gives an estimate of 20.6 with a 95% confidence interval between 20.6215 and 20.6206. The 95% confidence interval for the intercept is between -5.1E-5 and -9.0E-4. Due to the large number of samples, the error in the confidence interval is very small, but the estimate for the parameter is close to zero.
Examining the errors for the log of the errors correlation is 0.993 for the log-log data. The approximation for the slope of the log-log data gives an estimate of 1.003 with a 95% confidence interval between 0.72 and 1.28. The 95% confidence interval for the intercept is between 2.7 and 3.3. Note that the value of one is within the confidence interval making it difficult to claim that the relationship is not linear. The estimate for the slope, in fact, is very close to one indicating that the value of in equation (39) is close to one.
4 Overexploitation Phenomenon
Overexploitation refers to the phenomenon where excessive harvesting of a species can result in its extinction. This finds applications in conservation, biodiversity, cascade control and so on. Although there is a fair amount of literature on this in two species models [32], it is much less studied in three species models. To begin, we state the following theorem
Theorem 4.1 (Middle predator and Allee effect mediated overexploitation)
proof: We begin by looking at the equation for , and following the ideas in [12]
| (40) |
We will claim that for all , , and , , if . If not there exists a first time s.t., on and .
Due to , there exists an s.t , thus
| (41) | |||||
Thus satisfies
| (42) |
This easily follows via multiplying (2) by , and integrating by parts. We also notice that the solving the following equation, with , is a super solution to (3)
| (43) |
Multiplying through by , and integrating by parts yields
| (44) |
This implies
| (45) |
This implies a contradiction. Thus , which implies uniform convergence of a subsequence, say to 0 (where is a Galerkin truncation of and standard theory is adopted [22]), and by uniqueness of solutions, uniformly, as . This reduces the equation to
| (46) |
and it is easy to see that uniformly, as .
Now the equation reduces to
| (47) |
and if standard analysis yields
uniformly.
This proves the theorem.
Remark 4.2
Also, if the attack rate of the top predator is large enough, it could cause to go extinct, before does. Once goes extinct , again prohibiting overexploitation.
Theorem 4.3 (Top predator mediated overexploitation avoidance)
proof: We first derive a lower bound on . Trivially we have . Now
| (48) |
This yields
| (49) |
Next we will claim that for all , , and , , if . If not there exists a first time s.t., on and .
Due to the choice of , there exists an s.t , thus
Thus satisfies
| (51) |
By the restriction on , we see that trivially or . This implies
| (52) |
This implies a contradiction. Thus , which implies uniform convergence to 0 of a subsequence, say (where is a Galerkin truncation of and standard theory is adopted [22]), and by uniqueness uniformly as . Looking at the decay rate for , we see it converges to 0 faster than , so , when uniformly, and so then the equation reduces to
| (53) |
and we know via standard theory that now uniformly.
This proves the theorem.
Remark 4.4
This also happens if , or .
The following lemma describes persistence in the top predator.
Lemma 4.5 (Persistence in top predator)
proof: Note , due to positivity of . Thus we can compare the solution of (4) to the solution of the ODE
| (54) |
Remark 4.6
In the event that there is no Allee effect, or , uniformly as , hence always persists, independent of all other parameters or initial data . Thus in a three species system where the top predator is a generalist, and can switch its favorite food source, true overexploitation can only take place if an Allee effect is in place, and not otherwise.
Remark 4.7
All of the over exploitation theorems were verified numerically, for various ranges of parameter values.
5 Turing Instability
In this section we establish the condition needed to ensure a positive interior steady state for model system (2-4). We focus on deriving the condition necessary and sufficient for Turing instability to occur as a result of the introduction of diffusion. This phenomena is referred to as diffusion driven instability, which was first introduced by Alan Turing[29]. We first establish the steady state for model system (55-57)
5.1 Steady States
Before we can begin the analysis of Turing instability, we have to establish the conditions needed to ensure a positive interior steady state for the ODE version of model system (2)-(4), which is given as
| (55) | |||
| (56) | |||
| (57) |
Also all parameters associated with model system (55-57) are assumed to be positive constants and have the usual biological meaning.
The model system (55)-(57) has the following non-negative steady states
-
1.
Total Extinction of the three species: .
-
2.
Predator free steady state: .
-
3.
No primary food source for predator steady state: and .
-
4.
Top Predator free steady state: where if .
-
5.
Middle Predator free steady state: and .
-
6.
Coexistence of Species: where and is the real positive root of following equation:
(58) where
-
7.
Coexistence of Species with interior equilibrium population: is the solution of following equations:
(59a) (59b) (59c)
From (59) we have,
| (60) | |||
| (61) |
Putting the values of and from (60) and (61) into (59b), we get
| (62) |
where
,
,
,
.
is the real positive root of (62). Hence interior equilibrium point exists if . Knowing the value of we can find the values of and from (60) and (61) respectively.
Remark 5.1
5.2 Turing conditions
In this subsection we derive sufficient conditions for Turing instability to occur in (2)-(4) where the positive interior equilibrium point is stable in the absence of diffusion and unstable due to the addition of diffusion, under a small perturbation to . This is achieved by first linearizing model (2)-(4) about the homogenous steady state, by introducing both space and time-dependent fluctuations around . This is given as
| (63a) | |||
| (63b) | |||
| (63c) | |||
where , and . Conventionally we choose
where for are the corresponding amplitudes, is the wavenumber, is the growth rate of perturbation in time and is the spatial coordinate. Substituing (63) into (2)-(4) and ignoring higher order terms including nonlinear terms, we obtain the characteristic equation which is given as
| (67) |
where
and is a identity matrix.
For the non-trivial solution of (67), we require that
which gives a dispersion relation corresponding to . To determine the stability domain associated with , we rewrite the dispersion relation as a cubic polynomial function given as
| (68) |
with coefficients
According to Routh-Hurwitz criterion for stability, in model (2)-(4) around equilibrium point (i.e is stable) if and only if these conditions holds:
| (69) |
As violating either of the above conditions implies instability (i.e ).
We now require conditions where an homogenous steady state () will be stable to small perturbation in the absence of diffusion and unstable in the present of diffusion with certain vaules. Meaning, we require that around the homogenous steady state
where we consider to be real and positive even though can be complex. This behavior is called diffusion driven instability. Models that exhibits this sort of behavior in and species has been extensively studied in [33], where several different patterns was observed.
In order for homogenous steady state to be stable( in the absence of diffusion) we need
where as with diffusion () we look for conditions where we can drive the homogenous steady state to be unstable, this can be achieved by studying the coefficient of (68). In order to achieve this we need to reverse at least one of the signs in (69). By which we first study . Irrespective of the value of , will be positive since is always less than zero. Therefore we cannot depend on for diffusion driven instability to occur. Hence for diffusion driven instability to occur in our case, we only depend on the conditions which are
| (70) |
Both functions are cubic functions of , which are generally of the form
The coefficient of are given in Table 1.
| Coefficient of | |||
|---|---|---|---|
To drive either or to negative for some , we need to find the minimum referred to as the minimum turing point () such that . This minimum turing point occurs when
this when solved for yields
To ensures is real and positive such that , we require either
| (71) |
which ensures that
Therefore , if at
| (72) |
Hence (71)-(72) are necessary and sufficient conditions for to produce diffusion driven instability, leading to the emergence of patterns. Also to first establish stability when , in each case has to be positive. We state this via the following theorem
5.3 Effect of Allee threshold parameter on Turing Instability
In this section we investigate the effects of Allee threshold on Turing patterns. We focus on whether can induce Turing instabilities. We perform numerical simulation of model system (2)-(4) and the use of coefficient of dispersion relation, given in Table 1.
A Chebychev collocation scheme is employed for the approximation of
the time varying, one-dimensional
problem[11, 9].
Our one-dimensional numerical simulation employs the zero-flux boundary condition with a spatial domain of size . We define the spatial domain to be , in the nondimensionalistaion in appendix 7.1, where .
The initial condition as defined is a small perturbation around the positive homogenous steady state given as
where .
In the two-dimensional case, we numerically solve model system (2)-(4) using a finite difference method. A forward difference
scheme is used for the reaction part. A standard five-point explicit finite difference scheme is used for the two-dimensional diffusion terms. Model system (2)-(4) is numerically solved in two-dimension over mesh points with spatial resolution and time step .
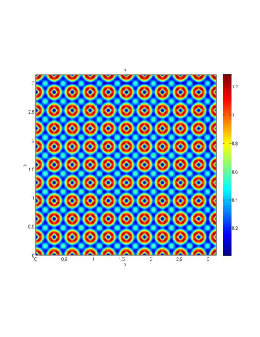
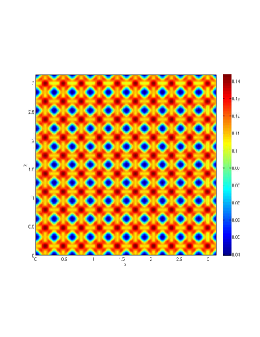
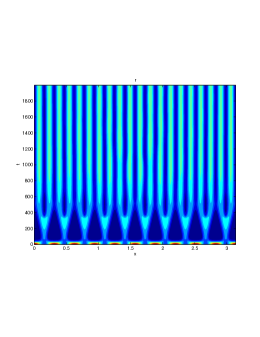
In our numerical simulation both in the one-dimensional and two-dimensional case, with specific parameter set as show in figure (3)-figure (7), different types of dynamics are observed as a result of the value of the Allee threshold .
From figure (3)-figure (4), we numerically observe that change in can result in disappearance of patterns or the appearance of patterns. Specifically from figure (3)-figure (4), patterns where observed when but these patterns change as gets larger and finally at , these patterns completely disappear. The critical Allee threshold , for patterns to disappear, depends on the parameter set being used. In some cases, patterns where observed when but as and beyond, these patterns disappeared.
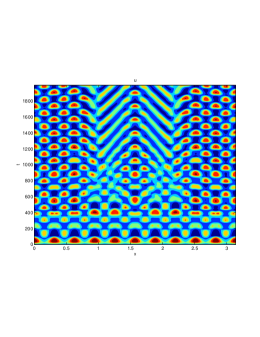
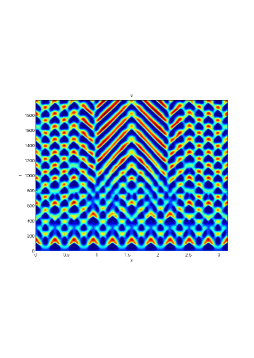
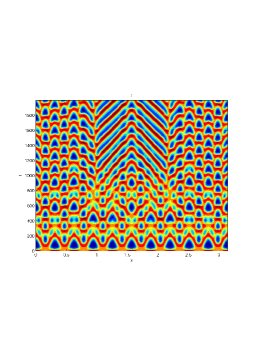
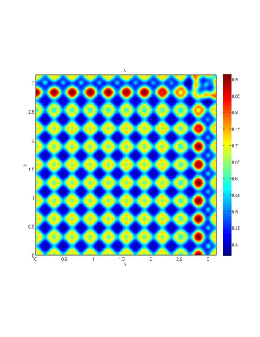
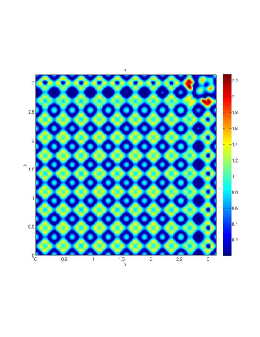
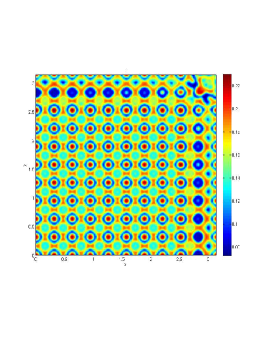
It is also conclusive from figure (5)-figure (7) that Allee threshold has an effect on the type of patterns that do form particularly, as in the case of figure (5) and (7), changing , can change spatio-temporal patterns to a fixed spatial patterns. This behavior can be observed using the dispersion relation as shown in figure (9).
In choosing for some , which will mostly result in fixed spatial patterns, changing the value of does not result in a change in the type of patterns formed, but parameters move out of the Turing space. Therefore in our numerical experiments we do not find parameters such that fixed spatial patterns can change to spatial-temporal patterns, as increases from zero.
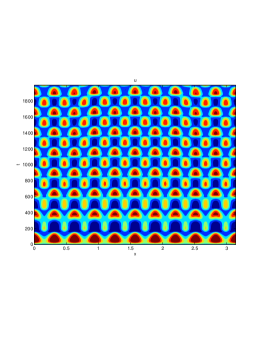
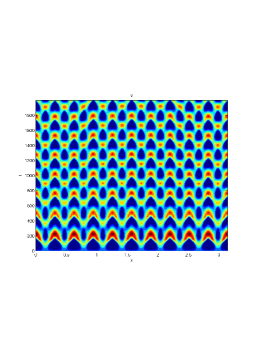
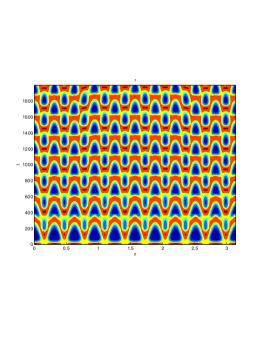
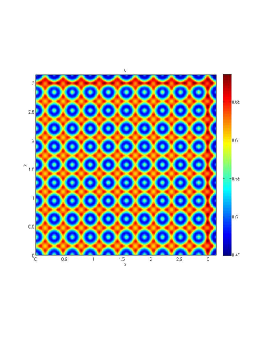
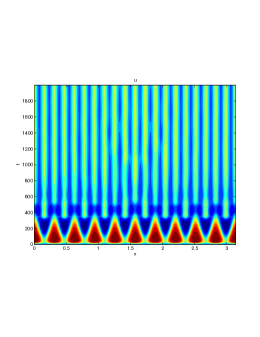
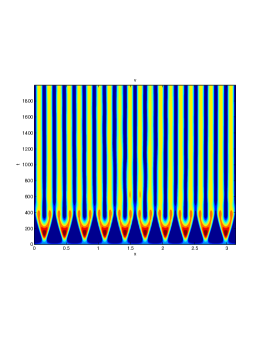
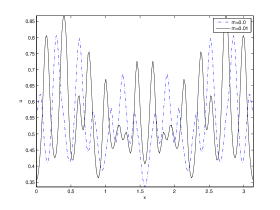
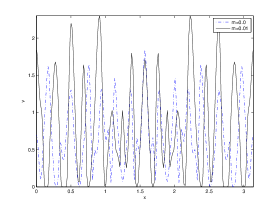
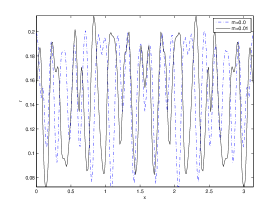
We next observe the densities at time t=1500 for (dashed line) vs (solid line), to see how the species density changes in space as the Allee threshold changes.
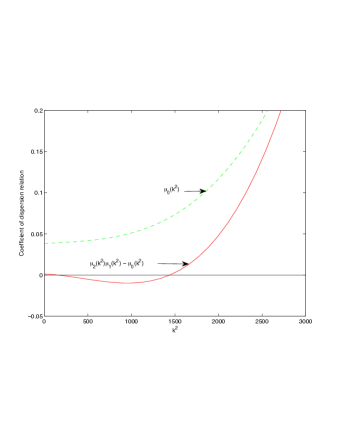
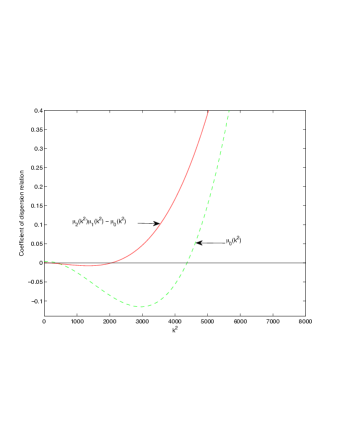
Table (2), also displays the fact that no patterns were observed as increases from to from figure (3) and figure (4) because can destabilizes an already stable equilibrium point in the ode model as in when . Hence as in figure (3) and figure (4) where produces patterns since is stable when , this stable () equilibrium point becomes unstable () even when .
| Pattern | |||
|---|---|---|---|
| Patterns may occur | |||
| Patterns may occur | |||
| No Patterns | |||
| No Patterns | |||
| No Patterns | |||
| No Patterns |
6 Discussion
In this manuscript we have considered a spatially explicit ratio dependent three species food chain model, with a strong Allee effect in the top predator. The model represents dynamics of three interacting species in “well-mixed” conditions and is applicable to ecological problems in terrestrial, as well as aquatic systems. Our goal is to understand the effect of the Allee threshold on the system dynamics, as there is not much work on Allee effects in multi-trophic level food chains, and we hope to address this here.
We first prove the existence of a global attractor for the model. In many systems an interesting question is to consider the effect on the global attractor, under perturbation of the physical parameters in the system. Most often continuity cannot be proven, but upper semi-continuity can. We show that the global attractor is upper semi-continuous w.r.t the Allee threshold parameter , that is , via theorem 3.3. To the best of our knowledge this is the first robustness result for a three-species model with strong Allee effect. Unless a systems dynamics are robust, there is no possibility to capture the same ecological behavior in a laboratory experiment, or natural setting.
The next question of interest, after one has proved such a result, is estimating the rate of decay, in terms of the physical parameter in question. Since there are no theoretical results to estimate the decay rate to the target attractor (that is when ), we choose to investigate this rate numerically. We find decay estimates of the order of , where is found explicitly to be slightly less, but very close to 1.
We also find that effects the spatiotemporal dynamics of the system in two distinct ways.
(1) It changes the Turing patterns that occur in the system, in both one and two spatial dimensions.
That is varying , has a distinct effect on the sorts of Turing patterns that form.
This can have interesting effects on the patchiness of spatially dispersing species. Our results say that if one can effect the Allee threshold in the top predator, one can effectively change the spatial concentrations of the species involved. This is best visualized in figure 8. This could have many potential applications in Allee mediated biological control, and conservation, as recently biologists have begun to consider Allee effects as beneficial in limiting establishment of an invading species [28].
(2) It facilitates overexploitation phenomenon. That is without , or when , one does not see extinction in top predator, as the origin becomes unstable. However,
introducing it stabilises the origin, and low initial concentrations of , may yield extinction, via theorems 4.1. This has many possible applications to top down trophic cascades and cascade control. This also tells us that in a three species system, where the top predator can switch its food source, only having an Allee effect in place can possibly drive it to extinction, thus bring about true overexploitation. This could have potential applications in Allee mediated biological control, if the top predator is an invasive species.
As future investigations it would be interesting to try to model weak Allee effects in top predator, and/or Allee effects in the other species as well, be they weak or strong. It has been stipulated with evidence, that two or more Allee effects can occur simultaneously in the same population[4]. Thus an extremely interesting question would be to consider different type of Allee effects in the different species, and investigate the interplay of the various Allee thresholds, as they affect the dynamics of the system. All in all our results would be of interest to both the mathematical and ecological communities, and in particular to groups that are interested in conservation efforts in food chain systems, cascade control, such as in many aquatic systems, and even Allee mediated biological control.
References
- [1] Peter A Abrams and Lev R Ginzburg. The nature of predation: prey dependent, ratio dependent or neither? Trends in Ecology & Evolution, 15(8):337–341, 2000.
- [2] Warder Clyde Allee. Co-operation among animals. American Journal of Sociology, pages 386–398, 1931.
- [3] Warder Clyde Allee, Orlando Park, Alfred Edwards Emerson, Thomas Park, Karl P Schmidt, et al. Principles of animal ecology. Number Edn 1. WB Saundere Co. Ltd., 1949.
- [4] Luděk Berec, Elena Angulo, and Franck Courchamp. Multiple allee effects and population management. Trends in Ecology & Evolution, 22(4):185–191, 2007.
- [5] Mathematical Bioeconomics. The optimal management of renewable resources, 1990.
- [6] Stephen R Carpenter, James F Kitchell, and James R Hodgson. Cascading trophic interactions and lake productivity. BioScience, pages 634–639, 1985.
- [7] Colin W Clark. The worldwide crisis in fisheries: economic models and human behavior. Cambridge University Press, 2006.
- [8] JM Drake and AM Kramer. Allee effects. Nat. Educ. Knowl, 3(10):2, 2011.
- [9] David Gottlieb and Liviu Lustman. The spectrum of the chebyshev collocation operator for the heat equation. SIAM journal on numerical analysis, 20(5):909–921, 1983.
- [10] Dan Henry. Geometric theory of semilinear parabolic equations, volume 840. Springer-Verlag New York, 1981.
- [11] Jan S Hesthaven, Sigal Gottlieb, and David Gottlieb. Spectral methods for time-dependent problems, volume 21. Cambridge University Press, 2007.
- [12] Yang Kuang and Edoardo Beretta. Global qualitative analysis of a ratio-dependent predator–prey system. Journal of Mathematical Biology, 36(4):389–406, 1998.
- [13] Martin Liermann and Ray Hilborn. Depensation: evidence, models and implications. Fish and Fisheries, 2(1):33–58, 2001.
- [14] Andrew Morozov, Sergei Petrovskii, and Bai-Lian Li. Bifurcations and chaos in a predator-prey system with the allee effect. Proceedings of the Royal Society of London. Series B: Biological Sciences, 271(1546):1407–1414, 2004.
- [15] James D Murray. Mathematical biology i: An introduction, vol. 17 of interdisciplinary applied mathematics, 2002.
- [16] Akira Okubo and Smon A Levin. Diffusion and ecological problems: modern perspectives, volume 14. Springer Science & Business Media, 2013.
- [17] Pallav Jyoti Pal and Prashanta Kumar Mandal. Bifurcation analysis of a modified leslie–gower predator–prey model with beddington–deangelis functional response and strong allee effect. Mathematics and Computers in Simulation, 97:123–146, 2014.
- [18] Rana D Parshad, Hamid Ait Abderrahmane, Ranjit Kumar Upadhyay, and Nitu Kumari. Finite time blowup in a realistic food-chain model. ISRN Biomathematics, 2013, 2013.
- [19] Rana D Parshad, Nitu Kumari, Aslan R Kasimov, and Hamid Ait Abderrahmane. Turing patterns and long-time behavior in a three-species food-chain model. Mathematical biosciences, 254:83–102, 2014.
- [20] Rana D Parshad and Ranjit K Upadhyay. Investigation of long time dynamics of a diffusive three species aquatic model. Dynamics of Partial Differential Equations, 7(3):217–244, 2010.
- [21] Sergei V Petrovskii, Andrew Y Morozov, and Ezio Venturino. Allee effect makes possible patchy invasion in a predator–prey system. Ecology Letters, 5(3):345–352, 2002.
- [22] George R Sell and Yuncheng You. Dynamics of evolutionary equations, volume 143. Springer Science & Business Media, 2013.
- [23] Moitri Sen, Malay Banerjee, and Andrew Morozov. Bifurcation analysis of a ratio-dependent prey–predator model with the allee effect. Ecological Complexity, 11:12–27, 2012.
- [24] Swarnali Sharma and GP Samanta. A ratio-dependent predator-prey model with allee effect and disease in prey. Journal of Applied Mathematics and Computing, 47(1-2):345–364, 2014.
- [25] Joel Smoller. Shock waves and reaction?diffusion equations, volume 258. Springer Science & Business Media, 1994.
- [26] Philip A Stephens and William J Sutherland. Consequences of the allee effect for behaviour, ecology and conservation. Trends in Ecology & Evolution, 14(10):401–405, 1999.
- [27] Roger Temam. Infinite-dimensional dynamical systems in mechanics and physics, volume 68. Springer Science & Business Media, 2012.
- [28] Patrick C Tobin, Luděk Berec, and Andrew M Liebhold. Exploiting allee effects for managing biological invasions. Ecology letters, 14(6):615–624, 2011.
- [29] Alan Mathison Turing. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of London B: Biological Sciences, 237(641):37–72, 1952.
- [30] Ranjit Kumar Upadhyay and Vikas Rai. Why chaos is rarely observed in natural populations. Chaos, Solitons & Fractals, 8(12):1933–1939, 1997.
- [31] George AK Van Voorn, Lia Hemerik, Martin P Boer, and Bob W Kooi. Heteroclinic orbits indicate overexploitation in predator–prey systems with a strong allee effect. Mathematical biosciences, 209(2):451–469, 2007.
- [32] Jinfeng Wang, Junping Shi, and Junjie Wei. Dynamics and pattern formation in a diffusive predator–prey system with strong allee effect in prey. Journal of Differential Equations, 251(4):1276–1304, 2011.
- [33] KAJ White and CA Gilligan. Spatial heterogeneity in three species, plant–parasite–hyperparasite, systems. Philosophical Transactions of the Royal Society B: Biological Sciences, 353(1368):543–557, 1998.
7 Appendix
7.1 Nondimensionalisation
The model system in (2)-(4) is a nondimensionalised version of the following system
| (73a) | ||||
| (73b) | ||||
| (73c) | ||||
is the self-growth rate of the prey population . the intrinsic death rate of the specialist predator in the absence of its only food , measures the rate of self-reproduction of the generalist predator . measures the strength of competition among individuals of the prey species . are the maximum values which per capita growth rate can attain. represents the residual loss in population due to severe scarcity of its favorite food . is the parameters that describes the handling time of the prey by predator , and is the parameter that describes the handling time of the prey by predator .
7.2 Global existence
Here we prove proposition 2.2. The positivity of solutions follow trivially from the form of the reaction terms, which are quasi positive. By the positivity of the first component of the solution to (2) on , we get from equation (2)
| (77) |
then we use a comparison argument [25]. That is, we can compare the solution of (77) to the solution , of the linear heat equation
| (78) |
where satisfies the same initial and boundary conditions as . Clearly , and since (being the solution of a linear heat equation) is bounded, so is , and we deduce
| (79) |
where is a constant depending only on . Then equation (3) gives
| (80) |
which implies by the same arguments
| (81) |
where is a constant depending only on . To get a bound on the component we apply Young’s inequality to yield
| (82) |
7.3 Apriori estimates
In all estimates made hence forth the constants are generic constants, that can change in value from line to line, and sometimes within the same line if so required. We estimate the gradient of by multiplying (4) by , and integrating by parts and using standard methods to obtain
| (84) |
We have to estimate . Note
Thus we obtain
| (85) |
We now proceed in 2 steps. We first assume .
Young’s Inequality with epsilon then gives us the following estimate
Then we obtain
This follows via (7.3). Thus we obtain
| (88) |
Here . Now we can use the sobolev embedding of , where is the embedding constant, to obtain
| (89) |
Thus
| (90) |
Now we invoke the estimate via (15), and the uniform Gronwall lemma to obtain
| (91) |
Now assume . Then we obtain
We now use the Sobolev embedding of to obtain
| (93) |
dropping the term yields
| (94) |
| (95) |
7.4 Apriori estimates independent of the parameter
Recall the following estimate
We then use Hölder’s inequality followed by Young’s inequality to obtain
Now we drop the term from the left hand side, to avoid the singularity caused by , the , and use the estimate on via (27), and the embedding of to obtain
| (97) |
Here, we assume , else we already have a bound for . Next we use Gronwall’s inequality to obtain
| (98) |
Thus for , we obtain
| (99) |
which is a uniform bound in that is independent of the Allee parameter , time and initial data.
We next focus on making estimates, that are independent of the Allee parameter .
| (100) |
Now we choose
| (101) |
Then, we can majorise the right hand side of the above by plugging in . Since the above quantities are not singular in , this is possible. Thus we obtain
| (102) |
| (103) |
Also note the integral in time estimate via (7.4) is now independent of . This allows us to apply the uniform Gronwall lemma on (103) with , and the estimate via (7.4) to yield the following bound
| (104) |
Thus the estimate for can be made independent of .
7.5 Upper semi-continuity of global attractors
In this section we prove upper semi continuity of global attractors. We first introduce certain concepts pertinent to the upper semicontinuity of attractors.
Definition 7.1 (Uniform dissipativity)
Suppose there is a family of semiflows on a Banach space , where is an open set in a Euclidean space of parameter , is called uniformly dissipative at , if there is a neighborhood of in and there is a bounded set such that is an absorbing set for each semiflow , , in common.
Definition 7.2 (Upper semicontinuity)
A family of semiflows on a Banach space , where is an open set in a Euclidean space of parameter , and that there exists a global attractor in for each semiflow . If and
with respect to the Hausdorff semidistance, then we say that the family of global attractors is upper semicontinuous at , or that is robust at .
We next recall the following lemma
Lemma 7.3 (Gronwall-Henry Inequality)
Let be a nonnegative function in and , such that the following inequality is satisfied:
| (105) |
where , and are positive constants. Then it holds that
| (106) |
where , is the gamma function, and the function is given by
| (107) |
We state the following theorem
Theorem 7.4
Consider the reaction diffusion equation described via (2)-(4) where is of spatial dimension . There exists a universal constant , independent of the Allee parameter that bounds uniformly in the family of global attractors . That is,
| (108) |
Where is the closed ball of radius in the space , with , where the is from (27).
This follows from the estimates via (27).
We next focus on the uniform dissipativity in . The uniform in parameter estimate via (99) enables us to state the following theorem
Theorem 7.5
Consider the reaction diffusion system described via (2)-(4) where is of spatial dimension . The family of semiflows for this system on , is uniformly dissipative at . Specifically there exists a constant such that the ball , which is the closed ball of radius in the space is a common absorbing set for the semiflows for all . Here , where the comes from lemma 2.4.
Next, let us choose . We know , the common absorbing ball in for the semiflow , , from theorem 7.5. We use the earlier and estimates on from lemma 2.4, noticing that they do not depend on , we also use (99) and (7.4) to obtain
| (109) |
This is true for any and . Now by invariance , and so . Where
| (110) |
This yields the following theorem
Theorem 7.6
Consider the reaction diffusion equation described via (2)-(4) where is of spatial dimension . There exists a universal constant , independent of the Allee parameter that bounds uniformly in the family of global attractors . That is,
| (111) |
where is the closed ball of radius explicitly given in (110).
We next show that the trajectories , are uniformly -bounded, with respect to . Since the estimate in (110) does not depend on , we can take a supremum over and still achieve the same bound. Thus we have the following result
Theorem 7.7
Consider the reaction diffusion equation described via (2)-(4). There exists a universal constant , independent of the Allee parameter such that
| (112) |
where, is the closed ball of radius in the space .
We next set in (4) and note that the corresponding estimates in lemma 2.4 hold for , and do not depend on the parameter . Thus we carry out the analysis as in (7.4) - (110) to still yield
| (113) |
Where is independent of the parameter . Thus we can state the following result
Theorem 7.8
The proof of the above theorem follows essentially via theorem 3.2.
Note, since is a bounded set in , we can state the following result ,
Theorem 7.9
Consider the reaction diffusion equation described via (2)-(4), with . The global attractor for this system , attracts the set , with respect to the -norm. That is
| (114) |
We now use the Gronwall-Henry lemma, to show uniform convergence in the parameter .
Theorem 7.10
Consider the reaction diffusion equation described via (2)-(4), and associated semi-group . Also consider (2)-(4), when , that is with associated semi-group . For any given , it holds that
| (115) |
For any given initial data , we note and , are both classical solutions, hence mild solutions. Thus we denote
| (116) |
Using the form of mild solutions, we can write down the following,
| (117) |
Here , is the semi-group generated by . Note
| (118) |
The above is easily seen to be Lipschitz continuous in , due to the Sobolev embedding of . Here , which is gotten by setting in the above, is also Lipschitz continuous, thus there is a Lipschitz constant , depending only on , where is given in (110), s.t
| (119) |
| (120) |
This follows via standard decay estimates on the semi-group [22], theorems 7.6, 7.7 and the Sobolev embedding of . We now apply the Gronwall-Henry inequality with to obtain
| (121) |
Here
| (122) |
Thus we get the uniform convergence as required, and
| (123) |
where the convergence is uniform in the parameter .