Low-Complexity Codebook Design for SCMA based Visible Light Communication

In the VLC system, the optical receiver (i.e., PD) measures the intensity of the incident optical signal and converts it into electrical signal. The interaction of the incoming photons with the matter of PD is a statistical process [20]. The fluctuations in the number of photons detected, results in fluctuating current which cause shot noise at the optical receiver. The generated shot noise depends on the incident optical signal itself [21, 22, 23]. Further, the thermal motion of the electronic carriers result in fluctuating voltage known as thermal noise. In case of strong ambient light, the impact of thermal noise is more and the shot noise becomes very low. Thus, the noises at the VLC system are assumed to be independent of the received signal [24, 25, 26]. However, in case of indoor scenario, the distance between transmitter and receiver is less and the dominant signal is LOS [27], thus the received power is large. However, in practical VLC systems, typical illumination and communication scenarios offer very high SNR[28, 29]. In case of indoor scenario (as considered in our work), since the received power is large, the shot noise is more dominant and cannot be neglected. The variance of shot noise is given as

where $q$ is the electronic charge, $x_{p}$ is the intensity of incident optical signal, $\mathfrak{R}$ is responsivity, $I_{B}$ is the background noise current, and $I_{2}$ is the noise-bandwidth factor, and B is the effective bandwidth of the optical receiver.
The thermal noise is assumed to be Additive white Gaussian noise (AWGN), which is independent of the intensity of the incident signal [21]. The shot noise affected optical intensity channel can be distinguished as an input-dependent Gaussian noise (IDGN), where variance of IDGN can be used to characterise the physical properties of the VLC system [21, 30]. Consequently, the received signal $y$ can be expressed as

where $Z_{1}\sim\mathcal{N}_{\mathbb{R}}[0,\varsigma^{2}\sigma^{2}]$ denotes a real Gaussian RV with zero mean and $\varsigma^{2}\sigma^{2}$ variance describing IDGN (shot noise), and $Z_{0}\sim~{}\mathcal{N}_{\mathbb{R}}[0,\sigma^{2}]$ describes the thermal noise. Here, $Z_{1}$ and $Z_{0}$ are assumed to be independent, and $\varsigma^{2}\in[1,10]$ denotes the strength of shot noise with respect to thermal noise. In an indoor scenario, as the transmitter and the receiver parameters change, the received power changes, and thus the shot noise varies. In this paper, the variation in shot noise has been depicted by considering different shot noise factor $\varsigma^{2}$ values.

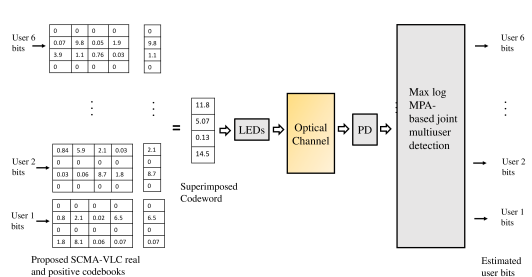
Consider a downlink indoor LOS VLC system where multiple users are being served, each equipped with a single receiving device. Every $J$ users are grouped together for SCMA, and each group is supported by $K$ REs (e.g., time or frequency slots), providing the load factor $\lambda=J/K$. In Fig.1, the data transmission and reception of six users ($J=6$) on four REs ($K=4$) with $\lambda=1.5$ is shown.

At the transmitter, $b=\text{log}_{2}M$ bits are mapped to $K$-dimensional real and positive codewords, with $M$ number of codewords in a CB. These codewords are sparse vectors with $N$ non-zero elements, $K>N$. Each user has a dedicated CB allotted to it. The CB of $j$th user can be expressed as

where $\textbf{V}_{j}\in\mathbb{B}^{K\times N}$ and $\textbf{C}_{j}\in\mathbb{R}_{>0}^{N\times M}$ denote the mapping matrix and constellation matrix of the $j$th user, respectively. The constellation matrix $\textbf{C}_{j}=[\textbf{c}_{j}^{1},\cdots,\textbf{c}_{j}^{M}]$, where $\textbf{c}_{j}^{m}\in\mathbb{R}_{>0}^{N\times 1}$ denotes the $m$th constellation point of $\textbf{C}_{j}$. The whole CB structure of SCMA can be represented by the factor graph matrix, $\textbf{F}=(\textbf{f}_{1},\textbf{f}_{2},\cdots,\textbf{f}_{J})$, where $\textbf{f}_{j}=\text{diag}(\textbf{V}_{j}\textbf{V}_{j}^{T})$. The user $j$ is being served by resource node (RN) $k$, if $\textbf{F}_{kj}=1$ $(1\leq k\leq K,1\leq j\leq J)$. For a $4\times 6$ SCMA block having $K=4$ REs and $J=6$ users, one example of the factor graph matrix of size $4\times 6$ is given as

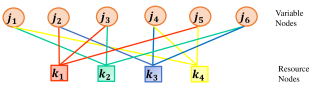
Fig. 2 shows an example of factor graph representation of six users (or Variable Nodes (VNs)) with four RNs, $N$=2 and data of $d_{f}$ users is being superimposed on each RN ($d_{f}=3$ for $\textbf{F}_{4\times 6}$ shown in (4)). The binary mapping matrices corresponding to the six users are given below

The set of CBs for $J$ users is dependent on the constellation matrices $\mathbf{C}_{j},~{}j=1,\cdots,J$ as the mapping matrices remain fixed as shown in (5). Assuming synchronous multiplexing between users, the received signal can be expressed as

where $\textbf{x}_{j}\in\mathbb{R}_{>0}^{K\times 1}$ is a codeword of $j$th user, $\text{diag}(\textbf{h}_{j})$ denotes the channel matrix of $j$th user, the second term represents the IDGN with $\textbf{n}_{sh}\sim\mathcal{N}_{\mathbb{R}}[\textbf{0},\varsigma^{2}\sigma^{2}\textbf{I}]$, and $\textbf{n}_{th}\sim\mathcal{N}_{\mathbb{R}}[\textbf{0},\sigma^{2}\textbf{I}]$. The channels are assumed to be unit vectors for simplicity, and the extension to the general VLC values is straight-forward. In case of the movement of the users, the channel characteristics of the users $((\textbf{h}_{j})$ of $j$th user in $(\ref{rec_sig_eqn}))$ will be affected. The random waypoint (RWP) mobility model is a simple and straightforward stochastic model that describes a human movement behavior in indoor scenarios [31]. In case of user mobility, the received signal expression remains same as (6), however the channel vector (h) varies as per the RWP model in (6).

Assuming perfect channel estimation and the set of CBs known to receiver, the SCMA multi-user codeword $\textbf{X}=[\textbf{x}_{1},\textbf{x}_{2},\cdots,\textbf{x}_{J}]$ can be detected by solving the joint maximum a-posteriori (MAP) probability mass function (PMF) of the transmitted codewords [7], [32]. The estimated X can be written as

where $\mathbb{A}_{j}$ represents the set of codewords allotted to the $j$th user. The marginal distribution of (7) with respect to $\textbf{x}_{j}$ (i.e., summing the joint PMF of multi-user codeword over all values of X except $\textbf{x}_{j}$) leads to $j$th user detected symbol as

Using Bayes’ rule

where $P(\textbf{X})$ denotes the joint a-priori PMF of all transmitted codewords and $f(\textbf{y}|\textbf{X})$ denotes the conditional pdf of the received vector. Assuming noise components are independent and identically distributed for all REs. Then (9) becomes

where $y_{k}$ denotes the received signal at the $k$th RE. Solving the above marginal product of function (MPF) problem with brute force will lead to exponential complexity. Taking advantage of sparse CBs, this problem can be approximately solved by iterative MPA with moderate complexity [7], [33]. MPA works as a decoding algorithm based on passing the extrinsic information between RNs and VNs. The first message is passed from the leaf node (node which has only one neighboring node), and a node of degree $d$ will remain idle until it has received messages from the $d-1$ number of neighboring nodes. MPA involves a large number of exponential operations which are of high complexity. A mathematical simplification is to move MPA to logarithm domain and use Jacobian logarithm, which gives a simpler version called Max-Log-MPA [34]. With Jacobian logarithm, the log-sum of exponentials can be approximated as a maximum operation as shown below:

The Max-Log-MPA for detection of SCMA codewords in VLC is based on three steps as shown in Algorithm 1. Let $\zeta_{j}$ and $\xi_{k}$, be the set of nodes connected to VN $j$ and RN $k$, respectively. Let $\eta_{k\rightarrow j}$ and $\eta_{j\rightarrow k}$ be the message passed from RN $k$ to VN $j$ and vice-versa. Also, $r\in\xi_{k}\setminus\{j\}$ denotes all the VNs of $\xi_{k}$ except VN $j$ and $d\in\zeta_{j}\setminus\{k\}$ denotes the RNs in $\zeta_{j}$ except the $k$th RN.

In Algorithm 1, it is assumed that the received signal y and all the CBs C_j, $\forall j=1,\cdots,J$ are known at the receiver. The total number of iterations considered in Step 2 are $N_{t}$ and, VNs and RNs are updated for each iteration $t$. Also, the channel coefficient between $k$th RN and $m$th VN is denoted by $h_{km}$ and the codeword element transmitted by $m$th VN on $k$th RN is denoted by $x_{km}$, respectively.

In the case of shot noise, the variance at each RN is different and dependent on the superimposed codeword element at the corresponding RN, while in the presence of only thermal noise, $\varsigma^{2}=0$, so $\rho^{2}=\sigma^{2}$ and variance will be the same for all RNs. In case of three users scenario, the factor graph would not be cyclic and number of elements being superimposed on each RN would be different ($d_{f}=2$ for $k=1,2$ and $d_{f}=1$ for $k=3,4$). Since $d_{f}$ is different for different REs, therefore, Algorithm 1 will change accordingly [35].

The computational complexity of standard MPA and Max-Log-MPA considering the effect of shot noise in decoding is shown in Table I [36]. The number of operations is shown for the update step of RN as shown in Step 2 (a) of Algorithm 1. Max-Log-MPA requires more addition operations and less multiplication operations than MPA. This gap of increase in addition and decrease in multiplication operations between MPA and Max-Log-MPA increases with the overloading factor.

In the AWGN channel, MED is taken as one of the key performance indicators for determining the performance of the designed SCMA CB. Let $\textbf{s}_{i}$ be a superimposed codeword from the combined constellation matrix $\mathbb{M}_{v}\in\mathbb{R}_{>0}^{K\times M^{J}}$. Then, the MED between $\textbf{s}_{i}\in\mathbb{M}_{v}$ and $\textbf{s}_{j}\in\mathbb{M}_{v}$ is given as

The MED emerge as a critical parameter because of the pair-wise error probability (PEP) for AWGN channel which is given as

However, in case of IDGN, the PDF of the received signal y is given as (assuming unit channel gain)

where $\Sigma_{i}=\text{diag}\{\varsigma^{2}\sigma^{2}\textbf{s}_{i}+\sigma^{2}\textbf{1}\}$ denotes the covariance matrix for the $\textbf{s}_{i}$th superimposed codeword. It can be seen from (14) that the variance is now dependent on the superimposed codeword.

In the case of only thermal noise, MED is taken as a critical parameter for designing CB where variance is independent of the superimposed codeword. However, in the case of shot noise, when variance is no longer independent, the conventional MED cannot serve as an optimal performance indicator. With the effect of shot noise, the shape of constellation points gets distorted. To mitigate the effect of IDGN, the authors in [16] introduced an improved optimization objective based on Rotated-MED for designing constellation matrices. The rotated Euclidean distance (RED) between superimposed codewords $\textbf{s}_{i}$ and $\textbf{s}_{j}$ can be expressed as

where $\textbf{G}_{i}=\varsigma^{2}\text{diag}\{\textbf{s}_{i}\}+\textbf{I}$, $\textbf{G}_{j}=\varsigma^{2}\text{diag}\{\textbf{s}_{j}\}+\textbf{I}$ and $\textbf{I}\in\mathbb{B}^{K\times K}$ represents the Identity matrix. It is to be noted from (15) that the new parameter RED incorporates the shot noise effect while computing the Euclidean distance between superimposed codewords. The authors in [16] aimed at maximizing the rotated minimum Euclidean distance (R-MED) subject to the power constraints. The objective function proposed in [16] for SCMA CB design is given as

where $\textbf{L}=\text{vec}(\textbf{C})$. This was further simplified as

where $d_{\text{min}}$ denotes the minimum value of RED. It has been verified in [16] that R-MED based CB outperforms the MED based CB for VLC systems affected by shot noise. The results in [16] have shown that for $J=3,K=4,M=4,\varsigma^{2}=5$ and $\sigma^{2}=0.01$, BER of $10^{-3}$ is achieved at $P_{e}=10$ and $P_{e}=7$ for MED and R-MED based CBs, where $P_{e}$ denotes the maximum electrical power allotted to a user. Since from the literature we can understand that RED works as an important parameter for designing CB than MED, we have included RED in our optimization problem. Further, the authors in [17] introduced the concept of distance range (DR) based on the maximum and the minimum values of the RED. They have mentioned that for the low to medium SNR region, the BER is no longer dependent on just R-MED. The optimization problem proposed in [17] for CB designing is

where $d_{\text{max}}$ denotes the maximum value of RED, and $\alpha>0$ denotes the weighting factor. The objective function shown in (18a) is dependent on $d_{\text{min}}$ and $d_{\text{max}}$. The real and positive optical signal constraint is considered in (18b) and maximum electrical power constraint is considered in (18c). All the REDs will lie between $d_{\text{min}}$ and $d_{\text{max}}$ (18d, 18e). Also, it is to be noted that, lesser the overlapping between the constellation points of a user, better the performance of the designed CBs.

The objective function mentioned in (16) considers all the REDs while designing and optimizing the CBs to get optimum results. However, considering all the REDs makes the objective function non-convex and non-differentiable [40]. To solve (16), authors in [17] have proposed the objective function as shown in (III-A). It should be noted that the numerical methods used for solving the nonlinear maxi-min problem aim at approximating the $F(x)=\min_{i}f_{i}(x)$ by close enough smooth functions, and the closeness of approximation decide the nearness to optimal solutions [41]. If we consider $\sum_{i}\phi(f_{i}(x))$, the approximation to $F(x)$ becomes better when $\phi(.)$ is a strong convex function (i.e., large positive second derivative). One approach to solve this non-convex problem is to use well known “log sum-exponentials” continuous approximation [42], [43]. With this approximation, the objective function in (16) transforms to

where $\beta>0$ is a tuning parameter which results in the smoothness of (19) and affects the accuracy of the model.

• •

  Example 1: Let $\beta=1$, and there are two distances $d_{1}\gg d_{2}$, then
  $-\text{ln}(e^{-d_{1}}+e^{-d_{2}})\\ \approx-\text{ln}(e^{-d_{2}})=d_{2}=\min\{d_{1},d_{2}\}.$

The function in (19) is differentiable but still non-convex; however, optimization algorithms based on the derivation of the Hessian of the objective function can find the local optimal solution [44]. Also, if the objective function is optimized number of times with initialization from small set of random numbers and choosing the $\beta$ parameter wisely, the likelihood of obtaining the global optimal solution increases [45]. Thus, the optimization problem is formulated as

where (20b) denotes the real positive intensity constraint of the transmitted codeword elements and (20c) denotes that the average electrical power of the generated codewords should be less than the maximum electrical power ($P_{e}$) allotted per user. The optimization problem in (20) can be solved using commercially available solvers like MATLAB’s $fmincon$. The procedure for solving the above optimization problem is summarized in Algorithm 2.

For the case of the proposed optimization problem in (20), initially, the set of all multiplexed vectors (or superimposed codewords) $\mathbb{M}_{v}$ is computed. With $J$ users and $M$ number of codewords in the CB, the number of superimposed codewords obtained are $M^{J}$, i.e., $|\mathbb{M}_{v}|=M^{J}$. Since the complexity of operations such as addition and subtraction is $O(1)$ therefore, the complexity of computing multiplexed vectors is $O(JM^{J})$. Next, for generating the covariance matrix ($\Sigma_{i}$ for $\textbf{s}_{i}$ superimposed codeword), each multiplexed vector is multiplied with the scalar $\varsigma^{2}$ which results in the complexity $O(KM^{J})$. The complexity of computing RED (as shown in (15)) between two multiplexed vectors is $O(K)$ as the length of each vector is $K$ and the total number of multiplexed vectors are $M^{J}$. Thus, the total number of REDs between $M^{J}$ multiplexed vectors is $\binom{M^{J}}{2}$ and the total complexity for calculating REDs will be $O(K~{}{\binom{M^{J}}{2}})$. Next, the complexity of computing the objective function (20a) is $\binom{M^{J}}{2}$. The complexity of constraints in (20b) and (20c) is $O(1)$ since it includes addition and square operations. The maximum value of $\beta$ at which the algorithm converges is denoted by $\beta_{max}$ and number of iterations for the MATLAB’s $fmincon$ solver is $N_{it}$, then total complexity to generate the constellation matrices for $J$ users using Algorithm 2 is $O_{Logsum}=[\beta_{max}N_{it}(JM^{J}+KM^{J}+{K~{}{\binom{M^{J}}{2}}}+{\binom{M^{J}}{2}}+1)]$. If we take the most dominant part resulting for complexity, it is equal to $O(\beta_{max}N_{it}K~{}{\binom{M^{J}}{2}})$.

In case of the DR based CB [17] optimization problem (as shown in (III-A)), the total complexity comes from the computation of the objective function and four constraints. The third and fourth distance based constraints (18d, 18e) are non-convex and are approximated using first order Taylor series [16]. From the calculation of multiplexed vectors, covariance matrices and REDs, the complexity is $O(JM^{J}+KM^{J}+{K~{}{\binom{M^{J}}{2}}})$. The complexity of intensity and power constraints (18b, 18c) is $O(1)$. For the approximation of two non-convex constraints (18d, 18e), firstly the coefficient matrix $\Pi_{i}$ is calculated to obtain multiplexed vector $\textbf{s}_{i}$ from L [16], and its complexity is $M^{J}KNMJ$. Next, we found that the derivative of RED has the highest complexity because of the kronecker product operation involved. The derivative term has the complexity $O({(KNMJ)^{2}~{}{\binom{M^{J}}{2}}})$. So, with $N_{out}$ as total number of outer loop iterations, the total complexity is $O_{DR}=[O(N_{out}N_{it}(JM^{J}+KM^{J}+{K~{}{\binom{M^{J}}{2}}}+{\binom{M^{J}}{2}}+1+M^{J}KNMJ+{(KNMJ)^{2}~{}{\binom{M^{J}}{2}}}))]$. Taking only the dominant part, the complexity becomes $O(N_{out}N_{it}{(KNMJ)^{2}~{}{\binom{M^{J}}{2}}})$. It can be observed that the proposed Log-sum-exp scheme (20) has reduced the computation complexity of SCMA CB design by a significant amount from DR based CB optimization problem shown in (III-A).

SCMA is a multi-carrier scheme, i.e., the superimposed transmitted codeword $\textbf{s}_{i}=[s_{i}^{1},\cdots,s_{i}^{K}]$ is a $K$ dimensional real codeword as discussed in Section II-B. In this section, the theoretical BER expression has been derived for the IDGN incorporated SCMA-VLC system. For only the thermal noise case, the PEP is given as (13). However, in the case of shot noise, the overall variance changes and is dependent on $\varsigma^{2}$ and the intensity of the incident optical signal. The error rate for the superimposed codeword $\textbf{s}_{i}$ is

where ${s}_{i}^{k}$ and ${s}_{i^{\prime}}^{k}$, denotes the $k$th element of the superimposed codeword $\textbf{s}_{i}$ and $\textbf{s}_{i^{\prime}}$, respectively. The $k$th diagonal element of the covariance matrix $\Sigma_{i}$ of the superimposed codeword $\textbf{s}_{i}$ is denoted by $\nu_{i,k}$. The diagonal element $\nu_{i,k}$ denotes the total variance at $k$th RE when $\textbf{s}_{i}$ was transmitted. The total probability of error is given as [46]

where $P_{a}(\textbf{s}_{i})$ denotes the a priori probability of $\textbf{s}_{i}$, $h_{d}(\textbf{s}_{i^{\prime}},\textbf{s}_{i})$ denotes the bit error when $\textbf{s}_{i^{\prime}}$ is chosen over $\textbf{s}_{i}$ and $P^{\prime}(\textbf{s}_{i}\rightarrow\textbf{s}_{i^{\prime}})$ denotes the PEP between $\textbf{s}_{i}$ and $\textbf{s}_{i^{\prime}}$.

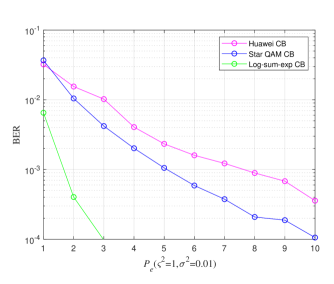
We consider the case where RF-based CBs are used for transmitting data over a VLC system. We consider the $4\times 6$ SCMA CBs from [37] and [47]. RF CBs cannot be employed as it is, as the VLC system has the requirement of real and positive signal transmission. So, the complex codeword elements are divided into real and imaginary parts, which are then DC biased to get real and positive codeword elements [37], [47]. These real and positive codewords are transmitted over different REs . This way, the data of six users is transmitted over eight REs. Further, we have generated the Log-sum-exp based CB for six users and eight REs scenario using Algorithm 2. Fig. 3 shows the bit error rate (BER) performance of the Star QAM based CB [37], Huawei CB [47] and Log-sum-exp CBs for $K=8$ and $\sigma^{2}=0.01$. It can be understood from Fig. 3 that CBs designed solely for the VLC system (proposed Log-sum-exp based CB) outperforms the RF-based CBs for shot noise incorporated VLC system. The performance gap observed in Fig. 3 motivated the authors to design CB especially for the SCMA-VLC system.

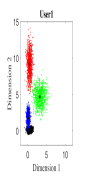
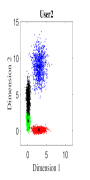
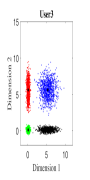
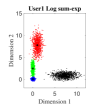
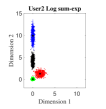
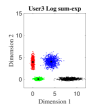
For the initial simulation, we consider the case where three users share four REs with $M=4$ and the number of non-zero elements in the codeword is $N=2$. The mapping matrices $\textbf{V}_{1},\textbf{V}_{2},\textbf{V}_{3}$ have the same values as shown in (5) (i.e., $d_{f}=2$ for $k=1,2$ and $d_{f}=1$ for $k=3,4$). For three users, the CBs (DR based and Log-sum-exp based) are generated by solving the optimization problems (III-A, 20) (CBs are shown in Appendix). For $J=3$, Algorithm 2 is found to be converging for low values of $\beta$ (i.e., $\beta=10$). Fig. 4. shows the 2-dimensional (2D) scatter plots of the generated DR based CBs (III-A) and the proposed Log-sum-exp based CBs (20) for $\varsigma^{2}=10$ and $P_{e}=30$. It can be noted that the constellation points under DR criterion (III-A) are substantially overlapping as shown in Fig. 4(a)-4(c). However, the overlapping between proposed Log-sum-exp based constellation points for all three users is negligible as shown in Fig. 4(d)-4(f). As the overlapping increases between different constellation points, it becomes difficult for the receiver to detect the symbols correctly, and thus, the overall performance deteriorates.

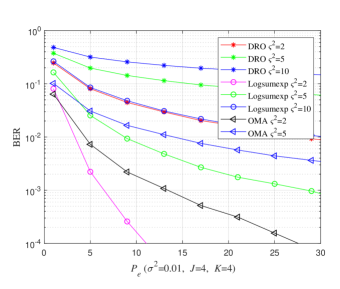
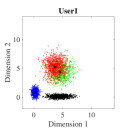
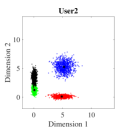
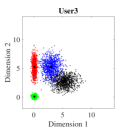
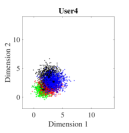
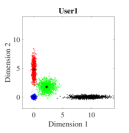
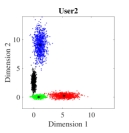
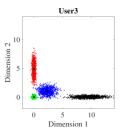
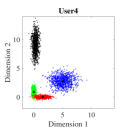
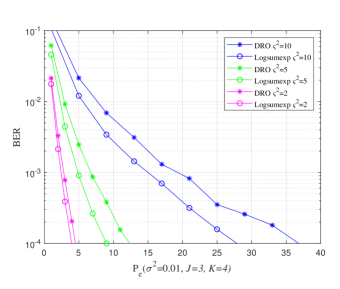
Fig. 5 shows the bit error rate (BER) performance for three users of the proposed Log-sum-exp based (20) SCMA CBs and the DR based CBs (III-A), respectively. The negligible overlapping in the case of log-sum-exp CBs as compared to DR CBs (in Fig. 4), reasons the performance gain obtained in Fig. 5. For both CBs (DR based and Log-sum-exp based), Max-Log-MPA (Algorithm 1) has been used for multi-user detection. It can be noticed that for the low value of $\varsigma^{2}$ (e.g., $\varsigma^{2}=2$), BER performance of both CBs is close, and for high values of $\varsigma^{2}$ (e.g., $\varsigma^{2}=5,10$), the proposed Log-sum-exp based CBs yield better performance gain as compared to DR based CBs. This suggests that the objective function with all the REDs results in better CB (i.e., Log-sum-exp based CB) than the CB with only minimum and maximum values of REDs (i.e., DR based CB). It is shown that our proposed CBs achieve the BER of $10^{-3}$ at $P_{e}=15$ while DR based CB achieve it at $P_{e}\approx 20$ for $\varsigma^{2}=10$. This suggests that for large values of $\varsigma^{2}$, the advantage of the proposed Log-sum-exp based CB is more significant than DR based CB. Further, from the results it can inferred that, we can reduce the dimming level to $\frac{30-4}{30}$ = 86.6% of designed power ($P_{e}=30$) for $\varsigma^{2}=2$.

The bivariate normal density is specified by the 2D constellation points and the variance of these points in different dimensions. Fig. 6 shows the lines of the equal probability density (EPD) functions of the bivariate Gaussian. The center of the ellipse is the 2D constellation point and its shape is determined by the covariance matrix of the 2D constellation points. The principal axes of these ellipses are given by the eigenvectors of the covariance matrix and, semi-major and semi-minor axis are dependent on the eigenvalues, respectively [48]. For $N=2$, the $m$th constellation point of the $j$th user is $\textbf{c}_{j}^{m}\in\mathbb{R}_{>0}^{2\times 1}$ and the covariance matrix of this 2D constellation point is denoted by $\mathbb{S}_{\textbf{c}_{j}^{m}}$. So, the center of the ellipse is $\textbf{c}_{j}^{m}$ and its shape is determined by $\mathbb{S}_{\textbf{c}_{j}^{m}}$. Fig. 6(a)-6(c) shows the lines of EPD for DR based constellation points and Fig. 6(d)-6(f) shows lines of EPD for Log-sum-exp based constellation points, respectively.

Consider the case where four users share four REs. The Log-sum-exp based CB is designed for four users using Algorithm 2, and its performance is compared with DR based CB. Fig. 7 shows the BER performance of four users where Log-sum-exp based CB outperforms DR based CBs for different values of $\varsigma^{2}$. The reason behind the performance difference can be understood from the level of overlapping between the constellation points for both CBs in Fig. 8. It can be observed in Fig. 8 that the DR based 2D constellation points suffer from significant overlapping, especially for user 1 (Fig. 8(a)) and user 4 (Fig. 8(d)), while Log-sum-exp based 2D constellation points are barely overlapping. This results in significant performance improvement for Log-sum-exp based CBs. Also in Fig. 7, the comparison with pulse amplitude modulation orthogonal multiple access (4 PAM-OMA) scheme is shown. It is noted that the proposed algorithm outperforms the OMA scheme for different values of $\varsigma^{2}$. This is expected as the OMA scheme offers no frequency diversity in contrast to the SCMA scheme.

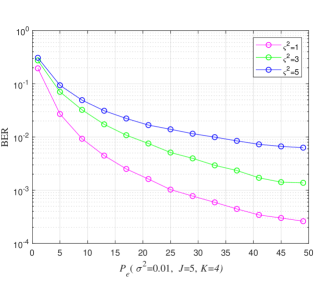
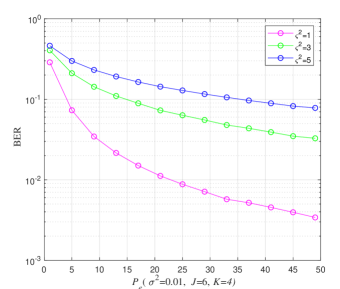
For five users, the complexity of generating DR based CB increases significantly. Further, the performance degrades drastically and requires a very high $P_{e}$ at BER of $10^{-3}$. Therefore, the effect of varying shot noise factor $\varsigma^{2}$ with only Log-sum-exp based CBs, when five users data is being transmitted over four REs ($\lambda=5/4)$ has been shown in Fig. 9. The BER performance with respect to increasing $P_{e}$ is shown in Fig. 10 for six users. Here, the effect of varying shot noise factor $\varsigma^{2}$ is shown when the proposed Log-sum-exp based CBs have been used for transmitting data over four REs.

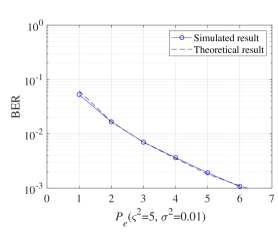
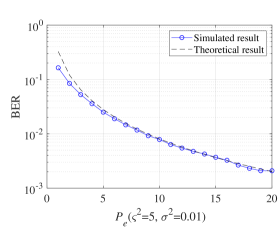
In Fig. 11, the theoretical and simulated BER performances are compared. We find that the simulated curves match with the theoretical curves, especially for the high signal power region. These results verify the correctness of the simulated results obtained in Fig. 5 and Fig. 7. The results from Fig. 5, 7, 9 and 10 have been summarized in Table II. From Table II, we have the electrical power required to achieve BER of $10^{-3}$ for different users and VLC systems with different shot noise factors.