PHENIX Collaboration
Lévy-stable two-pion Bose-Einstein correlations in GeV AuAu collisions
Abstract
We present a detailed measurement of charged two-pion correlation functions in 0%–30% centrality GeV AuAu collisions by the PHENIX experiment at the Relativistic Heavy Ion Collider. The data are well described by Bose-Einstein correlation functions stemming from Lévy-stable source distributions. Using a fine transverse momentum binning, we extract the correlation strength parameter , the Lévy index of stability and the Lévy length scale parameter as a function of average transverse mass of the pair . We find that the positively and the negatively charged pion pairs yield consistent results, and their correlation functions are represented, within uncertainties, by the same Lévy-stable source functions. The measurements indicate a decrease of the strength of the correlations at low . The Lévy length scale parameter decreases with increasing , following a hydrodynamically predicted type of scaling behavior. The values of the Lévy index of stability are found to be significantly lower than the Gaussian case of , but also significantly larger than the conjectured value that may characterize the critical point of a second-order quark-hadron phase transition.
I Introduction
Femtoscopy is a well-established sub-field of high energy particle and nuclear physics, that encompasses all the methods that allow for measuring lengths and time intervals on the femtometer (fm) scale. While the name was coined in 2001 Lednicky (2001), several earlier methods were developed in other fields of science that can be considered as predecessors. As femtoscopy typically deals with intensity correlations of particle pairs (or multiplets), the earliest intensity correlation measurements, that were performed in radio and optical astronomy to measure the angular diameters of main sequence stars by R. Hanbury Brown and R. Q. Twiss (HBT) Hanbury Brown and Twiss (1956) are considered as the experimental foundations of this field. The clear understanding of the HBT effect, as well as that of the lack of intensity correlations in lasers, by Roy J. Glauber is considered to be the opening of a new and prosperous field of science called quantum optics Glauber (1963, 2006a, 2006b).
Intensity correlations of identical pions were observed in proton-antiproton annihilation while searching for the meson Goldhaber et al. (1959), and these correlations were explained by G. Goldhaber, S. Goldhaber, W-Y. Lee and A. Pais on the basis of the Bose-Einstein symmetrization of the wave-function of identical pion pairs Goldhaber et al. (1960). Hence, in particle physics these correlations are also called GGLP or simply Bose-Einstein correlations. Because the two-particle Bose-Einstein correlation function is related to the Fourier transform of the phase-space density of the particle emitting source, by measuring the correlation function one can readily map out the particle source on a femtometer scale.
The discovery of the strongly coupled quark gluon plasma (sQGP) at the Relativistic Heavy Ion Collider Adcox et al. (2005); Adams et al. (2005a); Arsene et al. (2005); Back et al. (2005) (RHIC) relied also on the contribution from Bose-Einstein correlation studies, beyond other important observables, many of which were confirmed and further elaborated at the Large Hadron Collider (LHC). The approximate transverse mass () dependence of the measured Gaussian source radii () is (where and are constants), which is almost universal across collision centrality, particle type, colliding energy and colliding system size Adler et al. (2004); Afanasiev et al. (2009). This is a direct consequence of a strong longitudinal as well as radial hydrodynamical expansion Makhlin and Sinyukov (1988); Csörgő and Lörstad (1996); Chapman et al. (1995a, b); Csanád et al. (2004); Bekele et al. (2007); Lisa and Pratt (2008). Directional Hubble flows seem to be a crucial property of the sQGP formation in heavy ion collisions, or Little Bangs Makhlin and Sinyukov (1988); Csörgő and Lörstad (1996); Chapman et al. (1995a, b). The so-called RHIC HBT puzzle, the apparent contradiction between several hydrodynamical model predictions and the observed ratio of the HBT radii Adcox et al. (2005); Adams et al. (2005a), also turned out to be resolvable in a hydrodynamical picture with more realistic physics conditions and refined models of three dimensional Hubble flows Csörgő and Lörstad (1996); Csanád et al. (2004); Bekele et al. (2007); Pratt (2009); Heinz (2010); Bożek (2012). For a more detailed introduction and review of Bose-Einstein correlations and their application in high energy heavy ion collisions, see the review papers in Refs. Boal et al. (1990); Weiner (2000); Wiedemann and Heinz (1999); Csörgő (2002); Lisa et al. (2005); Tannenbaum (2006); Lisa and Pratt (2008); A. Kisiel, for the ALICE Collaboration (2011); Heinz and Snellings (2013); Adamczyk et al. (2015).
To fully exploit the power of HBT correlations (as observables deemed to provide insight into the dynamics of the matter produced in heavy-ion collisions), one can and must go beyond the Gaussian parameterization and the Gaussian source radii, as observed in collisions at the Large Electron-Positron Collider (LEP) Achard et al. (2011) and in pp, pPb and PbPb collisions at the LHC Khachatryan et al. (2011); F. Siklér, for the CMS Collaboration (2014); Astalos (2015). One of the observables that is rather sensitive to the actual shape of the Bose-Einstein correlation function is the so-called “intercept parameter” (or strength) of the correlation function, as its value depends on the result of an extrapolation of the observed correlation function to zero relative momentum. The experimental determination of the parameter for pions can provide information about the ratio of primordial pions to those that are decay products of long lived resonances Bolz et al. (1993); Csörgő et al. (1996), and may also give insight into the possibility of coherent pion production Bolz et al. (1993); Weiner (2000); Csörgő (2002). The shape of the correlation functions, in particular their non-Gaussian behavior, may also hint at the vicinity of the critical point of the quark-hadron phase transition Csörgő et al. (2005, 2004).
In this paper we present a precise measurement of two-pion HBT correlation functions in GeV AuAu collisions by the PHENIX experiment at RHIC. We use the data recorded in the 2010 data taking period. This data sample allows us to use a fine transverse mass binning, and to infer the shape of the correlation function more precisely than was possible with earlier data sets. The significance of this will become evident when we extract the source parameters. It turns out that the measured correlation functions cannot be described by a Gaussian approximation in a statistically acceptable way. A generalized random walk or anomalous diffusion suggests the appearance of Lévy-stable distributions for the phase-space density of the particle emitting source Metzler et al. (1999); Csörgő et al. (2004). We have investigated whether a Lévy-stable generalization of the Gaussian source distributions is consistent with our measurements, and found that (with the proper treatment of the final state Coulomb interaction) Lévy-stable source distributions – applied here for the first time in heavy ion HBT analyses – give a high quality, statistically acceptable description of the measured correlation functions.
The structure of this paper is as follows. Section II presents the PHENIX experimental setup with emphasis on the tracking and particle identification detectors that were used for this analysis. In Section III we present the measurement procedure of the two-pion correlation functions. In Section IV we discuss the shape analysis of the measured HBT correlation functions for Lévy-stable source distributions, and the procedure for determining the Lévy parameters. In Section VI we present our results, namely the extracted Lévy parameters of the source as a function of the transverse mass of the pair. We also discuss here some of the possible interpretations of these results. Finally we summarize and conclude.
II Experimental setup
The PHENIX experiment was designed to study various different particle types produced in heavy ion collisions, including photons, electrons, muons and charged hadrons, trading spatial acceptance for segmentation, good energy and momentum resolution, and high luminosity capability. Figure 1 shows a schematic beam view drawing of the PHENIX experiment during the 2010 data taking period. The detailed description of the basic experimental configuration (without the upgrades made after the early 2000s) can be found elsewhere Adcox et al. (2003a); here we give only a brief description of the detectors that played a role in this analysis.
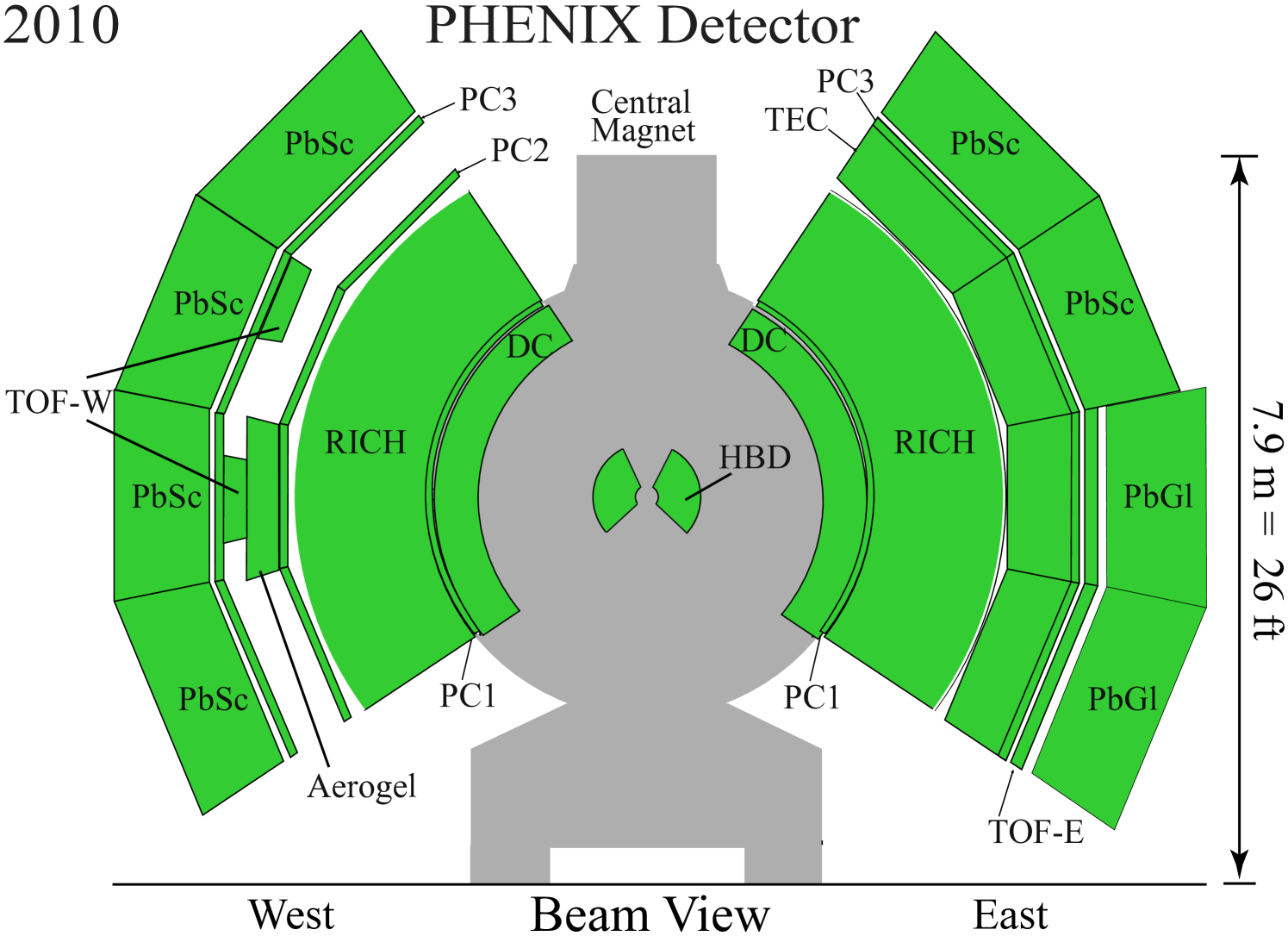
II.1 Event characterization detectors
This analysis uses the beam-beam counters (BBC) for event characterization. Its two arms (“North” and “South”) are located at cm along the beam axis ( axis) from the center of PHENIX, corresponding to the 3.03.9 pseudorapidity interval. Each arm of the BBC comprises 64 quartz Čerenkov counters, covering in azimuth. They provide minimum-bias (MB) triggering; the MB trigger condition requires at least two hits in coincidence in both BBC arms, thus capturing % of the total AuAu inelastic cross section Adare et al. (2013). The charge sum in both BBC arms is used for event centrality determination. The BBCs also measure the average hit time in the north and south arm photomultipliers (PMTs), thus providing collision vertex position measurements along the direction (from the hit time difference) as well as initial timing information for the collision. With an intrinsic timing resolution of 40 ps, the -vertex resolution is 0.5 cm and 1.5 cm in central and peripheral AuAu collisions, respectively.
II.2 Central arm tracking
PHENIX has two central arm spectrometers (“east” and “west”), each covering in pseudorapidity and in azimuth, as seen in Fig. 1. In each central arm, charged particle tracks are reconstructed using hit information from the drift chamber (DC), the first layer of pad chambers (PC1) and the collision -vertex position measured by the BBC Adcox et al. (2003b).
The DCs are located at a radial distance of 202–246 cm from the beam axis. They provide trajectory measurement in the transverse plane, with an angular resolution of 1 mrad. The PC1s are multiwire proportional chambers with pad readout, located immediately behind the DCs. They provide track position measurement both in the and in the direction, with a -resolution of 1.7 mm.
The PHENIX central arm spectrometer magnet generates a magnetic field approximately parallel to the beam line. It comprises two pairs of independently operable concentric coils, an inner and an outer coil pair, located at radial distances of 60 cm and 180 cm, respectively. The DCs are positioned so that they are in the reduced field region. Charged-particle-momentum determination is enabled by the measurement of the bending of the track in the magnetic field. The transverse momentum is determined by the bending angle measured by the DC, while the polar angle of the momentum is determined by the coordinate measured by PC1 and the -vertex coordinate from the BBC. Reconstructed tracks are then projected to the outer detectors used for track verification and timing measurement.
Because at not too low the momentum resolution is governed mainly by the angular resolution of the DC, high bending fields are desirable. Thus usually the two coil pairs are operated with currents flowing in the same direction (this is called “” or “” mode), to achieve the designed maximum total field integral of 1.1 T m (this is the relevant quantity for the bending, and in turn for the momentum measurement).
In 2010, the Hadron Blind Detector (HBD), a specialized Čerenkov counter located around the nominal collision point for the measurement of dielectron pairs, was installed Anderson et al. (2011). The operation of the HBD required a field-free region around the collision point, which was achieved by running the inner and outer coils in the opposite directions (in “” or “” modes). This reduced the field integral to 40% of its maximum value. However, the present analysis deals with low and intermediate hadrons (up to 0.85 GeV), so high momentum resolution is not crucial. (The momentum resolution for in the dataset used is estimated to be Adare et al. (2012). The momentum resolution has, in addition, a component stemming from the BBC -vertex resolution.) Moreover, the reduced magnetic field had a beneficial side effect for the present analysis. Namely, the low momentum acceptance of this dataset is extended to lower values of transverse momentum, enabling a relatively clean identified pion sample down to 0.2 GeV. This would have been much harder, if not impossible, with the normal or field setting, because of too large bending angles and residual bending outside of the DC nominal radius, which is not taken into account in the standard PHENIX track projection algorithm.
II.3 Particle identification detectors
In the present analysis, we identify charged pions by their time of flight from the collision point to the outer detectors. We use the lead-scintillator electromagnetic calorimeter (PbSc) as well as the high resolution time-of-flight detectors (TOF east and TOF west) Aizawa et al. (2003).
The PbSc is a sampling calorimeter located approximately 5.1 m radial distance from the beam axis. It covers 0.35 in both arms, and in terms of , it covers all acceptance of the west arm, and (i.e. half) of the east arm, as seen on Fig. 1. It is a finely segmented detector, consisting of 15,552 individual channels (“towers”). After careful tower-by-tower and energy dependent calibration, a timing resolution of 400–600 ps (depending on deposited energy, incident angle, individual channel electronics imperfections, etc.) was achieved for pions. The part of the east arm acceptance not covered by the PbSc is covered by the lead-glass (PbGl) calorimeter, which has a much worse timing resolution for hadrons and thus was not used for the present analysis.
The TOF east detector is also located at approximately a 5.1 m from the beam axis, and covers much of the PbGl acceptance in the east arm. It is made of 960 plastic scintillator slats, with 2 PMTs attached to each side of them. After calibration, the timing resolution was found to be 150 ps. Adare et al. (2016). The TOF west detector takes advantage of the multigap resistive plate chamber (MRPC) technology. It has two separate panels, each covering in the west arm, at around 4.8 m radial distance from the beam pipe. Each panel comprises 64 MRPCs and has 256 individual copper readout strips. After calibration, a timing resolution of 90 ps was achieved.
III Measurement of two-pion correlation functions
III.1 Event and track selection, particle identification
The MB-triggered data sample used in this analysis comprises GeV AuAu events recorded by PHENIX during the 2010 running period. This sample is reduced to events when we apply a 0%–30% centrality selection. The event -vertex position was constrained between cm in order to have an efficient BBC response as well as to avoid scattering in the central magnet steel.
We selected tracks of good quality, i.e. those where the DC and PC1 information was unambiguously matched. To reduce in-flight decays as well as random associations between tracks and hits in the PbSc/TOF detectors, a track matching cut of was applied for the difference between the projected track position and the closest hit position in these detectors, in both the and directions. As part of the systematic uncertainty investigation, we studied the dependence of the final results on these selection criteria.
For the present analysis, a clean sample of identified pions was necessary. Charged pion identification was performed with the help of time-of-flight information () from the PbSc/TOF detectors and the BBC, as well as using path length information () from the track model and the momentum value measured by the DC/PC1. The reconstructed squared mass of a track is then
| (1) |
and pions were selected by applying a cut in the distribution of the PbSc and the TOF detectors. For the range of interest in this analysis, the contamination in the pion sample caused by misidentified kaons or protons is negligible. A more important contamination in the pion sample comes from the random association of tracks and hits in the PbSc or the TOF detectors at low momentum, reaching 2%–3% for the TOF detectors, and as high as 8%–10% for the PbSc at or below GeV. This background quickly diminishes for even slightly higher (at GeV), as inferred from the observed distributions. However, even at low this is a gross overestimation of the contamination. Most of the tracks are pions, even those for which the track projection algorithm didn’t find the proper hit because of the residual bending at low momentum. The systematic uncertainty stemming from mis-identified particles is mapped out by varying the mentioned standard cut on the spectrum of pions, as detailed in Section V. In this analysis, we apply a GeV selection, including all identified pions above this threshold into our sample.
III.2 Construction of the correlation functions
In general, the two-particle correlation function is defined as
| (2) |
where , and are the one- and two-particle invariant momentum distributions at four-momenta and , and the superscript “spm” denotes that here the correlation function is written as a function of the single particle momenta.
There can be many causes of correlated particle production, such as collective flow, jets, resonance decays, conservation laws. In heavy ion collisions, the main cause of like-sign pion pairs correlation at small relative momentum is the quantum-statistical Bose-Einstein or HBT correlation stemming from the indistinguishability (and thus the symmetrical pair wave-function) of two identical bosons. This source of correlations grows with the mean number of pairs at small relative momentum, which is approximately proportional to the mean multiplicity squared. Other possible sources of correlations (for example pion pair production from resonance decays) increase only linearly with the mean multiplicity. Hence, for the large multiplicity heavy ion collisions, Bose-Einstein correlations dominate the correlation function at small relative momenta.
Experimentally the method of the measurement is the so called event-mixing. To discuss that in this subsection, let us denote any experimental choice for the measure of the two-pion relative momentum by , defining our particular choice later in subsection III.4. In the present subsection we discuss only those properties of the two-pion Bose-Einstein correlation functions that are generally valid, independently of the particular experimental choice of for the measure of the relative momentum of the pion pair.
Let us define as the actual distribution of pion pairs for a given average four-momentum , where both members of the pair stem from the same event. Note also that our choice for is detailed later in Section III.4. This distribution will contain effects which have to be excluded from the Bose-Einstein correlation function (such as resonance decay effects, kinematics, acceptance effects etc.). For this purpose, one defines a background distribution with pairs of pions from different events. Let us denote this background distribution with . A usual method is to construct the background distribution by keeping an event pool of a predefined size, and correlating each pion of the investigated event with all same charged pions of the background pool. However, in this case, multiple particle pairs will come from the same event pair. In this analysis we use the method described in Achard et al. (2011) that eliminates any possible residual correlation of this type as well. For each “actual” event, we form a “mixed” event by choosing pions (of the same number as in the actual event for each charge) from other randomly selected events within the background pool (that has to be larger than the maximal multiplicity of pions of a given charge), under the condition that no two tracks may originate from the same event. After this procedure, each “mixed” event comprises pions originating from different events. The background distribution is then created from the (same charge) pairs of this mixed event. It must also be noted that in order for the background event to exhibit the same kinematics and acceptance effects, one has to build the background event from the same event class (i.e. from events of similar centrality and of similar coordinate of the collision vertex). We used 3% wide centrality and 2 cm wide -vertex bins to achieve that goal.
If we now take the ratio of the actual and the background distributions, we get the prenormalized correlation function as
| (3) |
where the integral is performed over a range where the correlation function is not supposed to exhibit quantum statistical features. Let us note that the method described above is applied to pairs belonging to a given range of average momenta, and in that case denotes the mean of these average momenta in the given range. Furthermore, in the mixing technique described above, the number of actual and background pairs is the same – aside from the effect of two-track cuts, which is outlined in the next subsection.
III.3 Two-track cuts
When forming pairs to construct the aforementioned actual and background pair distributions, one has to take into account detector inefficiencies and peculiarities of the track reconstruction algorithm which sometimes doubles or splits one track into two (creating so-called ghost tracks). It is also possible that two different tracks are not well distinguished when they approach one another too closely. To remove these possible track splitting and track merging effects, we studied track separation distributions in each detector involved, in each of the transverse momentum bins used in this analysis. Then we applied the following cuts in the plane (in units of radians and cm, respectively) of pairs of hits in the given detector, associated with track pairs:
| (4) | ||||
| (5) | ||||
| (6) | ||||
| (7) |
We applied these two-track cuts to both the actual and the background sample.
In addition to these cuts, if we found multiple tracks that are associated with hits in the same tower of the PbSc, slat of the TOF east, or strip of the TOF west detector, we removed all but one of them. This ensured that we do not take into account any ghost tracks that would have remained in the sample after the above mentioned pair cuts.
Our analysis method is somewhat different from those of earlier measurements of Bose-Einstein correlations in heavy ion collisions, in particular with respect to the kinematic variables and the application of Lévy-stable distributions. Thus we proceed carefully here and provide a thorough and detailed description of the concepts and procedures that we applied in the determination of the proper kinematic variables and the shape analysis of the Bose-Einstein correlation functions.
III.4 Variables of the two-pion correlation function
The correlation function, as defined in Eq. (2), depends on single particle and pair momentum distributions. These can be calculated in the Wigner function formalism, assuming chaotic particle emission, from the single particle and pair wave functions, as detailed in Refs. Yano and Koonin (1978); Makhlin and Sinyukov (1988); Pratt et al. (1990); Csörgő (2002). For the pair momentum distribution, neglecting dynamical two-particle correlations, one obtains the Yano-Koonin formula Yano and Koonin (1978)
| (8) | ||||
by means of the phase-space density of the particle-emitting source , sometimes referred to as “source distribution” or simply as “source”, and , the symmetrized pair wave function. Neglecting final state Coulomb and strong interactions, as well as possible higher order wave-function symmetrization effects on the level of two-particle correlation functions, the pair wave-function is a properly symmetrized plane wave, i.e. in this case,
| (9) |
This approximation in turn leads to the expression of the pure quantum-statistical correlation function () as Yano and Koonin (1978); Makhlin and Sinyukov (1988); Pratt et al. (1990); Csörgő (2002)
| (10) |
where complex conjugation is denoted by ∗, the index signals that the Coulomb effect is not taken into account, the superscript “spm” denotes that the correlation function is written as a function of the single particle momenta, and from now on
| (11) |
stands for the difference of the four-momenta of particles 1 and 2 ( denotes energy difference, i.e. the zeroth component of the relative four-momentum ) and denotes the Fourier transform of the source
| (12) |
For source distributions and typical kinematic domains encountered in heavy ion collisions, the dependence of as defined in Eq. (12) is much smoother Lisa et al. (2005) in the original momentum variable than in the relative momentum , coming from the Fourier transform. Hence, it is customary to apply the approximation in Eq. (10), where
| (13) |
is the average four-momentum of the pair ( denotes the average energy of the pair, i.e. the zeroth component of the average four-momentum ). With this,
| (14) |
The validity of these approximations was reviewed in Refs. Csörgő (2002); Wiedemann and Heinz (1999) and for typically exponential single particle spectra the approximation was found to be within 5% of the more detailed and substantiated calculations.
If the above approximations are justified, the two-particle Bose-Einstein correlation function is unity plus a positive definite function of the relative momentum . In the GeV 0%–30% centrality AuAu data reported in this analysis, we found that Eq. (14) is consistent with the data; we did not observe the nonpositive definite, oscillatory behavior that was observed in collisions at LEP Achard et al. (2011), and in collisions at the LHC Khachatryan et al. (2011); Astalos (2015). Note that in collisions at LEP and in collisions at the LHC the smoothness approximation indicated above is not valid, but the Yano-Koonin formula of Eq. (8) still holds Achard et al. (2011); Khachatryan et al. (2011).
In general, as described above, the correlation function depends on four-momenta and or, equivalently, on and . However, the Lorentz product of and is zero, i.e. . Here and are defined as three-vector components of and as
| (15) |
This in turn implies
| (16) |
Based on this relation, one may transform the -dependent correlation function to depend on instead. If the particles contributing to the correlation function are similar in energy, then is approximately on-shell; thus the correlation function can be measured as a function of and .
As the dependence on in heavy ion reactions is typically smoother than on , one may think of as the “main” kinematic variable. Then one may assume a parameterization of the dependence, and explore the dependence of the parameters on . Close to midrapidity, instead of , the dependence on
| (17) |
or, alternatively, on the transverse mass
| (18) |
may be investigated, with being the particle (e.g. pion) mass. Note that the average four-momentum is not on mass-shell, but would be the transverse mass of a particle with momentum . Furthermore, also corresponds to the average transverse mass of the particle pair, in the limit of vanishing relative momentum . As earlier results were frequently given in terms of , which is a unique function of of Eq. (18), we decided to use instead of to characterize the transverse momentum of a pair of identical pions.
Let us also note that Eq. (14) can be reinterpreted if we introduce the pair distribution as
| (19) |
where is the pair separation four-vector and is the four-vector of the center of mass of the pair. Then the correlation function can be expressed as
| (20) |
where is defined with the Fourier transformation as
| (21) |
Thus the two-particle Bose-Einstein correlation function is connected to the pion pair distribution , so this is the quantity that can be reconstructed from two-particle correlation data directly. Different source distributions that keep invariant yield equivalent results from the point of view of two-particle Bose-Einstein correlation measurements.
At any fixed value of the average pair momentum , the correlation function can be measured as a function of various decompositions of the components of the relative momentum . The Bertsch-Pratt (BP) or side-out-longitudinal decomposition Pratt (1986); Bertsch et al. (1988) is frequently used. Here
| (22) |
with pointing in the beam direction, in the direction of the average transverse momentum , and the “side” direction orthogonal to these two directions. The transformation to the BP variables corresponds to a rotation in the transverse plane, depending on the direction of the average momentum. For the BP decomposition, it is particularly favorable to use the longitudinal co-moving system (LCMS) of the pair, where the average momentum is perpendicular to the beam axis. Here the BP decomposition of the average momentum is simply , as , and the temporal information of the source is coupled to the out component of the Bose-Einstein correlation function Wiedemann and Heinz (1999); Csörgő (2002).
However, the Bertsch-Pratt variables require three-dimensional Bose-Einstein correlation measurements, so a detailed shape analysis in terms of them can suffer from a lack of statistical precision. For example, it is very difficult to identify any non-Gaussian structure in a three-dimensional analysis of correlation functions. For this reason, sometimes the two-particle correlation function is measured as a function of a one-dimensional momentum variable Achard et al. (2011); F. Siklér, for the CMS Collaboration (2014). The Lorentz invariant relative momentum, corresponding to the Lorentz length of , is defined as
| (23) |
In the LCMS, using the Bertsch-Pratt variables is expressed as
| (24) |
where is the “average transverse speed” of the pair.
Let us introduce also the rest frame of the pair, here referred to as pair center-of-mass system (PCMS), and define the relative three-momentum in this system as . Then the variable can be expressed as
| (25) |
Equation (24) shows that can be very small at moderate , even for not very small values. It is also well known that the Bertsch-Pratt radii (, , ) are of similar magnitude in GeV AuAu reactions at RHIC, so the Bose-Einstein correlation functions are nearly spherically symmetric in the LCMS frame Adler et al. (2004); Adams et al. (2005b); Afanasiev et al. (2008, 2009). This also implies that the correlation function boosted to the PCMS frame is definitely not spherically symmetric (especially for intermediate or high , i.e. for values approaching 1). The conclusion is that is not a proper one-dimensional variable of Bose-Einstein correlations of pions in GeV AuAu collisions.
We look for a novel one-dimensional variable whose small value is only possible in the case when , , are all small. Hence, we introduce LCMS three-momentum difference This quantity is invariant for Lorenz boosts in the beam direction. For the sake of simplicity, we hereafter define
| (26) |
which can be expressed with the lab-system components of the individual particle momenta as
| (27) | |||
| (28) |
Because the correlation functions are approximately spherically symmetric in the LCMS, the measured correlation functions are approximately independent of the orientation of .
We thus conclude that can be introduced in a reasonable manner as the proper one-dimensional variable of the Bose-Einstein correlations in GeV AuAu collisions.
In order to perform a detailed shape analysis in the LCMS, we thus measured them as univariate functions of (for values in various ranges). Thus this one-dimensional analysis in the LCMS in terms of can be viewed as an approximation to a three-dimensional analysis with the approximation that the three HBT radii are equal.
In principle, a more complete picture of the source geometry can be obtained by a three-dimensional Lévy analysis, utilizing Eqs. (49)-(52) of Ref. Csörgő et al. (2004). Given that the details of these studies go beyond the scope of the current manuscript, let us make only some general remarks here. If the source is a symmetric three-dimensional Gaussian, then in a one-dimensional analysis (in our variable, measured in the LCMS), one would obtain for the Lévy shape parameter. If the source is an asymmetric 3D Gaussian, then non-Gaussian 1D correlation functions would be obtained, but also strong deviations from the Lévy shape could be observed. We investigated this using the method of Lévy expansion of the correlation functions Novák et al. (2016) for each bin, and found no first order deviations from the Lévy shape. However, an averaged correlation function shows deviations from the pure Lévy shape, which may be attributed to the dependence of . These observations suggest that the observed Lévy shapes do not originate from an asymmetric three-dimensional Gaussian source.
IV Strength and shape of two-pion correlation functions
We recapitulate some of the important general properties of the two-pion Bose-Einstein correlation functions. First we discuss the strength of the correlation functions, and the main features of its interpretation, following the lines of Refs. Bolz et al. (1993); Csörgő et al. (1996). Then we describe the shape assumption used in this paper, and the physical interpretation of the relevant parameters.
IV.1 Correlation strength and its implications
If the final-state-strong and Coulomb interactions can be neglected, then Eq. (14) implies that the correlation function takes the value at vanishing relative momentum, . However, experimentally the two-track resolution (corresponding to a minimum value of of at least 6–8 MeV, depending on track momentum) prevents the measurement correlation functions at . So the correlation function is measured at nonzero relative momenta and then extrapolated to . This extrapolated value in general can be different from the exact value at , and this can be quantified by defining
| (29) |
where may depend on average momentum .
In our analysis we measure the correlation functions as a ratio of actual and background distributions and , and we have carefully checked in our dataset that and in every transverse momentum range, indicating that the split tracks have been removed from our data sample. The two-track resolution, embodied into the values of two-track cuts as seen in Section III.3, corresponds to a maximum spatial resolution of fm. In our analysis, source details on spatial scales larger or equal to cannot be experimentally resolved.
This (perhaps with different values) is a general feature of any similar experiment, and it leads to the core-halo picture of Bose-Einstein correlations in high energy heavy ion reactions Bolz et al. (1993); Csörgő et al. (1996). The core-halo picture treats the particle emitting source as a composite one, corresponding to particle emission from a hydrodynamically behaving fireball-type core, surrounded by a halo of long-lived resonances. Such a picture is particularly relevant for pion production. Several long-lived resonances with decay widths of (like the , , mesons, and, depending on the experimental two-track resolution, maybe the meson) decay to pions that contribute to the halo region. The general structure of the core-halo model may hold not only for pion production but for the production of other mesons as well.
In short, is in general different from the exact value of which (independently of ) is 2 for a thermal, fully chaotic particle source. In most data sets, holds, see again the overview papers in Refs. Boal et al. (1990); Weiner (2000); Wiedemann and Heinz (1999); Csörgő (2002); Lisa et al. (2005); Tannenbaum (2006); Lisa and Pratt (2008); A. Kisiel, for the ALICE Collaboration (2011); Heinz and Snellings (2013); Adamczyk et al. (2015).
In the core-halo picture, for thermal particle emission, the intercept , the extrapolation of the measured resolvable part of the correlation function to zero relative momentum, is the square of the fraction of pions coming from the core, defined as
| (30) |
because both pions have to come from the core if they are to contribute to the resolvable correlation function. This requires a physical assumption, that the phase-space density of the pion emitting source is made up of two components, i.e.
| (31) |
each component having a Fourier transform defined as
| (32) | |||
| (33) |
where we again used the four-vector variables and . Then each component has a space-time integral corresponding to the contribution of the given component to the momentum distribution. We then may define
| (34) | ||||
| (35) |
Here the first equation in Eq. (34) and Eq. (35) represents our physical assumption about the phase-space density of the core and the halo, while the second equation in Eq. (34) and Eq. (35) indicates a mathematical identity about the Fourier transform. Taking these and Eq. (31) into account, we obtain
| (36) |
For the experimentally resolvable values, this system of physical assumptions yields the approximation
| (37) |
thus the correlation function () shown in Eq. (14) can be expressed as
| (38) | ||||
Hence, in the core-halo picture, at any given momentum
| (39) |
holds; see Ref. Csörgő et al. (1996) for details. Thus parameter can be interpreted as the squared fraction of pions from the core with respect to the total number of pions with a given average momentum . The dependent part in Eq. (38), i.e. the shape of the Bose-Einstein correlation function is connected to the core, . This source component is the one that may correspond to the perfect fluid, the hydrodynamically evolving central part of the fireball created in high energy heavy ion collisions.
If we assume that the source () is a sum of the core and the halo components as shown in Eq. (31), then it follows that the pair distribution () shown in Eq. (19), is a sum of the three components,
| (40) |
where subscript ‘c’ denotes the core and ‘h’ denotes the halo. It can be easily shown that the core-core component denoted by is resolvable, but the core-halo or type of pion pairs or the halo-halo or components are unresolvable (i.e. the width of their Fourier transform is below the minimal resolvable momentum difference). With this compared to Eq. (20), the correlation function of Eq. (38) can be re-expressed as
| (41) |
In summary, is an experimental finding, and so it is customary to introduce as an experimental parameter, defined as , and measured by extrapolating the correlation function to zero relative momentum. The core-halo model is then an interpretation of the value . It also relates the relative momentum dependent, resolvable part of the Bose-Einstein correlation function to , the core component of particle emission in high energy heavy ion collisions. From this interpretation it is particularly clear that while long-lived resonance effects dominate the variances of the source, they lead to a peak in the unresolvable part of the Bose-Einstein correlation function, with measurable effects only on . Particle emission from the hydrodynamically expanding fireball however, i.e. the core component of the source, is observable from the -dependent shape analysis of the Bose-Einstein correlation functions.
Thus one of the motivations for measuring the parameter is that it carries indirect information on the decays of long-lived resonances to the observable pion spectra. Of particular interest is the contribution of the meson to the low momentum pion yield. It is expected Kapusta et al. (1996) that in the case of chiral symmetry restoration in heavy-ion collisions, the in-medium mass of the meson (the ninth pseudoscalar meson, a would-be Goldstone boson) is decreased, thus its production cross section is heavily enhanced at low momentum. This (because the decay chain of the meson produces many charged pions) implies that at low transverse momentum, the parameter decreases Vance et al. (1998). A recent study Csörgő et al. (2010) of existing measurements (presented in greater detail in Ref Vértesi et al. (2011)) reported an indirect observation of a mass drop of the meson in GeV AuAu collisions at RHIC.
However, many of the earlier measurements were made with the assumption that the shape of the correlation function is a Gaussian one. Given the fact that the detailed analysis presented below indicates that the Gaussian approximation is a statistically unfavored assumption, we attempt here a precise shape analysis of the correlation functions. This is required for a precise measurement of the intercept parameter , as its value depends on the shape of the correlation function through the extrapolation of the measured correlation function to vanishing relative momentum.
Let us note here that the modification of the observable intercept parameter from unity can result from various reasons besides the core-halo model, for example coherence in the pion production Weiner (2000); Csörgő (2002). If a fraction of pions are created in a coherent manner, then two- and three-particle Bose-Einstein correlation functions at zero relative momentum are simply related to the fraction of coherently produced pions and to the fraction of pions coming from the core Csörgő (2002). Thus a simultaneous measurement of in two- and three-pion correlation functions offers the possibility of separating the component of a possibly coherent pion production, in addition to the resonance decay contribution. Such a simultaneous analysis of second, third and higher order correlations was recently reported at the LHC Adam et al. (2016). Also, more exotic quantum statistical effects like squeezed coherent states may modify the values of the intercept parameter (however, in the present analysis we have no compelling reason to consider this possibility). Hence, one of the goals of the paper is to measure precisely, without any physical assumption about the mechanism of the pion production.
In the following, we utilize a generalization of the usual Gaussian shape of the Bose-Einstein correlations, namely we analyze our data using Lévy-stable source distributions. We have carefully tested that this source model is in agreement with our data in all the transverse momentum regions studied. All the Lévy fits were statistically acceptable, as discussed in Section VI. We note that using the method of Lévy expansion of the correlation functions Novák et al. (2016), we investigated deviations from the Lévy shape. We have found that the coefficient of the first correction term is within uncertainties consistent with zero. Hence, we restrict the presentation of our results to the analysis of the correlation functions in terms of Lévy-stable source distributions.
IV.2 Lévy-type correlation functions and critical behavior
Past measurements of two-pion Bose-Einstein correlation functions in AuAu collisions that went beyond the Gaussian approximation show that the precise shape of Bose-Einstein correlations is indeed not Gaussian Afanasiev et al. (2008); Adler et al. (2007). The shape exhibits a power-law-like long-range component. In expanding systems, a generalized form of the central limit theorem and investigation of generalized random walk (also called anomalous diffusion) suggests the appearance of Lévy distributions as source functions Metzler et al. (1999); Csörgő et al. (2004). The one-dimensional, symmetric Lévy distribution is the generalization of the Gaussian distribution defined by the Fourier transform
| (42) |
Here is called the Lévy length scale parameter, and is called the Lévy index of stability. In the case we recover a Gaussian form; in the case, we have a Cauchy distribution. For , the Lévy distributions have a power-law-like tail, for (with ). Equivalently, for the angle-averaged Lévy distribution one gets
| (43) |
Thus Lévy distributions for have an infinite second moment or root-mean-square (RMS) radius. However, even in this case, the scale parameter provides a measure of the characteristic size of the system. In particular, the integral of the Lévy distribution is finite and proportional to . Note also that if the core part of the source () has a Lévy shape, then the core-core pair distribution () also has a Lévy shape, due to the fact that the autocorrelation of two identical Lévy distributions is also a Lévy distribution with the same index of stability ,
| (44) |
Thus the Lévy-type source distributions offer a more general description of the shape of the correlation function than a Gaussian would do. They provide a better handle on the intercept parameter as well. The Gaussian limit corresponds to the special case, so one can experimentally check how far given data are from the Gaussian limit. We illustrate the shape of Lévy-type source distributions () with various values in Fig. 2.
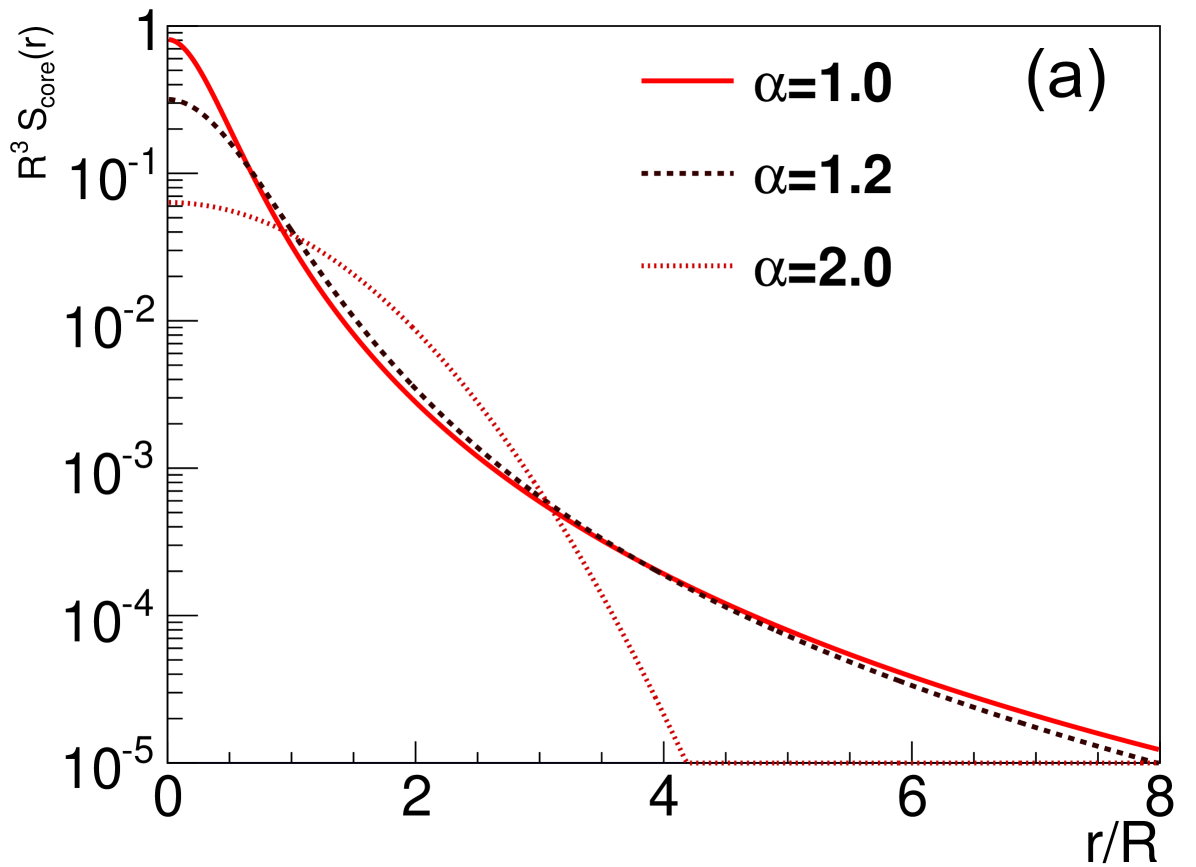
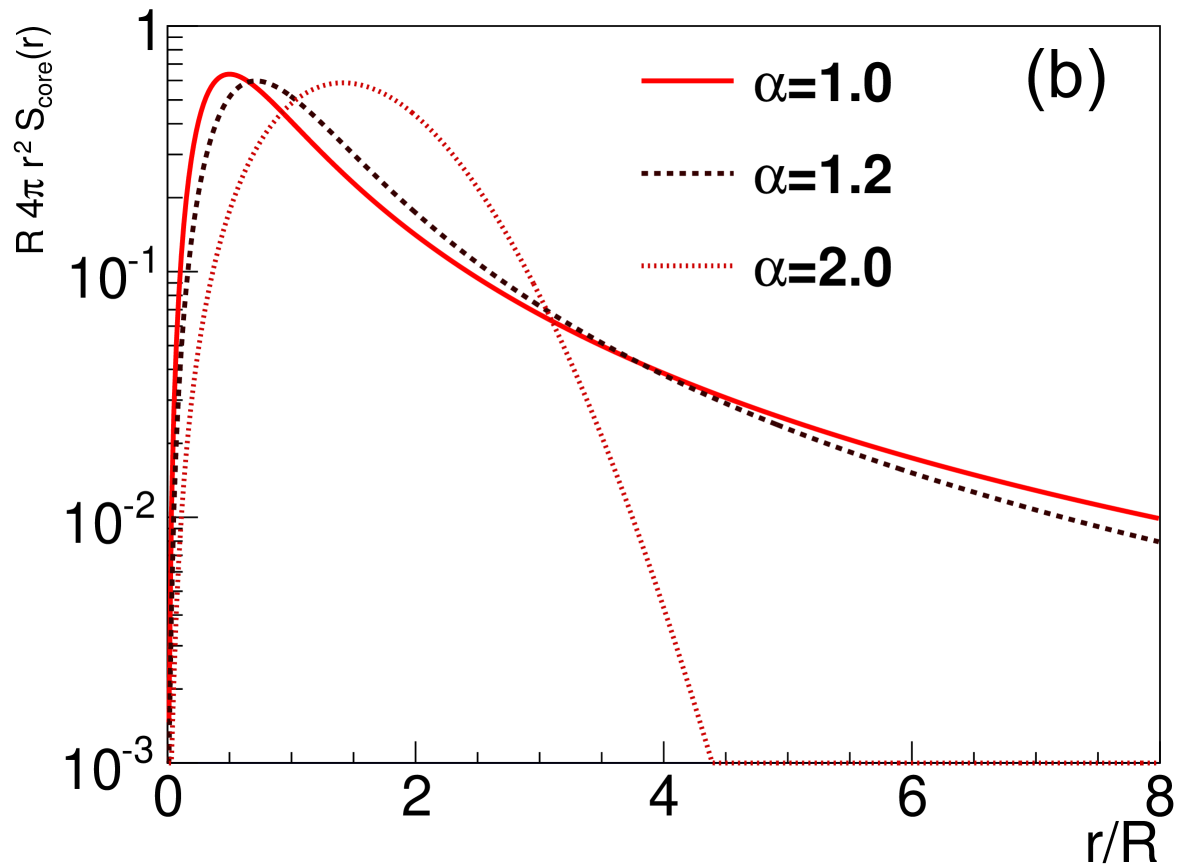
There is yet another motivation for Lévy distributions. Namely, the exponent of the Lévy distribution (that determines the power-law-like behavior of the distribution at large distances) is related to the critical exponent of a system at a second order phase transition Csörgő (2008). This exponent characterizes the power-law structure of the spatial correlation at the critical point. If an order parameter is introduced, its correlation function (in three dimensions, as a function of distance ) will be
| (45) |
As noted above in Eq. (43), the Lévy source distribution has the same limiting behavior, thus in this case, . According to lattice quantum chromodynamics (QCD) Aoki et al. (2006); Bhattacharya et al. (2014); Soltz et al. (2015) the quark-hadron transition is analytic (cross-over) at vanishing baryochemical potential , and is expected to be a first order phase transition at high values of . There may be a critical endpoint (CEP) at certain intermediate values of , where one has a second order phase transition, with a specific value of the exponent. This value is in the 3D Ising model El-Showk et al. (2014), and in the random field 3D Ising model Rieger (1995). Given that the second order QCD phase transition is expected to be in the same universality class as the 3D Ising model Halasz et al. (1998); Stephanov et al. (1998), the QCD critical point may be signaled by Lévy sources with a specific exponent. To locate and characterize the CEP is one of the most pressing present day challenges of experimental heavy-ion physics. It is thus desirable to measure for various colliding systems and collision energies, to map various parts of the plane, in a quest to find the location of the CEP of the quark-hadron transition. We present below the first determination of the Lévy index of stability in GeV AuAu collisions.
IV.3 Coulomb effect
Using the plane-wave approximation, and assuming a spherically symmetric, three dimensional Lévy-type source and using the core-halo model, the shape of the two-particle correlation function turns out to have the simple form of
| (46) |
with being the independent variable as introduced in Eq. (26), and with three fit parameters, which may depend on average momentum . The scale parameter , the strength (intercept) and the Lévy index (note that the fitting procedure is detailed in Section VI.1). However, one cannot fit the above functional form to the measured correlation functions before properly taking the final state Coulomb repulsion of the identically charged pions into account.
In the treatment of this effect, we follow the general lines of the Sinyukov-Bowler method Sinyukov et al. (1998); Bowler (1991). Coupling this with the core-halo picture, one has to average the modulus squared of the final state pair wave-function over the “core-core” spatial pair distribution , obtaining
| (47) |
where the Coulomb wave function is defined as
| (48) |
Here is the confluent hypergeometric function, is the Coulomb-parameter, is the fine structure constant, is the Gamma function, is a spatial integration variable representing the spatial pair separation, and is the three dimensional momentum difference in the pair rest frame, . The term represents a term similar to the first one, just with a mirrored . The above Coulomb wave function formula is a standard result in quantum scattering theory. Note that in Eq. (47), the right side does not depend on the direction of if the source is spherically symmetric. Hence, we modified the formula of Eq. (47) slightly to make it compatible with our analysis. We substitute , and thus obtain as a function of . We analyzed the error coming from this approximation by averaging values for various momenta at a given , and treated it as a source of uncertainty, as quantified next in Section V.
V Systematic uncertainties
| setting name | settings () | |
|---|---|---|
| 0 | PID arm | east, west, both |
| 1 | PID cut | 3 cut settings |
| 2 | PID det. matching cut | 3 cut settings |
| 3 | PC3 matching cut | 3 cut settings |
| 4 | PID det. pair cut | 3 cut settings |
| 5 | DC pair cut | 3 cut settings |
| 6 | Fit range () | 7 ranges |
| 7 | Fit range () | 3 ranges |
| 8 | Coulomb effect | 2 versions |
The extracted Bose-Einstein correlation functions depend on a number of experimental parameters and cut values, as discussed e.g. in subsections III.3 and III.1. The dependence is on the cut for identification in the spectrum (PID cut), the track matching cut in the PID detector and in PC3, the pair cuts in the PID detectors and in the DC, the choice of fit range and some other settings (like the choice of and binning, or the settings of the Coulomb-calculation) with negligible contributions. When performing fits to the correlation functions (note that the fitting procedure is detailed in Section VI.1), the fit parameters also depend on these settings. Then a given fit parameter (which represents here , or ) takes the value (where represents the number of the bin) if all cuts and settings are at their default values. However, the resulting fit parameter is , when a different setting (indexed by ) was chosen for the given setting (indexed by ). See a summary of the possible and values in Table 1. Then the systematic uncertainty of parameter at the given bin is calculated as the average deviation from the default value, for lower and upper uncertainties separately. This can be illustrated by the following formulas:
| (49) | ||||
| (50) |
where is the set of values where , and is the number of elements in this set. This number may vary from 0 (if both changes increase the fitted value of the given parameter) to the number of possible settings (if all changes decrease the fitted value of the given parameter). Similarly, is the set of values where , and is the cardinality of this set. In the above formulas, summing over is only done if or . The values for and were then averaged over the neighboring 5 bins (two bins at higher, and two bins at lower , in addition to the central, averaged value). This procedure allowed us to smooth out the apparently nonphysical large fluctuations in the upper or lower limits on the systematic uncertainties. Let us also note here that we found the different systematic uncertainty sources to be uncorrelated with each other, so the quadratic sum in the equation above is justified.
In addition to settings in the correlation function measurement, we have performed fit range studies by varying the initial and the final bin locations ( and ). The results were remarkably stable for adding or removing the first few (1–5) or the last few (10–20) data points at the beginning or the end of the fit. In fact we used this stability criteria to define the beginning and the end points of the fitted range. We have also investigated the stability of the fit results with respect to duplicating or halving the number of bins, and also with respect to doubling the bin size in , or splitting the bins into two equal parts. These sources of uncertainty had negligible effects on the fit parameters. We also analyzed the uncertainty of the fit results originating from the Coulomb calculation (as detailed in subsection IV.3).
Now that all the details of the formalism are described in detail, in the following we outline the experimental procedure of the measurement and the results on the Lévy parameters of two-pion ( and ) Bose-Einstein correlation functions in GeV AuAu collisions.
VI Results
We measured Bose-Einstein correlation functions of and pairs in 31 bins in the pair average transverse mass , from 228 MeV to 871 MeV. Our measurement was based on 2.2 billion 0%–30% centrality AuAu collisions at GeV colliding energy, selected from 7.3 billion MB events. Further centrality bins and their analysis is outside the scope of present manuscript.
VI.1 Fitting procedure
The formulas in Eqs. (47)–(48) cannot be evaluated analytically, and the numerical calculation is also cumbersome, so to accelerate the fitting process, we created a lookup table for this function, and used it for fitting. We denote our fit function based on Eqs. (47)–(48) as , and from now on we drop the notation of the dependence, and explicitly write out the parameter values, i.e.
| (51) |
However, it turned out that fits using this function resulted in a numerically fluctuating -landscape, so we applied an “iterative afterburner” where the fit function contained only analytic dependencies on the fit parameters. Our second round fit function was
| (52) | |||
| (53) |
where , , and are the fit parameters from the first round of fit. Let us call the resulting fit parameters of this next fit , and . If these differ substantially (more than 1% in squared sum) from , and , then we set , and , and do one more round of fitting. We continued this iterative procedure with a fit function of
| (54) |
until the previous parameter vector and the newly obtained parameter vector differed less than 1% in the squared sum. Note at this point that in the actual fits, a normalization parameter and a parameter that represents a possible but small background long-range correlation effect were also included. In practice and , and these parameters converge earlier in the fit than do the physical parameters , , and . For this reason only the physical parameters were used in the test of the convergence criteria. In this way the physical source parameters were extracted from the data in a reliable manner, with a self-consistent treatment for the Coulomb effect. Note that our procedure is in fact rather similar to the iterative Coulomb correction method applied by the NA44 Collaboration in Ref. Boggild et al. (1995). However, in our implementation, we use this iterative procedure also for the correction for the halo effects, by evaluating the Coulomb wave-functions only for the experimentally resolvable (core,core) type of pion pairs.
Pair multiplicities allowed us to use a minimization method (in contrast to the need for log-likelihood fitting methods if the value of in the given bin is obtained by the ratio of two small numbers and ; see details in Ref. Zajc (1982)). We applied MINUIT2 minimization libraries James and Roos (1975) when performing fits to the measured correlation functions. We accept the fit results if the following criteria are satisfied: (a) the status of the fit is “converged” (i.e. a valid minimum was reached), (b) the error matrix is “accurate” (i.e. fully calculable and positive definite), (c) the NDF values are acceptable, corresponding to a confidence level (CL) above 0.1%. Our fits satisfied these conditions, implying that the fit parameters represent the measurements in a statistically acceptable manner. We note here that fits with an constraint, i.e. fits with a Gaussian assumption were not acceptable. The CL of these Gaussian fits were many orders of magnitude below 0.1%, as the values ranged from 100–600 (for the lowest bins, where , and also for the highest bins, where NDF values are around 350) to 600–1000 (for 300–500 MeV, where NDF is about 150–220). In contrast, Lévy fits resulted in values in the 1–1.3NDF range. Note that the statistical acceptability of our Lévy fits to GeV AuAu RHIC data also confirms the validity of the assumption about the correlation function being unity plus a positive definite function.
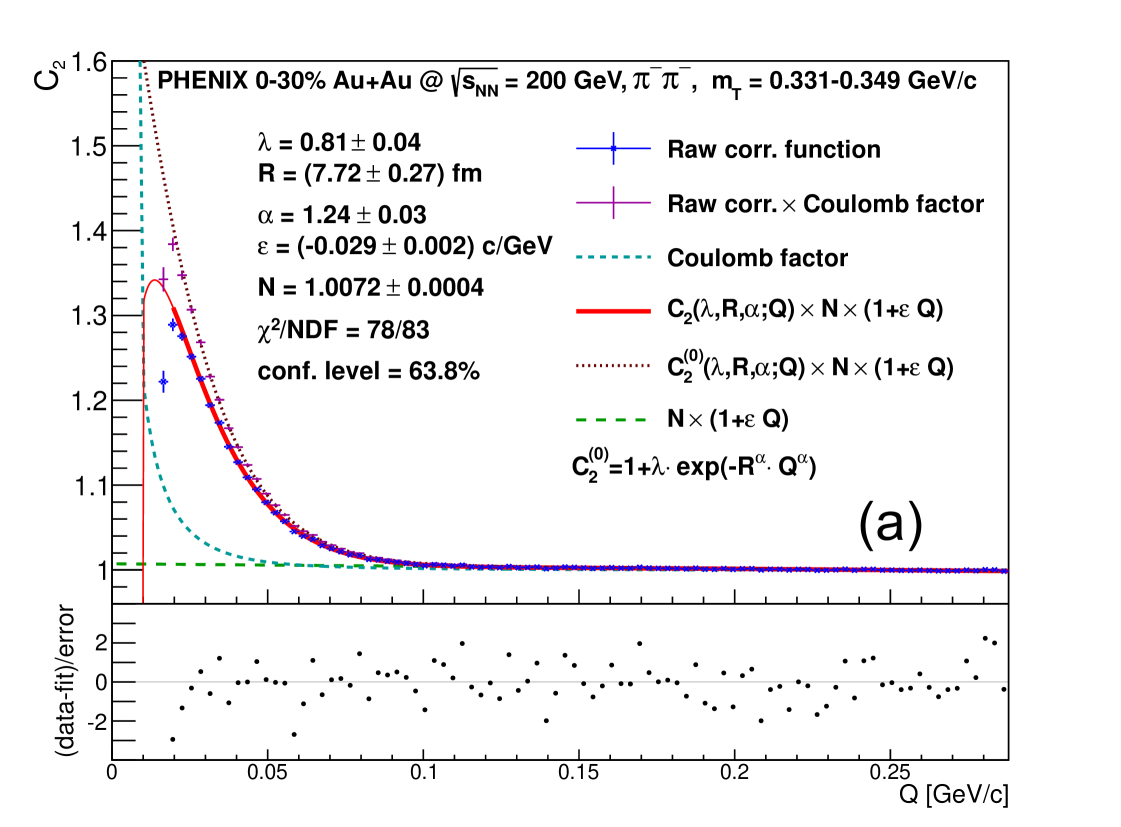
We fitted the measured correlation functions with the above outlined procedure. Figure 3 shows some examples of the measured Coulomb-distorted two-pion Bose-Einstein correlation function, the Coulomb correction factor and the resulting Coulomb-corrected two-pion Bose-Einstein correlation functions, together with the fits with Eqs. (52)-(53) that define the parameters of the Lévy-stable Bose-Einstein correlation functions.
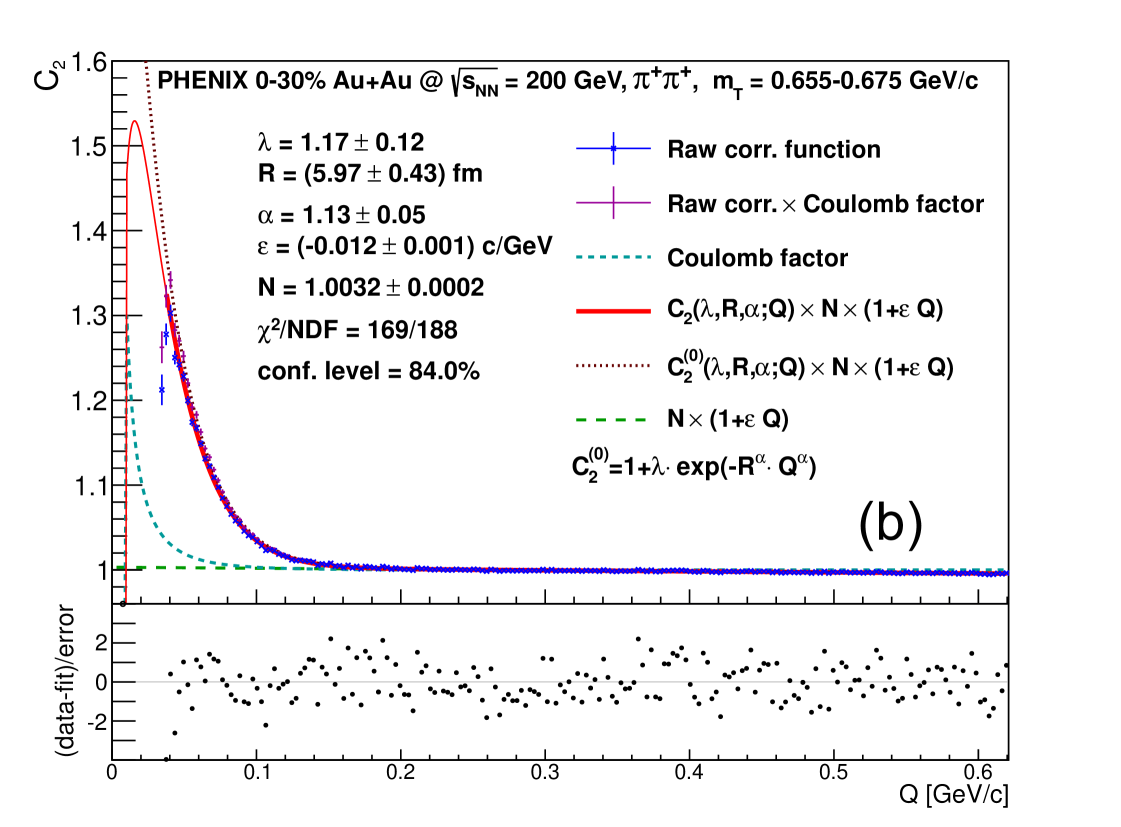
In Section VI.2, we present our results for the fits and for the trends of the fit parameters, versus average pair calculated from the of the pair.
VI.2 Results for the transverse momentum dependence of the fit parameters
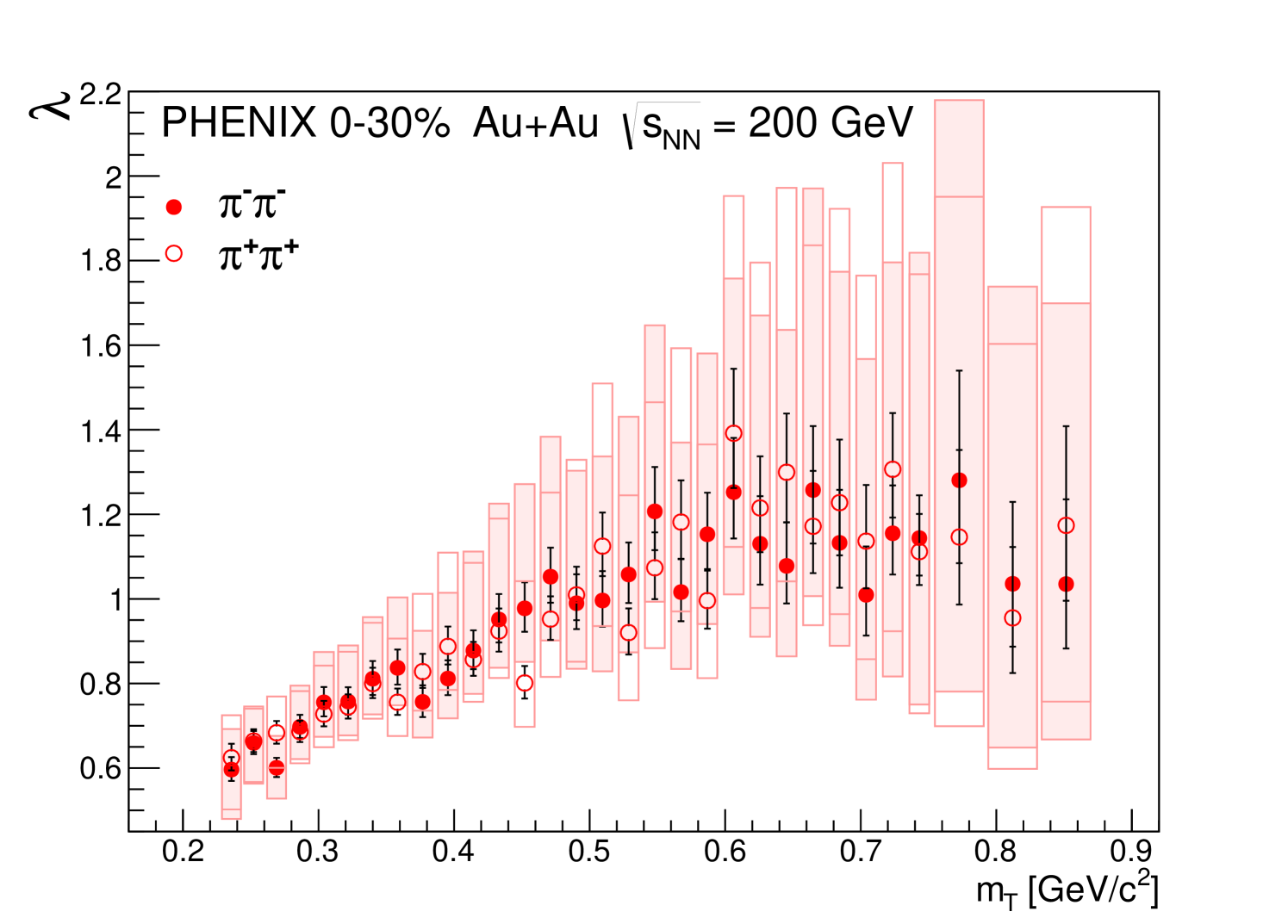
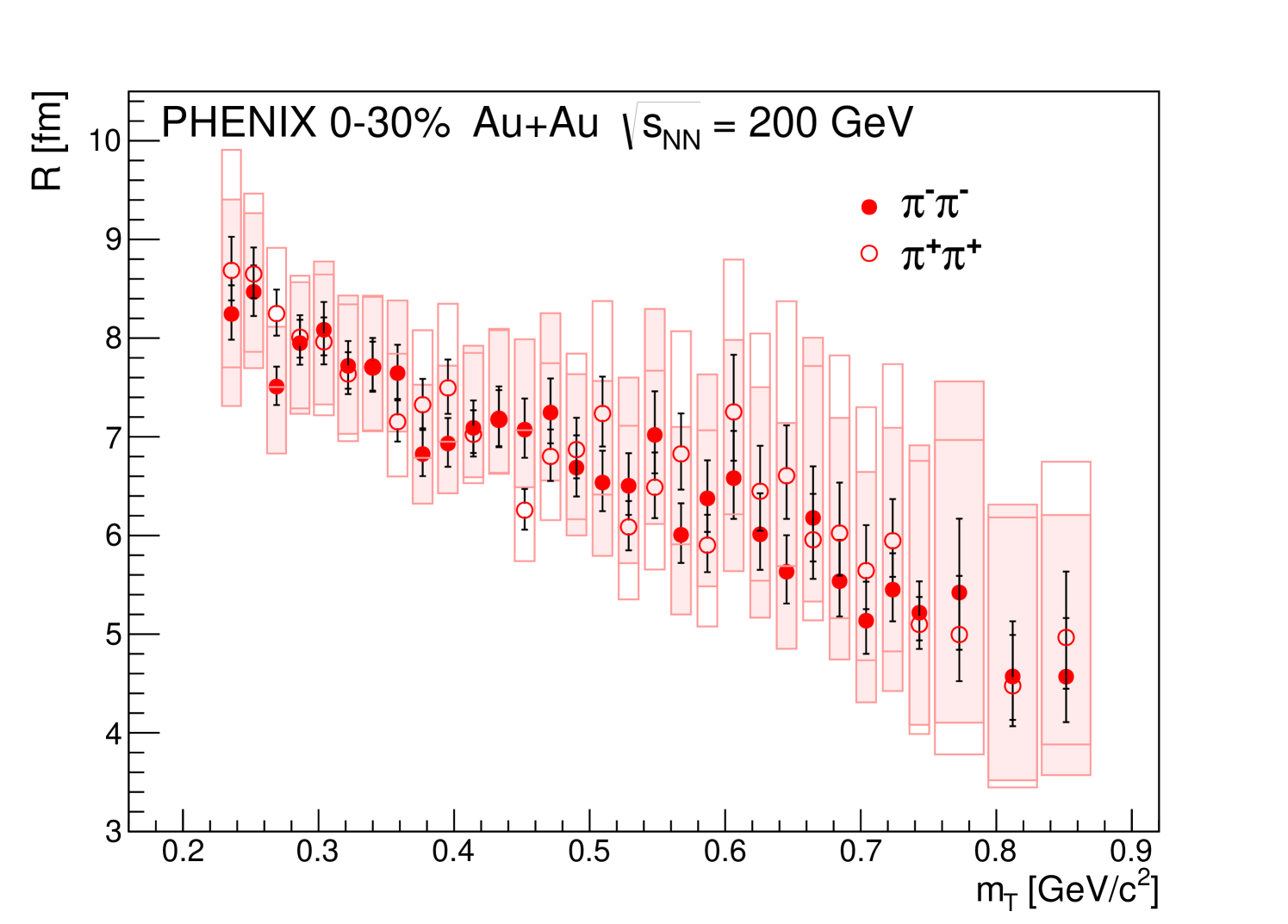
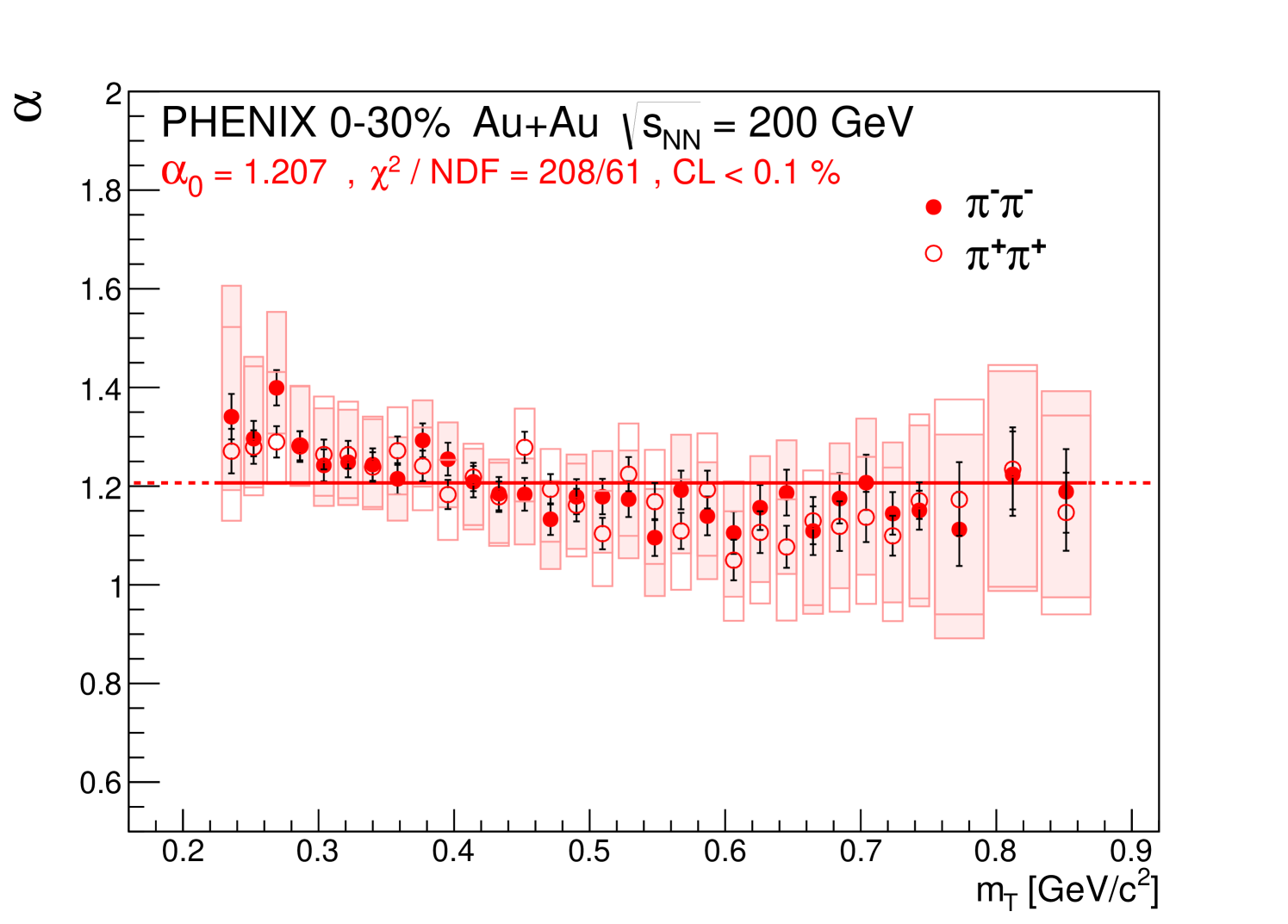
Parameters , and are the physical parameters of the fit, while and are the normalization and background-slope parameters. The dependence of the physical parameters is shown in Figs. 4, 5 and 6. The parameter values for and pairs in 0%–30% centrality collisions are given in Table 3, while the decomposition of their systematic uncertainties is detailed below in Table 3.
The intercept parameter seems to saturate at high . Even within the sizable systematic uncertainties of the measurement, a decrease of is clearly visible at low values of the average transverse mass , where the uncertainties of the analysis are reduced significantly.
The Lévy scale parameter indicates a characteristic decreasing trend, that is similar to the decrease predicted by hydrodynamical calculations of a three-dimensionally expanding source for the Gaussian case Makhlin and Sinyukov (1988); Csörgő and Lörstad (1996); Chapman et al. (1995a, b). Note that for we are not aware of any theoretical predictions for the dependence of the Lévy scale parameter .
The values of are significantly below the Gaussian limit of 2. In certain measurements of two-particle Bose-Einstein correlations, if the Gaussian approximation fails, the exponential approximation is attempted. In our analysis, we observe that our data are systematically above 1. Although the case of is closer to the measured values than the case of , it also is disfavored by the data. When we repeat the fits with fixed, the fits become statistically unacceptable in most of the bins.
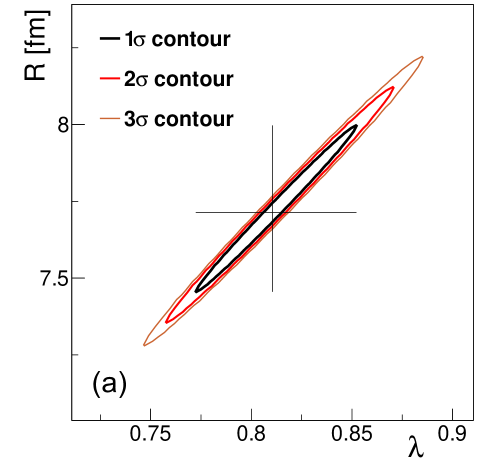
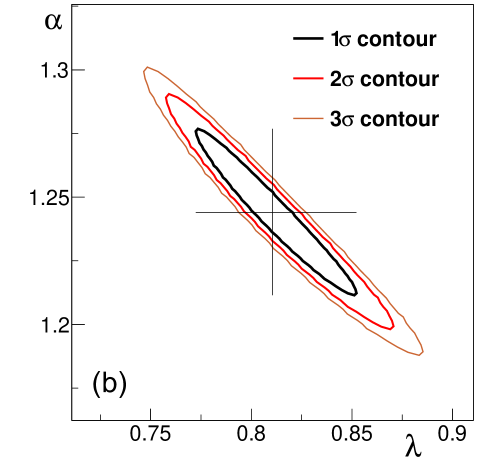
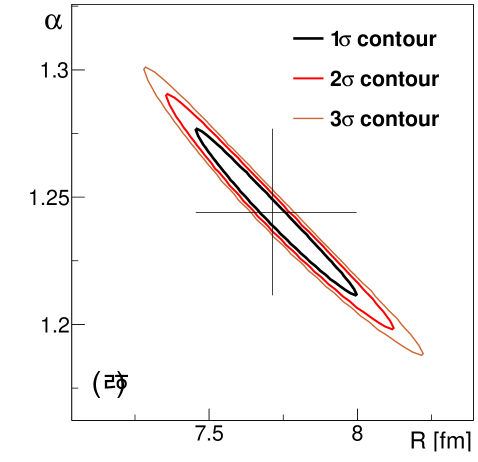
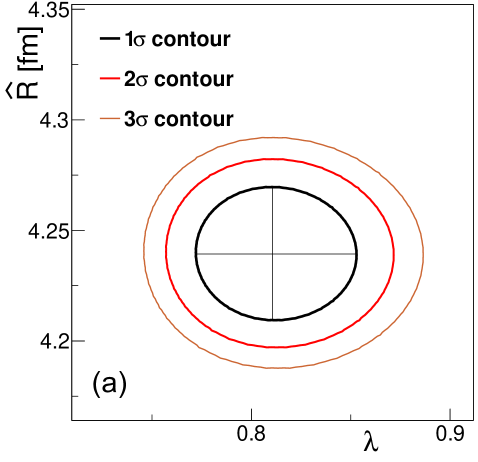
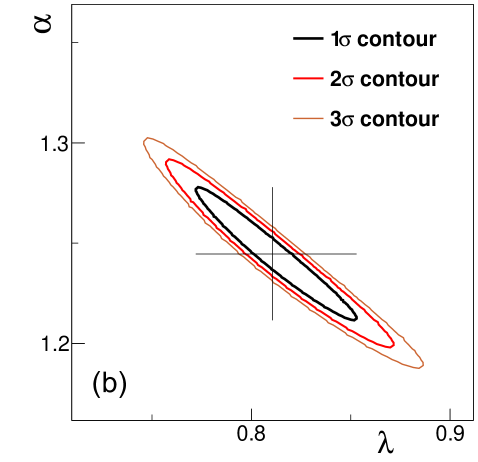
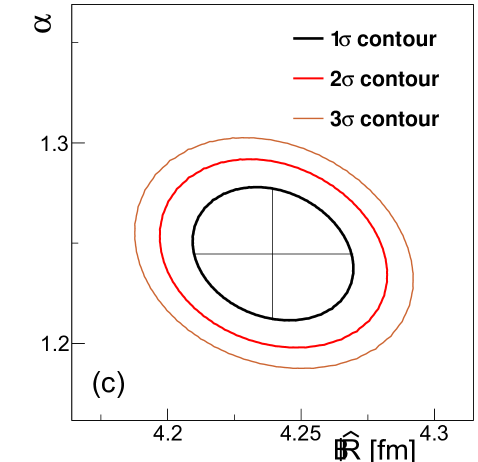
Let us also note that the error contours are all narrow tilted ellipses on the two-dimensional maps in the , and planes, as shown in Fig. 7. This illustrates that the parameters of the Lévy-stable fits of Eq. (52) are highly correlated. Typical values of the correlation coefficients for the , and coefficients are around %, % and %, respectively.
As discussed in Section V, the extracted parameters of Bose-Einstein correlation functions depend on a number of experimental parameters and settings. In Figs. 4–6 and Table 3, we indicate the corresponding total systematic uncertainty, bin by bin. A charge averaged, and (in two regions) averaged decomposition of the systematic uncertainties is given in Table 3 (both for the parameters introduced above, and those defined in the next subsections). Let us note here that the systematic uncertainties contain both -correlated and uncorrelated components. Uncertainties coming from the variations of pair-cuts are mostly uncorrelated, while the ones from the PID arm and fit extrapolation are -correlated. As for the other sources of uncertainties, they have an -correlated effect on , but an uncorrelated effect on and . There are clear differences in the systematic uncertainties between the two regions both in relative size and in distribution among the sources of uncertainty. This translates into differences in the -correlated nature of the systematic uncertainties as well. Let us also note here that the systematic uncertainties are further -correlated because of the averaging process described in Section V.
| (GeV/) | (fm) | (fm) | ||||
|---|---|---|---|---|---|---|
| 0.236 | ||||||
| 0.252 | ||||||
| 0.269 | ||||||
| 0.286 | ||||||
| 0.304 | ||||||
| 0.322 | ||||||
| 0.340 | ||||||
| 0.358 | ||||||
| 0.377 | ||||||
| 0.395 | ||||||
| 0.414 | ||||||
| 0.433 | ||||||
| 0.452 | ||||||
| 0.471 | ||||||
| 0.490 | ||||||
| 0.509 | ||||||
| 0.529 | ||||||
| 0.548 | ||||||
| 0.567 | ||||||
| 0.587 | ||||||
| 0.606 | ||||||
| 0.626 | ||||||
| 0.645 | ||||||
| 0.665 | ||||||
| 0.684 | ||||||
| 0.704 | ||||||
| 0.724 | ||||||
| 0.743 | ||||||
| 0.773 | ||||||
| 0.812 | ||||||
| 0.852 |
| MeV average uncertainties [%] | MeV average uncertainties [%] | ||||||||||||||||||||||
| PID arm | 8.9 | 9.6 | 8.5 | 5.8 | 9.2 | 4.9 | 5.4 | 6.0 | 12. | 20. | 28. | 12. | 17. | 6.9 | 4.9 | 7.4 | 5.6 | 4.2 | 16. | 12. | |||
| PID cut | 4.4 | 3.8 | 1.8 | 2.2 | 2.0 | 1.3 | 4.0 | 3.8 | 3.8 | 5.9 | 11. | 7.7 | 6.0 | 4.2 | 2.9 | 3.4 | 3.6 | 3.5 | 6.0 | 5.7 | |||
| PID det. matching cut | 4.0 | 13. | 2.2 | 1.8 | 1.4 | 1.5 | 2.9 | 2.0 | 1.8 | 1.8 | 3.8 | 22. | 2.4 | 4.2 | 2.7 | 1.6 | 1.2 | 0.5 | 2.4 | 1.9 | |||
| PID det. paircut | 4.4 | 3.0 | 2.2 | 1.8 | 1.5 | 1.5 | 3.1 | 2.3 | 8.0 | 4.3 | 7.7 | 7.5 | 4.3 | 5.1 | 3.5 | 2.5 | 2.9 | 2.1 | 4.1 | 4.5 | |||
| PC3 matching cut | 14. | 0.6 | 4.7 | 2.2 | 1.9 | 3.0 | 8.9 | 0.0 | 0.2 | 19. | 38. | 0.1 | 17. | 1.5 | 0.9 | 8.7 | 13. | 0.0 | 9.1 | 7.6 | |||
| DC paircut | 3.0 | 3.4 | 1.9 | 2.5 | 1.9 | 1.5 | 0.7 | 0.7 | 13. | 1.7 | 2.1 | 16. | 7.7 | 9.9 | 7.7 | 0.8 | 0.5 | 4.0 | 10. | 10. | |||
| Fit range () | 4.4 | 4.8 | 3.1 | 3.3 | 2.3 | 2.0 | 0.5 | 0.5 | 12. | 5.7 | 7.8 | 14. | 6.2 | 9.3 | 6.2 | 3.2 | 1.4 | 2.4 | 5.1 | 5.4 | |||
| Fit range () | 3.2 | 3.2 | 2.2 | 2.2 | 2.0 | 2.0 | 0.2 | 0.2 | 4.3 | 4.3 | 4.5 | 4.5 | 3.2 | 3.2 | 2.1 | 2.1 | 0.5 | 0.5 | 6.6 | 6.6 | |||
| Coulomb effect | 9.4 | 0.0 | 4.2 | 0.0 | 0.0 | 3.4 | 3.8 | 0.0 | 0.0 | 10. | 21. | 0.0 | 13. | 0.0 | 0.0 | 8.1 | 2.0 | 0.0 | 1.6 | 2.0 | |||
| Total | 21. | 18. | 12. | 8.5 | 11. | 7.8 | 13. | 7.8 | 24. | 31. | 54. | 35. | 30. | 18. | 12. | 15. | 15. | 7.5 | 24. | 21. | |||
VI.3 Discussion and interpretation of the results
In this subsection we discuss more subtle physical interpretations of the measured trends of the parameters of the two-pion Bose-Einstein correlation functions.
Starting with the Lévy exponent, we observe that in each of the investigated cases, values were slightly above 1. It is known that the value of the critical exponent of the random field 3D Ising model is 0.5 Rieger (1995), much larger than the value of the critical exponent in the 3D Ising model El-Showk et al. (2014) (without random external fields). It is also known that the 3D Ising model is expected to be in the same universality class as the second order QCD phase transition Halasz et al. (1998); Stephanov et al. (1998). Therefore, we observe that the measured values of the Lévy exponent in 0%–30% centrality AuAu collisions at GeV do not correspond to the conjectured value () of the exponent of the two-particle correlation function at the QCD critical point Csörgő (2009). The appearance of the critical point is not expected near GeV, thus we emphasize the need for similar measurements at lower collision energies.
Hydrodynamic calculations typically predict Gaussian shapes (i.e. ) for the Bose-Einstein correlation functions Akkelin and Sinyukov (1996, 1995); Csörgő et al. (1994); Csizmadia et al. (1998); Csörgő and Lörstad (1996); Csanád and Vargyas (2010). We may also note that in certain cases the freeze-out criteria may alter this behavior, interference terms between two different extrema in the source may lead to small deviations from Gaussian Bose-Einstein correlations Csörgő (2002, 2001). The measured correlation functions discussed in the present paper show large deviations from the Gaussian assumption. Our observations show that the source of charged pions in the investigated momentum range is a Lévy distribution with an average index of stability of , see Fig. 6.
Various scenarios may lead to such a source with a long power-law like tail, e.g. rescattering in an expanding medium with time-dependent mean free path, which is also called anomalous diffusion or Lévy flight. In such a scenario, the smaller the cross section, the longer the mean free path (at a given time), thus the longer the tail of the source distribution. This might be tested by comparing the Lévy source distributions for pions, kaons and protons Akiba et al. (1993); Csanád et al. (2007).
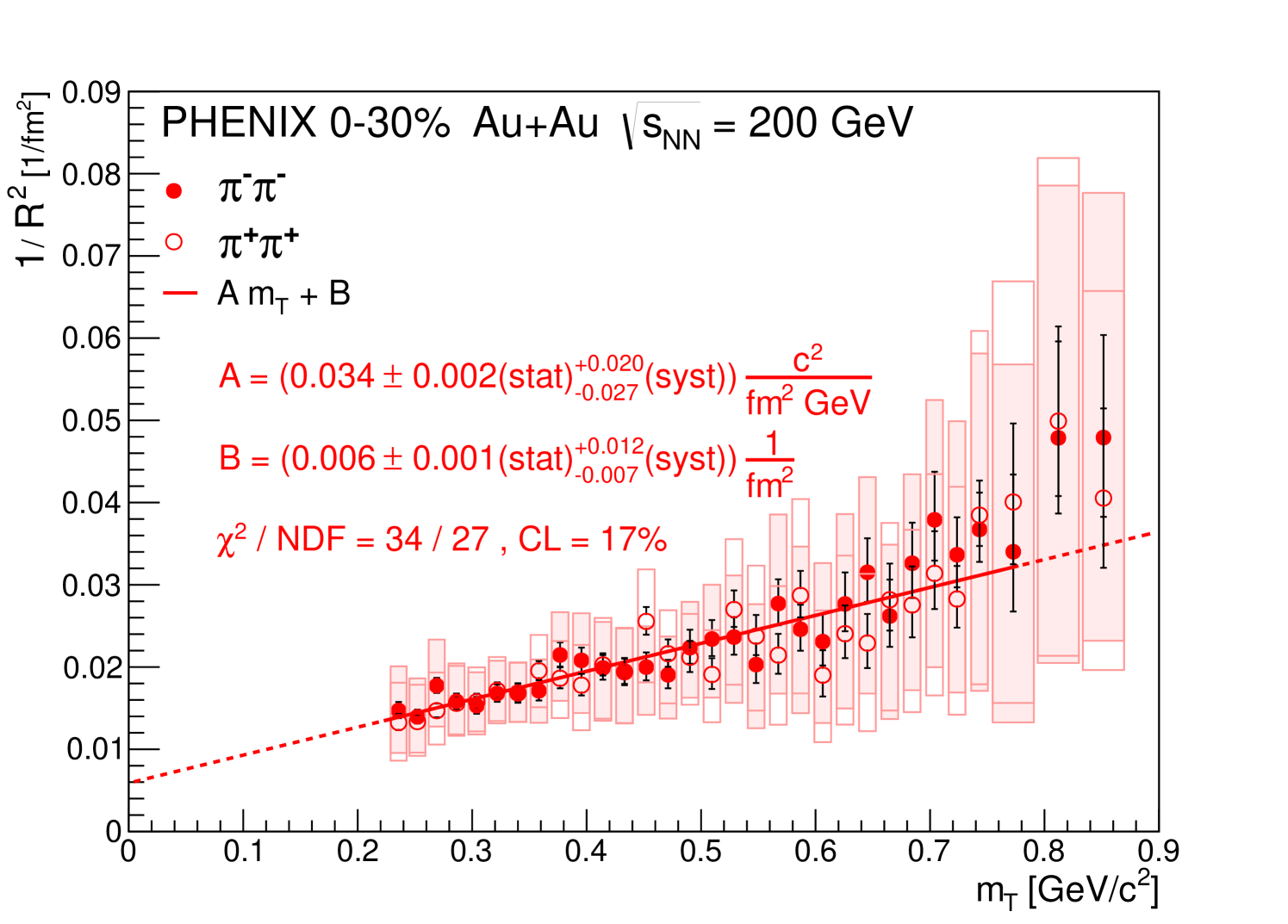
As the Lévy scale parameter defines the length scales of the particle-emitting source for particle emission with heavy tails, the dependence of these parameters is worth investigating in greater detail. It turns out (shown in Fig. 8) that a hydrodynamical type of scaling holds approximately, especially in the low region. This corresponds to the scaling predictions for the HBT radii from hydrodynamical calculations Makhlin and Sinyukov (1988); Csörgő and Lörstad (1996); Chapman et al. (1995a, b); Akkelin and Sinyukov (1996, 1995); Csörgő et al. (1994); Csizmadia et al. (1998); Csanád and Vargyas (2010). Although these predictions assumed , the scaling seems to hold remarkably even in this case of . We also show a linear fit to versus , taking into account only the statistical uncertainties when determining the best values and the statistical errors of the fit parameters. The resulting parameters turned out to be
| (55) | ||||
| (56) |
as noted in Fig. 8. Systematic uncertainties of the fit parameters were determined by performing a linear fit to versus obtained from measurements and fits with varied settings (listed e.g. in Table 3). The and parameters above can be converted to a simple
| (57) |
dependence, where one then gets fm and .
Because the estimators of Lévy parameters , and are strongly correlated, reasonably good (although not necessarily statistically acceptable) fits can be obtained with multiple sets of co-varied parameters. This motivated us to search for less correlated combinations of these parameters. Unexpectedly, and without any theoretical motivation for this new scaling law except perhaps the suggestions of Ref. Zajc (1993), we indeed found such a parameter, defined as
| (58) |
If this parameter is used as a fit parameter instead of the Lévy scale parameter (which is calculated as ), the obtained , and parameters are the same as before, but the correlation coefficients for and are reduced substantially, to the region of 20%–30%, which indicates small correlation as compared to the 95% values of the correlation coefficients between and (and all of them are negative in this case). The error contours obtained on the two-dimensional maps in the , and planes for one example fit are shown in Fig. 9. Also note that due to the reduction of the correlation, the uncertainty of is also significantly reduced compared to that of , as indicated in Fig. 10 and Table 4.
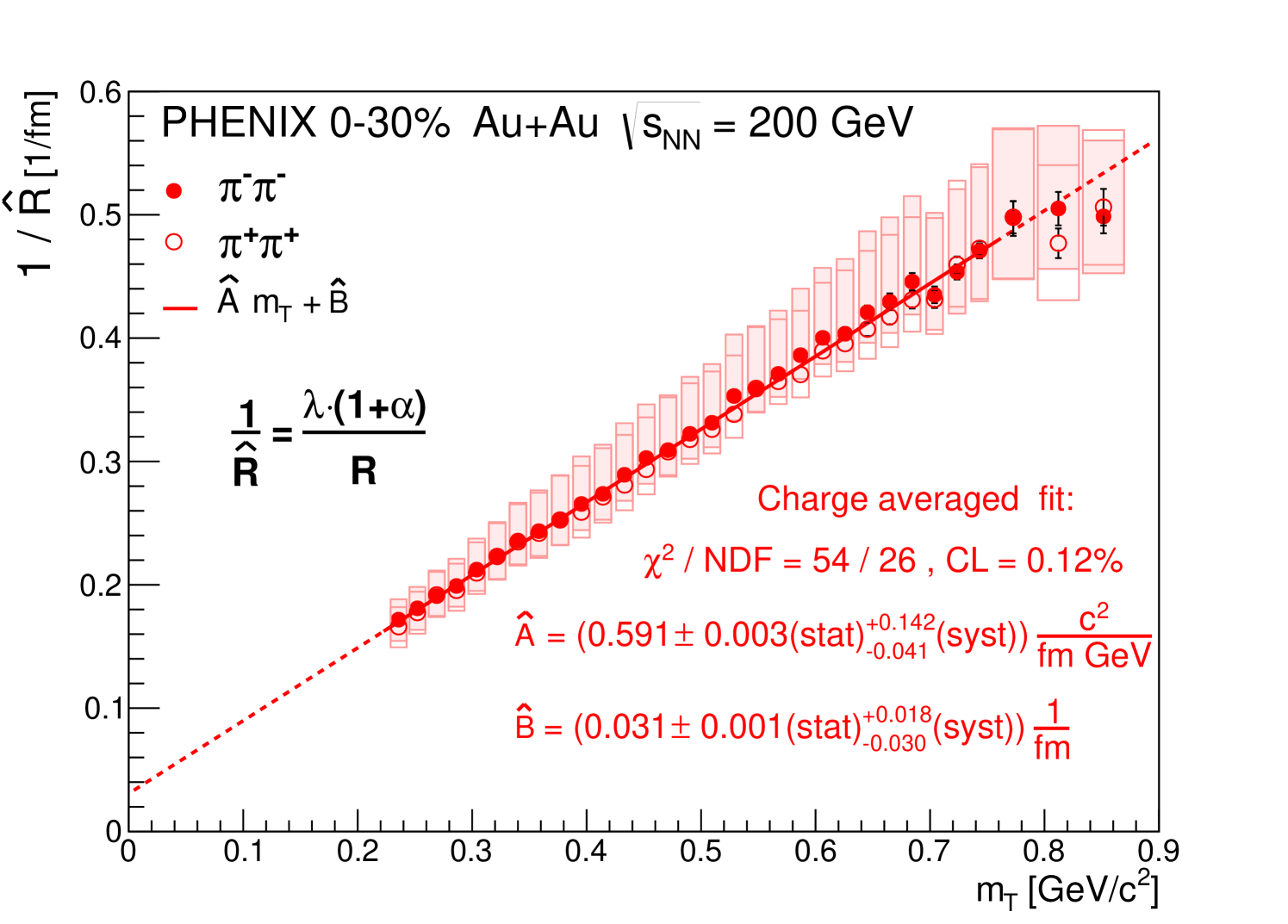
It is interesting to observe that scales linearly with , as shown in Fig. 10. The parameters of the linear fit to the charge averaged data are
| (59) | ||||
| (60) |
Statistical and systematic uncertainties were determined similarly to the fits to versus and versus .
The physical cause and possible interpretation of this remarkable affine linear dependence of (not its square, as in the case of the scale parameter ) on is entirely unknown to us.
One still may try to explain the newly observed scaling of by a simple scaling law for , based on the observation that both and scale linearly with , while is approximately constant. It is important to note however that both of these scalings are affine linear, thus the ratio of the two is not constant. In particular, the linear parameters of Eq. (59) can be converted to a simple dependence of
| (61) |
where then one gets fm and . This, together with the definition of and Eq. (57), yields
| (62) |
This (together with the assumption of being constant in ) would imply that at large transverse masses , however such a scaling is not meaningful, because , representing the fraction of pions contributing to Bose-Einstein correlations, typically cannot increase ad infinitum. In fact our data indicate a saturation of at large values of .
| (GeV) | (fm) | (fm) | |
|---|---|---|---|
| 0.236 | |||
| 0.252 | |||
| 0.269 | |||
| 0.286 | |||
| 0.304 | |||
| 0.322 | |||
| 0.340 | |||
| 0.358 | |||
| 0.377 | |||
| 0.395 | |||
| 0.414 | |||
| 0.433 | |||
| 0.452 | |||
| 0.471 | |||
| 0.490 | |||
| 0.509 | |||
| 0.529 | |||
| 0.548 | |||
| 0.567 | |||
| 0.587 | |||
| 0.606 | |||
| 0.626 | |||
| 0.645 | |||
| 0.665 | |||
| 0.684 | |||
| 0.704 | |||
| 0.724 | |||
| 0.743 | |||
| 0.773 | |||
| 0.812 | |||
| 0.852 |
As discussed in Section IV.1 and seen in Section VI.2, the strength of the correlation functions is not equal to unity, and not even constant as a function of , the reason for which may be the fact that a large fraction of low pions are produced from decays of long-lived resonances (, , , mesons, etc). The detailed shape of may be compared to predictions based on various resonance cocktails, including models that incorporate modified in-medium resonance masses or calculations based on partially coherent pion production.
Earlier measurements or simulations were frequently done within the Gaussian approximation, usually yielding smaller values compared to a Lévy analysis. This can be explained by the anticorrelation between and . If the correlation function has a nonzero slope at , then a Gaussian fit with zero slope at artificially forces to a lower value – such fits do not capture a key feature of the data.
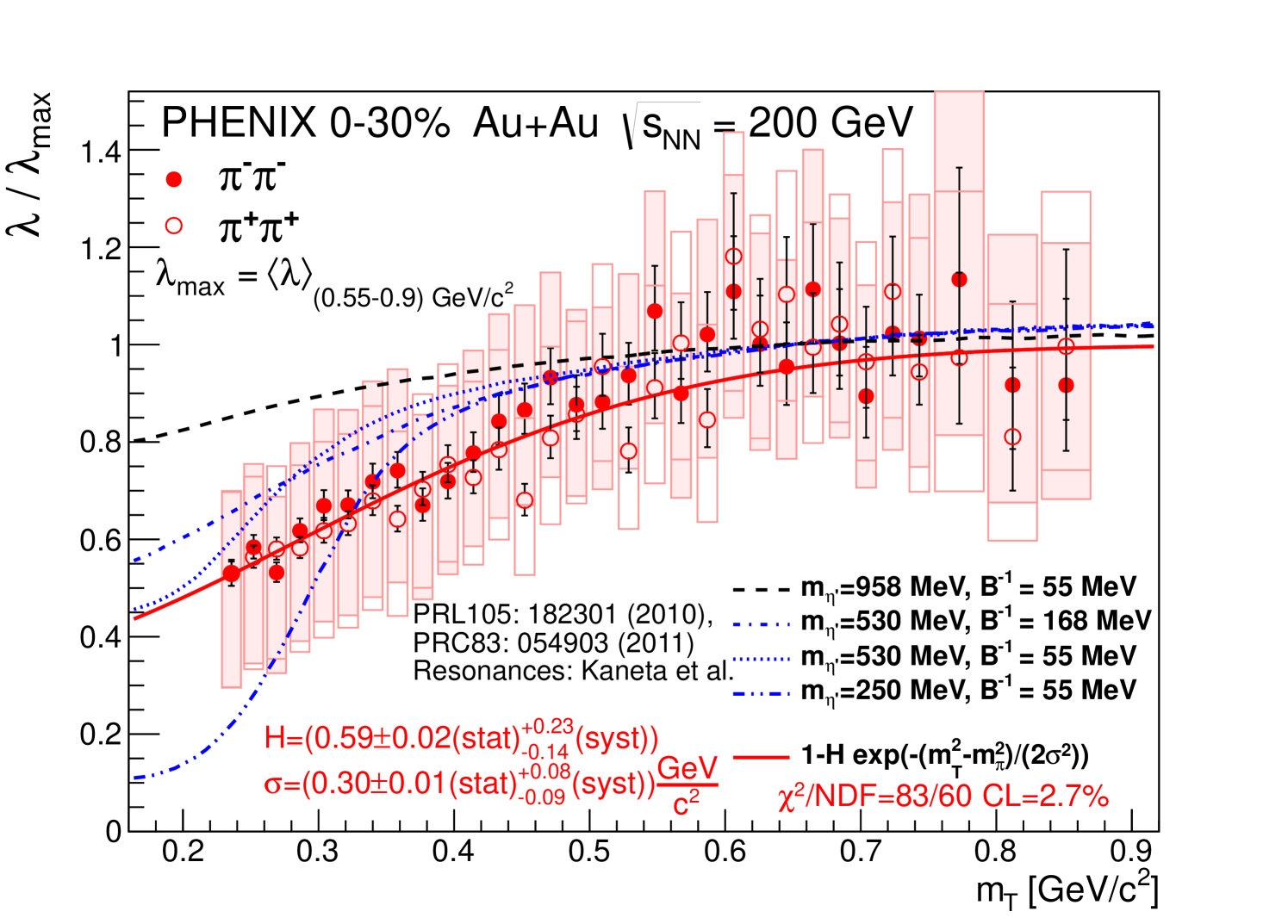
As seen in Fig. 4 appears to increase with until it saturates around GeV. To further study the dependence of on it is advantageous to use the ratio where is the saturated value of , which we determine in the region GeV. This is advantageous for two reasons: (i) the systematic uncertainties largely cancel in the ratio, and (ii) the ratio is less sensitive to the assumed shape of Bose-Einstein correlation functions M. Csanád for the PHENIX Collaboration (2006). Figure 11 shows the resulting dependence on .
To quantify this dependence the distribution is fit with the function
| (63) |
The parameters have a simple meaning. Parameter measures the depth (intercept at i.e. ), while parameter measures the width of the low- region of decrease. The following values of the parameters were determined:
| (64) | ||||
| (65) |
Only the statistical uncertainties of the points were taken into account in the fit. Here the statistical uncertainty of is treated as a normalization uncertainty. This uncertainty and the systematic uncertainty caused by the choice of range when calculating (both 1%) are negligible compared to other uncertainties. The systematic uncertainties of the fit parameters were determined by fitting versus obtained from measurements and fits with varied settings (listed e.g. in Table 3). It is important to note that the values are significantly different from zero, so the existence of the decrease in the data is statistically significant.
Partial coherence effects may suppress the strength of the two-pion Bose-Einstein correlation functions. However, in the model of Ref. Sinyukov and Tolstykh (1994) is not expected to depend on . An dependence given by Eq. (63) was derived in a pion-laser model Pratt (1993); Csörgő and Zimányi (1998). However this model gives an upper limit of given our measured values of and . Measurements of higher order Bose-Einstein correlation functions could shed more light on the contributions of partial coherence.
It has been suggested Vance et al. (1998) that symmetry restoration and its related in-medium mass reduction of the meson in hot, dense hadronic matter would cause a reduction in the value of at low . In Fig. 11, our data are compared with parameter scans from Refs. Vértesi et al. (2011); Csörgő et al. (2010) with the Kaneta-Xu model ratios of long-lived resonances Kaneta and Xu (2004), using different values for the in-medium mass and the condensate temperature (slope parameter) . Our data are seen to be suppressed compared to the prediction with no in-medium mass modification, MeV. Within systematics, our data are not inconsistent with selected parameter scan results of Refs. Vértesi et al. (2011); Csörgő et al. (2010) using a modified in-medium mass. These data thus provide strong new constraints for more detailed theoretical studies on symmetry restoration in hot and dense hadronic matter.
VII Summary and conclusion
In this paper we presented the measurement and analysis of two-pion Bose-Einstein correlations and their Lévy parameters, measured in 0%–30% centrality AuAu collisions at GeV colliding energies in the PHENIX experiment at the RHIC accelerator. After selecting the 2.2 billion 0%–30% centrality events from the 2010 data taking period, and after applying carefully chosen single track and two-track selection cuts, we performed a study of the proper variable and the shape of the two-pion Bose-Einstein correlation function and investigated their transverse mass dependence in 31 bins from 228 to 871 MeV.
We found that these data cannot be well represented by the usual Gaussian Bose-Einstein correlation functions. However, when Gaussian source distributions were generalized to Lévy-stable source distributions, and the final state Coulomb interaction between like-sign pions emitted from Lévy-stable source distributions was properly taken into account, the data could be described at a statistically acceptable level. We determined the dependence of the parameters of Lévy-stable source distributions.
The Lévy exponent was found to be inconsistent not only with the Gaussian case of and the exponential case of , but also with , the conjectured value at the QCD critical point. We have found, that is weakly dependent on the transverse momentum of the pair in 0%–30% centrality AuAu collisions, in qualitative agreement with simulations based on anomalous diffusion in an expanding medium. However, a fit with a constant value of to the data resulted in a statistically unacceptable confidence level.
Even though these values may indicate a nonhydrodynamical component in the pion production processes in GeV AuAu collisions, the bulk of pion production still seems to be of hydrodynamical origin. A hydrodynamical type of scaling behavior is found to represent the measured data remarkably well, especially in the low region. However, we are not aware of theoretical predictions of for Lévy-stable source distributions with .
We found a statistically significant decrease of the intercept parameter at low values of the transverse mass. Our new measurements are not consistent with predictions without in-medium mass modification. Clearly additional measurements are needed in the soft ( MeV) region, including other decay channels of the meson in order to clarify the role of mass modification.
Surprisingly, we also found an unpredicted, empirical new scaling variable that follows an affine linear scaling, which is stable against small variations of the exact value of the Lévy exponent . The origin of this new empirical scaling law is unknown to us.
The methods described in this manuscript demonstrate that it is possible to measure the Lévy exponent of the correlation function in high energy heavy ion reactions. Given that the value of the correlation exponent is expected to reach a specific value in second order phase transitions that is characteristic to the universality class of the given critical point, let us close this paper by proposing similar measurements at various collision energies, centralities, colliding system sizes and identified particle pair types, as well as analyses with two- or three-dimensional momentum difference variables, to improve our detailed understanding of the nature of the particle production in high energy heavy ion reactions, and to search for the vicinity of the critical end point of QCD, where the line of first order quark-hadron transitions in the plane ends, corresponding to a second order phase transition. Finally we emphasize the need for more detailed measurements, including measuring the centrality and collision energy, system size and particle type dependence of the Lévy fit parameters , and .
ACKNOWLEDGMENTS
We thank the staff of the Collider-Accelerator and Physics Departments at Brookhaven National Laboratory and the staff of the other PHENIX participating institutions for their vital contributions. We also thank S. Hegyi for significant theoretical contributions and discussions. We acknowledge support from the Office of Nuclear Physics in the Office of Science of the Department of Energy, the National Science Foundation, Abilene Christian University Research Council, Research Foundation of SUNY, and Dean of the College of Arts and Sciences, Vanderbilt University (U.S.A), Ministry of Education, Culture, Sports, Science, and Technology and the Japan Society for the Promotion of Science (Japan), Conselho Nacional de Desenvolvimento Científico e Tecnológico and Fundação de Amparo à Pesquisa do Estado de São Paulo (Brazil), Natural Science Foundation of China (People’s Republic of China), Croatian Science Foundation and Ministry of Science and Education (Croatia), Ministry of Education, Youth and Sports (Czech Republic), Centre National de la Recherche Scientifique, Commissariat à l’Énergie Atomique, and Institut National de Physique Nucléaire et de Physique des Particules (France), Bundesministerium für Bildung und Forschung, Deutscher Akademischer Austausch Dienst, and Alexander von Humboldt Stiftung (Germany), J. Bolyai Research Scholarship, EFOP, the New National Excellence Program (ÚNKP), NKFIH, and OTKA (Hungary), Department of Atomic Energy and Department of Science and Technology (India), Israel Science Foundation (Israel), Basic Science Research Program through NRF of the Ministry of Education (Korea), Physics Department, Lahore University of Management Sciences (Pakistan), Ministry of Education and Science, Russian Academy of Sciences, Federal Agency of Atomic Energy (Russia), VR and Wallenberg Foundation (Sweden), the U.S. Civilian Research and Development Foundation for the Independent States of the Former Soviet Union, the Hungarian American Enterprise Scholarship Fund, the US-Hungarian Fulbright Foundation, and the US-Israel Binational Science Foundation.
References
- Lednicky (2001) R. Lednicky, “Femtoscopy with unlike particles,” in International Workshop on the Physics of the Quark Gluon Plasma Palaiseau, France, September 4-7, 2001 (2001).
- Hanbury Brown and Twiss (1956) R. Hanbury Brown and R. Q. Twiss, “A Test of a new type of stellar interferometer on Sirius,” Nature 178, 1046 (1956).
- Glauber (1963) R. J. Glauber, “Photon correlations,” Phys. Rev. Lett. 10, 84 (1963).
- Glauber (2006a) R. J. Glauber, “Nobel Lecture: One hundred years of light quanta,” Rev. Mod. Phys. 78, 1267 (2006a).
- Glauber (2006b) R. J. Glauber, “Quantum Optics and Heavy Ion Physics,” Proceedings, 18th International Conference on Ultra-Relativistic Nucleus-Nucleus Collisions (Quark Matter 2005): Budapest, Hungary, August 4-9, 2005, Nucl. Phys. A 774, 3 (2006b).
- Goldhaber et al. (1959) G. Goldhaber, W. B. Fowler, S. Goldhaber, and T. F. Hoang, “Pion-pion correlations in antiproton annihilation events,” Phys. Rev. Lett. 3, 181 (1959).
- Goldhaber et al. (1960) G. Goldhaber, S. Goldhaber, W.-Y. Lee, and A. Pais, “Influence of Bose-Einstein statistics on the anti-proton proton annihilation process,” Phys. Rev. 120, 300 (1960).
- Adcox et al. (2005) K. Adcox et al. (PHENIX Collaboration), “Formation of dense partonic matter in relativistic nucleus-nucleus collisions at RHIC: Experimental evaluation by the PHENIX collaboration,” Nucl. Phys. A 757, 184 (2005).
- Adams et al. (2005a) J. Adams et al. (STAR Collaboration), “Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions,” Nucl. Phys. A 757, 102 (2005a).
- Arsene et al. (2005) I. Arsene et al. (BRAHMS Collaboration), “Quark gluon plasma and color glass condensate at RHIC? The Perspective from the BRAHMS experiment,” Nucl. Phys. A 757, 1 (2005).
- Back et al. (2005) B. B. Back et al., “The PHOBOS perspective on discoveries at RHIC,” Nucl. Phys. A 757, 28 (2005).
- Adler et al. (2004) S. S. Adler et al. (PHENIX Collaboration), “Bose-Einstein correlations of charged pion pairs in Au + Au collisions at 200 GeV,” Phys. Rev. Lett. 93, 152302 (2004).
- Afanasiev et al. (2009) S. Afanasiev et al. (PHENIX Collaboration), “Kaon interferometric probes of space-time evolution in Au+Au collisions at 200 GeV,” Phys. Rev. Lett. 103, 142301 (2009).
- Makhlin and Sinyukov (1988) A. N. Makhlin and Yu. M. Sinyukov, “Hydrodynamics of Hadron Matter Under Pion Interferometric Microscope,” Z. Phys. C 39, 69 (1988).
- Csörgő and Lörstad (1996) T. Csörgő and B. Lörstad, “Bose-Einstein correlations for three-dimensionally expanding, cylindrically symmetric, finite systems,” Phys. Rev. C 54, 1390 (1996).
- Chapman et al. (1995a) S. Chapman, P. Scotto, and U. W. Heinz, “A new cross term in the two particle HBT correlation function,” Phys. Rev. Lett. 74, 4400 (1995a).
- Chapman et al. (1995b) S. Chapman, P. Scotto, and U. W. Heinz, “Model independent features of the two particle correlation function,” Heavy Ion Phys. 1, 1 (1995b).
- Csanád et al. (2004) M. Csanád, T. Csörgő, B. Lörstad, and A. Ster, “Indication of quark deconfinement and evidence for a Hubble flow in 130-GeV and 200-GeV Au+Au collisions,” Ultra-relativistic nucleus-nucleus collisions. Proceedings, 17th International Conference, Quark Matter 2004, Oakland, USA, January 11-17, 2004, J. Phys. G 30, S1079 (2004).
- Bekele et al. (2007) S. Bekele et al., “Status and Promise of Particle Interferometry in Heavy-Ion Collisions,” Braz. J. Phys. 37, 31 (2007).
- Lisa and Pratt (2008) M. A. Lisa and S. Pratt, “Femtoscopically Probing the Freeze-out Configuration in Heavy Ion Collisions,” (2008), arXiv:0811.1352.
- Pratt (2009) S. Pratt, “Resolving the HBT Puzzle in Relativistic Heavy Ion Collision,” Phys. Rev. Lett. 102, 232301 (2009).
- Heinz (2010) U. W. Heinz, “Early collective expansion: Relativistic hydrodynamics and the transport properties of QCD matter,” in Landolt-Börnstein- Group I Elementary Particles, Nuclei and Atoms 23 (Relativistic Heavy Ion Physics), edited by R. Stock (Springer-Verlag Berlin Heidelberg, 2010) Chap. Primordial Bulk Plasma Dynamics in Nuclear Collisions at RHIC.
- Bożek (2012) P. Bożek, “Flow and interferometry in 3+1 dimensional viscous hydrodynamics,” Phys. Rev. C 85, 034901 (2012).
- Boal et al. (1990) D. H. Boal, C. K. Gelbke, and B. K. Jennings, “Intensity interferometry in subatomic physics,” Rev. Mod. Phys. 62, 553 (1990).
- Weiner (2000) R. M. Weiner, “Boson interferometry in high-energy physics,” Phys. Rept. 327, 249 (2000).
- Wiedemann and Heinz (1999) U. A. Wiedemann and U. W. Heinz, “Particle interferometry for relativistic heavy ion collisions,” Phys. Rept. 319, 145 (1999).
- Csörgő (2002) T. Csörgő, “Particle interferometry from 40-MeV to 40-TeV,” NATO Advanced Study Institute on Particle Production Spanning MeV and TeV Energies (Nijmegen 99) Nijmegen, Netherlands, August 8-20, 1999, Heavy Ion Phys. 15, 1 (2002).
- Lisa et al. (2005) M. A. Lisa, S. Pratt, R. Soltz, and U. Wiedemann, “Femtoscopy in relativistic heavy ion collisions,” Ann. Rev. Nucl. Part. Sci. 55, 357 (2005).
- Tannenbaum (2006) M. J. Tannenbaum, “Recent results in relativistic heavy ion collisions: From ’a new state of matter’ to ’the perfect fluid’,” Rept. Prog. Phys. 69, 2005 (2006).
- A. Kisiel, for the ALICE Collaboration (2011) A. Kisiel, for the ALICE Collaboration, “Overview of the femtoscopy studies in Pb Pb and p p collisions at the LHC by the ALICE experiment,” Proceedings, 7th Workshop on Particle Correlations and Femtoscopy (WPCF 2011): Tokyo, Japan, September 20-24, 2011, PoS WPCF2011, 003 (2011).
- Heinz and Snellings (2013) U. Heinz and R. Snellings, “Collective flow and viscosity in relativistic heavy-ion collisions,” Ann. Rev. Nucl. Part. Sci. 63, 123 (2013).
- Adamczyk et al. (2015) L. Adamczyk et al. (STAR Collaboration), “Beam-energy-dependent two-pion interferometry and the freeze-out eccentricity of pions measured in heavy ion collisions at the STAR detector,” Phys. Rev. C 92, 014904 (2015).
- Achard et al. (2011) P. Achard et al. (L3 Collaboration), “Test of the -Model of Bose-Einstein Correlations and Reconstruction of the Source Function in Hadronic Z-boson Decay at LEP,” Eur. Phys. J. C 71, 1648 (2011).
- Khachatryan et al. (2011) V. Khachatryan et al. (CMS Collaboration), “Measurement of Bose-Einstein Correlations in Collisions at and 7 TeV,” JHEP 05, 029 (2011).
- F. Siklér, for the CMS Collaboration (2014) F. Siklér, for the CMS Collaboration, “Femtoscopy with identified hadrons in pp, pPb, and peripheral PbPb collisions in CMS,” (2014), arXiv:1411.6609.
- Astalos (2015) R. Astalos, Bose-Einstein correlations in 7 TeV proton-proton collisions in the ATLAS experiment, Ph.D. thesis, Radboud University (2015).
- Bolz et al. (1993) J. Bolz, U. Ornik, M. Plümer, B. R. Schlei, and R. M. Weiner, “Resonance decays and partial coherence in Bose-Einstein correlations,” Phys. Rev. D 47, 3860 (1993).
- Csörgő et al. (1996) T. Csörgő, B. Lörstad, and J. Zimányi, “Bose-Einstein correlations for systems with large halo,” Z. Phys. C 71, 491 (1996).
- Csörgő et al. (2005) T. Csörgő, S. Hegyi, T. Novák, and W. A. Zajc, “Bose-Einstein or HBT correlations and the anomalous dimension of QCD,” Proceedings, 34th International Symposium on Multiparticle dynamics (ISMD 2004): Rohnert Park, USA, July 26-August 1, 2004, Acta Phys. Polon. B 36, 329 (2005).
- Csörgő et al. (2004) T. Csörgő, S. Hegyi, and W. A. Zajc, “Bose-Einstein correlations for Lévy stable source distributions,” Eur. Phys. J. C 36, 67 (2004).
- Metzler et al. (1999) R. Metzler, E. Barkai, and J. Klafter, “Anomalous Diffusion and Relaxation Close to Thermal Equilibrium: A Fractional Fokker-Planck Equation Approach,” Phys. Rev. Lett. 82, 3563 (1999).
- Adcox et al. (2003a) K. Adcox et al. (PHENIX Collaboration), “PHENIX detector overview,” Nucl. Instrum. Methods Phys. Res., Sec. A 499, 469 (2003a).
- Adare et al. (2013) A. Adare et al. (PHENIX Collaboration), “Spectra and ratios of identified particles in Au+Au and +Au collisions at GeV,” Phys. Rev. C 88, 024906 (2013).
- Adcox et al. (2003b) K. Adcox et al. (PHENIX Collaboration), “PHENIX central arm tracking detectors,” Nucl. Instrum. Methods Phys. Res., Sec. A 499, 489 (2003b).
- Anderson et al. (2011) W. Anderson et al., “Design, Construction, Operation and Performance of a Hadron Blind Detector for the PHENIX Experiment,” Nucl. Instrum. Methods Phys. Res., Sec. A 646, 35 (2011).
- Adare et al. (2012) A. Adare et al. (PHENIX Collaboration), “Deviation from quark-number scaling of the anisotropy parameter of pions, kaons, and protons in Au+Au collisions at GeV,” Phys. Rev. C 85, 064914 (2012).
- Aizawa et al. (2003) M. Aizawa et al. (PHENIX Collaboration), “PHENIX central arm particle ID detectors,” Nucl. Instrum. Methods Phys. Res., Sec. A 499, 508 (2003).
- Adare et al. (2016) A. Adare et al. (PHENIX Collaboration), “Dielectron production in AuAu collisions at =200 GeV,” Phys. Rev. C 93, 014904 (2016).
- Yano and Koonin (1978) F. B. Yano and S. E. Koonin, “Determining Pion Source Parameters in Relativistic Heavy Ion Collisions,” Phys. Lett. B 78, 556 (1978).
- Pratt et al. (1990) S. Pratt, T. Csörgő, and J. Zimányi, “Detailed predictions for two pion correlations in ultrarelativistic heavy ion collisions,” Phys. Rev. C 42, 2646 (1990).
- Pratt (1986) S. Pratt, “Coherence and Coulomb Effects on Pion Interferometry,” Phys. Rev. D 33, 72 (1986).
- Bertsch et al. (1988) G. Bertsch, M. Gong, and M. Tohyama, “Pion Interferometry in Ultrarelativistic Heavy Ion Collisions,” Phys. Rev. C 37, 1896 (1988).
- Adams et al. (2005b) J. Adams et al. (STAR Collaboration), “Pion interferometry in Au+Au collisions at 200 GeV,” Phys. Rev. C 71, 044906 (2005b).
- Afanasiev et al. (2008) S. Afanasiev et al. (PHENIX Collaboration), “Source breakup dynamics in Au+Au Collisions at 200 GeV via three-dimensional two-pion source imaging,” Phys. Rev. Lett. 100, 232301 (2008).
- Novák et al. (2016) T. Novák, T. Csörgő, H. C. Eggers, and M. de Kock, “Model independent analysis of nearly Lévy correlations,” Proceedings, 11th Workshop on Particle Correlations and Femtoscopy and NICA Days 2015 (WPCF 2015): Warsaw, Poland,November 3-7, 2015, Acta Phys. Polon. Supp. 9, 289 (2016).
- Kapusta et al. (1996) J. I. Kapusta, D. Kharzeev, and L. D. McLerran, “The return of the prodigal Goldstone boson,” Phys. Rev. D 53, 5028 (1996).
- Vance et al. (1998) S. E. Vance, T. Csörgő, and D. Kharzeev, “Partial U(A)(1) restoration from Bose-Einstein correlations,” Phys. Rev. Lett. 81, 2205 (1998).
- Csörgő et al. (2010) T. Csörgő, R. Vértesi, and J. Sziklai, “Indirect observation of an in-medium ’ mass reduction in GeV Au+Au collisions,” Phys. Rev. Lett. 105, 182301 (2010).
- Vértesi et al. (2011) R. Vértesi, T. Csörgő, and J. Sziklai, “Significant in-medium ’ mass reduction in GeV Au+Au collisions at the BNL Relativistic Heavy Ion Collider,” Phys. Rev. C 83, 054903 (2011).
- Adam et al. (2016) J. Adam et al. (ALICE Collaboration), “Multipion Bose-Einstein correlations in p p, p Pb, and Pb Pb collisions at energies available at the CERN Large Hadron Collider,” Phys. Rev. C 93, 054908 (2016).
- Adler et al. (2007) S. S. Adler et al. (PHENIX Collaboration), “Evidence for a long-range component in the pion emission source in Au + Au collisions at GeV,” Phys. Rev. Lett. 98, 132301 (2007).
- Csörgő (2008) T. Csörgő, “Correlation Probes of a QCD Critical Point,” High-p(T) physics at LHC. Proceedings, 3rd International Workshop, HIGH-pTLHC, Tokaj, Hungary, March 16-19, 2008, PoS HIGH-PTLHC08, 027 (2008).
- Aoki et al. (2006) Y. Aoki, G. Endrődi, Z. Fodor, S. D. Katz, and K. K. Szabó, “The order of the quantum chromodynamics transition predicted by the standard model of particle physics,” Nature 443, 675 (2006).
- Bhattacharya et al. (2014) T. Bhattacharya et al., “QCD Phase Transition with Chiral Quarks and Physical Quark Masses,” Phys. Rev. Lett. 113, 082001 (2014).
- Soltz et al. (2015) R. A. Soltz, C. DeTar, F. Karsch, S. Mukherjee, and P. Vranas, “Lattice QCD Thermodynamics with Physical Quark Masses,” Ann. Rev. Nucl. Part. Sci. 65, 379 (2015).
- El-Showk et al. (2014) S. El-Showk, M. F. Paulos, D. Poland, S. Rychkov, D. Simmons-Duffin, and A. Vichi, “Solving the 3d Ising Model with the Conformal Bootstrap II. c-Minimization and Precise Critical Exponents,” J. Stat. Phys. 157, 869 (2014).
- Rieger (1995) H. Rieger, “Critical behavior of the three-dimensional random-field Ising model: Two-exponent scaling and discontinuous transition,” Phys. Rev. B 52, 6659 (1995).
- Halasz et al. (1998) M. A. Halasz, A. D. Jackson, R. E. Shrock, M. A. Stephanov, and J. J. M. Verbaarschot, “On the phase diagram of QCD,” Phys. Rev. D 58, 096007 (1998).
- Stephanov et al. (1998) M. A. Stephanov, K. Rajagopal, and Edward V. Shuryak, “Signatures of the tricritical point in QCD,” Phys. Rev. Lett. 81, 4816 (1998).
- Sinyukov et al. (1998) Yu. Sinyukov, R. Lednicky, S. V. Akkelin, J. Pluta, and B. Erazmus, “Coulomb corrections for interferometry analysis of expanding hadron systems,” Phys. Lett. B 432, 248 (1998).
- Bowler (1991) M. G. Bowler, “Coulomb corrections to Bose-Einstein correlations have been greatly exaggerated,” Phys. Lett. B 270, 69 (1991).
- Boggild et al. (1995) H. Boggild et al. (NA44 Collaboration), “Directional dependence of the pion source in high-energy heavy ion collisions,” Phys. Lett. B 349, 386 (1995).
- Zajc (1982) W. A. Zajc, Two pion correlations in heavy ion collisions, Ph.D. thesis, LBL, Berkeley (1982).
- James and Roos (1975) F. James and M. Roos, “Minuit: A System for Function Minimization and Analysis of the Parameter Errors and Correlations,” Comput. Phys. Commun. 10, 343 (1975).
- Csörgő (2009) T. Csörgő, “Critical Opalescence: An Optical Signature for a QCD Critical Point,” Proceedings, 5th International Workshop on Critical point and onset of deconfinement (CPOD 2009): Upton, USA, June 8-12, 2009, PoS CPOD2009, 035 (2009).
- Akkelin and Sinyukov (1996) S. V. Akkelin and Yu. M. Sinyukov, “The HBT-interferometry of expanding inhomogeneous sources,” Z. Phys. C 72, 501 (1996).
- Akkelin and Sinyukov (1995) S. V. Akkelin and Yu. M. Sinyukov, “The HBT interferometry of expanding sources,” Phys. Lett. B 356, 525 (1995).
- Csörgő et al. (1994) T. Csörgő, B. Lörstad, and J. Zimányi, “Quantum statistical correlations for slowly expanding systems,” Phys. Lett. B 338, 134 (1994).
- Csizmadia et al. (1998) P. Csizmadia, T. Csörgő, and B. Lukács, “New analytic solutions of the nonrelativistic hydrodynamical equations,” Phys. Lett. B 443, 21 (1998).
- Csanád and Vargyas (2010) M. Csanád and M. Vargyas, “Observables from a solution of 1+3 dimensional relativistic hydrodynamics,” Eur. Phys. J. A 44, 473 (2010).
- Csörgő (2001) T. Csörgő, “Particle interferometry, binary sources and oscillations in two particle correlations,” Multiparticle production: New frontiers in soft physics and correlations on the threshold of the third millennium. Proceedings, 9th International Workshop, Torino, Italy, June 12-17, 2000, Nucl. Phys. Proc. Suppl. 92, 223 (2001).
- Akiba et al. (1993) Y. Akiba et al. (E-802 Collaboration), “Bose-Einstein correlation of kaons in Si + Au collisions at 14.6-A/GeV/c,” Phys. Rev. Lett. 70, 1057 (1993).
- Csanád et al. (2007) M. Csanád, T. Csörgő, and M. Nagy, “Anomalous diffusion of pions at RHIC,” Particle correlations and femtoscopy. Proceedings, 2nd Workshop, WPCF 2006, Sao Paulo, Brazil, September 9-11, 2006, Braz. J. Phys. 37, 1002 (2007).
- Zajc (1993) W. A. Zajc, “A pedestrian’s guide to interferometry,” NATO Advanced Study Institute on Particle Production in Highly Excited Matter Castelvecchio Pascoli, Italy, July 12-24, 1992, NATO Sci. Ser. B 303, 435 (1993).
- M. Csanád for the PHENIX Collaboration (2006) M. Csanád for the PHENIX Collaboration, “Measurement and analysis of two- and three-particle correlations,” Nucl. Phys. A 774, 611 (2006).
- Sinyukov and Tolstykh (1994) Yu. M. Sinyukov and Y. Yu. Tolstykh, “Coherence influence on the Bose-Einstein correlations,” Z. Phys. C 61, 593 (1994).
- Pratt (1993) S. Pratt, “Pion lasers from high-energy collisions,” Phys. Lett. B 301, 159 (1993).
- Csörgő and Zimányi (1998) T. Csörgő and J. Zimányi, “Analytic solution of the pion- laser model,” Phys. Rev. Lett. 80, 916 (1998).
- Kaneta and Xu (2004) M. Kaneta and N. Xu, “Centrality dependence of chemical freeze-out in Au+Au collisions at RHIC,” in Write-up of a poster presented at the 17th International Conference on Ultra-relativistic Nucleus-Nucleus Collisions, Oakland, USA (2004).