^†^†footnotetext: English title: Teaching of mathematics through classical problems.

M simdh nia e matematik s n p rmjet problemeve klasike

Bedri Shaska 48619 Stoneridge Dr
Northville, MI 48168 bshaska@risat.org and Tanush Shaska Department of Mathematics and Statistics
Oakland University
368 Mathematics Science Center
Rochester MI 48309-4479 shaska@oakland.edu Kushtuar ish-student ve tan t t gjitha moshave.

Abstract.

N k t artikull ne trajtojm se si m simdh nia e matematik s n shkollat 9-vje are dhe t mesme mund t p rmir sohet n m nyr t ndjeshme kur motivimi i koncepteve dhe ideve b het n p rmjet problemeve klasike dhe historis s matematik s. Kjo p rmir son intuit n e student ve, zgjon kuriozitetin e tyre, shmang m simin p rmend sh t formulave t panevojshme, dhe i vendos konceptet n k ndv shtrimin e duhur historik.

Abstract.

In this paper we discuss how teaching of mathematics for middle school and high school students can be improved dramatically when motivation of concepts and ideas is done through the classical problems and the history of mathematics. This improves the intuition of students, awakens their curiosity, avoids memorizing useless formulas, and put concepts in a historical prospective.

PII:

ISSN: 1930-1235; (2016)

The first author taught mathematics in middle school and high school in Albania during the period 1960-1995. In 1996, he was awarded the medal "M sues i popullit" from the President of Albania for his services in teaching, the highest award awarded in teaching in Albania.

Mathematics Subject Classes 2010: 94B05; 97A30; 97C70; 97D40

Keywords: mathematics education; teaching methods; mathematics curriculum

1. Hyrje

Programet m simore t matematik s gjithmon kan shkaktuar diskutime jo vet m mbi p rmbajtjen e tyre, por edhe mbi k ndv shtrimin pedagogjik, psikollogjik, dhe filozofik q duhet t ken programe t tilla. Diskutime k to q kan ndodhur jo vet m n vendin ton , por n gjith vendet e tjera. Pikat kryesore t diskutimit jan t nj jta pothuajse n gjith vendet e bot s dhe p rmblidhen n p rgjigjen e pyetjes q vijon: Cili sht q llimi apo objektivi i programit t matematik s n arsimin 12-vje ar?

Pyetja kjo q ka p rgjigje t ndryshme t cilat varen kryesisht nga politikat arsimore t do vendi. Pak a shum p rgjigjet p rmblidhen si m posht :

•

T pregatis nx n s me nj formim t p rgjithsh m matematik p r t p rballuar me sukses sfidat e jet s. K tu futet kryesisht grupi i nx n sve p r t cil t njohurit matematike nuk p rb jn baz n e profesionit t tyre.
•

T pregatis nx n s me nj formimin e nevojsh m matematik p r student t e shkencave dhe inxhinjerive. K tu futet kryesisht grupi i nx n sve p r t cil t njohurit matematike do t jen baza e profesionit t tyre.
•

T pregatis matematikan t e ardhsh m apo m suesit e ardhsh m t matematik s.

Zakonisht sisteme t ndryshme arsimore p rpiqen q t realizojn t tre k to objektiva, pavar sisht se metodat dhe rruga ndryshon sipas vendeve t ndryshme. Duhet theksuar se tashm edhe tek profesionet ku roli i matematik s konsiderohej minimal si shkencat shoq rore, mjek sore,juridike, roli i matematik s n dekadat e fundit është rritur n m nyr t konsiderueshme fal rolit t statistik s, "big data", aplikimeve t matematik s n mjek si, n shkencat biologjike, etj.

Nga ana pedagogjike diskutimi kryesor sht se cila sht rruga m e mir p r t realizuar k to objektiva? N k t artikull modest, ne do t p rpiqemi t sygjerojm disa ide se si t rrisim efektivitetin e m simdh nies n or n e matematik s.

Ideja kryesore e k tij artikulli është q m simdh nia e matematik s duhet t b het n p rmjet problemeve klasike q kan zhvilluar matematik n si shkenc dhe historia e zhvillimit t matematik s duhet t jet pjes e m simdh nies. Kjo i jep matematik s jet n klas dhe e b n t jet di ka m shum se nj grup formulash t thata. P r m tep r kjo motivon konceptet baz dhe u jep nx n sve nj arsye m shum p rse k to koncepte jan t rend sishme dhe duhen m suar.

N pro esin e studimit t literatur s s k tij artikulli ne zbuluam nj sasi t konsiderueshme artikujsh t tjer q kan m shtetur k t ide. M i njohuri dhe m i p rkushtuari pas k saj ideje është Felix Klein n [MR0076336, MR0015349, MR0055397, MR0080930, MR549187, MR2098410, MR3495524, MR3495525]. Filozofia e Klein ka dominuar pedagogjin e matematik s n fillimet e shekullit t XX, megjith se mund t themi se implementimi i k saj filozofie n mas l shum p r t d shiruar. K to sh nime jan organizuar si m posht :

N Kreun 2, ne japim nj p rshkrim t shkurt r t disa problemeve dhe koncepteve ku nj m sues i talentuar mund t zgjerohet m shum n program dhe si pasoj t ler nj mbres t thell n formimin matematik t nx n sve. Ne nuk pretendojm se lista e problemeve q ne sygjerojm është e plot , Nj list e till mund t plot sohet m tep r duket pasur parasysh eksperiencat individuale t secilit m sues dhe grupin e nx n sve.

N Kreun 3 ne diskutojm rolin kritik dhe konstruktiv t historis s shkenc s n formimin e student ve t matematik s. Ky rol duhet t jet i ingranuar me programin. Ne duhet t p rpiqemi t’u shpjegojm nx n sve jo vet m teorit q i mbijetuan koh s, por edhe p rpjekjet e d shtuara pasi nga k to d shtime n shumic n e rasteve m sohet shum .

N Kreun 4 ne p rq ndrohemi tek problemi m klasik dhe m themelor i matematik s, ai i zgjidhjes s ekuacioneve polinomiale. Pjesa kryesore e matematik s mund t lidhet me k t tem . Pik risht algjebra, gjeometria, gjeometria algjebrike, nj pjes e mir e analiz s, kriptografia, teoria e kodeve, etj i kan themelet e tyre tek polinomet ose zgjidhja e ekuacioneve polinomiale ose si quhen ndryshe ekuacione algjebrike. Si mund t trajtohet kjo tem n kontekstin e duhur historik duke i m suar nx n sit jo thjesht formul n e zgjidhjes s ekuacionit kuadratik, por edhe diskriminantin, polinomet simetrike, teorin Galua, format binare, algjebr n lineare, teorin e invariant ve, serit e Taylor, varietetet algjebrike, kurbat eliptike dhe hipereliptike e shum koncepte t tjera t matematik s bashk kohore?

N Kreun 5 ne trajtojm konceptin e diskriminantit nga nj k ndv shtrim intuitiv dhe historik. Esht ndoshta shembulli m i mir q nj koncept kaq intuitiv është kthyer nga programet m simore ne nj koncept t that dhe n nj formul q shumica e nx n sve dhe m suesve nuk ja kuptojn vler n. Duhet pranuar se ky nuk është vet m problem i shkollave tona. Shumica e student ve t matematik s m sojn p r diskriminantin n algjebr n e lart dhe edhe at her thjesht formulat baz dhe asgj m shum . Cila është lidhja e diskriminantit t nj polinomi dhe determinantit (ose p rcaktorit) t nj matrice, kur filluan k to dy koncepte t ndaheshin nga njeri-tjetri n historin e matematik s?

Format binare trajtohen n Kreun 6. Koncepti i formave sht nj nga konceptet baz t matematik s q ka luajtuar dhe vazhdon t luaj nj rol t r nd sish m n matematik , por q udit risht trajtohet shum pak n programet e matematik s s shkoll s s mesme. Ne trajtojm vet m format kuadratike megjith se me fare pak p rpjekje gjith teoria mund t trajtohet p r gjith format me grad $n\geq 2$ . Edhe vet m me format kuadratike ne mund t ngrem nj teori t t r dhe t drejtojm nx n sin tek koncepte fondamentale t matematik s si hap sirat vektoriale, veprimi i nj grupi mbi nj bashk si, ndryshimi i koordinatave, teoria e invariant ve dhe puna kolosale e matematikan ve te shekullit t XIX si Clebsch, Gordan, Bolza, Hilbert, etj.

Format kuadratike mund t hapin edhe horizonte t tjera si teorin e reduktimit (shih Beshaj [MR3579531]), bashk sit Julia [MR3532882], gjeometrin hiperbolike, etj. Ne zhvillojm aq teori n Kreun 6 sa t klasifikojm gjith prerjet konike dhe sip rfaqet quadratike. Q kjo t realizohet sakt ne duhet t prezantojm nx n sit me matricat, eigenvlerat dhe eigenvektor t, procesin e diagonalizimit t nj matrice, gjetjen e baz s ortonormale t eigenhap sirave. Ky është nj kurs i plot i algjebr s lineare i cili vjen si nj aplikim i nj ushtrimi n dukje elementar atij t klasifikimit t prerjeve konike. N t v rtet kjo është edhe ana historike se si k to koncepte jan zhvilluar. Kush i m son k to koncepte pa kuptuar motivimin e tyre historik duhet t ndihet sikur ka par nj film q nuk e kuptoi dot kurr .

N Kreun 7 ne studiojm nd rtimet gjeometrike. Nd rtimet gjeometrike jan probleme klasike q mund t implementohen me sukses q n klasat e 5-ta dhe t 6-ta. Nga nd rtimet gjeometrike mund t zhvillohet koncepti i fush s dhe shtrirjes algjebrike. Ne japim nj p rshkrim t shkurt r t nd rtimeve algjebrike dhe v rtetimin e rezultateve kryesore. Ne supozojm se lexuesi ka njohuri mbi fushat t krahasueshme me nivelin e [alg].

Ja vlen t p rmendet se edhe nj program ideal nuk do t funksiononte n se efektivi m simdh n s nuk sht n gjendje t kuptoj dhe implementoj me sukses k to koncepte intuitive. Pik risht p r k t , formimi i nj plejade matematikan sh me koncepte t qarta sht m se i nevojsh m.

Ne japim nj sasi t konsiderueshme t literatur s, sidomos t disa botimeve t fundme n gjuh n Shqipe ku disa nga k to tema trajtohen n detaje [alg, kalk, lin-alg]. Duke mos pretenduar se kjo është fjala e fundit p r m simdh nien e matematik s, ne shpresojm q m suesit e matematik s do ti gjejn k to ide nj ndihm n profesion e tyre t v shtir .

2. Nj v shtrim i shkurt r mbi disa probleme t ve anta n programin e matematik s

Njer z t ndrysh m kan perceptime t ndryshme mbi nivelin a nx n sve tan sidomos para vitit 1990. Pjesa m e madhe me t drejt mendojn se nx n sit tan ishin t pregatitur mjaft mir nga ana matematike. Nga ana tjeter nuk mund t mos mohohet se programi i matematik s ka pasur dhe vazhdon t ket probleme t shumta. Ajo ka vihet re nga nx n sit shqiptar q shkojn me studime jasht shtetit sht se n shumic n e rasteve ata jan t pregatiur n m nyr t pranueshme nga shkollat tona. Ajo far nuk kuptohet nga shumica e njer zve sht se nx n sit shqiptar k t e kan arritur me nj pun t jasht zakonshme, se avantazhi m i madh i tyre karshi student ve t tjer ka qen pik risht disiplina n pun . Duke i shtuar k saj edhe njohurit e p rfituara nga nj sistem ku shkohej n shkoll gjasht dit n jav , ku b hej matematik do dit p r 12 vjet me rradh , at her nx n si i mir i dal nga shkollat tona kishte nj avantazh t madh me shumic n e bashk moshatar ve te vet nga vendet e tjera.

Para shum vjet sh nj nx n s i vitit t tret t nj prej gjimnazeve t Vlor s, i b ri k t pyetje nj rit prej autor ve t k tij artikulli: Profesor, m kan th n q shkolla n Amerik sht m e leht se n Shqip ri. Esht e v rtet ?

Ka di ka me substanc n k t pyetje. Natyrisht ne po shohim p rtej faktit q nx n s t shk lqyer tan t shkojn n shkolla mesatare n Amerik apo vende t tjera. A jan programet e matematik s apo tekstet q p rdoren m t thjeshta p r nx n sin n vendet e tjera? A mund t p rmir sohen programet tona q m simdh nia e matematik s t b het m efi ente? P rgjigja është "po". P r nx n sin e mir shkolla është m e leht n Amerik , sepse ka programe solide, tekste t shk lqyera dhe pedagog q kuptojn jo vet m subjektin q japin, por edhe shum m tej.

M posht po japim disa shembuj konkret ku disa koncepte mund t trajtoheshin m mira n programin e matematik s.

Problem 1.

Gjeni bashk sin e p rcaktimit t funksionit

f(x)=\frac{1}{\sqrt{x^{2}-4}}

Shumica e nx n sve tan t vitit IV, do ta b jn pa v shtir si k t ushtrim, por problemi q ndron diku tjet r. far sht bashk sia e p rcaktimit? Ne p rdorim termin p rkufizim dhe jo p rcaktim. Ndryshimi midis dy termave n gjuh n Shqipe sht i qart . At her p rse ky konfuzion n matematik ? Ne i kemi ngjitur nj koncepti fare t qart matematik nj term tep r konfuz. N fakt termi bashk sia e p rkufizimit duhet p rdorur sepse ne p rkufizojm nj funksion nuk e p rcaktojm at .

Vazhdojm me nj shembull nga fizika.

Problem 2.

Nj nga konceptet kryesor n historin e shkenc s eshte koncepti i shpejt sis (ose ajo ka n Anglisht quhet velocity). Natyrisht koncepti i sakt i shpejt sis jepet vet m n p rmjet derivatit.

A e kuptojn nx n sit dhe m suesit tan ndryshimin midis shpejt sis dhe shpejt sis mesatare (n Anglisht velocity dhe speed). N fjal t e nj studente shqiptare q studion n Princeton, - "Ndryshimin e kuptova vet m n Princeton".

A kuptohet nga nx n sit dhe m suesit tan r nd sia historike e p rkufizimit t sakt t shpejt sis (pra t derivatit t funksionit). Ishte pik risht nevoja e p rkufizimit sakt t shpejt sis ajo q detyroi Newtonin s pari t zhvillonte Kalkulusin dhe s dyti t formulonte tre ligjet baz te mekanik s t cilat ishin pik nisja e fizik s dhe e gjith shkenc s moderne.

Shumica e gjuh ve sot kan terma t ve ant p r shpejt sin dhe shpejt sin mesatare, por n tekstet dhe programet tona k to nd rthuren si pa t keq. P r shembull, kur nj m sues i klas s s tret jep problemin:

Nj udh tar shkoi nga Vlora n Fier p r 5 or . Distanca Vlor -Fier sht 35 km. Sa sht shpejt sia?.

Esht e qart se k tu b het fjal p r shpejt sin mesatare dhe jo shpejt sin e astit. Madje n t folur n e p rditshme shumica e p rdorin fjal n shpejt si si shpejt si mesatare. Jan pik risht k to pakujdesi q gjenden kudo n tekstet tona q i bejn gj rat tep r t v shtira p r nx n sit tan .

2.1. Koncepti i dallorit t polinomeve

Vazhdojm me nj shembull tjet r nga matematika e klas s s 10-t . Dallori i polinomeve sht nj nga konceptet themelore t matematik s. N programet tona trajtohet fare cek t. Supozojm se u japin nj grupi nx n sish dhe student sh problemin e m posht m:

Pyetje 1.

Jepet polinomi quadratic

f(x)=ax^{2}+bx+c

P rkufizoni dallorin e $f(x)$ .

Shumica e nx n sve t shkollave t mesme si dhe gjith m sues t e matematik s do t japin p rgjigjen e menj hershme

\Delta=b^{2}-4ac

A sht kjo p rgjigja e sakt ? Shum prej lexuesve do t thon se ’po’. Por n se pyetja sht t p rkufizohet dallori i polinomit t grad s s tret

f(x)=ax^{3}+bx^{2}+cx+d,

at her shumica d rrmuese e nx n sve dhe m suesve nuk do t jen n gjendje t japin nj p rgjigje t sakt . Kjo p rforcohet edhe m shum n se pyesim p r dallorin e nj polinomi t grad s $n\geq 4$ . Pra ’ sht dallori? A e kuptojn nx n sit dhe m suesit tan konceptin e dallorit?

N se n algjebr n e lart jepet problemi q vijon:

Problem 3.

Jepet nj polinom $p(x)$ i grad s $n\geq 2$

p(x)=a_{n}x^{n}+\dots a_{1}x+a_{0}.

P rkufizoni dallorin e këtij polinomi.

A sht gati nx n si t p rgjithsoj konceptin e dallorit t polinomit kuadratik tek nj polinom e grad s $n\geq 2$ ?

Natyrisht, gj ja m e leht nga ana pedagogjike është t flas sh p r zgjidhjen e ekuacionit kuadratik kur $\Delta<0$ . Esht pik risht k tu q n m nyr fare t vazhdueshme mund t prezantohen numrat kompleks dhe jo vet m t prezantohen, por t shpenzohet koh e mjaftueshme me bashk sin e numrave kompleks .

2.2. Nj shembull nga trigonometria, rrethi nj si

Nx n sit tan kan b r trigonometri, n programin para 1990, p r gjith vitin III-t t shkoll s s mesme. Kjo siguronte nj baz solide p r gjith student t e mir . N fakt n shumic n e programeve t matematik s n vendet per ndimore trigonometria b het vet m nj simest r ose nd rthuret n simestra t ndrysh m, por asnj her nuk z koh n ekuivalente me dy simestra. Funksionet trigonometrike jan :

f(x)=\sin x,\quad f(x)=\cos x,\quad f(x)=\tan x,\quad f(x)=\cot x,

N rrethin nj si ato paraqiten si n figur .

Nj problem disi interesant nga klasa e 9-t sht t shpreh sh gjith funksionet trigonometrike si funksione racionale t $\tan\frac{\alpha}{2}$ . Nj k rkes e till i duket disi e uditshme nj nx n si t vitit t III-t .

Problem 4.

Shprehni funksionet $\sin\alpha$ dhe $\cos\alpha$ n var si t funksionit $\tan\frac{\alpha}{2}$ .

Shumica e nx n sve jan n gjendje ta b jn k t ushtrim dhe t v rtetojn formulat e m poshtme:

\sin\alpha=\frac{2\tan\frac{\alpha}{2}}{1+\tan^{2}\frac{\alpha}{2}},\qquad\cos\alpha=\frac{1-\tan^{2}\frac{\alpha}{2}}{1+\tan^{2}\frac{\alpha}{2}}

Historia n programet tona mbyllet k tu, por kjo duhet t ishte vet m fillimi i nj dashurie t bukur midis nx n sit dhe trajetoreve algjebrike.

Ne do t shohim m posht se si nj ushtrim kaq i thjesht mund t p rdoret p r t prezantuar nx n sit me ide dhe koncepte t thella matematike si ai i pikave racionale n trajektoret algjebrike.

Ndoshta nj problem fare i natyrsh m q mund t b hej me leht si n trigonometri ishte koncepti i rrenj ve t nj sis . P r shembull, sa nga nx n sit apo m sues t tan mund ti p rgjigjen sakt pyetje s m poshtme.

Pyetje 2.

Gjeni gjith rr nj t e ekuacionit

x^{3}=1

Koncepti i rr nj ve t nj sis me shum leht si na on tek numrat kompleks , shum zimi i numrave kompleks , grupi i rrethit nj si, dhe grupet ciklik .

2.3. Integrimi i funksioneve racional

Le t supozojm se audienc s son i shtrojm pyetjen:

Pyetje 3.

Jepet funksioni racional

f(x)=\frac{p(x)}{q(x)},

ku $p(x),q(x)$ jan polinome me koeficient real . P rshkruani nj m nyr p r t llogaritur integralin

\int f(x)\;dx

Ndoshta pyetja e m sip rme mund t thjeshtohet n nj pyetje m konkrete,

Shembull 1.

Njehsoni $\int\frac{2x^{2}-x+4}{x^{3}+4x}dx$ .

A sht n gjendje maturanti yn t mbaroj nj ushtrim t till ? P r m tep r sht nj nga klasat m elementare t funksioneve. P r nj trajtim t k saj teme lexuesi mund t lexoj [kalk, Kap. 6].

M posht po japin nj zgjidhje t k tij ushtrimi p r t kuptuar q trajtimi është fare elementar. Meq n se $x^{3}+4x=x(x^{2}+4)$ dhe nuk mund t faktorizohet m tej mbi numrat real , at her ne mund t shkruajm

\frac{2x^{2}-x+4}{x^{3}+4x}=\frac{A}{x}+\frac{Bx+C}{x^{2}+4}

Duke shum zuar t dy an t me $x(x^{2}+4)$ , kemi

2x^{2}-x+4=A(x^{2}+4)+(Bx+C)x=(A+B)x^{2}+Cx+4A

Duke barazuar koefi ent t pran fuqive t nj jta t $x$ , kemi $A=1$ , $B=1$ , dhe $C=-1$ dhe prej k tej

\int\frac{2x^{2}-x+4}{x^{3}+4x}\;dx=\int\left(\frac{1}{x}+\frac{x-1}{x^{2}+4}\right)\;dx

N m nyr q t integrojm termin e dyt , e ndajm at n dy pjes :

\int\frac{x-1}{x^{2}+4}\;dx=\int\frac{x}{x^{2}+4}\;dx-\int\frac{1}{x^{2}+4}

B jm z vend simin $u=x^{2}+4$ n integralin e par t k saj pjese, k shtu q $du=2x\;dx$ dhe p rfundimisht kemi

	$\displaystyle\int\frac{2x^{2}-x+4}{x^{3}+4x}dx$	$\displaystyle=\int\frac{1}{x}dx+\int\frac{x}{x^{2}+4}dx-\int\frac{1}{x^{2}+4}dx$
		$\displaystyle=\ln\|x\|+\frac{1}{2}\ln(x^{2}+4)-\frac{1}{2}\tan^{-1}(x/2)+K$

A mund t p rgjithsohet kjo teknik tek gjith integralet e funksioneve racional ? Cila sht teorema nga ana teorike q kjo metod t funksionoj p r gjith funksionet racional ?

P r udi kjo metod elementare nuk është trajtuar n programet tona megjith se bazohet n nj fakt n dukje elementar, por shum themelor nga ana teorike.

Lemma 1.

do polinom me koefi enta real faktorizohet si prodhim faktor sh linear ose kuadratik .

Arsyeja q kjo lem është e v rtet është sepse fusha e numrave real është invariant n n konjugimin kompleks. Pra nj tjet r rezultat goxha i pafajsh m n dukje por me rend si të madhe teorike.

2.4. Elipsi dhe rrethi

Le t konsiderojm disa ide nga gjeometria. Jepet ekuacioni i nje elipsi

\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1

Pyetje 4.

A mund t gjeni formula p r sip rfaqen dhe perimetrin e k tij elipsi?

Nx n sit e mir padyshim q mund ta zgjidhnin nj ushtrim t till . Duke e zgjidhur k t ekuacion n lidhje me $y$ , ne marrim

\frac{y^{2}}{b^{2}}=1-\frac{x^{2}}{a^{2}}=\frac{a^{2}-x^{2}}{a^{2}}

ose

y=\pm\frac{b}{a}\sqrt{a^{2}-x^{2}}.

Meq elipsi sht simetrik n lidhje me t dy boshtet koordinative, sip rfaqja totale $A$ sht kat rfishi i sip rfaqes s kuadrantit t par .

Pjesa e elipsit n kuadrantin e par jepet nga funksioni

(1)

y=\frac{b}{a}\sqrt{a^{2}-x^{2}}\ \ \ 0\leq x\leq a

dhe k shtu

\frac{1}{4}A=\int_{0}^{a}\frac{b}{a}\sqrt{a^{2}-x^{2}}dx

P r t gjetur k t integral b jm z vend simin

\boxed{x=a\sin t}.

At her $dx=a\cos t\;dt$ . P r t ndryshuar kufijt e integrimit, shohim se kur $x=0$ , $\sin t=0$ , pra $t=0$ nd rsa kur $x=a$ , $\sin t=1$ , pra $t=\pi/2$ . Gjithashtu

\sqrt{a^{2}-x^{2}}=\sqrt{a^{2}-a^{2}\sin^{2}t}=\sqrt{a^{2}\cos^{2}t}=a|\cos t|=a\cos t

meq $0\leq t\leq\pi/2$ . Prej nga,

\begin{split}A&=4\frac{b}{a}\;\int_{0}^{a}\sqrt{a^{2}-x^{2}}\;dx=4\frac{b}{a}\;\int_{0}^{\pi/2}a\cos t\cdot a\cos t\;dt\\ &=4ab\int_{0}^{\pi/2}\cos^{2}t\;dt=4ab\int_{0}^{\pi/2}\frac{1}{2}\left(1+\cos 2t\right)\;dt\\ &=\left.2ab\left[t+\frac{1}{2}\sin 2t\right]\right|_{0}^{\pi/2}=2ab\left(\frac{\pi}{2}+0-0\right)=\pi ab.\\ \end{split}

V rtetuam k shtu se sip rfaqja e elipsit me gjysm boshte $a$ dhe $b$ sht

\boxed{A=\pi ab}

N ve anti kur marrim $a=b=r$ , kemi v rtetuar formul n se sip rfaqja e rrethit me rreze $r$ sht $\pi r^{2}$ .

N nivelin e shkollave tona ku lloj integrali sht e mundur q t b het. Ajo ka sht e vecanta sht se na orienton n dy probleme interesante. S pari, p rgjith simi i z vend simit t m sip rm na on tek z vend simet trigonometrike dhe prej andej tek formulat e integrimit p r

\int\sqrt{a^{2}-x^{2}}\;dx,\quad\int\sqrt{a^{2}+x^{2}}\;dx,\quad\int\sqrt{x^{2}-a^{2}}\;dx

S dyti, gjetja e perimetrit t elipsit na on drejt nj l ndine plot me lule, at t integraleve eliptike.

Gjat sia e grafikut t nj funksioni $y=f(x)$ , $a\leq x\leq b$ jepet nga formula

L=\int_{a}^{b}\sqrt{1+\left[f^{\prime}(x)\right]^{2}}\;dx,

shihni [kalk, Kapitulli 9]. N rastin ton , $f(x)$ jepet ne Eq. (1). Derivati i tij sht

f^{\prime}(x)=\frac{b}{2a}\;\frac{1}{\sqrt{a^{2}-x^{2}}}\;(-2x)=-\frac{b}{a}\,\frac{x}{\sqrt{a^{2}-x^{2}}}

Pra perimetri i elipsit sht

P=4\int_{0}^{a}\sqrt{1+\frac{b^{2}}{a^{2}}\cdot\frac{x^{2}}{a^{2}-x^{2}}}\;dx=4\;\int_{0}^{a}\sqrt{\frac{a^{2}-e^{2}x^{2}}{a^{2}-x^{2}}}

ku $e=\frac{a^{2}-b^{2}}{a^{2}}$ . Duke b r z vend simin

\boxed{x=a\sin t}

lexuesi t v rtetoj se

P=4a\int_{0}^{\frac{\pi}{2}}\sqrt{1-e^{2}\sin^{2}t}\;dt

Ky quhet nj integrali i plot eliptik i llojit t dyt . Prej tij marrin emrin trajektoret eliptike q jan nga objektet mjaft popullore t matematik s. Integralet eliptike ishin edhe pik nisja e pun s s Abelit dhe Jacobit q vazhdoi m pas me Riemann.

Esht p r t ardhur keq q n programet e shkollave t mesme integralet eliptike nuk trajtohen fare. Ato jan t v shtira p r tu zgjidhur, por nj pjes e konsiderueshme e matematik s moderne nisi pik risht nga integrale t tilla si p r shembull funksionet theta [MR3525572], integralet hypereliptike dhe supereliptike, trajektoret hipereliptike dhe supereliptike [MR3525570], etj.

M posht po japim nj tjet r problem n dukje shum af r problemit t m sip rm, por q na on n nj fush tjet r t matematik s.

Pyetje 5.

A mundet qe ky elips t transformohet n nj rreth me nj ndryshim koordinatash t planit? A ndryshojn sip rfaqja dhe perimetri gjat k tij transformimi?

Zgjidhja e k tij problemi është nj mund si p r t prezantuar nx n sit me transformimet lineare dhe matricat ortogonale. Ne flasim pak p r to n vijim.

2.5. Prerjet konike

Kjo ideja e transformimeve na on edhe m thell . Naturisht n se ne transformojm planin n nj sistem tjet r koordinativ, p r shembull origjina shkon tek pika $(2,3)$ , at her ekuacioni i elipsit b het

\frac{(x-2)^{2}}{a^{2}}+\frac{(y-3)^{2}}{b^{2}}=1.

Ekuacion q ndryshe shkruhet

b^{2}x^{2}+a^{2}y^{2}-2b^{2}x-6a^{2}y=a^{2}b^{2}-4b^{2}-9a^{2}

Ne e dim qe ky sht ekuacioni i nj elipsi, edhe pse kjo nuk sht plot sisht e leht t verifikohet.

A mund ta p rgjithsojm k t rast n nj teori m t p rgjithshme. P r shembull, jepet ekuacioni i p rgjithsh m i grad s s dyt

ax^{2}+bxy+cy^{2}+dx+fy+s=0

Pyetje 6.

P r ’vlera t koefi ent ve $a,b,c,d,f,s$ grafiku i m sip rm sht nj rreth, elipse?

Por ndoshta edhe m themelore është pyetja

Pyetje 7.

Jepet ekuacioni i grad s s dyt

(2)

ax^{2}+bxy+cy^{2}+dx+ey=\lambda

far paraqet nj ekuacion i till nga ana grafike? A mund t gjendet nj metod q k saj pyetje t’i jepet p rgjigje thjesht nga koefi ent t $a,b,c,d,e,\lambda$ , pa nd rtuar grafikun?

Nx n si yn e di se grafik t e ekuacineve t tilla jan grafik t e prerjeve konike, pra prerjet e nj koni t dyfisht me nj plan si n figur n m posht .

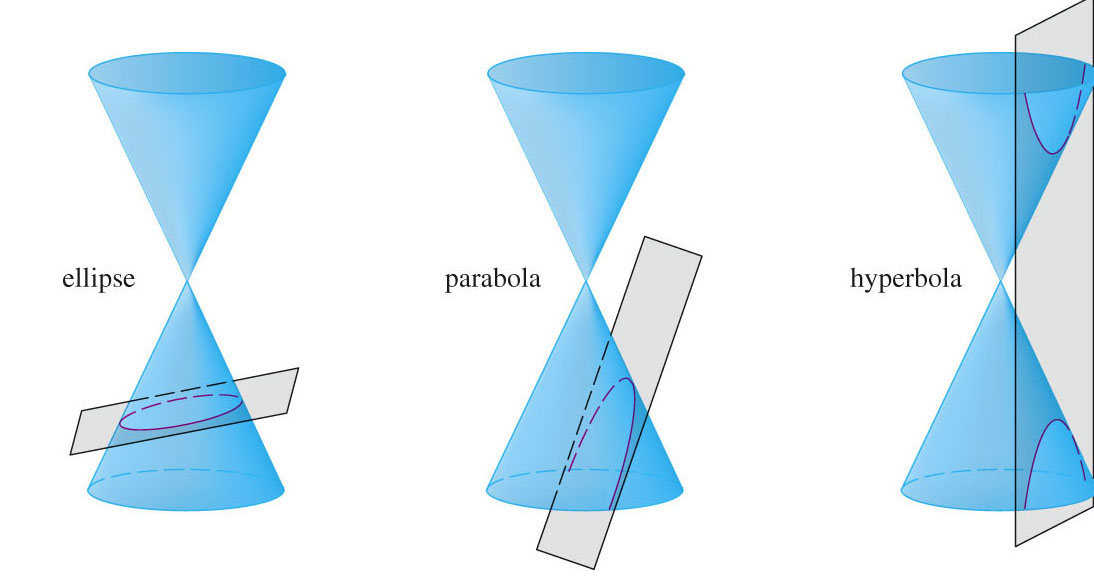
Refer to caption — Figure 1. Prerjet konike

Nx n sit e shkollave tona e din q , elipsi, parabola, dhe hiperbola kan p rkat sisht ekuacione

(3)

\frac{x^{2}}{\lambda_{1}^{2}}+\frac{y^{2}}{\lambda_{2}^{2}}=1,\qquad y^{2}=4\lambda_{1}x,\qquad\frac{x^{2}}{\lambda_{1}^{2}}-\frac{y^{2}}{\lambda_{2}^{2}}=1

p r disa vlera jozero $\lambda_{1},l_{2}$ . Rrethi është rasti i ve ant i elipsit kur $\lambda_{1}=\lambda_{2}$ .

Secili prej k tyre ekuacioneve është shum her m i thjesht se ekuacioni Eq. (2) dhe kjo sepse sistemi koordinativ është zgjedhur n qendr n e rrethit, elipsit, hiperbol s, apo kulmin e parabol s dhe boshtet n m nyr t p rshtatshme. K to ekuacione kan t mir n e madhe q ne e dim form n e grafikut thjesht duke par ekuacionin. At her shtrohet pyetja, e kuptueshme nga do gjimnazist:

Pyetje 8.

Si duhet ndryshuar sistemi yne koordinativ q ekuacioni (2) t transformohet n nj nga ekuacionet e m sip rme?

R nd sia e k saj pyetje dhe konceptet q mund t zhvillohen duke ju p rgjigjur k saj pyetje jan nj mrekulli e v rtet . P r her t par nx n si ekspozohet tek ideja q ekuacionet jan di ka pak e r nd sishme, di ka q ndryshon. Esht objekti gjeometrik ai q nuk ndryshon. Apo ka vall ndonj koncept sasior q mund t shprehet n var si t koefi ent ve dhe q nuk ndryshon pavar sisht ndryshimit t sistemit koordinativ?

Si pa kuptuar ne jemi futur n teori invariantesh, nj nga deg t m aktive t matematik s s shekullit XIX. Gjithashtu, pik risht ky diskutim kaq modest sht fillimi i gjeometris ose m mir i gjeometris algjebrike, nj nga deg t m aktive t matematik s moderne. Ne do ti japim zgjidhje pyetjes s m sip rme ne kreun n vazhdim.

Pyetje 9.

A mund t gjejm nj parametrizim racional t prerjeve konike? Ose me konkretisht, a mund t shprehet ekuacioni i do prerje konike si ekuacion parametrik $(x(t),y(t))$ ku $x(t)$ dhe $y(t)$ jan funksione racional ?

Kujtoni q është nj problem elementar q zakonisht është b r me nx n sit e mir q ekuacionet parametrik i elipsit është

x=a\cos\theta,\qquad y=b\sin\theta

i parabol s

x=at^{2},\qquad y=2at

dhe i hiperbol s

x=a\sec\theta,\qquad y=b\tan\theta.

Natyrisht parabola ka nj parametrizim racional. P r elipsin dhe hiperbol n mjafton t zevend sojm $t=\tan\frac{\theta}{2}$ dhe ne baz t Problemit 4 ne marrim nj parametrizim racional. Pra kemi se prerjet konike gjithmon kan nj parametrizim racional. P r entuziastuet e gjeometris algjebrike, kjo do t thot se prerjet konike jan trajektore algjebrike me genus zero. Kjo konkluzion na hap nj pyetje tjet r:

Pyetje 10.

A ka ndonj r nd si ky parametrizimi racional?

Si pa dashur jemi futur n problemin klasik t Diofantit, at t gjetjes s zgjidhjeve integrale (n m nyr ekuivalente racionale p r ekuacionet homogjen ) t ekuacioneve algjebrik .

Ne nuk do t zgjerohemi shum n k t fush , por thjesht duam t theksojm se gjith teoria moderne e numrave v rtitet rreth k tij problemi. Duam gjithashtu t theksojm q nj ekuacion algjebrik q ka nj parametrizim racional ka nj bashk si t pafundme zgjidhjesh racionale.

Esht gjithashtu me vler p r tu theksuar se shumica e ekuacioneve polinomiale kan vet m njue num r t fund m zgjidhjesh racionale. Kjo është teorema Faltings (83) dhe konsiderohet si teorema e shekullit t XX.

Pra prerjet konike nga ky k ndv shtrim duken mjaft speciale dhe nga nj ushtrim elementar i trigonomestris ne kuptojm p rse ato jan tue tilla.

2.6. Maximumet dhe minimumet lokale te funksioneve

Vazhdojm me nj shembull tjet r nga analiza. Nj pjes e mir e vitit IV n analiz kalohet me gjetjen e maksimumeve dhe minimumeve lokale t funksioneve me nj ndryshore. Nx n sit harxhojn me jav t t ra duke b r probleme optimizimi. Asnj fjal n analiz n e vitit IV nuk thuhet p r funksionet me dy ndryshore. Mendoni sa kuriozitet do t zgjonte tek nx n si ideja e gjetjes se majave t kodrave dhe thell sive t detit, apo llogaritja e sip rfaqes s nj relievi. Ishtje nj pyetje q shqet sonte autorin e dyt t k tij artikulli si adoleshent: Sa sip rfaqe reale tok ka Shqip ria?

Pra problemi i m posht m mund shtrohet tek maturant t tan dhe ndoshta t punohet vet m me ata m t talentuarit.

Problem 5.

Jepet nj sip rfaqe

z=f(x,y)

e p rkufizuar n nj zon $D\subset\mathbb{R}^{2}$ . T gjenden maksimumet dhe minimumet lokale t k saj sip rfaqeje.

Natyrisht analiza është nj minier e v rtet idesh dhe aplikimesh. Gjetja e vorbull s s nj lumi, volumi i nj kodre, kurbatura e nj kthese, shpejt sia dhe nxitimi i nj objekti q l viz n hap sir , ligjet e Keplerit, etj. Duhet pranuar se analiza e funksioneve me shum ndryshore edhe n programet tona universatere është b r cek t dhe ilustrimi me aplikime nga fizika dhe inxhinjerit gjithmon ka qen i varf r.

Gjithashtu ja vlen t p rmendet se shum prej k tyre temave trajtohen n shkollat e mesme n shum vende. P r shembull n Amerik nx n sit q jan t orientuar drejt shkencave dhe inxhinjerive futen ne klasa t avancuara dhe marrin lend si Kalkulusi I dhe Kalkulusi II q n shkoll t mesme.

2.7. Nd rtimet gjeometrike

Ata q kuptojn historin e matematik s t pakt n nj her n jet n e tyre duhet t shkojn t vizitojn varrezat Albani në Gottingen ku pushon nj prej njer zve m me influenc n historin e njer zimit, Carl Friedrich Gauss. Gauss është i njohur p r shum rezultate t famshme në matematik dhe nj prej tyre ishte edhe nd rtimi me vizore dhe kompas i nj 17-k nd shi të rregullt ose si quhet ndryshe heptadecagon, pas 2000 vjet sh p rpjekje nga matematikan t shumt . Ishte nj nga arritjet q e b nin Gaussin krenar m shum se do gj tjet r. far është kaq e v shtir p r k to nd rtimet gjeometrike q i dha Gausit kaq fam dhe krenari?

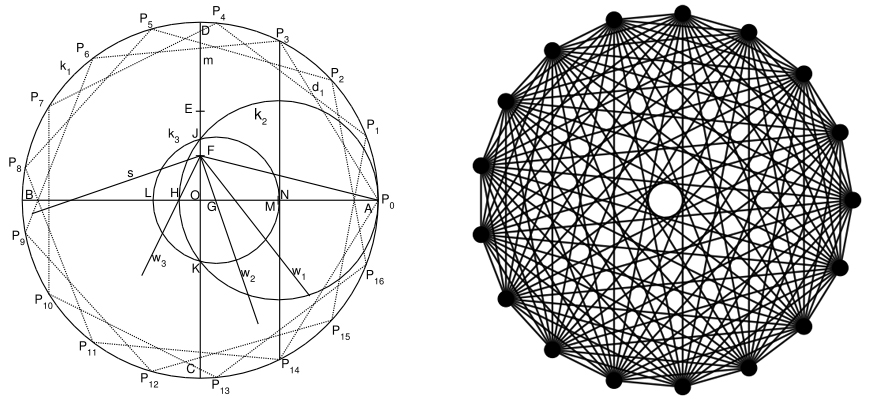
N tekstet tona t shkoll s 8-vje are dhe t mesme, gjithmon ka pasur cop za historike mbi nd rtimet gjeometrike, por k to nuk jan shfryt zuar p r t nd rtuar koncepte matematike mbi to. Nj lib r i shk lqyer i Petro Priftit, Probleme t zgjidhura t gjeometris ka pasur plot probleme t vlefshme, por ky tekst ishte gjithmon di ka q shfryt zohej vet m nga student t e talentuar. Pak p rdoreshin probleme t tilla p r t orientuar nx n sin drejt koncepteve t matematik s bashk kohore, madje shumica e m suesve nuk ishin fare n dijeni t k tij libri kaq t vyer. Le t p rpiqemi ti organizojm disi k to probleme klasike t gjeometris .

N Greqin e lasht kishte disa problema klasike. K to probleme jan nga gjeometria n natyr dhe p rfshijn nd rtimet vet m me vizore dhe kompas. Problemet mund t formulohen si m posht .

(1)

Jepet nj k nd i çfar dosh m, a mund ta ndajm k ndin n tre k nde t barabart duke p rdorur vet m vizore dhe kompas?
(2)

Jepet nj rreth i çfar dosh m, a mund t nd rtojm nj katror me t nj jt n sip rfaqe, duke p rdorur vet m vizore dhe kompasin?
(3)

Jepet nj kub, a mund t nd rtojm brinj n e nj kubi tjet r, i cili t ket dyfishin e v llimit t kubit origjinal duke p rdorur vet m vizore dhe kompas.
(4)

P r cilat $n$ , $n$ -k nd shi i rregullt sht i nd rtuesh m?

Pas p rpjekjeve dymij vjeçare nga ana e matematikan ve, u tregua, nd rtimet n tre problemet e para jan t pamundura. N Kreun 6 ne do t japim disa ide se si k to tema mund t trajtohen q n shkoll t mesme.

3. Historia e shkenc s - nj mjet kritik dhe konstruktiv p r programin e matematik s

Ka mendime dhe k ndv shtrime t ndryshme p r pregatitjen e nx n sve n matematik . K to pik pamje kan lidhje me shoq rin , tradit n e nj vendi, filozofin e shkoll s p rkat se. Ajo q pothuajse është e pranueshme nga t gjithe është që intuita matematike zhvillohet n nj mosh t vog l dhe konceptet merren her t. Diskutimet sot n ambjentet pedagogjike jan kryesisht mbi rrug t q duhen ndjekur me moshat e reja.

Shkolla jon ka t theksuar p rs ritjen e vazhdueshme dhe p r nj koh t gjat dhe kjo shpesh është b r n kurriz t an s intuitive. Po t kemi parasysh se para viteve 1990 f mij t shkonin 6 dit në shkoll dhe b nin p rdit matematik , at her duhet t pranojm se femij t shqiptar harxhonin nj pjes t konsiderueshme t f mij ris me matematik n. Po t shoh sh materialin q b hej p r 12 vjet shkoll është m pak se shumica e vendeve t tjera. Ky material p rs ritej aq her sa b hej i m rzitsh m, sidomos p r nx n sit e mir . ’mund t b het me k ta nx n s? Si mund t zhvillohet intuita tek t gjith nx n sit dhe ve an risht tek nx n sit me prirje n matematik ?

Zakonisht rruga m e mir është kur konceptet zhvillohen n m nyr n n t cil n jan zbuluar. Pra shtrohet pyetja, orientohen nx n sit drejt ideve t dukshme edhe pse ato mund t jen t gabuara. Esht e nevojshme që nx n si t kuptoj se far nuk funksionon dhe t detyrohet vet , ndoshta edhe duke vuajtur pak, q t gjej zgjidhjen e duhur. Faktet historike, v nia e do teoreme n ambjentin historik është nj ndihm shum e madhe. Historia e matematik s moderne është nj dram e ngjeshur emocionale e shekujve XVIII, XIX, XX.

Edukimi i p rgjithsh m i matematik s sot është distancuar nga kjo lloj m simdh nie. Ne shkojm n klas me nj tuf teoremash dhe faktesh dhe detyrojm nx n sit ti m sojn ato. Nj m nyr tep r komode p r m suesin mediok r, por tep r katastrofike p r nx n sin. Megjithat ka plot raste dhe shkolla ku matematika m sohet ndryshe. Ne do ti sygjeronin lexuesit librin Perfect rigor [MR2598223], mbi jet n e nj prej matematikan ve m t medhenj t k tij shekulli Grigory Perelman. Nje pjes e mir e librit flet p r Nj shkoll t mrekullueshme ku Grigory 12-vje ar trajnohej p rdit .

Nj shkoll tjet r e nisur vitet e fundit është The Proof school në San Francisco, ku intuita dhe konceptet klasike t matematik s marrin p rpar si.

Natyrisht v shtir sia m e madhe n k t lloj shkolle është mungesa e m suesve t aft , t cil t t ken njohuri t thella t matematik s s lart dhe t din se si k to koncepte ti ingranojn n programet m simore. Matematika, kur m sohet nga njer zit e duhur hap shum dyer dhe labirinte t thella n mendjen e nj f mije. Problemi është se si mund ti gjejm k ta vizioner , k ta njer z t duhur q kuptojn se ’donte t b nte Gauss, Abel, Jakobi, q njohin thell matematik n e shekullit XIX, q jan gati t sakrifikojn karier n e tyre shkencore p r tu m suar disa 12-vje ar ve matematik . K ta nuk është e leht ti gjesh! Prandaj shoq ria duhet t b j nj p rpjekje t madhe q t rekrutoj dhe pregatis njer z t till .

P r m suesit e apasionuar t cil t duan t gjejn rrug t reja se si historia e matematik s mund t futet n klas n e matematik s ne do t’u sygjeronim librat e Felix Klein [MR0076336, MR0015349, MR0055397, MR0080930, MR549187, MR2098410, MR3495524, MR3495525], Wilder [MR0297501], Roberts [MR767867], dhe ve an risht librin nga Arnold [MR3409220],

4. Ekuacionet algjebrike

Tani japin disa ide mbi disa tema q jan themelore n historin e zhvillimit t matematik s dhe q mund t futen me sukses ne programet e shkollave t mesme.

4.1. Ekuacionet me grade 2 dhe 3

Zgjidhja e ekuacioneve polinomiale ka qen dhe vazhdon t jet nj nga problemet themelore t matematik s q ka nxitur zhvillimin e disa prej deg ve m elegante dhe m produktive t matematik s si teoria Galua, gjeometria algjebrike, gjeometria Diofantine, etj. M posht japim nj ide se si zgjidhen disa nga ekuacionet me grad t vog l me nj ndryshore. T gjith polinomet kan koefiçient n $\mathbb{C}$ .

Kur kemi t b jm me nj ekuacion me nj ndryshore

(4)

x^{n}\ +\ a_{n-1}x^{n-1}\ +\ \dots\ +\ a_{1}x\ +\ a_{0}\ =\ 0

thjeshtimi i par sht t z vend sojm

x\ =\ y\ -\ \frac{a_{n-1}}{n}

i cili rezulton n nj ekuacion

y^{n}\ +\ b_{n-2}y^{n-2}\ +\ \dots\ +\ b_{0}\ =\ 0

me termin $y^{n-1}$ zero. Ky e zgjidh ekuacionin kuadratik (duke plot suar katrorin). Pra p r $n=2$ , ne thjesht marrim $y^{2}=-b_{0}$ .

Konsiderojm tani rastin p r $n=3$ , pra, ekuacionin

(5)

y^{3}\ +\ ay\ +\ b\ =\ 0.

Duke z vend suar $y=u+v$ , marrim

(6)

u^{3}\ +\ v^{3}\ +\ 3\ \left(uv+\frac{a}{3}\right)\ (u+v)\ +\ b\ =\ 0

qe sht i v rtet , n qoft se $u$ dhe $v$ k naqin

(7)

u^{3}\ +\ v^{3}\ \ =\ -b,\ \ \ \ \ uv\ \ =\ -\frac{a}{3}

Ekuacioni i fundit na jep

(Z-u^{3})\ (Z-v^{3})\ =\ Z^{2}\ +\ bZ\ -\ \frac{a^{3}}{27}

pra,

(8)

\begin{split}u^{3}\ &=\ \frac{-b\ +\ \sqrt{b^{2}\ +\ \frac{4a^{3}}{27}}}{2}\\ v^{3}\ &=\ \frac{-b\ -\ \sqrt{b^{2}\ +\ \frac{4a^{3}}{27}}}{2}\\ \end{split}

Nga ana tjet r, ne mund t zgjedhim $u$ dhe $v$ si rr nj kubike t p rshtatshme t an s s djatht , t tilla q , Eq. (6) t jet i v rtet . At her $u+v$ sht nj nga zgjidhjet e Eq. (5), t tjerat i marrim nga zgjedhjet e ndryshme t rr nj ve kubike. M sakt , n qoft se, $\epsilon$ sht nj rr nj primitive e tret e nj shit, pra $\epsilon^{3}=1$ , at her zgjidhjet e Eq. (4), jan

y_{1}=\ u\ +\ v,\ \ \ y_{2}=\ \epsilon u\ +\ \epsilon^{2}v,\ \ \ Y_{y}=\ \epsilon^{2}u\ +\ \epsilon v,

t cilat mund t verifikohen duke faktorizuar $(y-y_{1})(y-y_{2})(y-y_{3})$ . K to jan formulat Kardano, t cilat zakonisht shkruhen si

(9)

y_{i}\ =\ \left(-\frac{b}{2}\ +\ \sqrt{\frac{b^{2}}{4}\ +\ \frac{a^{3}}{27}}\right)^{1/3}\ +\ \left(-\frac{b}{2}\ -\ \sqrt{\frac{b^{2}}{4}\ +\ \frac{a^{3}}{27}}\right)^{1/3}

Shohim se, k to formula kan disa simetri, duke filluar nga zgjedhjet e ndryshme t rr nj ve katrore, t rr nj ve kubike dhe gjithashtu nga zgjedhja e nj rr nje t tret t nj shit. Gj ja pozitive sht , q ç shtja e simetrive midis zgjidhjeve mund t p rkufizohet pa p rdorur formul n e shtjellur t zgjidhjeve.

Ideja themelore e teoris Galois tani mund t formulohet thjesht si vijon:
P r do $n\geq 4$ , z vend sojm formul n e shtjellur p r zgjidhjet (megjith se ajo nuk ekziston) duke p rdorur grupin Galois.

P r m tep r p r zgjidhjen e ekuacioneve dhe nj prezantim mbi teorin e Galois shihni [alg].

N fakt koncepti i grupit n algjebr n moderne lindi pik risht nga koncepti i bashk sis s simetrive midis rr nj ve t nj polinomi. Megjith rolin q ndror t teoris Galua n algjeb r, n programet tona, duke p rfshir edhe ato universitare, kjo teori as p rmendej fare. Pra student t tan t shkencave asnj her nuk arrit n t b jn lidhjen apo t kuptojn motivimin se p rse studioheshin grupet apo fushat n universitet. Dhe kur ata vet nuk e kuptonin k t lidhje nuk mund t pretendosh q ata t’u shpjegonin nx n sve n klas n e X deg zimet apo idet q dalin nga zgjidhja e ekuacionit.

5. Diskriminanti dhe identitetet e Newtonit

N pro esin e diskutimit t rr nj ve t nj polinomi sht shum i r nd sish m fakti n se ndonj prej k tyre rr nj ve p rs ritet. N fund t fundit, ekuacioni

(x-2)^{4}\,(x-3)^{5}=0

sht m i leht p r tu zgjidhur edhe pse sht i grad s 9. Pyetje e m poshtme sht fare e natyrshme p r do nx n s s klas s IX apo X.

Pyetje 11.

Jepet polinomi i grad s $n\geq 2$

f(x)\ \ =\ a_{n}x^{n}\ +\ a_{n-1}x^{n-1}\ +\dots+\ a_{0}\ \ =\ a_{n}(x-\alpha_{1})\dots(x-\alpha_{n})

ku $a_{n}\neq 0$ . A mund t gjeni nj kriter p r koefi ent t $a_{0},\dots,a_{n}$ q $f(x)$ t ket rr nj q p rs riten?

Ky nuk sht nj problem i v shtir , por na on n nj nga konceptet m t r nd sish m t matematik s, at t dallorit ose diskriminantit. Le ti rradhisim gjith rr nj t si m posht

\alpha_{1},\alpha_{2},\dots,a_{n-1},\alpha_{n}

dhe marrim prodhimin

\Delta_{f}\ =\ \Pi_{i\neq j}(\alpha_{i}-\alpha_{j})

Natyrisht, kemi nj factor $(-1)$ q varet nga renditja e rr nj ve. P r ta b r $\Delta_{f}$ t pandjesh m nga kjo renditje e rr nj ve si edhe nga koefi enti udh heq s $a_{n}\neq 0$ ne modifikojm p rkufizimin si m posht :

(10)

\Delta_{f}\ =(-1)^{n(n-1)/2}\,\cdot\,a_{n}^{2n-2}\,\cdot\,\Pi_{i\neq j}(\alpha_{i}-\alpha_{j})

At her , lema e m poshtme sht e besueshme p r do nx n s

Lemma 2.

$f(x)$ ka rr nj q p rs riten atëherë dhe vetëm atëherë kur $\Delta_{f}=0$ .

Pik risht, sht $\Delta_{f}$ n Eq. (10) se si duhet t p rkufizohet discriminanti i do polinomi. Ky sht koncepti i natyrsh m, koncepti q mbahet mend, dhe koncepti q na tregon vetit e diskriminantit.

Megjithat ne ende nuk i jemi p rgjigjur pyetjes s m sip rme. Ne nuk i njohim rr nj t e $f(x)$ . Pra, a mund t themi di ka p r shum fishm rin e rr nj ve pa i gjetur rr nj t? Kjo pyetje sht ekuivalente me

Pyetje 12.

Jepet polinomi

f(x)\ \ =\ a_{n}x^{n}\ +\ a_{n-1}x^{n-1}\ +\dots+\ a_{0}\ \ =\ a_{n}(x-\alpha_{1})\dots(x-\alpha_{n})

A mund t shprehet diskriminanti $\Delta_{f}$ n var si t koefi ent ve $a_{0},\dots,a_{n}$ ?

Ushtrimi i m posht m sht nj ushtrim q do nx n s duhet ta ket b r t pakt n nj her n jet .

Ushtrim 1.

Jepet polinomi quadratik

f(a)\ =a\ x^{2}\ +\ bx\ +\ c\ =\ a\ (x-\alpha_{1})\ (x-\alpha_{2}).

At her , nga p rkufizimi dallori sht

\Delta_{f}=a^{2}\,(\alpha_{1}-\alpha_{2})^{2}

V rtetoni se

\Delta_{f}\ =\ b^{2}\ -\ 4ac.

Natyrisht, zgjidhja e ushtrimit t m posht m k rkon vet m njohuri elementare t algjebr s dhe mund t b het nga shumica e nx n sve t klas s X.

Ushtrim 2.

Jepet polinomi kubik

f(a)\ =ax^{3}+bx^{2}+cx+d

At her , v rtetoni se

\Delta_{f}\ =b^{2}c^{2}-4ac^{3}-4b^{3}d-27a^{2}d^{2}+18abcd.\,

Tani le t p rpiqemi t nxjerrim nj formul t shtjellur p r discriminantin. Le t jepet $f(x)$ si vijon

f(x)\ \ =\ \ x^{n}\ +\ a_{n-1}x^{n-1}\ +\dots+\ a_{0}\ \ =\ \ (x-\alpha_{1})\dots(x-\alpha_{n})

dhe p rkufizojm

\Delta\ \ =\ \ \prod_{i\neq j}\ (\alpha_{i}-\alpha_{j})

Matrica

X:=\ \ \ \begin{pmatrix}1&\dots&1\cr\alpha_{1}&\dots&\alpha_{n}\cr.&\dots&.\cr.&\dots&.\cr.&\dots&.\cr\alpha_{1}^{n-1}&\dots&\alpha_{n}^{n-1}\end{pmatrix}

\det(X)\ \ \ =\ \ \ \prod_{i>j}\ (\alpha_{i}-\alpha_{j})

nga formula e mir njohur e p rcaktorit t matric s Vandermonde.

Shembull 2.

V rtetoni formul n

\Delta=\det(X)^{2}=\det(XX^{t})=\det\begin{pmatrix}S_{0}&S_{1}&\dots&S_{n-1}\cr S_{1}&S_{2}&\dots&S_{n}\cr.&.&\dots&.\cr.&.&\dots&.\cr.&.&\dots&.\cr S_{n-1}&S_{n}&\dots&S_{2n-2}\end{pmatrix}

S_{\mu}\ :=\ \ \ x_{1}^{\mu}\ +\ \dots\ +\ x_{n}^{\mu}.

V rtetim. Duhet t shprehim shumat fuqi $S_{\mu}$ n lidhje me funksionet simetrik elementar

\sigma_{\nu}\ \ =\ \ \sum_{i_{1}<i_{2}<\dots<i_{\nu}}\ x_{i_{1}}x_{i_{2}}\ \dots\ x_{i_{\nu}}

(ku vetia baz e tyre sht , q $\sigma_{\nu}(x_{1},\dots,x_{n})\ =\ (-1)^{\nu}\ a_{n-\nu}$ ). Kjo mb shtetet te identitetet e Newtonit (c.f. Cox et al., p. 317):

\begin{split}&S_{\mu}-\sigma_{1}S_{\mu-1}+\dots+(-1)^{\mu-1}\sigma_{\mu-1}S_{1}+(-1)^{\mu}\mu\sigma_{\mu}=0,\ \ \mbox{for }1\leq\mu\leq n\\ &S_{\mu}-\sigma_{1}S_{\mu-1}+\dots+(-1)^{n-1}\sigma_{n-1}S_{\mu-n+1}+(-1)^{n}\sigma_{n}S_{\mu-n}=0,\ \ \ \mbox{for}\ \mu>n\end{split}

Jepet $z$ nj variab l i ri, p rkufizojm

\sigma(z)\ \ =\ \ \prod_{i=1}^{n}\ (1\ -\ x_{i}z)

At her

(11)

\begin{split}&\frac{-z\sigma^{\prime}(z)}{\sigma(z)}\ \ =\ \ \frac{z\ \sum_{i=1}^{n}\ x_{i}\prod_{jni}\ (1\ -\ x_{j}z)}{\sigma(z)}\ \ =\ \ \sum_{i=1}^{n}\ \frac{x_{i}z}{1\ -\ x_{i}z}\\ &=\,\sum_{i=1}^{n}\ \sum_{\nu=1}^{\infty}\ x_{i}^{\nu}z^{\nu}\ \ =\ \ \sum_{\nu=1}^{\infty}\ (\sum_{i=1}^{n}\ x_{i}^{\nu})\ z^{\nu}\ \ =\ \ \sum_{\nu=1}^{\infty}\ S_{\nu}\ z^{\nu}\end{split}

K shtu q , ne marrim identitetin n vazhdim nd rmjet serive fuqi formale n $z$ :

\sigma(z)\ \sum_{\nu=1}^{\infty}\ S_{\nu}\ z^{\nu}\ \ =\ \ -z\sigma^{\prime}(z)

Vetia baz e funksioneve simetrik elementar na çon n

\sigma(z)\ \ =\ \ \sum_{\mu=0}^{n}\ (-1)^{\mu}\sigma_{\mu}z^{\mu}

K shtu q ,

\sum_{j=0}^{n}\ (-1)^{j}\sigma_{j}z^{j}\ \cdot\ \sum_{\nu=1}^{\infty}\ S_{\nu}\ z^{\nu}\ \ =\ \ \sum_{\mu=1}^{n}\ (-1)^{\mu+1}\mu\sigma_{\mu}z^{\mu}

Duke krahasuar koefiçient t marrim at , q duam.

∎

Shembull 3.

do polinom kubik $f(x)$ mund t shkruhet n form n

f(x)\ =\ x^{3}\ +\ ax\ +\ b

V rtetoni se

\Delta_{f}\ =\ -4a^{3}\ -\ 27b^{2}.

K shtu q , formulat Kardano b hen

x_{i}\ =\ \left(-\frac{b}{2}\ +\ \sqrt{\frac{-\Delta_{f}}{108}}\right)^{1/3}\ +\ \left(-\frac{b}{2}\ -\ \sqrt{\frac{-\Delta_{f}}{108}}\right)^{1/3}

6. Format quadratike dhe nj hyrje n algjebr n lineare

Teoria e formave sht nj nga m t vjetrat dhe m t bukurat e matematik s. Ka vlera t paz vend sueshme nga ana metodike sepse motivon p rkufizimin e matricave (n fakt matricat lind n pik risht nga format kuadratike), nj pjes t mir t terminollogjise s algjebr s lineare (p.sh. definitisht pozitive, matricat simetrike, etj), dhe na jep ilustrime t shk lqyera t aplikimit t algjebr s si per shembull klasifikimi i prerjeve konike, klasifikimi i sip rfaqeve algjebrike, etj.

Nj form binare kuadratike është nj polinom homogjen i grad s s dyt me dy ndryshore, pra nj polinom i form s

(12)

f(x,y)=ax^{2}+bxy+cx^{2}

Pra është thjesht polinomi kuadratik ku ne fusim nj ndryshore t re $y$ dhe i b jm t gjitha termat me grad totale dy. N fakt ky pro es është i r nd sish m n matematik n e lart dhe quhet homogjenizim i polinomeve. M posht ne do t spjegojm k t pro es p r polinomet e grad s m t lart , por p r momentin le t p rq ndrohemi tek polinomet kuadratike. Ne duam t studiojm k to polinome kuadratike dhe rr njet e tyre.

Le t v rejm fillimisht disa veti t formave kuadratike.

Lemma 3.

P r do dy forma kuadratike $f(x,y)$ dhe $g(x,y)$ shuma e tyre

(f+g)(x,y):=f(x,y)+g(x,y)

është p rs ri nj form kuadratike. P r do konstante $\lambda\in\mathbb{C}$ , polinomi $h(x,y):=\lambda f(x,y)$ është nj form kuadratike.

V rtetimi i k saj leme është elementar, por r nd sia e saj është e madhe. Ky rezultat elementar na jep p rkufizimin e par t nj hap sire vektoriale. Pra bashk sia e gjith formave kuadratike me koefi ent n $k$ , ku $k$ është secila prej $\mathbb{Q},\mathbb{R},\mathbb{C}$ është nj hap sir vektoriale edhe pse nj nx n s i klas s IX apo X nuk e ka d gjuar m par k t koncept.

Nj form kuadratike $f(x,y)$ si n Eq. (12) p rcaktohet n m nyr t vetme nga treshja e renditur e numrave $(a,b,c)$ dhe nga ifti i renditur i ndryshoreve $(x,y)$ . N nj far m nyre ne duam q t organizojme k to treshe t renditura n se duam t studiojm format kuadratike. Gauss dhe me von Hermite filluan ti vinin k to treshe n tabela t tipit

\begin{bmatrix}a&b\\ b&c\end{bmatrix},

e cila quhet matric . N fakt Gauss filloi t p rdorte $M$ dhe $\mathbf{v}$ si m posht

M=\begin{bmatrix}a&\frac{b}{2}\\ \frac{b}{2}&c\end{bmatrix},\quad\textit{ and }\quad\mathbf{v}=\begin{bmatrix}x\\ y\end{bmatrix}

Kjo terminollogji ishte mjaft efi ente me marr veshjen q

\begin{bmatrix}a&b\\ b&c\end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}ax+by\\ cx+dy\end{bmatrix}

dhe

[x,y]\begin{bmatrix}a&b\\ b&c\end{bmatrix}=[ax+by,bx+cy]

N vend t $[x,y]$ ne shpesh p rdorim simbolin $\mathbf{v}^{t}$ dhe e quajm transpose t $\mathbf{v}$ -s . At her forma kuadratike $f(x,y)$ jepet si m posht

f(x,y)=\mathbf{v}^{t}M\mathbf{v}=(x,y)\,\begin{bmatrix}a&\frac{b}{2}\\ \frac{b}{2}&c\end{bmatrix}\,\begin{bmatrix}x\\ y\end{bmatrix}\ =\ ax^{2}+bxy+cx^{2}.

Pra, kemi nj korespondenc biunivoke midis formave kuadratike dhe matricave t form s

\begin{bmatrix}a&r\\ r&c\end{bmatrix}

P r nj form t dh n $f(x,y)$ matrica koresponduese sh nohet me $M_{f}$ .

Pozicionet n nj matric sh nohen me $(i,j)$ ku $i$ tregon numrin e rradh s dhe $j$ numrin e kolon s. Matricat e m sip rme $M$ quhen matrica $2\times 2$ meq n se kan 2 rradh dhe 2 kolona. Nj matric $2\times 2$ quhet matric simetrike kur termat n pozicionet $(1,2)$ dhe $(2,1)$ jan t barabarta. Pra matricat tona q korespondojn me format kuadratike jan matrica $2\times 2$ dhe simetrike.

Perfundiminsht, kemi rezultatin si m posht :

Lemma 4.

Ekziston nj korespondenc biunivoke midis formave kuadratike dhe matricave $2\times 2$ , simetrike. M konkretisht, kjo korespondenc jepet si m posht

f(x,y)=ax^{2}+bxy+cy^{2}\;\mapsto M_{f}=\begin{bmatrix}a&\frac{b}{2}\\ \frac{b}{2}&c\end{bmatrix}.

Matrica $M_{f}$ quhet matrica koresponduese e form s $f(x,y)$ .

Shihni pra se pa njohuri shtes dhe pa shum pun ne mund t prezantojm nx n sin me konceptin e polinomeve homogjen , matricave, matricave simetrike, shum zimit t matricave, hap sir s vektoriale. Pra thjesht polinomi i grad s s dyt është nj miner floriri. Dhe ne vet m sa kemi filluar.

Diskriminanti if nj forme kuadratike p rkufizohet nj soj si diskriminanti i polinomit $f(x,1)$ . Pra, diskriminanti i $f(x,y)$ dh n n Eq. (12) është $\Delta_{f}=b^{2}-4ac$ .

P r nj matric $A=\begin{bmatrix}a_{1,1}&a_{1,1}\\ a_{2,1}&a_{2,2}\end{bmatrix}$ ne p rkufizojm determinantin $\det A$ (ose p rcaktorin si p rdoret n Shqip) si

\det A=a_{1,1}a_{2,2}-a_{2,1}a_{1,2}

At her ,

\det M_{f}=ac-\frac{b^{2}}{4}

V rtetimi i Lem s s m poshtme tani është nj ushtrim elementar.

Lemma 5.

Diskriminanti $\Delta_{f}$ i nj forme kuadratike $f(x,y)$ është zero atëherë dhe vetëm atëherë kur $\det M_{f}=0$ . P r m tep r,

\Delta_{f}=-4\,\det M_{f}

Ka shum autor q i p rkufizojn format kuadratike si

f(x,y)=ax^{2}+2b\,xy+cy^{2}

n m nyr q matrica koresponduese është $M_{f}=\begin{bmatrix}a&b\\ b&c\end{bmatrix}$ . At her , diskriminanti $\Delta_{f}=ac-b^{2}$ n vend t $b^{2}-4ac$ . Kjo është thjesht shtje preference, n se autori preferon ta nis nga format kuadratike apo nga matricat.

6.1. Ekuivalenca e formave, matricat e ngjashme

I kthehemi edhe nj her problemit t prerjeve konike, pra Prob. (10). Jepet nj prerje konike

ax^{2}+bxy+cy^{2}+dx+ey=\lambda

Si duhet ndryshuar sistemi koordinativ , pra $\begin{bmatrix}x\\ y\end{bmatrix}$ q kjo prerje konike t jet nj nga format standart. S pari vem re se grada e ekuacionit t ri nuk mund t ndryshoj pasi n k t rast nuk do t kishim m nj prerje konike. Pra trasformimet e mundshme jan vet m transformimet

T:(x,y)\mapsto\left(\lambda_{1}x+\lambda_{2}y,\lambda_{3}x+\lambda_{4}y\right)

Me fjal t tjera, ne kemi nj sistem t ri koordinatash q jepet nga

\begin{bmatrix}x^{\prime}\\ y^{\prime}\end{bmatrix}=\begin{bmatrix}\lambda_{1}&\lambda_{2}\\ \lambda_{3}&\lambda_{4}\end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix}.

Funksioni $T(x,y)$ quhet transformim linear dhe matrica $C=\begin{bmatrix}\lambda_{1}&\lambda_{2}\\ \lambda_{3}&\lambda_{4}\end{bmatrix}$ quhet matrica e transformimit $T$ . $T(x,y)$ sht funksion bijektiv dhe i anasjellti i tij $T^{-1}$ është gjithashtu linear. Pra ekziston nje matric p r $T^{-1}$ qe ne e sh nojm me $C^{-1}$ . Matrica $C^{-1}$ quhet matrica e anasjellt e matric s $C$ . At her paraqisim edhe nj her problemin ton :

Problem 6.

Gjeni numrat $\lambda_{1},\lambda_{2},\lambda_{3},\lambda_{4}$ t till q prerja konike transformohet n ekuacionin standart.

Kjo motivon p rkufizimin e m posht m. Dy forma kuadratike $f(x,y)$ dhe $g(x,y)$ do t quhen ekuivalente në qoftë se ekzistojn $\lambda_{1},\dots,\lambda_{4}\in\mathbb{C}$ t till q

f\left(\lambda_{1}x+\lambda_{2}y,\,\lambda_{3}x+\lambda_{4}y\right)=g(x,y).

Vini re se

\begin{split}f\left(\lambda_{1}x+\lambda_{2}y,\,\lambda_{3}x+\lambda_{4}y\right)&=\mathbf{x}^{t}\,M_{f}\,\mathbf{x}=\left(\begin{bmatrix}\lambda_{1}&\lambda_{2}\\ \lambda_{3}&\lambda_{4}\end{bmatrix}\cdot\begin{bmatrix}x\\ y\end{bmatrix}\right)^{t}\,M_{f}\,\left(\begin{bmatrix}\lambda_{1}&\lambda_{2}\\ \lambda_{3}&\lambda_{4}\end{bmatrix}\cdot\begin{bmatrix}x\\ y\end{bmatrix}\right)\\ &=[x,y]\,\left(\begin{bmatrix}\lambda_{1}&\lambda_{2}\\ \lambda_{3}&\lambda_{4}\end{bmatrix}^{t}\,M_{f}\,\begin{bmatrix}\lambda_{1}&\lambda_{2}\\ \lambda_{3}&\lambda_{4}\end{bmatrix}\right)\,\begin{bmatrix}x\\ y\end{bmatrix}\\ \end{split}

Pra

f\left(\lambda_{1}x+\lambda_{2}y,\,\lambda_{3}x+\lambda_{4}y\right)=\mathbf{x}^{t}\,M_{f}\,\mathbf{x}

\mathbf{x}=\begin{bmatrix}\lambda_{1}&\lambda_{2}\\ \lambda_{3}&\lambda_{4}\end{bmatrix}\cdot\begin{bmatrix}x\\ y\end{bmatrix}

Matricat koresponduese t dy formave ekuivalente i quajm matrica t ngjashme.

Ushtrim 3.

Dy matrica $A$ dhe $B$ jan t ngjashme atëherë dhe vetëm atëherë kur ekziston nj matric $C$ e till q

A=C^{-1}BC

Ushtrimi i m posht m është standart n shkollat tona.

Shembull 4.

P r nj polinom kuadratik

f(x)=ax^{2}+bx+c

me koefi ent real , shenja e vler s s $f(x)$ p rcaktohet si vijon: $f(x)$ ka shenj n e kundert t $a$ -s n intervalin $(-\alpha_{1},\alpha_{2})$ dhe ka shenj n e $a$ -s kudo tjet r.

x		$\alpha_{1}$		$\alpha_{2}$
f(x)	a		-a		a

Table 1. Studimi i shenj s s polinomeve kuadratike.

Nj form kuadratike $f(x,y)$ quhet definitisht pozitive në qoftë se $f(x,1)>0$ p r do $x\in\mathbb{R}$ .

Ushtrim 4.

$f(x,y)$ është definitisht pozitive atëherë dhe vetëm atëherë kur $a>0$ dhe $\Delta_{f}<0$ .

P r nj matric fardo

A=\begin{bmatrix}a&b\\ c&d\end{bmatrix}

ne quajm eigenvlera t matric s zgjidhjet e ekuacionit

(\lambda-a)(\lambda-c)-bc=0

6.2. Klasifikimi i prerjeve konike

Le t p rpiqemi tani ti p rgjigjemi Pyetjes 7. Pra jepet Equacioni (2), ’mund t themi p r form n e grafikut?

N se ekuacioni n (2) do t kishte $b=0$ atëherë ky do t ishte nj ushtrim elementar. Ne plot sonim katrorin p r $ax^{2}+dx$ si edhe katrorin p r $cy^{2}+ey$ dhe do t merrnim njue ekuacion t form s

A(x+\alpha)^{2}+B(x+\beta)^{2}=C.

Me z vend simet $X=x+\alpha$ dhe $Y=y+\beta$ ne kemi

AX^{2}+BY^{2}=C,

i cili është bashk si boshe n $\mathbb{R}^{2}$ kur $C<0$ , nj elips kur $A,B$ jan me t nj jt n shenj , dhe nj hiperbol kur $A,B$ jan me shenja t ndryshme.

Forma kuadratike

G(x,y)=\lambda_{1}x^{2}+\lambda_{2}y^{2},

quhet form diagonale dhe matrica koresponduese

M_{g}=\begin{bmatrix}\lambda_{1}&0\\ 0&\lambda_{2}\end{bmatrix}

është njue matric diagonale.

Pra termi $b\,xy$ është fare ne duam t bejm zero q t p rcaktojm form n e grafikut. Ne mund t supozojm q pas plot simit t katror ve dhe z vend simeve p rkat se, ekuacioni na është dh n n form n $ax^{2}+bxy+cy^{2}=\lambda$ .

Pra kemi problemin e m posht m

Problem 7.

Jepet forma kuadratike

F(x,y)=Ax^{2}+Bxy+Cy^{2}.

Gjeni z vend simet e nevojshme algjebrike (pra ndryshimin e sistemit koordinativ)

x=ax+by,\qquad y=cx+dy

q forma $G(x,y)=F(ax+by,cx+dy)$ është diagonale.

Ne po i shmangim detajet e zgjidhjes s k tij problemi pasi ky problem është thjesht nj rast i va ant i problemit pasardh s. Po anallogjia është e qart , matrica $M_{F}$ diagonalizohet ne m nyr ortogonale, pra

M_{F}=\begin{bmatrix}a&b\\ c&d\end{bmatrix}^{-1}\;\begin{bmatrix}\lambda_{1}&0\\ 0&\lambda_{2}\end{bmatrix}\;\begin{bmatrix}a&b\\ c&d\end{bmatrix}

e till qe $\lambda_{1},\lambda_{2}$ jan eigenvlerat e $M_{F}$ . Lema n vijim p rcakton form n e grafikut t $F(x,y)=k$ , p r do konstant $k\in\mathbb{R}^{\ast}$ .

Lemma 6.

Grafiku

F(x,y)=ax^{2}+bxy+cy^{2}=k

është elipse në qoftë se t dy egeinvalutat e $M_{F}$ jan pozitive dhe hiperbol n se nj ra është pozitive dhe tjetra negative.

Ne i sygjerojm lexuesit t shoh [lin-alg] p r detajet.

6.3. Sip rfaqet kuadratike dhe klasifikimi i tyre

Ne mund t homogjenizojm ekuacionin e dh n n Ek. (2) si m posht

ax^{2}+by^{2}+cz^{2}+dxy+exz+fyz

duke futur nj ndryshore t re $z$ . Pra ne kalojm nga plani $\mathbb{R}^{2}$ n sistemin n hap sir $\mathbb{R}^{3}$ . Prerjet tona konike tashm jan thjesht projeksione n plan t grafikut t sip rfaqes s m sip rme. Pa ndonj kusht shtes ne mund t supozojm se koefi ent t $d,e,f$ jan $2d,2e,2f$ .

Nj form ternare kuadratike quhet polinomi homogjen kuadratik me tre ndryshore $x$ , $y$ , $z$ . Pra nj polinom i form s

F(x,y,z)=ax^{2}+by^{2}+cz^{2}+2dxy+2exz+2fyz

ku koefi ent t $a,b,c,d,e,f$ jan numra real . Konsiderojm ekuacionin

F(x,y,z)=h.

p r ndonj $h\in\mathbb{R}$ . N m nyr plot sisht t ngjashme me format binare, ky ekuacion mund t shkruhet

F(x,y,z)\;=\;\mathbf{x}^{t}\,M_{F}\,\mathbf{x}

\mathbf{x}=\begin{bmatrix}x\\ y\\ z\end{bmatrix}\quad\textit{dhe}\quad M_{F}=\left[\begin{tabular}[]{rrr}a&d&e\\ d&b&f\\ e&f&c\\ \end{tabular}\right]

$M_{F}$ quhet matrica koresponduese e $F(x,y,z)$ . Teoria e formave binare p rgjith sohet n k t rast fjal p r fjal .

Pyetje 13.

’mund t themi p r grafikun

F(x,y,z)=h,

n var si t koefi ent ve t $F(x,y,z)$ .

Grafiku është nj sip rfaqe kuadratike n $\mathbb{R}^{3}$ . Nj p rshkrim i detajuar i k tyre sip rfaqeve jepet n [kalk]. Ne po i p rkufizojm m posht shkurtimisht.

Nj prej llojeve t sip rfaqeve kuadratike sht elipsoidi, i cili jepet me ekuacionin

\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1

N rastin kur $a^{2}=b^{2}=c^{2}$ ekuacioni i elipsoidit paraqet nj sfer . Prerjet t rthore t tij me planet koordinative jan elipsa. Elipsoidi sht nj nga sip rfaqet m t pergjithshme kuadratike, sferoidi dhe sferat jan raste t ve anta t ellipsoidit.

Ekziston nj tjet r elipsoid q quhet imagjinar dhe ka ekuacion

\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=-1

P r detaje t m tejshme shih [kalk].

Paraboloidi eliptik sht nj tjet r sip rfaqeje kuadratike ekuacioni i s cil s sht i form s:

\qquad\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=\frac{z}{c}

Prerjet me planet paralele me planin $xy$ jan elipse, nd rsa prerja me vet planin $xy$ sht nj pik e vetme.

Figura tregon rastin kur $c>0$ , nd rsa kur $c<0$ , sip rfaqja sht e kthyer me kok posht . N rastin kur $a=b$ , sip rfaqja sht nj cilind r.

Nj tjet r sip rfaqe kuadratike sht paraboloidi hiperbolik q jepet me ekuacionin

\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=\frac{z}{c}

Pra, nj nga ndryshoret sht e grad s s par kurse pjesa tjet r sht diferenca e dy katror ve t ndryshoreve t tjera. Paraboloidi hiperbolik jep nj shembull t atyre q ne i quajm pika shal t cilat jan edhe maksimume lokale edhe minimume lokale; shih kapitujt mbi analiz n me disa ndryshore n [kalk].

Ne sygjerojm ushtrimin e m posht m.

Ushtrim 5.

Diskutoni se far v ndi gjeometrik mund t jet prerja e nj sferoidi me nj paraboloidi hiperbolic. A sht kjo gjithmon nj kurb konike?

Nj lloj tjet r sip rfaqesh kuadratike është hiperboloidi me nj flet i cili jepet me ekuacionin:

\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=1

P r hiperboloidin me nj flet , prerja t rthore me do plan paralel me planin $xy$ sht nj elips, nd rsa prerjet t rthore me plane paralele me planet $xz$ ose $yz$ jan hiperbola. P rjashtim b jn rastet e ve anta kur $x=\pm a$ dhe $y=\pm b$ ; n k to plane prerjet jan ifte drejt zash prer se.

Hiperboloidi me dy flet sht sip rfaqja kuadratike ekuacioni i t cilit është

\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=1

P r hiperboloidin me dy flet , prerja t rthore me do plan paralel me planet $xy$ ose $yz$ sht nj hiperbol . Me planin $yz$ nuk ka prerje t rthore, sepse p r $x=0$ ekuacioni

-\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=1

nuk ka zgjidhje. Me do plan paralel me planin $yz$ p r t cilin $|x|>a$ , prerja sht elips.

N vijim ne do t m sojm se si t klasifikojm gjith sip rfaqet kuadratike sipas k tyre llojeve.

Cilindri parabolik është sip rfaqja kuadratike ku nj nga ndryshoret është n fuqi t dyt dhe tjetra n fuqi t par , ndryshorja e tret nuk ekziston. Pra nj sip rfaqe e till

x^{2}=\lambda z

Megjith se ka forma t tjera t sip rfaqeve kuadratike, secila prej tyre mund t p rftohet si nj degjenerim i formave t m sip rme.

I kthehemi tani problemit ton ku na jepet nj sip rfaqe kuadratike e p rgjithshme dhe duam t gjejm llojin a saj n var si t koefi ent ve. Si n rastin e prerjeve konike, është e p rshtatshme q t rrotullojm sistemin koordinativ q termat $xy,yz,xz$ t zhduken. Forma t tilla, pa termat $xy,yz,xz$ , quhen forma kuadratike diagonale.

P rkufizojm inercin $\mbox{in }M_{F}$ e nj forme quadratike $F(x,y,z)$ si treshen e renditur

\mbox{in }M_{F}:=(n_{1},n_{2},n_{3}),

ku $n_{i}$ , $i=1,2,3$ është p rkat sisht numri pozitiv, negativ, dhe zero i eigenvlerave t $M_{F}$ -s . At her kemi lem n e m poshtme.

Lemma 7.

Jepet forma kuadratike ternare $F(x,y,z)$ dhe matrica koresponduese $A$ . Pohimet e m poshtme jan t v rteta:

i)

Në qoftë se $\mbox{in }M_{F}=(3,0,0)$ , at her sip rfaqja kuadratike sht nj ellipsoid.
ii)

Në qoftë se $\mbox{in }M_{F}=(2,0,1)$ , at her sip rfaqja kuadratike sht nj paraboloid eliptik.
iii)

Në qoftë se $\mbox{in }M_{F}=(2,1,0)$ , at her sip rfaqja kuadratike sht nj hyperboloid me nj flet .
iv)

Në qoftë se $\mbox{in }M_{F}=(1,2,0)$ , at her sip rfaqja kuadratike sht nj hyperboloid me dy flet .
v)

Në qoftë se $\mbox{in }M_{F}=(1,1,1)$ , at her sip rfaqja kuadratike sht nj paraboloid hiperbolik.
vi)

Në qoftë se $\mbox{in }M_{F}=(1,0,2)$ , at her sip rfaqja kuadratike sht nj cylinder parabolic.

V rtetimi i Lem s mund t gjendet n [lin-alg] dhe bazohet n faktin se numri i engenvlerave pozitive, negative, ose zero nuk ndryshon pavar sisht sistemit koordinativ t zgjedhur. N fund t fundit nj konfirmim q forma e sip rfaqes nuk ndryshon, pra nj elipsoid nuk mund t b het parabolois apo anasjelltas. Nj koncept q nx n si e beson shum m kollaj sepse bazohet n intuit n gjeometrike.

M posht po japim shkurtimisht metod n se si p rkaktohet forma diagonale dhe zevend simet algjebrike q e b jn k t t mundur.

Problem 8.

Gjeni diagonalizimin ortogonal t nj matrice simetrike $A$ .

Pra, ne duam t gjejm nj matric ortogonale $S$ dhe nj matric diagonale $D$ t till q

A=S^{T}DS.

Kujtoni q p r matricat ortogonale $S^{T}=S^{-1}$ ; shihni [lin-alg] p r detajet.

S pari gjejm gjith eigenvlerat e $A$ -s

\lambda_{1},\dots,\lambda_{r},

dhe shumfishm rit e tyre.

S dyti, p r do eigenvler $\lambda_{i}$ gjejm nj baz ortonormale

\mathcal{B}=\{v_{i,1},\dots,v_{i,s_{i}}\}

S treti, krijojm matric n

S=\left[v_{1,1}\,|\,\dots\,|v_{1,s_{1}}|v_{2,1}|\dots|v_{2,s_{2}}|\dots|v_{r,s_{r}}\right]

dhe matric n diagonale

D=\mbox{diag }(\lambda_{1},\dots,\lambda_{r})

q jan matricat e k rkuara.

Problemi i m sip rm ka vler p r do matric simetrike (pra n m nyr ekuivalente p r do form kuadratike, jo vet m format binare dhe ternare). Nj nx n s q kupton gjith hapat e zgjidhjes s k tij problemi mund t thuhet se ka nj baz t shendosh t algjebr s lineare.

I p rshtatur p r sip rfaqet kuadratike ky problem b het:

Problem 9.

Konsideroni form n kuadratike

q(x,y,z)=x^{2}+y^{2}+z^{2}+2xy+2xz+2yz

i) Gjeni matrioc n koresponduese $A$ t $q(x,y,z)$ .

ii) Gjeni matricat $C$ dhe $D$ t tilla q $A=C^{-1}DC$ , ku $C$ është ortogonale dhe $D$ matric diagonale.

iii) P rcaktoni z vend simet lineare

\begin{split}x^{\prime}&=a_{1}x+b_{1}y+c_{1}z,\\ y^{\prime}&=a_{2}x+b_{2}y+c_{2}z,\\ z^{\prime}&=a_{3}x+b_{3}y+c_{3}z,\\ \end{split}

t tilla q $q(x^{\prime},y^{\prime},z^{\prime})$ transformohet n nj form diagonale q i korespondon $D$ -s .

iv) Gjeni $q(x^{\prime},y^{\prime},z^{\prime})$ algjebrikisht p r t kontrolluar q v rtet i korespondon matric s diagonale $D$ .

v) far është forma e sip rfaqes $q(x^{\prime},y^{\prime},z^{\prime})=4$ ? ’mund t thoni p r form n e sip rfaqes $q(x,y,z)=4$ ?

Kur ushtrimi i m sip rm është metodollogjik dhe p rmban brenda t pakt n nj simest r t algjebr s lineare dhe nj simest r t gjeometris analitike, t gjitha keto njohuri mund t b hen n shkoll n e mesme dhe nx n si arrin nivelin e nj studenti t vitit t dyt t universitetit.

Problemi i m posht m, n dukje m ino ent, është nj shembull konkret i metod s s m sip rme.

Problem 10.

Klasifikoni sip rfaqen kuadratike

x^{2}+y^{2}-z^{2}+3xy-5xz+4yz=1.

7. Nd rtimet gjeometrike

K tu po japim nj permbledhje elementare t materialit t trajtuar ne Kapitullin 14 të [alg]. Ne supozojm njohuri elementare t algjebr s dhe konceptin e fush s. N rast se ky koncept nuk sht zhvilluar, m suesi mund t z vend soj fjal n fush me nj nga bashk sit $\mathbb{Q},\mathbb{R}$ , ose $\mathbb{C}$ .

Gjithashtu ne supozojm se nx n si kupton konceptin e zgjerimit t fushave ose n nfushe e nj fushe t dh n . Pra ne do t p rdorim shtrirjet algjebrike t fushave. Nj material pregatitor p r t lexuar k t material është materiali elementar n Kapitullin 13 në [alg].

7.1. Numrat e nd rtuesh m

Nj num r real $\alpha$ sht i nd rtuesh m, në qoftë se mund t nd rtojm nj segment me gjat si $|\alpha|$ n nj num r t fund m hapash nga nj segment nj si, duke p rdorur nj vizore dhe nj kompas.

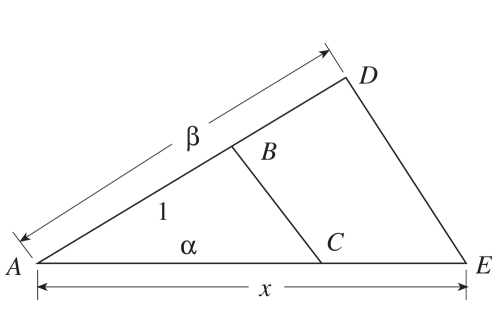
Theorem 1.

Bashk sia t gjith numrave real t nd rtuesh m formon nj n nfush $F$ , t fush s s numrave real $\mathbb{R}$ .

V rtetim. Le t jen $\alpha$ dhe $\beta$ , numra t nd rtuesh m. ne duhet t v rtetojm se, $\alpha+\beta$ , $\alpha-\beta$ , $\alpha\beta$ , dhe $\alpha/\beta$ ( $\beta\neq 0$ ), jan gjithashtu numra t nd rtuesh m. Ne mund t supozojm , q t dy $\alpha$ dhe $\beta$ , jan pozitiv , ku $\alpha>\beta$ . sht pothuajse e qart , sesi t nd rtojm $\alpha+\beta$ dhe $\alpha-\beta$ . P r t gjetur nj segment me gjat si $\alpha\beta$ , supozojm , q $\beta>1$ dhe nd rtojm trek nd shin n Figur n 3, i till q , trek nd shat $\triangle ABC$ dhe $\triangle ADE$ jan t ngjash m. Meq n se $\alpha/1=x/\beta$ , segmenti $x$ ka gjat si $\alpha\beta$ . Nj nd rtim i ngjash m mund t b het, në qoftë se $\beta<1$ . Po e l m si ushtrim t v rtetoni se, i nj jti trek nd sh mund t p rdoret p r t nd rtuar $\alpha/\beta$ , p r $\beta\neq 0$ . ∎

Lemma 8.

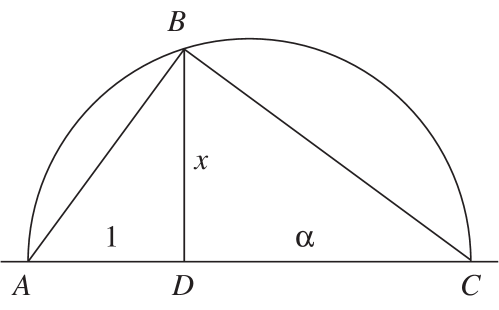
Në qoftë se $\alpha$ sht nj num r i nd rtuesh m, at her edhe $\sqrt{\alpha}$ sht num r i nd rtuesh m.

V rtetim. N Figur n 4 trek nd shat $\triangle ABD$ , $\triangle BCD$ , dhe $\triangle ABC$ jan t ngjash m; pra, $1/x=x/\alpha$ , ose $x^{2}=\alpha$ . ∎

Lema e m poshtme mund t jet nj detyr e p rshtatshme.

Lemma 9.

sht i mundur nd rtimi i trek nd shave t ngjash m.

Ne mund t gjejm n plan do pik $P=(p,q)$ , e cila ka koordinata racionale $p$ dhe $q$ . Ne duam t dim se, cilat pika t tjera mund t nd rtohen me kompas dhe vizore, nga pikat me koordinata racionale.

Lemma 10.

Le t jet $F$ nj n nfush e $\mathbb{R}$ .

i) Në qoftë se nj drejt z p rmban dy pika n $F$ , at her ajo ka ekuacionin $ax+by+c=0$ , ku $a$ , $b$ , dhe $c$ jan n $F$ .

ii) Në qoftë se nj rreth e ka qendr n n nj pik me koordinata n $F$ dhe me rreze, cila sht gjithashtu n $F$ , at her ai ka ekuacionin $x^{2}+y^{2}+dx+ey+f=0$ , ku $d$ , $e$ , dhe $f$ jan n $F$ .

V rtetim. Le t jen $(x_{1},y_{1})$ dhe $(x_{2},y_{2})$ , pika t nj drejt ze me koordinata n $F$ . Në qoftë se $x_{1}=x_{2}$ , at her ekuacioni i drejt z s, q kalon nga dy pikat sht $x-x_{1}=0$ , i cili ka form n $ax+by+c=0$ . Në qoftë se $x_{1}\neq x_{2}$ , at her ekuacioni i drejt z s, q kalon nga dy pikat jepet nga

y-y_{1}=\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)(x-x_{1}),

i cili mund t kthehet n form n e duhur.

P r t v rtetuar pjes n e dyt t lem s, supozojm se, $(x_{1},y_{1})$ sht qendra e nj rrethi me rreze $r$ . At her rrethi ka ekuacionin

(x-x_{1})^{2}+(y-y_{1})^{2}-r^{2}=0.

Ky ekuacion mund t shkruhet leht n form n e duhur.

∎

Duke filluar me fush n e numrave t nd rtuesh m $F$ , kemi tre m nyra t ndryshme p r t nd rtuar pikat shtes n $\mathbb{R}$ me kompas dhe vizore .

(1)

P r t gjetur pika e reja t mundshme n $\mathbb{R}$ , ne mund t marrim prerjen e dy drejt zave, ku seicila prej tyre kalon nga dy pika t dh na me koordinata n $F$ .
(2)

Prerja e nj drejt ze, e cila kalon nga dy pika me koordinata n $F$ me nj rreth, qendra e t cilit i ka koordinatat n $F$ me gjat si rrezje n $F$ , do t na jap pika t reja n $\mathbb{R}$ .
(3)

Ne mund t p rftojm pika t reja n $\mathbb{R}$ , duke prer dy rrath , qendrat e t cil ve i kan koordinatat n $F$ dhe gjat sit e rrezeve t tyre jan n $F$ .

Rasti i par , nuk na jep pika t reja n $\mathbb{R}$ , meq zgjidhja e dy ekuacioneve t form s $ax+by+c=0$ , me koefiçient n $F$ , gjithmon do t jet n $F$ . Rasti i tret mund t sillet te rasti i dyt . Le t jen

	$\displaystyle x^{2}+y^{2}+d_{1}x+e_{1}x+f_{1}=0$
	$\displaystyle x^{2}+y^{2}+d_{2}x+e_{2}x+f_{2}=0$

ekuacionet e dy rrath ve, ku $d_{i}$ , $e_{i}$ , dhe $f_{i}$ jan n $F$ p r $i=1,2$ . K ta rrath kan t nj jt n prerje si, rrethi

x^{2}+y^{2}+d_{1}x+e_{1}x+f_{1}=0

dhe drejt za

(d_{1}-d_{2})x+b(e_{2}-e_{1})y+(f_{2}-f_{1})=0.

Ekuacioni i fundit, sht ai i kord s, q kalon n pikat e prerjes s dy rrath ve. Pra, prerja e dy rrath ve mund t sillet n rastin e prerjes s nj drejt ze me nj rreth.

Konsiderojm rastin e prerjes s nj drejt ze me nj rreth, duhet t p rcaktojm natyr n e zgjidhjeve t ekuacioneve.

	$\displaystyle ax+by+c$	$\displaystyle=$	$\displaystyle 0$
	$\displaystyle x^{2}+y^{2}+dx+ey+f$	$\displaystyle=$	$\displaystyle 0.$

Në qoftë se eleminojm $y$ nga k to ekuacione, p rftojm nj ekuacion t form s $Ax^{2}+Bx+C=0$ , ku $A$ , $B$ , dhe $C$ jan n $F$ . Koordinata $x$ e pikave t prerjes jepet nga

x=\frac{-B\pm\sqrt{B^{2}-4AC}}{2A}

dhe sht n $F(\sqrt{\alpha}\,)$ , ku $\alpha=B^{2}-4AC>0$ . Kemi v rtetuar lem n n vazhdim.

Lemma 11.

Le t jet $F$ fusha e numrave t nd rtuesh m. At her pikat e prerjes s drejt zave dhe rrath ve n $F$ , ndodhen n fush n $F(\sqrt{\alpha}\,)$ p r ndonj $\alpha$ n $F$ .

Theorem 2.

Nj num r real $\alpha$ sht num r i nd rtuesh m, at her dhe vet m at her , kur ekziston nj varg fushash

\mathbb{Q}=F_{0}\subset F_{1}\subset\cdots\subset F_{k}

t tilla q , $F_{i}=F_{i-1}(\sqrt{\alpha_{i}}\,)$ ku $\alpha\in F_{k}$ . N veçanti, ekziston nj num r i plot $k>0$ , i till q , $[\mathbb{Q}(\alpha):\mathbb{Q}]=2^{k}$ .

V rtetim. Ekzistenca e $F_{i}$ -ve dhe e $\alpha_{i}$ -ve sht pasoj direkte e Lem s së m sip rme dhe e faktit, q

[F_{k}:\mathbb{Q}]=[F_{k}:F_{k-1}][F_{k-1}:F_{k-2}]\cdots[F_{1}:\mathbb{Q}]=2^{k}.

∎

Rrjedhim 1.

Fusha e gjith numrave t nd rtuesh m sht nj shtrirje algjebrike e $\mathbb{Q}$ .

Siç mund ta shihni nga fusha e numrave t nd rtuesh m, jo do shtrirje algjebrike e nj fushe sht shtrirje e fundme.

7.2. Dyfishimi i nj kubi dhe katrori i rethit

Tani jemi gati t shqyrtojm problemet klasike t dyfishimit t kubit dhe t kthimit t rrethit n katror. Ne mund t p rdorim fush n e numrave t nd rtuesh m p r t treguar me sakt si se, kur nj nd rtim i veçant algjebrik mund t realizohet.

Dyfishimi i kubit sht i pamundur. Kur jepet brinja e kubit, sht e pamundur t nd rtosh me vizore dhe kompas brinj n e kubit, i cili ka dyfishin e v llimit t kubit origjinal. Le t jet kubi origjinal me brinj me gjat si 1 dhe me v llim po 1. Në qoftë se mund t nd rtojm nj kub me v llim 2, at her ky kub i ri do ta ket brinj n me gjat si $\sqrt[3]{2}$ . Megjithat , $\sqrt[3]{2}$ sht nj rr nj e polinomit t pathjeshtuar $x^{3}-2$ , mbi $\mathbb{Q}$ ; pra,

[\mathbb{Q}(\sqrt[3]{2}\,):\mathbb{Q}]=3

Kjo sht e pamundur, sepse 3 nuk sht fuqi e 2.

Theorem 3.

sht e pamundur, q t dyfishojm kubin.

V rtetim. Marrim nj kub me v llim 1. P r t dyfishuar kubin duhet t nd rtojm nj $x$ , t till q ,

x^{3}=2.

Polinomi

f(x)=x^{3}-2

sht i pathjeshtuesh m mbi $\mathbb{Q}$ dhe prandaj, p r do rr nj $\alpha$ t $f(x)$ , kemi $[\mathbb{Q}(\alpha):\mathbb{Q}]=3$ , e cila nuk sht fuqi e 2.

∎

7.3. Kthimi i rrethit n katror

Supozojm , q kemi nj rreth me rreze 1. Sip rfaqja e rrethit sht $\pi$ ; prandaj, ne duhet t nd rtojm nj katror me brinj $\sqrt{\pi}$ . Kjo sht e pamundur, sepse si $\pi$ dhe $\sqrt{\pi}$ jan t dy transhendent . K shtu q , me p rdorimin e vizores dhe kompasit, sht e pamundur t nd rtosh nj katror me t nj jt n sip rfaqe sa t rrethit.

Theorem 4.

sht e pa mundur ta kthesh rrethin n katror.

V rtetim. Jepen $r$ i nd rtuesh m dhe nj rreth me rreze $r$ . Duam t nd rtojm nj katror me brinj $x$ , i till q ,

x^{2}=\pi r^{2}

Meq n se $\pi$ nuk sht as num r algjebrik, at her rr nj t e ekuacionit t m sip rm nuk jan as algjebrik dhe prandaj nuk mund t jen t nd rtueshme.

∎

7.4. Ndarja n tresh e nj k ndi

Ndarja n tresh e nj k ndi t çfar dosh m sht e pamundur. Do t v rtetojm se, sht e pamundur t nd rtosh nj k nd $20^{\circ}$ . P r pasoj , nj k nd $60^{\circ}$ nuk mund t ndahet n tresh. Si fillim, duhet t llogaritim formul n e k ndit trefish p r kosinusin:

(13)

\cos 3\theta=4\cos^{3}\theta-3\cos\theta.

K ndi $\theta$ mund t nd rtohet, at her dhe vet m at her , kur $\alpha=\cos\theta$ sht i nd rtuesh m. Le t jet $\theta=20^{\circ}$ . At her $\cos 3\theta=\cos 60^{\circ}=1/2$ . Nga formula e k ndit t trefisht p r kosinusin,

4\alpha^{3}-3\alpha=\frac{1}{2}.

K shtu q , $\alpha$ sht nj rr nj e $8x^{3}-6x-1$ . Ky polinom nuk ka faktor n $\mathbb{Z}[x]$ , pra sht i pathjeshtuesh m mbi $\mathbb{Q}[x]$ . K shtu q , $[\mathbb{Q}(\alpha):{\mathbb{Q}}]=3$ . P r pasoj , $\alpha$ nuk mund t jet nj num r i nd rtuesh m.

Theorem 5.

sht e pamundur t ndahet nj k nd n tresh.

V rtetim. T ndash n tresh nj k nd $3\alpha$ , sht nj soj si t nd rtosh $\cos\alpha$ , kur jepet $\cos 3\alpha$ . Ekuacioni (13) na jep polinomin

f(x)=4x^{3}-3x-\cos 3\alpha,

p r t cilin $\cos\alpha$ sht rr nj . P r disa vlera t $\alpha$ polinomi $f(x)$ sht i pathjeshtuesh m dhe $[\mathbb{Q}(\cos\alpha):\mathbb{Q}]=3$ , e cila nuk sht fuqi e 2. Marrim $\alpha=20^{\circ}$ . At her ,

f(x)=8x^{3}-6x-1

sht i pathjeshtuesh m mbi $\mathbb{Q}$ . Pra, n qoft se, $\alpha$ sht rr nj e $f(x)$ , at her $[\mathbb{Q}(\alpha):\mathbb{Q}]=3$ , e cila nuk sht fuqi e 2.

∎

Shembull 5.

P rcakto n se k ta k nde mund t ndahet n tresh.

i) K ndi $\beta$ , i till q , $\cos\beta=\frac{1}{3}$ .

ii) $\beta=120^{\circ}$

Solution: T ndash n tresh nj k nd $\beta=3\alpha$ , sht nj soj si t nd rtosh $\cos\alpha$ , kur jepet $\cos 3\alpha$ . Ekuacioni

\cos 3\alpha=4\cos^{3}\alpha-3\cos\alpha

na jep polinomin

f(x)=4x^{3}-3x-\cos 3\alpha,

p r t cilin $\cos\alpha$ sht rr nj .

i) N qoft se, $\cos 3\alpha=\frac{1}{3}$ , at her $\cos\alpha$ sht nj rr nj e polinomit

f(x)=4x^{3}-3x-\frac{1}{3}

i cili sht i pathjeshtuesh m. At her , $[\mathbb{Q}(\cos\alpha):\mathbb{Q}]=3$ , i cili nuk sht fuqi e 2. Pra, ky k nd nuk mund t ndahet n tresh.

ii) N qoft se, $\beta=120^{\circ}$ , at her $\cos\beta=-\frac{1}{2}$ . At her

f(x)=4x^{3}-3x+\frac{1}{2}

i cili sht i pathjeshtuesh m mbi $\mathbb{Q}$ dhe, si m lart, k ndi nuk mund t ndahet n tresh.

∎

7.5. Nd rtimi i nj shum k nd shi t rregullt

Theorem 6.

$n$ -k nd shi sht i nd rtuesh m, at her dhe vet m at her , kur

n=2^{k}\cdot p_{1}\cdots p_{s},

ku $p_{i}$ jan numrat e thjesht Fermat, t dalluar, pra t form s $p=2^{2^{r}}+1$ .

V rtetim. Nd rtimi i nj $n$ -k nd shi sht ekuivalent me nd rtimin e $\cos\frac{2\pi}{n}$ . Sh nojm me $e_{n}=\cos\frac{2\pi}{n}+i\sin\frac{2\pi}{n}$ rr nj n primitive t nj sis . At her , $\cos\frac{2\pi}{n}=(\varepsilon_{n}+\varepsilon_{n}^{-1})/2$ . Pra, $\mathbb{Q}(\varepsilon_{n})$ sht nj shtrirje e $\mathbb{Q}(\frac{2\pi}{n})$ . Ne e mbarojm v rtetimin vet m p r $n$ num r t thjesht $p$ , pjesa tjet r do t v rtetohet n kapitullin e fush s ciklotomike në [alg]. Pra, $\cos\frac{2\pi}{n}$ sht i nd rtuesh m, n qoft se, $\frac{p-1}{2}=2^{r}$ p r ndonj $r\geq 0$ . K shtu q , kjo sht e mundur vet m p r numra t thjesht $p$ , t form s $p=2^{k}+1$ . K ta jan sakt sisht numrat e thjesht Fermat dhe ata jan t form s $p=2^{2^{r}}+1$ . ∎

Disa problema t p rshtatsh m p r gjeometrin e shkoll s s mesme jan :

Problem 11.

V rtetoni se, 9-k nd shi i rregullt nuk sht i nd rtuesh m me vizore dhe kompas kurse 20-k nd shi i rregullt sht i nd rtuesh m.

Problem 12.

V rtetoni se, kosinusi i nj grade ( $\cos 1^{\circ}$ ) sht algjebrik mbi $\mathbb{Q}$ , por nuk sht i nd rtuesh m.

Problem 13.

V rtetoni se në qoftë se $\alpha$ dhe $\beta$ jan numra t nd rtuesh m, të till q $\beta\neq 0$ , at her i till sht edhe $\alpha/\beta$ .

Problem 14.

Jepni nj m nyr gjeometrike p r t nd rtuar nj $n$ -gon t rregullt, p r

n=3,4,5,6,8,10,12,15,16,17,20,24

Nd rtimi i $n$ -k nd shit t rregullt p r $n=3,\dots,6$ zakonisht është trajtuar b programet tona të gjeometris . Natyrisht, nga kjo rastet $n=8,10,12,16,20,24$ jan rrjedhime elementare. Rasti $n=15$ është nj problem interesant p r nx n sin e vitit t dyt t gjimnazit. Rasti $n=17$ është m i v shtiri.

References

\ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry \ProcessBibTeXEntry