Magnetic ground state of monolayer CeI2: Occupation matrix control and DFT+U calculations
Abstract
The magnetic ground state is crucial for the applications of the two-dimension magnets as it decides fundamental magnetic properties of the material, such as magnetic order, magnetic transition temperature, and low-energy excitation of the spin waves. However, the simulations for magnetism of local-electron systems are challenging due to the existence of metastable states. In this study, occupation matrix control (OMC) and density functional theory plus Hubbard calculations are applied to investigate the magnetic ground state of monolayer CeI2. Following the predicted ferromagnetic (FM) order, the FM ground state and the FM metastable states are identified and found to have different values of the magnetic parameters. Based on the calculated magnetic parameters of the FM ground state, the Curie temperature is estimated to be K for monolayer CeI2. When spin-orbit coupling (SOC) is considered, the FM ground state is further confirmed to contain both off-plane and in-plane components of magnetization. SOC is shown to be essential for reasonably describing not only magnetic anisotropy but also local electronic orbital state of monolayer CeI2.
I Introduction
The two-dimension(2D) magnets exhibit magnificent potential in spintronic devices and magnetic storage devices due to their unique properties and the nanoscale size. Although Mermin-Wagner theorem Mermin denies the possibility of long-range magnetic order in 2D systems at non-zero temperature, a series of experimental studies Jiang2021 ; Huang2017 ; Tian2019 ; Cai2019 ; Zhang2019 ; Banerjee2017 ; Zhou2019 ; Bonilla2018 ; Li2018 ; Hara2018 ; Gong2017 ; Wang2016 ; Kim2019 ; Flem1982 ; Fei2018 ; May2019 have confirmed the presence of magnetic orders in 2D materials. These findings encourage people to further explore 2D magnetic materials with superior properties, such as robust dynamic stability, high magnetic transition temperature, and unique magnetic anisotropy.
The magnetic ground state (GS) of a 2D material is significant. It not only dominates the behaviour about magnetism at low temperature, but decides the low-energy excitation of the spin waves at finite temperature. For magnetic crystals, a comprehensive description of the magnetic GS should contain the information of two aspects: the specific magnetic structure and the electronic states of the magnetic sites. For the former part, spin-polarized scanning tunneling microscope (SP-STM), Ramam spectroscopy, and the observation of anomalous Hall effect have been adopted to examine the magnetic order of 2D magnetic insulators and 2D magnetic metals Huang2017 ; Gong2017 ; May2019 ; Lee2016 ; Tian2016 ; Deng2018 . For the latter part, x-ray magnetic circular dichroism (XMCD) and x-ray magnetic linear dichroism(XMLD) are two techniques which help to obtain the local electronic configuration Liu2016 ; Laan1999 . Nonetheless, exploring magnetic ground states of 2D materials experimentally is still challenging. The limitations include the acquirement of high quality samples, strict experimental conditions, and even expensive costs on economy and time. From this point of view, exploring 2D magnetic materials by using density functional theory (DFT) calculations is another feasible scheme. The DFT tool gives the prediction of the magnetic ground state without synthesizing actual samples. It has been applied to study a series of 2D magnetic materials such as layered -RuCl3, VSe(Te)2, CrGe(Si)Te3, etc. Sarikurt2018 ; Kim20161 ; Sandilands2015 ; Li2014 ; Ataca2012 ; Chen2020 ; Fuh2016 ; Pan2014 ; Kan2014 ; Lin2017 ; Lin2016 For 2D CrI3 and CrBr3, DFT calculations give quite consistent prediction of magnetic features with the experiments, including the magnetic structure and Curie temperature () Wang20162 ; Zhang2015 ; Liu20162 ; Jiang20212 . With the assistance of DFT calculations, the studying progress of 2D magnetic materials has been accelerated significantly.
In 2D magnetic insulators and semiconductors, the spin magnetic moments are commonly contributed by polarized electrons from partially filled or f atomic shells. These electrons are localized around the lattice sites and need extra corrections for strong electronic correlation. Therefore, the density functional theory plus Hubbard (DFT+U) scheme Liechtenstein ; Dudarev is widely applied to give reasonable electronic structures of the correlated systems. In fact, the conventional DFT+U computational scheme faces challenges in locating the ground state of the localized electrons due to the presence of metastable states, especially when the d and f shells are less filled. In other words, although a specific magnetic ordered state can be determined by DFT+U calculations, however, the obtained electronic state of the localized electrons may be not identical for different researchers. This phenomenon has occurred in the DFT+U studies of Ti-based systems Watson , Ce-based systems Watson ; Shick , U-based systems Miskowiec ; Dorado ; Dorado1 ; Dorado2 ; Matthew ; Claisse , cubic fluorite PuO2 Jomard ; Hou2022 , and monolayer VX3 (X=Cl, Br, I) hou2024 etc., and the metastable states can originate from 3, 4, or 5 localized electrons (not found in 4 or 5 electronic systems yet, to our knowledge). Moreover, these works have also shown that the occurrence of trapping into metastable states is not relevant to the form of adopted exchange-correlation functional. Local density approximation (LDA) Shick , generalized gradient approximation (GGA) Watson ; Miskowiec ; Dorado ; Dorado1 , strongly constrained appropriate normed (SCAN) type meta-GGA Hou2022 , and HSE06 type hybrid Jollet ; Ratcliff functionals have been adopted in the studies and this accident still happens constantly. To solve the problem, a few techniques have been applied including U-ramping Claisse ; Meredig , quasi-annealing Geng , occupation matrix control (OMC) Watson ; Dorado ; Claisse ; Amadon ; Zhou2011 ; Zhou2022 , DFT+DMFT Amadon2012 and even the combination of them Rabone . These techniques help to reduce the probability of trapping into metastable states to some extent. However, it remains an open question as to how the ground state of the localized electrons can be strictly obtained.
Recently, the monolayer CeI2 was predicted to be an in-plane ferromagnetic (FM) semiconductor with a high of K by DFT+U calculations Sheng . The dynamic stability of the monolayer CeI2 was supported by both phonon calculations and a molecular dynamics simulation at room temperature. In the monolayer CeI2, two 6s electrons of the Ce atom move away to form the Ce-I bond, leaving a electronic configuration for the Ce2+ ion. According to above analysis, a number of metastable states originated from the highly localized electrons should be expected. Owing to the importance for both basic physics and potential applications, it is necessary to provide a systematic analysis of the magnetic GS of monolayer CeI2.
In this study, we perform DFT+U calculations combined with OMC to investigate the magnetic GS of monolayer CeI2. The magnetic structure is once again confirmed to be FM. The FM GS as well as twenty-three FM metastable states of monolayer CeI2 with different local electronic states are identified. Our results show that the computed isotropy exchange parameter and magnetic anisotropy energy are distinguishable for the GS and metastable states. Based on the exchange parameters of the magnetic GS, the is estimated to be about K by using Monte Carlo simulations. To reasonably analyze the contributions to the total energies, the Coulomb potential energies of the 4f electron with different occupied electronic orbitals in the crystal field are discussed. Furthermore, we take spin-orbit coupling (SOC) into consideration. The magnetic structure of monolayer CeI2 then becomes FM with both in-plane and off-plane components of magnetic moments and the easy axis of magnetization is coupled with the crystal structure. The single Ce- electron occupies another distinguishable electronic orbital compared to the situation without SOC, which illustrates that SOC is essential to describe the magnetic GS of monolayer CeI2. A fully off-plane FM state is confirmed to be a metastable state of monolayer CeI2 whose total energy is just slightly higher than the magnetic GS. We anticipate that achieving saturation magnetization in the off-plane direction for monolayer CeI2 is feasible under appropriate external conditions.
II Computational Methods
The DFT+U calculations are carried out by employing the Vienna ab-initio simulation package (VASP) code Kresse . OMC is implemented by applying the patch of Allen et al. tailored for VASP Watson . The adopted atomic pseudo potentials are constructed by the project augmented wave (PAW) method Blochl ; Kresse2 ; Blochl2 . The cut-off energy of the plane wave bases is set to eV. The first Brillouin Zone is sampled by a -center -point mesh. The convergence of both cut-off energy and -point mesh has been carefully examined. The crystal structures are relaxed until the Feynman-Hellman force on each atom is smaller than eV/Å. The optimizing of the charge density is ended when the energy difference is smaller than eV between the current two steps of the iteration. We make use of the DFT+U method of Dudarev et al. Dudarev with a form of
| (1) |
where is the matrix element of the occupation matrix with spin . The standard DFT part here is handled by the Perdew-Burke-Ernzerhof (PBE) type GGA exchange-correlation functional. Perdew The Hubbard and Hund for the Ce- electron are set to be eV and eV, respectively, which have been applied in previous study Sheng ; Larson . To be cautious, a discussion is also made to demonstrate the rationality of the parameter (see Section A of the Supporting Information SI ). Based on the computed Bloch states with plane waves bases, Wannier90 code Mostofi is used to construct the tight-binding Hamiltonian. TB2J code He is used to calculate the Green’s function and then the isotropic exchange parameter for magnetic properties is obtained. The is gained by Monte Carlo simulations based on the heat bath algorithms Miyatake . The visualizations of the crystal structure and spin densities in this work is achieved by VESTA Momma . The VASPKIT code is used to process the data of the DFT calculations Wang2021 .
III OMC of the electronic state
A quantum state of a single electron can be express as a linear combination of a group of complete and orthogonal bases in the Hilbert space. In the limitation of localized electrons of an isolated atom, the dimension of the space is equal to , where is the angular quantum number of that electron. In monolayer CeI2, is no longer a good quantum number for the electron of Ce2+ since the electron is not well localized. Additionally, the delocalized electron has a more plane-wave-like charge density rather than the atom-orbital-like charge density of the electron. Hence only the electron is accompanied by high risks of falling into metastable states in DFT+U calculations. Its electronic orbital requires careful control and observation.
The occupation matrix is the density matrix in particle-number representation and a occupation matrix is sufficient to represent the electronic state of the single electron exactly. Here the general set of 4f atomic orbitals is used as the bases, which are , , , , , , , , , , , , , and , respectively. The spin-quantization axis is chosen to be along direction of the Cartesian coordinate system. We firstly do not take SOC into consideration. Since there is only one localized electron in the shell of Ce2+, any quantum state of the single electron with both spin up and spin down components is unphysical. We thus neglect the spin index and a quantum state of the single electron can be written as
| (2) |
where () is the complex expansion coefficient of the basis. There should be
| (3) |
For simplicity, we mark the quantum state as (, , , , , , ) for the following part of this paper. The eigenvectors and eigenvalues of the occupation matrix are actually quantum states and the corresponding occupation numbers, respectively.
An OMC procedure is to set an initial occupation matrix artificially for the localized electrons in the DFT+U calculations. The initial occupation matrix has also been called the starting point Zhou2022 . Different starting points may access to different final states of the localized electrons. In our calculations, we make our starting points for the Ce- electron all diagonal with a average occupation on several orbital bases. The down spin block and the two off-diagonal blocks of the occupation matrix are null matrices. The up spin block of the occupation matrix has a form of
| (4) |
with
| (5) |
where is the number of orbital bases whose occupation number is non-zero. The trace of the up spin block is the number of occupying electrons, which is equal to for the Ce- shell here. Hence there is
| (6) |
Based on Eqs. (4)-(6), we have different starting points for the DFT+U calculations. After the self-consistent iteration processes based on different starting points, we obtain twenty-four final states of monolayer CeI2, whose electronic states are different with each other. A detailed discussion of the OMC procedure for the SOC situation is provided in Section B of the Supporting Information. SI
IV Magnetic properties of the GS and metastable states
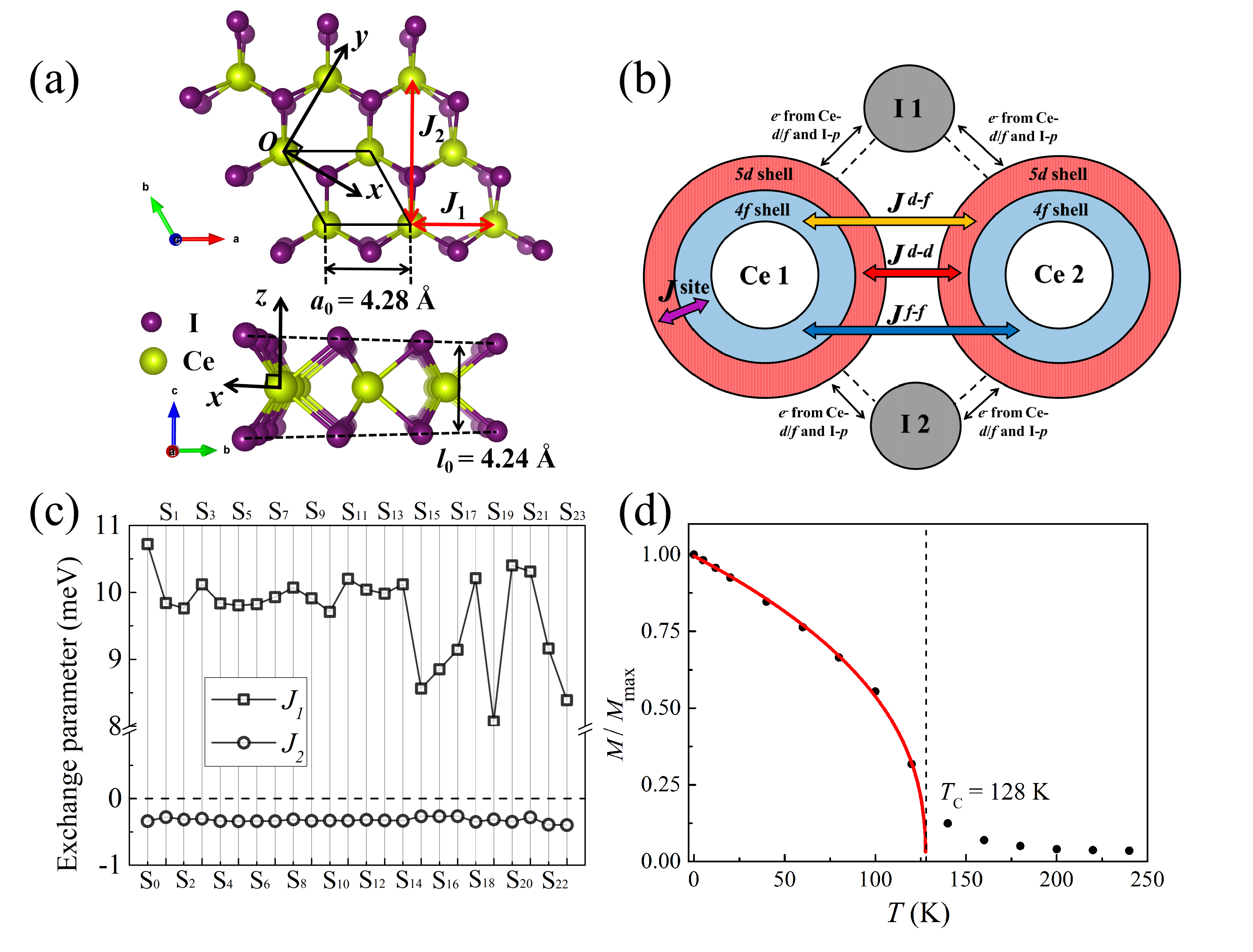
The optimized crystal structure of monolayer CeI2 is shown in Fig. 1(a). Each Ce2+ ion is surrounded by six nearest I- ions which form a regular triangle prism (RTP). The distance between two nearest Ce2+ ions is Å which makes the direct exchange from different Ce sites negligible. The main reason that causes the magnetic order should be the superexchange interaction mediated by I- electrons. Since both Ce- and Ce- electrons contribute to the superexchange interaction, the total inter-site exchange strength can be decomposed to , , and , as shown in Fig. 1(b). These are the exchange parameter between shell and shell, shell and shell, and shell and shell from different sites, respectively. Meanwhile, with the help of coordinated I- ions, the hybridization on each Ce site should be considered. This on-site exchange parameter is denoted by , as shown in Fig. 1(b). For the inter-site exchange parameters, we only consider the first nearest exchange parameter and second nearest exchange parameter as shown in Fig. 1(a). Hence the total Hamiltonian of CeI2 can be express as
| (7) |
with
| (8) |
where is the spin-independent part of the total energy. and denote different sites in the unit cell.
All the following discussions for monolayer CeI2 are based on the fact that the magnetic structure of the GS is FM no matter which orbital the localized electron is occupying. This feature of CeI2 can be verified by our computed total energies of the magnetic structures, as well as the computed values of the exchange parameters, which will be discussed later. With OMC applied, the relative energies of the GS and the metastable states of FM CeI2 are listed in Table I. It is noteworthy that the FM state studied by the previous study Sheng is confirmed to be a metastable state (S20) in our work.
By using a model Hamiltonian of spin interactions like Eq. (7) in combination with the DFT total energies of different magnetic structures, one can fit the values of the exchange parameters. However, this scheme is invalid for monolayer CeI2 because the exchange parameter is not identical for different magnetic structures. A detailed discussion about it is given in Section C of the Supporting Information. SI Here, we make use of the obtained Bloch states by a self-consistent calculation to construct tight-binding Hamiltonian and calculate the exchange parameter by using Green’s function method He . The values of and for monolayer CeI2 with different local electronic states are shown in Fig. 1(c). One can find that is always positive and is always negative for all the states. The absolute value of is far greater than , which favors FM order of monolayer CeI2. Note that is quite sensitive to the electronic states and S0 has the largest .
The exchange parameters of the ground state S0 are used to simulate the of monolayer CeI2. There are meV and meV. Monte-Carlo method is used and is estimated to be about K as shown in Fig. 1(d). It is important to note that the presence of metastable states of monolayer CeI2 can lead to different values of the inter-site exchange parameters, potentially affecting the reliability of the predicted for the material. Therefore, it is also recommended to exclude the metastable states before conducting further calculations for other local-electron systems, in addition to monolayer CeI2.
| electronic state | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| S0 | |||||||||
| S1 | |||||||||
| S2 | |||||||||
| S3 | |||||||||
| S4 | |||||||||
| S5 | |||||||||
| S6 | |||||||||
| S7 | |||||||||
| S8 | |||||||||
| S9 | |||||||||
| S10 | |||||||||
| S11 | |||||||||
| S12 | |||||||||
| S13 | |||||||||
| S14 | |||||||||
| S15 | |||||||||
| S16 | |||||||||
| S17 | |||||||||
| S18 | |||||||||
| S19 | |||||||||
| S20 | |||||||||
| S21 | |||||||||
| S22 | |||||||||
| S23 |
In the case of weak SOC (common in electronic systems), the orbital state of localized electrons is primarily decided by on-site Coulomb interactions and the crystal field. Thus, SOC can be treat as an additional perturbation. In other words, the SOC energy can be safely gained based on the simulated charge density which does not include SOC effect. The SOC Hamiltonian is written as
| (9) |
where parameter denotes the strength of SOC. Applying this approximation to FM monolayer CeI2, the relative energies of different spin directions are computed. As shown in Table I, all the magnetic states have the highest energy when the spin is along direction. The easy axis of spin polarization varies depending on the specific orbital state of the 4f electron. For S0 (the GS), both and directions are the easy axes which are eV lower in energy than the direction. Hence, monolayer CeI2 is recognized as an isotropic in-plane FM material within the theoretical framework of weak SOC.
In order to better understand the origin of the FM order in monolayer CeI2, the components of are computed and listed in Table I. It is observed that the values of , , and are always in the order of for different states. is primarily contributed by , which is similar to the situation in GdI2 (Gd2+: ) Wang2020 . According to Eq. (7), can be obtained from the energy difference of the two spin configurations and for each state, which is denoted as . The computed values of for different states are listed in Table I. The positive values of helps to stabilize the saturated spin moment of Ce2+, i.e. spin configuration is favorable in energy for monolayer CeI2 rather than spin configuration, although the spin singlet state (1G) has been recommended by laser spectroscopy for Ce atoms Worden . The magnetic moment is 2 per Ce coming from the two parallel spins. Furthermore, S0 has the largest value of , which is one of the reason why it leads to the lowest total energy referring to Eq. (7).
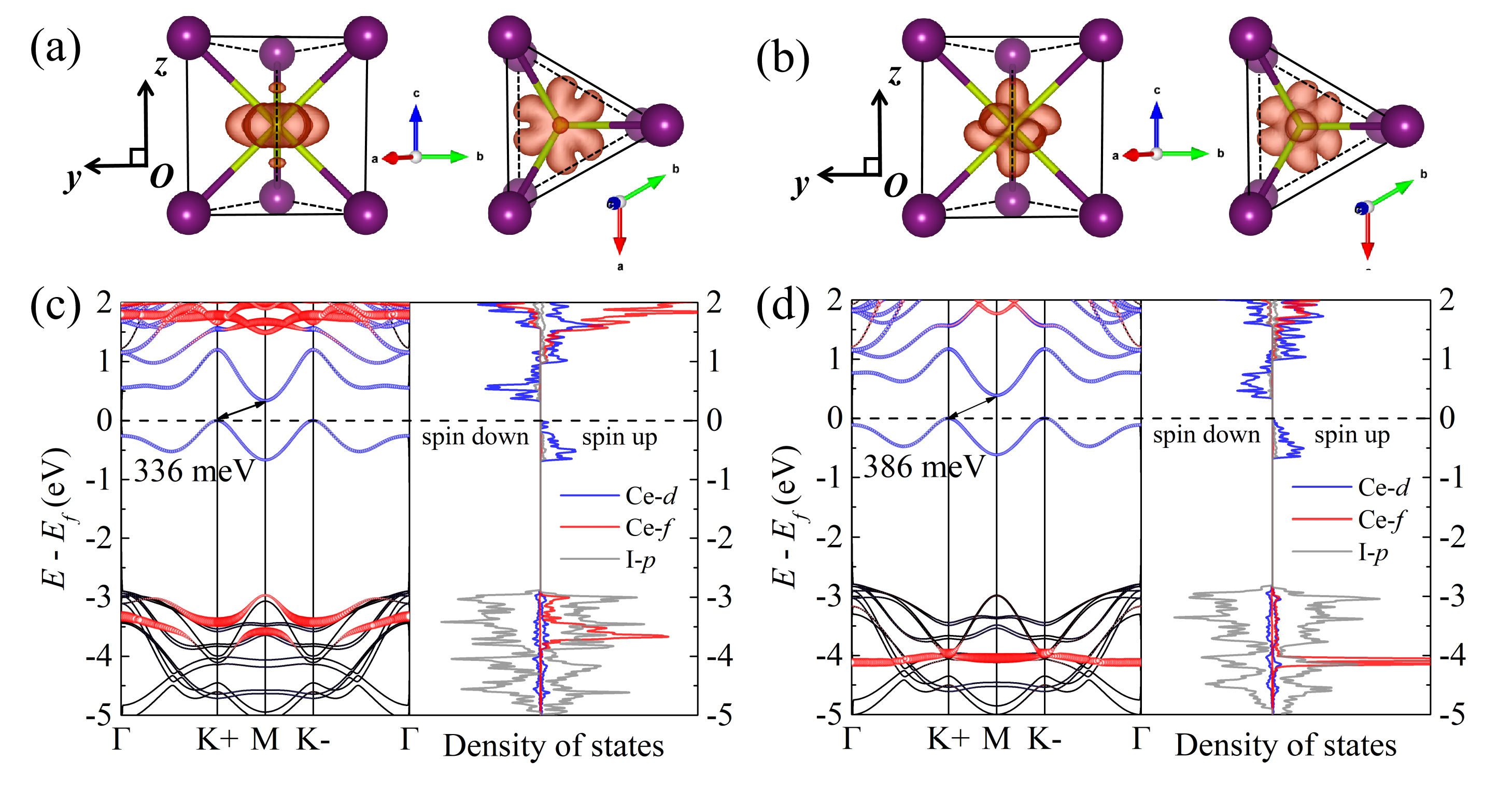
The spin densities and electronic structures of S20 and S0 are illustrated in Fig. 2. The significant difference between the two states can be noticed by inspecting the spin densities. Meanwhile, S0 exhibits more low-energy contributions to the bands from orbitals than that of S20. The dispersion of the electron is much more weak for S0, almost forming a flat band at eV. Since there is hybridization on each Ce site mediated by I- ions, the electronic states are slightly affected by the electronic states as well. The energy gaps of S0 and S20, which are caused by the spin splitting of the electrons, are meV and meV, respectively. In fact, there exists another degenerate ground state S, whose electronic state is (0.66, 0, 0, 0.74, 0, 0, 0). This state is recognized to show exactly the same magnetic properties as S0. The detailed discussion about S is given in Section F of the Supporting Information. SI The spin densities and electronic structures of all the other metastable states are also shown in Section F of the Supporting Information. SI
V Electronic orbital energy in the RTP crystal field
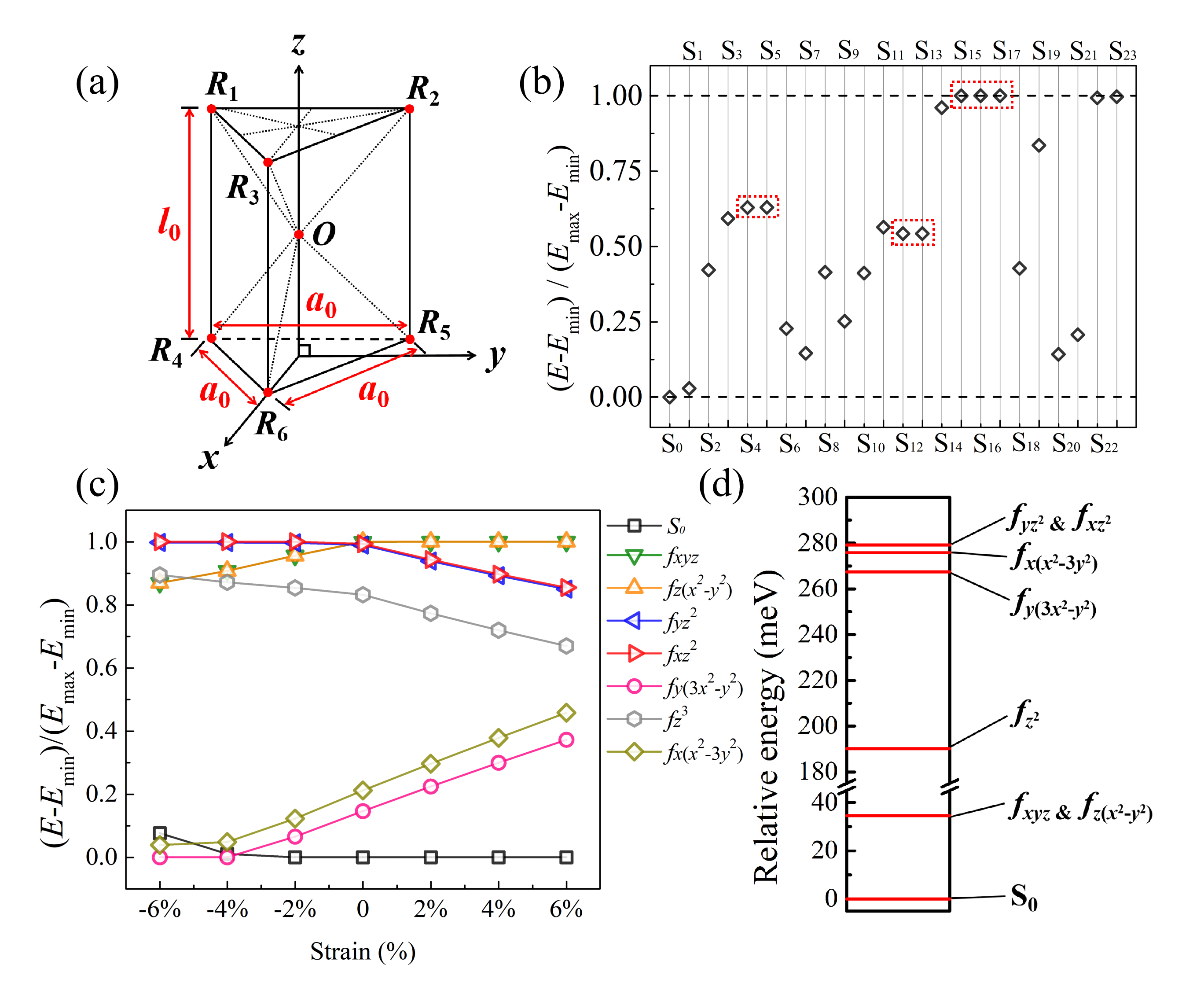
In order to have a better understanding of the ground state of FM monolayer CeI2, we calculate the electronic orbital energies of the single electron when occupying different orbitals in the RTP crystal field. This so-called orbital energy is originated from pure Coulomb interactions. As shown in Fig. 3(a), the single electron is located at , with six surrounding anions located at (, , ) () in the Cartesian coordinate system. The height of the RTP is denoted as and the edge length of the bottom surface is denoted as . and are taken to be Å and Å, respectively, which are based on the relaxed monolayer CeI2 by DFT calculations. The orbital energy can be expressed as
| (10) |
where is the wave function of the single electron and is the crystal field potential energy with a from of
| (11) |
in which the constant term has been set to be unity for simplicity in the calculations. The charge densities of the six I- ions are treated as point charges. Since the single electron of CeI2 is localized, the numerical integration for Eq. (10) is calculated within a integral area :
| (12) |
where denotes the spherical area . The integral radius is set to be times of the Wigner-Seitz radius of Ce to reasonably describe both the local character and the hybridization of the electron.
The orbital energies of all the identified electronic states listed in Table I are computed. As shown in Fig. 3 (b), the electronic state of S0 has the lowest orbital energy in the simulated RTP crystal field environment of the relaxed monolayer CeI2. Now besides the largest value of , the RTP crystal field in monolayer CeI2 also helps to stabilize the ground state S0 by attaching the lowest electronic orbital energy. In the RTP crystal field with D point group symmetry, the original seven-fold orbitals split into three non-degenerate levels , , and a pair of two-fold levels and . The degeneracy of the symmetry-protected orbitals is well-reflected in Fig. 3(b). The orbital states are , , and for S15, S16 and S17, respectively. As and are belong to degenerate , the numerical results of crystal orbital energy are the same for these two orbitals along with their linear combination. The similar degeneracy occurs in S4 and S5, or S12 and S13, which originates from the degenerate : and . What’s more, the degenerate crystal field orbitals also access to exactly equal on-site exchange energy and total energy for monolayer CeI2 referring to Table I. This feature reflects the strong constrain from orbital symmetry for the system.
We explore how the orbital energies are influenced by biaxial strain of monolayer CeI2. We examine the seven general atomic orbitals and the electronic orbital of S0, as shown in Fig. 4 (c). The degeneracy of two groups of orbitals : & and : & are maintained under biaxial strain, since biaxial strain does not change the D3h point group symmetry of monolayer CeI2. The electronic orbital of S0: keeps its lowest orbital energy until the compressive strain reaches 4% of the lattice parameter. Fig.3 (c) reveals the change of relative energies among different atomic orbitals caused by strain of the crystal structure. Although the orbital energy itself does not dominate the local-electron ground state of monolayer CeI2, we expect potential strain-caused phase transition of local electronic state in magnetic transition systems, where the crystal field plays a more important role than electronic systems.
Since OMC is applied, the DFT total energy of the system with the electron occupying arbitrary orbital is able to be gained as long as the corresponding electronic state is metastable. Due to the high symmetry of the crystal field in monolayer CeI2, the seven general atomic orbitals are almost metastable. The corresponding DFT total energies are excerpted from Table I into Fig. 3 (d). Fig.3 (d) shows the feasibility of simulating crystal field excitation by using DFT plus OMC for crystals. This approach includes electronic interactions from the whole crystal field environment, such as non-nearest ligand field and orbital characters of the ligands, which is not that of point charges like in a simple crystal field model. Thus, the simulated crystal field excitation energy is expected to agree with experiments better than model calculations.
So far three kinds of electronic interactions have been verified to have influence on the FM ground state of monolayer CeI2 in this paper. They are inter-site exchange interaction, on-site exchange interaction and crystal field Coulomb interaction. In fact, it is natural to take the crystal field energy of the electron into account. However, with both local and itinerant characters, the simulations for the electron are complicated and are beyond our study. A qualitative discussion about the electronic states in monolayer CeI2 is given in Section E of the supportting information.
VI The magnetic GS with strong SOC
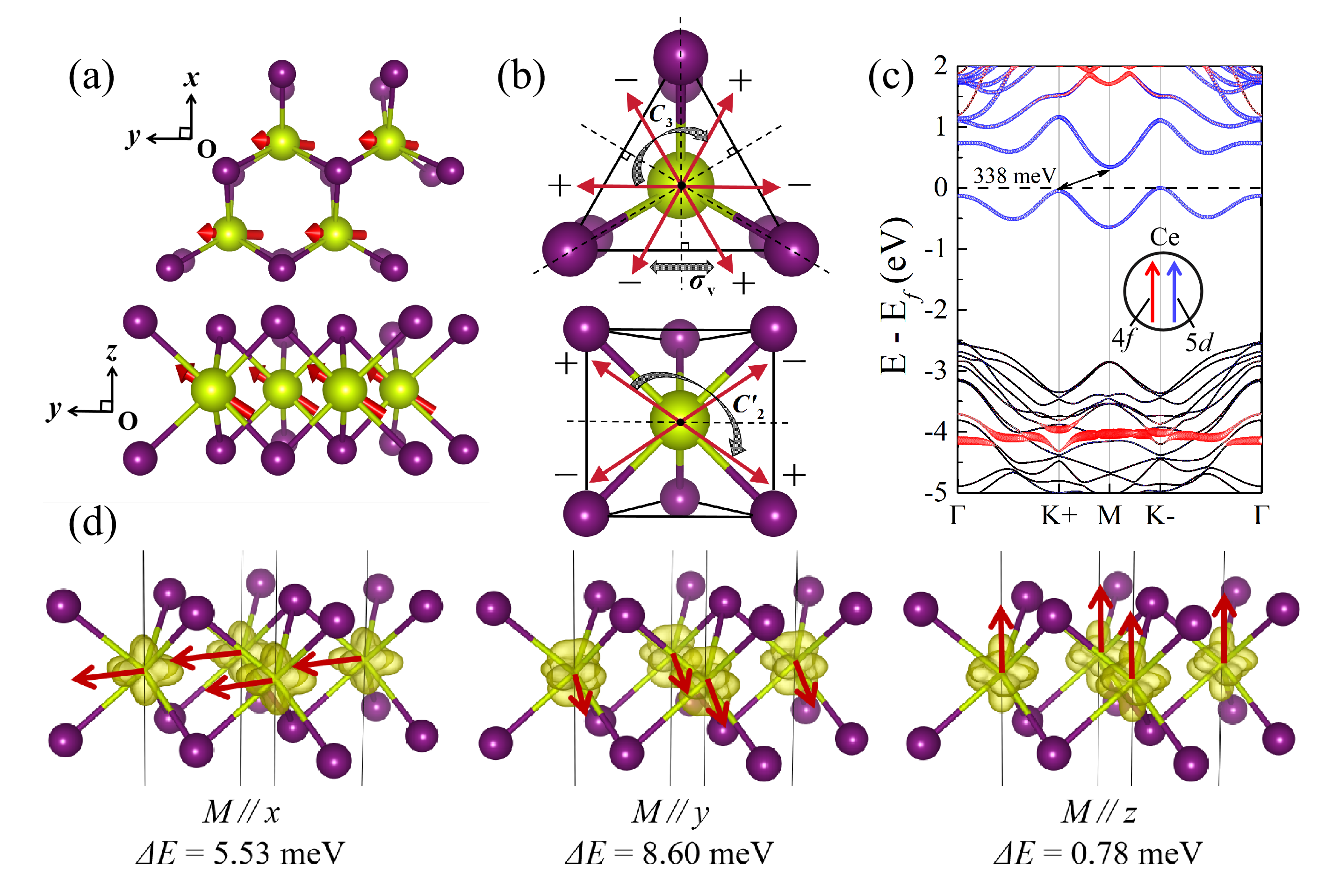
In the more realistic situation, the electronic state of the localized 4f electron in monolayer CeI2 is not only decided by electronic interactions, but also decided by strong SOC. Thus, the acquirement of the magnetic GS requires fully unconstrained noncollinear self-consistent calculations Worden with SOC included in the DFT+U energy functional. Here OMC is once again applied to exclude metastable states. With SOC being considered, the magnetic ground state of monolayer CeI2 still favors FM order, but the magnetic moments are with components of both and directions, as shown in Fig. 4(a). The easy axis of magnetization is coupled with the crystal field, which makes the magnetic moments point toward certain directions of the crystal structure. The ratio of the off-plane () and in-plane () components of the total magnetic moment is . The net magnetic moment for each Ce is about which is contributed by both spin magnetic moment and orbital moment.
The DFT calculations also recommend a 12-fold degenerate magnetic GS for monolayer CeI2 with SOC included, as displayed in Fig. 5(b). All thedegenerate states can be related to the FM GS shown in Fig. 4(a) by the symmetry operations of D3h point group, i.e. {, , , , and }. Due to SOC, the symmetry operations act on both electronic orbitals and spins. Thus these degenerate states can be clearly distinguished by the different orientations of magnetization. Except for the original FM GS, the and rotation operations give birth to another five degenerate states with identical chirality of the electronic orbital. This identical chirality is marked by “” in Fig. 5(b). The inversion operations then double the number of degenerate states, and produce six more states with opposite chirality of the electronic orbital. This opposite chirality is marked by “” in Fig. 5(b). We expect this 12-fold degenerate magnetic GS of monolayer CeI2 could be experimentally verified by magnetic measurements.
The SOC bands of monolayer CeI2 is shown in Fig. 4(c). The two spins from and shells are still parallel to benefit the total energy. No significant and qualitative changes are detected for the electronic structure near the fermi level when compared with the situation without SOC. In spite of this, SOC is essential to reasonably describe the magnetic anisotropy in monolayer CeI2. As shown in Fig. 4(d), with the strong enough external magnetic field along , , and direction, respectively, the total energies of the corresponding magnetized states are meV, meV, and meV higher per Ce than the magnetic GS. These energy differences are one order larger than the situation that SOC is treated as a perturbation. The variation of the electronic orbital contributes to these energy differences, in addition to the SOC energy introduced by Eq. (9). Hence the conclusion that monolayer CeI2 is an isotropic in-plane FM material is no longer satisfied when getting away from the framework of weak SOC which is discussed in Section IV.
The fully off-plane ( direction) FM state is concerned due to its potential application in spintronic devices. A comparison between this FM metastable state and the FM GS is shown in Table II. The included angle of the magnetic moments from the two FM states is 57∘. The fully off-plane FM state is 0.78 meV higher per Ce in total energy that the FM GS. Apparently an appropriate external magnetic field can help to achieve saturated magnetization in the off-plane direction from the GS. We also expect other measures that can tune the magnetic characters of monolayer CeI2 such as electric field or strain.
| (meV) | electronic states | ||
|---|---|---|---|
VII Conclusions
In this work, the ab-initio DFT+U calculations combined with OMC are performed to investigate the magnetic GS of monolayer CeI2. The FM GS and FM metastable states are identified. It is shown that the metastable states have different magnetic properties with the magnetic GS. We recommend that something ought to be done to prevent the metastable states from producing errors when predicting the magnetic properties of such local-electron systems by DFT calculations. The of monolayer CeI2 is simulated to be about K based on the magnetic ground state, not above room temperature as mentioned before. The calculations of on-site exchange parameter and electronic orbital energy imply that the GS of monolayer CeI2 with FM order requires the harmony of multiple types of electron-electron interactions to minimize the total energy. With SOC included, the easy axis of magnetization is found to be coupled with the crystal structure. The FM GS with both in-plane and off-plane components of magnetic moments, and a fully off-plane FM metastable state of monolayer CeI2 are confirmed to be close in total energy. Our work shows it is necessary to absorb SOC into the energy functional to allow SOC to affect the electronic state of the local electrons during the self-consistent calculations. Only in this way could the reliable magnetic GS of monolayer CeI2 be obtained and the magnetic anisotropy be reliably described.
For other systems with local-electron magnetism, the identification of the local electronic states are also significant. However, the phenomenon of trapping into metastable states during the calculations is quite common and it causes confusions if no extra information is given. Here it is recommended to give the specific representation of the computed local electronic state in one’s research. This action helps to enhance the repeatability and normalization of the computational studies for magnetic materials. (All the representations of the used starting points and corresponding final states in our work have been shown in Section G of the Supporting Information. SI )
Acknowledgements.
We thank Doctor Yuan Hong from Institute of Applied Physics and Computational Mathematics for his useful discussions with us. We thank our referees for the time they paid on our manuscript. We are grateful for their helpful comments and suggestions. This work was supported by the National Natural Science Foundation of China (Grant No. 12175023, and No. 12104034).References
- (1) N. D. Mermin and H. Wagner, Absence of ferromagnetism or antiferromagnetism in one-or two-dimensional isotropic Heisenberg models, Phys. Rev. Lett. 17, 1133 (1966).
- (2) X. Jiang, Q. Liu, J. Xing, N. Liu, Y. Guo, Z. Liu, and J. Zhao, Recent progress on 2D magnets: Fundamental mechanism, structural design and modification, Appl. Phys. Rev. 8, 031305 (2021).
- (3) B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero, and X. Xu, Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature 546, 270 (2017).
- (4) S. Tian, J.-F. Zhang, C. Li, T. Ying, S. Li, X. Zhang, K. Liu, and H. Lei, Ferromagnetic van der Waals crystal VI3, J. Am. Chem. Soc. 141, 5326 (2019).
- (5) X. Cai, T. Song, N. P. Wilson, G. Clark, M. He, X. Zhang, T. Taniguchi, K. Watanabe, W. Yao, D. Xiao, M. A. McGuire, D. H. Cobden, and X. Xu, Atomically Thin CrCl3: An in-plane layered antiferromagnetic insulator, Nano Lett. 19, 3993 (2019).
- (6) Z. Zhang, J. Shang, C. Jiang, A. Rasmita, W. Gao, and T. Yu, Direct photoluminescence probing of ferromagnetism in monolayer two-dimensional CrBr3, Nano Lett. 19, 3138 (2019).
- (7) A. Banerjee, J. Yan, J. Knolle, C. A. Bridges, M. B. Stone, M. D. Lumsden, D. G. Mandrus, D. A. Tennant, R. Moessner, and S. E. Nagler, Neutron scattering in the proximate quantum spin liquid -RuCl3, Science 356, 1055 (2017).
- (8) B. Zhou, Y. Wang, G. B. Osterhoudt, P. Lampen-Kelley, D. Mandrus, R. He, K. S. Burch, and E. A. Henriksen, Possible structural transformation and enhanced magnetic fluctuations in exfoliated -RuCl3, J. Phys. Chem. Solids 128, 291 (2019).
- (9) M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M.-H. Phan, and M. Batzill, Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates, Nature Nanotechnol. 13, 289 (2018).
- (10) J. Li, B. Zhao, P. Chen, R. Wu, B. Li, Q. Xia, G. Guo, J. Luo, K. Zang, Z. Zhang, H. Ma, G. Sun, X. Duan, and X. Duan, Synthesis of ultrathin metallic MTe2 (M = V, Nb, Ta) single-crystalline nanoplates, Adv. Mater. 30, 1801043 (2018).
- (11) D. J. O’Hara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta, D. W. McComb, and R. K. Kawakami, Room temperature intrinsic ferromagnetism in epitaxial manganese selenide films in the monolayer limit, Nano Lett. 18, 3125 (2018).
- (12) C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia, and X. Zhang, Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature 546, 265 (2017).
- (13) X. Wang, K. Du, Y. Y. F. Liu, P. Hu, J. Zhang, Q. Zhang, M. H. S. Owen, X. Lu, C. K. Gan, P. Sengupta, C. Kloc, and Q. Xiong, Raman spectroscopy of atomically thin two-dimensional magnetic iron phosphorus trisulfide (FePS3) crystals, 2D Mater. 3, 031009 (2016).
- (14) K. Kim, S. Y. Lim, J. Kim, J.-U. Lee, S. Lee, P. Kim, K. Park, S. Son, C.-H. Park, J.-G. Park, and H. Cheong, Antiferromagnetic ordering in van der Waals 2D magnetic material MnPS3 probed by Raman spectroscopy, 2D Mater. 6, 041001 (2019).
- (15) G. Le Flem, R. Brec, G. Ouvard, A. Louisy, and P. Segransan, Magnetic interactions in the layer compounds MPX3 (M= Mn, Fe, Ni; X= S, Se), J. Phys. Chem. Solids 43, 455 (1982).
- (16) Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J. H. Chu, and X. Xu, Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2, Nat. Mater. 17, 778 (2018).
- (17) A. F. May, D. Ovchinnikov, Q. Zheng, R. Hermann, S. Calder, B. Huang, Z. Fei, Y. Liu, X. Xu, and M. A. McGuire, Ferromagnetism near room temperature in the cleavable van der Waals crystal Fe5GeTe2, ACS Nano 13, 4436 (2019).
- (18) J.-U. Lee, S. Lee, J. H. Ryoo, S. Kang, T. Y. Kim, P. Kim, C.-H. Park, J.-G. Park, and H. Cheong, Ising-type magnetic ordering in atomically thin FePS3, Nano Lett. 16, 7433 (2016).
- (19) Y. Tian, M. J. Gray, H. Ji, R. J. Cava, and K. S. Burch, Magneto-elastic coupling in a potential ferromagnetic 2D atomic crystal, 2D Mater. 3, 025035 (2016).
- (20) Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen, and Y. Zhang, Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2, Nature 563, 94 (2018).
- (21) W. Liu, Y. Xu, S. Hassan, J. Weaver, and G. van der Laan, in Handbook of Spintronics, edited by Y. Xu, D. D. Awschalom, and J. Nitta (Springer, Dordrecht, Netherlands, 2016), pp. 709–756.
- (22) G. van der Laan, Magnetic linear x-ray dichroism as a probe of the magnetocrystalline anisotropy, Phys. Rev. Lett. 82, 640 (1999).
- (23) S. Sarikurt, Y. Kadioglu, F. Ersan, E. Vatansever, O. U. Akturk, Y. Yuksel, U. Akıncı, and E. Akturk, Electronic and magnetic properties of monolayer -RuCl3: a first-principles and Monte Carlo study, Phys. Chem. Chem. Phys. 20, 997 (2018).
- (24) H.-S. Kim and H.-Y. Kee, Crystal structure and magnetism in : An ab initio study, Phys. Rev. B 93, 155143 (2016).
- (25) L. J. Sandilands, Y. Tian, K. W. Plumb, Y.-J. Kim, and K. S. Burch, Scattering continuum and possible fractionalized excitations in -RuCl3, Phys. Rev. Lett. 114, 147201 (2015).
- (26) F. Li, K. Tu, and Z. Chen, Versatile electronic properties of VSe2 bulk, few-Layers, monolayer, nanoribbons, and nanotubes: A computational exploration, J. Phys. Chem. C 118, 21264 (2014).
- (27) C. Ataca, H. Sahin, and S. Ciraci, Stable, single-layer MX2 transition-metal oxides and dichalcogenides in a honeycomb-like structure, J. Phys. Chem. C 116, 8983 (2012).
- (28) W. Chen, J.-m. Zhang, Y.-z. Nie, Q.-l. Xia, and G.-h. Guo, Electronic structure and magnetism of mte2 (m= ti, v, cr, mn, fe, co and ni) monolayers, J. Magn. Magn. Mater. 508, 166878 (2020).
- (29) H.-R. Fuh, C.-R. Chang, Y.-K. Wang, R. F. L. Evans, R. W. Chantrell, and H.- T. Jeng, Newtype single-layer magnetic semiconductor in transition-metal dichalcogenides VX2 (X = S, Se and Te), Sci. Rep. 6, 32625 (2016).
- (30) H. Pan, Electronic and magnetic properties of vanadium dichalcogenides monolayers tuned by hydrogenation, J. Phys. Chem. C 118, 13248 (2014).
- (31) M. Kan, S. Adhikari, and Q. Sun, Ferromagnetism in mnx2 (x= s, se) monolayers, Phys. Chem. Chem. Phys. 16, 4990 (2014).
- (32) G. T. Lin, H. L. Zhuang, X. Luo, B. J. Liu, F. C. Chen, J. Yan, Y. Sun, J. Zhou, W. J. Lu, P. Tong, Z. G. Sheng, Z. Qu, W. H. Song, X. B. Zhu, and Y. P. Sun, Tricritical behavior of the two-dimensional intrinsically ferromagnetic semiconductor CrGeTe3, Phys. Rev. B 95, 245212 (2017).
- (33) M.-W. Lin, H. L. Zhuang, J. Yan, T. Z. Ward, A. A. Puretzky, C. M. Rouleau, Z. Gai, L. Liang, V. Meunier, B. G. Sumpter, P. Ganesh, P. R. C. Kent, D. B. Geohegan, D. G. Mandrus, and K. Xiao, Ultrathin nanosheets of CrSiTe3: a semiconducting two-dimensional ferromagnetic material, J. Mater. Chem. C 4, 315 (2016).
- (34) H. Wang, F. Fan, S. Zhu, and H. Wu, Doping enhanced ferromagnetism and induced half-metallicity in CrI3 monolayer, Europhys. Lett. 114, 47001 (2016).
- (35) W.-B. Zhang, Q. Qu, P. Zhu, and C.-H. Lam, Robust intrinsic ferromagnetism and half semiconductivity in stable two-dimensional single-layer chromium trihalides, J. Mater. Chem. C 3, 12457 (2015).
- (36) J. Liu, Q. Sun, Y. Kawazoe, and P. Jena, Exfoliating biocompatible ferromagnetic Cr-trihalide monolayers, Phys. Chem. Chem. Phys. 18, 8777 (2016).
- (37) W. Jiang, Y. Hou, S. Li, Z. Fu, and P. Zhang, Magnetic phase diagram of single-layer CrBr3, Chinese Phys. B 30, 127501 (2021).
- (38) A. I. Liechtenstein, V. I. Anisimov, J. Zaanen, Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators, Phys. Rev. B 52, R5467 (1995).
- (39) S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+ U study, Phys. Rev. B 57, 1505 (1998).
- (40) Jeremy P. Allen and Graeme W. Watson, Occupation matrix control of d- and f- electron localisations using DFT+ U, Phys. Chem. Chem. Phys. 16, 21016-21031 (2014).
- (41) A. B. Shick, W. E. Pickett, and A. I. Liechtenstein, Ground and metastable states in -Ce from correlated band theory, Journal of Electron Spectroscopy and Related Phenomena 114–116, 753-758 (2001).
- (42) A. Miskowiec, Metastable electronic states in uranium tetrafluoride, Phys. Chem. Chem. Phys. 20, 10384-10395 (2018).
- (43) B. Dorado, B. Amadon, M. Freyss, and M. Bertolus, DFT+U calculations of the ground state and metastable states of uranium dioxide, Phys. Rev. B 79, 235125 (2009).
- (44) B. Dorado, G. Jomard, M. Freyss, and M. Bertolus, Stability of oxygen point defects in UO2 by first-principles DFT+U calculations: Occupation matrix control and Jahn-Teller distortion, Phys. Rev. B 82, 035114 (2010).
- (45) B. Dorado, M. Freyss, B. Amadon, M. Bertolus, G. Jomardand P. Garcia, Advances in first-principles modelling of point defects in UO2: f electron correlations and the issue of local energy minima, J. Phys.: Condens. Matter 25, 333201 (2013).
- (46) M. S. Christian, E. R. Johnson,and Theodore M. Besmann, Interplay between London dispersion, Hubbard U, and metastable states for uranium compounds, J. Phys. Chem. A 125, 2791-2799 (2021).
- (47) A. Claisse, M. Klipfel, N. Lindbom, M. Freyss, and P. Olsson, GGA+ U study of uranium mononitride: A comparison of the U-ramping and occupation matrix schemes and incorporation energies of fission products, Journal of Nuclear Materials 478, 119-124 (2016).
- (48) G. Jomard, B. Amadon, F. Bottin, and M. Torrent, Structural, thermodynamic, and electronic properties of plutonium oxides from first principles, Phys. Rev. B 78, 075125 (2008).
- (49) Y. Hou, W. Jiang, S. Li, Z. Fu, and P. Zhang, Magnetic ground state of plutonium dioxide: DFT+ U calculations, Chinese Phys. B 32, 027103 (2022).
- (50) L. Camerano and G. Profeta, Symmetry breaking in vanadium trihalides, 2D Mater. 11, 025027 (2024).
- (51) F. Jollet, G. Jomard, B. Amadon, J. P. Crocombette, and D. Torumba, Hybrid functional for correlated electrons in the projector augmented-wave formalism: Study of multiple minima for actinide oxides, Phys. Rev. B 80, 235109 (2009).
- (52) L. E Ratcliff, L. Genovese, H. Park, P. B Littlewood and Alejandro Lopez-Bezanilla, Exploring metastable states in UO2 using hybrid functionals and dynamical mean field theory, J. Phys.: Condens. Matter 34, 094003 (2022).
- (53) B. Meredig, A. Thompson, H. A. Hansen, C. Wolverton, and A. van de Walle, Method for locating low-energy solutions within DFT+U, Phys. Rev. B 82, 195128 (2010).
- (54) H. Y. Geng, Y. Chen, Y. Kaneta, M. Kinoshita, and Q. Wu, Interplay of defect cluster and the stability of xenon in uranium dioxide from density functional calculations, Phys. Rev. B 82, 094106 (2010).
- (55) B. Amadon, F. Jollet, and M. Torrent, and cerium: calculations of ground-state parameters, Phys. Rev. B 77, 155104 (2008).
- (56) F. Zhou and V. Ozolins, Crystal field and magnetic structure of UO2, Phys. Rev. B 83, 085106 (2011).
- (57) S. Zhou, H. Ma, E. Xiao, K. Gofryk, C. Jiang, M. E. Manley, D. H. Hurley, and C. A. Marianetti, Capturing the ground state of uranium dioxide from first principles: Crystal distortion, magnetic structure, and phonons, Phys. Rev. B 106, 125134 (2022).
- (58) B. Amadon, A self-consistent DFT + DMFT scheme in the projector augmented wave method: applications to cerium, Ce2O3 and Pu2O3 with the Hubbard I solver and comparison to DFT + U, J. Phys.: Condens. Matter 24, 075604 (2012).
- (59) J. Rabone, and M. Krack, A procedure for bypassing metastable states in local basis set DFT+ U calculations and its application to uranium dioxide surfaces, Computational Materials Science 71, 157–164 (2013).
- (60) K. Sheng, Q. Chen, H. K. Yuan, and Z. Y. Wang, Monolayer CeI2: An intrinsic room-temperature ferrovalley semiconductor, Phys. Rev. B 105, 075304 (2022).
- (61) Kresse G. and Furthmuller J., Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996).
- (62) Blöchl P. E., The projector augmented wave method: ab-initio molecular dynamics with full wave functions, Phys. Rev. B 50, 17953 (1994).
- (63) Kresse G., Joubert D., From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B 59, 1758 (1999).
- (64) Blöchl P. E., Först C. J., and Schimpl J. B., Projector augmented wave method:ab initio molecular dynamics with full wave functions, Bull. Mater. Sci. 26, 33 (2003).
- (65) Perdew J. P., Burke K., and Wang Y., Generalized gradient approximation for the exchange-correlation hole of a many-electron system, Phys. Rev. B 54, 16533 (1996).
- (66) P. Larson, W. R. L. Lambrecht, A. Chantis, and M. van Schilfgaarde, Electronic structure of rare-earth nitrides using the LSDA+U approach: Importance of allowing 4f orbitals to break the cubic crystal symmetry, Phys. Rev. B 75, 045114 (2007).
- (67) A. A. Mostofi, J. R. Yates, Y. Lee, I. Souza, D. Vanderbilt, N. Marzari, wannier90: A tool for obtaining maximally-localised Wannier functions, Computer Physics Communications 178, 685–699 (2008).
- (68) X. He, N. Helbig, M. J. Verstraete, and E. Bousquet, TB2J: A python package for computing magnetic interaction parameters, Computer Physics Communications 264, 107938 (2021).
- (69) Y. Miyatake, M. Yamamoto, J. J. Kim, M. Toyonaga and O. Nagai, On the implementation of the heat bath algorithms for Monte Carlo simulations of classical Heisenberg spin systems, J. Phys. C: Solid State Phys. 19, 2539 (1986).
- (70) K. Momma and F. Izumi, VESTA: a three-dimensional visualization system for electronic and structural analysis, J. Appl. Cryst. 41, 653-658 (2008).
- (71) V. Wang, N. Xu, J. Liu, G. Tang, and W. Geng, VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code, Computer Physics Communications 267, 108033 (2021).
- (72) B. Wang, X. Zhang, Y. Zhang, S. Yuan, Y. Guo, S. Dong and J. Wang, Prediction of a two-dimensional high-TC f-electron ferromagnetic semiconductor, Mater. Horiz. 7, 1623-1630 (2020).
- (73) E. F. Worden, R. W. Solarz, and J. A. Paisner, First ionization potentials of lanthanides by laser spectroscopy, J. Opt. Soc. Am. 68 (1978).
- (74) See Supporting Information [link to be inserted by publisher] for more discussions and simulated results about monolayer CeI2.