Magnetic Monopoles and Exotic States in
$SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}$

Thomas W. Kephart 0000-0001-6414-9590 tom.kephart@gmail.com Department of Physics and Astronomy, Vanderbilt University, Nashville, TN 37235, USA Qaisar Shafi Bartol Research Institute, Department of Physics and Astronomy, University of Delaware, Newark, DE 19716, USA

(May 2, 2025)

Abstract

Abstract:
In the Pati-Salam gauge symmetry $SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}$ (4-2-2, for short), the observed quarks and leptons of each family reside in the bi- fundamental representations $(4,2,1)$ and $({\bar{4}},1,2)$ . There exist, however, the fundamental representations $(4,1,1)$ , $(1,2,1)$ and $(1,1,2)$ and their hermitian conjugates, which show the presence, in principle, of yet to be discovered color triplets that carry electric charge $\pm{e/6}$ , and color singlet particles with charges of $\pm{e/2}$ . These Standard Model charges are in full accord with the fact that the 4-2-2 model predicts the presence of a topologically stable finite energy magnetic monopole that carries two quanta of Dirac magnetic charge, i.e., $4\pi/e$ , as well as color magnetic charge that is screened beyond the quark confinement scale. The 4-2-2 model therefore predicts the existence of exotic baryons, mesons and leptons that carry fractional ( $\pm{e/2}$ ) electric charges. Since their origin lies in the fundamental representations of 4-2-2, these exotic particles may turn out to be relatively light, in the TeV mass range or so. The 4-2-2 magnetic monopole mass depends on the 4-2-2 symmetry breaking scale which may be as low as a few TeV.

I Introduction

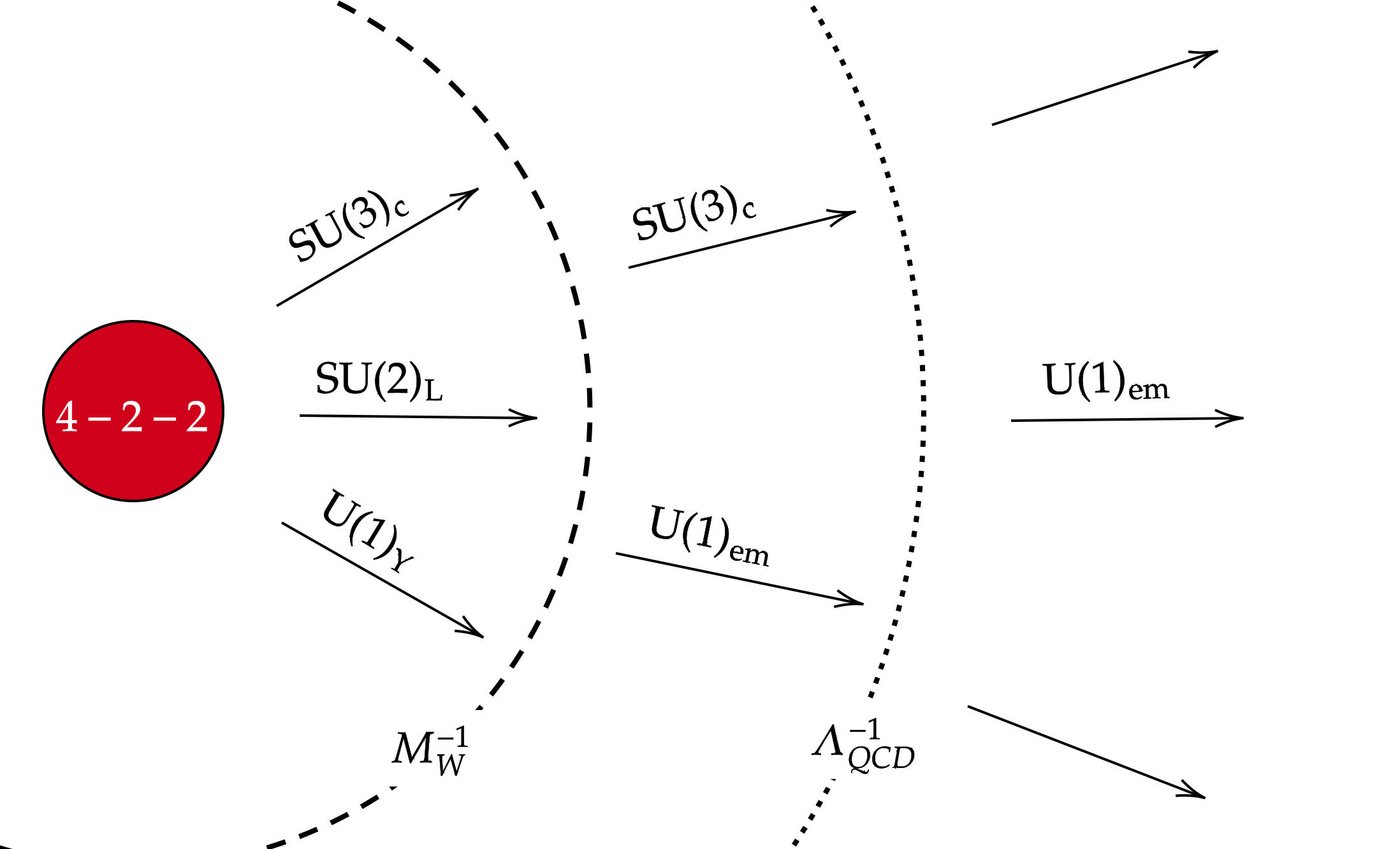
In this article we study some low energy consequences of the Pati-Salam gauge symmetry $SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}$ (4-2-2) [1], which can be spontaneously broken to the Standard Model (SM) in a number of different ways. Along with a right-handed neutrino the observed quarks and leptons of each family reside in the bi-fundamental representations $(4,2,1)$ and $({\bar{4}},1,2)$ of 4-2-2. This feature is nicely explained if the 4-2-2 symmetry is embedded inside the grand unified symmetry group $SO(10)$ (more precisely $Spin(10)$ ). The decomposition of the 16 dimensional spinor representation of $SO(10)$ under 4-2-2 then yields the desired bi- fundamental representations.

However, if we do not assume that the 4-2-2 symmetry is embedded inside SO(10), we are led to consider the possibility that fields (bosons and/or fermions) in the fundamental representations (and their Hermitian conjugates) of 4-2-2 may exist in nature. Among other consequences, this means that the electric charge in 4-2-2 is quantized in units of $\pm{e/6}$ , and the particles carrying this charge are also color triplets, hence exotic quarks, or e-quarks. Because of the $SU(4)_{c}$ symmetry there also appear color singlet leptons with electric charges of $\pm{e/2}$ , i.e., e-leptons. These SM charges are compatible with the fact that the 4-2-2 model contains a topologically stable finite energy monopole that carries two quanta ( $4\pi/e$ ) of Dirac magnetic charge [2] as well as color magnetic field [3].

Recall that topologically stable finite energy monopoles arise from the spontaneous symmetry breaking of a gauge symmetry $G$ with manifest electric charge quantization to the SM. ‘t Hooft [4] and Polyakov [5] provided the first example of this phenomenon based on a toy model in which an SU(2) gauge symmetry is spontaneously broken with a scalar Higgs triplet to a $U(1)$ symmetry. Identifying the three gauge bosons in this toy $SU(2)$ model with $W^{+}$ , $W^{-}$ and photon, and $U(1)_{em}$ as the unbroken symmetry, these authors showed the appearance of a topologically stable monopole in this model carrying two units ( $4\pi/e$ ) of Dirac magnetic charge and with a mass proportional to the symmetry breaking scale of the $SU(2)$ gauge symmetry.

The 4-2-2 monopole mass is proportional to the symmetry breaking scale of the underlying symmetry which may even lie in the low TeV range. As we increase the 4-2-2 breaking scale the monopole mass rises and can even approach the superheavy scale of order $10^{17}$ GeV, which is normally associated with the GUT monopole.

The exotic quarks in the $(4,1,1)+({\bar{4}},1,1)$ representations of the 4-2-2 gauge symmetry give rise to exotic baryons and mesons carrying fractional electric charge ( $\pm{e/2}$ .) The masses of these states can vary anywhere from the TeV region to the superheavy scale. Below we designate all exotically charges particles by appending an “e” prefix as above for e-leptons, e-quarks, and likewise for e-baryons, e-mesons, etc. For a study of exotic states and magnetic monopoles in trinification models based on $SU(3)_{c}\times SU(3)_{L}\times SU(3)_{R}$ (see Raut et al., [6] and references therein.)

II $SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}$ monopole

An elegant extension of the standard model is based on the gauge symmetry G = $SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}$ [1]. The observed quarks and leptons of each family reside in the bi-fundamental representations $({4},{2},{1})$ and $(\overline{4},{1},{2})$ of G. The electric charge generator is given by

Q_{em}=\frac{(B-L)}{2}\;+\;\frac{T_{3R}}{2}\;+\;\frac{T_{3L}}{2},

(1)

where $B$ and $L$ denote baryon and lepton numbers, and $T_{3L}$ , $T_{3R}$ denote the third generators of $SU(2)_{L}$ and $SU(2)_{R}$ respectively. We normalize the $U(1)$ generators as in Ref. [7], so that they have the minimal integer charges compatible with a period of $2\pi$ . Note that G here is a global direct product of the three symmetry groups, and so the first homotopy group of G is trivial. Among other things, this implies that electric charge is quantized in units of $e/6$ . This can be seen by considering the fundamental representation $(4,1,1)$ of G whose components carry electric charges given by ( $e/6,e/6,e/6,-e/2$ ). The first three components are $SU(3)_{c}$ color triplets, and the fourth component is a color singlet particle with electric charge $e/2$ [For a related discussion and additional references, see [6, 8, 9, 10]]. If the 4-2-2 symmetry is spontaneously broken to the SM at a few TeV, as discussed in [11], the predicted monopole acquires a mass in the multi-TeV range and may be accessible at an upgraded LHC or future colliders. Being highly relativistic such a monopole may be accessible in cosmic ray searches [12, 10, 13].

Next let us calculate the minimum Dirac magnetic charge the 4-2-2 monopole carries.

Refer to caption — Figure 1: Schematic diagram showing the structure of the 4-2-2 monopole. The red core represents the region where the 4-2-2 symmetry is restored. Outside the 4-2-2 core and until $M_{W}^{-1}$ , the magnetic fluxes are associated with $SU(3)_{c}$ , $SU(2)_{L}$ , and $U(1)_{Y}$ . Beyond $M_{W}^{-1}$ and until $\Lambda_{\text{QCD}}^{-1}$ , only $SU(3)_{c}$ and $U(1)_{\text{em}}$ fluxes are present. Beyond $\Lambda_{\text{QCD}}^{-1}$ , only the electromagnetic flux remains. This monopole carries two units $(4\pi/e)$ of Dirac charge and its color magnetic flux is screened beyond $\Lambda^{-1}_{QCD}$ .

i) We first consider the direct breaking of 4-2-2 to the SM. The SM hypercharges of the fundamental representation $(4,1,1)$ are given by

Y=\left(\frac{1}{6},\frac{1}{6},\frac{1}{6},-\frac{1}{2}\right).

(2)

Note that in this case the hypercharge $Y$ coincides with the electric charge generator $Q_{em}$ . To identify the 4-2-2 monopole we note that a $4\pi$ rotation with $Y$ in Eq. (2) yields an identity element in the fourth component, but in the first three elements we end up with $e^{2i\pi/3}$ , which lies in $SU(3)_{c}$ . We therefore perform a $4\pi$ rotation along the color hypercharge generator $diag(1/3,1/3,-2/3,0)$ , which brings us back to the identity element.

We conclude that the 4-2-2 monopole carries two quanta $(4\pi/e)$ of Dirac magnetic charge, as well as some color magnetic charge which is subsequently screened beyond the quark confinement radius (see Figure 1). Note that the $4\pi$ rotation above corresponds to a $2\pi$ rotation along the $SU(4)_{c}$ generator $B-L+\frac{2}{3}T_{c}^{8}=diag(1,1,-1,-1)$ . This yields a closed loop in $SU(4)_{c}$ , which is consistent with the fact that $SU(4)_{c}$ is simply connected.

ii) Another way to examine the 4-2-2 monopole is to consider the breaking of this symmetry to the SM via the the phenomenologically interesting subgroup $SU(3)_{c}\times SU(2)_{L}\times SU(2)_{R}\times U(1)_{B-L}$ [14, 15, 16]. To find a stable monopole, we study the first homotopy group,

\pi_{1}\bigl{(}SU(3)_{c}\times SU(2)_{L}\times SU(2)_{R}\times U(1)_{B-L}\bigr{)}.

(3)

Acting on the quarks, a $2\pi$ rotation along the generator $B-L$ leads us to the center of $SU(3)_{c}$ . Acting on the leptons it brings us to the identity element. Next we preform a $2\pi$ rotation along $\frac{2}{3}T_{c}^{8}$ , which brings us back to the identity also in the quark sector. (Note that $U(1)_{B-L}$ intersects $SU(3)_{c}$ in its center.) Furthermore, since the first homotopy groups of $SU(2)_{R}$ and $SU(2)_{L}$ are topologically trivial, we can include $2\pi$ rotations along the generators $T_{3R}$ and $T_{3L}$ without impacting the previous argument.

Put differently, a $4\pi$ rotation along the generator

\frac{\bigl{(}B-L\bigr{)}}{2}\;+\;\frac{T_{3R}}{2}\;+\;\frac{T_{3L}}{2}\;+\;\frac{T_{c}^{8}}{3}\ =Q_{em}+\frac{T_{c}^{8}}{3}\

(4)

brings us back to the identity, which corresponds to a 4-2-2 monopole carrying two units $(4\pi/e)$ of Dirac magnetic charge. The presence of the color hypercharge generator shows that the monopole also carries color magnetic charge.

It is worth pointing out that the direct breaking of SO(10) to the left-right symmetry group in Eq.(3) yields a monopole that carries only a single unit ( $2\pi/e$ ) of Dirac magnetic charge [17]. This is intimately related to the fact that the embedding of left-right symmetry in $SO(10)$ yield new intersections between the topological spaces.

iii. Another interesting 4-2-2 symmetry breaking pattern is as follows:

\begin{split}SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}&\longrightarrow SU(4)_{c}\times SU(2)_{L}\times U(1)_{R}\\ &\longrightarrow SU(3)_{c}\times SU(2)_{L}\times U(1)_{Y}\end{split}

(5)

The first step in the breaking produces a monopole associated with a $2\pi$ rotation along the generator $T_{R}^{3}$ . Since both $SU(4)_{c}$ and $SU(2)_{L}$ are simply connected spaces, we can include $2\pi$ rotations along their respective generators $X=B-L+2/3Y_{c}^{8}$ and $T_{L}^{3}$ , without affecting the preceding topological argument. In other words, we have a monopole associated with a $4\pi$ rotation along the generator $Q_{em}+1/3Y_{c}^{8}$ , where $Q_{em}$ is the generator of electromagnetic charge in 4-2-2, as shown in Eq.(5). Thus, the topologically stable finite energy 4-2-2 monopole carries two units $4\pi/e$ of Dirac magnetic charge as well as some color magnetic charge.

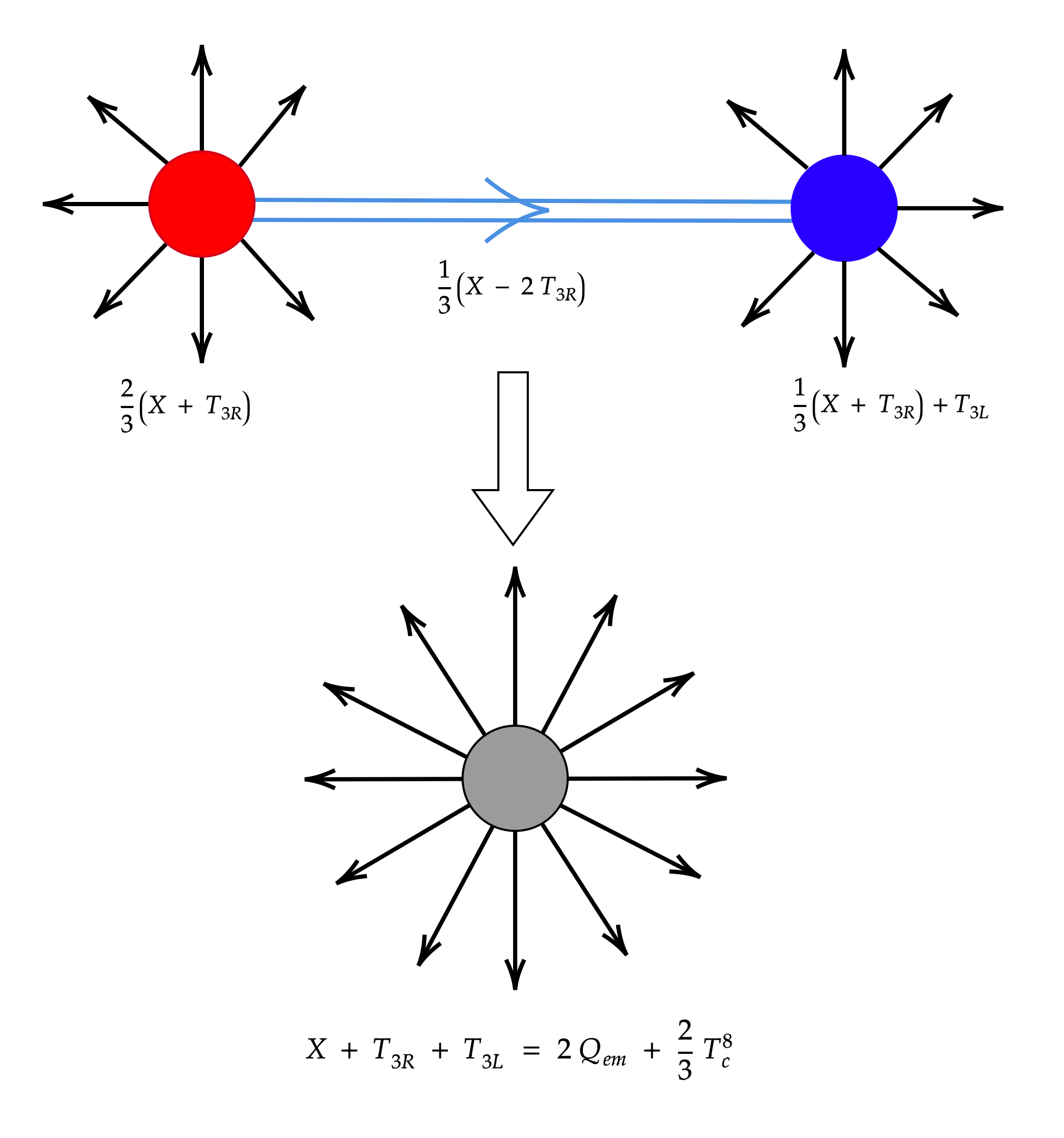
iv. Finally, let us consider the breaking of 4-2-2 to the SM via the breaking chain:

\begin{split}SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}&\longrightarrow SU(3)_{c}\times U(1)_{B-L}\times SU(2)_{L}\times U(1)_{R}\\ &\longrightarrow SU(3)_{c}\times SU(2)_{L}\times U(1)_{Y}\end{split}

(6)

The first breaking yields two kinds of magnetic monopoles which correspond to the breaking of $SU(4)_{c}$ to $SU(3)_{c}\times U(1)_{B-L}$ , and $SU(2)_{R}$ to $U(1)_{R}$ . They were coined red and blue monopoles respectively in Ref. [18]. The breaking of $U(1)_{B-L}\times U(1)_{R}$ to $U(1)_{Y}$ generates a tube that connects a red with a blue monopole, and which pulls the two monopoles together, to form the 4-2-2 monopole, as illustrated in Figure 2. For more details see Refs. [18, 19]. Following Ref. [20], we could refer to the red and blue monopoles as ‘magnetic quarks’ which carry Coulomb as well as confined magnetic flux and do not therefore exist as isolated states. Their merger yields the 4-2-2 monopole, namely a ‘magnetic hadron’ that carries a conserved magnetic charge. It remains to be seen if the topological structure shown in Figure 2 can be found in condensed matter physics.

III Primordial (4-2-2) monopoles

III.1 Production

In many scenarios magnetic monopoles are produced, often in abundance, in early Universe phase transitions. The number density of monopoles emerging from a phase transition is determined by the Kibble mechanism [21], where approximately one monopole or anti-monopole is produced per correlated volume. The resulting monopole number density today is [22]

n_{M}\sim 10^{-19}\,(T_{c}/10^{11}{\rm GeV})^{3}(l_{H}/\xi_{c})^{3}\,{\rm cm}^{-3},

(7)

where $\xi_{c}$ is the phase transition correlation length, bounded from above by the horizon size $l_{H}$ at the time when the region relaxes to the broken–symmetry phase. In a strongly first order transition, the correlation length is much smaller than the horizon size. In a second order or weakly first order phase transition, the correlation length is comparable to the horizon size. While monopoles could have been diluted by annihilation or inflation, they may still exist in detectable numbers today in some models. Next we consider three scenarios according to which an observable number density of primordial monopole may be present in our galaxy. The first example is based on the following symmetry breaking of SO(10), which yields intermediate scale 4-2-2 monopoles:

SO(10)\longrightarrow SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}\longrightarrow SU(3)_{c}\times SU(2)_{L}\times U(1)_{Y}

(8)

The first breaking yields the superheavy GUT monopole, while the second breaking yields a topologically stable intermediate mass 4-2-2 monopole. According to the inflation model described in [23], the GUT monopole is inflated away, but the 4-2-2 monopole with mass comparable to the Hubble parameter during inflation experiences a limited number of e-foldings. The 4-2-2 monopole number density is estimated as follows:

After reheating, the monopole yield $Y_{M}$ takes the form

Y_{M}\equiv\frac{n_{M}}{s}\simeq\frac{\frac{\xi_{c}^{-3}}{10}\exp(-3N_{M})\left(\frac{\tau}{\tau_{r}}\right)^{2}}{\frac{2\pi^{2}}{45}g_{*}T_{r}^{3}},

(9)

where $\xi_{c}\;=\;\min\;\bigl{(}H^{-1},\;m_{\mathrm{eff}}^{-1}\bigr{)},$ specifies the corrolation length at the time of production. The term in the denominator is the entropy density after reheating. The parameter $N_{M}$ denotes the number of e-folds during which monopoles are produced, while $\tau$ , $t_{r}$ , $g_{*}$ , and $T_{r}$ represent the inflation decay time, reheating time, effective number of relativistic degrees of freedom, and temperature at reheating, respectively. The two major effects that reduce the final monopole abundance are the exponential dilution from inflation, $\exp(-3N_{M})$ , and the additional dilution from inflation oscillations, $\left(\tau/t_{r}\right)^{2}$ . In light of the current experimental constraints, the MACRO collaboration sets an upper limit $Y_{M}\lesssim 10^{-27}$ . On the other hand, for any feasible detection, one would typically require $Y_{M}\gtrsim 10^{-35}$ .

Our second example comes from a recent paper [24] that shows how an observable number density of superheavy monopoles can arise from quantum mechanical tunneling in the early universe. This scenario exploits inflation, metastable cosmic strings and the presence of red and blue monopoles as shown in Figure 2.

In our final example [25], which can be extended to the 4-2-2 model, the monopole is associated with a waterfall field which experiences a limited number of $e$ -foldings.

IV Magnetic Monopoles as Cosmic Rays

Magnetic monopoles (MMs) are natural candidates for ultra high energy cosmic rays (UHECRs). See [12, 26] and references therein. In this section we summarize the expected interactions of various types of monopoles with matter and the possibilities of their detection in cosmic ray observatories.

IV.1 Monopole Acceleration

What makes magnetic monopoles such interesting candidates for UHECRs is that all types of monopoles can be accelerated to energies above $\sim 10^{20}$ eV without invoking speculative mechanisms. All one needs are magnetic fields, which are abundant all over the Universe. A free monopole is accelerated along the field lines to high energies.

The kinetic energy gained by a magnetic monopole on traversing a magnetic field along a path is [12]

E_{K}=g\int_{\rm{path}}\vec{B}\cdot\vec{dl}\,\sim\sqrt{n}\,\,g\,B\,\ell\,,

(10)

where

g=e/2\alpha=3.3\times 10^{-8}\,\,dynes/G

(11)

is the magnetic charge, $B$ is the magnetic field strength, $\ell$ is the field’s coherence length, and $\sqrt{n}$ is a factor to roughly approximate the random–walk through the $n$ domains of coherent fields traversed by the monopole path.

	$B/\mu$ G	$\ell$ /Mpc	$gB\ell$ /eV
normal galaxies	$3\;{\rm to}\;10$	$10^{-2}$	$(0.5\;{\rm to}\;1.7)\times 10^{21}$
starburst galaxies	$10\;{\rm to}\;50$	$10^{-3}$	$(1.7\;{\rm to}\;8)\times 10^{20}$
AGN jets	$\sim 100$	$10^{-4}\;{\rm to}\;10^{-2}$	$1.7\times(10^{20}\;{\rm to}\;10^{22})$
galaxy clusters	$5\;{\rm to}\;30$	$10^{-4}\;{\rm to}\;1$	$3\times 10^{18}\;{\rm to}\;5\times 10^{23}$
Extragal. sheets	$0.1\;{\rm to}\;1.0$	1 to 30	$1.7\times 10^{22}\;{\rm to}\;5\times 10^{23}$

Table 1: Estimated magnetic field strength

{\bf B}

, coherence length

\ell

and energies in eV for some astrophysical environments, and the associated monopole energies for a single transit through the regions. For more details and references see [26].

IV.1.1 Magnetic Field Regions

Table 1 list the typical energy gained by a MM in traversing various regions of the Universe. In the table we collect the cosmic magnetic fields and their coherence lengths, inferred from observations of synchrotron radiation, Faraday rotation, and models. The typical monopole kinetic energies that result are all above the Greisen–Zatsepin–Kuzmin (GZK) bound [27, 28].

IV.2 Summary of UHECR Observations

The GHZ bound limits the distance ultra high energy cosmic ray (UHECR) protons can travel due to interactions with cosmic background photons.

p+\gamma\rightarrow\Delta^{*}\rightarrow p+\pi\rightarrow p+...

(12)

The threshold for this process is about $5\times 10^{19}$ eV, leading to a pileup of cosmic ray protons at this energy. But, super GZK energy events have been seen. This implies the initial protons were accelerated nearby, since the mean free path of a super GZK proton is a few Mpc, or that some of the observed events are not protons.

The highest energy cosmic ray ever seen is the HiRes (The High Resolution Fly’s Eye Ultra High Energy Cosmic Ray Observatory) event at energy

3.12\times 10^{20}\,\,eV.

There are now several dozen events above the GZK cutoff. Remarkably, some come from the direction of the local void. As an example, the recently observed Amaterasu event of energy

2.40\times 10^{20}\,\,eV,

tied (within error bars) for second with two other events from the AGASSA observatory, is one such event. The local void is about 45 Mpc across with no known sources of ultra high energy protons and so it is about 10 proton mean free paths (mfps) across, making the idea that the Amaterasu event may be a magnetic monopole primary seem not unlikely.

There are a number of other UHECR events of transGZK energies that appear to be coming reom the direction of the local void. For a discussion see [29].

IV.3 Detection

While all MMs will accelerate to the same energy in a magnetic field, up to a factor of the charge of the monopole, where its charge is some integer $n$ times the Dirac charge, the behavior of the monopoles when interacting with matter can be very different, depending on their characteristics, including mass, charge, and their interaction strengths–strong, weak and/or electromagnetic. Even though there are a large number of possible monopole types, they should each have their own signature. Some could be best seen in air showers, others may need ICE CUBE or something else. But cosmic ray detectors have the best and perhaps only realistic chance of seeing them. However, as low mass monopoles could potentially be see in accelerators, we refer the reader to [30] for a discussion of magnetic monopole phenomenology at future hadron colliders.

IV.3.1 Detectors/Experiments/Observatories

Pioneering UHECR observations were carried out at Volcano Ranch, Haverah Park, SUGAR, Yakutsk, and Akeno arrays which led to new more ambitious observatories with improved detection techniques by the AGASA, Fly’s Eye, HiRes, Auger, Ice Cube and Telescope Array experiments. For reviews see [31, 32].

IV.3.2 Magnetic Monopole Cosmic Ray Shower Development

Monopole CR shower development depends on the monopole mass and structure. The showers from monopoles that only have electromagnetic interactions are slow to develop (They keep most of their energy after a collision, so these monopoles remain at high energy and allow the shower to be are continuously initiated.) By contrast, hadronic monopole showers can develop quickly and can look similar to proton or nucleus showers. The 4-2-2 monopole, we recall, carries color magnetic charge.

IV.3.3 Detection of Monopoles via Electromagnetic Interactions

Monopole electromagnetic energy losses are dominated by the following three processes [26]:
(i) Collisional Energy Loss; (ii) Pair Production; (iii) Monopole Photonuclear Interaction.
At low $\gamma$ the monopole energy loss is dominated by collisional loss. This persists until about $\gamma=10^{4}$ where pair production takes over. This continues until approximately $\gamma=10^{6}$ where photo-nuclear processes take over and dominate asymptotically in $\gamma$ . Other processes like Monopole Bremsstrahlung are always subdominant.

Note that the polarization of Cherenkov radiation from monopoles is rotated 90 degrees from that of protons. This provides the potential to identify monopoles early during shower development.

IV.3.4 Ice Cube

Recently Ice Cube [33] has set new limits on relativistic magnetic monopoles with $0.5\leq\gamma\leq 0.995$ . This improves on their previous bound [34], and agrees with bounds from the ANTARES experiment [35].

IV.3.5 Detection of Hadronic Monopoles

The constituents of hadronic (baryonic or mesonic) monopoles carry magnetic charge and are attached via magnetic flux tubes. The red-blue mesonic case discussed above and shown in Figure 2 is an example. Another example, not studied in this work, is the topologically stable triply charged baryonic monopole [20] from the symmetry breaking $G\rightarrow SU(3)_{c}\times SU(2)_{L}\times U(1)_{Y_{L}}\times U(1)_{Y_{R}}\times U(1)_{R}\rightarrow SU(3)_{c}\times SU(2)_{L}\times U(1)_{Y}\rightarrow SU(3)_{c}\times U(1)_{em}$ , where the constituents are an $SU(2)_{R}$ monopole connected by a flux tube to an $SU(3)_{L}$ monopole which, in turn, is connected to an $SU(3)_{R}$ monopole by a superconducting flux tube. The constituent monopoles are pulled together to form the stable triply charged monopole.

The initial energy of an UHECR is $E_{cr}\sim 10^{20}$ eV or about $10^{8}$ TeV. We assume that the symmetry breaking where a monopole appears is around or just above the electroweak scale, $\Lambda_{SB}\sim 1$ TeV. However, that monopole has mass $M\sim\Lambda_{SB}/\alpha$ , and hence is about two orders of magnitude heavier than $\Lambda_{SB}$ . The center of mass energy of an UHECR monopole colliding with an atmospheric proton is $E_{cm}=\sqrt{m_{p}^{2}+M^{2}+2m_{p}E_{cr}}\sim 10^{3}$ TeV. The magnetic flux tubes can only break by producing a $M{\bar{M}}$ pair, and the flux tube carries energy $\Lambda_{SB}$ per unit length. Hence the tube can stretch by a factor of $\Lambda_{SB}/\alpha$ before breaking. This leads to a cross section that grows by a factor of $\sim 100$ after the first collision, assuming the flux tube has a similar cross section per unit length to the monopole itself. Hence the excited monopole-flux tube system’s cross section approaches that of a typical QCD hadronic cross section. We conclude that the excitation of the initial highly relativistic ( $\gamma\sim 10^{7}$ ) monopole of energy $E_{cr}$ and mass $M\sim 10$ TeV can emulate an ultra high energy proton shower.

V Free Fractional Electric Charge

Monopoles and fractionally-charged color singlets go hand in hand in the class of models that include the 4-2-2 model discussed here. If the minimally charged monopole has multiple Dirac charge, then this implies a fractionally-charged color singlets must be in the theory due to the relation $\frac{eg}{4\pi}=\frac{n}{2}.$ Fractional electric charge has been of interest since Fairbanks et al. [36] redid the Millikan oil drop experiment of the early $20^{th}$ century. In [36] a superconducting magnetic levitation experiment was used. Two of the levitated niobium balls were found to have residual charges of $(+0.337\pm 0.009)$ e and $(-0.331\pm 0.070)$ e.

If free fractional charges exist, they could bind to form atoms. Suppose we have a massive $-\frac{1}{3}e$ charge particle [37, 38] which binds to a proton and forms a hybrid hydrogen atom. The spectral lines in this case resemble hydrogen, but are shifted due to the potential’s change of charge factor from $e^{2}$ to $e^{2}/3.$

Likewise, a free $+e/2$ charged particle, as predicted by the 4-2-2 model, could bind directly to an electron. Again the solution to the Schrodinger equation should be similar to that for the hydrogen atom where $e^{2}\rightarrow e^{2}/2$ everywhere. Since the energy levels for hydrogen are $E_{n}=-(me^{4})/(2\hbar^{2}n^{2})$ , for this new exotic atom we get $E_{n}=-(me^{4})/(8\hbar^{2}n^{2})$ . The spectrum is the same as hydrogen, except it is scaled by a factor of 4. (It looks like it has been red shifted.) So one could search for e-hydrogen by looking for weak shifted hydrogen like lines in stellar atmospheres or gas clouds.

V.0.1 Current Fractional Charge Searches

A variety of experiments are currently searching for magnetic monopoles and related fractionally charged particles [39, 40, 41, 42, 33, 43, 44, 45]. There is an extensive list of bifundamental models with fractional charged color singlets and multi-charged monopoles yet to be fully explored, however these models are beyond the scope of this work [46].

V.0.2 The CMS Search for Fractional Charge

Recently, the CMS Collaboration at CERN has searched for fractionally charged particles via a Drell-Yan-like production mode with $q<e$ in proton-proton collisions at $\sqrt{s}=13$ TeV [47]. They find the most stringent limits to date and exclude masses up to 640 GeV and charges as low as $e/3$ at the 95% confidence level. We emphasize that the lightest exotic charged particle must be stable since charge is conserved.

V.0.3 CUORE and the Search for Fractional Charge

The Cryogenic Underground Observatory for Rare Events (CUORE) at the Laboratori Nazionali del Gran Sasso (LNGS), is a cryogenic calorimetric experiments able to search for fractionally-charged particles [48]. They have recently placed a bound on the flux $\Phi$ of e-particles in the range $e/24$ to $e/2$ at $\Phi<6.9\times 10^{-12}cm^{-2}s^{-1}Sr^{-1}$ (90% C.L.) [49].

VI Summary

Relatively light monopoles in models based on the gauge symmetry $SU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}$ should be accessible at an upgraded LHC or future colliders. This model also predicts e-particles, the existence of particles in exotic color singlet states that carry fractional electric charge. Heavier and intermediate mass monopoles can be searched for in cosmic ray experiments as well as with neutrino detectors. Progress has recently been made in understanding how the superheavy monopole can survive primordial inflation and which may be present in our galaxy at an observable level. For a discussion of magnetic monopole phenomenology at future hadron colliders see [30].

Acknowledgements.

We thank Dr. Rinku Maji for helpful discussions. Q.S. thanks Dr. Amit Tiwari for discussion and collaboration.

References

Pati and Salam [1974] J. C. Pati and A. Salam, Lepton Number as the Fourth Color, Phys. Rev. D 10, 275 (1974), [Erratum: Phys.Rev.D 11, 703–703 (1975)].
Dirac [1931] P. A. M. Dirac, Quantised singularities in the electromagnetic field,, Proc. Roy. Soc. Lond. A 133, 60 (1931).
Lazarides et al. [1980] G. Lazarides, M. Magg, and Q. Shafi, Phase Transitions and Magnetic Monopoles in SO(10), Phys. Lett. B 97, 87 (1980).
’t Hooft [1974] G. ’t Hooft, Magnetic Monopoles in Unified Gauge Theories, Nucl. Phys. B 79, 276 (1974).
Polyakov [1974] A. M. Polyakov, Particle Spectrum in Quantum Field Theory, JETP Lett. 20, 194 (1974).
Raut et al. [2022] D. Raut, Q. Shafi, and A. Thapa, Monopoles, exotic states and muon $g-2$ in TeV scale trinification, Eur. Phys. J. C 82, 803 (2022), arXiv:2201.11609 [hep-ph] .
Slansky [1981] R. Slansky, Group Theory for Unified Model Building, Phys. Rept. 79, 1 (1981).
Kephart and Shafi [2001] T. W. Kephart and Q. Shafi, Family unification, exotic states and magnetic monopoles, Phys. Lett. B 520, 313 (2001), arXiv:hep-ph/0105237 .
Kephart et al. [2007] T. W. Kephart, C.-A. Lee, and Q. Shafi, Family unification, exotic states and light magnetic monopoles, JHEP 01, 088, arXiv:hep-ph/0602055 .
Kephart et al. [2017] T. W. Kephart, G. K. Leontaris, and Q. Shafi, Magnetic Monopoles and Free Fractionally Charged States at Accelerators and in Cosmic Rays, JHEP 10, 176, arXiv:1707.08067 [hep-ph] .
Dolan et al. [2021] M. J. Dolan, T. P. Dutka, and R. R. Volkas, Lowering the scale of Pati-Salam breaking through seesaw mixing, JHEP 05, 199, arXiv:2012.05976 [hep-ph] .
Kephart and Weiler [1996] T. W. Kephart and T. J. Weiler, Magnetic monopoles as the highest energy cosmic ray primaries, Astropart. Phys. 4, 271 (1996), arXiv:astro-ph/9505134 .
Frampton and Kephart [2024] P. H. Frampton and T. W. Kephart, The Amaterasu cosmic ray as a magnetic monopole and implications for extensions of the standard model, Phys. Lett. B 855, 138777 (2024), arXiv:2403.12322 [hep-ph] .
Mohapatra and Pati [1975a] R. N. Mohapatra and J. C. Pati, Left-Right Gauge Symmetry and an Isoconjugate Model of CP Violation, Phys. Rev. D 11, 566 (1975a).
Mohapatra and Pati [1975b] R. N. Mohapatra and J. C. Pati, A Natural Left-Right Symmetry, Phys. Rev. D 11, 2558 (1975b).
Senjanovic and Mohapatra [1975] G. Senjanovic and R. N. Mohapatra, Exact Left-Right Symmetry and Spontaneous Violation of Parity, Phys. Rev. D 12, 1502 (1975).
Maji and Shafi [2025] R. Maji and Q. Shafi, C-parity, magnetic monopoles and higher frequency gravitational waves, (2025), arXiv:2502.10135 [hep-ph] .
Lazarides and Shafi [2019] G. Lazarides and Q. Shafi, Monopoles, Strings, and Necklaces in $SO(10)$ and $E_{6}$ , JHEP 10, 193, arXiv:1904.06880 [hep-ph] .
Lazarides et al. [2023] G. Lazarides, Q. Shafi, and A. Tiwari, Composite topological structures in SO(10), JHEP 05, 119, arXiv:2303.15159 [hep-ph] .
Lazarides and Shafi [2021] G. Lazarides and Q. Shafi, Triply Charged Monopole and Magnetic Quarks, Phys. Lett. B 818, 136363 (2021), arXiv:2101.01412 [hep-ph] .
Kibble [1980] T. W. B. Kibble, Some Implications of a Cosmological Phase Transition, Phys. Rept. 67, 183 (1980).
Kolb [2019] E. W. Kolb, The Early Universe, Vol. 69 (Taylor and Francis, 2019).
Maji and Shafi [2022] R. Maji and Q. Shafi, Monopoles, Strings and Gravitational Waves in Non-minimal Inflation, (2022), arXiv:2208.08137 [hep-ph] .
Lazarides et al. [2024] G. Lazarides, R. Maji, and Q. Shafi, Quantum tunneling in the early universe: stable magnetic monopoles from metastable cosmic strings, JCAP 05, 128, arXiv:2402.03128 [hep-ph] .
Moursy and Shafi [2024] A. Moursy and Q. Shafi, Primordial monopoles, black holes and gravitational waves, (2024), arXiv:2405.04397 [hep-ph] .
Wick et al. [2003] S. D. Wick, T. W. Kephart, T. J. Weiler, and P. L. Biermann, Signatures for a cosmic flux of magnetic monopoles, Astropart. Phys. 18, 663 (2003), arXiv:astro-ph/0001233 .
Greisen [1966] K. Greisen, End to the cosmic ray spectrum?, Phys. Rev. Lett. 16, 748 (1966).
Zatsepin and Kuzmin [1966] G. T. Zatsepin and V. A. Kuzmin, Upper limit of the spectrum of cosmic rays, JETP Lett. 4, 78 (1966).
Kephart and Padgett [pear] T. W. Kephart and M. J. Padgett, Trans-GZK magnetic monopoles from the local void, (2025, to appear).
Ahmed et al. [2024] I. Ahmed, S. Swalheen, M. U. Rehman, and R. Tariq, Magnetic monopole phenomenology at future hadron colliders (2024), arXiv:2404.10871 [hep-ph] .
Nagano and Watson [2000] M. Nagano and A. A. Watson, Observations and implications of the ultrahigh-energy cosmic rays, Rev. Mod. Phys. 72, 689 (2000).
Dawson et al. [2017] B. R. Dawson, M. Fukushima, and P. Sokolsky, Past, Present and Future of UHECR Observations, PTEP 2017, 12A101 (2017), arXiv:1703.07897 [astro-ph.HE] .
Abbasi et al. [2022] R. Abbasi et al. (IceCube), Search for Relativistic Magnetic Monopoles with Eight Years of IceCube Data, Phys. Rev. Lett. 128, 051101 (2022), arXiv:2109.13719 [astro-ph.HE] .
Aartsen [2016] M. G. Aartsen, et al., searches for relativistic magnetic monopoles in icecube, The European Physical Journal C 76, 10.1140/epjc/s10052-016-3953-8 (2016).
Albert [2017] A. Albert, et al., search for relativistic magnetic monopoles with five years of the antares detector data, Journal of High Energy Physics 2017, 10.1007/jhep07(2017)054 (2017).
LaRue et al. [1977] G. S. LaRue, W. M. Fairbank, and A. F. Hebard, Evidence for the existence of fractional charge on matter, Phys. Rev. Lett. 38, 1011 (1977).
Goldberg et al. [1981] H. Goldberg, T. W. Kephart, and M. T. Vaughn, Fractionally Charged Color Singlet Fermions in a Grand Unified Theory, Phys. Rev. Lett. 47, 1429 (1981).
Frampton and Kephart [1982] P. H. Frampton and T. W. Kephart, Fractionally Charged Particles as Evidence for Supersymmetry, Phys. Rev. Lett. 49, 1310 (1982).
Acharya et al. [2024] B. Acharya et al. (MoEDAL), MoEDAL Search in the CMS Beam Pipe for Magnetic Monopoles Produced via the Schwinger Effect, Phys. Rev. Lett. 133, 071803 (2024), arXiv:2402.15682 [nucl-ex] .
ATL [2024] Search for magnetic monopole pair production in ultraperipheral Pb+Pb collisions at $\sqrt{s_{\textrm{NN}}}=5.36$ TeV with the ATLAS detector at the LHC, (2024).
Aad et al. [2023] G. Aad et al. (ATLAS), Search for magnetic monopoles and stable particles with high electric charges in $\sqrt{s}$ = 13 TeV pp collisions with the ATLAS detector, JHEP 11, 112, arXiv:2308.04835 [hep-ex] .
Wulz [2021] C.-E. Wulz (ATLAS, CMS), Searches for Anomalous Ionizing Particles, SIMPs, and Monopoles at the LHC, PoS LHCP2021, 009 (2021).
Frank et al. [2024] M. J. Frank, A. Antoshkin, D. Coveyou, E. C. Dukes, R. Ehrlich, and L. Panda (NOvA), Latest Magnetic Monopole Search Results from NOvA, PoS EPS-HEP2023, 441 (2024).
Panda and Swain [2024] L. Panda and S. Swain, Search for Fast Magnetic Monopoles with NOvA Far Detector, Springer Proc. Phys. 304, 1058 (2024).
Acero et al. [2021] M. A. Acero et al. (NOvA), Search for slow magnetic monopoles with the NOvA detector on the surface, Phys. Rev. D 103, 012007 (2021), arXiv:2009.04867 [hep-ex] .
Sheridan and Kephart [2023] E. Sheridan and T. W. Kephart, A survey of family unification models with bifundamental matter, Nucl. Phys. B 987, 116108 (2023), arXiv:2206.13309 [hep-ph] .
Collaboration [2024] C. Collaboration, Search for fractionally charged particles in proton-proton collisions at $\sqrt{s}$ = 13 tev (2024), arXiv:2402.09932 [hep-ex] .
Arnaboldi et al. [2004] C. Arnaboldi et al. (CUORE), CUORE: A Cryogenic underground observatory for rare events, Nucl. Instrum. Meth. A 518, 775 (2004), arXiv:hep-ex/0212053 .
Adams et al. [2024] D. Q. Adams et al. (CUORE Collaboration), Search for fractionally charged particles with cuore, Phys. Rev. Lett. 133, 241801 (2024).

Magnetic Monopoles and Exotic States in S​U​(4)c×S​U​(2)L×S​U​(2)RSU(4)_{c}\times SU(2)_{L}\times SU(2)_{R}