Magnetic nano-fluctuations in a frustrated magnet

Frustrated systems exhibit remarkable properties due to the high degeneracy of their ground states. Stabilised by competing interactionsSeul1995 , a rich diversity of typically nanometre–sized phase structures appear in polymerSeo2012 and colloidalAdams1998 systems, while the surface of ice pre-meltsWatkins2011 due to geometrically frustrated interactions. Atomic spin systems where magnetic interactions are frustrated by lattice geometry provide a fruitful source of emergent phenomena, such as fractionalised excitations analogous to magnetic monopolesLadak2010 ; Castelnovo2012 . The degeneracy inherent in frustrated systems may prevail all the way down to absolute zero temperatureBalents2010 , or it may be lifted by small perturbationsShokef2011 or entropic effects Savary2012 . In the geometrically frustrated Ising–like magnet Ca₃Co₂O₆, we follow the temporal and spatial evolution of nanoscale magnetic fluctuations firmly embedded inside the spin–density–wave magnetic structure. These fluctuations are a signature of a competing ferrimagnetic phase with an incommensurability that is different from, but determined by the host. As the temperature is lowered, the fluctuations slow down into a super-paramagnetic regime of stable spatiotemporal nano-structures.

The Ising model on a two-dimensional (2D) triangular lattice with antiferromagnetic nearest-neighbour interactions $J_{\mathrm{ab}}>0$ has long embodied the archetype of a geometrically frustrated spin systemWannier1950 ; Houtappel1950 . It is convenient to divide the triangular lattice into three sublattices, whereby every elementary triangle contains one site of each sublattice connected by three antiferromagnetic bonds that cannot be simultaneously satisfied. One bond per triangle remains frustrated at the minimum energy. The extensive ground-state degeneracy, equal to $\exp(0.323N)$ as the number of spins $N\to\infty$, means that the system is a spin liquid at finite temperatures above the $T=0$ critical pointWannier1950 ; Houtappel1950 . The residual entropy can be lifted by increasing the dimensionality through the stacking of layers of triangular lattices on top of each other. Since the interaction $J_{c}$ along the stacking direction $c$ is unfrustrated, the ground state degeneracy reduces to $\exp(0.323N^{2/3})$. The result is a transition at $T>0$ to a partially disordered antiferromagnetic (PDA) state. This state has long-range order along $c$ but only two out of three sublattices are ordered within the $ab$ plane, while the third fluctuates. The competing ferrimagnetic state, with the third sublattice direction fixed, has equal energy to the PDA, but the PDA is favoured for entropic reasonsJiang2006 .

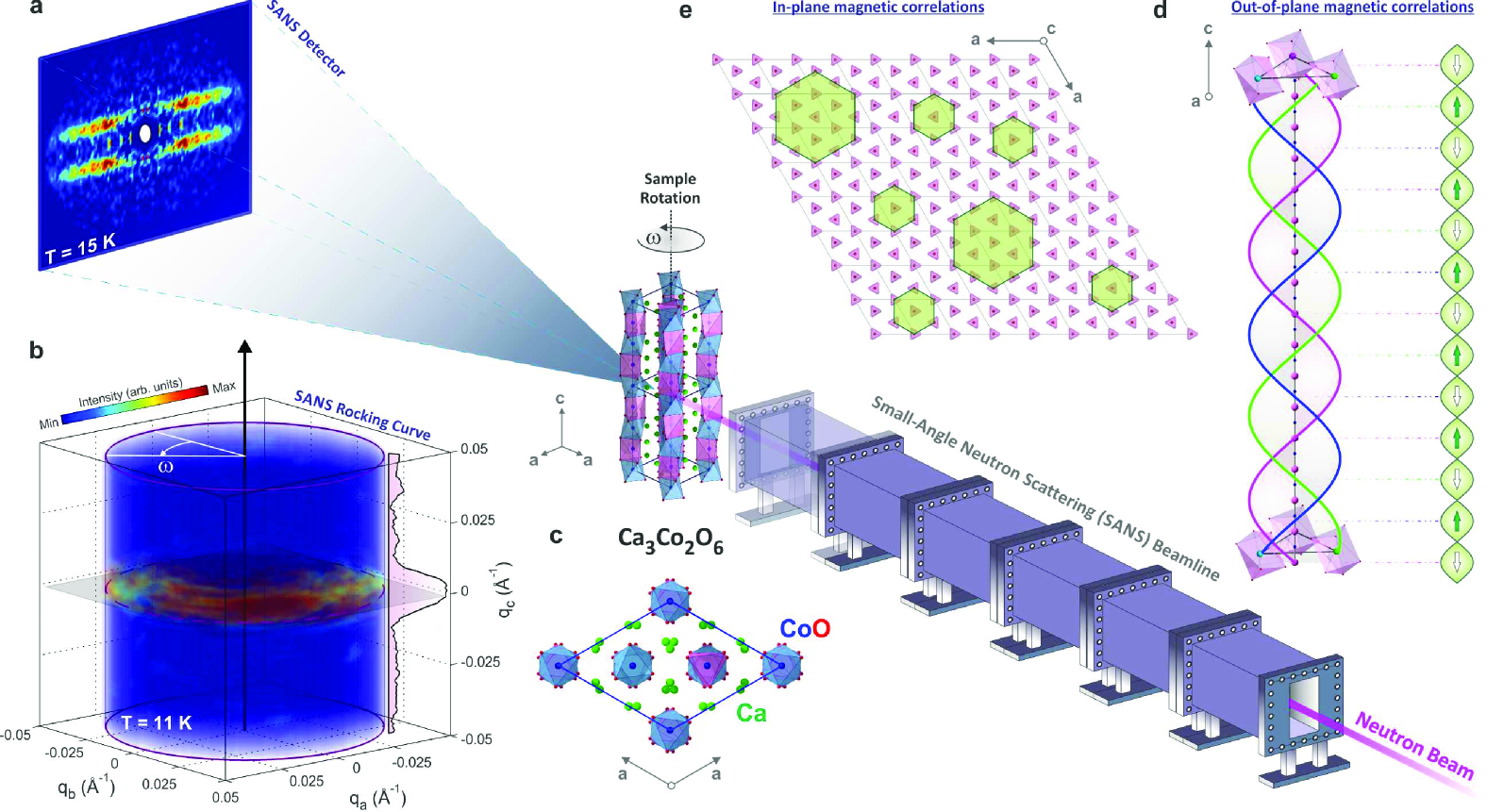
Small angle neutron scattering (SANS) experiments were performed on Ca₃Co₂O₆ to investigate the small $\mathbf{Q}$ reciprocal space structure (Fig.1, central schematic and a). In the frustrated magnet Ca₃Co₂O₆, the magnetic Co³⁺ ions form structural chains along the $c$-axis, with a buckled triangular arrangement in the $ab$ plane (Fig. 1c) resembling the stacked triangular model. The moments point along the chains with an Ising–like anisotropyWu2005 ; Jain2013 , but below the ordering temperature at $T=T_{\mathrm{N}}\simeq 25$ K are amplitude–modulated by an incommensurate longitudinal spin density wave (SDW) propagating along the $c$-axis, with a phase shift of $120^{\circ}$ between adjacent chainsAgrestini2008PRB ; Agrestini2008PRL (Fig. 1d). Every one–sixth of the modulation period, a rigorous PDA condition (an “up”–“down”–“zero” expectation value for the sublattice magnetizations) holds, presumably accompanied by a strong fluctuation of the Ising–like spins. This modulation is thought to be stabilised by interchain interaction pathwaysFresard2004 ; Chapon2009 ; Kamiya2012 .

Here, we uncover ferrimagnetic nanoscale fluctuations forming within the SDW ordered state at all $T<T_{\mathrm{N}}$ in Ca₃Co₂O₆ (Fig. 1a). To scatter neutrons through small angles by reciprocal vectors $\mathbf{Q}$ in the vicinity of the $\mathbf{Q}=\mathbf{0}$ position, a local ferromagnetic component of spin correlations suffices. These dynamic objects produce two parallel streaks at incommensurate positions on the 2D SANS detector (Figs. 2a-b) running perpendicular to the $c$-axis which is aligned in the plane of the detector. This incommensurability is connected with a third of the real-space periodicity $d/3$ of the SDW modulation along $c$, reflecting the strong PDA–like fluctuation points in the ground state of the material (Fig. 1c). The scattering pattern does not change when the sample is rotated about the $c$-axis (Fig. 1b, also see Suppl. Info), implying that correlations are isotropic in the $ab$ plane. Accordingly, we can separate the along-chain ($Q_{\mathrm{c}}$) and the isotropic in-plane ($Q_{\mathrm{ab}}$) components, and the scattered neutron intensity $I(\mathbf{Q})$ is then described by

where $C_{\mathrm{ab}}(r)$ is the spin-spin correlation in the $ab$-plane.

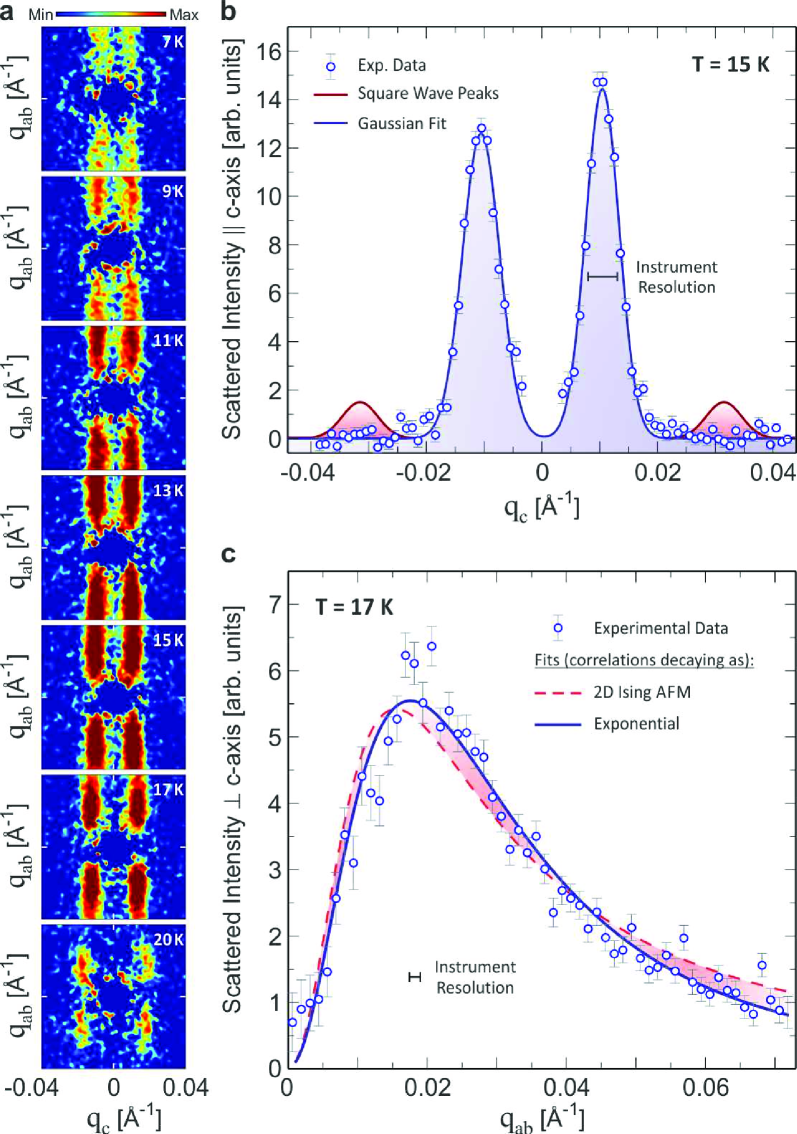
Spin correlations are further studied by looking at the $Q_{\mathrm{ab}}$ dependence of the scattering along the streaks (Fig. 2c). From Eq. (1), such profiles are Hankel transforms of the in-plane spin-spin correlation function $C_{\mathrm{ab}}(r)$ multiplied by $Q_{\mathrm{ab}}^{2}/Q_{\mathrm{c}}^{2}$. This multiplicative factor is a consequence of the dipolar interaction between neutrons and the atomic moments aligned along $c$. In Fig. 2c, we show the measured profile compared to two model spin-spin correlation functions (more are compared in the Supplementary Information): (i) the finite-temperature expression for the 2D triangular lattice antiferromagnet (TLA), $C_{\mathrm{ab}}(r)\sim r^{-\frac{1}{2}}\exp(-r/\xi_{\mathrm{ab}})$, where we have ignored the antiferromagnetic $\cos(2\pi r/3)$ modulationWojtas2009 and (ii) a purely exponentially decaying correlation, $C_{\mathrm{ab}}(r)\sim\exp(-r/\xi_{\mathrm{ab}})$. For both models $\xi_{\mathrm{ab}}$ is temperature dependent. The intensity scale and correlation length $\xi_{\mathrm{ab}}$ are considered as fit parameters to the measured data-set. Model (i) might be anticipated to describe ferromagnetic correlations arising as perturbations of the PDA state, and for a 2D TLA we would expect $\xi_{\mathrm{ab}}\sim 1/|\ln\tanh(1/T)|$ to increase as $T$ (here in units of the model’s coupling constant) decreases. However, the measured $Q_{\mathrm{ab}}$ profiles are seen to flatten as $T$ decreases, implying a decreasing $\xi_{\mathrm{ab}}$. The form of the curves of all the measured datasets (c.f. Supplementary Information) are best described by the exponentially decaying correlations of model (ii). Fitting the data of Fig. 2a to model (ii) gives the correlation length $\xi_{\mathrm{ab}}$ as a function of temperature (Fig. 3a) — indeed showing a decrease of $\xi_{\mathrm{ab}}$ with decreasing temperature. The in–plane exponential decay of spin-spin correlation could be consistent with ferrimagnetic regions existing at the walls between PDA domainsMatsubara1987 or a thermally induced effective interactions within the disordered sublattice (see Supplementary Information). The correlation length along the $c$ axis follows a trend with temperature similar to $\xi_{\mathrm{ab}}$ (Fig. 3a) but is longer due to the stronger interactions along the chains. At 15 K, this structure is extended $\sim 5$ interatomic distances in the $ab$ direction and $\sim 90$ interatomic distances along the $c$ direction in real space (Fig. 1d).

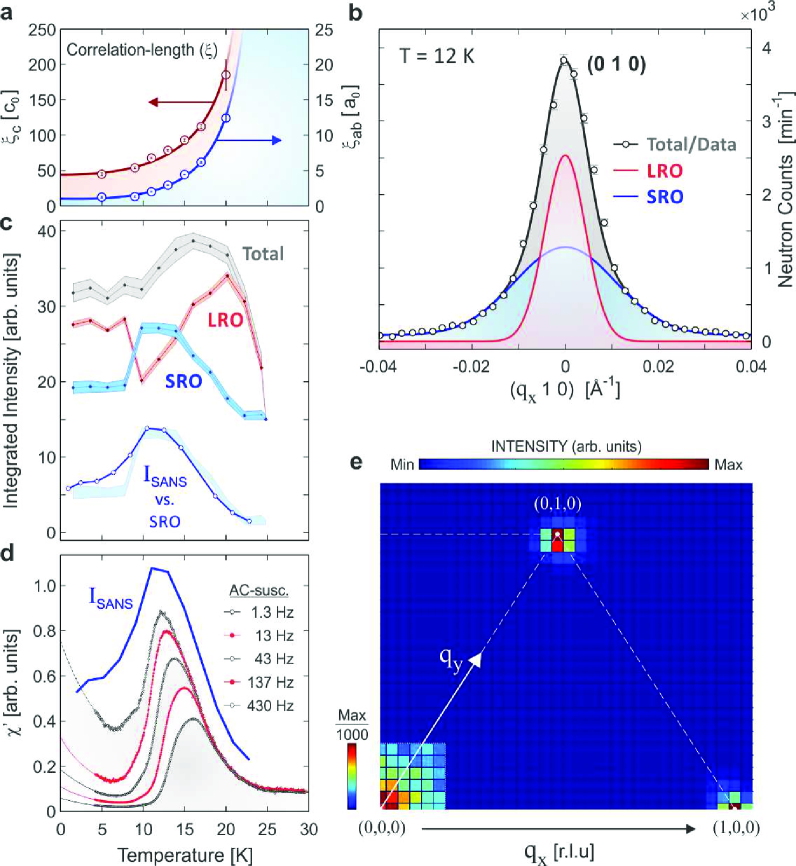
The nanofluctuations originate from, but are distinct from the PDA background. The latter phase is well ordered over large lengthscales $>0.5$ $\mu$m at $T\lesssim 25$ KAgrestini2008PRB , producing resolution-limited antiferromagnetic Bragg peaks in our neutron diffraction data (Fig. 3b). Here the nano-fluctuations generate broad features superimposed on the sharp antiferromagnetic peaksAgrestini2008PRL that are seen to share a common temperature dependence with the SANS signal (Fig. 3c). This is a signature of ferrimagnetic nano-scale objects, which would give broad anti-ferromagnetic and $\textbf{Q}=0$ peaks. The temperature dependences of the integrated intensities reveal a competition between the two components, since the embedded nano-structures exist at the expense of magnetic volume fraction for the host.

Microscopic ferrimagnetism in the compound also explains the experimentally observed magnetic response functions. In agreement with previous studiesHardy2004 , we find a large cusp in the linear susceptibility $\chi^{\prime}$ at temperatures above 12 K (Fig. 3d). The susceptibility curve resembles the SANS intensity, indicative of a common origin. The position in temperature $T_{f}$ of the peak shifts with the ac frequency $f$, a dependence that is characterised by the quantity $g=\Delta T_{f}/[T_{f}\Delta(\log f)]$. Here we find $g=0.17$, which is too big to be consistent with spin glass ($g\lesssim 0.01$) or cluster glass ($g\approx 0.05$) relaxationsMahendiran2003 . Instead larger spin structures are implied, tying in with values $g\gtrsim 0.1$ exhibited by frequency-dependent blocking transitions in superparamagnetic nanostructuresMahendiran2003 . The observed frequency dependence directly reveals the characteristic temporal scales of the nano-fluctuations. As the temperature is lowered, they slow down from the millisecond (16 K) to the second (12 K) timescale, effectively producing stable spatiotemporal objects. Large spin structures are also supported by nonlinear susceptibility measurements (see Supplementary information).

To shed some light on the origin of the nanophases in Ca₃Co₂O₆, we studied the simplified system of the strongly anisotropic stacked triangular lattice. Our Monte Carlo simulations confirm a finite-temperature order–by–disorder phase transition from the disordered high-temperature phase into the partially ordered PDA. This transition is signaled by an extensive peak at the anti-ferromagnetic points in the Brillouin zone (see Fig. 3e and the Supplementary Information). Theoretically it is known that the ferrimagnetic state (which has the same energy as the PDA state) unsuccessfully competes with the PDA stateJiang2006 ; Moessner2001 . Despite this, our Monte Carlo simulations evidence residual ferrimagnetic fluctuations in the structure factor around $\mathbf{Q}=0$ which are non-extensive in their magnitude. The fact that such fluctuations do occur for our model Hamiltonian suggests that additional interactions may further stabilise ferrimagnetic fluctuations in Ca₃Co₂O₆, leading to a plausible explanation for the observed nanophases. These additional interactions will likely entail a coupling of the magnetism to other degrees of freedom. Recent dielectric measurementsBasu2013 indicate magnetoelectric coupling in Ca₃Co₂O₆, which might be envisaged to help stabilise nanophases via local distortions of oxygen octahedraBindu2009 , in a manner analagous to the structural nano-phase separation recently reported in the frustrated antiferromagnet $\alpha$-NaMnO₂Zorko2014 or to the accommodation-strain-mediated phase separation in the colossal magnetoresistant manganitesAhn2004 .

Methods Summary Susceptibility measurements were performed on a CryoBIND ac susceptometer. Direct measurements of the ferrimagnetic nanophases using small-angle neutron scattering were made using the SANS-I and SANS-II instruments at the Swiss Spallation Neutron Source (SINQ) and the D22 instrument at the Institut Laue Langevin. Neutron diffraction measurements on our single crystals were performed on the TASP and Rita-II triple-axis instruments at SINQ.

Acknowledgements K.P. thanks A. Zheludev (ETH Zürich) for discussions. Technical assistance at PSI by M. Bartkowiak and M. Zolliker is highly appreciated. The work at Rutgers University was supported by the DOE under Grant No. DE-FG02-07ER46382.