Magnetic phase diagram of Cu_4-xZn_x(OH)₆FBr studied by neutron-diffraction and $\mu$SR techniques

Two-dimensional (2D) kagome antiferromagnetic (AFM) system has attracted great interests since its strong geometrical frustration effects can give rise to various ground states Messio et al. (2012); Bieri et al. (2015); Iqbal et al. (2015); Gong et al. (2016); Liao et al. (2017); Mei et al. (2017); Wang et al. (2018). Especially, it has been suggested to be one of the best platforms to realize quantum spin liquids (QSLs), which are highly entangled quantum magnetism that typically, although not necessarily, shows no long-range magnetic order down to zero K Savary and Balents (2017); Zhou et al. (2017). Up to now, the most well-studied kagome $S$ = 1/2 magnetic material is the herbertsmithite, ZnCu₃(OH)₆Cl₂, which is believed to host a QSL ground state Norman (2016); Shores et al. (2005); Bert et al. (2007); Mendels et al. (2007). However, there is no consensus on whether its low energy excitations are gapped or gapless Helton et al. (2007); de Vries et al. (2009); Han et al. (2012, 2016a); Fu et al. (2015); Khuntia et al. (2020), which is crucial for us to understand the nature of the QSL state. One of the major difficulties lies in the fact that there are always a few percent of Cu²⁺ ions sitting on Zn²⁺ sites, which mainly affect the low-energy spin excitations Han et al. (2016a); Nilsen et al. (2013).

Recently, there are increasing new materials that also consist of 2D Cu²⁺ kagome layers Sun et al. (2016); Okuma et al. (2017); Feng et al. (2017, 2018a); Puphal et al. (2018); Wei et al. (2019a); Iida et al. (2020). While most of them have magnetic orders, the Zn-doped barlowite (Cu₃Zn(OH)₆FBr) provides a promising new platform to study the QSL physics. The structure of barlowite Cu₄(OH)₆FBr is composed of 2D Cu²⁺ kagome layers with Cu²⁺ ions in between and shows long-range AFM order at 15 KHan et al. (2014); Feng et al. (2018b); Tustain et al. (2018). Substituting interlayer Cu²⁺ with Zn²⁺ can completely destroy the order and when the substitution is 100%, one expects a QSL ground state Feng et al. (2018b); Smaha et al. (2020); Tustain et al. (2020). Indeed, the system shows no magnetic ordering down to 50 mK although its dominate AFM exchange interaction is about 200 K Feng et al. (2017). More interestingly, both NMR and inelastic neutron scattering results suggest it has a gapped QSL ground state Feng et al. (2017); Wei et al. (2019b). Compared to the herbersmithite, it has higher crystal symmetry, which gives rise to smaller Dzyaloshinskii-Moriya interaction (DMI) Han et al. (2016b); Zorko et al. (2008) and thus makes it further away from the quantum phase transition resulted from the DMI interaction Cépas et al. (2008). Moreover, symmetry lowering has been observed in the herbertsmithite but not in Cu₃Zn(OH)₆FBr Zorko et al. (2017); Laurita et al. (2019); Norman et al. (2020); Li et al. (2020).

While the Zn-doped barlowite shows its advantages in studying the QSL physics on a 2D kagome lattice, it still suffers the same magnetic-impurity issues as the herbertsmithite Feng et al. (2017); Wei et al. (2019b). To further address the role of interlayer Cu²⁺ spins, we systematically study the Cu_4-xZn_x(OH)₆FBr system by the neutron-diffraction and $\mu$SR techniques. The long-range magnetic order and low-temperature orthorhombic structure are observed in the neutron-diffraction experiments for $x$ up to 0.23 and 0.43, respectively. The ZF $\mu$SR spectra can be fitted by a phenomenological function, which gives two parameters $A_{0}$ and $\lambda$, corresponding to the extrapolated zero-time asymmetry and long-time relaxation rate, respectively. By combining all the results, we provide a phase diagram of the Cu_4-xZn_x(OH)₆FBr system by combining previous bulk and $\mu$SR results Feng et al. (2018b); Tustain et al. (2020). Our results are consistent with a gapped ground state in Cu₃Zn(OH)₆FBr.

Polycrystalline Cu_4-xZn_x(OH)₆FBr were synthesized by the hydrothermal method as reported previously Feng et al. (2018b). The neutron-diffraction data were obtained on SPODI at FRM-II, Germany, WOMBAT at ANSTO, Australia, and the instrument E9 at HZB, Germany. The nuclear and magnetic structures are refined by the FULLPROF program Rodriguez-Carvajal (1993). The $\mu$SR experiments were carried out in the longitudinal field (LF) geometry at MuSR and EMU spectrometers of the ISIS Facility at the Rutherford Appleton Laboratory, Oxfordshire, U.K. The samples were mounted on a 99.995% silver plate, applying dilute GE varnish covered with a high-purity silver foil. The $\mu$SR data were analyzed by the MantidPlot software Arnold et al. (2014).

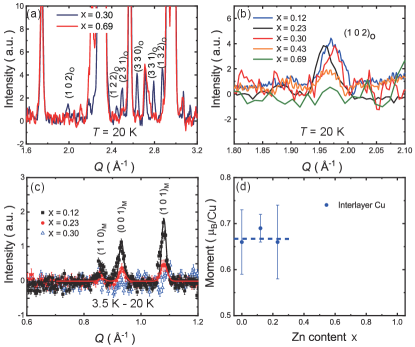
Figure 1(a) shows the neutron-powder-diffraction intensities of the $x$ = 0.3 and 0.69 samples at 20 K. It has been shown that the low-temperature nuclear strucutre of the $x$ = 0 sample is orthorhombic with the space group of $Pnma$ Feng et al. (2018b). To see whether the orthorhombic structure exists in these two samples, the panel only plots the magnification of the data at large $Q$’s, which shows several orthorhombic peaks for the $x$ = 0.3 sample but not for the $x$ = 0.69 sample. Refinements on the data demonstrate that the lattice space group of the $x$ = 0.3 sample is $Pnma$, the same as that in the $x$ = 0 sample Feng et al. (2018b). The structure of the $x$ = 0.69 sample is hexagonal with the space group of $P6_{3}/mmc$ as that of the $x$ = 0.92 sample Feng et al. (2017). Figure 1(b) gives the (1,0,2)_O peak for different samples, which shows that the orthorhombic structure may still present in the $x$ = 0.43 sample. Future studies with large $Q$’s data are need to determine at which doping level the orthorhombic structure disappears.

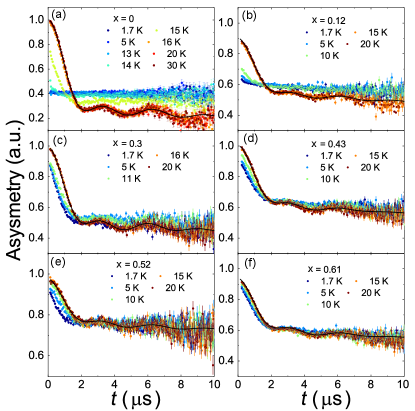
Figure 1(c) shows the first three magnetic peaks for the $x$ = 0.12 and 0.23 samples, which can be refined by the same magnetic structure as in barlowite Feng et al. (2018b). In this structure, the ordered moment mainly comes from the interlayer Cu²⁺ spins, while the magnetic configuration for the kagome spins is rather hard to be determined due to their weak ordered moments Feng et al. (2018b); Tustain et al. (2018). The doping dependence of the ordered interlayer moment is shown in Fig. 1(d), which suggests that its value does not change with doping. The decrease of the magnetic-peak intensities is mainly due to the substitution of nonmagnetic Zn²⁺ ions. While our neutron-diffraction data cannot distinguish whether there is magnetic order for the $x$ = 0.3 sample because of its very weak signal (Fig. 1(c)), previous $\mu$SR has shown that the magnetically ordered phase can survive up to 0.32 Tustain et al. (2020).

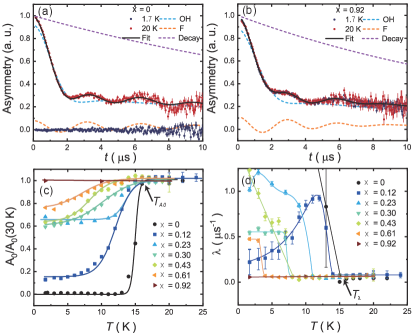
Figure 2 provides the time-dependent ZF $\mu$SR spectra for the Cu_4-xZn_x(OH)₆FBr system. At high temperatures, all of them show oscillation behaviors. With decreasing temperature, the oscillation is completely suppressed in the time range measured here for the low-doping samples but still presents for the middle doping samples. It has been shown that the oscillation is associated with both $\mu$-OH and $\mu$-F complexes Tustain et al. (2020). The actual description of the $\mu$SR spectra needs detailed information of the asymmetry at very low time scale close to zero, which is not accessible for our data. We thus simply introduce the following equation to account for the oscillation,

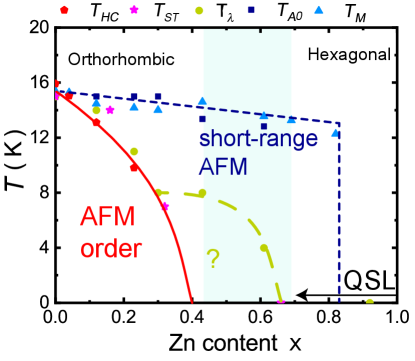
Figure 3(a) and 3(b) further provide detailed analysis of the muon spectra for the $x$ = 0 and 0.92 samples, respectively. The initial fast drop of the asymmetry is mainly due to the $\mu$-OH complex, while the $\mu$-F complex mainly contributes to the oscillation above about 2 $\mu$s Tustain et al. (2020). The relaxation term exp$(-\lambda t)$ is also determined by the long-time data, which may be related to the $\mu$-F complex. Figure 3(c) and 3(d) show the temperature dependence of the fitted parameters $A_{0}$ normalized by its 30-K value and $\lambda$, respectively. For the $x$ = 0 sample, significant changes are found at $T_{N}$ for both $A_{0}$ and $\lambda$. The temperatures are marked as $T_{A0}$ and $T_{lambda}$, respectively. With increasing Zn substitution, both $T_{A0}$ and $T_{\lambda}$ decrease but with different rate. While the former is still above 10 K for the $x$ = 0.61 sample, the latter has already dropped to about 4 K.

Figure 4 gives the phase diagram of Cu_4-xZn_x(OH)₆FBr by summarizing our results and previous studies Feng et al. (2018b); Tustain et al. (2020). It has been previously suggested that the magnetic transition temperatures detected by the heat capacity and magnetic susceptibility, i.e. $T_{HC}$ and $T_{M}$, become different in the Zn-substituted samples Feng et al. (2018b). Here we found that $T_{HC}$ is close to $T_{ST}$, which is defined as the temperature where the frozen volume fraction obtained from the $\mu$SR spectra becomes non-zero Tustain et al. (2020). Since both the heat capacity and frozen volume fraction are measuring the bulk properties, and our neutron-diffraction data also clearly show magnetic peaks up to $x$ = 0.23, we conclude that the region for the long-range order AFM order are marked by $T_{HC}$ and $T_{ST}$.

Figure 4 also demonstrates that $T_{M}$ and $T_{A0}$ are very close to each other, which suggests they have the same origin. As shown above, the value of $A_{0}$ is not the asymmetry at time zero but rather the extrapolated zero-time value after the very-fast initial drop that cannot be detected here. For the $x$ = 0 sample, this kind of drop is due to the local fields from the long-range magnetic order Tustain et al. (2020). With Zn substitution, the long-range order is suppressed but the magnetic clusters, most likely formed by the interlayer Cu²⁺ ions, can still survive and provide local magnetic fields to depolarize the muon spins, which will result in the fast initial drop of the asymmetry. This is consistent with previous discussions on the origin of the $T_{M}$ Feng et al. (2018b). Therefore, the area marked by $T_{M}$ and $T_{A0}$ is associated with the short-range AFM from the interlayer moments. It should be noted that for low-doping samples, the system enters into the short-range AFM first and then becomes long-range ordered with decreasing temperature, which suggests that the long-range AFM order should involve kagome spins.

Tracing the doping dependence of $T_{\lambda}$ shows that it ends at about $x$ = 0.66, which is clearly not associated with either the long-range or the short-range AFM. While its origin is unclear, there are a few results that may be related to it. First, the crossover from the orthorhombic to the hexagonal structure may also happen at the same doping range, as illustrated by the shaded area in Fig. 4. The change of the structure should result in the change of the exchange energies within the kagome planes. Second, it has been shown that the $\mu$SR spectra do not change any more for $x\geq$ 0.66 Tustain et al. (2020), which suggests that the ground states for 0.66 $\leq x\leq$ 1 may be the same. The regime for 0.32 $<x<$ 0.66 is suggested to be the crossover between the static and dynamic ground states. This is consistent with our observation of the regime between red line for the AFM order and green dashed line for $T_{\lambda}$, where the ground state of kagome planes is changing from the 3D order to the gapped quantum spin liquid though an unknown intermediate state. Third, the value of $\lambda$ is mainly determined by the long-time relaxation and thus related to the $\mu$-F complex. The position of the fluorine makes it not sensitive to interlayer spins, as shown by the ¹⁹F NMR measurements Feng et al. (2017). As the low-energy spin excitations become gapped Feng et al. (2017); Wei et al. (2019b), one expect that $\mu$SR spectra from the $\mu$-F complex, which only detect very low-energy excitations, will not change with the temperature any more. These results suggest that the change of $\lambda$ at low temperatures for $x<$ 0.66 may be related to the kagome spins and the gapped QSL state in the $x$ = 1 sample could be extended down to 0.66. It should be noted that the unknown crossover region labeled by the question mark and the QSL state should not be treated as within the short-range magnetic order, but rather as solely coming from the kagome spin system, which is phase-separated from the interlayer spin system.

In conclusions, we establish the magnetic phase diagram of the Cu_4-xZn_x(OH)₆FBr system by comparing several techniques Feng et al. (2018b); Tustain et al. (2020). The short-range spin correlations of the interlayer Cu²⁺ moments can persist up to $x\approx$ 0.82, while the whole spin system only become long-range ordered below $x\approx$ 0.4. The slow exponential decay of the long-time $\mu$SR spectra disappears above $x$ = 0.66, which is consistent with a gapped QSL state. Our results suggest that the kagome and interlayer spin systems are decoupled at high-Zn-doping levels and may help us to further understand the actual magnetic ground state of the 2D kagome antiferromagnet Cu₃Zn(OH)₆FBr.