Magnetized massive stars as magnetar progenitors

Ren-Yu Hu¹ and Yu-Qing Lou¹^,2^,3¹¹footnotemark: 1
¹Physics Department and Tsinghua Centre for Astrophysics (THCA), Tsinghua University, Beijing 100084, China
²Department of Astronomy and Astrophysics, The University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
³National Astronomical Observatories, Chinese Academy of Science, A20, Datun Road, Beijing, 100012, China E-mail: hu-ry07@mails.tsinghua.edu.cn (RYH) and louyq@tsinghua.edu.cn, lou@oddjob.uchicago.edu (Y-QL)

(Accepted 2009 February 16. Received 2009 February 06; in original form 2008 December 16)

Abstract

The origin of ultra-intense magnetic fields on magnetars is a mystery in modern astrophysics. We model the core collapse dynamics of massive progenitor stars with high surface magnetic fields in the theoretical framework of a self-similar general polytropic magnetofluid under the self-gravity with a quasi-spherical symmetry. With the specification of physical parameters such as mass density, temperature, magnetic field and wind mass loss rate on the progenitor stellar surface and the consideration of a rebound shock breaking through the stellar interior and envelope, we find a remnant compact object (i.e. neutron star) left behind at the centre with a radius of $\sim 10^{6}$ cm and a mass range of $\sim 1-3$ M_⊙. Moreover, we find that surface magnetic fields of such kind of compact objects can be $\sim 10^{14}-10^{15}$ G, consistent with those inferred for magnetars which include soft gamma-ray repeaters (SGRs) and anomalous X-ray pulsars (AXPs). The magnetic field enhancement factor critically depends on the self-similar scaling index $n$ , which also determines the initial density distribution of the massive progenitor. We propose that magnetized massive stars as magnetar progenitors based on the magnetohydrodynamic evolution of the gravitational core collapse and rebound shock. Our physical mechanism, which does not necessarily require ad hoc dynamo amplification within a fast spinning neutron star, favours the ‘fossil field’ scenario of forming magnetars from the strongly magnetized core collapse inside massive progenitor stars. With a range of surface magnetic field strengths over massive progenitor stars, our scenario allows a continuum of magnetic field strengths from pulsars to magnetars. The intense Lorentz force inside a magnetar may break the crust of a neutron star into pieces to various extents. Coupled with the magnetar spin, the magnetospheric configuration of a magnetar is most likely variable in the presence of exposed convection, differential rotation, equatorial bulge, bursts of interior magnetic flux ropes as well as rearrangement of broken pieces of the crust. Sporadic and violent releases of accumulated magnetic energies and a broken crust are the underlying causes for various observed high-energy activities of magnetars.

keywords:

magnetohydrodynamics (MHD) — shock waves — stars: magnetic fields — stars: neutron — supernova remnants — white dwarfs

^†^†pagerange: LABEL:firstpage–LABEL:lastpage^†^†pubyear: 2008

1 Introduction

Magnetars are believed to be neutron stars with surface magnetic field strengths considerably stronger than the quantum critical value of $B_{\rm QED}=4.4\times 10^{13}$ G. There are two main types of observational manifestations for magnetars: (i) Soft Gamma-ray Repeaters (SGRs) and (ii) Anomalous X-ray Pulsars (AXPs). Up to now, six SGRs and ten AXPs have been identified observationally (see Mereghetti 2008 for a latest list and an extensive review as well as very recent powerful explosions of SGR J1550-5418 with a shortest spin period of 2.07 s). Most recently, a new Galactic magnetar is reported with very fast optical flares (Kouveliotou, 2008; Stefanescu et al., 2008; Castro-Tirado et al., 2008), alluding a continuum from ordinary dim isolated neutron stars to magnetars. The ultra-intense surface magnetic fields on magnetars are unique in the Universe and they are responsible for various high-energy activities, for example the giant $\gamma$ -ray flare of SGR 1806-20 (e.g. Hurley et al., 2005; Palmer et al., 2005). Magnetar-like X-ray emissions are also detected from a rotation-powered pulsar PSR J1846-0258 with an inferred intense magnetic field of $\sim 4.9\times 10^{13}$ G at the centre of supernova remnant Kes75 (e.g. Gavriil et al., 2008; Archibald et al., 2008).

Recent observations have also provided clues connecting magnetars with very massive progenitor stars, for example an infrared elliptical ring or shell was discovered surrounding the magnetar SGR 1900+14 (e.g. Wachter et al., 2008). However, the formation of magnetars, especially the origin of the ultra-intense magnetic field, remains an important open issue. There are two major contending physical scenarios, viz. the dynamo scenario versus the fossil-field scenario.

Duncan & Thompson (1992) and Thompson & Duncan (1993) explored the turbulent dynamo amplification, occurring primarily in the convection zone of the progenitor, as well as in a differentially rotating nascent neutron star, and concluded that very strong magnetic field, in principle up to $\sim 3\times 10^{17}$ G, may be created. The dynamo mechanism requires an extremely rapid rotation of a nascent neutron star with a spin period of a few milliseconds. However, the current population of magnetars appears to be slow rotators, having spin periods in the range of $\sim 2-12$ s (e.g. Mereghetti, 2008). Therefore, neutron star dynamo scenario for magnetars faces a considerable challenge to account for the fact of slowly rotating magnetars as observed so far.

The fossil-field scenario for the magnetism of compact objects was first proposed to explain magnetic white dwarfs (e.g. Braithwaite & Spruit, 2004; Wickramasinghe & Ferrario, 2005; Ferrario & Wickramasinghe, 2005; Lou & Wang, 2007). It is conceivable that the magnetic field of white dwarfs may be of fossil origin from the main-sequence phase of their progenitors, and the attempt to link magnetic white dwarfs with their main-sequence progenitors naturally makes the chemically peculiar Ap and Bp stars as plausible candidates. Observations of Aurière et al. (2003) have shown that chemically peculiar Ap and Bp stars are generally magnetic indeed, with a surface magnetic field of $\sim$ 100 G by Zeeman splittings. In general, magnetic field strengths fall in the range of $\sim 3\times 10^{2}-3\times 10^{4}$ G (e.g. Braithwaite & Spruit 2004 and references therein). Magnetic white dwarfs may be created as a result of rebound shock explosion (Lou & Wang, 2007) and may further give rise to novel magnetic modes of global stellar oscillations (Lou 1995). By the magnetic flux conservation during the stellar evolution, Ferrario & Wickramasinghe (2005) argued that stellar magnetic fields ( $\sim$ 100 G) in their main-sequence phase can be enhanced up to the range of $\sim 10^{6}-10^{9}$ G on the surface of magnetic white dwarfs. This fossil-field scenario is supported by the statistics for the mass and magnetic field distributions of magnetic white dwarfs.

Based on the same scenario and a similar physical argument, Ferrario & Wickramasinghe (2006) further suggested that the ultra-intense magnetic field over the surface of magnetars may also come from fossil magnetic fields. The progenitors of magnetars are expected to be O stars and early B stars with high surface magnetic fields of $\sim 1000$ G. Ferrario & Wickramasinghe (2008) presented a population synthesis study of the observed properties of magnetars and found that magnetars arise from high mass progenitor stars (20M ${}_{\odot}\;\lower 4.0pt\hbox{${\buildrel\displaystyle<\over{\sim}}$}\;$ M ${\buildrel\displaystyle<\over{\sim}}$ 45M_⊙).

Up to now magnetic fields are directly measured for two O stars, namely $\theta^{1}$ Ori C ( $\sim$ 1 kG, e.g. Donati et al. 2002) and HD 191612 ( $\sim 1.5$ kG, e.g. Donati et al. 2006), and a couple of early B stars, for example the B0.5V star HD 37061 ( $\sim$ 650 G, e.g. Hubrig et al. 2006). Petit et al. (2008a, b) carried out systematic spectropolarimetric observations to search for magnetic fields on all massive OB stars in the Orion Nebula Cluster star-forming region. Strong magnetic fields of the order of kG were inferred on 3 stars out of a sample of 8. The existence of strong magnetic fields on OB stars even appears somewhat overwhelming in contrast to very few magnetars that have been discovered so far.

With the assumption that neutron stars form during the collapse of massive progenitors in the Galactic disc with $8\;\lower 4.0pt\hbox{${\buildrel\displaystyle<\over{\sim}}$}\;M/M_{\odot}\;\lower 4.0pt\hbox{${\buildrel\displaystyle<\over{\sim}}$}\;45$ (stellar masses in the main-sequence phase), and $\sim 8$ percent of massive stars have surface magnetic fields higher than $\sim 1000$ G, Ferrario & Wickramasinghe (2006) estimated that these high-field massive progenitors gave birth to 24 neutron stars with magnetic field $\;\lower 4.0pt\hbox{${\buildrel\displaystyle>\over{\sim}}$}\;10^{14}$ G, consisting a major part of magnetars. While the fossil-field scenario appears plausible from the perspective of statistics, it is highly instructive to have a more direct magnetohydrodynamic (MHD) model description for the core collapse of high-field massive progenitor stars and to check whether compact remnants left behind MHD rebound shocks do possess ultra-intense magnetic fields.

In this paper, we attempt to model magnetized massive progenitor stars with a quasi-spherical general polytropic magnetofluid under the self-gravity (Wang & Lou 2008; Lou & Hu 2009). We examine semi-analytic and numerical solutions to explore the self-similar MHD evolution emerging from dynamic processes of core collapse and rebound shock travelling in the stellar envelope with a wind mass loss. More specifically, we adopt a general polytropic equation of state (EoS) $p=\kappa(r,\ t)\rho^{\gamma}$ with $p$ , $\rho$ , $\gamma$ , and $\kappa$ respectively being the gas pressure, mass density, polytropic index and a proportional coefficient dependent on radius $r$ and time $t$ . Here, $\kappa$ is closely related to the ‘specific entropy’ and is not necessarily a global constant. By ‘specific entropy’ conservation along streamlines, another key parameter $q$ arises in self-similar dynamics (see Wang & Lou, 2008). For $\kappa$ being a global constant, or equivalently $q=0$ , the general polytropic EoS reduces to a conventional polytropic EoS. By further setting $\gamma=1$ , a conventional polytropic gas reduces to an isothermal gas (e.g. Lou & Shen 2004). We also require $\gamma\geqslant 1$ to ensure a positive specific enthalpy $p/(\gamma-1)$ .

Chiueh & Chou (1994) studied the isothermal MHD by including the magnetic pressure gradient force in the radial momentum equation. Yu & Lou (2005), Yu, Lou, Bian & Wu (2006), Wang & Lou (2007) and Wang & Lou (2008) generalized the self-similar hydrodynamic framework by including a completely random transverse magnetic field with the approximation of a ‘quasi-spherical’ symmetry (e.g. Zel’dovich & Novikov 1971); the radial component of such magnetic field is much weaker than the transverse components. We conceive a simple ‘ball of thread’ scenario for random magnetic fields in a massive progenitor star. In other words, a magnetic field line follows the ‘thread’ meandering within a thin spherical ‘layer’ in space in a completely random manner. Strictly speaking, there is always a weak radial magnetic field component such that field lines in adjacent ‘layers’ remain physically connected throughout in space. In particular, we emphasize that the nature of the random magnetic fields inside a progenitor star may be either those generated by dynamo mechanism probably linked with convection and differential rotation (e.g. Spruit, 2002; Heger, Woosley & Spruit, 2005), or those of ‘fossil fields’ entrained from molecular clouds in dynamic processes of star formation (e.g. Wang & Lou, 2007, 2008).

According to numerical simulations of differentially rotating magnetized stars by Heger et al. (2005), the dynamo-powered radial magnetic fields in a progenitor star are about 3 to 4 orders of magnitude weaker than the transverse magnetic fields during the pre-supernova evolution. In line with this hint, we simplify the treatment by only dealing with the dominant transverse field and focus on their dynamic effects on the bulk motion of gas in the radial direction. By taking the ensemble average of magnetic fields in each thin spherical ‘layer’, we smooth out small-scale magnetic field structures and are left with ‘layers’ of large-scale transverse magnetic fields. We also presume that small-scale non-spherical flows as a result of the magnetic tension force may be neglected as compared to large-scale mean radial bulk flow motions. Therefore on large scales, a completely random magnetic field contributes to the dynamics in the form of the average magnetic pressure gradient force and the average magnetic tension force in the radial direction.

This theoretical model framework of self-similar MHD has been applied to gravitational core collapse and rebound shock processes within progenitor stars for supernovae. Lou & Wang (2006, 2007) modelled the hydrodynamic and MHD rebound shocks of supernovae in the self-similar phase of evolution. Hu & Lou (2008b) presented preliminary results for a shock breakout to reproduce the early X-ray light curve of supernova SN 2008D (e.g. Soderberg et al., 2008; Mazzali et al., 2008). In this paper, we demonstrate that such a self-similar MHD process may give birth to a compact remnant with a nuclear density and a range of ultra-intense surface magnetic fields. We will see that massive progenitor stars whose collapsing cores have magnetic fluxes similar to those of magnetars will eventually collapse into neutron stars with a magnetar level of magnetic fluxes because of the magnetic flux conservation. In our model scenario, the neutron star dynamo processes and the required initial rapid spins of nascent neutron stars may not be necessary.

2 General polytropic self-similar magnetohydrodynamics

Under the approximation of quasi-spherical symmetry and based on the physical idea outlined in the introduction, the ideal MHD equations involve mass conservation, radial momentum equation, specific entropy conservation along streamlines and the magnetic induction equation (see Wang & Lou 2008). We highlight the essential parts of this formulation of nonlinear MHD equations below.

2.1 Theoretical MHD Model Formulation

The ideal magnetic induction equation (without the resistivity) implying the frozen-in condition for the magnetic flux can be cast into the following form

\bigg{(}\frac{\partial}{\partial t}+u\frac{\partial}{\partial r}\bigg{)}(r^{2}<B_{t}^{2}>)+2r^{2}<B_{t}^{2}>\frac{\partial u}{\partial r}=0\ ,

(1)

where $u$ is the bulk radial flow speed and $<B_{t}^{2}>$ is the ensemble mean square of a random transverse magnetic field. The weak radial component of the magnetic field is determined by equations (10) and (11) of Yu & Lou (2005). With the self-similar MHD transformation of Wang & Lou (2008), the ideal MHD equations together with the magnetic flux frozen-in condition and the general polytropic EoS can be readily reduced to a set of nonlinear MHD ODEs in the highly compact form of

{\cal X}(x,\alpha,v)\alpha^{\prime}={\cal A}(x,\alpha,v)\ ,\ \ {\cal X}(x,\alpha,v)v^{\prime}={\cal V}(x,\alpha,v)\ ,

(2)

where the prime ^′ stands for the first derivative $d/dx$ , and the three functionals ${\cal X}$ , ${\cal A}$ and ${\cal V}$ are defined by

	$\displaystyle\!\!\!\!\!\!\!\!\!{\cal X}(x,\ \alpha,\ v)\equiv C\bigg{[}2-n+\frac{(3n-2)}{2}q\bigg{]}$
	$\displaystyle\quad\times\alpha^{1-n+3nq/2}x^{2q}(nx-v)^{q}+h\alpha x^{2}-(nx-v)^{2}\ ,$

	$\displaystyle\!\!\!\!\!\!\!\!\!{\cal A}(x,\ \alpha,\ v)\equiv 2\frac{x-v}{x}\alpha\big{[}Cq\alpha^{1-n+3nq/2}x^{2q}(nx-v)^{q-1}$
	$\displaystyle\quad+(nx-v)\big{]}-\alpha\bigg{[}(n-1)v+\frac{(nx-v)}{(3n-2)}\alpha+2h\alpha x$
	$\displaystyle\quad+Cq\alpha^{1-n+3nq/2}x^{2q-1}(nx-v)^{q-1}(3nx-2v)\bigg{]}\ ,$

	$\displaystyle\!\!\!\!\!\!\!\!\!{\cal V}(x,\ \alpha,\ v)\equiv 2\frac{(x-v)}{x}\alpha\bigg{[}C\bigg{(}2-n+\frac{3n}{2}q\bigg{)}$
	$\displaystyle\quad\times\alpha^{-n+3nq/2}x^{2q}(nx-v)^{q}+hx^{2}\bigg{]}$
	$\displaystyle\quad-(nx-v)\bigg{[}(n-1)v+\frac{(nx-v)}{(3n-2)}\alpha+2h\alpha x$
	$\displaystyle+Cq\alpha^{1-n+3nq/2}x^{2q-1}(nx-v)^{q-1}(3nx-2v)\bigg{]}\ .$		(3)

In this straightforward yet somewhat tedious derivation, we have useful relations $m=\alpha x^{2}(nx-v)$ and $q\equiv 2(n+\gamma-2)/(3n-2)$ and we have performed the following MHD self-similar transformation for a general polytropic gas, viz.

	$\displaystyle r=k^{1/2}t^{n}x,\qquad\qquad u=k^{1/2}t^{n-1}v\ ,\$

	$\displaystyle\rho=\frac{\alpha}{4\pi Gt^{2}}\ ,\qquad\qquad p=\frac{kt^{2n-4}}{4\pi G}C\alpha^{\gamma}m^{q},\$

	$\displaystyle M=\frac{k^{3/2}t^{3n-2}m}{(3n-2)G},\qquad\ <B_{t}^{2}>=\frac{kt^{2n-4}}{G}h\alpha^{2}x^{2},$		(4)

where $G=6.67\times 10^{-8}\hbox{ g}^{-1}\hbox{ cm}^{3}\hbox{ s}^{-2}$ is the gravitational constant, $M$ is the enclosed mass at time $t$ within radius $r$ , $x$ is the independent self-similar variable, $v(x)$ is the reduced flow speed, $\alpha(x)$ is the reduced mass density, $m(x)$ is the reduced enclosed mass, $k$ , $n$ and $C$ are three parameters, and the dimensionless coefficient $h$ is referred to as the magnetic parameter such that $<B_{t}^{2}>=16h\pi^{2}G\rho^{2}r^{2}$ . It follows that $q=2/3$ leads to $\gamma=4/3$ for a relativistically hot gas. Only for the case of $q=2/3$ , can the parameter $C$ be independently chosen; otherwise for $q\neq 2/3$ , $C$ can be set to 1 without loss of generality (Lou & Cao 2008; Lou & Hu 2009). The magnetosonic critical curve (MCC) is determined by the simultaneous vanishing of the numerator and denominator on the right-hand sides (RHS) of ODEs (2) and (3). Once solutions are obtained for $v(x)$ and $\alpha(x)$ , the mean magnetic field strength $<B_{t}^{2}>^{1/2}$ can be readily determined from self-similar MHD transformation (4). With proper asymptotic conditions as well as eigen-derivatives across the MCC, nonlinear MHD ODEs (2) and (3) can be numerically integrated by using the standard fourth-order Runge-Kutta scheme (e.g. Press et al., 1986).

It is straightforward to treat MHD shock conditions for self-similar solutions to cross the magnetosonic singular surface ${\cal X}(x,\alpha,v)=0$ . By the conservations of mass, radial momentum, and energy as well as magnetic induction equation in the comoving framework of reference across an MHD shock front, we obtain a set of jump conditions for an MHD shock that can be cast into a self-similar form (see Appendix A, Wang & Lou 2008 and Lou & Hu 2009). Note that the so-called ‘sound’ parameter $k$ in self-similar MHD transformation (4) is related to the polytropic sound speed and changes across a shock front, with the relations $k_{2}=\lambda^{2}k_{1},\ h_{1}=h_{2}=h,\ x_{1}=\lambda x_{2}$ where subscripts $1$ and $2$ refer to the immediate upstream and downstream sides of a shock and $\lambda$ is a dimensionless scaling parameter. Strictly speaking, magnetic fields have very weak radial components normal to the shock front. Our treatment of magnetic field coplanar with the shock front represents a very good approximation for our purposes.

2.2 Analytic Asymptotic MHD Solutions

The analytic asymptotic solutions at large $x$ of nonlinear coupled MHD ODEs (2) and (3) are

	$\displaystyle\!\!\!\!\!\!\!\!\alpha=Ax^{-2/n}+\cdots,$

	$\displaystyle\!\!\!\!\!\!\!\!v=Bx^{1-1/n}+\bigg{\{}-\bigg{[}\frac{n}{(3n-2)}+\frac{2h(n-1)}{n}\bigg{]}A$
	$\displaystyle\qquad+2(2-n)n^{q-1}A^{1-n+3nq/2}\bigg{\}}x^{1-2/n}+\cdots\ ,$		(5)

where $A$ and $B$ are two integration constants, referred to as the mass and velocity parameters (Wang & Lou, 2008). To ensure the validity of asymptotic MHD solution (5), we require $2/3<n\leqslant 2$ ; the inequality $n>2/3$ is directly related to self-similar MHD transformation (4) where a positive $M$ is mandatory on the ground of physics. For $2/3<n\leqslant 1$ , both mass and velocity parameters $A>0$ and $B$ are fairly arbitrary. In case of $1<n\leqslant 2$ , we should require $B=0$ to avoid a divergent $v(x)$ at large $x$ unless a flow system is truncated. Using this asymptotic solution at large $x$ as initial conditions, the key scaling index $n$ determines the initial mass density distribution as $\rho\propto r^{-2/n}$ . In our self-similar scenario, the valid range of exponent $n$ corresponds to a range of density power laws $\rho\propto r^{-3}$ to $\rho\propto r^{-1}$ .

By setting $v=0$ for all $x$ in nonlinear MHD ODEs (2) and (3), we readily obtain an exact global magnetostatic solution, namely

\alpha=A_{0}x^{-2/n}\ ,

(6)

where the proportional coefficient $A_{0}$ is given by

A_{0}=\bigg{[}\frac{n^{2}-2(1-n)(3n-2)h}{2(2-n)(3n-2)}n^{-q}\bigg{]}^{-1/(n-3nq/2)}\ .

(7)

This describes a magnetostatic singular polytropic sphere (SPS) with a substantial generalization of $q\neq 0$ ; the case of $q=0$ or $n+\gamma=2$ is included here and corresponds to a conventional polytropic gas in magnetostatic equilibrium. A further special case of $n=\gamma=1$ corresponds to a magnetostatic singular isothermal sphere (SIS). Physically, expression (7) requires $q\neq 2/3$ and $h<h_{c}\equiv n^{2}/[2(1-n)(3n-2)]$ for the existence of the global magnetostatic SPS solution in a general polytropic gas. For $n=4/5$ , $h_{c}$ reaches the minimum value $h_{c}=4$ . This places a constraint only when $n<1$ ; while for $n\geqslant 1$ , parameter $h>0$ is fairly arbitrary.

There exists an analytic asymptotic MHD solution approaching the magnetostatic SPS solution at small $x$ (referred to as the ‘quasi-magnetostatic’ asymptotic solution), namely $v=Lx^{K}$ and $\alpha=A_{0}x^{-2/n}+Nx^{K-1-2/n}$ where $K$ is the root of the following quadratic equation

\bigg{[}\frac{n^{2}}{2(3n-2)}+nh+\frac{(3n-2)}{2}Q\bigg{]}\bigg{[}K^{2}+\frac{(3n-4)}{n}K\bigg{]}

\ +\frac{2(2-n)(1-n)}{n}h+\frac{n^{2}+(3n-2)^{2}(1-4/n)Q}{(3n-2)}=0\ ,

(8)

where $Q\equiv q\big{\{}n^{2}/[2(2-n)(3n-2)]-(1-n)h/(2-n)\big{\}}$ is introduced for notational clarity (Lou & Wang 2006, 2007). In a certain regime, at least one root of quadratic equation (8) satisfies $\Re(K)>1$ and therefore quasi-magnetostatic solutions do exist. The two coefficients $L$ and $N$ are simply related by the following algebraic expression

n(K-1)N=(K+2-2/n)A_{0}L\ .

(9)

In this case, the magnetic Lorentz force (i.e. magnetic pressure and tension forces together) and the gas pressure force are in the same order of magnitude in the regime of small $x$ .

It can be proved that the parameter regimes where quasi-magnetostatic solutions exist are $\gamma\geqslant 1$ , $h<h_{c}$ , $q<2/3$ , $n<0.8$ and $\gamma\geqslant 1$ , $h<h_{c}$ , $q>2/3$ . With parameters outside these two regimes, the so-called strong-field asymptotic solutions at small $x$ , for which the magnetic force dominates over the thermal pressure force, have been shown to exist (Yu et al., 2006; Wang & Lou, 2007, 2008).

3 Formation of Compact Magnetars

3.1 Model Progenitors and Compact Remnants

To be specific, the radial range of our model solutions is set within $r_{\rm i}<r<r_{\rm o}$ , where $r_{\rm i}=10^{6}$ cm if the compact object is a neutron star or black hole, and $r_{\rm o}=10^{12}$ cm as the radius of a typical massive main-sequence star (e.g. Herrero et al., 1992; Schönberner & Harmanec, 1995). Massive stars may have undergone tremendous mass losses before the onset of gravitational core collapses, and a progenitor immediately before a core collapse may have already lost the entire hydrogen envelope and become a compact Wolf-Rayet star with a radius of $\sim 10^{11}$ cm and a mass of $\sim 4-8M_{\odot}$ (see e.g. Soderberg et al. 2008 and Mazzali et al. 2008 for recent observations). We attempt to further identify plausible conditions of forming magnetars by gravitational core collapses of massive progenitor stars.

At the initial time of our analysis, the model should approximately represent the final stage of a massive progenitor star before the gravitational core collapse. The mass density, temperature and magnetic field on the progenitor stellar surface can be inferred from the observed range. From these quantities, one estimates the dimensionless magnetic parameter $h$ , which plays an important role in the MHD evolution of quasi-magnetostatic solutions. By self-similar MHD transformation (4) and the ideal gas law, we have

Ck^{1-3q/2}=\frac{k_{B}T}{\mu(4\pi G)^{\gamma-1}G^{q}(3n-2)^{q}\rho^{\gamma-1}M^{q}}\ ,

(10)

where $T$ is the gas temperature, $k_{B}$ is Boltzmann’s constant, and $\mu$ is the mean molecular (atomic) weight for gas particles. For a gas mainly of ionized hydrogen and a stellar mass of several solar masses, one can estimate parameter $k$ according to expression (10) from $\gamma$ and the local density $\rho$ and temperature $T$ . For typical values of $\rho\sim 10^{-5}$ g cm^-3 and $T\sim 10^{5}-10^{6}$ K on the stellar surface of a massive progenitor in the late phase (just before the gravitational core collapse) and $\gamma=1.3$ and $n=0.7$ , we estimate a range of $k\sim 10^{16}-10^{17}$ cgs unit.

With $t\rightarrow 0^{+}$ and/or $r\rightarrow\infty$ (i.e. for the regime of large $x$ ), self-similar MHD solutions follow asymptotic form (5). For such analytic asymptotic solutions, the mass density simply scales as

\rho=\frac{Ak^{1/n}}{4\pi G}r^{-2/n}\

(11)

and is independent of time $t$ . The reason to refer $A$ as the mass parameter is now apparent. With asymptotic mass density scaling (11), one can estimate $A$ from the surface mass density of a progenitor star. We have the radial flow velocity

u=Bk^{1/(2n)}r^{1-1/n}\ ,

(12)

also independent of $t$ . The radial flow velocity near the stellar surface relates to the mass accretion rate or mass loss rate by

\dot{M}=-4\pi r^{2}\rho u\ .

(13)

With expressions (12) and (13), one can determine velocity parameter $B$ from the stellar mass loss rate for $B>0$ or mass accretion rate for $B<0$ . Observationally, mass loss rates of Galactic OB stars fall in the range of $\sim 10^{-5}-10^{-7}$ M_⊙ yr^-1 (e.g. Lamers & Leitherer, 1993). Mass loss rates of Wolf-Rayet stars are much higher than massive main-sequence stars, falling in the range of $\sim 10^{-4}-10^{-6}$ M_⊙ yr^-1 (e.g. Singh, 1986). Very recently, Puls, Vink & Najarro (2008) provide an extensive review on mass loss rates of massive stars.

In summary, with the mass density, temperature, magnetic field and mass loss rate specified at the surface of a massive progenitor star, one can determine all parameters of asymptotic solution (5) and integrate nonlinear MHD ODEs (2) and (3) inwards to produce an MHD profile for the progenitor interior and envelope. We still have the freedom to choose the rebound shock position after the gravitational core collapse. Physically, the speed of the rebound shock depends on the core collapse, for example the EoS and the neutrino reheating, etc. Here we simply treat it as an adjustable parameter to search for downstream solutions within the shock front as $x\rightarrow 0^{+}$ .

With $t\rightarrow\infty$ and/or $r\rightarrow 0^{+}$ (i.e. for the regime of small $x$ ), the final evolution may approach either a quasi-magnetostatic solution (Lou & Wang 2007) or the strong-field solutions (Wang & Lou 2007, 2008). It is desirable that after a long lapse (i.e. $t\rightarrow\infty$ ), the enclosed mass within $r_{\rm i}$ evolves towards a constant value and form a compact remnant of nuclear mass density. Asymptotically, the enclosed mass takes the form of

M=\frac{nk^{1/n}A_{0}}{(3n-2)G}r^{3-2/n}

(14)

for quasi-magnetostatic solutions and becomes independent of $t$ . This appears consistent with the scenario of forming a central compact object with a strong magnetic field (Lou & Wang, 2007). In a companion paper, we will show that the asymptotic enclosed mass for strong-field solutions depends on $t$ , and may be invoked to model a continuous accretion or outflow around a nascent neutron star (Hu & Lou 2009, in preparation). As quasi-magnetostatic solutions require that $h<h_{c}$ , we arrive at an interesting situation, i.e. in order to give birth to a stable neutron star with an ultra-intense magnetic field, the massive progenitor star needs to be magnetized but not too much. We shall see presently that $h<h_{c}$ is generally satisfied for massive main-sequence stars.

We now introduce the outer initial mass $M_{\mbox{o,ini}}$ and the inner ultimate mass $M_{\mbox{i,ult}}$ in the same manner as done in Lou & Wang (2006, 2007) and regard them as rough estimates for the the initial progenitor mass and the final mass of the remnant compact object, respectively. The ratio of these two masses is given by $M_{\mbox{o,ini}}/M_{\mbox{i,ult}}=\lambda^{*}(r_{\mbox{o}}/r_{\mbox{i}})^{(3-2/n)}$ with $\lambda^{*}\equiv(A/A_{0})\lambda^{-2/n}$ . The ratio of outer initial magnetic field at the surface of the progenitor star to the inner final magnetic field of the central compact remnant is $<B_{\mbox{o,ini}}^{2}>^{1/2}/<B_{\mbox{i,ult}}^{2}>^{1/2}=\lambda^{*}(r_{\mbox{o}}/r_{\mbox{i}})^{(1-2/n)}$ . The factor $\lambda^{*}$ is insignificant as compared to the radial variation of magnetic field, i.e. the very radial dependence of $r^{(1-2/n)}$ . As $n\rightarrow 2/3$ and the polytropic index $\gamma$ approaches $4/3$ , this scaling approaches $r^{-2}$ . With $r_{\mbox{o}}=10^{12}$ cm and $r_{\mbox{i}}=10^{6}$ cm, the magnetic field strength can be rapidly enhanced by a factor up to $\sim 10^{12}$ . Thus, for a magnetar (i.e. neutron star) to have a surface magnetic field strength of $<B_{\mbox{i,ult}}^{2}>^{1/2}\sim 10^{15}$ G, we need a magnetic field of $\sim 10^{3}$ G over the progenitor stellar surface, which is attainable for magnetic massive OB stars.

3.2 Numerical Model Calculations

The initial time to apply our solutions is estimated by the time when the rebound shock crosses $r_{\rm i}$ , viz. $t_{1}=[r_{\rm i}/(k^{1/2}x_{s})]^{1/n}$ (Lou & Wang, 2006). Here we suppose that roughly from $t_{1}$ on the collapse and rebound shock inside the progenitor star have already evolved into a self-similar phase (typically this process takes a few milliseconds). The rebound shock travels outwards through the stellar interior into the envelope in $\sim 10^{4}-10^{6}$ s (e.g. Lou & Wang, 2007; Lou & Hu, 2009; Hu & Lou, 2008a). We set $t_{2}$ as the time when the rebound shock reaches $r_{\rm o}$ , roughly around the shock breakout. We will also show self-similar MHD solutions at $t_{m1}=1$ s as an intermediate time between $t_{1}$ and $t_{2}$ , and at $t=\infty$ .

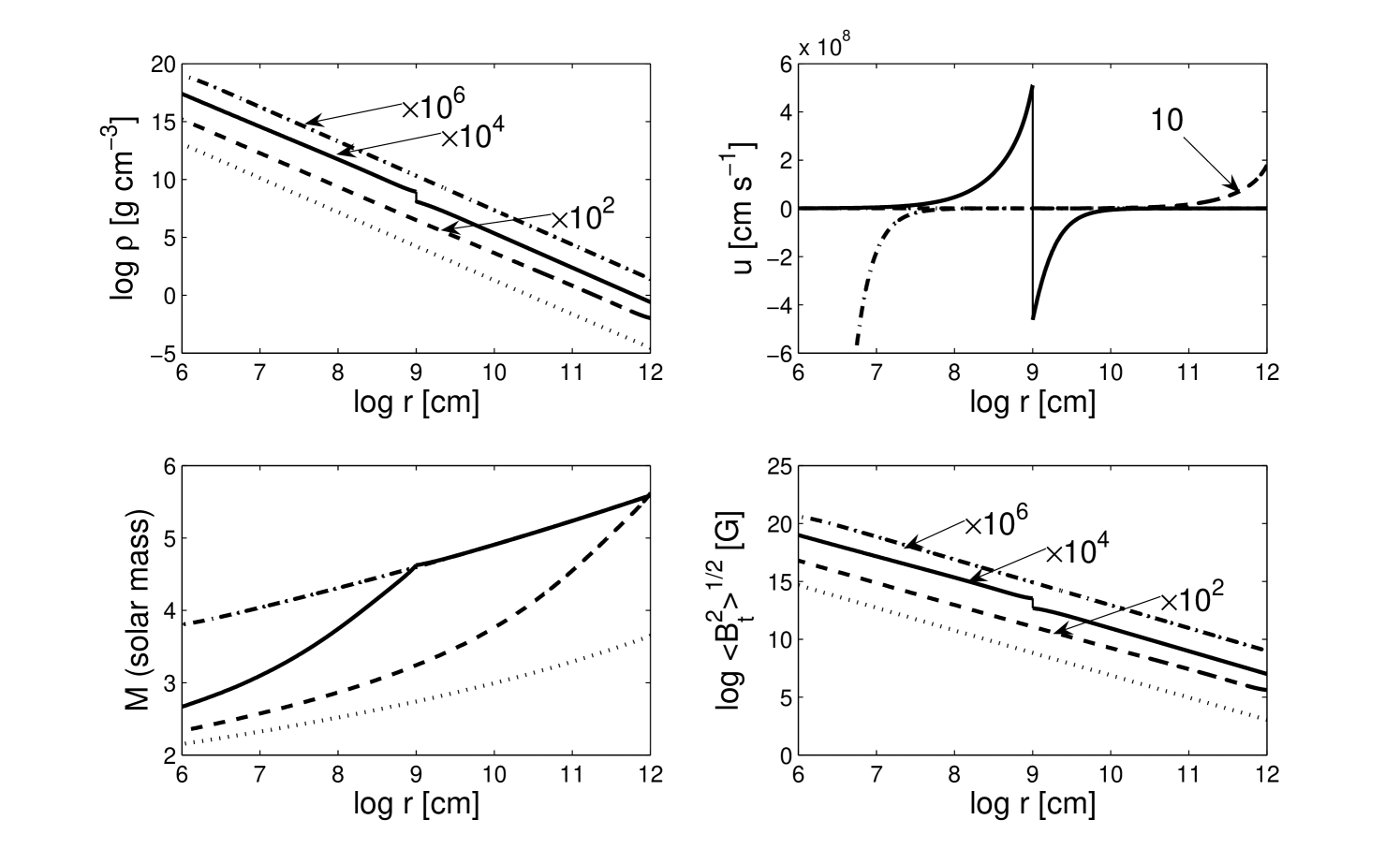
Refer to caption — Figure 1: The radial profiles of mass density, radial flow velocity, enclosed mass and transverse magnetic field at four different epochs. For all panels, the dash-dotted, solid, dashed and dotted curves are at $t_{1}$ , $t_{m1}$ , $t_{2}$ , and $t=\infty$ , respectively. Mass density, velocity and magnetic field profiles are multiplied by numerical factors marked along the curves for a compact presentation.

As an example of illustration, we choose $n=0.673,\ q=0,\ \gamma=1.327$ for a conventional polytropic gas. From the analysis in subsection 3.1, solutions with a smaller $n$ ( $>2/3$ ) tend to give a larger $M_{\mbox{i,ult}}$ and $<B_{\mbox{i,ult}}^{2}>^{1/2}$ . The choice of parameters here is a compromise among multiple numerical tests. With a typical surface mass density of $2.5\times 10^{-5}$ g cm^-3, a surface temperature $3\times 10^{4}$ K, a mass loss rate $10^{-6}$ M_⊙ yr^-1, and a surface magnetic field strength $10^{3}$ G for a massive progenitor star, we estimate $k_{1}=1.55\times 10^{16}$ cgs unit, $A=8.4378$ , $B=1.27\times 10^{-7}$ and $h=1.52\times 10^{-4}$ . Such parameter $h$ ensures that a stellar core collapse evolves into a quasi-magnetostatic manner for small $x$ . Here, inequality $h<h_{c}$ is readily satisfied for this set of adopted parameters. We set a rebound shock reaching a radius $r=10^{9}$ cm at $t=1$ s, which fixes the shock location and travel speed. With these parameters, a global self-similar rebound shock solution can be constructed and the temporal evolution is shown in Figure 1 at sampled epochs $t_{1}=3.49\times 10^{-5}$ s, $t_{m1}$ , $t_{2}=2.87\times 10^{4}$ s and $t=\infty$ .

The initial progenitor mass is around 5.59 M_⊙, consistent with observations of Soderberg et al. (2008). At epoch $t_{1}$ (dash-dotted curve), the rebound shock has not yet emerged. The radial velocities around the surface of the proto-neutron star point inwards, corresponding to a core collapse process leading to a subsequent rebound shock travelling outwards inside the progenitor envelope. Meanwhile, the outer part of the progenitor envelope still flows slowly outwards for a stellar wind. Such kind of self-similar shock manifestation with a collapsing inner part and an expanding outer part is made possible from the quasi-magnetostatic asymptotic solutions (see Lou & Wang, 2006) and is another form of envelope expansion with core collapse (EECC) proposed by Lou & Shen (2004). At epoch $t_{m1}$ (solid curve), the outgoing rebound shock emerges and travels within the stellar envelope. Figure 1 clearly shows this discontinuity across the outgoing MHD shock front. The rebound shock evolves in a self-similar manner with an outgoing speed decreasing with time $t$ for $n<1$ (see Lou & Hu 2008 and Hu & Lou 2008b for a comparison with numerical simulations). The immediate downstream side of the shock has an outward velocity and the immediate upstream side has an inward velocity. The enclosed mass of the downstream side decreases rapidly towards the centre while that of the upstream side remains nearly unchanged. Across the shock front, both mass density and magnetic field strength are enhanced by a factor of 6.96. It can be derived that $<B_{t}^{2}>^{1/2}_{1}/<B_{t}^{2}>^{1/2}_{2}=\rho_{1}/\rho_{2}=2/[(\gamma+1){\cal M}_{1}^{2}]+(\gamma-1)/(\gamma+1)$ where ${\cal M}_{1}$ is the upstream Mach number in the comoving shock framework of reference. The maximum enhancement across the shock is $(\gamma+1)/(\gamma-1)=7.12$ for our adopted value of polytropic index $\gamma=1.327$ .

This rebound shock breaks out from the stellar envelope in $t_{2}\sim 3\times 10^{4}$ s. We see at that moment the flow velocity within the spherical volume previously occupied by the progenitor star becomes very much reduced in the wake of the rebound shock, and the gas there gradually approaches the quasi-magnetostatic phase of evolution. Coupled with radiation mechanisms, for instance the thermal bremsstrahlung of hot electrons with a temperature $T\;\lower 4.0pt\hbox{${\buildrel\displaystyle>\over{\sim}}$}\;10^{7}$ K, and using the dynamic profiles shown in Figure 1, one may compute the radiation detected and reproduce the X-ray or $\gamma$ -ray light curves observed (e.g. Hu & Lou, 2008b; Soderberg et al., 2008; Mazzali et al., 2008). Eventually, flow velocities of the entire system tend to zero and the enclosed masses at all radii remain unchanged. From Figure 1, we see that for the initial and final stages of the MHD evolution, the mass density and magnetic field distributions obey power laws, consistent with the asymptotic analysis in subsection 3.1. Finally, within radius $r_{\rm i}$ of the inner compact remnant, the enclosed mass is 2.15 M_⊙ with a mean density of $1.02\times 10^{15}$ g cm^-3 for a neutron star. As the mean surface magnetic field strength is $<B_{\mbox{i,ult}}^{2}>^{1/2}\sim 4.70\times 10^{14}$ G, this neutron star should be indeed regarded as a magnetar.

Numerical explorations indicate that the ultimate magnetic field on the neutron star is proportional to the initial magnetic field on the progenitor stellar surface. However, the magnetic enhancement factor $<B_{\mbox{i,ult}}^{2}>^{1/2}/<B_{\mbox{o,ini}}^{2}>^{1/2}$ and the mass ratio $M_{\mbox{i,ult}}/M_{\mbox{o,ini}}$ indeed depend on model parameters and in particular, on shock properties and self-similar scaling indices $n$ and $q$ . As long as the density scales as $r^{-2/n}$ , index $n$ must be set to approach the limiting value 2/3 to ensure a sufficiently massive progenitor star. In Figure 2, we plot these two ratios versus the selected rebound shock radii at $t=1$ s. The two curves suggest that a shock with a medium travel speed is associated with a minimum magnetic field enhancement. The magnetic enhancement factor appears grossly proportional to the mass ratio. We illustrate the relation between these two ratios in Figure 3. Note that the magnetic enhancement factor does not exceed $10^{12}$ .

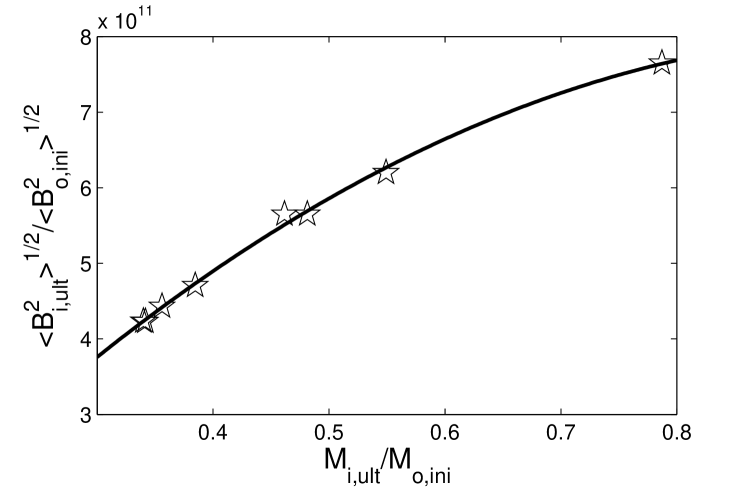
We further examine the influence of parameter $q$ for a general polytropic magnetofluid shown in Fig. 4. With a larger $q$ , both the mass ratio and magnetic enhancement factor become less. The qualitative behaviours of quasi-magnetostatic solutions in general polytropic cases are similar to the conventional polytropic cases.

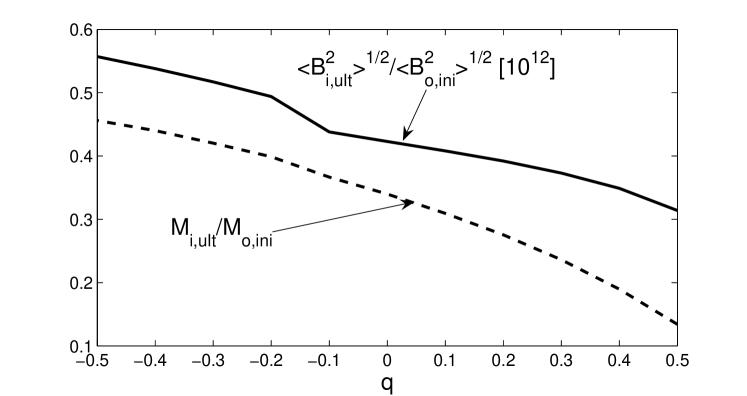
Our self-similar MHD rebound shock model analysis suggests that should there be a continuum of stellar surface magnetic field strengths over massive progenitor stars, there is then a corresponding continuum from normal radio pulsars to magnetars in terms of magnetic field strengths over the compact stellar surface. The key factors that decide whether a remnant neutron star possesses an ultra-intense magnetic field include scaling indices $n$ and $q$ , the initial surface magnetic field of progenitor star, and the strength (or speed) of the rebound shock. Our analysis also resolves the difficulty posed by the survey of Petit et al. (2008b). That is, a massive progenitor star with a proper range of surface magnetic field strengths is most likely but not necessarily leads to a magnetar after the gravitational core collapse and the emergence of a rebound shock. There are additional constraints to be satisfied. Both Figures 2 and 4 demonstrate that the magnetic enhancement factor cannot exceed $\sim 10^{12}$ , and may be as low as $\sim 10^{11}$ even as $n\rightarrow 2/3$ . This implies that the conditions for producing magnetars are fairly strict. Another major limit arises as the fact that the magnetic enhancement factor correlates to the mass ratio. If this mass ratio is too high, the compact remnant mass may exceed the Tolman-Oppenheimer-Volkoff (TOV) limit ( $\sim 3-3.2$ M_⊙; Rhoades & Ruffini 1974), and the core object would collapse further to form a black hole. The upper bound for the mass of neutron stars then places a limit on their surface magnetic field strengths.

4 Conclusions and Discussion

We combine semi-analytic and numerical self-similar MHD solutions to model the gravitational core collapse, the rebound shock explosion of a magnetized massive progenitor star, and the formation of a central remnant compact magnetar. As natural extension and generalization to recent supernova rebound shock models of Lou & Wang (2006, 2007), we invoked quasi-magnetostatic asymptotic solutions and asymptotic solutions far away from the centre for a general polytropic magnetofluid. With the magnetic frozen-in condition imposed, the surface magnetic field of a nascent neutron star can be very much stronger than that of its progenitor by a factor of $\sim 10^{11}-10^{12}$ during processes of the gravitational core collapse and the self-similar rebound shock breakout. Therefore if the progenitor is a magnetic massive star with a surface magnetic field strength of $\sim 10^{3}$ G, it would have a good chance to produce a magnetar at the centre of its supernova remnant. Here we propose that magnetars may be produced through powerful supernova explosions of magnetized massive progenitor stars. Such physical origin is also supported by statistical inferences from observational surveys (e.g. Ferrario & Wickramasinghe, 2006). While the magnetic flux of the collapsing core inside the progenitor star may come from either main-sequence stellar dynamo processes or ‘fossil fields’ of molecular clouds, it will be dragged and squeezed into the newborn neutron star by the conservation of magnetic fluxes. At least for magnetic massive stars as magnetar progenitors, the post-supernova dynamo processes inside the remnant neutron star may not be necessary for producing the ultra-intense surface magnetic field. Magnetic field strengths in the interior of such magnetars thus produced are expected to be even stronger and are gravitationally buried and confined by the nuclear-density matter.

If the surface magnetic field strength of a massive progenitor happens to be even higher, possibly up to $\sim 3\times 10^{4}$ G or more, a nascent compact magnetar may then possess an ultra-intense surface magnetic field up to $\sim 10^{15}-3\times 10^{16}$ G or higher. Such strong magnetic fields can give rise to various stellar activities and magnetic reconnection can release stored magnetic energy sporadically and violently (e.g. Low & Lou 1990). For example, if one approximates the magnetospheres of SGRs, AXPs, and radio pulsars as in gross force-free equilibria (i.e. electric currents parallel to magnetic fields), then the magnetic energies retained in such magnetospheric systems are higher than the corresponding potential field configurations with the same footpoint magnetic field at the stellar surface. A loss of equilibrium most likely triggered by magnetic reconnections may then lead to outbursts of available magnetic energies. In the solar and stellar contexts, such processes correspond to solar/stellar flare activities and coronal mass ejections. For compact stellar object like neutron stars, this type of dramatic magnetic energy releases might fuel ‘magnetic fireballs’ which produce short-hard gamma-ray bursts, such as those reported giant flares (e.g. Hurley et al., 2005) as well as very recent outbursts of SGR J1550-5418 and SGR 1627-41. After giant flares, a neutron star may still recover surface magnetic fields of order of $\sim 10^{14}-10^{15}$ G manifested as either an AXP or a SGR.

For an intense magnetic field buried inside a magnetar, there is yet another possible source of activities. The magnetic Lorentz force may break the crust of a neutron star into pieces to various levels. Coupled with the magnetar spin, a broken crust can give rise to various activities. For examples, chunks of crust may pile up around the equatorial bulge and rearrange themselves to generate stellar seismic activities in a random manner; interior magnetic flux ropes may burst into the magnetar magnetosphere randomly at weak points of a crust; if the crust is more or less destroyed by the Lorentz force, then footpoints of magnetic field lines can be moved around by convective motions and possible differential rotations of a magnetar; the manoeuvre of magnetic footpoints over the surface of a magnetar leads to variable configurations of the magnetosphere and thus produces magnetic activities including analogues of ‘flares’ and ‘coronal mass ejections’ mentioned earlier.

Regarding observed magnetar-like X-ray emissions from a rotation-powered pulsar PSR J1846-0258 inside supernova remnant Kes75 (e.g. Gavriil et al., 2008; Archibald et al., 2008), our model can accommodate this pulsar resulting from a magnetized massive progenitor yet with a lower surface magnetic field strength. Such magnetar-like activities are physically associated more with strong magnetospheric field strengths. With the current observational evidence, it appears not necessary to postulate that magnetars evolve from fast spinning radio pulsars.

In our ‘ball of thread’ scenario for a random magnetic field within a massive progenitor star, the large-scale mean of such a random magnetic field is idealized as dominantly transverse with a fairly weak radial component. By the approximation of quasi-spherical symmetry, low-amplitude small-scale deviations, oscillations or fluctuations are randomly distributed about the mean flow profile and are expected to co-evolve with large-scale MHD profiles (e.g. Lou & Bai 2009 in preparation; Cao & Lou 2009 in preparation). During the processes of the gravitational core collapse and the MHD rebound shock breakout, a remnant neutron star forms with high nuclear density and ultra-intense magnetic field, while a major portion of the interior and envelope of the massive progenitor star is driven out into the interstellar space by the rebound shock with entrained strong magnetic field. Our semi-analytic model describes a large-scale self-similar MHD evolution for the supernova explosion of a magnetized massive progenitor. Along with this large-scale evolution, the central magnetar and the thrown-out stellar materials may certainly follow their own courses of adjustment or rearrangement (e.g. Lou 1994). For example, considerable radial components of magnetic field should emerge in a random turbulent manner. In fact, magnetars are expected to possess magnetospheres with various possible configurations (see Low & Lou 1990 for constructing force-free stellar magnetic field configurations). By numerical simulations with ‘fossil fields’, Braithwaite & Spruit (2004) illustrated examples of processes for magnetic field rearrangement to occur within a few Alfvén timescales. The emergent stable structure of magnetic field for magnetic Ap stars appears always of ‘offset dipole’ type (with complex and twisted magnetic field configurations inside), consistent with observations. By this analogy, we presume that such magnetic field rearrangement processes could take place very rapidly during the formation of intensely magnetized neutron stars, whose Alfvén timescale is of the order of $\sim 0.1$ s. Eventually, a magnetar can possess a variety of magnetic field configurations (e.g. Low & Lou 1990).

Magnetars observed so far appear to be slow rotators, while massive stars are in general rapid rotators with typical equatorial speeds of $\sim 200$ km s^-1 (e.g. Fukuda 1982). Therefore, significant angular momentum transfer may have taken place in the stellar evolution of magnetic massive stars. Spruit (1999, 2002) has shown that magnetic fields can be created in stably stratified layers inside a differentially rotating star. Heger et al. (2005) gave detailed rotating stellar evolution calculations for stars in the mass range of $\sim 12-35$ M_⊙ incorporating the dynamo-powered magnetic field. In general, it is found that magnetic breaking decreases the final spin rate of the collapsing iron core by a factor of $\sim 30-50$ when compared with the nonmagnetic case. The ‘fossil’ (or primordial) magnetic fields may have similar dynamic effects regarding the re-distribution of angular momentum inside a massive star. In particular, for magnetar formation, high magnetic fields may lead to stronger core-envelope coupling during the hydrogen and helium burning phase of the SN progenitor, and the collapsing iron core and the compact supernova remnant is expected to be even slower rotators. This is in accordance with the population of slowly rotating magnetars observed.

In our model at this stage of development, the stellar rotation is not included to simplify the mathematical treatment. Conceptually, it could be possible to design an axisymmetric MHD problem to accommodate stellar differential rotation in order to explore the re-distribution of angular momentum during the processes of gravitational core collapse, MHD rebound shock as well as collimated MHD outflows from polar regions with shocks (e.g. shocked MHD jets). The overall magnetic field configuration could be predominantly toroidal but a relatively weak radial magnetic field component is necessary to exert an effective magnetic torque to break or slow down the stellar core rotation. As the core materials rapidly collapse towards the centre under the gravity, the mechanical angular momentum is transferred outwards in an outgoing envelope with shock. Along the rotation axis, collimated outflows or jets may emerge to breakthrough the polar stellar envelope and part of the mechanical angular momentum is carried outwards by rotating polar collimated outflows. For a semi-analytic self-similar approach to this time-dependent problem, one might be able to perform a self-similar transformation combining time $t$ with two spatial coordinates, say $r$ and $\theta$ . It might be possible to derive asymptotic solutions in the regime of slow rotators for this two-dimensional magnetar formation problem. One also expects the existence of several MHD singular surfaces in deriving flow solutions. Physically, such a scheme if tractable semi-analytically and/or numerically can be applied to a wide range of gravitational collapses of rotating systems, including magnetars, pulsars, magnetic white dwarfs, protostars, planets and so forth.

In addition to the quasi-magnetostatic asymptotic solutions adopted and exemplified in this paper, it may be possible that a magnetized massive progenitor star evolves towards the strong-field asymptotic solutions ultimately (Yu et al., 2006; Wang & Lou, 2007, 2008), involving a material fall-back process towards the central remnant neutron star. Under this situation, the enclosed mass within a certain radius keeps increasing until the mass of the neutron star exceeds the TOV limit. Such an MHD fall-back process offers a possible means to form stellar mass black holes as compact remnants in supernova and hypernova explosions. We emphasize that such a mechanism requires a strong magnetic field inside a progenitor and the magnetic force becomes dominant during the fall-back process.

Acknowledgments

This research was supported in part by Tsinghua Centre for Astrophysics (THCA), by the National Natural Science Foundation of China (NSFC) grants 10373009 and 10533020 and by the National Basic Science Talent Training Foundation (NSFC J0630317) at Tsinghua University, and by the SRFDP 20050003088 and 200800030071 and the Yangtze Endowment from the Ministry of Education at Tsinghua University. The hospitality of Institut für Theoretische Physik und Astrophysik der Christian-Albrechts-Universität Kiel Germany and of International Center for Relativistic Astrophysics Network (ICRANet) Pescara, Italy is gratefully acknowledged.

References

Archibald et al. (2008) Archibald A. M., Kaspi V. M., Livingstone M. A., McLaughlin M. A., 2008, ApJ, 688, 550
Aurière et al. (2003) Aurière M., et al., 2003, A Peculiar Newsletter, Vol. 39
Braithwaite & Spruit (2004) Braithwaite J., Spruit H. C., 2004, Nature, 431, 819
Castro-Tirado et al. (2008) Castro-Tirado A. J., et al., 2008, Nature, 455, 506
Chiueh & Chou (1994) Chiueh T., Chou J.-K., 1994, ApJ, 431, 380
Donati et al. (2002) Donati J.-F., Babel J., Harries T. J., Howarth I. D., Petit P., Semel M., 2002, MNRAS, 333, 55
Donati et al. (2006) Donati J.-F., Howarth I. D., Bouret J.-C., Petit P., Catala C., Landstreet J., 2006, MNRAS, 365, 6
Duncan & Thompson (1992) Duncan R. C., Thompson C., 1992, ApJ, 392, L9
Ferrario & Wickramasinghe (2005) Ferrario L., Wickramasinghe D. T., 2005, MNRAS, 356, 615
Ferrario & Wickramasinghe (2006) Ferrario L., Wickramasinghe D. T., 2006, MNRAS, 367, 1323F
Ferrario & Wickramasinghe (2008) Ferrario L., Wickramasinghe D. T., 2008, MNRAS, 389, L66
Fukuda (1982) Fukuda I., 1982, PASP, 94, 271
Gavriil et al. (2008) Gavriil F. P., Gonzalez M. E., Gotthelf E. V., Kaspi V. M., Livingstone M. A., Woods P. M., 2008, Science, 319, 1802
Heger, Woosley & Spruit (2005) Heger A., Woosley S. E., Spruit H. C., 2005, ApJ, 626, 350
Herrero et al. (1992) Herrero A., Kudritzki R. P., Vilchez J. M., Kunze D., Butler K., Haser S., 1992, A&A, 261, 209
Hu & Lou (2008a) Hu R.-Y., Lou Y.-Q., 2008, MNRAS, 390, 1619
Hu & Lou (2008b) Hu R.-Y., Lou Y.-Q., 2008, AIP Proceedings of “2008 Nanjing GRB Conference”, 1065, 310
Hubrig et al. (2006) Hubrig S., Briquet M., Schöller M., De Cat P., Mathys G., Aerts C., 2006, MNRAS, 369, 61
Hurley et al. (2005) Hurley K., et al., 2005, Nature, 434, 1098
Kouveliotou (2008) Kouveliotou C., 2008, Nature, 455, 477
Lamers & Leitherer (1993) Lamers H. J. G. L. M., Leitherer C., 1993, ApJ, 412, 771
Lou (1994) Lou Y.-Q., 1994, ApJ, 428, L21
Lou (1995) Lou Y.-Q., 1995, MNRAS, 275, L11
Lou & Cao (2008) Lou Y.-Q., Cao Y., 2008, MNRAS, 384, 611
Lou & Hu (2009) Lou Y.-Q., Hu R.-Y., 2009, submitted
Lou & Shen (2004) Lou Y.-Q., Shen Y., 2004, MNRAS, 348, 717
Lou & Wang (2006) Lou Y.-Q., Wang W.-G., 2006, MNRAS, 372, 885
Lou & Wang (2007) Lou Y.-Q., Wang W.-G., 2007, MNRAS, 378, L54
Low & Lou (1990) Low B. C., Lou Y.-Q., 1990, ApJ, 352, 343
Mazzali et al. (2008) Mazzali P. A., et al., 2008, Science, 321, 1185
Mereghetti (2008) Mereghetti S., 2008, Astron. Astrophys. Rev., 15, 225
Palmer et al. (2005) Palmer D. M., et al., 2005, Nature, 434, 1107
Petit et al. (2008a) Petit V., Wade G. A., Drissen L., Montmerle T., Alecian E., 2008, MNRAS, 387, L23
Petit et al. (2008b) Petit V., Wade G. A., Drissen L., Montmerle T., 2008, AIP Conference Proceedings, 983, 399
Press et al. (1986) Press W. H., Flannery B. P., Teukolsky S. A., Vetterling W., 1986, Numerical Recipes (Cambridge: Cambridge University Press)
Puls, Vink & Najarro (2008) Puls J., Vink J. S., Najarro F., 2008, A&A Review, in press
Rhoades & Ruffini (1974) Rhoades C. E., Ruffini R., 1974, Phys. Rev. Lett., 32, 324
Schönberner & Harmanec (1995) Schönberner D., Harmanec P., 1995, A&A, 294, 509
Singh (1986) Singh M., 1986, ApSS, 120, 115
Soderberg et al. (2008) Soderberg A. M., et al., 2008, Nature, 453, 469
Spruit (1999) Spruit H. C., 1999, A&A, 349, 189
Spruit (2002) Spruit H. C., 2002, A&A, 381, 923
Stefanescu et al. (2008) Stefanescu A., Kanbach G., Sowikowska A., Greiner J., McBreen S., Sala G., 2008, Nature, 455, 503
Thompson & Duncan (1993) Thompson C., Duncan R. C., 1993, ApJ, 408, 194
Wachter et al. (2008) Wachter S., et al., 2008, Nature, 453, 626
Wang & Lou (2007) Wang W.-G., Lou Y.-Q., 2007, ApSS, 311, 363
Wang & Lou (2008) Wang W.-G., Lou Y.-Q., 2008, ApSS, 315, 135
Wickramasinghe & Ferrario (2005) Wickramasinghe D. T., Ferrario L., 2005, MNRAS, 356, 1576
Yu & Lou (2005) Yu C., Lou Y.-Q., 2005, MNRAS, 364, 1168
Yu et al. (2006) Yu C., Lou Y.-Q., Bian F.-Y., Wu Y., 2006, MNRAS, 370, 121
Zel’dovich & Novikov (1971) Zel’dovich Ya. B., Novikov I. D., Stars and Relativity – Relativistic Astrophysics, Vol. 1, The University of Chicago Press, Chicago (1971)

Appendix A MHD Shock Conditions

In the shock comoving framework of reference, the MHD shock jump conditions in terms of the reduced self-similar variables are

	$\displaystyle\alpha_{1}(nx_{1}-v_{1})=\lambda\alpha_{2}(nx_{2}-v_{2})\ ,$		(15)

	$\displaystyle\qquad C\alpha_{1}^{2-n+3nq/2}x_{1}^{2q}(nx_{1}-v_{1})^{q}$
	$\displaystyle\qquad\quad+\alpha_{1}(nx_{1}-v_{1})^{2}+\frac{h\alpha_{1}^{2}x_{1}^{2}}{2}$
	$\displaystyle\qquad\qquad=\lambda^{2}\bigg{[}C\alpha_{2}^{2-n+3nq/2}x_{2}^{2q}(nx_{2}-v_{2})^{q}$
	$\displaystyle\qquad\qquad\quad+\alpha_{2}(nx_{2}-v_{2})^{2}+\frac{h\alpha_{2}^{2}x_{2}^{2}}{2}\bigg{]}\ ,$		(16)

	$\displaystyle\frac{2\gamma}{(\gamma-1)}C\alpha_{1}^{1-n+3nq/2}x_{1}^{2q}(nx_{1}-v_{1})^{q}$
	$\displaystyle\qquad\qquad\qquad+(nx_{1}-v_{1})^{2}+2h\alpha_{1}x_{1}^{2}$
	$\displaystyle\qquad\quad=\lambda^{2}\bigg{[}\frac{2\gamma}{(\gamma-1)}C\alpha_{2}^{1-n+3nq/2}x_{2}^{2q}(nx_{2}-v_{2})^{q}$
	$\displaystyle\qquad\qquad\qquad\qquad+(nx_{2}-v_{2})^{2}+2h\alpha_{2}x_{2}^{2}\bigg{]}\$		(17)

(Wang & Lou, 2008). Once we have $(x_{2},\ \alpha_{2},\ v_{2})$ on the immediate downstream side of a shock front, we can obtain $(x_{1},\ \alpha_{1},\ v_{1})$ explicitly for the immediate upstream side using MHD shock relations (15) $-$ (17) (Wang & Lou, 2008; Lou & Hu, 2009) or vice versa. In the case of $q=2/3$ , there are only two independent relations among equations (15) $-$ (17) and we could choose parameter $\lambda>0$ arbitrarily. Hence we can set $k_{1}=k_{2}$ or $\lambda=1$ in this situation. This treatment will not alter the relations of the resulting dimensional physical variables. In general, the outgoing travel speed of a rebound shock varies with time $t$ for $n\neq 1$ : shock accelerates for $n>1$ , shock speed remains constant for $n=1$ , and shock decelerates for $n<1$ .