Mass loss from OB-stars
Abstract
We review recent developments regarding radiation driven mass loss from OB-stars. We first summarize the fundamental theoretical predictions, and then compare these to observational results (including the VLT-FLAMES survey of massive stars). Especially we focus on the mass loss-metallicity dependence and on the so-called bi-stability jump.
Subsequently we concentrate on two urgent problems, weak winds and wind clumping, that have been identified from various diagnostics and that challenge our present understanding of radiation driven winds. We discuss the problems of “measuring” mass-loss rates from weak winds and the potential of the near infrared, Br-alpha line as a tool to enable a more precise quantification, and comment on physical explanations for mass-loss rates that are much lower than predicted by the standard model.
Wind clumping, conventionally interpreted as the consequence of a strong instability inherent to radiative line-driving, has severe implications for the interpretation of observational diagnostics, since derived mass-loss rates are usually overestimated when clumping is present but ignored in the analyses. Simplified techniques to account for clumping indicate overestimates by factors of 2 to 10, or even more. If actually true, these results would have a dramatic impact on the evolution of, and the feedback from, massive stars. We discuss ongoing attempts (including own work) to interprete the corresponding observations in terms of more sophisticated models. By allowing for porosity in density and velocity space, and for a non-void inter-clump medium, such models might require only moderate reductions of mass-loss rates.
Keywords:
Mass loss and stellar winds:
97.10.Me1 Introduction
Massive stars are critical agents in galactic evolution, both in the present and in the early Universe (e.g., re-ionization and first enrichment). Mass loss is a key process, which modifies chemical profiles, surface abundances, and luminosities. Furthermore, mass loss has to be understood quantitatively in order to describe and predict massive star evolution in a correct way. The standard theory to describe hot, massive star winds is based on radiative line-driving, and has been proven to work successfully in most evolutionary phases (OB-stars, A-supergiants, and LBVs in their “quiet” phase). Also for the pivotal Wolf-Rayet (WR) stadium, line-driving is still the most promising acceleration mechanism (Gräfener and Hamann, 2005, 2008).
In this review, we summarize fundamental predictions of the theory, as well as corresponding observational evidence, and subsequently concentrate on two urgent problems that challenge our understanding of line-driven winds, the so-called weak-wind problem and wind clumping. We concentrate on the winds from “normal” OB-stars in all evolutionary phases (for corresponding results and problems regarding WR-winds and additional material, see the contributions by Hamann and Hillier, this volume).
2 Line-driven winds from hot stars – theoretical predictions
To be efficient, radiative line-driving requires a large number of photons, i.e., a high luminosity . Since , not only OB-supergiants, but also hot dwarfs and A-supergiants undergo significant mass loss via this mechanism. Typical mass-loss rates are of the order of 0.1 … 10 , with terminal velocities 200 … 3,000 . Another prerequisite is the presence of a multitude of spectral lines, with high interaction probabilities, close to flux maximum, implying that the strength of line-driven winds should strongly depend on metallicity.
Pioneering work on this subject was performed by Lucy and Solomon (1970) and Castor, Abbott & Klein ((Castor et al., 1975), “CAK”), where the latter still builds the theoretical foundation of our present understanding. Improvements with respect to a quantitative description and first applications were provided by Friend and Abbott (1986) and Pauldrach et al. (1986), whereas recent reviews on the topic have been published by Kudritzki and Puls (2000) and Puls et al. (2008).
The principle idea of radiative line-driving relies on two processes.
1. Momentum is transferred to the wind matter via line absorption/emission
processes, mostly resonance scattering, with a net change in radial
momentum
| (1) |
where and are the frequencies of the absorbed and emitted photons, and is the angle between the photon’s direction and the radial unit vector. Thanks to the fore-aft symmetry of the emission process, on average , whereas , since (most) of the absorbed photons originate from the stellar surface. Thus, , and the total radiative acceleration exerted on a mass element per time interval can be derived from considering all participating lines,
| (2) |
2. Due to the huge number of metallic lines as compared to the few dozens from hydrogen and helium, mostly just the metal ions are directly accelerated. Their momentum needs to be transferred to the bulk plasma (H, He), via Coulomb collisions. The velocity drift of the metal ions with respect to H/He is compensated for by a frictional force (“Stokes law”) as long as the ratio between drift and thermal velocity is small (e.g., (Springmann and Pauldrach, 1992; Krtička and Kubát, 2000; Owocki and Puls, 2002)). Otherwise (at very low wind-densities) the metallic ions might decouple from the wind, and the wind no longer becomes accelerated.
The real challenge is to evaluate Eq. 2 (see also Owocki and Gayley, this volume). Following CAK, this is conventionally done by (i) applying the Sobolev theory (Sobolev, 1960) to approximate the line optical depths and thus the interaction probabilities, and (ii) to replace the summation by appropriate integrals over the line-strength distribution (resulting from detailed NLTE calculations), where the line-strength is the line-opacity measured in units of the Thomson-scattering opacity. This distribution can be fairly well approximated by a power-law, , with the effective (flux-weighted) number of lines and 0.6…0.7 (e.g., (Puls et al., 2000)). Note that both quantities depend on metallicity and spectral type. As a final result, , i.e., depends on the spatial velocity gradient and on the inverse of the density.
Scaling relations and WLR. Once the above quantities are inserted into the hydrodynamic equations (adopting stationarity), the latter can be solved (almost) analytically, returning the following scaling relations for mass-loss rate, velocity law, and terminal velocity:
| (3) |
with Eddington-, (photospheric) escape velocity , and , where describes the run of the ionization (Abbott, 1982). The velocity-field exponent, , is of the order of 0.8 (for O-stars) to 2 (for BA-supergiants).
Using these scaling relations, a fundamental prediction for line-driven winds becomes apparent if one calculates the so-called modified wind-momentum rate,
| (4) |
and accounts for the fact that is of the order of 2/3. Then the wind-momentum rate becomes independent on mass and , and can be expressed in terms of the wind-momentum luminosity relation (WLR), discovered first by Kudritzki et al. (1995),
| (5) |
with slope and offset , which depends on and thus on metallicity and spectral type. Originally, it was proposed to exploit the WLR for measuring extragalactic distances on intermediate scales (up to the Virgo cluster), but nowadays the relation is mostly used to test the theory itself (see below).
Theoretical 1-D models. Though the basic scaling relations for line-driven winds are known since the key paper by CAK (and updates by (Abbott, 1982; Friend and Abbott, 1986; Pauldrach et al., 1986)), quantitative predictions require consistent NLTE/radiative-transfer calculations, to derive the line-force as a function of spectral type and metallicity, as well as the inclusion of processes neglected in the original work, for example line-overlap (e.g., (Friend and Castor, 1983; Puls, 1987)).
The most frequently cited theoretical wind models (stationary, 1-D, homogeneous) are those from Vink et al. (2000, 2001). Based on the Monte-Carlo approach developed by Abbott and Lucy (1985), they allow multi-line effects to be considered. In these models, the mass-loss rate is derived (iterated) from global energy conservation, whilst the (-) velocity field is pre-described and the NLTE rate equations are treated in a simplified way. Pauldrach (1987) and Pauldrach et al. (1994, 2001), on the other hand, obtain a consistent hydrodynamic solution by integrating the (modified) CAK equations based on a rigorous NLTE line-force using Sobolev line transfer. Moreover, Krtička and Kubát (2000, 2001, 2004, 2009) and Krtička (2006) solve the equation of motion by means of a NLTE, Sobolev line-force, including a more-component description of the fluid (accelerated metal ions plus H/He) that allows them to consider questions regarding drift-velocities, non-thermal heating, and ion decoupling. Also, Kudritzki (2002) (see also Kudritzki et al. (1989)) provides an analytic “cooking recipe” for mass-loss rate and terminal velocity, based on an approximate NLTE treatment, and Gräfener and Hamann (2005, 2008) obtain self-consistent solutions (applied to WR winds) by means of a NLTE line-force evaluated in the comoving frame (see Mihalas et al. (1975, 1976a, 1976b, 1976c) and Hamann, this volume). Finally, Lucy (2007a, b) and Müller and Vink (2008) derive the wind-properties from a regularity condition at the sonic point, in contrast to most other solutions that invoke a singularity condition at the CAK-critical point of the wind (see comments by Owocki, this volume).
Results and predictions from hydrodynamic modeling. Most of the various approaches yield consistent results, e.g., when comparing the “mass-loss recipe” from Vink et al. (2000) with similar investigations utilizing different codes (Kudritzki, 2002; Pauldrach et al., 2001; Krtička and Kubát, 2004). Moreover, the WLR concept is impressively confirmed by the simulations performed by Vink et al.: The obtained modified wind-momenta follow an almost perfect power-law with respect to stellar luminosity alone, independent of luminosity class, and, for solar abundances, “only” two distinct relations covering the complete spectral range have been found, one for 50 kK 27.5 kK and the other for 22.5 kK 12 kK, respectively. In other words, the spectral type dependence of and in Eq. 5 seems to be rather mild.
3 Observations vs. Theory
In the last decade, various spectroscopic NLTE analyses of hot stars and their winds have been undertaken, in the Galaxy and in the Magellanic Clouds, in the UV, in the optical, and in a combination of both. For a compilation of these publications (without Galactic Center objects and objects analyzed within the flames survey of massive stars, see below), see Tables 2 and 3 in Puls (2008), to be augmented by the UV-Pv investigation of Galactic O-stars by Fullerton et al. (2006), the UV+optical analysis of Galactic O-dwarfs by Marcolino et al. (2009), and the optical analysis of LMC/SMC O-stars by Massey et al. (2009). Most of this work has been performed by means of 1-D, line-blanketed, NLTE, atmosphere/spectrum-synthesis codes allowing for the presence of winds, in particular cmfgen (Hillier and Miller (1998)), wm-basic (Pauldrach et al. (2001)), and fastwind (Puls et al. (2005)).
Central results. The results of these investigations can be roughly summarized as follows. (i) The mass-loss rates from SMC stars (with , see (Mokiem et al., 2007a) and references therein) are indeed lower than those from their Galactic counterparts. (ii) For O- and early B-stars, the theoretically predicted WLR from Vink et al. (2000) is met, except for O-supergiants with rather dense winds, in which the observed wind-momenta are higher (by factors around three) than the predictions (which might be explained by wind-clumping effects, see Sect. 5), and for a number of late O-dwarfs (and a few O-giants), in which the observed wind-momenta are much lower than the predictions (this is the so-called “weak-wind problem”, see Sect. 4). (iii) B-supergiants below the “bi-stability jump” ( 22 kK) show lower wind-momenta than predicted, as outlined in the following.
The bi-stability jump: predictions and observations. A fundamental prediction by Vink et al. (2000) is the occurrence of two distinct WLRs, one for hotter objects and one for cooler objects, with the division located around 252.5 kK. This rather abrupt change is due to the so-called bi-stability mechanism111denoted after some peculiar behaviour of theoretical models for the wind of P Cygni (Pauldrach and Puls, 1990)., which relies on the fact that the mass-loss rates of line-driven winds are, for typical chemical compositions, primarily controlled by the number and distribution of iron-lines, because of their dominant contribution (50%) to the total line acceleration in the lower wind (Puls et al., 2000; Vink et al., 2000; Krtička, 2006). Below roughly 25 kK, the ionization of iron is predicted to switch abruptly from Fe iv to Fe iii, and since Fe iii has more driving lines than Fe iv at flux maximum, the mass-loss rate must increase. Quantitatively, Vink et al. (2000) predict an increase in by a factor of five and a decrease of by a factor of two, so that, overall, B-supergiants (except for the earliest sub-types) should have higher wind-momenta than their O-star counterparts at the same luminosity.
Observations confirm the “velocity-part” of this picture, at least qualitatively. For stars with 23 kK, the observed ratio is 3, whereas it decreases gradually towards cooler temperatures, reaching values of 1.3…1.5 for stars with 18 kK (Evans et al., 2004; Crowther et al., 2006; Markova and Puls, 2008). With respect to the predicted increase in , however, the situation is different. As shown by Markova and Puls (2008), the mass-loss rates of B-supergiants below the observed bi-stability jump ( 22 kK) actually decrease or at least do no change. This is a first indication that there are still problems in our understanding of line-driven winds.
The flames survey of massive stars. Further progress has been obtained within the flames survey of massive stars (P.I. S. Smartt), a project that performed high resolution multi-object spectroscopy of stars located within eight young and old clusters in the Galaxy and the Magellanic Clouds. In total, 86 O-stars and 615 B-stars were observed (for introductory papers and a brief summary, see Evans et al. (2005, 2006, 2008)). The major scientific objectives of this survey were to investigate (i) the relation between stellar rotation and abundances (i.e., to test the present theory of rotational mixing), (ii) the role of binarity, and (iii) stellar mass-loss as a function of metallicity.
Regarding the last objective, Mokiem et al. (2006, 2007b) analyzed a total of O- and early B-stars in the SMC and LMC, by means of fastwind and using a genetic algorithm (Mokiem et al., 2005). The results were combined by Mokiem et al. (2007a) with data from previous investigations, to infer the metallicity dependence of line-driven mass-loss based on a significant sample of stars. Using mean abundances of (LMC) and (SMC), a metallicity dependence of , and a correction for clumping effects (see below) following Repolust et al. (2004), they derived an empirical relation
| (6) |
with rather narrow confidence intervals. This result is consistent with theoretical predictions, both from line-statistics (Puls et al., 2000) and from hydrodynamic models (see above).
4 Weak winds
The results as summarized above imply that line-driven mass loss seems to be basically understood, though certain problems need further consideration. In particular, from early on there were indications that the (simple) theory might break down for low-density winds. E.g., Chlebowski and Garmany (1991) have derived mass-loss rates for late O-dwarfs that are factors of ten lower than expected. By means of UV-line diagnostics, Kudritzki et al. (1991) and Drew et al. (1994) have derived mass-loss rates for two BII stars that are a factor of five lower than predicted, and Puls et al. (1996) have shown that the wind-momentum rates for low-luminosity dwarfs and giants ( 5.3) lie well below the empirical relation for “normal” O-stars.
The last investigation illuminated an immediate problem arising for low-density winds. For , the conventional mass-loss indicator, Hα, becomes insensitive, and only upper limits for can be derived (for a recent illustration of this problem, see (Marcolino et al., 2009)). Instead, unsaturated UV resonance lines (C iv, Si iv, C iii) might be used to obtain actual values for (e.g., (Martins et al., 2004; Puls et al., 2008; Marcolino et al., 2009)).
By means of such UV-diagnostics, strong evidence has accumulated that a large number of late type O-dwarfs (and a few giants of intermediate spectral type) have mass-loss rates that are factors of 10 to 100 lower than corresponding rates from both predictions and extrapolations of empirical WLRs. In particular, such weak winds have been found in the Magellanic Clouds (O-dwarfs in NCG 346 (LMC): Bouret et al. (2003); extremely young O-dwarfs in N81 (SMC): Martins et al. (2004)) and in the Milky Way (O-dwarfs and giants: Martins et al. (2005); late O-dwarfs: Marcolino et al. (2009)).
Two points have to be stressed. (i) Until now, it is not clear whether all or only part of the late type dwarfs are affected by this problem. (ii) The derived UV mass-loss rates are not very well constrained, since they might be contaminated222via a modified ionization equilibrium. from X-rays embedded in the wind (due to shocks, see next Section). The higher the X-ray emission, the weaker the lines, and the higher the actual mass-loss rates (see Figs. 19 and 20 in Puls et al. (2008)). However, to “unify” the present, very low, -values with “normal” mass-loss rates by invoking X-rays, unrealistically high X-ray luminosities would be required (Marcolino et al., 2009).
The weak-wind problem is a prime challenge for the radiative line-driven wind theory. Martins et al. (2004) investigated a variety of candidate processes (e.g., ionic decoupling, shadowing by photospheric lines, curvature effects of velocity fields), but none of those turned out to be strong enough to explain the very low mass-loss rates that seem to be present. At the end of this review, we will return to this problem.
5 Wind clumping
During the last years, overwhelming direct and indirect evidence has accumulated that one of the standard assumptions of conventional wind models, homogeneity, needs to be relaxed. Nowadays the winds are thought to be clumpy, consisting of small scale density inhomogeneities, where the wind matter is compressed into over-dense clumps, separated by an (almost) void inter-clump medium (icm). Details on observations and theory can be found in the proceedings of a recent workshop, “Clumping in hot star winds” (Hamann et al., 2008).
Theoretically, such inhomogeneities are considered related to structure formation due to the line-driven (“de-shadowing”) instability, a strong instability inherent to radiative line-driving (cf. Owocki, this volume). Time-dependent hydrodynamic models allowing for this instability to operate have been developed by Owocki and coworkers (1-D:(Owocki et al., 1988; Runacres and Owocki, 2002, 2005); 2-D:(Dessart and Owocki, 2003, 2005)) and by Feldmeier (Feldmeier, 1995; Feldmeier et al., 1997), and show that the wind, for , develops extensive structure consisting of strong reverse shocks separating slower, dense material from high-speed rarefied regions in between. Such structure is the most prominent and robust result from time-dependent modeling, and the basis for our interpretation and description of wind clumping. Within the shocks, the material is heated to a couple of million Kelvin, and subsequently cooled by X-ray emission (which has been observed by all X-ray observatories), with typical X-ray luminosities (for newest results, see Sana et al. (2006)).
Clumping effects. Until now, most diagnostic methods to investigate the effects of clumping use the following assumptions: The clumps are optically thin, the icm is void, the velocity field remains undisturbed, and the so-called clumping factor, , measures the over-density inside the clumps with respect to the average density. This simple model of micro-clumping allows one to incorporate clumping into NLTE-codes without any major effort, namely by multiplying the average (wind-) density by and by multiplying all opacities/emissivities by the inverse of (i.e., by the volume filling factor).
The most important consequence of such optically thin clumps is a reduction of any derived from -dependent diagnostics (e.g., recombination based processes such as Hα or radio-emission), assuming smooth models, by a factor of . That there is a reduction is conceivable, since, under the assumptions made, the square of the over-density “wins” against the smaller absorbing/emitting volume. Thus, a lower is sufficient to produce the same optical depths/emission measures as in smooth models.
Note, however, that in this scenario any derived from -dependent diagnostics (e.g., UV-resonance lines) remains uncontaminated, since in this case the over-density cancels against the smaller absorbing/emitting volume. Finally, it should be mentioned that a clumpy medium also affects the ionization equilibrium, due to enhanced recombination (e.g., (Bouret et al., 2005)).
Results from NLTE-spectroscopy allowing for micro-clumped winds are as follows. (i) Typical clumping factors are 10…50, and clumping starts at or close to the wind base, the latter in conflict with theoretical predictions. Derived mass-loss rates are factors of 3 to 7 lower than previously thought (Crowther et al., 2002; Hillier et al., 2003; Bouret et al., 2003, 2005). In strong winds, the inner region is more clumped than the outer one (), and the minimum reduction of smooth Hα mass-loss rates is by factors between 2 and 3 (Puls et al., 2006).
The P v problem. From a mass-loss analysis using the FUV P v resonance line333unsaturated due to the low phosphorus abundance. for a large sample of O-stars, Fullerton et al. (2006) (see also (Massa et al., 2003)) concluded that the resulting mass-loss rates are a factor of 10 or more lower than derived from Hα and/or radio emission using homogeneous models, implying 100! Similar results have been found from unsaturated P Cygni lines from lower luminosity B-supergiants (Prinja et al., 2005).
If such large reductions in were true, the consequences for stellar evolution and feed-back would be enormous. Note that an “allowed” reduction from evolutionary constraints is at most by a factor of 2 to 4 (Hirschi (2008)).
Porosity and vorosity. A possible resolution of this dilemma might be provided by considering the porosity (Owocki et al., 2004) of the medium, also suggested to explain the observed X-ray line emission (cf. the contributions by Oskinova et al. and Cohen et al. in (Hamann et al., 2008), and particularly the discussion on X-rays). Whenever the clumps become optically thick for certain processes, as might be true for the P v-line, the geometrical distribution of the clumps becomes important (size vs. separation, shape). In this macro-clumping approach (see also Hamann, this volume), the effective opacity becomes reduced, i.e., the wind becomes more transparent (“porous”), because radiation can propagate through the “holes” provided by the icm. Additionally, clumps hidden behind other clumps become ineffective because the first clump is already optically thick.
Oskinova et al. (2007) used a simple, quasi-analytic treatment of macro-clumping (still assuming a smooth velocity law) to investigate P v in parallel with Hα from Pup. Whereas macro-clumping had almost no effect on Hα, since the transition is optically thin in the clumps, P v turned out to be severely affected. Thus, only a moderate reduction of the smooth mass-loss rate (factors 2 to 3) was necessary to fit the observations, consistent with the evolutionary constraints from above.
This model has been criticized by Owocki (2008), who pointed out that not only the distribution/optical thickness of the clumps is important, but also the distribution of the velocity field, since the interaction between photons and lines is controlled by the Doppler-effect. Also the “holes” in velocity space, due to the non-monotonic character of the velocity field, lead to an increased escape (thus, he called this process velocity-porosity = “vorosity”), whilst the different velocity gradients inside the clumps lead to an additional modification of the optical depth.
Resonance line formation with porosity and vorosity. To clarify in how far the above arguments/simulations depend on the various assumptions, and to characterize/quantify the various effects from inhomogeneous winds of different sub-structures, a current project in our group investigates the resonance-line formation in such winds. To this end, pseudo 2-D hydrodynamic models (based on different snapshots of corresponding 1-D models from Owocki and Feldmeier, aligned as independent slices of opening angle ), as well as 2-D models based on a stochastic description, have been created (Fig. 1, left panel). For these models then, a detailed Monte-Carlo line transfer (discarding the Sobolev-approximation) is performed. The right panel of Fig. 1 shows prototypical profiles from such simulations, based on the stochastic 2-D wind description, for an intermediate strong line that would be marginally saturated in smooth models (dashed). The grey dashed-dotted profile displays the effects of porosity alone (i.e., a smooth velocity field has been used), using a rather low clumping factor, , and an average separation of clumps in the outer wind. Already here, a strong de-saturation of the profile is visible. The grey dashed-dotted-dotted line displays the other extreme, namely vorosity alone (i.e., now the density is smooth), using a stochastic description of the velocity field, characterized by a “velocity clumping factor” (as defined in (Owocki, 2008), Fig. 1) = 0.3. Interestingly, the de-saturation of the profile is similar to the porosity-effect alone. The solid black line displays the combined effect from porosity and vorosity, with a further de-saturation. If compared to a line from a smooth model of similar profile strength (dotted), it turns out that the effective opacity in the structured model(s) has been reduced by a factor of 20, i.e., the actual would be a factor of 20 higher than derived from a smooth model. Thus, structured models invoking porosity and vorosity might indeed resolve the discordance between the results by Fullerton et al. and evolutionary constraints.
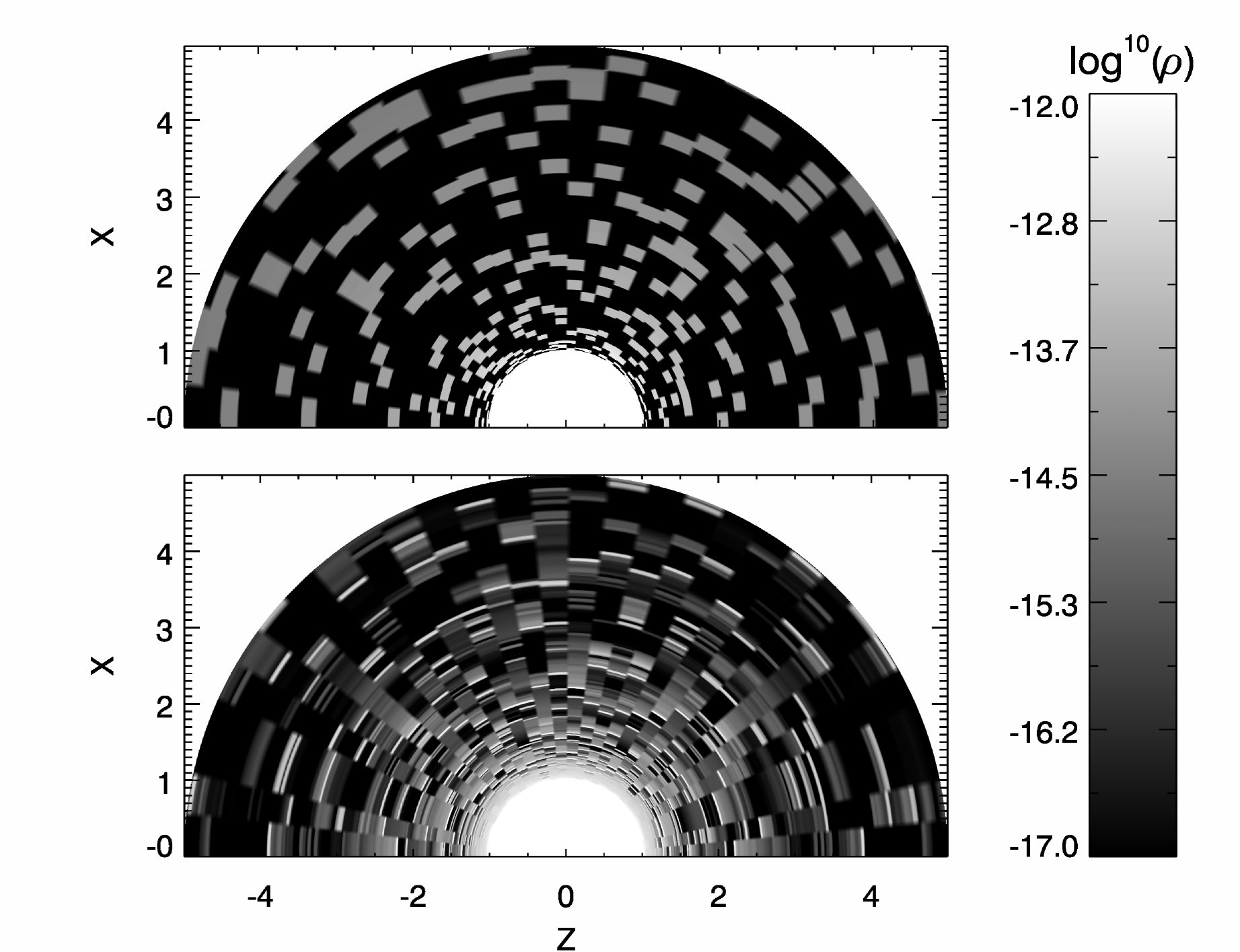

We note, however, that the profile-strength reduction presented in Fig. 1 corresponds to a “most favourable case”, using rather ideal parameters. Our investigations have shown how details on porosity, vorosity, and the icm, all are important for the formation of the line profiles. In fact, the strengths of similar profiles calculated from our pseudo 2-D hydrodynamic models are only reduced by , because of insufficient vorosity inherent to structures from present time-dependent modeling (see also Owocki (2008)). Such a modest reduction is much lower than needed to alleviate the discrepancy discussed above. Also, as it turns out, the icm is a crucial parameter if to de-saturate intermediate strong lines and, at the same time, allowing the formation of the observed saturated profiles. Tests have shown that, with a void icm, the formation of saturated profiles is only possible if the average clump separation (controlling the porosity) is very small, but then the de-saturation of intermediate strong lines becomes marginal. Only by assuming an icm with sufficient density () we have been able to form saturated lines in parallel with de-saturated ones of intermediate strength. This finding is consistent with results from Zsargó et al. (2008), who pointed out that the icm is crucial for the formation of highly ionized species such as O vi.
Further details and results from our investigations will be given in a forthcoming paper (Sundqvist et al., in prep for A&A), including a systematic investigation of different key parameters and effects. Future plans include a comparison with emission lines, and the development of simplified approaches to incorporate porosity/vorosity effects into NLTE models.
6 Weak winds again – Brα as a diagnostic tool
In the preceeding paragraphs, we have argued that (i) mass-loss rates from unsaturated UV line-profiles are much lower than those from Hα or radio emission, and that (ii) this discordance might be mitigated by porosity/vorosity effects. Recall here that the mass-loss rates from weak winds discussed so far (Sect. 4) rely on the same UV-line diagnostics, and the question arises whether one encounters a similar problem, i.e., an under-estimation of the “true” mass-loss rates due to insufficient physics accounted for in the diagnostics. Thus, to clarify in how far the weak wind problem is a real one, independent diagnostics are required!
Already in 1969 Auer and Mihalas (1969), based on their first generation of NLTE, hot-star model atmospheres, predicted that the IR Brα-line should show significant photospheric core emission, due to an under-population of its lower level () relative to the upper one (), resulting from a very efficient decay channel . Indeed, such core emission has meanwhile been observed in various weak wind candidates such as Sco (B0.2V), HD 36861 (O8III(f)), and HD 37468 (O9.5V) (Najarro, Hanson and Puls, in prep. for A&A). Recent simulations (Puls et al. (2008), Figs. 21/22) actually show that such photospheric + wind emission can fit the observations quite nicely, and that the core of Brα is a perfect tracer for the wind density also for thinner winds (as opposed to Hα). Astonishingly, the height of the peak increases for decreasing , which is related to the onset of the wind, i.e., the density/velocity structure in the transition zone between photosphere and wind, and not due to radiative transfer effects. The higher the wind-density, the deeper (with respect to optical depth) this onset, which subsequently suppresses the relative under-population of due to efficient pumping from the hydrogen ground-state. Moreover, Brα is only weakly affected by the presence of X-rays, and thus an ideal tool to infer very low mass-loss rates. From fits to the observations, it turns out that is actually very low (of the order of for HD 37468, and even lower, if the wind-base were clumped). Thus, weak winds seem to be a reality!
What may then be the origin of weak winds? Krtička and Kubát (2009) argue that weak-winded stars display enhanced X-ray emission, maybe related to extended cooling zones because of the low wind density. Already Drew et al. (1994) pointed out that strong X-ray emission can lead to a reduced line acceleration, because of a modified ionization equilibrium, and since higher ions have fewer lines. Thus, weak-winded stars might be the result of strong X-ray emission. Let us now speculate whether such strong emission might be related to magnetic fields. Note that weak winds can be strongly affected by relatively weak -fields, of the order of 40 Gauss according to the scaling relations provided by ud-Doula and Owocki (2002), which is below the present detection threshold. In this case then, colliding loops might be generated, which in turn generate strong and hard X-ray emission in the lower wind, which finally might influence the ionization and thus radiative driving. Future simulations coupling magneto-radiation-hydrodynamic wind codes with a self-consistent description of the line-acceleration will tell whether this mechanism might work.
References
- Gräfener and Hamann (2005) G. Gräfener, and W.-R. Hamann, A&A 432, 633–645 (2005).
- Gräfener and Hamann (2008) G. Gräfener, and W.-R. Hamann, A&A 482, 945–960 (2008).
- Lucy and Solomon (1970) L. B. Lucy, and P. M. Solomon, ApJ 159, 879–893 (1970).
- Castor et al. (1975) J. I. Castor, D. C. Abbott, and R. I. Klein, ApJ 195, 157–174 (1975).
- Friend and Abbott (1986) D. B. Friend, and D. C. Abbott, ApJ 311, 701–707 (1986).
- Pauldrach et al. (1986) A. Pauldrach, J. Puls, and R. P. Kudritzki, A&A 164, 86–100 (1986).
- Kudritzki and Puls (2000) R.-P. Kudritzki, and J. Puls, ARA&A 38, 613–666 (2000).
- Puls et al. (2008) J. Puls, J. S. Vink, and F. Najarro, A&ARv 16, 209–325 (2008).
- Springmann and Pauldrach (1992) U. W. E. Springmann, and A. W. A. Pauldrach, A&A 262, 515–522 (1992).
- Krtička and Kubát (2000) J. Krtička, and J. Kubát, A&A 359, 983–990 (2000).
- Owocki and Puls (2002) S. P. Owocki, and J. Puls, ApJ 568, 965–978 (2002).
- Sobolev (1960) V. V. Sobolev, Moving envelopes of stars, Cambridge: Harvard University Press, 1960, 1960.
- Puls et al. (2000) J. Puls, U. Springmann, and M. Lennon, A&AS 141, 23–64 (2000).
- Abbott (1982) D. C. Abbott, ApJ 259, 282–301 (1982).
- Kudritzki et al. (1995) R.-P. Kudritzki, D. J. Lennon, and J. Puls, “Quantitative Spectroscopy of Luminous Blue Stars in Distant Galaxies,” in Science with the VLT, edited by J. R. Walsh, and I. J. Danziger, 1995, p. 246.
- Friend and Castor (1983) D. B. Friend, and J. I. Castor, ApJ 272, 259–272 (1983).
- Puls (1987) J. Puls, A&A 184, 227–248 (1987).
- Vink et al. (2000) J. S. Vink, A. de Koter, and H. J. G. L. M. Lamers, A&A 362, 295–309 (2000).
- Vink et al. (2001) J. S. Vink, A. de Koter, and H. J. G. L. M. Lamers, A&A 369, 574–588 (2001).
- Abbott and Lucy (1985) D. C. Abbott, and L. B. Lucy, ApJ 288, 679–693 (1985).
- Pauldrach (1987) A. Pauldrach, A&A 183, 295–313 (1987).
- Pauldrach et al. (1994) A. W. A. Pauldrach, R. P. Kudritzki, J. Puls, K. Butler, and J. Hunsinger, A&A 283, 525–560 (1994).
- Pauldrach et al. (2001) A. W. A. Pauldrach, T. L. Hoffmann, and M. Lennon, A&A 375, 161–195 (2001).
- Krtička and Kubát (2001) J. Krtička, and J. Kubát, A&A 369, 222–238 (2001).
- Krtička and Kubát (2004) J. Krtička, and J. Kubát, A&A 417, 1003–1016 (2004).
- Krtička and Kubát (2009) J. Krtička, and J. Kubát, MNRAS p. 323 (2009).
- Krtička (2006) J. Krtička, MNRAS 367, 1282–1296 (2006).
- Kudritzki (2002) R.-P. Kudritzki, ApJ 577, 389–408 (2002).
- Kudritzki et al. (1989) R.-P. Kudritzki, A. Pauldrach, J. Puls, and D. C. Abbott, A&A 219, 205–218 (1989).
- Mihalas et al. (1975) D. Mihalas, P. B. Kunasz, and D. G. Hummer, ApJ 202, 465–489 (1975).
- Mihalas et al. (1976a) D. Mihalas, P. B. Kunasz, and D. G. Hummer, ApJ 203, 647–659 (1976a).
- Mihalas et al. (1976b) D. Mihalas, P. B. Kunasz, and D. G. Hummer, ApJ 206, 515–524 (1976b).
- Mihalas et al. (1976c) D. Mihalas, P. B. Kunasz, and D. G. Hummer, ApJ 210, 419–433 (1976c).
- Lucy (2007a) L. B. Lucy, A&A 468, 649–655 (2007a).
- Lucy (2007b) L. B. Lucy, A&A 474, 701–706 (2007b).
- Müller and Vink (2008) P. E. Müller, and J. S. Vink, A&A 492, 493–509 (2008).
- Puls (2008) J. Puls, “Physical and Wind Properties of OB-Stars,” in IAU Symposium, edited by F. Bresolin, P. A. Crowther, and J. Puls, 2008, vol. 250 of IAU Symposium, pp. 25–38.
- Fullerton et al. (2006) A. W. Fullerton, D. L. Massa, and R. K. Prinja, ApJ 637, 1025–1039 (2006).
- Marcolino et al. (2009) W. L. F. Marcolino, J. . Bouret, F. Martins, D. J. Hillier, T. Lanz, and C. Escolano, ArXiv e-prints (2009), 0902.1833.
- Massey et al. (2009) P. Massey, A. M. Zangari, N. I. Morrell, J. Puls, K. DeGioia-Eastwood, F. Bresolin, and R.-P. Kudritzki, ApJ 692, 618–652 (2009).
- Hillier and Miller (1998) D. J. Hillier, and D. L. Miller, ApJ 496, 407 (1998).
- Puls et al. (2005) J. Puls, M. A. Urbaneja, R. Venero, T. Repolust, U. Springmann, A. Jokuthy, and M. R. Mokiem, A&A 435, 669–698 (2005).
- Mokiem et al. (2007a) M. R. Mokiem, A. de Koter, J. S. Vink, J. Puls, C. J. Evans, S. J. Smartt, P. A. Crowther, A. Herrero, N. Langer, D. J. Lennon, F. Najarro, and M. R. Villamariz, A&A 473, 603–614 (2007a).
- Pauldrach and Puls (1990) A. W. A. Pauldrach, and J. Puls, A&A 237, 409–424 (1990).
- Evans et al. (2004) C. J. Evans, D. J. Lennon, C. Trundle, S. R. Heap, and D. J. Lindler, ApJ 607, 451–459 (2004).
- Crowther et al. (2006) P. A. Crowther, D. J. Lennon, and N. R. Walborn, A&A 446, 279–293 (2006).
- Markova and Puls (2008) N. Markova, and J. Puls, A&A 478, 823–842 (2008).
- Evans et al. (2005) C. J. Evans, S. J. Smartt, J.-K. Lee, and 23 coauthors, A&A 437, 467–482 (2005).
- Evans et al. (2006) C. J. Evans, D. J. Lennon, S. J. Smartt, and C. Trundle, A&A 456, 623–638 (2006).
- Evans et al. (2008) C. Evans, I. Hunter, S. Smartt, D. Lennon, A. de Koter, R. Mokiem, C. Trundle, P. Dufton, R. Ryans, J. Puls, J. Vink, A. Herrero, S. Simón-Díaz, N. Langer, and I. Brott, The Messenger 131, 25 (2008).
- Mokiem et al. (2006) M. R. Mokiem, A. de Koter, C. J. Evans, J. Puls, S. J. Smartt, P. A. Crowther, A. Herrero, N. Langer, D. J. Lennon, F. Najarro, M. R. Villamariz, and S.-C. Yoon, A&A 456, 1131–1151 (2006).
- Mokiem et al. (2007b) M. R. Mokiem, A. de Koter, C. J. Evans, J. Puls, S. J. Smartt, P. A. Crowther, A. Herrero, N. Langer, D. J. Lennon, F. Najarro, M. R. Villamariz, and J. S. Vink, A&A 465, 1003–1019 (2007b).
- Mokiem et al. (2005) M. R. Mokiem, A. de Koter, J. Puls, A. Herrero, F. Najarro, and M. R. Villamariz, A&A 441, 711–733 (2005).
- Repolust et al. (2004) T. Repolust, J. Puls, and A. Herrero, A&A 415, 349–376 (2004).
- Chlebowski and Garmany (1991) T. Chlebowski, and C. D. Garmany, ApJ 368, 241–251 (1991).
- Kudritzki et al. (1991) R.-P. Kudritzki, J. Puls, R. Gabler, and J. H. M. M. Schmitt, “Hot Stars - what can be Learned from Extreme Ultraviolet Spectroscopy,” in Extreme Ultraviolet Astronomy, edited by R. F. Malina, and S. Bowyer, 1991, p. 130.
- Drew et al. (1994) J. E. Drew, M. G. Hoare, and M. Denby, MNRAS 266, 917 (1994).
- Puls et al. (1996) J. Puls, R.-P. Kudritzki, A. Herrero, A. W. A. Pauldrach, S. M. Haser, D. J. Lennon, R. Gabler, S. A. Voels, J. M. Vilchez, S. Wachter, and A. Feldmeier, A&A 305, 171 (1996).
- Martins et al. (2004) F. Martins, D. Schaerer, D. J. Hillier, and M. Heydari-Malayeri, A&A 420, 1087–1106 (2004).
- Bouret et al. (2003) J.-C. Bouret, T. Lanz, D. J. Hillier, S. R. Heap, I. Hubeny, D. J. Lennon, L. J. Smith, and C. J. Evans, ApJ 595, 1182–1205 (2003).
- Martins et al. (2005) F. Martins, D. Schaerer, D. J. Hillier, F. Meynadier, M. Heydari-Malayeri, and N. R. Walborn, A&A 441, 735–762 (2005).
- Hamann et al. (2008) W.-R. Hamann, A. Feldmeier, and L. M. Oskinova, editors, Clumping in Hot-Star Winds, Potsdam: Universitätsverlag Potsdam, 2008.
- Owocki et al. (1988) S. P. Owocki, J. I. Castor, and G. B. Rybicki, ApJ 335, 914–930 (1988).
- Runacres and Owocki (2002) M. C. Runacres, and S. P. Owocki, A&A 381, 1015–1025 (2002).
- Runacres and Owocki (2005) M. C. Runacres, and S. P. Owocki, A&A 429, 323–333 (2005).
- Dessart and Owocki (2003) L. Dessart, and S. P. Owocki, A&A 406, L1–L4 (2003).
- Dessart and Owocki (2005) L. Dessart, and S. P. Owocki, A&A 437, 657–666 (2005).
- Feldmeier (1995) A. Feldmeier, A&A 299, 523 (1995).
- Feldmeier et al. (1997) A. Feldmeier, J. Puls, and A. W. A. Pauldrach, A&A 322, 878–895 (1997).
- Sana et al. (2006) H. Sana, G. Rauw, Y. Naze, E. Gosset, and J.-M. Vreux, MNRAS 372, 661–678 (2006).
- Bouret et al. (2005) J.-C. Bouret, T. Lanz, and D. J. Hillier, A&A 438, 301–316 (2005).
- Crowther et al. (2002) P. A. Crowther, D. J. Hillier, C. J. Evans, A. W. Fullerton, O. De Marco, and A. J. Willis, ApJ 579, 774–799 (2002).
- Hillier et al. (2003) D. J. Hillier, T. Lanz, S. R. Heap, I. Hubeny, L. J. Smith, C. J. Evans, D. J. Lennon, and J. C. Bouret, ApJ 588, 1039–1063 (2003).
- Puls et al. (2006) J. Puls, N. Markova, S. Scuderi, C. Stanghellini, O. G. Taranova, A. W. Burnley, and I. D. Howarth, A&A 454, 625–651 (2006).
- Massa et al. (2003) D. Massa, A. W. Fullerton, G. Sonneborn, and J. B. Hutchings, ApJ 586, 996–1018 (2003).
- Prinja et al. (2005) R. K. Prinja, D. Massa, and S. C. Searle, A&A 430, L41–L44 (2005).
- Hirschi (2008) R. Hirschi, “The impact of reduced mass loss rates on the evolution of massive stars,” in Clumping in Hot-Star Winds, edited by W.-R. Hamann, A. Feldmeier, and L. M. Oskinova, 2008, p. 9.
- Owocki et al. (2004) S. P. Owocki, K. G. Gayley, and N. J. Shaviv, ApJ 616, 525–541 (2004).
- Oskinova et al. (2007) L. M. Oskinova, W.-R. Hamann, and A. Feldmeier, A&A 476, 1331–1340 (2007).
- Owocki (2008) S. P. Owocki, “Dynamical simulation of the “velocity-porosity” reduction in observed strength of stellar wind lines,” in Clumping in Hot-Star Winds, edited by W.-R. Hamann, A. Feldmeier, and L. M. Oskinova, 2008, p. 121.
- Zsargó et al. (2008) J. Zsargó, D. J. Hillier, J.-C. Bouret, T. Lanz, M. A. Leutenegger, and D. H. Cohen, ApJ 685, L149–L152 (2008).
- Auer and Mihalas (1969) L. H. Auer, and D. Mihalas, ApJ 156, L151 (1969).
- ud-Doula and Owocki (2002) A. ud-Doula, and S. P. Owocki, ApJ 576, 413–428 (2002).