Mass-Matrix Differential-Algebraic Equation Formulation for Transient Stability Simulation

The proposed mass-matrix formulation is given by

where $\bm{M}$ is a $(n+m)\times(n+m)$ possibly-diagonal matrix with its upper-left $n\times n$ block being $\bm{M_{x}}$. $\bm{\hat{f}}$ ($\bm{\hat{f}}:\mathbb{R}^{m+n+o}\Rightarrow\mathbb{R}^{n}$) is chosen based on $\bm{f}$ and determines the diagonality of $\bm{m}$.

The choice of $\bm{\hat{f}}$ is not unique. For transient stability simulations, the simplest choice of $\bm{\hat{f}}$ is the numerators of $\bm{f}$ if $\bm{f}$ is a fraction expression with a constant parameter as the denominator. In such case, $\bm{M_{x}}$ becomes a time-invariant diagonal matrix with the element $\mu_{i,i}$ $(i\in[1,n])$ being

The proposed mass-matrix formulation in (5) has the following relationships with the existing ones:

1. 1.

   (5) is a special case of (4) when one let $\bm{\tilde{f}}=\bm{\hat{f}}$, $\bm{T(x,y)}=\bm{M_{x}}$ and $\bm{R(x,y)}=\bm{0}$.

2. 2.

   (2) is a special case of (5) when one let $\bm{\hat{f}}=\bm{f}$ and $\bm{M}=\bm{\Gamma}$.

3. 3.

   (1) is a special case of (2) when one let $\bm{\Gamma}=\bm{I_{n}}$, an $n\times n$ identity matrix. Due to the fact that the traditional formulation has already been proven to be all-encompassing for power system models, (5), as a superset of (1), can naturally accommodate for all power system equation formulations.

Such relationships can be represented as:

The main advantages of (5) are two-fold:

1. 1.

   As a general formulation, it is directly supported by a broad spectrum of full-fledged DAE solvers. Power system researchers can thus focus on formulating models without worrying about the details in solution techniques.

2. 2.

   Simple to implement. The only required change to the traditional formulation is to separate the parameters (typically, time or mass constants) from the denominators of $\bm{f}$ into the mass matrix. Mixing models in the mass-matrix and the traditional formulations is allowed, as the latter is a special case.

In addition, the mass-matrix formulation shares the same advantage as the semi-implicit formulation that allows model simplification by setting some time constants to zero.

This section presents some basic transfer functions and synchronous generators in the mass-matrix formulation, in order to demonstrate the implementation simplicity.

The mass-matrix formulation of DAE can be solved by a variety of numerical integration methods. Implicit numerical integration schemes are known for their good performance for Ordinary Differential Equations (ODEs) and DAEs that are stiff, which is the case for transient simulation. At each step, ITM solves a set of nonlinear equations consisting of both differential and algebraic equations simultaneously through Newton’s iteration. This subsection discusses the form of iteration for the mass-matrix formulation.

The nonlinear equations to solve for (1) at time $t$ are given by

where $h$ is the step size, and $\bm{x}_{t-h}$ and $\bm{f}_{t-h}$ are the differential states and equation RHS computed at the previous time ($t-h$). Note that for $\bm{g}$, the sign and the scaling factor $\gamma$ can be chosen arbitrarily, and a small $\gamma$ close to $h$ improves the convergence. Accordingly, solutions are obtained by iteratively updating variables using (16), where the increments are calculated using (17).

Comparing (5) with (1), we can observe that the mass-matrix formulation can be derived by multiplying $\bm{M}$ to both sides of the equation. Therefore, mutltiplying $\bm{M}$ to (17) yields

The Jacobian matrix for calculating increments is given by:

Comparing (19) to (17), one can notice that the only required change to the solver is to substitute the identity matrix $\bm{I_{n}}$ with the mass matrix $\bm{M_{x}}$. Therefore, numerical integration routines can be readily adapted for the proposed formulation.

In terms of computational complexity, (5) is not more demanding than (1). When one uses a constant diagonal mass-matrix formulation, the number of division operations can be slightly reduced for evaluating $\bm{\hat{f}}$ and the subsequent Jacobian elements. Such effect, however, is negligible in actual test cases mostly because the number of reduced operations is small w.r.t. the total operations.

The most significant advantage of the mass-matrix formulation is its compatibility with fine-tuned DAE solver packages, which usually come with a multitude of solution methods and error control mechanisms and have undergone rigorous tests. Such compatibility allows power system researchers to focus on modeling while utilizing the state-of-the-art numerical solvers.

For example, the DifferentialEquations.jl package [5] provides four categories of methods that naturally support the mass-matrix formulation: Rosenbrock methods and Rosenbrock-Wanner methods (for small stiffness systems), and Implicit Runge-Kutta methods and multistep methods (for stiff problems). An overview of the interfaced solvers in this work is shown in Table I, where “A” or “L” in the stability column indicates an algorithm being A-stable or L-stable [6]. Details of the solvers can be found in [5] and the accompanying documentation.

The proposed work has been implemented in ANDES [4], a Python-based hybrid symbolic-numeric library for power systems, and interfaced with the solvers in the Julia language with the Jacobian callback provided. Case studies utilize Python 3.7.6, ANDES 1.0.8, Julia 1.5.0, and DifferentialEquations 6.15.0. Simulations are executed on an Intel Xeon W-2133 CPU with 32 GiB of RAM running Ubuntu 16.04 LTS.

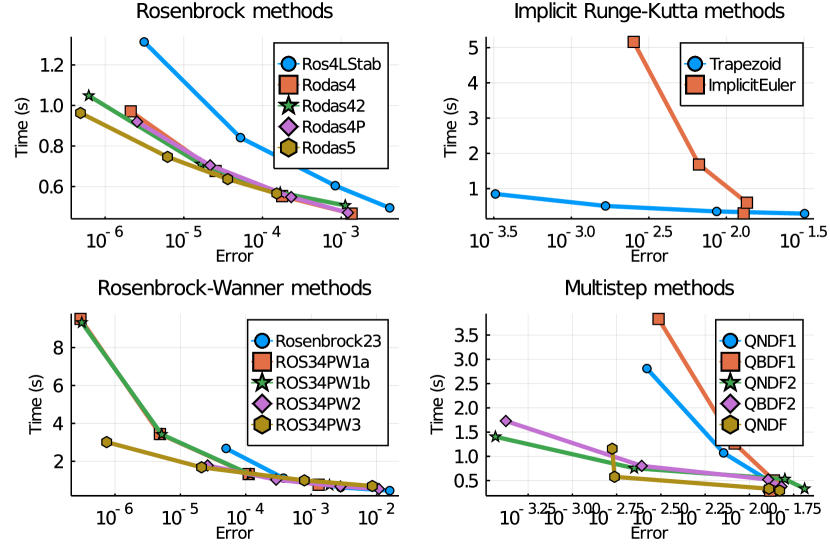
First, the Kundur’s system modeled in the proposed formulation is used for solver benchmarking. The system contains 52 differential states and 140 algebraic variables, and the rank of the mass matrix is 48 (two generators are reduced with $T_{d0}^{\prime\prime}=T_{q0}^{\prime\prime}=0$). The response following a line trip at $t=0.1$ s and a reconnection after 50 ms is simulated for 5 s. The baseline “accurate” solution is obtained using Rodas5, which is efficient in high accuracy, with both absolute and relative tolerances set to $10^{-12}$. Next, each solver is given four pairs of absolute and relative tolerances, chosen from $(10^{-5},10^{-6},10^{-7},10^{-8})$, and $(10^{-1},10^{-2},10^{-3},10^{-4})$, respectively. Errors are obtained as the difference between the accurate and the actual solutions at the final simulation step. Each case is run for five times to compute the average time. The results shown in Figure 1, and some observations are:

1. 1.

   The commonly used Trapezoidal method is balanced in speed and accuracy. ImplicitEuler is neither efficient nor accurate.

2. 2.

   Depending on the stiffness, the Rosenbrock methods can be faster than the Trapezoid method at some accuracy levels.

3. 3.

   The Rosenbrock-Wanner methods allow approximate Jacobians. When accurate Jacobians are used (in our case and most other transient stability simulation tools), the Rosenbrock-Wanner methods tend to be slower than the Rosenbrock ones.

4. 4.

   The QNDF method has similar speed and accuracy to the Trapezoid method. QBDF1 performs similarly to Implicit Euler.

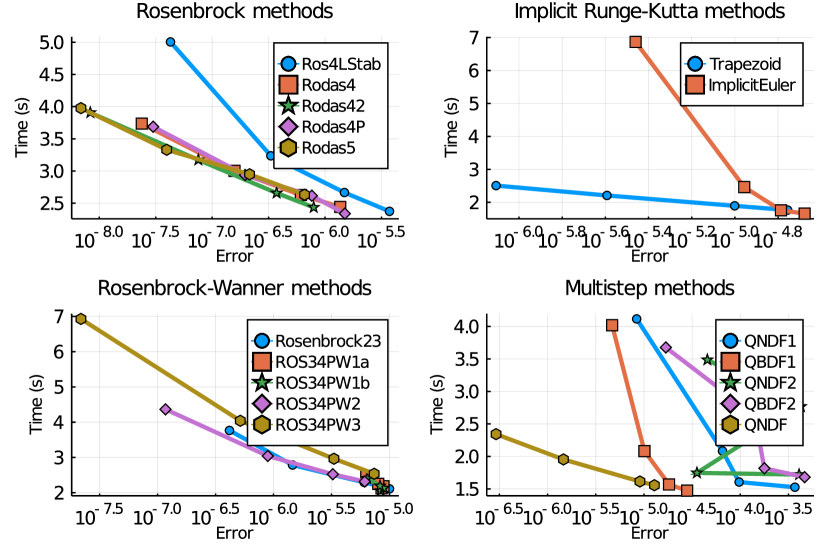
Next, the Great Britain (GB) 2,224-bus system [7] with dynamics is used for benchmarking. The system contains 788 state variables and 9,176 algebraic variables. A disturbance of line trip at $t=1.0$ s and a reconnection after 100 ms is simulated for 5 s. Benchmark results are shown in Figure 2. The observations from the Kundur’s system also apply to this case. For a different system, one can perform similar benchmarks to identify the best solvers that satisfy the speed and accuracy requirements.