Massive quantum superpositions using magneto-mechanics

In a general framework we can describe both our schemes as the creation of superposition on a massive quantum harmonic oscillator. For this, we consider a three-dimensional quantum harmonic oscillator (a levitated spherical magnet or a levitated flux qubit) with a mass denoted as $m$ and which is susceptible to external magnetic actuation. We assume a coordinate system with the origin at this equilibrium position of the oscillator and consider one of the axes, which we denote as $z-$ axis. We denote the oscillation frequency along this axis as $\omega_{\mathrm{z}}$. We consider that this oscillator is in its motional ground state [46, 38], with a ground state width (denoted as $\delta z_{zpm}$), $\delta z_{zpm}=\sqrt{\hbar/(2M\omega_{z})}$, where $\hbar$ is the reduced Planck’s constant. For the creation of superposition states, we consider logical states $|0\rangle$ and $|1\rangle$ based on superconducting flux qubits.

We consider superconducting flux qubit that is made from type-I superconductor (Aluminium). We assume that the operating temperatures for our schemes are at 300 mK or lower and that the magnetic field at the location of the flux qubit is well below its critical magnetic field strength of 9.78 mT to be in the superconducting state [47]. The superconducting flux qubit only allows integer numbers of magnetic flux quantum ($\Phi_{0}=h/2e=2.068\times 10^{-15}\>{\rm Wb}$) threading the qubit loop and the flux qubit will generate a supercurrent to compensate any non-integer flux quanta threading through its loop. We assume the superposition currents in the flux qubit to be $I=\pm{1}\>{\rm\mu A}$ for simplicity in our model. This current can be estimated based on magnetic flux threading the qubit loop as $p\Phi_{0}=\mu_{0}I\pi R/2$, where $p$ is a dimensionless number defining whether the magnetic flux quanta threading through the loop is an integer or not, $\mu_{0}$ and $R$ are vacuum permeability and the Radius of the flux qubits in our schemes.

Since flux qubits’ logical states are determined by the direction of large circulating persistent currents in a superconducting ring (currents flow either clockwise or counterclockwise) [46, 48], the flux qubit can generate logical state-dependent magnetic forces. We denote these logical state-dependent magnetic forces generated by flux qubit as $\vec{F}^{|q\rangle}_{\mathrm{FQ}}$, where $|q\rangle$ is the logical state. In general, $\vec{F}^{|q\rangle}_{\mathrm{FQ}}$due to the logical states $|0\rangle$ and $|1\rangle$ are in opposite directions and we consider they are along $+\hat{z}$ and $-\hat{z}$ respectively. This force displaces the equilibrium position of the oscillator away from $z=0$, to the new position $z=z_{\mathrm{eq}}$ ($z=-z_{\mathrm{eq}}$), for $|0\rangle$ ($|1\rangle$) state. However, a restoring force along the z-axis which can be expressed as $\vec{F}_{\mathrm{TR}}=-\hat{z}m\omega_{\mathrm{z}}^{2}z$ acts on the displaced oscillator that pulls the oscillator back from either $\hat{z}$ directions towards $z=0$. As a result the oscillator reaches new equilibrium position where $\vec{F}^{|q\rangle}_{\mathrm{FQ}}+\vec{F}_{\mathrm{TR}}=0$. When the qubits are put into the superposition state $\sim(|0\rangle+|1\rangle)$, the oscillator is pushed to a macroscopic spatial superposition of spatial extent $\Delta z=2z_{\mathrm{eq}}$. We express the spatial extent in terms of a dimensionless factor defined as $\chi=\Delta z/\delta z_{zpm}$.

The generation of macroscopic quantum superposition is possible if the oscillator stays close to its motional ground state. However, the coherent oscillation of the oscillator in its motional ground state will cease after a finite amount of time due to its undesired interaction with the surroundings [49]. We can consider the $Q-$factor of the oscillator which is the ratio of oscillation frequency to the damping rate and its value is determined by the dominating damping mechanism. The larger the motional $Q-$factor the longer it will remain close to this ground state with a spatial extent of $\delta z_{\mathrm{zpm}}$ [50]. We consider that the main source of damping on the oscillator is due to the collisions of gas molecules surrounding the oscillator and assume that the average velocity of the oscillator is much smaller than the velocity of the surrounding gas molecules as in the experiment reported in [51]. Thus the Q factor of the oscillation for the two types of oscillators we are considering can be generally written as [52, 51], $Q\approx(\pi\rho r\omega_{z}/(6P_{\mathrm{g}}))\times\sqrt{(3k_{\mathrm{B}}T)/M_{\mathrm{g}}}$, where $P_{g}$ is the pressure of the gas, $k_{\mathrm{B}}$ is the Boltzmann’s constant, $T$ is the temperature at which the experiments are performed, $M_{\mathrm{g}}$ is the mass of the gas molecule, $\rho$ is the density of the oscillator and $r$ is the radius (cross-sectional radius) for a spherical (toroid shaped ) oscillator(see [SM]). To estimate this Q-factor we assume that the gas surrounding the oscillator is Helium [51].

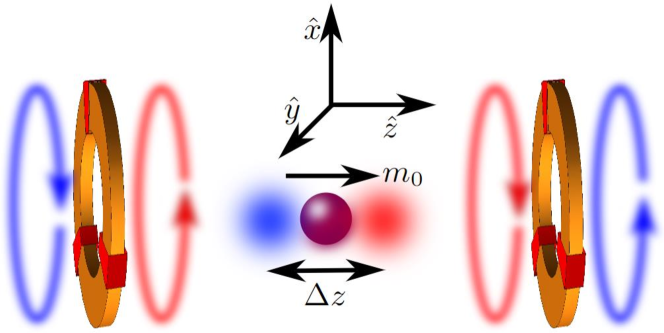
In this scheme, we consider a spherical magnet (for example Yttrium Iron Garnet (YIG) magnetic micro-particle), held in a three-dimensional trap as shown in Fig. 1) as the quantum oscillator. The three-dimensional trapping of such a spherical magnet can be experimentally realised either via magnetic levitation [51, 53] or via optical levitation.

We consider the primary axis for the optical trapping is along the $x-$axis, which is defined using the axes depicted in Fig. 1. The trapping force is strongest along the $x-$axis and weakest along the $y-$ and $z-$ axes. We consider the magnetic moment of the YIG micro-sphere, which we denote as $\vec{m}_{0}$ is directed along $+\hat{z}$ in Fig. 1, similar to the experimental study in [51] with a different type of spherical magnet. This can be also arranged using an asymmetric optical trap and asymmetric micro-particle as well. The asymmetric trap will yield motional modes which are highly differentiated in frequency avoiding cross-mode coupling and allows us to manipulate the $z-$ motional mode specifically. We approximate the YIG sphere as a magnetic dipole due to the spherical shape of the YIG particle. Thus we can write the dipole moment as $\vec{m}_{0}=~{}\mu_{0}^{-1}{B_{\mathrm{r}}}V\hat{z}$, where $B_{\mathrm{r}}$ is the remnant magnetic field. Furthermore, we consider a pair of flux qubits that is driven and connected such that identical supercurrents which we denote as $I$ flow with opposite helicity in each qubit. The flux qubit loops are arranged as shown in Fig. 1, and are placed co-axial with the $z-$axis symmetrically on either side of the trapped YIG particle. We assume that any change in the magnetic field produced by this YIG at the locations of the flux qubit due to the movement of the YIG within the trap is negligible or compensated appropriately in the experimental implementation.

We model the two flux qubits as superconducting ring with a radius $R$ [SM]. The flux qubits have supercurrents $I$ circulating in each ring. The supercurrents generate magnetic fields emanating from each flux qubit such that when each qubit is in the $|0\rangle$ state, these magnetic fields oppose each other and the magnetic field at the midpoint between the two flux qubits vanishes and varies linearly around there, $B_{z}(z)\propto z$. This magnetic field arrangement corresponds to an anti-Helmholtz configuration. When the flux qubits are flipped to be in the $|1\rangle$ state the magnetic field at the mid-point again vanishes, it is still in an anti-Helmholtz configuration, but with the linear dependence on $z$ reversed, e.g. $B_{z}(z)\propto-z$. Thus we can generate a logic state-dependent magnetic field gradient, $(\partial\vec{B}_{z}/\partial z)_{|q\rangle}$, which gives $\vec{F}^{|q\rangle}_{\mathrm{FQ}}=\vec{m}_{0}\cdot(\partial\vec{B}_{z}/\partial z)_{|q\rangle}$.

We find that the non-vanishing magnetic field gradient at the origin is maximum when each of these flux qubits is symmetrically located at a distance $z^{FQ}_{\pm}=\pm R/2$, along the z-axis around the origin [SM] and thus we consider this as the location of the flux qubits for the present scheme. Then the spatial extent of the superposition can be obtained by solving the equation [SM],

Counter-intuitively, from equation 1, we can see that $\Delta z$ is independent of the size of the magnetic sphere but depends only on the magnet’s density and remnant magnetization.

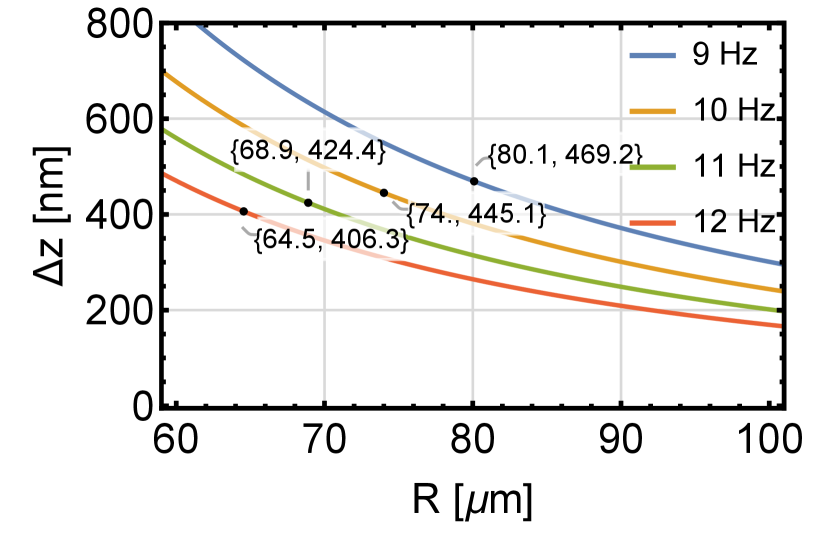
We now numerically study the extent of spatial superposition of the YIG sphere in the considered scheme and the results are shown in Fig. 2. In Fig. 2 (a) we show how the spatial superposition extent $\Delta z$ changes as a function of changing the radius of the flux qubits. We evaluate this numerically from Eq. (1). The numerical values of parameters used for the numerical estimations are given in the supplementary material.

If the levitation of the spherical magnet is via optical means one has to be careful about laser-induced heating of the flux qubit. In order to avoid any direct exposure of the light required for the optical trapping irradiating the flux qubits the latter should be located outside the optical beam path [SM]. One has to be also careful about the optical power required for the trapping considering the low cooling power of dilution refrigeration at mK temperatures. In the case of magnetic levitation of the YIG sphere, we work in the regime where the magnetic field produced by the flux qubits does not affect the levitation mechanism. From Fig. 2 (a) we can see that for the present scheme we can achieve superposition separation $\Delta z$ of the order of a hundreds of nanometers and it is independent of the size of the microparticle. The trapping of spherical magnets (not YIG) of radius of around 23.2 $\mu$m and of around 25 $\mu$m have been experimentally demonstrated via magnetic levitation in references [53] and [51] respectively. For the present scheme, we can achieve the $\chi$ of the order of $10^{6}$ [SM] with a spherical magnet (YIG) with a radius 25 $\mu$m. For a YIG sphere with radius 25 $\mu$m, within the frequency range considered in Fig. 2 we estimate $Q\sim 10^{8}$, due to the damping induced by the surrounding gas collisions on the sphere.

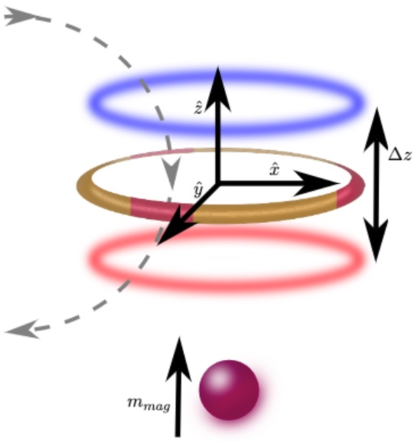
We now consider a complementary scheme with an isolated superconducting flux qubit as the oscillator, which itself is magnetically levitated above a spherical magnet as shown schematically in Fig. 3. As we show in the supplementary material [SM], the Q-factor for the oscillator in this scheme can be of the order of 10⁷.

We first consider a ring-shaped superconducting flux qubit which is cooled down to the Meissner state via the zero-field cooling method [54]. When the flux qubit is moved above a magnet sphere with a magnet moment $m_{mag}$, current will be induced in the qubit to conserve the threading flux, and the flux qubit will feel a repulsive force. Thus the flux qubit can be stably levitated above the magnet at a height $h$ when we have the flux qubit with proper size (see [SM] for more details on the levitation). We consider an additional superconducting driver circuit situated nearby the flux qubit without any direct galvanic contact to drive the flux qubit. The supercurrent in this driver circuit can generate a magnetic field to change the magnetic flux threading the flux qubit. When the magnetic flux is close to half integer of the flux quantum $\Phi_{0}$, clockwise and anti-clockwise currents will be induced in the flux qubit to compensate for the flux of half flux quantum. So we can inductively drive the flux qubit into the current superposition of $|0\rangle$ or $|1\rangle$ states. We denote the modulus of the supercurrent as $I$. The flux qubit acquires a resultant qubit state-dependent dipole moment $\vec{m}_{|q\rangle}=(-1)^{q}\>\vec{m}$ (where $\vec{m}=\hat{z}I\pi R^{2}$) which points downward (upward) when it is $|0\rangle$ $\left(|1\rangle\right)$ state. We can then write $\vec{F}_{\mathrm{Q}}$ for this scheme using the dipole model as, $\vec{F}_{\mathrm{Q}}^{|q\rangle}=\vec{m}_{|q\rangle}\cdot(\partial\vec{B}_{z}/\partial z)$, where $\vec{B}_{z}/\partial z$ is the gradient of the magnetic field generated by the fixed spherical magnet. We find $\vec{F}^{|0\rangle}=\hat{z}3\mu_{0}m_{mag}IR^{2}/(2(z+h)^{4})$ and $\vec{F}^{|1\rangle}=-\hat{z}3\mu_{0}m_{mag}IR^{2}/(2(z+h)^{4})$, where $z$ is the displacement from the equilibrium height. For $\Delta z\ll h$, the spatial position extent is obtained analytically as,

From equation (2), we can see that the spatial superposition can be increased by increasing $R$ and decreasing both $\omega_{\mathrm{z}}$ and $h$. The equilibrium levitation height $h$ can be decreased by either reducing the magnetic moment of the magnetic sphere (e.g. by decreasing its radius) or using a higher-density material for the levitated flux qubit. However, to obtain realistic values for this parameter, one needs to analyze the magnetic trapping of the flux qubit above the spherical magnet in detail. When there is no inductive driving, we can approximate the scheme as a levitation of a superconducting ring using a point dipole, due to the spherical nature of the lifting. This problem has been studied analytically in reference [54], but the model does not capture the significant back-action of the superconductor on the magnetic fields that trap it by the Meissner expulsion. Due to the complexity of the problem, a complete analytical solution of the scheme including this backaction is beyond the scope of this present letter. However, to illustrate the effect of back action and how this can be studied analytically we consider a simpler example setup: the Meissner trapping of an SC sphere by two nearby homogenous magnetic spheres (which we consider as magnetic dipoles), arranged in an anti-Helmholtz configuration (see [SM] for more details). We derive an analytical solution for the trap properties along the trapping axis using an exact method not shown before in the literature, to the best of our knowledge, and find that the key parameter, the vertical trap stiffness is modified by almost $62.5\%$ from the case when no backaction is taken into account. Hence, we simulate the magnetic trapping of the flux qubit above the spherical magnet in the commercial finite element method (FEM) package COMSOL. We find FEM simulation results for the Meissner trapping of an SC sphere which match very well with the analytical solutions (see [SM] for more details).

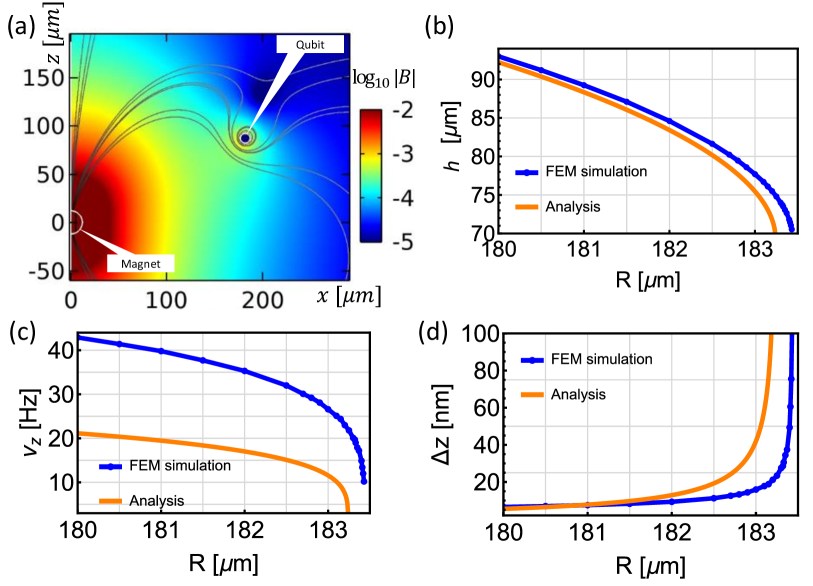
Using FEM simulation, we find that the large ring-like flux qubit experience complete rigid-body trapping (see [SM] for more details), and we present the results in Fig. 4. We find comparable results based on analytical solutions from reference [54] (see [SM] for more details). In Fig. 4 (a), we present one of the examples from our FEM simulations showing the cross-section of magnetic trapping of the flux qubit. From 4(a), we can see that the magnetic field strength at the location of the ring is very small ($|B|<1\>{\rm mT}$) and this ensures proper working of the flux qubit in our scheme. Furthermore, we observe significant perturbation of the fields surrounding the flux-qubit which is expected due to the backaction of the superconducting ring. From the cross-section plot Fig. 4(a), we can see that as $R$ (the flux-qubit radius) increases, the magnetic field seen by the flux qubit decreases and we expect the trapping stiffness (and thereby the $\omega_{\mathrm{z}}$ and $h$) to drop as $R$ increases. We identify this region of $R$ as shown in Fig. 4(b) and (c), there is a critical value of the radius above which the flux qubit cannot be stably trapped. We show the resultant massive spatial superposition in this region, in Fig. 4(d). We obtain a massive spatial superposition of $\Delta z\sim 100\>{\rm nm}$, when $\nu_{z}\sim 15\>{\rm Hz}$ for a radius of $183.4\>\mu m$ and the corresponding $\chi\sim 10^{6}$ with a Q-factor of around $Q\sim 2.8\times 10^{7}$. Larger values of $\Delta z$ are predicted from theory but are probably not feasible in experiments due to potential instabilities in a very low-frequency trap.

In this letter, we have introduced two magnetically-driven methods to achieve macroscopic motional superposition states for massive objects. In the first method, a levitated YIG microsphere with a motional $Q\sim 10^{8}$, can be driven into motional superposition state using adjacent magnetic flux qubits at both sides of the trapped YIG to apply quantum magnetic forces. The results show that the superposition spatial separation is independent of the size of the YIG particle in principle. In the second part, we propose a reversed scheme where the macroscopic spatial superposition can be realized directly on a flux qubit that is levitated above a magnetic microsphere, with a ring motional $Q\sim 10^{7}$. In both the schemes, massive superposition separation extents reach the extreme value $\chi\sim 10^{6}$. One needs to maximize the motional $Q$-factor to permit coherent dynamics for a duration long enough to prepare the superposition state and thereby utilise such large superposition states for quantum sensing applications [38]. The motional Q-factor can be improved further by working at even further low pressure ($P_{g}<10^{-11}\>{\rm mbar}$), by keeping the low frequency considered in this work. With improved flux qubit coherence times, both these macroscopic motional superposition states could be achieved experimentally which can pave the way to explore more fundamental quantum physics and ultra-sensitive applications.

This work was supported by Australian Research Council centre of Excellence for Engineered Quantum Systems (CE170100009) and the Okinawa Institute for Science and Technology Graduate University.