Mathematical analysis of an extended cellular model of the Hepatitis C Virus infection with non-cytolytic process
Abstract
The aims of this work is to analyse of the global stability of the extended model of hepatitis C virus(HCV) infection with cellular proliferation, spontaneous cure and hepatocyte homeostasis. We first give general information about hepatitis C. Secondly, We prove the existence of local, maximal and global solutions of the model and establish some properties of this solution as positivity and asymptotic behaviour. Thirdly we show, by the construction of an appropriate Lyapunov function, that the uninfected equilibrium and the unique infected equilibrium of the model of HCV are globally asymptotically stable respectively when the threshold number and when . Finally, some numerical simulations are carried out using Maple software confirm these theoretical results.
keywords : HCV model; global solutions; non-cytolytic process;
invariant set; Lyapunov functions; basic reproduction number;
equilibrium points.
AMS Classification Subject 2010 : 92B99, 34D23, 92D25.
1 Introduction
Hepatitis C infection is a viral disease caused by Hepatitis C Virus
(HCV) and being transmitted mainly by blood contact between an
infected person and a healthy person. This virus that attacks the
hepatocytes is one of the main causes of chronic diseases of the
liver such as hepatocellular carcinoma, liver cancer and cirrhosis
of the liver [1, 19]. According to the WHO [22]
global report published in April 2017 on hepatitis, 200 to 300
million people worldwide are infected with HCV, and between 60
et 85 of these people develop chronic liver disease [22, 23]. Although there is considerable progress in the research for
the fight against this infection whose virus was discovered in 1989
[1, 19] and which presents today six genotypes, ranked
from 1 to 6 according to [19]. There is no vaccine for
prevention yet [20, 22]. Concerning the treatment of HCV
infection, since 2014, the new direct-acting antivirals combined
with Interferon- and Ribavirin have been able to cure about
90 of cases of chronic infection, but leaves the chronic
diseases whose infection has caused. HCV infection is therefore a
major public health problem.
To understand the dynamics of HCV viral load and its infectious
process, mathematical models have become an important and almost
unavoidable tool[2, 16]. A model is a system of
mathematical equations accounting for all known experimental data of
the studied biological phenomenon. It makes it possible to better
understand the phenomenon under consideration and to act on the
system optimally. Until 2009, most research work on the modeling of
viral dynamics of HCV only took into account the level of
circulating virus in a human population, the case in vivo was almost
ignored as it provides a better understanding of the pathogenesis of
the virus as Harel Dahari et al [8] and Chong et
al.[1].
Our goal is therefore to analyze the stability of an extended model
of HCV infection in a patient with cell proliferation and
spontaneous healing presented in [7, 20] to reveal
significant information on pathogenesis and dynamics of this virus.
The work is organized as follows : In section 1, first focuses on
presentation of the epidemiological model and give some properties
of its solutions, then we calculate the basic reproduction ratio , which is an indispensable element in the study and
analysis of the models. is considered in the
virus dynamics as a metric. We theoretically analyze the local
stability and the global stability of the model by the linearization
and Lyapounov’s functions respectively in section 2 and in section 3
we perform numerical simulations using biologically plausible
parameter values in Table 1 to confirm the results obtained
theoretically and we complete the work by an appendix.
2 A dynamical model of HCV infection and some properties of the solutions of the differential system associated to the model
Mathematical modeling applies to the study of dynamics of infectious diseases seems to be one of the most interesting tool for designing control or eradication strategies of a disease like hepatitis C. It allows to test on computer different prevention scenarios and so help the decision-making in public health [14]. In the following sections, we will firstly present epidemiology and brief history of HCV dynamics, then describe the model itself, show the existence of solutions and establish some properties of these solutions and finally calculate the basic reproduction rate which is an important tool in epidemiology.
2.1 Epidemiology and history of HCV
2.1.1 HCV infection
HCV is a virus that attacks the cells of the liver and causes inflammation of the latter. This virus is present in the blood of an infected person and is, according to the WHO, mandatory declaration. It can live for about 5 to 7 weeks in the open air. In the long term, there may be very serious consequences such as cirrhosis and in some cases, liver cancer . This virus can remain for decades in the body without any apparent symptoms. According to [14, njou] six main genotypes HCV were identified whereas several subtypes play an important role in the severity of the disease and its response to treatment.
2.1.2 Epidemiology of HCV Infection
HCV infection is a major public health problem. Worldwide, the
number of chronic HCV carriers is estimated at about
170 million,
or of the world’s population,
and the incidence is between
3 and 4 million infections per year according to the
statistics
published by the World Health Organization in 2014. The actual
incidence is uncertain because the distinction between acute and
chronic forms is difficult to make. HCV was only identified in 1989
with the advent of modern molecular cloning techniques.
In
Cameroon, about 10,000 people die each year from hepatitis (A, B, C,
D, …). The country is one of the 17 most affected worldwide, with
a prevalence rate of about , that is 2.5 million people
infected.
2.1.3 Natural history of HCV infection
According to WHO’s global report on hepatitis C published in April 2017 the first phase of HCV infection is said Acute: It can cause jaundice, but remains asymptomatic in the majority of cases (70 to 80 ), hence the risk of going unnoticed. It is estimated that 20 to 30 people infected will spontaneously clear the virus within the first six months after initial contact. If the virus persists, hepatitis progresses to chronicity. The liver reacts to HCV aggression by an inflammatory reaction, one of the components of which is fibrogenesis. Hepatic fibrosis is the main complication of chronic hepatitis C. Hepatitis C is likely to evolve at the chronic phase in about 25 of cases to cirrhosis within a period of 5 to 20 years. In case of cirrhosis, the incidence of hepatocellular carcinoma is high: on the order of 1 to 4 per year [14].(See figure 1).
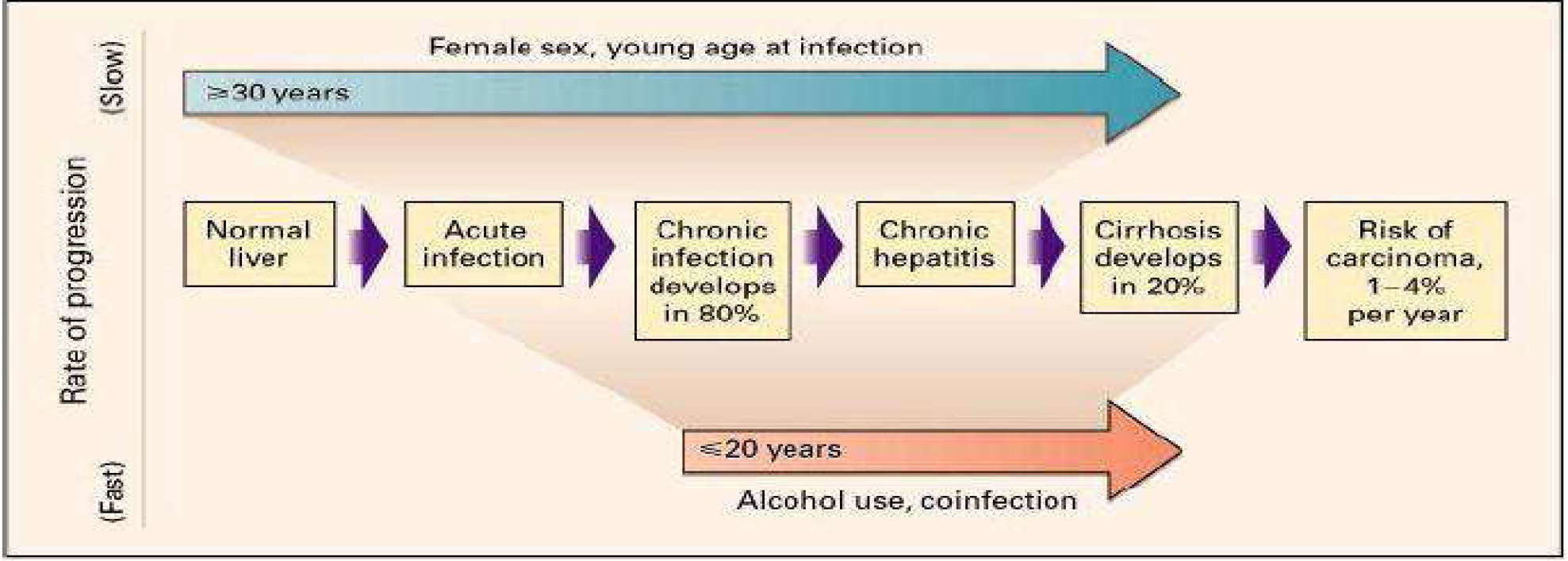
In order to achieve our various goals, we first describe the model and its parameters.
2.2 Description of the HCV model with compartmental diagram
There are two mathematical models of HCV dynamics : the original model or model of Newmann [17] and its extended models like that of Dahari [1, fashion]. Each model can be represented by a compartmental scheme. A compartmental scheme is a scheme for estimating the variation in the number of individuals in each compartment over time. Figure 2 is the schematic representation of the extended model, which we will study, of HCV with cellular proliferation and spontaneous healing designed by T. C. Reluga et al. [20]. This model expands the viral dynamics of the original model of infection and the disappearance of HCV by incorporating the proliferation and death density dependence. In addition to cell proliferation, the number of uninfected hepatocytes may increase through immigration or differentiation of hepatocyte precursors that develop into hepatocytes at a constitutive rate of or by spontaneous infected hepatocyte healing by a non-cytolytic process at the rate .
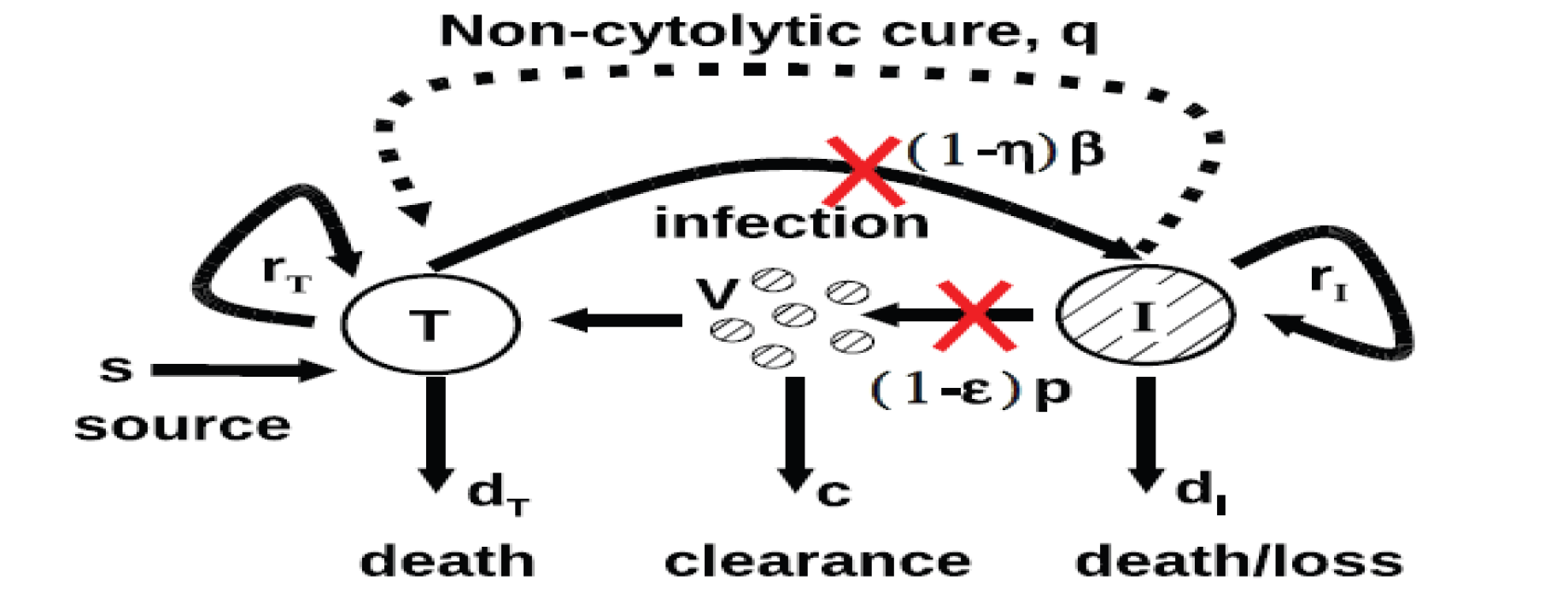
The model proposed by Dahari and coworkers [8, 4]
expands on the standard HCV viral-dynamic model [17]
of
infection and clearance by incorporating density-dependent
proliferation and death. Uninfected hepatocytes or noninfected
hepatocytes, T, are infected at a rate per free virus per
hepatocyte. Infected cells, I, produce free virus at rate per
cell but also die with rate . Free virus is cleared at rate
by immune and other degradation processes. Besides infection
processes, hepatocyte numbers are influenced by homeostatic
processes. Uninfected hepatocytes die at rate . Both infected
and uninfected hepatocytes proliferate logistically with maximum
rates and , respectively, as long as the total
number of hepatocytes is less than . Besides proliferation,
uninfected hepatocytes may increase in number through immigration or
differentiation of hepatocyte precursors that develop into
hepatocytes at constitutive rate , or by spontaneous cure of
infected hepatocytes through a noncytolytic process at rate .
Treatment with antiviral drugs reduces the infection rate by a
fraction and the viral production rate by a fraction
. It should be noted that and are
parameters which values are non-negative and less than one.
The interpretations and biologically plausible value of other
parameters are listed in following Table 1 , and a further
comprehensive survey on the description of the model is given in
[7, 6, 20].
Thus, the variation of healthy hepatocytes T is expressed by the
following expression :
| (1) |
The variation of infected hepatocytes I is expressed by the following expression:
| (2) |
And the variation of the viral load V is expressed by the following expression :
| (3) |
It follows that the dynamics of T, I and V is governed by the following differential system :
Given the meanings of and , the term
represents the mass action principle; is the
rate of infection of healthy T cells by interaction with
virus V.
For biological significance of the parameters, three assumptions are
employed. (1) Due to the burden of supporting virus replication,
infected cells may proliferate more slowly than uninfected cells,
i.e. . (2) To have a physiologically realistic
model, in an uninfected liver when is reached, liver size
should no longer increase, i.e. . (3) Infected
cells have a higher turnover rate than uninfected cells, i.e. . The interpretations and biologically plausible values
of other parameters are listed in Table 1, and a further
comprehensive survey on the description of (4) is given in
[20]. Besides HCV infection, the similar model of (4)
is also used to describe the dynamics of HBV or HIV infection, in
which the full logistic terms mean the proliferation of
uninfected/infected hepatocytes [3, 15, 5], or the
mitotic transmission of uninfected/infected CD4+T.
The range of variation of each parameter is recorded in table 1
[20].
Table 1
Estimated parameter ranges for hepatitis C when modeled with system [20]. The , , and parameters are not independently identifiable, so common practice is to fix prior to fitting
|
This table tells us in which interval varies each parameter of the model. For the study of stability and for simulations these ranges of values will have to be respected for a good decision-making.
2.3 Theorems of existence and some properties of solution to the cauchy problem (4), (5)
2.3.1 Existence of local solutions
Theorem 2.1
Proof. We will use the local Cauchy-Lipschitz theorem
to proof this. Since the system of equations (4)
is autonomous, it is enough to show that the function
|
is locally Lipschitzian with:
| (6) |
| (7) |
| (8) |
According to L. Perko [18], it is also enough to prove that
is a class function.
The jacobian matrix of
at
is:
i.e.
Each component of this matrix being continuous, they are locally bounded for all . Therefore possesses continuous and bounded partial derivatives on any compact of . Thus is locally Lipschitzian with respect to . By the Cauchy-Lipschitz theorem, there is a local solution defined on This completes the proof of this theorem 2.1.
2.3.2 positivity of the system (4)
Theorem 2.2
Let be a solution of the system (4) over an
interval
such that et .
If are positive, then , and
are also positive for all .
Proof. We are going to prove by contradiction. so
suppose there is such that
or or .
Let
Let also be the smallest of all in the interval such that and
for a certain .
Then each of the equations of the
system
(4) can be written where is a non negative function and
any function.
Thus,
with
and
similarly;
with
and
and
with
and
Without loss the generality, suppose that .
As hypothesized, is positive on ,
it follows that
from where
Yet
is a solution of (4). , , are class class
functions.
They are continuous on
and therefore are bounded on .
Thus is bounded on .
There exists a constant such that
By integrating this previous expression on , we get
Where
This is a
contradiction because .
Similarly, assuming that , as hypothesized,
is positive on ,
it follows that
Thus,
Yet is a solution of system (4); , ,
are class functions. They are therefore continuous on
and consequently are bounded on .
Therefore is bounded on .
Thus, there exists a constant such that
Integrating, the last expression on , yields
Therefore
This is a contradiction because
.
As far as that goes, assuming that .
By hypothesis, is positive on , we
obtain i.e
Hence integrating on we obtain
This is a contraction.
Conclusion: , , are positive on .
It will now be shown, with the help of the continuation criterion
the existence of global solutions of problem (4), (5).
2.3.3 Existence of global solutions
Theorem 2.3
Proof. To prove this it is enough to show that all variables
are bounded on
an arbitrary finite interval . Using the positivity, by
the theorem 2.2, of the solutions it is enough to show that all
variables
are bounded above.
Taking the sum
of equations (1), (2) shows that :
and hence that . Thus and are bounded on any finite interval. The third equation, i.e.
then shows that cannot grow faster than linearly and is also bounded on any finite interval. This completes the proof of this theorem.
2.3.4 Asymptotic behaviour
Proof. Summing equations (1) and (2), we get:
Let , , , and let us solve the following equation
| (9) |
Coupled to equation (9) the initial condition :
| (10) |
The resolution of the problem (9), (10) gives for all ,
As for all , it follows that :
i.e.
Let
we obtain :
Therefore
Since T and I are
positive and , so it
follows that and .
From (3), we have:
According to Gronwall inequality,
with
This completes the proof of theorem 2.4.
Remark 2
It follows that all solutions of the system (4) are asymptotically uniformly bounded in compact subset defined by
2.4 Basic reproduction ratio
One of the most important concerns about any infectious disease is its ability to invade a population. Many epidemiological models have a disease free equilibrium (DFE) at which the population remains in the absence of disease. These models usually have a threshold parameter, known as the basic reproduction number, , such that if , then the DFE is locally asymptotically stable, and the disease cannot invade the population, but if , then the DFE is unstable and invasion is always possible. In other words, we have the following definition :
Definition 2.5
[9] The basic reproduction ratio or the basic reproduction number or basic reproductive ratio is defined as the expected number of secondary cases produced, in a completely susceptible population, by a typical infected individual during its entire period of infectiousness.
Determine in function of the parameters of the model allow us to guess the conditions under which the disease invade the population.
2.4.1 Determination of the uninfected equilibrium or virus-free equilibrium or noninfected equilibrium
Proposition 2.6
Proof. When there is no viral infection, the uninfected hepatocytes dynamic is determined by :
| (11) |
The quantity of the free-virus equilibrium point
is solution of the equation .
Hence, let us solve the following equation :
Its discriminant is given by :
which yields :
Thus, in the absence of viral infection, the amount of susceptible cells or uninfected hepatocytes attend to a positive constant level , which is :
This completes the proof.
2.4.2 Computation of the basic reproduction number
We are going to use Van Den Driessche and Watmough method
[9, 21] for calculating the basic reproduction ratio
of the model (4).
Let us first present briefly the method.
Considering population whose population are grouped into
homogeneous compartments where
is the number of individuals in compartment .
For clarity we sort the compartments ,
so that
the first compartments correspond to
infected individuals. The distinction between infected and
uninfected compartments must be determined from the epidemiological
interpretation of the model and cannot be deduced from the structure
of the equations alone.
We define to be the set of all disease free states. That is
:
Let be the rate of appearance of new infections in
compartment that is the infected individuals coming from other
compartments and enter
into .
be the rate of transfer of individuals into compartment
by all other means (displacement, healing, aging).
be the rate of transfer of individuals out of
compartment (mortality, change of statut).
It is assumed that each function is continuously
differentiable at
least twice in each variable.
Figure 3 below shows the variations of the number of
individuals in compartment in a population.

The variation of the number of individuals in compartment is given by :
where
Due to the nature of the epidemiological model, we have the following properties :
-
If then , and .
Since each function represents a directed transfer of individuals. -
If then .
Indeed, If a compartment is empty, then there can be no transfer of individuals out of the compartment by death, infection, nor any other means : it is the essential property of a compartmental model. -
Pour , .
In fact, the compartments with an index greater than are ”uninfected”. By definition, it can not appear in these compartments infected individual. -
Si alors et pour , .
Indeed, to ensure that the disease free subspace is invariant, we assume that if the population is free of disease then the population will remain free of disease. That is, there is no (density independent) immigration of infectives. This is Lavoisier’s principle. There is no spontaneous generation.
Let and
.
Let also the uninfected equilibrium point of the
corresponding model.
Let and denote the jacobian matrices of F
and V respectively at the point .
It follows that is a positive matrix and
a Metzler matrix (matrix whose the
extra diagonal terms are greater or equal than zero ). Thus we have
the following equivalent definition of :
2.4.3 Expression of the basic reproduction number associated to the system (4)
Proposition 2.8
The expression of the basic reproduction number associated to the system (4) is given by :
| (12) |
where
Proof. Concerning the model (4) that we study here, the system of infected states is the following :
The expression of the quantities , , ,
and are given by:
, ,
,
,
From those quantities, we obtain:
= .
Let . It follows that :
Therefore :
which completes the proof of the proposition.
Remark 4
denotes the overall effectiveness rate of the drug .
Remark 5
Henceforth, we will let and .
At the end of this section, we note that HCV is a major
health problem in the world and particularly in Cameroon where it
affects almost 13% of population.
For the model (4) which is the
subject of our work, we have shown the existence of the global
solution
and
establish some properties like positivity. The calculation of
has been done.
In the
next section, we will determine the infected equilibrium point
and
establish
the conditions on for which stability of the
model occurs.
3 Stability analysis of the model
In this section, we study the local stability and global stability
of the equilibrium points and we present some numerical
simulations
of the theoretical results obtained. Specifically, we prove by
Lyapunov’s theory that the uninfected equilibrium point
is
globally asymptotically stable if
and the infected equilibrium
point is globally asymptotically stable when it exists.
Before that we establish a number of essential preliminary
results for the next steps
3.1 Invariant set of the model
Theorem 3.1
Proof. Let . We shall show that :
-
(i)
If then for all , .
-
(ii)
If then for all , .
- i)
- ii)
3.2 Existence of the infected equilibrium point
When it exists, the infected equilibrium point is given by: where , and are positive constants that we are going to determine.
Lemma 3.2
exists if and only if
Proof. Let us consider the following system of algebraic equations :
| (13) | |||||
| (14) | |||||
| (15) |
(15) yields :
| (16) |
It follows that,
Let
we have :
| (19) |
with :
Since , the polynomial (19) has a unique positive root if and only if :
This completes the proof of Lemma 3.2.
Suppose that , we have the following results :
Lemma 3.3
If , then :
-
i)
if and only if
-
ii)
if and only if .
Remark 6
of Lemma 3.3 is the solution of equation i.e
Proposition 3.4
Lemma 3.5
.
Lemma 3.6
if and only if .
Proof. We have :
Since , the equivalence of the
Lemma 3.6 allows us to write .
The following proposition establishes the link between
and the existence of the equilibrium point
when .
Proposition 3.7
Suppose that exists, and , then :
-
i)
if .
-
ii)
if .
Proof. Recall that if and only if
and if and
only if
Using the expression of given in (19) we have :
Thus
Yet
and
Hence,
Since and , we get :
and
This completes the proof of Proposition 3.7.
Suppose now , then equation (19) admits a
unique positive solution and we have the following
results:
Lemma 3.8
Suppose that , then :
-
•
if and only if .
-
•
if and only if .
Remark 7
of lemma 3.8is the solution of equation , i.e
Proposition 3.9
We state the following two lemmas whose the proofs are analogous of those of lemma 3.5 and lemma 3.6 respectively. These lemmas will help us to complete the conditions of existence of the infected equilibrium point
Lemma 3.10
Lemma 3.11
if and only if .
Proposition 3.12
Suppose that : and .
Then if , and
if
.
Proof. Recall that if and only if and if and only if From the expression of given by (19) we have :
Thus :
yet
Hence :
Since and , we get :
-
•
if .
-
•
if .
This completes the the proof.
The conditions of existence of an infected equilibrium point
have been established, we are going in the following
subsection give its expression.
3.3 Expression of the equilibrium points
3.3.1 Uninfected equilibrium point
By the proposition 2.6, the uninfected equilibrium point is given by where
3.3.2 Infected equilibrium point
Lemma 3.13
When it exists, is defined by :
where :
and
Proof. When exists, it will be a positive solution of the equation of second degree :
| (20) |
with :
Let
then (20) becomes :
Let also :
then (20) becomes :
Let :
hence the previous equation yields :
Its discriminant is:
i.e.
Hence
Where
We have :
with
It follows that :
The combination of the proposition 3.4, proposition 3.12 and the lemma 3.13 leads to the following theorem :
Theorem 3.14
When the unique equilibrium is the uninfected equilibrium point or the infection-free steady state .
3.4 Local stability analysis of the model 1 at the equilibrium points
For the study of local stability of the model (4) at the equilibrium points, let us consider once more the functions , et given by (6), (7) and (6) respectively.
3.4.1 Case of the uninfected equilibrium point or infection-free steady state
Theorem 3.15
The infection-free steady state of model (4) is locally asymptotically stable if and unstable if .
Proof. The Jacobian matrix
of the system (4) at is as the following :
i.e.
Since
it follows that :
Now let us show that the eigenvalues of the matrix have
negative real part if and only if .
Considering the expression of ,
is a negative
eigenvalue of the matrix . Now let us consider the
sub-matrix defined by :
| (24) |
The trace of is :
and the determinant of is:
The system (4) est locally asymptotically stable at if and only if
and
i.e.
Therefore the model (4), is locally asymptotically stable at when and unstable when This completes the proof of theorem 3.15
3.4.2 Case of infected equilibrium point
We start this subsection by two preliminary lemmas.
Proof. See the Appendice for the proof.
Lemma 3.17
The characteristic equation of the Jacobian matrix of the system (4) at is given by the following cubic equation :
where :
Proof. See the appendice for the proof of lemma 3.17.
Theorem 3.18
For model (4), when is valid, the unique endemic equilibrium is locally asymptotically stable if and unstable if .
Especially, we have :
Corollary 3.19
The infected steady state during the therapy of the model (4) is locally asymptotically stable if and unstable if .
Proof. Since , , it remains to show that .
where,
and
| (25) |
Since , it remains to show that .
From (1) we have :
yet
hence,
Thus,
it follows that ;
Reporting this previous expression in (25) yields :
Taking especially and , we obtain :
. Thus,
and , therefore the system (4) is locally asymptotically stable at This completes the proof of Corollary 3.19.
3.5 Global stability analysis of the system at equilibrium points
The global stability analysis of a dynamical system is usually a very complex problem. One of the most efficient methods to solve this problem is Lyapunov’s theory. To build the functions of Lyapunov we will follow the method proposed by A. Korobeinikov [11, 12, 13].
3.5.1 Case of infection-free steady state
Theorem 3.20
The infection-free steady state of the model (4) is globally asymptotically stable if the basic reproduction number and unstable if .
Proof. Consider the Lyapunov function :
is defined, continuous and positive definite for all , , . Also, the global minimum occurs at the infection free equilibrium . Further, function , along the solutions of system (1), satisfies :
yet
hence, further collecting terms, we have :
Furthermore ,
hence
Since and
, we have
and if and only if and
simultaneously.
Therefore, the largest compact invariant subset of the set
is the singleton . By the Lasalle invariance principle[10], the infection-free equilibrium is globally asymptotically stable if . We have seen previously that if , at least one of the eigenvalues of the Jacobian matrix evaluated at has a positive real part. Therefore, the infection-free equilibrium is unstable when . This completes the proof of the theorem.
3.5.2 Case of infected equilibrium point
We recall :
Theorem 3.21
Suppose that , and .
Then the infected steady state during therapy of model
(4) is globally
asymptotically stable as soon as it exists.
Proof. Consider the Lyapunov function defined by :
Let us show that and
if and only if
, , simultaneously.
The time
derivative of along the trajectories of system (4) is :
Collecting terms, and canceling identical terms with opposite signs, yields :
| (26) | |||||
Reporting equalities of remark 9 into (26), we have :
Note that
and
According to (13),
furthermore,
hence,
By hypothesis, this leads to :
Yet
since the geometric mean is less than
or equal to the arithmetic mean.
It should be noted that and holds if and only if take the steady
states values . Therefore the infected
equilibrium point is globally asymptotically stable. This
completes the proof of this theorem.
3.6 Some numerical simulations
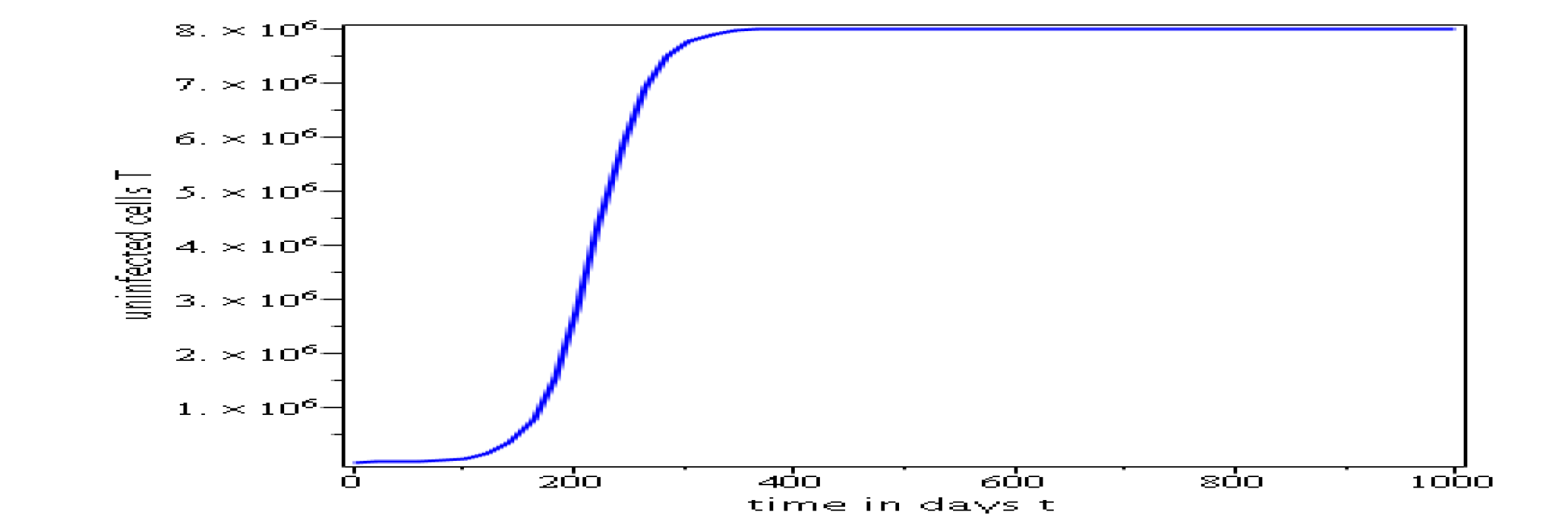
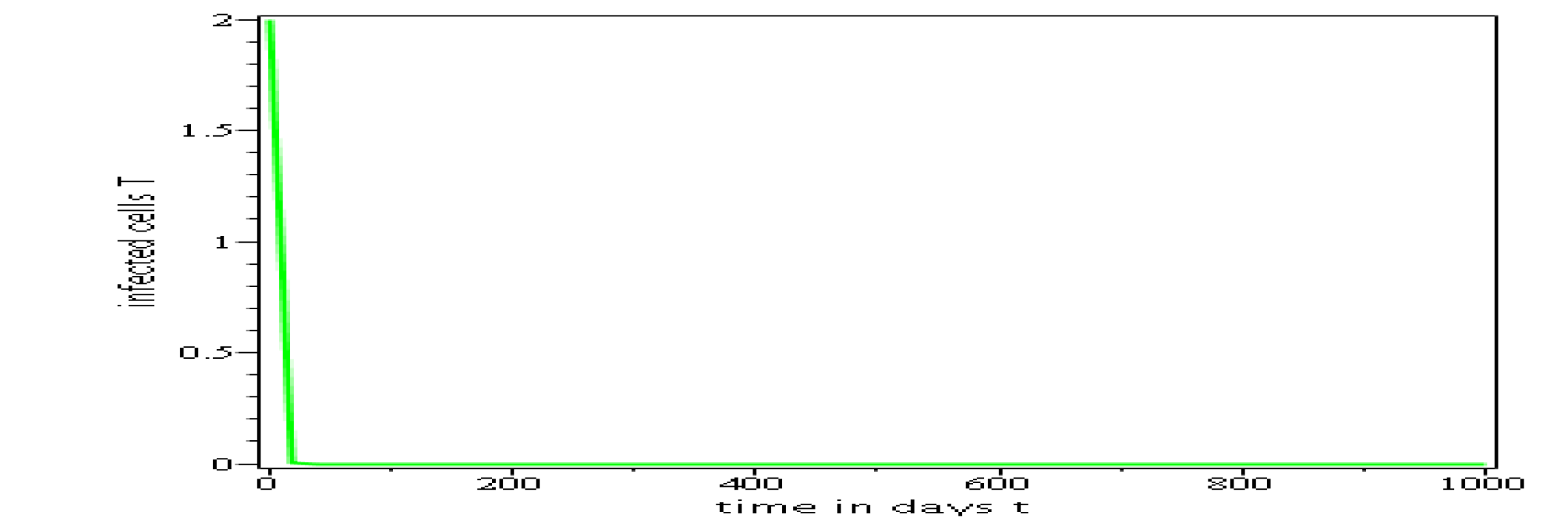
Some numerical simulations have been done in the case
to confirm theoretical result obtain on global stability for the
uninfected equilibrium.
The following curves, obtained
using the Maple software, show the real-time evolution of uninfected
hepatocytes, infected hepatocytes and viral load. The values of the
parameters are taken in the parameter range defined by the
table (2.2) and the initial conditions are ,
and .
3.6.1 Evolution in time of uninfected cells, infected cells and viral load when
. Parameters values : , , , , , , , , , , , . These parameters values yields : and .
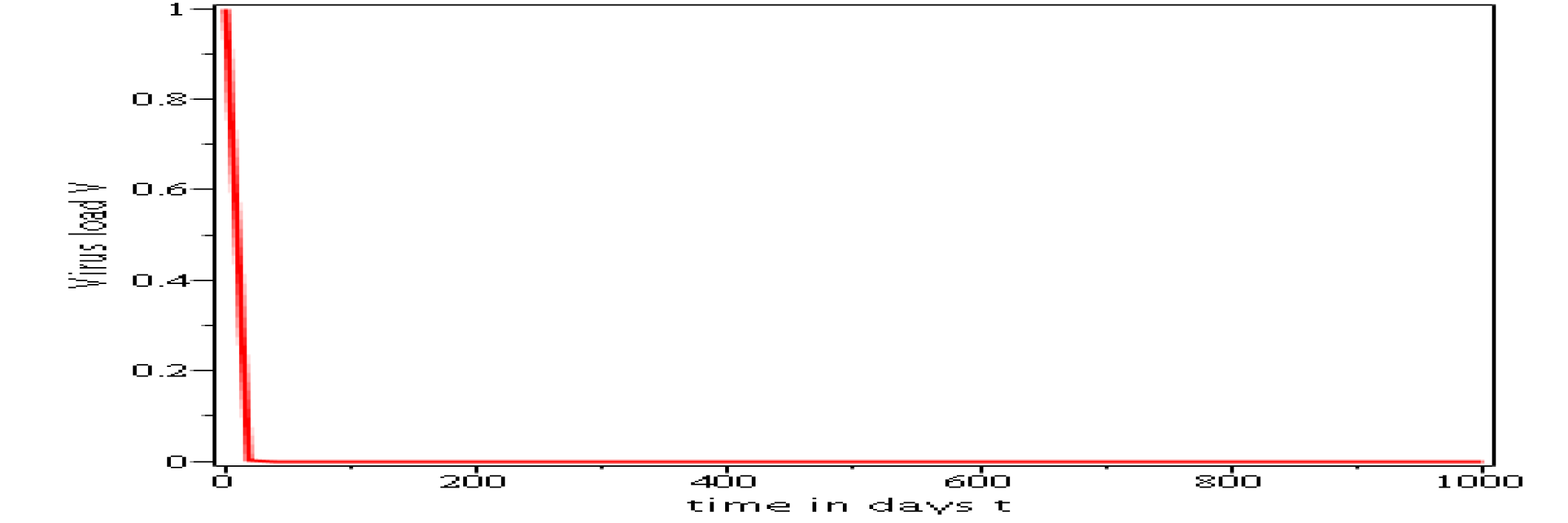
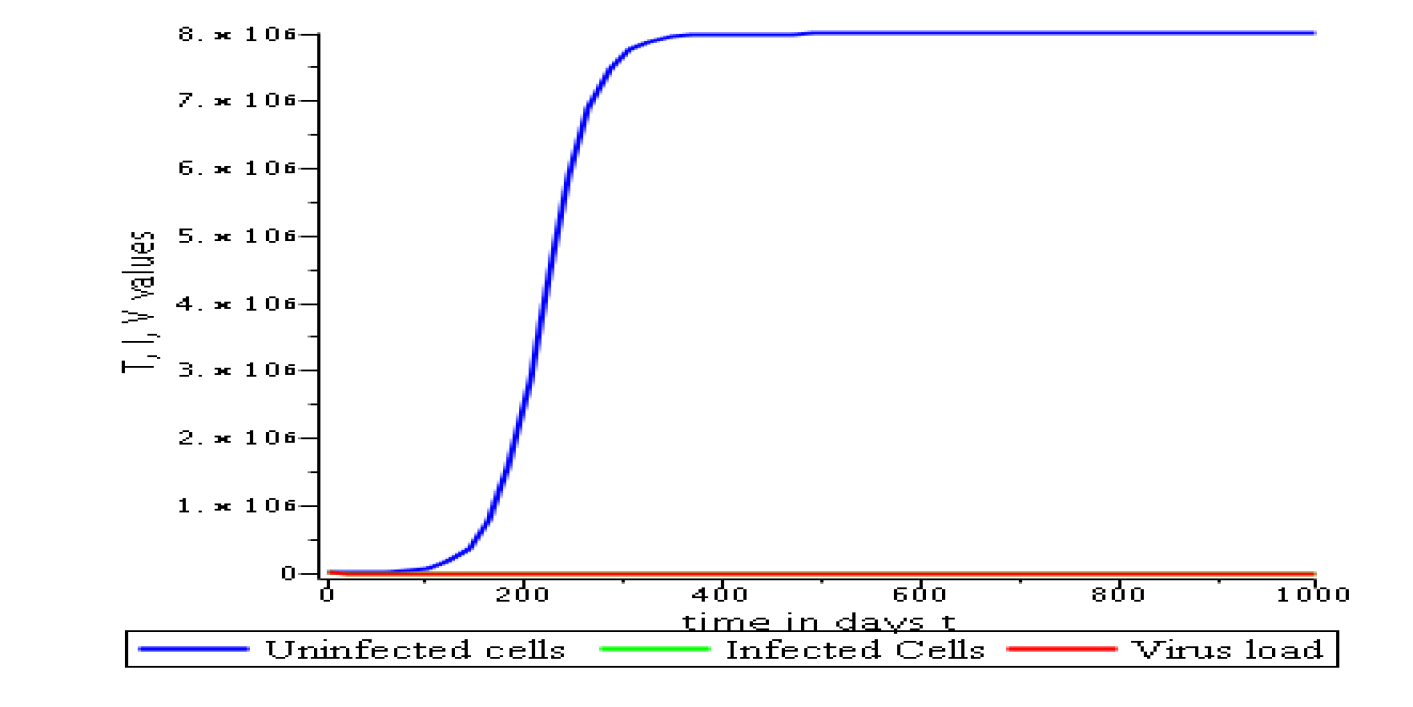
3.6.2 Evolution in time of uninfected cells, infected cells and viral load when .
Parameters values: , , , , , , , , , , , . These parameters values yields: et .
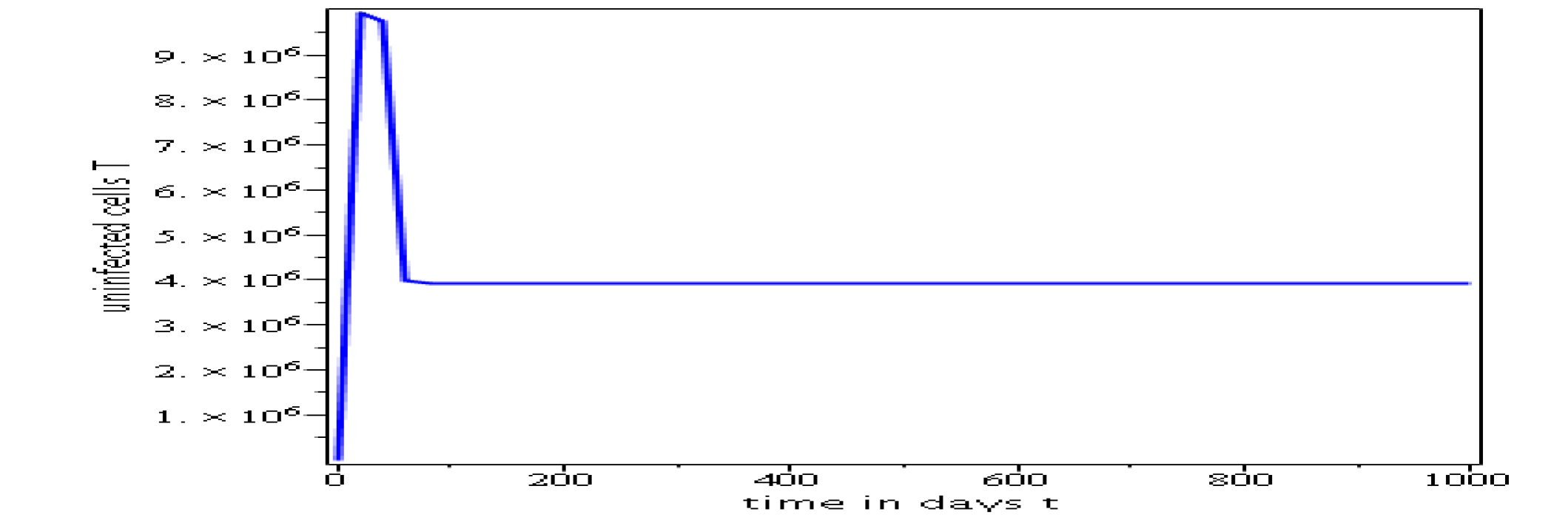
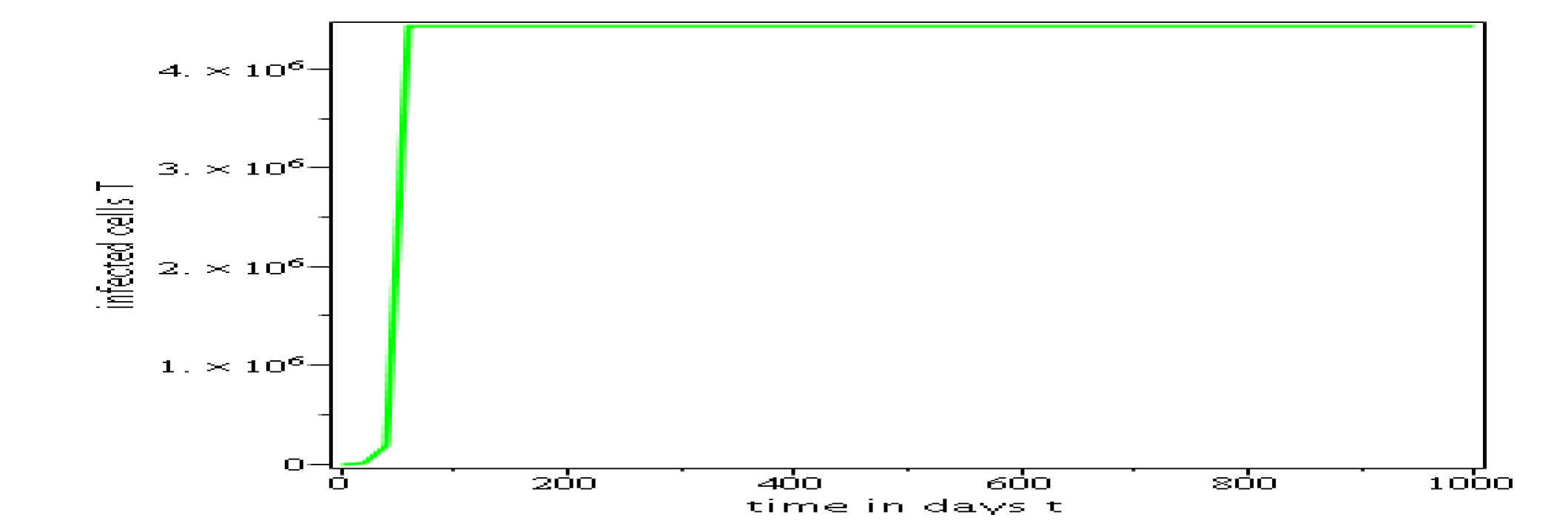
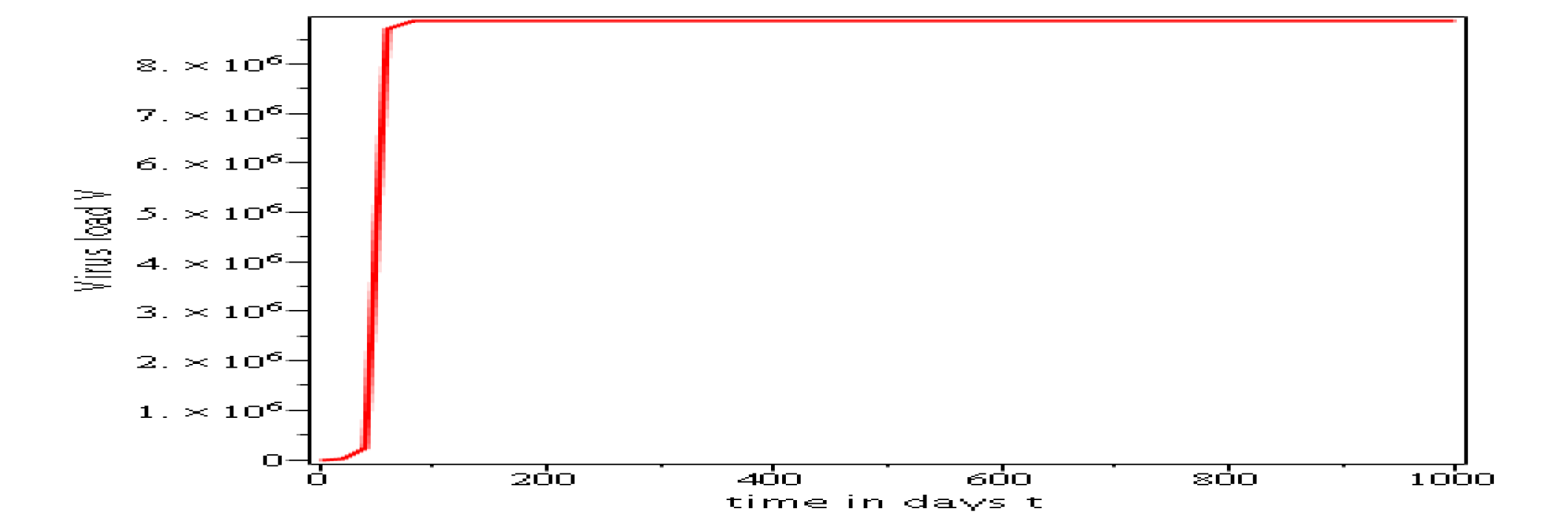
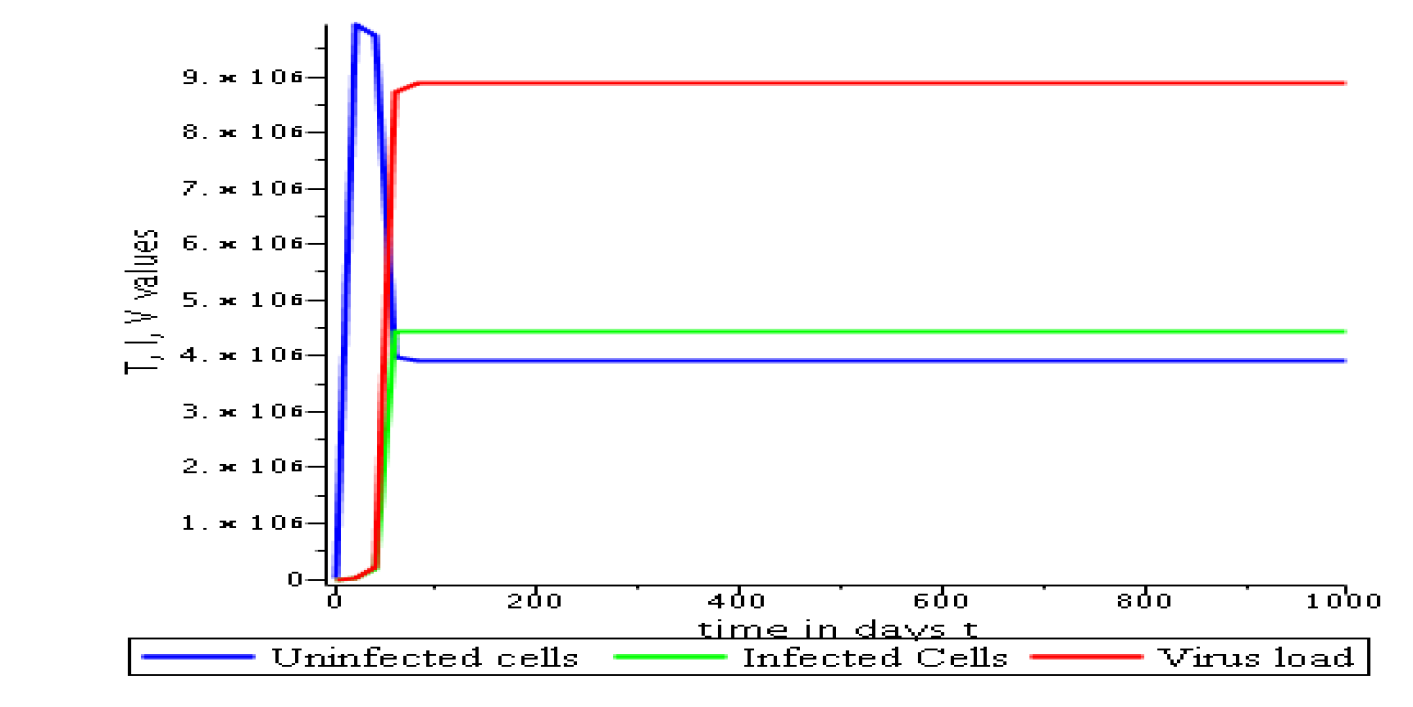
In short, in this section, it was a question to study the global stability of the model (4). We have established that the model (4) is globally asymptotically stable at equilibrium points and when and unstable when . the numerical simulations has been carried out using the Maple software confirming theoretical results.
Acknowledgement(s)
I am grateful to Professor Alan Rendall for valuable and tremendous discussions. I wish to thank him for introducing me to Mathematical Biology and to its relationship with Mathematical Analysis. I also thank the Higher Teacher’s Training College of the University of Maroua were this paper were initiated.
Conclusion and discussions
Having reached the end of our work, it emerges from all the
investigations presented that hepatitis C is a major health problem
in the world and especially in Cameroon. To understand the dynamics
of HCV and its infectious processes, mathematical models are present
as an important and unavoidable tool. Global stability analysis
has been done, by the technique of Lyapunov, to the model of HCV
infection with proliferation cell and spontaneous healing, for
revealing significant information for making good decision for the
fighting against hepatitis C. We first show the existence of the
global solution to the Cauchy problem (4), (5); then we
have calculated the basic reproduction ratio .
We finally show that the only infected equilibrium point
for the model is globally
asymptotically stable when and unstable when
under others hypotheses. Furthermore
uninfected equilibrium point
for the model is globally
asymptotically stable when and unstable
when
. These theoretical results have been
confirmed by numerical simulations done using the software Maple.
Given the results obtained, this work is the beginning point of very
interesting other future investigations.
We plan to extend our
analysis by focusing on more realistic models such as:
-
1.
models with delay which involve delay ordinary differential equations;
-
2.
models taking into account space which involve Partial differential equations;
-
3.
models taking into account random phenomena which evolve stochastic differential equations.
We also plan to focus on others methods of studying global stability like the geometric method that can provides results with less hypotheses on model (4).
References
- [1] M. S. F. Chong, L.S.M.Crossley and Madzvamuse, The stability analyses of the mathematical models of hepatitis C virus infection. Modern Applied Science, 9 (3). pp. 250-271. ISSN 1913-1844, Article (Published Version) Anotida (2015), 23 pages. http://sro.sussex.ac.uk/52312/
- [2] Y. Cherruault, Biomath matiques, Presses Universitaire de France, 1983, 108, boulevard Saint-Germain, 75006 Paris 2014, 132 pages.
- [3] S. M. Ciupe, R. M. Ribeiro, P. W. Nelson and A. S. Perelson, Modeling the mechanisms of acute hepatitis B virus infection, J. Theor. Biol. 247 (2007) 23 35.
- [4] H. Dahari, R. M. Ribeiro, and A. S. Perelson, Triphasic decline of HCV RNA during antiviral therapy, Hepatology, 46 (2007), pp. 16 21.
- [5] H. Dahari, E. Shudo, R. M. Ribeiro, and A. S. Perelson, Modeling complex decay profiles of hepatitis B virus during antiviral therapy, Hepatology, to appear (DOI: 10.1002/hep.22586).
- [6] H. Dahari, J. E. Layden-Almer, E. Kallwitz, R. M. Ribeiro, S. J. Cotler, T. J. Layden and A. S. Perelson, A mathematical model of hepatitis C virus dynamics in patients with high baseline viral loads or advanced liver disease, Gastroenterology 136 (2009) 1402 1409.
- [7] H. Dahari, M. Major, X.Zhang, K.Mihalik, C. M. Rice, A. S. Perelson, S. M. Feinstone and A.U.Neumann Mathematical Modeling of Primary Hepatitis C Infection: Noncytolytic Clearance and Early Blockage of Virion Production, Gastroenterology 128 2005:1056 1066.
- [8] H. Daharia, A. Loa, R. M. Ribeiroa, A. S. Perelson; Modeling hepatitis C virus dynamics: Liver regeneration and critical drug efficacy. Journal of Theoretical Biology 247 (2007) 371 381, 2007, P.371-381. www.sciencedirect.com.
- [9] O. Diekmann, J.A.P. Heesterbeek, J.A.J. Metz, On the definition and the computation of the basic reproduction ratio in models for infectious diseases in heterogeneous populations, J. Math. Biol. 28 (1990) 365.
- [10] Khalil, H., 2002. Nonlinear Systems, 3rd edn. Prentice Hall, New York.
- [11] A. Korobeinikov, Global Properties of Basic Virus Dynamics Models, doi: 10.1016/2004.02.001 879-883, Bulletin of Mathematical Biology (2004)66. 2016, 63 pages.
- [12] A. Korobeinikov, Lyapunov functions and global properties for SEIR and SEIS epidemic models, Mathematical Medicine and Biology (2004).
- [13] A. Korobeinikov, G. C. Wake; Lyapunov Functions and Global Stability for SIR, SIRS, and SIS Epidemiological Models, Applied Mathematics Letters 15 (2002) P.955-960
- [14] C. Laou nan, Utilisation des modèles dynamiques pour l´ évaluation des traitements de l´hépatite C, Thèse de Mathématiques de l’Université Paris Diderot (Paris 7) Sorbonne Paris Cité, juillet 2014, 113 pages.
- [15] Q. Li, F. Lu, G. Deng and K. Wang, Modeling the effects of covalently closed circular DNA and dendritic cells in chronic HBV infection, J. Theor. Biol. 357 (2014) 1 9.
- [16] J.D. Murray, Mathematical Biology I: An introduction, Editors S.S. Antman J.E. Marsden L. Sirovich S. Wiggins, 2001.
- [17] A. U. Neumann, N. P. Lam, H. Dahari, D. R. Gretch, T. E. Wiley, T. J. Layden, and A. S. Perelson, Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-alpha therapy, Science, 282 (1998), pp. 103 107.
- [18] L. Perko, Differential Equations and Dynamical Systems,Springer, Third Edition, Editors J.E. Marsden L. Sirovich M. Golubitsky, 571 pages.
- [19] S. Banerjee, R. Keval, S. Gakkhar, Modeling the dynamics of Hepatitis C Virus with combined antiviral drug therapy: Interferon and Ribavirin, arXiv:1105.3669v1 [q-bio.CB] 18 May 2011 Bulletin of Mathematical Biology.
- [20] T. C. Reluga, H. Dahari, and A. S. Perelson, analysis of hepatitis C virus infection models with hepatocyte homeostasis.SIAM J. APPL. MATH.Vol. 69, No. 4, pp. 999 1023, 2009, P.999-1023. http://www.siam.org/journals/ojsa.php.
- [21] P. Van den Driessche and J. Watmough. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences, 2002 180 2948.
- [22] WHO, Global hepatitis repport 2017, ISBN 978-92-4-156545-5, www.who.int/mediacentre/factsheets/fs164/en/.
- [23] N. Yousfi, K. Hattaf and M. Rachik; Analysis of a HCV Model with CTL and Antibody Responses, Applied Mathematical Sciences, Vol. 3, 2009, no. 57, P.2835-2846.
4 Appendices
Appendix A Proof lemma 3.16
Proof. The Jacobian matrix of the system (4) at is given by :
Let us determine the coefficients of that Jacobian matrix .
Yet
and
hence ,
Therefore,
This completes the proof of the
lemma 3.16.
Appendix B Proof of lemma 3.17
Proof. The characteristic equation is given by ,
i.e.
=0.
With
it follows that :
if and only if i.e.
i.e
.
By developing the different factors in the previous equation, we get
:
.
Let:
we have:
Let also :
we have :
Let once more :
We get :
Therefore,
with