Matrix Formulae and Skein Relations for Quasi-Cluster Algebras
Abstract.
In this paper, we give matrix formulae for non-orientable surfaces that provide the Laurent expansion for quasi-cluster variables, generalizing the orientable surface matrix formulae by Musiker-Williams. We additionally use our matrix formulas to prove the skein relations for the elements in the quasi-cluster algebra associated to curves on the non-orientable surface.
1. Introduction
Cluster algebras were first defined by Fomin and Zelevinksy in the early 2000’s in an effort to study problems regarding dual canonical bases and total positivity [5]. Since their axiomatization, endowing mathematical objects with a cluster structure has become a rapidly growing field of interest across many different disciplines in math and physics. For instance, Fomin and Shapiro defined a cluster structure associated to orientable topological surfaces (which actually generalized the deep geometric work on Fock and Goncharov in [2, 3] and Gekhtman, Shapiro, and Vainshtein [6]). The cluster algebra structure associated to an orientable surface has a completely topological description, but also can be bolstered to include more geometric significance. Namely, the cluster structure also arises from coordinate rings for the decorated Teichml̈ler space associated to the surface. The cluster variables can be thought of as hyperbolic lengths of geodesics on the surfaces also known as Penner coordinates [9]. Because of this interpretation, the Teichmüller theory was connected to combinatorics by associating elements in to arcs on the surface in order to obtain the Laurent expansions of the associated cluster variables. This result was first studied by Fock and Goncharov in [2, 3] in the coefficient-free case and generalized by Musiker and Williams in [8].
More recently, cluster-like structures were defined for non-orientable surfaces by Dupont and Palesi [1]. They defined quasi-cluster algebras associated to non-orientable surfaces drawing inspiration from the orientable case in [4]. The way they define their mutation or exchange relations is also inspired from the Teichmüller theory and geometry from [2, 3]. Positivity for quasi-cluster algebras was recently proven by Wilson through using snake and band graph combinatorics in [11] inspired by the original proof for positivity for cluster algebras from orientable surfaces in [7].
In our paper, we create explicit matrix formulae for non-orientable surfaces that give the Laurent expansions for quasi-cluster variables in the associated quasi-cluster algebra. That is, we associate a product of matrices in to a curve on a non-orientable surface so that the Laurent expansion for the associated element of the quasi-cluster algebra can be extracted from the matrix. Our method provides the first non-recursive way to compute Laurent expansions for quasi-cluster variables directly on the non-orientable surface. Our process modifies the construction by Musiker and Williams [8] by associated an element of when traversing through the non-trivial topology of a non-orientable surface. We in turn prove our result by relying on the combinatorics of snake and band graphs and a coefficient system using the language of laminations and Shear coordinates for non-orientable surfaces developed by Wilson in [11]. We also use our results to prove the skein relations for non-orientable surfaces.
Our paper is organized as follows: in Section 2 we review the cluster-like structure of non-orientable surfaces and topological notions we use throughout the paper. Section 3 introduces the combinatorics of snake and band graphs in order to state the expansion formula for quasi-cluster variables as in [11]. Section 4 introduces the coefficient system via laminations that give arbitrary coefficients for quasi-cluster algebras. Section 5 recalls the matrix formulae by Musiker and Williams for cluster algebras from orientable surfaces and also extends their results to the context of prinicipal laminations. This paves the way to our main results Theorem 6.4 and Theorem 6.8 that is then proven in Section 6. Finally, Section 7 proves the skein relations for non-orientable surfaces.
Acknowledgements. The authors would like to thank Chris Fraser for suggesting this project and helping us with the beginning stages of learning the relevant background. We would also like to thank Gregg Musiker for helpful comments and discussions.
2. Quasi-Cluster Algebras
In this section, we review the definition of quasi-cluster algebras defined in [1]. We give explicit computations for the so-called quasi-mutation rules that come from skein relations as this was missing from the literature.
Definition 2.1.
Let be a compact, connected Riemann surface with boundary . Let be a finite set of points, we call marked points, contained in such that each connected component of has at least one point of . We say the pair is a marked surface.
We call marked points on the interior of punctures.
Definition 2.2.
A regular arc in a marked surface is a curve in , considered up to isotopy relative its endpoints such that
-
(1)
the endpoints of are ,
-
(2)
has no self-intersections, except possibly at its endpoints,
-
(3)
except for its endpoints, does not intersect ;
-
(4)
and does not cut out a monogon or bigon.
We say the arc is a generalized arc if intersects itself, dropping condition (2). We say the arcs that connect two marked points and lie completely on are boundary arcs.
In our paper, we will be analyzing the specific case when is non-orientable. By the classification of compact surface, any non-orientable surface is homeomorphic to the connected sum of projective planes. By this fact, we refer to as the non-orientable genus of the surface. Recalling that the projective plane is a topological quotient of the 2-sphere by the antipodal map, we visualize these surfaces with crosscaps . This symbol denotes the removal of a closed disk with the antipodal points identified.
On a non-orientable surface , a closed curve is said to be two-sided if it admits an orientable regular neighborhood. It a closed curve does not admit such a neighborhood, it is said to be one-sided. Since one-sided curves reverse the local orientation, they may only be contained in a non-orientable surface.
As in the orientable case, an arc is an isotopy class of a simple curve in .
Definition 2.3.
A quasi-arc in is either an arc or a simple one-sided closed curve in the interior of .
We say that two arcs in are compatible if up to isotopy, they do not intersect one another. More formally, define to be the minimum of the number of crossings of and ’ where is an arc isotopic to and is an arc isotopic to
where ranges over arcs that are isotopic to and ranges over arcs isotopic to .
We say regular arcs are compatible if . A maximal collection of pairwise compatible arcs in is called a quasi-triangulation of . If none of the arcs in this collection is a quasi-arc, we say it is simply a triangulation.
All (quasi-)triangulations of a non-orientable surface are reachable via sequences of quasi-mutations [1, Proposition 3.12]. These quasi-mutations are a larger class of local moves on the surface that are motivated by the skein relations, studied in cluster algebra theory by [4, 8]. To discuss mutations we require the notion of a quasi-seed.
Let be the rank and the number of boundary components of the marked surface and a field of rational functions in indeterminates. For each boundary component , we associate a variable such that is algebraically independent in . We refer to as the ground ring.
Definition 2.4.
A quasi-seed associated with in is a pair such that
-
•
is a quasi-triangulation of ;
-
•
is a free generating set of the field over .
The set is called the quasi-cluster of the quasi-seed . We say a quasi-seed is a seed if the corresponding quasi-triangulation is a triangulation.
Definition 2.5.
An anti-self-folded triangle is any triangle of a quasi-triangulation with two edges identified by an orientation-reversing isometry.
For example, in Figure 1, the triangle with sides is an anti-self-folded triangle.
Before stating the quasi-mutation rules, we derive two of the mutations from the skein relations. The other, significantly longer, computation is given in the appendix.
Example 2.6.
Let be an arc in the anti-self-folded triangles with sides , and let be a one-sided curve in an annuli with boundary . Figure 1 demonstrates how to resolve the crossing of and using the Ptolemy relation, which yields the relation . We explain how to push a loop through the crosscap in the appendix. With this we can derive the second and third quasi-mutations given in Definition 2.7.
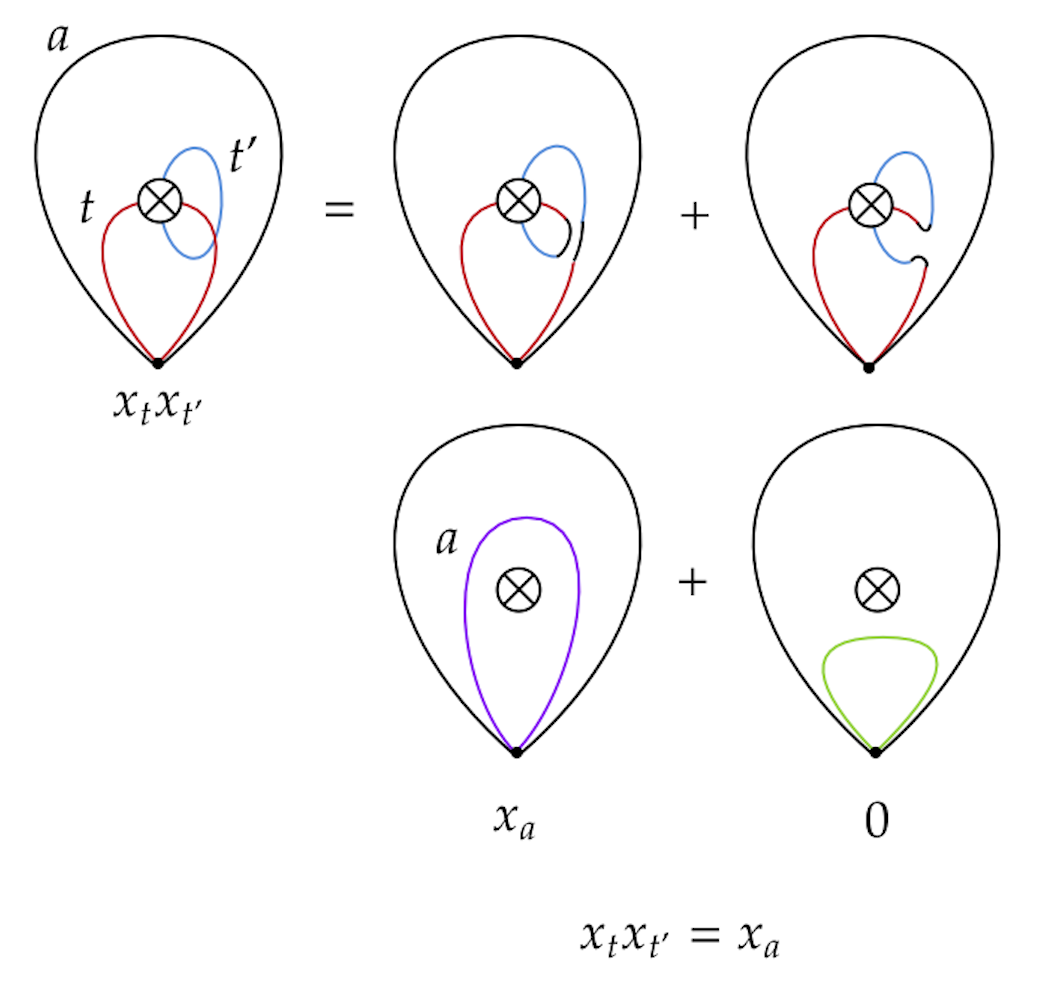
The justification for pushing the loop through the crosscap is given in the appendix.
With this motivation, we have the following definitions of quasi-mutation.
Definition 2.7.
Given , the quasi-mutation of in the direction as the pair where and such that is defined as follows:
-
(1)
If is an arc separating two distinct triangles with sides and , then the relation is given by the Ptolemy relation for arcs .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/skein-reln-1-ptolemy.png)
-
(2)
If is an arc in an anti-self-folded triangle with sides , then the relation is .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/skein-reln-2.png)
-
(3)
If is a one-sided curve in an annuli with boundary , then the relation is .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/skein-reln-3.png)
-
(4)
If is an arc separating a triangle with sides and an annuli with boundary and one-sided curve , then the relation is .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/skein-reln-4.png)
Now that we have the necessary topological notions, we are ready to define the cluster structure for these non-orientable surface. This was first defined in [1] which was inspired by work in [4] in the orientable setting.
Definition 2.8.
Let be the collection of all quasi-cluster variables obtained by iterated quasi-mutation from an initial seed . The quasi-cluster algebra is the polynomial ring generated by the quasi-cluster variables over the ground ring i.e. .
3. Expansion Formula via Snake and Band Graphs for Non-Orientable Surfaces
In this section, we review the expansion formulae for quasi-cluster variables in terms of snake and band graphs [11] without coefficients. We postpone the discussion on coefficients until 4. We begin by defining the notion of a snake graph as in [7] and then review the definition of band graphs that come from non-orientable surfaces as in [11].
Definition 3.1.
A tile is a copy of the cycle graph on four vertices, embedded in as a square with four cardinal directions, see Figure 2.
We glue tiles together in a particular way to obtain a snake or band graph. In particular, a snake or band graph can be thought of as a sequence of tiles glued along either the North or East edge of the previous tile. We describe how to construct a snake graph from an arc on a triangulated orientable surface.
Definition 3.2.
Let be an arc overlayed on a triangulation of an orientable surface . The snake graph associated to is a sequence of tiles where
-
•
the tiles correspond to the arc of that intersects;
-
•
and we attach to along the unique shared edge of the local quadrilaterals containing and .
Label the N, E, S, W edges of each tile with the corresponding arcs in the local quadrilateral so that the relative orientation of the tiles alternate, see [7, 11] for details.
We now give the definition of a band graph associated to a one-sided closed curve as in [11].
Definition 3.3.
Let be a one-sided closed curve overlayed on a quasi-triangulation , without quasi-arcs, of a non-orientable surface . Let be a point on . Consider the orientable double cover of along the the lifts of , and . Note that is a triangulation of , is an orientable closed curve and , of are antipodal points on .
Let be the snake graph of the arc corresponding to tracing along from to clockwise. If we continue along through one more intersection with , we’d obtain where and are lifts of the same local quadrilateral in . Let be the glued edge between and and be the corresponding edge in . The band graph associated to , denoted is the snake graph with and identified.
Remark 3.4.
Up to isomorphism, the choice of point on the one-sided closed curve does not affect the band graph or expansion formulae [11].
To state the expansion formulae, we need the notion of (good) perfect matchings on snake (band) graphs.
Definition 3.5.
A perfect matching of a snake graph is a subset of the edges of that covers each vertex exactly once. A good perfect matching of a band graph , glued along the edge from , is a perfect matching of the un-identified underlying snake graph where and are either matched with two edges are on or on .
Now, we state the expansion formula for regular arcs without coefficients as in Theorem 5.19 in [11]:
Theorem 3.6.
[11] Let be a regular arc overlayed on a quasi-triangulation without quasi-arcs of a non-orientable . Let be one of the two lifts of on the orientable double cover . Let be the snake graph associated to and be the set of perfect matchings on . Then the quasi-cluster variable can be expressed as follows:
where cross is the crossing monomial which keeps track of the arcs of the triangulation that crosses, counting multiplicities, and is the product of all the edge labels of in .
The analogous expansion formula for quasi-arcs without coefficients is given in Theorem of [11]:
Theorem 3.7.
[11] Let be a one-sided closed curve overlayed on a quasi-triangulation without quasi-arcs of a non-orientable . Let be the lift of on the orientable double cover . Let be the band graph associated to and be the set of good perfect matchings on . Then the quasi-cluster variable can be expressed as follows:
where cross is the crossing monomial which keeps track of the arcs of the triangulation that crosses, counting multiplicities, and is the product of all the edge labels of in .
4. Coefficients Using Principal Laminations
We review the arbitrary coefficients defined in [11] via principal laminations that complete the expansion formula mentioned in Section 3. We will then take inspiration from this coefficient system to define a poset structure of the set of good perfect matchings associated to a quasi-arc in a marked surface .
Definition 4.1.
A set of self-non-intersecting and pairwise non-intersecting curves on a marked surface is called a lamination if each is any of the following curves:
-
•
a one-sided closed curve;
-
•
a two-sided closed curve that does not bound a disk, or a Möbius strip;
-
•
a curve that connected two points on that is not isotopic to a boundary arc.
A multilamination of is a finite collection of laminations of .
Example 4.2.
The figure below is an example of a multilamination in red on the Klein bottle with four marked points.
We now define a principal lamination for marked surfaces in the unpunctured case.
Definition 4.3.
Let be an arc in . We associate the lamination to the curve via the following:
-
•
if is a regular arc, take to be a lamination that runs along in a small neighborhood, but turns clockwise (counterclockwise) at the marked point and ends when at the boundary.
-
•
if is a quasi-arc, take to be either a lamination that runs along in a small neighborhood and has endpoints on the boundary or take to be the 1 sided closed curve that is compatible with .
Definition 4.4.
Let be a triangulation of . Taking the collection of all laminations associated to the arcs is called a principal lamination. That is, a multilamination of the form is a principal lamination.
In order to define the coefficients seen in [11], we must use the notion of a principal lamination to define Shear coordinates, a coordinate we place on the diagonal of a local quadrilateral in a triangulation.
Definition 4.5.
Let be an arc in some triangulation of , let be a lamination and let is the local quadrilateral that is a diagonal of. The Shear coordinate of and with respect to , denoted , is given by
where -(respectively -) intersections are illustrated in Figure 4.
We now use the notion of Shear coordinate to connect laminations to snake/band graphs and their perfect matchings. Namely, each diagonal or label of a tile of a snake/band graph corresponds to some arc in a triangulation. We use the following definition to assign a to an orientation of a diagonal associated to a tile in a snake/band graph.
Definition 4.6.
Let be a snake (respectively band) graph and let be a perfect matching (respectively good perfect matching) of . For each tile of labeled on its diagonal, induces an orientation on the diagonal of . The orientation of is governed by the unique path from the SW vertex of to the NE vertex of taking alternating edges along and the diagonals of .
Example 4.7.
The orientation of each tile in a snake graph allows for the following definition:
Definition 4.8.
Let be the snake (respectively band) graph associated to the curve and triangulation of . Let be a principal lamination of . A diagonal of is -oriented with respect to a perfect matching (respectively good perfect matching) if:
-
•
The tile is indexed odd and either:
-
–
and the diagonal on the tile is oriented down, or
-
–
and the diagonal on the tile is oriented up.
-
–
-
•
The tile is indexed even and either:
-
–
and the diagonal on the tile is oriented up, or
-
–
and the diagonal on the tile is oriented down.
-
–
This definition of oriented tells us exactly how to assign coefficients in our expansions.
Definition 4.9.
Given a (good) perfect matching of , the coefficient monomial is given by
With these coefficients, we state Wilson’s complete expansion formula, Theorem 5.44 in [11], following the setup from Theorem 3.7 for quasi-arcs:
Theorem 4.10.
[11] Let be a one-sided closed curve overlayed on a quasi-triangulation , let be a principal lamination and be the set of good perfect matchings of band graph . The Laurent expansion for the quasi-cluster variable can be expressed as follows:
where is the product of all the edge labels of in , is the coefficient monomial and bad is an error term counting the number of “bad encounters” as in Definition 5.40 in [11].
5. Matrix Formulae on Orientable Surfaces with Respect to Principal Laminations
In this section, we present our main results in Theorem 5.8, Theorem 5.15, and then our main results in Theorem 6.4 and Theorem 6.8.
We generalize the matrix formulae from [8] so they work when using coefficients from an arbitrary principal lamination, rather than just principal coefficients, i.e. the case where for all . This will be necessary when we eventually generalize these matrix formulae to non-orientable surfaces, for if we lift an arc on a non-orientable surface to an orientable surface, it will lift to two arcs and , one of which will have an -intersection, while the other will have a -intersection. With this in mind, many of the results on cluster algebras found in this section will naturally carry over to quasi-cluster algebras due to the existence of the orientable double cover.
Fix a marked surface , triangulation of and principal lamination . To a generalized arc or closed loop , we will be associating a cluster algebra element using products of matrices in . This can be achieved by recreating via a concatenation of various elementary steps, each of which has an associated matrix. The ensuing path created by adjoining these elementary steps will be referred to as an -path. Upon taking the product of these matrices, is either the upper right entry or the trace of the resulting matrix, depending on whether was a generalized curve or a closed loop, respectively. The expansion for achieved in this manner coincides with what one finds using more traditional means, such as mutation or the snake graph poset structure.
The definitions and results that we will be stating, and in some instances adjusting, from this section can be found in Sections 4 and 5 of [8]. In order to define the aforementioned elementary steps and their matrices, we first need to establish some preliminary notation.
Elementary steps do not go from marked point to marked point, rather, they go between points which are close to marked points, but are not marked points themselves. With the above in mind, for each marked point , we draw a small horocycle locally around , and if is on the boundary, we just consider . We may assume the circles are small enough so that for distinct marked points . For each arc , and marked point incident to , we let denote the intersection point and we let (resp. ) denote a point on which is very close to but in the clockwise (resp. counterclockwise) direction from .
We now give the definition of elementary steps from [8] with a slight modification.
Definition 5.1 (Elementary Steps).
-
•
For the first type of step, we consider two arcs and from which are both incident to a marked point and which form a triangle with third side . Then the first step is a curve that goes between and along . The matrix associated to this step is where the sign of is positive if the orientation is clockwise and it is negative otherwise.
-
•
For the second type of step, we cross by following between and . The associated matrix is if we travel clockwise and otherwise. Here, is the Kronecker delta.
-
•
For the third type of step, we travel along a path parallel to a fixed arc connecting two points and associated to distinct marked points . The associated matrix is , where we use if this step sees on the right and otherwise.
Remark 5.2.
The first and third elementary steps are identical to those in [8]. However, the second step is modified in order to reflect the underlying coefficient system using principal laminations.
With the adjusted type two step, we must formally restate and reprove the major results from Section 5 of [8] with the additional case in mind, as there are a few differences that manifest.
By concatenating these elementary step segments to make a path, we can associate a matrix to an arc or a loop in the following way.
Definition 5.3.
[8] Given , and a generalized arc in from to , we choose a curve satisfying the following:
-
•
It begins at points of the form and ends at points of the form where are arcs of incident to and , respectively.
-
•
It is a concatenation of the elementary steps from Definition 5.1, and is isotopic to the segment of between and .
-
•
The intersections of with are in bijection with the intersections of with .
An analogous definition holds when is a closed loop as well, with the exception that we must have that is isotopic to . In either instance, we refer to as the -path. If we have a decomposition into elementary steps , then we define , and the identity matrix is the matrix associated to the empty path.
Notation 5.4.
Given a matrix , let denote (the upper-right entry of ) and denote the trace of .
Remark 5.5 ([8]).
The matrices corresponding to elementary steps of type two are not in . For some applications, we can instead use the matrices
If we make this replacement, we write , which is a product of matrices in .
While and depend on their choice of , it turns out that their trace and upper right entry depend only on .
Lemma 5.6.
[8, Lemma 4.8] Let and be a generalized arc and a closed loop, respectively, without contractible kinks. Then if and are two -paths associated to , then
Analogously, for any two -paths associated to , we have
The lemma above allows us to make the following definition.
Definition 5.7.
Let be a generalized arc and be closed loop, and let and denote arbitrary -paths associated to and , respectively. We associate the following algebraic quantities to and :
-
(1)
and .
-
(2)
and .
With the necessary definitions out of the way, we will now work towards proving the following result, which generalizes Theorem 4.11 of [8] so that our matrix formulae now account for any choice of principal lamination .
Theorem 5.8.
Let be marked surface with a triangulation and let be the corresponding triangulation. Let be the corresponding cluster algebra associated to the principal lamination .
-
•
Suppose is a generalized arc in without contractible kinks. Let be the snake graph of with respect to . Then
where the sum is over all perfect matchings of . It follows that when is an arc, then is the Laurent expansion of with respect to .
-
•
Suppose that is a closed loop which is not contractible and has no contractible kinks. Then
where the sum is over all good matchings of the band graph . Again, is the Laurent expansion of with respect to .
To prove Theorem 5.8, we will show coincides with the perfect (good) matching enumerator associated to their respective snake (band) graph. The process will be similar to that of [8]; however, with the additional case, we will need to make a few changes to the set-up as well as a few adjustments to the statements of the results. The proof of Theorem 5.8 can be found at the end of Section 5.2.
5.1. Matchings of Snake and Band Graphs
To begin the proof, we will associate matrices to the parallelograms of a snake graph, which will then give us a way of representing the Laurent expansion of our graph in terms of products of matrices. The exposition defining the snake and band graphs is taken from [8].
Definition 5.9 (Abstract snake graph).
An abstract snake graph with tiles is formed by concatenating the following pieces:
-
•
An initial triangle
-
•
parallelograms , where each is either a north facing or east-pointing parallelogram:
-
•
A final triangle based on whether is odd or even
We then erase all diagonal edges from the figure.
Definition 5.10 (Abstract band graph).
An abstract band graph for a one-sided curve with tiles is formed by concatenating the following puzzle pieces:
-
•
An initial triangle
-
•
parallelograms , where each is as before.
-
•
A final triangle based on whether is odd or even.
We then identify the edges and , the vertices and , and the vertices and . Lastly, we erase all diagonal edges from the figure.
Just like a traditional snake and band graph, we can consider perfect matchings of an abstract snake graph and good matchings of an abstract band graph. Furthermore, we can associate to each perfect/good matching its weight and coefficient monomials and by letting .
Definition 5.11.
Let be an abstract snake or band graph with tiles. For each parallelogram of , we associate a matrix , where is either
In either case, the following conditions determine which of the two matrices we use:
-
•
is of the first type if is a north-pointing parallelogram, and otherwise it is of the second type.
-
•
for , is of the first type if both and have the same shape, and otherwise, it is of the second type.
We can then define a matrix associated to defined by when . Otherwise, .
Remark 5.12.
The upcoming sequence of results generalize Proposition 5.5, Corollary 5.6 and Theorem 5.4 from [8] to principal laminations. Despite the additional case that stems from having -shape intersections, the proof techniques largely stay the same and the statements generalize in an expected manner.
Proposition 5.13.
Let be an abstract snake graph with tiles. Write
For ,
-
•
When we have
-
•
When we have
For , the formulae remain the same, but the cases are determined by the sign of .
Here, and are the sets of perfect matchings of which use the edges and , respectively.
Proof.
The case where is exactly Proposition 5.5 in [8], so we only consider the case where . Additionally, we note that differences between the two cases will only involve changes in . This is due to the fact that, despite the change in principal lamination, the perfect matchings on the abstract snake graph remain the exact same, meaning will not change when flipping from a -shape intersection to a -shape intersection, or vice versa.
We perform a proof by induction on , and consider what happens when one adds one more tile to a snake graph. When , we just have a single tile
meaning and . When , we get , hence , as desired.
Just like Proposition 5.5 in [8], for , we let denote the graph obtained by gluing together the initial triangle, parallelograms and the final triangle. For convenience, we label the final triangle in with and and note the orientation of this triangle depends on whether is odd or even. By changing labels, the graph is isomorphic to the subgraph of consisting of the first tiles. In particular, we either replace the edge label with and with , or vice versa.
With this in mind, when considering , we have may assume it has the following shape and labeling:
One can quickly check that when and then meanwhile, when and then . Regardless, both matrices match the equations found in Definition 5.11.
To finish the proof, we simply observe that the bijections between the various perfect matchings utilized in the proof of Proposition 5.5 of [8] apply here as well, regardless of our principal lamination. As such, by applying induction, we may conclude the following. Under the initial labeling scheme (used in the base cases), we obtain the following two cases depending on the sign of :
Likewise, under the other labeling scheme we obtain the following cases, again, depending on the sign of :
Comparing these two equations with Definition 5.11, we see the various cases agree with the cases of the definition of . ∎
Corollary 5.14.
Let be an abstract snake graph with tiles. Write .
-
•
When , then
(5.1) -
•
When , then
(5.2)
where the sum is over all perfect matchings of .
The above corollary immediately implies the next theorem.
Theorem 5.15.
Suppose is an abstract snake graph with tiles. Then its perfect matching enumerator is given by
-
•
-
•
By adjusting our labeling by substituting for , for , and for (see Definition 5.10), we obtain a sequence of statements and results for abstract band graphs that will be analogous to Proposition 5.7 and Corollary 5.8 of [8], but with respect to principal laminations. We end up with the following theorem.
Theorem 5.16.
Suppose is an abstract band graph with tiles. Then its good matching enumerator i.e. the weighted sum of good perfect matchings of with respect to is given by
-
•
-
•
5.2. The Standard -path
Arcs do not have a unique associated -path, but there is an algorithm for assigning a “standard -path” to a curve that we will utilize in order to facilitate proofs. Here we recall the definition of a standard -path for both an arc and a closed loop. Despite working with principal laminations for coefficients, the standard -paths for generalized arcs and closed curves will not change. The only difference that will occur on the -path side will involve adjusting our step two matrix, depending on whether the arc’s corresponding lamination is an -intersection or a -intersection.
Definition 5.17 (Standard -paths).
The definitions below are Definitions 5.9 and 5.11 from [8]. In Definition 6.7, we generalize this construction for one-sided closed curves.
Generalized Arcs: We begin with the case where we have a generalized arc . Let be a generalized arc that goes from point to a point , crossing the arcs in order. We label the initial triangle that intersects with sides , and in clockwise order so that is the intersection of and . We label the final crossed triangle with sides and in clockwise order, with being the intersection of the arcs and .
The path begins at the point , where the sign is chosen so the point lies in the triangle. The first two steps of consists of traveling along and then jumping from to , i.e., we perform a step three and then a step one move. After these two moves, we are at a point of the form , but we have not yet crossed .
Until we reach the the final triangle, we follow the steps illustrated in Figure 6 depending on whether is counterclockwise or clockwise from . That is, if is counterclockwise to , the next steps of will consist of a step two move that crosses and then a step one move from to . If is clockwise from , we cross with a step two move, then we reach through a step one move to reach , then a step three move to travel along and we finish with a step one move to arrive at .
After transitions, we reach the final triangle. We cross with a step three move, we then apply a step one move to get to and then we travel along with a step three move to reach the point . We call this the standard -path associated to .
Closed Loops: In the case where is a closed loop, the process is largely the same. To begin, we choose a triangle in such that two of its arcs are crossed by and we label the two arcs and so that is clockwise from . We label the third side of by . Let be a point on which lies in and has the form . We then let denote the ordered sequence of arcs which are crossed by , when one travels from away from . The standard -path associated to is defined just like it was for generalized arcs, that is, by following the sequences of steps illustrated by Figure 6, depending on whether is counterclockwise or clockwise from . The standard -path begins and ends at the point and we consider the indices modulo .
If is not a standard -path, for the generalized arc or loop , then one can deform into a standard -path by making local adjustments that do not influence the upper right entry or trace.
We are now ready to prove Theorem 5.8, which states that, with our additional adjustments, the matrix formulae of [8] hold for arbitrary principal laminations.
Proof of Theorem 5.8.
We first consider the case where is a generalized arc and consider its standard -path, . The first two steps of this path correspond to the matrix product
while the last three steps correspond to
In between the first and the last steps, for the portion between and , where , we have the following four cases that depend on the sign of and whether lies clockwise or counterclockwise from .
Here, is the third side of the triangle with sides .
By Definition 5.7 and Theorem 5.15, we find
-
•
-
•
where the middle matrix is obtained by multiplying together a sequence of matrices of the four forms mentioned previously. The term has an interpretation in terms of perfect matchings of some abstract snake graph . Namely, the abstract snake graph is precisely associated to , meaning from Definition 5.11, which justifies the right-most equality and the proof is complete.
The case where is a closed loop is virtually the same, the only difference being that our initial and final steps are different. By construction of the standard -path, we have that is in the clockwise direction of . This implies the final steps of corresponds to either
By Definition 5.7, Theorem 5.16 and using the interpretation of in terms of good matchings of some abstract band graph , we obtain
-
•
-
•
where again is a obtained by multiplying together a sequence of matrices of the four forms mentioned previously and can be interpreted as the matrix for . ∎
5.3. Example with Closed Curve
Consider the triangulation and closed loop with band graph pictured in Figure 7.
We compute as well as and show they are equal. The perfect matchings and how they relate to one another are pictured in Figure 8. Taking the sum of each monomial in the Figure 8, we find
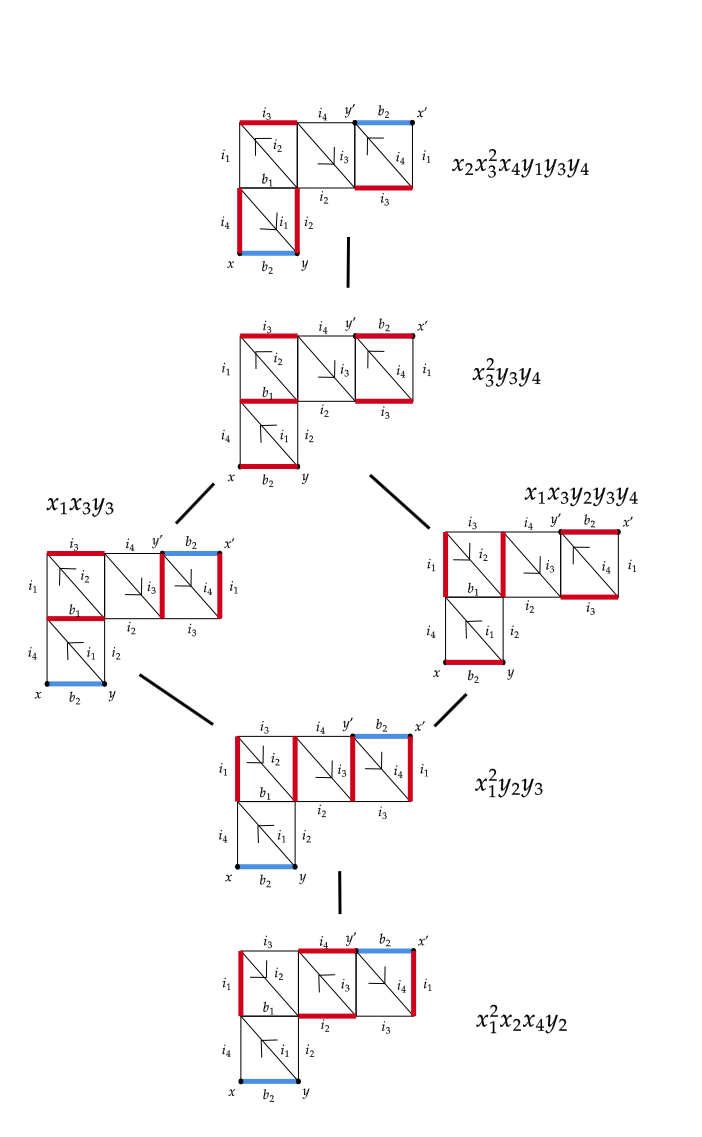
Meanwhile, the matrix formula yields
Letting and rearranging the terms in our numerator, we conclude
Remark 5.18 (Comparision to Example 3.23 in [8]).
We chose to revisit Example 3.23 from [8] using a different principal lamination to demonstrate the differences in our construction. In [8], they use the same triangulation and closed curve with the principal lamination defined by for each . For our example, we consider defined by taking and changing from to and keeping everything else the same.
With these differences, Musiker and Williams obtain
whereas, we have
Remark 5.19.
Also, notice that Figure 8 is arranged to look like the Hasse diagram for a poset. Although we may always arrange the set of (good) perfect matchings as a poset with the cover relation given by “flipping” local tiles as in [7], the coefficient variables cannot be directly recovered without the lamination. For instance, the minimal element in this poset has a non-trivial height monomial of . This is not typically how the -coefficients or height monomial is classically defined. In general, there will exist a choice of isotopic representative of arc that gives the classical poset structure interpretation of the coefficients, but perturbations of this arc will change the poset structure. An example of this can be seen comparing the poset we obtain in Figure 15 and Figure 12 in Section 6.
6. Expansion formula for one-sided closed curves using matrix products
In this section, we will prove the matrix formulae in the previous section can be used to find the Laurent expansion for one-sided closed curves. To prove this result, we will be following the general guidelines found in Section 5 of this paper. That is, we will be associating matrices to the parallelograms of a band graph, which will then give us a way of representing the good matching enumerator of our graph in terms of the trace of a product of matrices. To conclude this section, we will show that the matrix product associated with the band graphs of one-sided curves coincides with the matrix product associated to a canonical -path associated to the one-sided curve.
6.1. Good matching enumerators for one-sided closed curves.
The basic ingredients used to construct band graphs for one-sided curves are largely the same as those found in Definition 5.10, but there is a slight twist.
For two-sided closed curves, we always glue together sides with the same sign, but when working with the one-sided closed curve, we will now be identifying edges that have the opposite sign. With this in mind, the following abstract band graph will differ from the one defined earlier.
Definition 6.1 (Abstract band graph for one-sided curves).
An abstract band graph for a one-sided curve with tiles is formed by concatenating the following puzzle pieces:
-
•
An initial triangle
-
•
parallelograms , where each is as before.
-
•
A final triangle based on whether is odd or even.
Just like the orientable case, we associate various matrices to the parallelograms of our graph that will be determined by comparing the shape of the parallelograms and , as well as the principal lamination used for coefficients. See Definition 5.11.
We now provide a description of the entries of in terms of weight and coefficient monomials and for good matchings of our new variant of abstract band graphs. The following proposition is an immediate corollary of Proposition 5.13 after relabeling the edges of our graph.
Proposition 6.2.
Let be an abstract snake graph with -tiles, but with a labeling obtained by substituting with , with and with . Write
For ,
-
•
When we have
-
•
When we have
For , the formulae remain the same, but the cases are determined by the sign of .
Here, and are the sets of perfect matchings of which use the edges and , respectively.
The following comes as a direct corollary of Proposition 6.2.
Corollary 6.3.
Let be an abstract band graph corresponding to a one-sided closed curve with tiles. Write .
-
•
When , then
(6.1) -
•
When , then
(6.2)
where the sum is over all good matchings of .
Proof.
Following the notation from Proposition 6.2, we consider the sets and . If is our snake graph from Proposition 6.2 and is the band obtained from identifying and , then every perfect matching from and descends to a good matching of after removing either or . On the other hand, no perfect matching from descends to a good matching of . As all good matchings of are obtained uniquely from perfect matchings in or , the result follows. ∎
The corollary above immediately proves the following theorem.
Theorem 6.4.
Suppose is an abstract band graph with tiles that corresponds to a one-sided closed curve. Then its good matching enumerator is given by
-
•
-
•
where the sum is over all good matchings of .
6.2. The standard -path for a one-sided closed curve.
In this section, for any one-sided closed curve , we will associate to it a standard -path and show that the associated matrix formula will have the same form as Equations (6.1) and (6.2) found in Corollary 6.3.
The elementary steps used in the standard -path will be the same as those used in the orientable case; however, we will need to make an adjustment to the matrix corresponding to the type III step that travels through the crosscap, as we will now be traveling along an arc from a point of the form () to another point of the form ().
Definition 6.5 (Elementary Step of Type 3’).
For this variation of the third type of elementary step, we travel through the crosscap along a path parallel to a fixed arc connecting two points and associated to distinct marked points . The associated matrix is , where we use if this step sees on the right and otherwise.
An illustration of the type 3’ elementary step can be found in Figure 10 of Section 6.3. The next lemma is a quick check verification that Lemma 5.6 still holds with our new type three step.
Lemma 6.6.
Fix and . Let be a one-sided closed curve. Then for any two -paths, and associated to , we have
Proof.
First, we observe if we have an -path , then
for all , so the trace is invariant under the starting point of our -path. The original three elementary steps are covered already by Lemma 5.6.
Furthermore, we have the equality
which implies, with respect to , crossing with a step two move and then passing through the crosscap with the adjusted step three move is the same as first passing through the crosscap and then crossing . ∎
Despite working on a non-orientable surface, the algorithm for constructing the standard -path for the one-sided closed curve will be reminiscent to the algorithm for creating standard -paths for closed curves on orientable surfaces. The differences being that we require the first arc to be counter-clockwise from the last; and we require that the final step of the path corresponds to traveling through the crosscap.
Definition 6.7.
(Standard -path for a one-sided closed curve) Let be a one-sided closed curve which crosses arcs of a fixed triangulation (counted with multiplicity). Choose a triangle in such that two of its arcs are crossed by . We label these two arcs as and , where is in the counterclockwise direction from . We label the third side with . Let be a point on which lies in and has the form . Letting, denote the ordered sequence of arcs that are crossed by as we move from and , we have that the standard -path associated to is the same as Definition 5.17, starting and ending at and traveling along elementary steps based on whether is counterclockwise or clockwise from . The final elementary steps of will be determined by the fact that is in the counterclockwise direction from and that, to return to , we must travel parallel to through the crosscap. We consider indices modulo . See Figure 10 for an example of a such a standard -path.
We’re ready to prove the main theorem of this section.
Theorem 6.8.
Let be a marked non-orientable surface with a triangulation , and let be the corresponding triangulation. Let be the corresponding cluster algebra associated to the principal lamination .
Suppose is a one-sided closed curve which is not contractible, and has no contractible kinks. Then
where the sum is over all good matchings of the band graph .
Proof.
We consider the standard -path of defined in Definition 6.7. For the indices from to , we have the following four cases that depend on the sign of and whether lies clockwise or counterclockwise from .
| (6.3) | |||
| (6.4) | |||
| (6.5) | |||
| (6.6) |
Here, is the third side of the triangle with sides .
As is in the counterclockwise direction from , and we must travel parallel along through the crosscap in order to return to , the final few steps of are represented by one of the two matrices:
| (6.7) | |||
| (6.8) |
By Definition 5.7, Theorem 6.4 and using the interpretation of in terms of good matchings on some abstract band graph we have
-
•
-
•
If is a non-standard -path for the one-sided closed curve , then can be deformed into a standard -path by the local adjustments found in Lemma 4.8 of [8] and Lemma 6.6.
Lemma 6.9.
If we use the standard -path, Definition 6.7, for a one-sided closed curve with no contractible kinks, then every coefficient of is positive.
Proof.
Given a one-sided closed curve with no contractible kinks, let denote the corresponding standard -path. The proof of this lemma comes from the simple observation that all entries of matrices of the forms (6.3), (6.4), (6.5), (6.6), (6.7) and (6.8) are positive. As such, is a sum of positive terms and is thus positive. ∎
Corollary 6.10.
The quantity is a Laurent polynomial with all coefficients positive. This verifies and provides another proof of the positivity result by Wilson in [11].
Next, we need to make sure that if we fix a principal lamination , then the isotopic representations of a one-sided curve share the same Laurent polynomial. That is, if and are isotopic one-sided closed curves, then
Throughout this segment, we will write
While this statement may seem straightforward, there is some difficulty that occurs due to the fact that, in most situations, the band graphs of and are not isomorphic to one another and hence yield different poset structures. This is illustrated in Figure 18.
Lemma 6.11.
Let be a one-sided closed curve and be a principal lamination on the triangulation . Let be the reflection of about the crosscap. Then
Proof.
By definition, we have ; furthermore, one can obtain the band graph of by taking and reversing the relative orientation of each tile. This ensures that the set of perfect matchings on both graphs are the same, and for each perfect matching . Note, the minimal matching on is the maximum matching on (and vice versa); however, reflecting across the crosscap has the effect of changing -intersections into -intersections (and vice versa).
As a corollary, for this specific matching. The remaining matchings on both band graphs are found by taking , flipping the orientation of certain diagonals and repeating this process until conclusion. We thus have
∎
Proposition 6.12.
Let and be isotopic one-sided closed curves. Then
Proof.
We begin by setting up some notation. Let be the arcs of our triangulation and let be a principal lamination. As a reminder, each lifts to two arcs in the orientable double cover that will have opposite signs with respect to the principal lamination. Let be the copy of that lifts to an -shape intersection and be the copy that lifts to a -shape intersection.
To prove this result, we show is invariant under “rotations” of the one-sided closed curve around the crosscap. In other words, if and are the first two arcs that intersects and is the final arc intersects, then we will assume intersects first and last (see Figure 17) and show . Note that the ’s in and correspond to arcs on the orientable surface with opposite sign with respect to . By Lemma 6.11, we may assume without loss of generality, that lies counterclockwise to . This implies that on the other side of the crosscap, lies clockwise to (otherwise, we can reflect across the crosscap). Further, we will assume the that crosses lifts to , while the that crosses lifts to .
By Theorem 6.8 and the fact for two matrices and , we have
Remark 6.13.
One could also prove this by making use of the band graphs of these curves. Namely, a rotation of the amounts to moving the first tile of the graph to the end of the graph and then flipping the sign of the lamination. This method is far more difficult to prove in generality than the matrix method used above.
6.3. Möbius Band Example
In this subsection, we illustrate the techniques used above in a few examples involving the Möbius Band. We will first compute the Laurent expansion by computing the trace of the -path matrix and then we will compare it to the Laurent expansion obtained from the good matching enumerator.
Notation 6.14.
Throughout this section, if we have an arc in the triangulation, we let denote the coefficient corresponding to .
The one-sided curve on and each step of the standard -path are shown in Figure 10. We assume each arc that intersects lifts to an -intersection in the orientable double cover and will look at what happens on different laminations later. The matrices associated to each of step of the standard -path are listed here:
Therefore, we have
where the closed brackets, in the product, group the matrices by triangle and the final matrix, , corresponds to going through the crosscap.
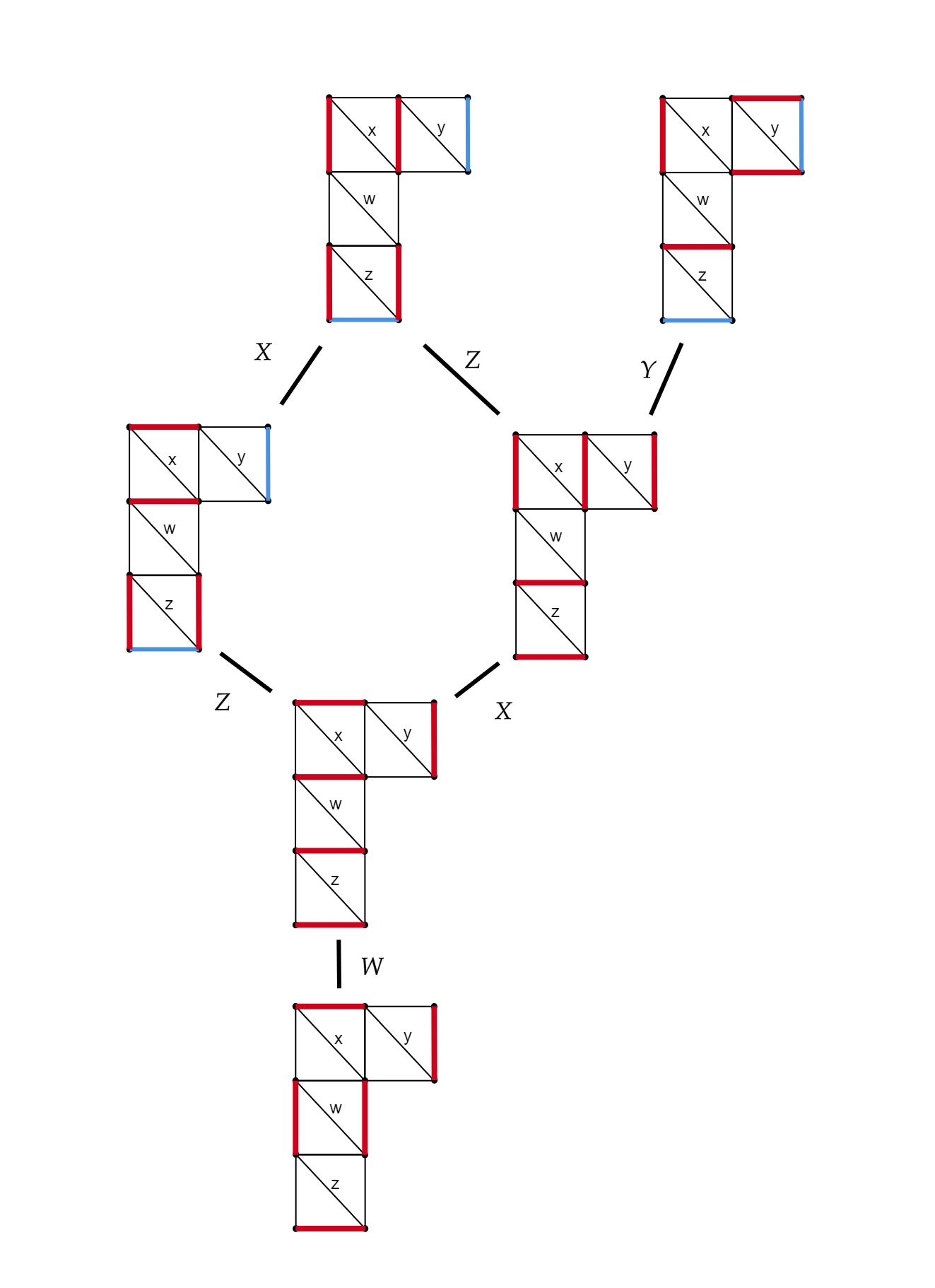
Meanwhile, we have the band graph shown in Figure 11. With this band graph, the good matchings are demonstrated in Figure 12.
Computing the good matching enumerator, we find
and we see the two methods of computing the expansion agree with one another.
6.4. Reflection and Rotation Example
If we instead considered the curve given by reflected across the crosscap, which we will denote by , then we get the -path found in Figure 13. The expansion is given by
which agrees with out previous computation. Observe that when flipping across the crosscap, every counterclockwise sequence becomes clockwise and vice-versa. Additionally, the sign of the principal lamination changes as we are now intersecting arcs that lift to -intersections, so we must change each matrix of type two in the standard -path.
The corresponding band graph is shown in Figure 14. Observe that it is the same as the band graph shown in Figure 11 with the exception that we have used the opposite relative orientation.
Observe that the minimal matching shown in Figure 12 (the bottommost graph of the figure), becomes the maximal matching for (see Figure 16); however, as we are now lifting to -intersections, the coefficient monomial remains the exact same as the previous example. A similar logic applies to the other good matchings on and the set of good matchings is shown to give comparison in Figure 15.
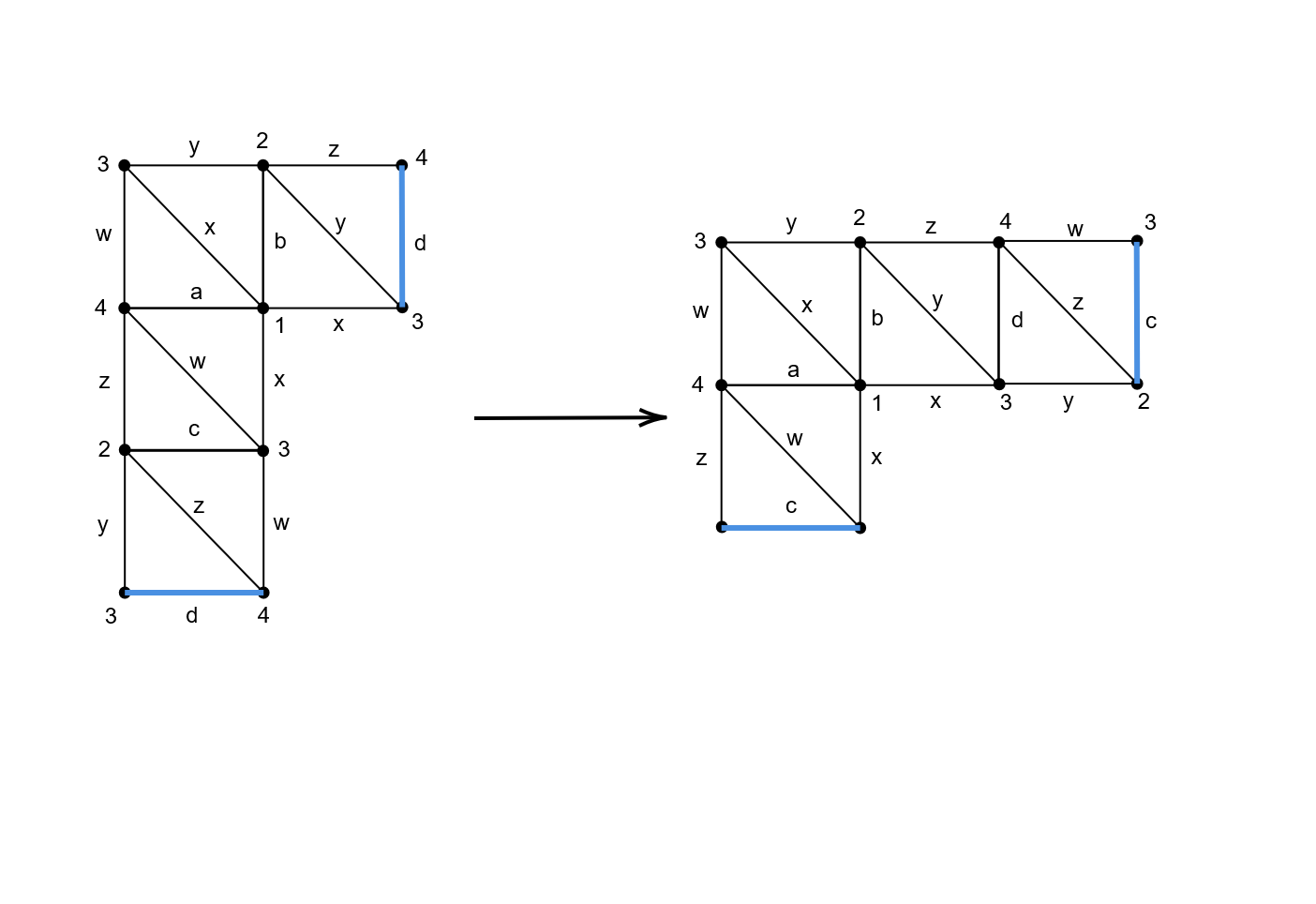
Next, we will look at a “rotation” of . Let be the arc depicted in Figure 10 and let be the one-sided closed curve shown in Figure 17. The matrices corresponding to the individual steps of the standard -path for are listed below. The first ten matrices appear in the matrix product for as well, i.e, the matrices in purple text.
The proof of Proposition 6.12 shows that the trace of the matrix product associated to agrees with the trace of the matrix product associated to . This can be seen explicitly by computing the matrix product via Macaulay2. One finds
A similar computation can be done with the other rotations of .
7. Skein Relations for One-Sided Closed Curves
To conclude this paper, we briefly show how the theory we have developed throughout this paper can be used to prove skein relations on non-orientable surfaces. Skein relations on non-orientable surfaces have already been proven for -coordinates in Section 4.3 of [1]; however, with our matrix formulae, we can show these equations hold true when considering coefficients that come from principal laminations.
There are only a few cases that we need to consider, and most follow from basic adjustments to the arguments found in [8] using Sections 5 and 6 of this paper. Throughout this section, we will let denote the number of crossings between the generalized arc/loop/one-sided closed curve and the arc .
Case One: Intersection of Generalized Arcs
In this case, we do not consider one-sided closed curves, so we can simply lift to the orientable double cover and apply Proposition 6.4 from [8]. Considering general principal laminations rather than principal coefficients, the statement becomes the following.
Proposition 7.1.
Let and be two generalized arcs which intersect each other at least once; let be a point of intersection; and let and be the two pairs of arcs obtained by resolving the intersection of and at . Then
where and .
Case Two: Intersection of Generalized Arc/Loop with Generalized Loop/One-sided Closed Curve
When is a generalized arc or loop and is a generalized loop, then Proposition 6.5 from [8] applies after lifting to the orientable double cover. When is a one-sided closed curve, we note that the only new type of step in the standard -path is the elementary step of type 3’, from Definition 6.5, when going through the crosscap at the end, see Definition 6.7. Specifically, the steps of type 1 and 2 remain the same as in the orientable case, meaning we can directly apply the arguments from Lemma 6.10 and Proposition 6.5 from [8] to prove Proposition 7.2.
Proposition 7.2.
Let be a generalized arc or loop and let be a generalized loop or one-sided closed curve, such that and intersect each other at least once; let be a point of intersection; and let and be the two arcs/curves obtained by resolving the intersection of and at . Then
where and .
Case Three: Non-simple Generalized Arc/Loop/One-sided Closed Curve
Just like the previous case, when is a generalized arc or closed curve with a self-intersection at , me may lift to the orientable surface and apply Proposition 6.6 from [8]. When is a one-sided closed curve, using the standard -path for one-sided closed curves, we may directly apply the arguments from Lemma 6.10 and Proposition 6.6 of [8] to conclude Proposition 7.3.
Proposition 7.3.
Let be a generalized arc, closed curve or one-sided closed curve with a self-intersection at . Let and be the generalized arcs/loops/one-sided curves obtained by resolving the intersection at . Then
where and .
Case Four: Intersection of Homotopic One-sided Closed Curves
The case that requires the most care occurs when we have two homotopic one-sided closed curves that intersect one another. It’s worth noting that any two curves homotopic to a one-sided closed curve will have at least one intersection point, meanwhile, in the orientable case, two homotopic two-sided curves can always be adjusted so that they are disjoint.
For the next proposition, we follow the notation from Proposition 4.6 of [1]. Namely, if is a one-sided closed curve, then will denote the one-sided closed curve of multiplicity two, see Figure 21 below. In terms of the orientable double cover, one can interpret as the concatenation of the two lifts of on the orientable surface, as such, is a two-sided closed curve enclosing the crosscap. The following proposition generalizes Proposition 4.6 of [1].
Proposition 7.4.
Let be a one-sided closed curve, and let be the two sided-closed curve enclosing the crosscap obtained from resolving an intersection of with another one-sided closed curve homotopic to , then
Proof.
Let be the reflection of about the crosscap, as in Lemma 6.11. We can write
where is the reduced standard -path of with the final step excluded (so we do not go through the crosscap). Similarly, we can write
With this notation, we have . With all of this information in mind, from earlier results from this paper, as well as other basic considerations, we have
-
•
-
•
-
•
-
•
Lastly, when are matrices with and , we have
Putting everything together, we have
∎
8. Appendix
In this appendix, we explicitly demonstrate the skein relation manipulations referred to in Section 2. We begin by demonstrating the missing step in the computation for the quasi-mutation depicted in the body of the paper. Namely, we show on the double cover why we can push a loop through the crosscap.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/cross-cap-loop.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/cross-cap-loop-comp.png)
Included below is the skein relation derivation of the fourth quasi-mutation relation given in Definition 2.7. We restate the mutation relation for reference.
Given , the quasi-mutation of in the direction as the pair where and such that is defined as follows: If is an arc separating a triangle with sides and an annuli with boundary and one-sided curve , then the relation is .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/skein-reln-4.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/skein-reln-4-compa.png)
The above computation shows that this crossing resolution yields the relation where is a two sided-closed curve enclosing the crosscap. It remains to show that . Let be the arc passing through the crosscap. We now show the resolution of the crossing of the arc and the two-sided closed curve which encloses the crosscap, which yields the relation .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/skein-reln-4-compb.png)
Finally, we show that by resolving the remaining crossings. With this computation, we have implying that . This completes the derivation of the fourth mutation relation from Definition 2.7.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b1a5ad5c-cf28-43b9-a6c8-d87364ba9821/skein-reln-4-compc.png)
References
- [1] Grégoire Dupont and Frédéric Palesi “Quasi-cluster algebras from non-orientable surfaces” In Journal of Algebraic Combinatorics 42.2 Springer ScienceBusiness Media LLC, 2015, pp. 429–472 DOI: 10.1007/s10801-015-0586-1
- [2] Vladimir Fock and Alexander Goncharov “Moduli spaces of local systems and higher Teichmüller theory” In Publications Mathématiques de l’IHÉS 103, 2006, pp. 1–211
- [3] Vladimir V. Fock and Alexander B. Goncharov “Dual Teichmüller and lamination spaces” In Handbook of Teichmüller theory. Vol. I 11, IRMA Lect. Math. Theor. Phys. Eur. Math. Soc., Zürich, 2007, pp. 647–684 DOI: 10.4171/029-1/16
- [4] Sergey Fomin, Michael Shapiro and Dylan Thurston “Cluster algebras and triangulated surfaces. Part I: Cluster complexes” In Acta Mathematica 201.1 Springer Netherlands, 2008, pp. 83–146 DOI: 10.1007/s11511-008-0030-7
- [5] Sergey Fomin and Andrei Zelevinsky “Cluster Algebras I: Foundations” In Journal of the American Mathematical Society 15.2, 2002, pp. 497–529
- [6] Michael Gekhtman, Michael Shapiro and Alek Vainshtein “Cluster algebras and Weil-Petersson forms”, 2005
- [7] Gregg Musiker, Ralf Schiffler and Lauren Williams “Positivity for cluster algebras from surfaces” In Adv. Math. 227.6, 2011, pp. 2241–2308 DOI: 10.1016/j.aim.2011.04.018
- [8] Gregg Musiker and Lauren Williams “Matrix Formulae and Skein Relations for Cluster Algebras from Surfaces” In International Mathematics Research Notices 2013.13, 2013, pp. 2891–2944 DOI: 10.1093/imrn/rns118
- [9] Robert C Penner “The decorated Teichmüller space of punctured surfaces” In Communications in Mathematical Physics 113 Springer, 1987, pp. 299–339
- [10] Ralf Schiffler “A Cluster Expansion Formula ( case)” In The Electronic Journal of Combinatorics, 2008, pp. R64–R64
- [11] Jon Wilson “Positivity for quasi-cluster algebras” arXiv:1912.12789, 2019 arXiv:1912.12789 [math.CO]