Mean curvature flow with multiplicity convergence in closed manifolds
Abstract.
We construct new examples of immortal mean curvature flow of smooth embedded connected hypersurfaces in closed manifolds, which converge to minimal hypersurfaces with multiplicity as time approaches infinity.
1. Introduction
The mean curvature flow is the gradient flow of the area functional. This feature makes it one of the most natural extrinsic geometric flows. Mean curvature flow is widely used to study geometry and topology, and we refer the readers to some of the applications in [Gra89, Wan02, HK19, BHH21, BHH19, GLP21]. A central topic in the study of mean curvature flow is to understand the singular behavior and long-time behavior, and it is particularly important to the potential applications.
Among the possible exotic phenomena that may show up, higher multiplicity convergence is one of the most significant phenomena and has attracted much attention. Roughly speaking, higher multiplicity convergence means that the hypersurfaces can be decomposed into several connected components outside a small set, and each one of the connected components converges to the limit hypersurface smoothly. Recently, the Multiplicity One Conjecture proposed by Ilmanen was resolved by Bamler-Kleiner [BK23], showing that higher multiplicity can not show up as the blow-up of a singularity of a mean curvature flow of closed embedded surfaces in . In contrast, the authors [CS23] constructed an immortal mean curvature flow in , showing that higher multiplicity convergence can show up as the long-time behavior of mean curvature flow of connected surfaces in .
In this paper, we construct new examples of mean curvature flow in closed manifolds that converge to higher multiplicity minimal hypersurfaces as time goes to infinity. Recall that an immortal mean curvature flow is a smooth mean curvature flow that exists for all positive time. In the following, suppose equips the round metric and equips the standard product metric. It is not too hard to see that is a minimal hypersurface.
Theorem 1.1.
For all , there exists a smooth embedded connected immortal mean curvature flow in such that converges to with multiplicity as .
Of course, one can close up to get a compact manifold, or extend it to a complete noncompact manifold.
This new family of examples shows that the higher multiplicity convergence of mean curvature flow can occur for compact mean curvature flow in a closed manifold. In particular, there exists an infinite time singularity. This contrasts with a result of Jingyi Chen and Weiyong He [CH10], which proved that in manifold with certain curvature and growth conditions, the mean curvature flow can only have finite time singularities. We note that their growth condition does not hold for .
Our new examples enhance our understanding of using mean curvature flow to construct minimal hypersurfaces. When higher multiplicity convergence shows up, the geometry and topology of the limit hypersurface may be different from the flow. This phenomenon has been discovered in other fields of geometric analysis, such as the Min-max theory. In [WZ22], Zhichao Wang and Xin Zhou constructed an example to show higher multiplicity minimal surfaces can show up in the Almgren-Pitts min-max theory. In [WZ23], Zhichao Wang and Xin Zhou observed that the possible obstruction to the existence of minimal spheres in with an arbitrary metric is the higher multiplicity convergence in the min-max theory.
Motivated by the generic multiplicity property in the min-max theory proved by Xin Zhou [Zho20], we expect that higher multiplicity convergence is a non-generic property.
Conjecture 1.2.
Starting from a generic closed hypersurface in a Riemannian manifold, either the long-time limit has multiplicity , or the hypersurface breaks into different connected components, and each one of the connected components converges to a multiplicity limit.
We remark that the limit minimal surfaces in our examples are stable. Also motivated by the min-max theory and the resolution of the Multiplicity One Conjecture by Bamler and Kleiner [BK23], we expect that higher multiplicity convergence can not occur if the limit minimal hypersurface is unstable.
Conjecture 1.3.
Suppose is a Riemannian manifold, is a mean curvature flow of closed embedded hypersurfaces. if the limit of as is a minimal hypersurface with multiplicity , and is unstable, then .
Now we discuss the strategy of the proof. The main idea is similar to [CS23] in which the authors used an interpolation argument. Here we also constructed a family of initial data , which are rotationally symmetry under the action on the sphere factor, and reflective symmetry along and the equators of s. Moreover, when is small, the mean curvature flow starting from would generate a neck singularity at the north pole of , and when is large, the mean curvature flow starting from would shrink to a point on the equator of . Then there exists an in between such that the mean curvature flow starting from exists for all future time, namely it is an immortal flow.
It remains to show this immortal flow converges to with multiplicity . To do so, we need to use some barriers to control the immortal flow. In [CS23], we used the planes, the catenoids, and the Angenent torus as barriers. In this paper, we find analogous barriers: the spherical minimal hypersurfaces, the spherical catenoids, and -Angenent torus. We will discuss these special solutions in the preliminary section.
2. Preliminary
2.1. Metric on and rotationally symmetric mean curvature flows
We equip with the standard metric, namely the induced metric on as a hypersurface in . Then we equip with the product metric, denoted by . We can also view as the hypersurface in , equipped with the induced metric.
We consider the action rotating the hyperplane generated by the first coordinates of . This action can be induced to naturally. Any hypersurface in is called rotationally symmetric if it is invariant under this action. After taking the quotient, becomes , and we use and to denote the coordinates on and respectively.
Given a rotationally symmetric hypersurface in , there is an associated curve called profile curve , while can be an interval or , such that is generated by rotating . That says, if we write , then we can parameterize as follows:
The area form of this parametrization is given by
After taking integration and using Fubini’s theorem, we see that the area of , up to a constant, equals the length of the curve under the metric
| (2.1) |
We will be interested in mean curvature flows with initial data that are rotationally symmetric, reflexive symmetric with respect to the middle sphere , and reflexive symmetric with respect to the hypersurface . We call a smooth hypersurface in with all above symmetry conditions as a desired hypersurface. By the short-time existence and uniqueness of the mean curvature flow, we know the rotational symmetry and reflexive symmetry are preserved under the mean curvature flow. Consider a mean curvature flow of desired hypersurfaces on . For each hypersurface , after taking the quotient of the action and the two reflections, we get a curve in the region , and we name as the section curve of (note this is the top left part of the profile curve). We say is an ascending section curve if it is the graph of an increasing function, and let denote the set of function such that the graph of is an ascending section curve of a desired hypersurface in .
The reflexive symmetry implies that the curve intersects the two sides , orthogonally. We name the intersection point of with as the head point. This curve can be expressed as the union of two graphs of smooth functions and , and we call the vertical graph function and call its graph as the vertical graph; we call as the horizontal graph function and call its graph as the horizontal graph. See the picture below for an example.
Let and be the vertical graph function and the horizontal graph function of the initial curve . Suppose after reflecting and rotating we get a hypersurface in . Then a family of hypersurfaces is said to be a mean curvature flow with initial condition if the corresponding vertical graph function, horizontal graph function , of satisfy the following equations (see Appendix A):
| (2.2) |
2.2. Minimal hypersurfaces as barriers
Suppose and are two curves in . We say that is on top of , if for all pairs such that , it holds that . Recall the comparison principle for mean curvature flow:
Proposition 2.1 (Comparison principle).
Suppose is a closed manifold, and are two mean curvature flows of smooth embedded hypersurfaces in . If does not intersect , then does not intersect for all .
Therefore, we can use barriers that are either on top of the flow or under the flow at the initial time to control the behavior of the flow at a later time. We will frequently use the following special solutions as barriers in this paper.
Firstly, we consider the static solutions known as the minimal hypersurfaces. The simplest possible examples are the horizontal graphs given by for a constant . Such a minimal hypersurface is just a section of , and we call it a minimal sphere. There is only one constant vertical graph given by . It is the Cartesian product of the geodesic hypersphere in with , and we still call it a geodesic hypersphere.
Another class of minimal hypersurfaces is the analog of the catenoids, and we call them spherical catenoids. Given a parameter , we can solve the ODE
| (2.3) |
with initial condition and . First, (2.3) is invariant under , so the solution must be an even function, and hence we only need to study the part of the solution where . It is straightforward to see that , and hence in a neighborhood of . Multiplying both sides of (2.3) by yields the identity
and then we can conclude that there exists a constant such that
By plugging in we obtain
Then we obtain that for all , where . We may write the expression of as
We can also obtain the information of by looking at the inverse function , which satisfies the equation
| (2.4) |
where and , and as or . dividing both sides of (2.4) by yields the identity
Therefore, there exists such that
Let , we have . Then we obtain
| (2.5) |
This implies that for all , and . Then we can show that . It is also clear that .
Lemma 2.2.
We have the following asymptotic of :
| (2.6) |
Proof.
By (2.5) and , we have
Using the fact , for , we have
By letting , we see that . On the other hand,
Thus
Since , thus
∎
Remark 2.3.
Using the fact that , by a similar estimate, we can show that .
In fact, the spherical catenoids are periodic in the factor, and is half of the period. See Figure 3 for a picture.
2.3. -Angenent curves
In his pioneer work [Ang92], Angenent constructed a rotationally symmetric self-shrinking mean curvature flow in that is topological before it becomes singular. More precisely, Angenent constructed a closed embedded hypersurface that is rotationally symmetric, such that is a mean curvature flow.
It was observed by Huisken [Hui84] that if is a mean curvature flow, then satisfies the equation , and such is called a shrinker. Moreover, Huisken observed that a shrinker in is the critical point of the Gaussian area functional . Therefore, Angenent reduced the existence of a rotationally symmetric shrinker to the existence of a closed embedded geodesic in the half-plane equipped with the metric .
Angenent used a shooting method to construct such a closed embedded geodesic. The idea is to examine the trajectory of the geodesics starting from with unit tangent vector as varies. Then an interpolation argument asserts the existence of a geodesic trajectory that will get back to some again with tangent vector . Reflecting this geodesic trajectory along the -axis gives a desired closed embedded geodesic.
We would like to point out that if we replace by some , all the proofs in [Ang92] still work (See Appendix B for an explanation). We call a closed embedded geodesic in the half-plane equipped with the metric a -Angenent curve. Such curves will be the barriers. In fact, when , we can just use the -dimensional Angenent torus as the barrier. Only in the case we need a -Angenent curve as the barrier for .
3. Main result
Throughout this paper, to simplify the notation, we will use the names of the hypersurfaces (minimal spheres, geodesic hyperspheres, spherical catenoids, etc.) to denote their profile curves and section curves as well.
3.1. Rotationally symmetric mean curvature flow
In this section, we study the solutions to the equation (2.2).
We will introduce the following notations throughout this section. is a rotationally symmetric mean curvature flow in . The section curve of is , and can be expressed as the graph of . Therefore is a solution to the equation (2.2). , will denote the vertical graph function and the horizontal graph function of .
Proposition 3.1.
If the initial section curve is an ascending section curve and is the first singular time, then is an ascending section curve for all .
Proof.
is an ascending section curve means , and besides the boundary. Since , are solutions to the equation (2.2), we know that and satisfies the following equation
| (3.1) | ||||
By the strict maximum principle of the quasilinear equation, we claim that for ,
| (3.2) |
∎
From now on we will assume that the initial section curve is ascending. It follows from Proposition 3.1 that is an ascending section curve, thus the height of (i.e. the maximum of ) is given by . We prove in the next lemma that it is monotone.
Lemma 3.2.
If is an ascending section curve, then the height of is strictly decreasing in .
Proof.
The horizontal line is on top of the curve , and remains static under the mean curvature flow. By Proposition 2.1, for any , is on top of the curve , thus . Moreover, if is not a constant function, then the strong maximum principle yields the result.
∎
Although Lemma 3.2 shows that the height of the section curve of the flow strictly decreases, we do not have a quantitative estimate of the decreasing rate. To obtain such a bound, we need to construct a new family of barriers.
Given , Consider a smooth function such that
and for .
By similar arguments as in authors’ previous paper [CS23], there exists a smooth solution to the horizontal graph equation with initial data , and boundary condition . We have the following lemmas which are based on the maximum principle and Sturmian theorem (see [CS23, Lemma 3.4, 3.5]).
Lemma 3.3.
There exist a constant and a time such that for all .
Lemma 3.4.
Given , there exists a continuous nonincreasing function that only depends on the head point of the initial condition (i.e. ) and , such that
holds for all , .
Next, we examine the behavior of the head point when the singularity appears during the mean curvature flow. By Lemma 3.2, we know the limit of the height exists. The gradient estimate in Lemma 3.4 implies that if the height of the function tends to , then the head point must tend to the boundary .
Corollary 3.5.
If , then .
Proof.
We prove this by contradiction. Suppose not, then there exists and an increasing sequence such that , .
Then is well-defined on . Let , , then by Lemma 3.4,
Hence for all . Moreover , which contradicts to .
∎
On the other hand, if the limit of the height is not zero, we obtain an improved gradient estimate.
Lemma 3.6.
If the height , then for any , let , there exists a constant such that for all , . In addition, .
Proof.
For , is well-defined on and for . We know satisfies the vertical graph equation
Define , then for , and
Hence for . Since for all , let , . Then on , thus
Therefore is a subsolution, and is a supersolution of the PDE on the interval . Initially we have , and at the two endpoints of the interval , , . By the classical maximum principle, we conclude for all . Therefore
This implies .
∎
Now we are ready to describe the possible singular behaviors of the mean curvature flow with a desired hypersurface as the initial condition. Recall that we assume the initial section curve is ascending. In [CS23], we used the Evans-Spruck estimates ([ES92, Corollary 5.3], also see [AAG95, Page 303]) of the gradient of the graph function of mean curvature flow in . We need a generalization of this graph estimate to in [BM12].
In the following, for , we use to denote a given ball of radius in .
Lemma 3.7.
Given , there exists with the following significance: Suppose is a function such that the graph of is a mean curvature flow in , then for ,
| (3.3) |
Proof.
The proof can be found in [BM12]. In the following, is the distance function on from the point , and for , . Using the proof of [BM12, Theorem 7], we can obtain that for any ,
| (3.4) | ||||
Then when is sufficiently small, we can choose appropriate such that to derive a desired bound for .
∎
Proposition 3.8.
The flow first becomes singular at time if and only if or . In addition, if such doesn’t exist, then the mean curvature flow exists for all future time.
Proof.
As shown in equation (2.2), the mean curvature of the hypersurfaces near the head point is given by , thus a singularity appears when . If , then the section curve collapses, and singularity appears at the geodesic hypersphere. Now we assume neither of the above happens, and we want to show that is not a singular time.
We prove by contradiction and assume that a singularity appears at time . By Corollary 3.5, . We claim that there exists such that for all . Otherwise there exists a sequence in such that . Up to extracting from a subsequence, we can assume converges to . Since , , and a singularity appears at the origin at time , which is a contradiction.
By a similar argument, we can also assume that for all .
For any , by Lemma 3.6, we know . Let , we know .
We claim that is smooth at . This follows from , a priori estimate for in Lemma 3.4, and hence (see [LSU68]) for all higher derivatives of in the interior. Therefore the singularity can only appear on the boundary, i.e. at .
Now consider the horizontal graph function , which is defined for , , and we can extend this function smoothly on to by the symmetry. This function is uniformly bounded by the height of the initial condition, and it is a solution of the horizontal graph equation. Let , for any , consider the flow of on . By Lemma 3.7, , as well as all higher space derivatives of , are uniformly bounded on the region . Hence uniformly in as . We have also shown that is uniformly bounded for , , hence cannot be a singular point.
∎
In the following proposition, we show that the appearance of the singularity on the boundary (i.e. the rotation axis in the manifold) is an open condition.
Proposition 3.9.
Let denote the set of function such that the solution to the equation (2.2) with initial condition becomes singular in finite time, and for some , then is an open set in with respect to the norm.
Proof.
The idea is similar to the proof of [CS23, Proposition 3.10]. We can isometrically embed into . Then the mean curvature flow corresponds to in can be interpreted as a mean curvature flow with additional force in . We refer the readers to [HZ23] for some properties of mean curvature flow with additional force. In particular, by the classification of rotationally symmetric self-shrinkers, the tangent flow at the singular point of is modeled by a cylinder . That says, if we dilate the half-space by , then for any , the profile curve of will converge to the straight line as in .
By the smooth dependence of the initial data, for any , if is sufficiently close to in , then the mean curvature flow will be very close to on , in particular, also very close to the straight line in . Then using the appropriate dilation of the -Angenent curve as a barrier, we see that can only have singularity on the rotation axis. This shows the openness of . ∎
3.2. Interpolation family of hypersurfaces
In this section, we construct an immortal flow using the interpolation argument. By Lemma 2.2, there exists such that . Then for the spherical catenoid constructed in Section 2.2 with parameter , the restriction of its profile curve onto the region has a connected segment that joins the head point and . We denote this segment of the profile curve by .
Next, we introduce two constants . The Angenent curve is constructed in Appendix B, we will let in the following. We can choose a constant and dilate the Angenent curve such that the upper half of the dilated Angenent curve is contained in the region , and we denote this segment of curve as , and let be the time at which collapses to a point under mean curvature flow. We choose a constant such that is on top of the curve .
We consider a family of initial data that forms a smooth foliation of a subset of the region . is the graph of an increasing smooth function with vertical graph function and horizontal graph function . After reflecting with respect to the lines and , we get a smooth curve in , in other word, all odd order derivatives of at and at vanish. also has the following properties:
| (3.5) |
| (3.6) |
By property (3.5) and the fact that forms a foliation, we know for , the curve is on top of . By property (3.6), the height of is , since , thus the height of is at most . Therefore by property (3.5) and the choice of , is on top of .
Let be the family of solutions to the equation (2.2) with initial data . Denote the vertical graph function and the horizontal graph function of by .
Lemma 3.10.
Given , if , then for all time before the singularity occurs.
Proof.
Since , we know the height of is less than . By Lemma 3.2, we know for all time .
If at some time before the singularity occurs, then by the choice of , is on top of the graph of . Then by Theorem 2.1, is on top of the graph of for all time , which implies that for all . We get a contradiction with the assumption .
∎
We are now ready to prove the existence of an immortal flow on . We first sketch the picture of the two main comparison results that are used to apply the interpolation argument, See Figure 3. We compare the family of initial data to the curves and . The head point of the initial curve in the first picture will tend to in finite time, meanwhile, the initial curve in the second picture will remain away from before the singular time.
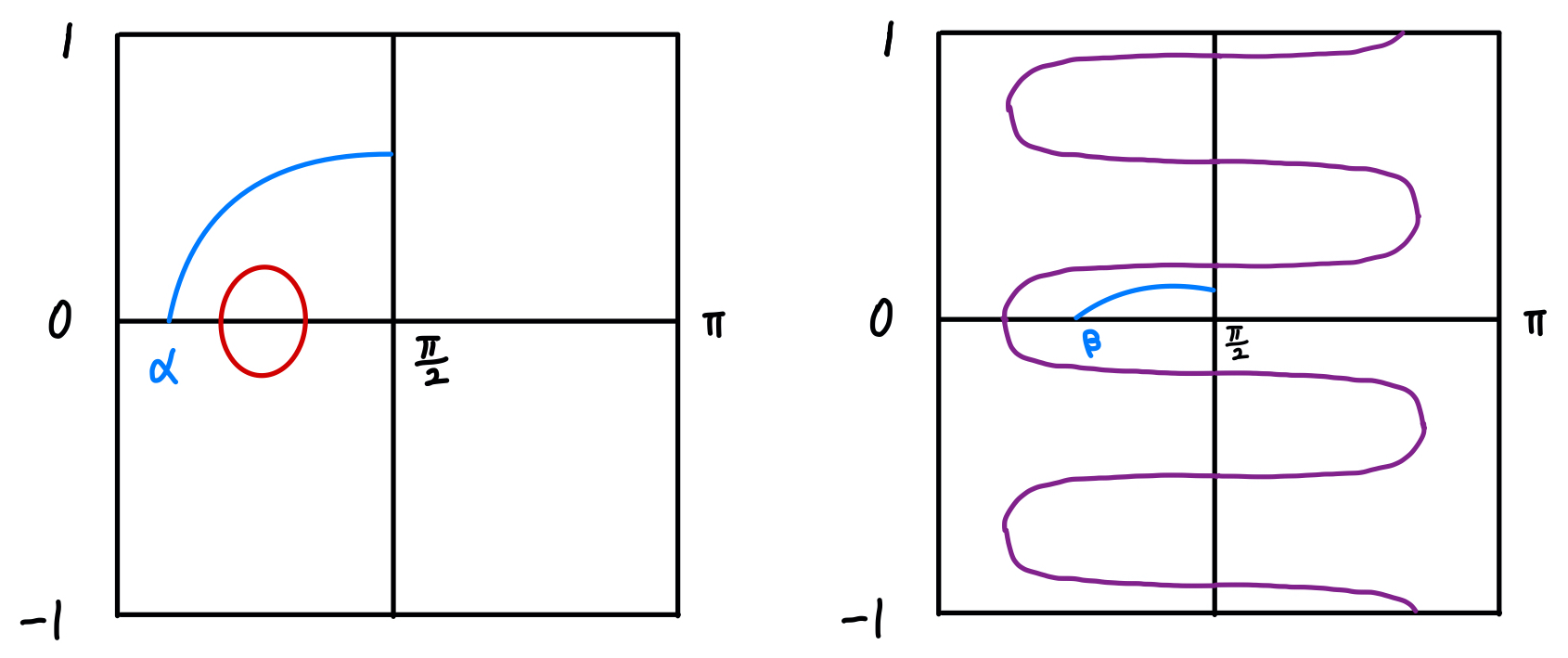
Theorem 3.11.
There exists an immortal nonstatic rotationally symmetric mean curvature flow of hypersurfaces in .
Proof.
For , we know that the curve is on top of . We restricted the curve and onto the region , and view these two segments as the graph of a function of . In this region, the function value is bounded above by , thus
Hence (i.e., the solution to (B.2) with initial condition ) is a supersolution to the vertical graph equation, and initially is on top of the curve . By maximum principle, remains on top of the graph of for all time . The head point of the Angenent curve tends to in finite time , which forces at some time . By Proposition 2.1, if in finite time, then in finite time for all .
For , is on top of the curve . By Proposition 2.1, is on top of the graph of for all time , which implies for all .
Hence, by continuous dependence of the initial data (see e.g. [Ama88]) and Proposition 3.9, there exists a maximal interval such that for any within this interval, converges to in finite time. As indicated in the preceding argument, . By Proposition 2.1 and Proposition 3.8, the singular time is strictly increasing in , and its limit as has to be , otherwise will converge to in finite time by the continuous dependence. By the selection of , never reaches in finite time. Combining this with Lemma 3.10, we conclude that for and , we have . By continuous dependence and the fact that , we can deduce that for all .
As a result, does not converge to either or within any finite time, by Proposition 3.8, the solutions and exist for all time .
∎
3.3. Multiplicity convergence
From the construction above, we know that the solution to the equation (2.2) exists for all time . In the following, we will show the mean curvature flow induced from will converge to the minimal sphere with multiplicity . In fact, outside a neighborhood of the north pole and south pole of , we can show the mean curvature flow has two connected components, and each component converges to outside a neighborhood of the north pole and south pole smoothly.
By a similar height decreasing argument as in [CS23, Lemma 3.15], we show that the head point of the function converges to as , i.e. . We can also use as a barrier to obtain a linear upper bound of the function .
Lemma 3.12.
for all and .
Proof.
We prove this by contradiction. Suppose not, then for some , , then the graph of is on top of the dilated Angenent curve , which implies that has a finite time singularities. This is a contradiction. ∎
We are ready to prove the key long-time gradient estimate of .
Proposition 3.13.
Given , for any , there exist a constant depending on , and a time depending on , such that
for all , . In addition, .
Proof.
Given any . Since , we know that there exists such that for any , . Then is a smooth function over for all . For simplicity, we will use to express the function restricted on the interval , which is smooth for all time . We know
Let , , . Then , and . Then
Moreover,
Therefore,
| (3.7) |
Let and be a positive constant to be determined later. Define . Then for , , we have
Then
Since , we have , and there exists such that for all . Let , then for , ; for , .
Thus
Now we can apply the parabolic maximum principle to conclude that for all and . On the other hand, for any ,
Thus there exists such that for all and , . In summary, for , , we have the gradient estimate
| (3.8) |
Next, integrating this gradient bound yields
Let ,
Let ,
Since can be chosen arbitrarily small, we have .
∎
The gradient estimate yields the following two corollaries, which can be combined to show that will converge to .
Corollary 3.14.
converges to uniformly as , for all .
Proof.
Let , we get . Since is a strictly increasing function, thus converges to as and this convergence is uniform in .
∎
Corollary 3.15.
Given , converges to uniformly as , for all .
Proof.
For any , there exists and such that , and . Let , be as determined in Proposition 3.13. Then there exists such that for , . By Proposition 3.13, for , ,
∎
Let denote the desired hypersurface with the graph of as its section curve.
Theorem 3.16.
is an immortal mean curvature flow on , and the forward limit of this flow is the minimal sphere with multiplicity .
Proof.
Following from the proof of Theorem 3.11, we only need to prove that for any , converges to in . Given , we know that there exists such that for . So is well defined for all . By Lemma 3.12, is contained in the rectangle for . By Corollary 3.14 and 3.15, we know converges to as . This completes the proof.
∎
Appendix A Curves in the plane with conformal metrics
Given a function defined on an open subset of the plane, let us consider the metric , and the corresponding Levi-Civita connection . We present some computations related to curves in in this section.
By standard calculations, we can write down the Christoffel symbols:
Suppose is a -curve, where can be an interval or . We consider the coordinate expression . Then and the length of is . Let . Then the geodesic curvature vector of is given by
| (A.1) |
Choose the unit normal vector field , where is the normal vector of the curve in the Euclidean metric. This implies that
Therefore, the curvature vector is given by
| (A.2) |
Note that we can interpret this as
| (A.3) |
where and are the curvature and normal projection of the gradient of the curve under the Euclidean metric respectively.
Example A.1.
Consider only depending on . Suppose is chosen such that the curves in give the area of the hypersurface that is rotating the curve in some Riemannian manifold, for example, (gives the area of rotationally symmetric hypersurfaces in ) or (gives the area of rotationally symmetric hypersurfaces in ). Suppose the curve is .
After taking the quotient of action, we identify the mean curvature vector as , and the unit normal vector as . Then from the first variational formula, we have , and . After taking the quotient of the mean curvature flow of the hypersurfaces, the profile curves satisfy the equation
| (A.4) |
Under the conformal metric, this can be expressed as
| (A.5) |
Notice that this curvature flow is different from the curve shortening flow under the metric up to the conformal factor.
Now we derive the equation of the graphs under this flow. Suppose , we obtain that
| (A.6) |
Plugging in , , , gives
| (A.7) |
Similarly, suppose , we have
| (A.8) |
Appendix B -Angenent curves
Let . Consider the metric with , defined on the right half plane . We call a closed embedded geodesic under the metric a -Angenent curve. When , rotating the curves by action gives the Angenent doughnut in .
Suppose is a -Angenent curve. Let
for . Because is a geodesic under the metric , following the computations in Section A, we have .
From now on we will use the Euclidean coordinates on . Suppose is a parametrization of a part of , then . Therefore we can conclude that
being a geodesic implies that
namely
| (B.1) |
In summary, we obtain the equation
| (B.2) |
Angenent proved the existence of a simple closed -Angenent curve in [Ang92]. To have the same notation as [Ang92], let us temporarily change the domain of the right-half plane to the upper-half plane by a rotation, and we use the as the coordinate in the upper-half plane. Namely, we want to construct a simple closed geodesic in the upper-half plane equipped with the metric . Although in [Ang92], Angenent only discussed the cases that for positive integers , the proof indeed works for general verbatim, by replacing in [Ang92, Page 9-16] by . We refer the readers to [Ang92] for the proof.
It is worth noting that Drugan-Nguyen [DN18] also constructed shrinking doughnuts using a variational method. It is still an open question that whether their construction coincides with Angenent’s construction. It seems that their method can also be applied to construct -Angenent curves.
References
- [AAG95] Steven Altschuler, Sigurd B. Angenent, and Yoshikazu Giga. Mean curvature flow through singularities for surfaces of rotation. J. Geom. Anal., 5(3):293–358, 1995.
- [Ama88] Herbert Amann. Dynamic theory of quasilinear parabolic equations. I. Abstract evolution equations. Nonlinear Anal., 12(9):895–919, 1988.
- [Ang92] Sigurd B Angenent. Shrinking doughnuts. In Nonlinear diffusion equations and their equilibrium states, 3, pages 21–38. Springer, 1992.
- [BHH19] Reto Buzano, Robert Haslhofer, and Or Hershkovits. The moduli space of two-convex embedded tori. Int. Math. Res. Not. IMRN, (2):392–406, 2019.
- [BHH21] Reto Buzano, Robert Haslhofer, and Or Hershkovits. The moduli space of two-convex embedded spheres. J. Differential Geom., 118(2):189–221, 2021.
- [BK23] Richard H Bamler and Bruce Kleiner. On the multiplicity one conjecture for mean curvature flows of surfaces. arXiv preprint arXiv:2312.02106, 2023.
- [BM12] Alexander A. Borisenko and Vicente Miquel. Mean curvature flow of graphs in warped products. Trans. Amer. Math. Soc., 364(9):4551–4587, 2012.
- [CH10] Jingyi Chen and Weiyong He. A note on singular time of mean curvature flow. Math. Z., 266(4):921–931, 2010.
- [CS23] Jingwen Chen and Ao Sun. Mean curvature flow with multiplicity 2 convergence. arXiv preprint arXiv:2312.17457, 2023.
- [DN18] Gregory Drugan and Xuan Hien Nguyen. Shrinking doughnuts via variational methods. J. Geom. Anal., 28(4):3725–3746, 2018.
- [ES92] Lawrence C Evans and Joel Spruck. Motion of level sets by mean curvature iii. The Journal of Geometric Analysis, 2(2):121–150, 1992.
- [GLP21] Marco AM Guaraco, Vanderson Lima, and Franco Vargas Pallete. Mean curvature flow in homology and foliations of hyperbolic -manifolds. arXiv preprint arXiv:2105.07504, 2021.
- [Gra89] Matthew A. Grayson. Shortening embedded curves. Ann. of Math. (2), 129(1):71–111, 1989.
- [HK19] Robert Haslhofer and Daniel Ketover. Minimal 2-spheres in 3-spheres. Duke Math. J., 168(10):1929–1975, 2019.
- [Hui84] Gerhard Huisken. Flow by mean curvature of convex surfaces into spheres. J. Differential Geom., 20(1):237–266, 1984.
- [HZ23] Sven Hirsch and Jonathan J Zhu. Uniqueness of blowups for forced mean curvature flow. arXiv preprint arXiv:2310.08005, 2023.
- [LSU68] Olga Aleksandrovna Ladyzhenskaia, Vsevolod Alekseevich Solonnikov, and Nina N Ural’tseva. Linear and quasi-linear equations of parabolic type, volume 23. American Mathematical Soc., 1968.
- [Wan02] Mu-Tao Wang. Long-time existence and convergence of graphic mean curvature flow in arbitrary codimension. Invent. Math., 148(3):525–543, 2002.
- [WZ22] Zhichao Wang and Xin Zhou. Min-max minimal hypersurfaces with higher multiplicity. arXiv preprint arXiv:2201.06154, 2022.
- [WZ23] Zhichao Wang and Xin Zhou. Existence of four minimal spheres in with a bumpy metric. arXiv preprint arXiv:2305.08755, 2023.
- [Zho20] Xin Zhou. On the multiplicity one conjecture in min-max theory. Ann. of Math. (2), 192(3):767–820, 2020.