Mean field limits of particle-based stochastic reaction-drift-diffusion models
Abstract.
We consider particle-based stochastic reaction-drift-diffusion models where particles move via diffusion and drift induced by one- and two-body potential interactions. The dynamics of the particles are formulated as measure-valued stochastic processes (MVSPs), which describe the evolution of the singular, stochastic concentration fields of each chemical species. The mean field large population limit of such models is derived and proven, giving coarse-grained deterministic partial integro-differential equations (PIDEs) for the limiting deterministic concentration fields’ dynamics. We generalize previous studies on the mean field limit of models involving only diffusive motion, with care to formulating the MVSP representation to ensure detailed balance of reversible reactions in the presence of potentials. Our work illustrates the more general set of PIDEs that arise in the mean field limit, demonstrating that the limiting macroscopic reactive interaction terms for reversible reactions obtain additional nonlinear concentration-dependent coefficients compared to the purely diffusive case. Numerical studies are presented which illustrate that two-body repulsive potential interactions can have a significant impact on the reaction dynamics, and also demonstrate the empirical numerical convergence of solutions to the PBSRDD model to the derived mean field PIDEs as the population size increases.
1. Introduction
We consider particle-based stochastic reaction-drift-diffusion (PBSRDD) models where particles move via diffusion and drift induced by one- and two-body potential interactions. We formulate the dynamics of the particles as measure-valued stochastic processes (MVSPs), which describe the stochastic evolution of the concentration fields of each chemical species as a sum of functions encoding the position and type of each particle. Our goal is to formulate an appropriate MVSP model for such systems, and then rigorously investigate the large population limit of the MVSP dynamics, deriving partial-integral differential equations (PIDEs) that represent the limiting mean-field dynamics.
Particle-based stochastic reaction-diffusion (PBSRD) models have a long history of use in modeling the diffusion of, and reactions between, individual molecules. PBSRDD models are more macroscopic descriptions than millisecond-timescale quantum mechanical or molecular dynamics models of a few molecules [42], but more microscopic descriptions than deterministic 3D reaction-diffusion PDEs for the average concentration field of each chemical species. One of the most popular PBSRDD models for studying biological processes is the volume reactivity (VR) model of Doi [47, 9, 10]. In the Doi model, the positions of individual molecules are typically represented as points undergoing Brownian motion. Bimolecular reactions between two substrate molecules occur with a probability per unit time based on their current positions [9, 10]. Unimolecular reactions are typically assumed to represent internal processes, and as such are modeled as occurring with exponentially distributed times based on a specified reaction-rate constant.
In our prior work [28], we investigated the large population limit of PBSRD models (i.e. in the absence of drift). Allowing drift makes the models more relevant for applications, but complicates the model formulation and the analysis needed to prove the mean field limit. Many models of biological systems involve drift induced by background potential fields and/or by potential interactions. In modeling cellular processes, the former has been used to model how volume exclusion by DNA fibers impedes protein diffusion in the nucleus [29, 32], and to model membrane-bound protein motion induced by actin contraction in T cell synapses [43]. Two-body potential interaction fields have been used to more accurately account for attractive or repulsive interactions between molecules [23], including to model volume exclusion due to the physical size of molecules [4, 43]. More generally, such interactions can arise in diverse classes of agent-based models including models for the spread of infections or innovations within populations [20], or for interactions between cells. In addition, as our numerical studies in Section 7 demonstrate, the inclusion of potential interactions can have non-trivial effects on the behavior of the system. We therefore now investigate the large population limit PBSRDD models where particles move via diffusion and drift term induced by one-body and two-body potentials.
For simplicity, we will work in free space as in [28, 27], and as such, we will study the large population mean field limit via an increasing scaling parameter, , which can physically represent Avogadro’s number. The “large system size” limit is where one typically obtains more macroscopic coarse-grained partial-integral differential equation (PIDE), PDE, SPIDE, or SPDE models for biological systems that model diffusion and reaction via the evolution of continuous concentration fields [18, 28, 2, 36, 20, 38, 40]. To determine the limit for PBSRDD models we adopt the classical Stroock-Varadhan Martingale approach [12, 46] that previously allowed us to rigorously identify and prove the large population limit of the MVSP representation for PBSRDD models [28]. We note that this method has been successful in many instances to study large population dynamics and general interacting particle systems, see [14, 15, 6, 7, 8, 25, 37, 44]. We identify a new macroscopic system of partial integro-differential equations (PIDEs) whose solution corresponds to the large population limit of the MVSP, and we rigorously prove the convergence (in a weak sense) of the MVSP to this solution.
We also note here that the bottom-up approach that we take in this paper allows us to derive the new macroscopic PIDEs corresponding to the true population limit of the underlying spatial PBSRDD model. This is to be contrasted with the well-known macroscopic reaction-drift-diffusion PDE models of chemical reactions at a cellular scale, which are often derived by modifying standard ODE models for non-spatial reaction systems via the addition of drift-diffusion operators to give a (phenomenological) spatial model. Note, in the absence of potential interactions (i.e., particles move only via diffusion), in [27] we proved that such models can be seen as limits of the rigorous mean field limit we derived in [28] when bimolecular reaction kernels are short-range and averaging.
For our model, consider to be the set of indices of particles of species . In the absence of reactions, suppose that the th particle is of species and located at position at time . The th particle then moves according to
| (1) | ||||
Here denotes the one-body potential experienced by a particle of type when at position , and the two-body potential between particles at locations and of types and respectively. denotes the total number of particles at time , and is a vector consisting of the mean field limit scaling parameter, , and a displacement range parameter, . In the large population mean field limit, plays the role of a system size (e.g., Avogadro’s number, or in bounded domains the product of Avogadro’s number and the domain volume)[1]. represents a regularization parameter we introduce to rigorously handle -function placement densities for reaction products, which are commonly used in many PBSRDD models, see Section 5. Finally, represents the diffusion coefficient for a particle of species , and is a countable collection of standard independent Brownian motions in .
From (1), we see each particle follows the gradient of a potential landscape, the so-called suitability landscape, and also experiences an additional force derived from the two-body potentials. The scaling in front of the pair-wise potentials is the mean field scaling, which, at least formally, preserves the total strength of the interaction at order one so that we have a well-defined large population mean field limit in the absence of reactions, see [33].
From a mathematical point of view, adding drift due to potential interactions makes the rigorous formulation of the particle model more complicated, and gives rise to a number of new terms that need to be appropriately handled for a coarse-grained mean field limit to exist. Specifically, in moving from PBSRD (purely-diffusive) to PBSRDD models (drift due to potential interactions) reactive interaction functions, which determine the probability per time substrates react and produce products at specified positions, may require modification. Such modifications ensure detailed balance of reaction fluxes, i.e., the statistical mechanical property that the pointwise forward and backward reaction fluxes should balance at equilibrium [31, 13, 17]. When formulating PBSRDD reactive interaction terms to be consistent with detailed balance at equilibrium, the needed modifications result in a dependence on the full potential of the system (hence adding a dependence on the positions of non-reactant particles). We specifically formulate these modifications as an extra rejection/acceptance probability appearing within reactive interaction functions, following the approach proposed in [13], but note our results should be straightforward to adapt should one instead modify reaction rates or product placement mechanisms to ensure detailed balance. One of the contributions of this work is that we make all of these modifications precise in a general fashion via the MVSP formulation. We illustrate our results for a specific, but important, choice of rejection/acceptance probabilities based on the functional choices proposed by Fröhner and Noé [13]. The modified reactive interaction functions we employ then give rise to additional nonlinear concentration-dependent coefficients within the limiting reactive terms of the resulting mean field PIDEs, giving rise to a new deterministic, macroscopic reaction-drift-diffusion model.
To illustrate the main result of this paper, consider the reversible reaction as an example. Denote the forward reaction by and the backward reaction by . Let us represent by the stochastic process for the number of species A molecules at time , and label the position of th molecule of species A at time by the stochastic process . The quantity
corresponds to the stochastic, singular molar concentration field of species A at point at time . We define and in a similar fashion, and let . For each species we assume a spatially-constant diffusivity, and , respectively.
For , let denote the probability per time that one A molecule at and one molecule at react. The product molecule is then placed at following the probability density , conditioning on substrates at and . Here the displacement range parameter represents a mollification parameter for singular -function placement densities. We further incorporate a rejection/acceptance mechanism via an acceptance probability , which indicates the probability that the above reaction is accepted, i.e. alllowed to occur, and generates a product at given the positions of the substrates at and , and of the non-substrate and non-product particles molecules at . We define and analogously for the reverse reaction . Finally, we assume that the acceptance probabilities can be equivalently rewritten as a function of the substrate positions, product positions, and the pre-reaction concentration fields, and . In Section 6 we illustrate that this assumption holds for the specific choices of rejection/acceptance probabilities proposed in [13].
Note that and all depend on . In the large population limit that and jointly, denoted as , let and denote their respective (possibly rescaled) limits. We will specify our assumptions on the mean field limits and scalings of , , and , as well as specific functional examples for them, in Sections 2, 4 and 6.
In this work, we derive the large population (thermodynamic) limit and prove, in a weak sense, that as ,
with representing the limiting deterministic mean-field molar concentration fields. The latter satisfy the system of reaction-drift-diffusion PIDEs that
The paper is organized as follows. In Section 2, we go over the notation and definitions that are used throughout this work. We then present the stochastic equation for the PBSRDD model, which describes the evolution of the empirical measure (MVSP) of the chemical species in path space, in Section 3. In Section 4, we summarize the basic assumptions we make about the form of the reaction rate functions, product placement densities, and acceptance probabilities. In Section 5, we present our main result on the mean field limit, Theorem 5.1, which describes the evolution equation satisfied by the empirical measures for the molar concentration of each species in the large population limit for general reaction networks. As illustrative examples, we also present the mean field limits for specific chemical systems. In Section 6, we discuss a specific formulation of the acceptance probability in the generalized Fröhner-Noé model [13], and examine its large-population limit. We also examine a number of reversible reactions and give the corresponding acceptance probabilities. In Section 7, we present numerical studies illustrating the empirical convergence of numerical solutions to the PBSRDD model to the derived mean field PIDEs as . Our numerical examples also demonstrate that the potential interactions can have significant impacts on the statistical and dynamical behavior of the system. Finally, in Section 8, we give the proof of Theorem 5.1. Appendix 9 includes the verification that the Fröhner-Noé type of acceptance probabilities satisfy the relevant assumptions made in Section 4, and provides the proof of a mollification-type result used in Section 8.
2. Notations and preliminary definitions
We consider a collection of particles with different types, and for the rest of the paper, we will interchangeably use the terms particle or molecule and type or species. Let denote the set of different possible types, with the value of the species of the th particle. We also assume an underlying probability triple, , on which all random variables are defined.
In our model, molecules diffuse in space subject to drift arising from potential interactions, and can undergo possible types of reactions, denoted as . We use non-negative integer stoichiometric coefficients and to describe the th reaction, , as
and the multi-index vectors and to collect the coefficients of the th reaction. We denote the substrate and product orders of the reaction by and . The implicit assumption that all reactions are at most second order is justified by the assumption that the probability that three substrates in a dilute system simultaneously have the proper configuration and energy levels to react is small. It is further justified since reactions of order three and above are often considered to be approximations of sequences of bimolecular reactions in biological models. For subsequent notational purposes, we label the reactions such that the first reactions correspond to those that have no products, i.e., annihilation reactions of the form
for . We assume that the remaining reactions have one or more product particles.
Let label the diffusion coefficient for the th particle, taking values in , where is the diffusion coefficient for species . We assume drift is imparted to particles via one- and two-body potentials. Let denote a background potential that imparts drift to a particle of species located at . Similarly, we let represent a two-body potential experienced between a particle of species at and a particle of species at . Note, the inverse scaling here is the standard mean field scaling to keep the total strength of the interaction fixed as more particles are added in the mean field limit [33]. We denote by the position of the th particle, , at time . In the absence of reactions, the dynamics for are governed by (1). A particle’s state can be represented as a vector in , the combined space encoding particle position and type. This state vector is subsequently denoted by .
We now formulate our representation for the (number) concentration, equivalently number density, fields of each species. Let be a complete metric space and the collection of measures on . Let be the subset of consisting of all finite, non-negative point measures of the form
For and , define
We will frequently have , in which case we omit the subscript and simply write . For each , we define the concentration (i.e., number density) of particles in the system at time by the distribution
| (3) |
where borrowing notation from [3], represents the stochastic process for the total number of particles at time . To investigate the behavior of different types of particles, we denote the marginal distribution on the th type, i.e., the concentration field for species , by
a distribution on . will similarly label the total number of particles of type at time . Note that in the remainder, in any rigorous calculation and will be measures and treated as such. We will, however, abuse notation and also refer to them as concentration fields, i.e., number densities. Strictly speaking, the latter should refer to the densities associated with such measures, but we ignore this distinction in subsequent discussions. For any fixed particle distribution of the form (3), we will also use an alternative representation in terms of the marginal distributions for particles of type ,
| (4) |
In considering the mean field large population limit, we will take a simultaneous limit in which the population scaling parameter , and the (convenience) displacement range parameter (see Section 4 for the definition of the latter). As mentioned in the introduction, this dual limit is encoded via the vector limit parameter
In studying this limit we will work with rescaled measures for each species, denoted by
When corresponds to Avogadro’s number, physically corresponds to the measure for which the associated density would represent the molar concentration field for species at time (but we will again abuse notation and also refer to as the molar concentration field). We similarly let
and define the vector of the molar concentrations for each species by
In the remainder, we will often write and to make explicit that and depend on .
In addition to having notations for representing particle concentration fields, we will also use state vectors to store the positions of particles of a given type. Define the particle index maps , which encode a fixed ordering for the positions of particles of species , , arising from an (assumed) fixed underlying ordering on . Following the notation established in [3] (see Section 6.3 therein), we let and let such that
| (5) |
represents the position state vector for type particles. We analogously let label the th entry of the vector . Note that the zero entries after the term merely serve as placeholders. As commented in [3], this function allows us to address a notational issue. In particular, choosing a particle of a type uniformly among all particles in amounts to choosing an index uniformly in the set , and then choosing the individual particle from the arbitrary fixed ordering.
As particles of the same type are assumed indistinguishable, there is no ambiguity in the value of in the case that two particles of type have the same position. Using this notation we will often write the marginal distribution of species as
| (6) |
With the preceding definitions, and analogously to [28], we introduce a system of notation to encode substrate and particle positions and configurations that are needed to later specify reaction processes.
Definition 2.1.
To describe the dynamics of , we will sample vectors containing the indices of the specific substrate particles participating in a single -type reaction from the substrate index space
For the allowable reactions considered in this work, we label the elements of according to their species types:
-
(1)
For of the form
-
(2)
For of the form
-
(3)
For of the form with
-
(4)
For of the form
We write a particular sampled set of substrate indices as
Definition 2.2.
We define the substrate particle position space analogously to as
with an element represented by . For , a sampled substrate position configuration for one individual reaction, then labels the sampled position for the th substrate particle of species involved in the reaction. Let be the corresponding volume form on which also naturally defines an associated Lebesgue measure.
Definition 2.3.
For reaction with , i.e., having at least one product particle, define the product position space analogously to ,
with an element written as . For a sampled product position configuration for one individual reaction, then labels the sampled position for the th product particle of species involved in the reaction. Let be the corresponding volume form on , which also naturally defines an associated Lebesgue measure.
Definition 2.4.
Consider a fixed reaction , with and corresponding to a fixed particle distribution given by (3) with representation (4). We define the th projection mapping as
When substrates with indices in particle distribution are chosen to undergo a reaction of type then gives the vector of the corresponding substrate particles’ positions. For simplicity of notation, in the remainder, we will sometimes evaluate with inconsistent particle distributions and index vectors. In all of these cases the inconsistency will occur in terms that are zero, and hence not matter in any practical way.
Definition 2.5.
Consider a fixed reaction , with a fixed particle distribution given by (3) with representation (4). Using the notation of Definition 2.1, we define the allowable substrate index sampling space as
Note that in the calculations that follow will change over time due to the fact that changes over time, but this will not be explicitly denoted for notational convenience.
Definition 2.6.
Consider a fixed reaction , with any element of with the representation (4). We define the th substrate measure mapping evaluated at via
Definition 2.7.
For reaction , define a subspace by removing all particle substrate position vectors in for which two particles of the same species have the same position. That is
3. Generator and process level description
To formulate the process-level model, it is necessary to specify more concretely the reaction process between individual particles. We make assumptions on and that are analogous to what we assumed in the introduction for the reaction.
For reaction , denote by the rate (i.e., probability per time) that substrate particles with positions react. As described in the next section, we assume this rate function has a specific scaling dependence on . Let be the placement density when the substrates at react and generate products at . We assume that for each and fixed is bounded. We let denote the probability that a candidate reaction between the substrates located at , given the non-substrate and non-product particles at , is accepted and produces products at . We assume that this acceptance probability can equivalently be written in terms of , , and the molar concentration of each species (rather than the specific positions, of each non-substrate and non-product particle). Therefore, we will usually write the acceptance probability as . Note that we assume the acceptance probability may have an explicit dependence on . See Section 6 for explicit examples that demonstrate this dependence.
To describe a reaction with no products, i.e., , we associate with it a Poisson point measure on . Here gives the sampled substrate configuration, with labeling the th sampled index of species . The corresponding intensity measure of is given by . Analogously, for each reaction with products, i.e., , we associate with it a Poisson point measure on . Here gives the sampled substrate configuration, with labeling the th sampled index of species . gives the sampled product configuration, with labeling the sampled position for the th newly created particle of species . The corresponding intensity measure is given by
The existence of the Poisson point measure follows as the intensity measure is -finite (see Theorem in [24] or Corollary in [35]). Let be the compensated Poisson measure, for . For any measurable set such that , which is true if for example A is bounded, is a Poisson process and is a martingale (see Proposition in [35]). Similarly, we can define , for . In this case, given any measurable set such that , we then have that is a Poisson process and is a martingale.
3.1. Process level description.
We now formulate a weak representation for the time evolution of scaled empirical measures , . Denote by a countable collection of standard independent Brownian motions in . For a test function and for each species , a weak representation of the dynamics of are given by (see also (23)),
| (7) |
Formula (7) captures the dynamics of our particle system. Recall that here denotes the total number of particles in the system at time , with the number of particles of type at time . labels the diffusion coefficient for the th molecule, taking values in , where is the diffusion coefficient for species . The drift and diffusion of each particle are modeled by the four integrals on the first four lines of (7). The fifth to sixth lines model reactions with no products, while the seventh to ninth lines model reactions with products. The integrals involving the Poisson measures model the different components of the reaction processes, and correspond to sampling the times at which reactions occur, which substrate particles react, where reaction products are placed, and whether the proposed reaction is accepted.
When the th reaction happens for (and analogously for ), with probability per time given by the kernel , the system loses substrate particles and gains product particles. A sampling of possible reaction occurrences according to occurs through the indicator functions on the sixth and eighth lines. The corresponding loss and gain of particles are encoded by the sums of delta functions on the fifth and seventh lines. Product positions are sampled according to the placement density through the indicator function on the eighth line. For reactions with products, the reaction then fires according to the acceptance probability through the indicator function on the ninth line. The indicators over elements of the sets ensure that reactions can only occur between particles that correspond to a possible set of substrates. We access particle positions via the state vector , as the particle labeled by in (7) will change dynamically as reactions occur.
For a test function and for each species , let us define the following generators for the drift-diffusion of particles
| (8) |
and the corresponding formal adjoint operators,
| (9) |
We will subsequently assume that is uniformly bounded in time in Assumption 4.1. The stochastic integral with respect to Brownian motion in is then a martingale for a fixed . Taking the expectation, we obtain for the mean that
4. Assumptions for the Mean Field Limit and Main Results
4.1. Assumptions for the Mean Field Limit.
With the introduction of general one and two-body drift terms, we will constrain our choices of the potential functions, the reaction kernels, placement densities, and acceptance probabilities through the following assumptions, along with assuming some basic properties of the underlying reaction network.
4.1.1. Assumptions on the molar concentration fields
Assumption 4.1.
We assume that the total (molar) population concentration satisfies for all , i.e., is uniformly in time bounded by some constant .
Assumption 4.2.
We assume that for all , the initial distribution weakly as , where is a compactly supported measure with finite mass.
4.1.2. Assumptions on potentials
Assumption 4.3.
For all and , the one-body potential and the (unscaled) pairwise potential have bounded and function norms respectively, i.e., there is some constant such that for all and
4.1.3. Assumptions on reaction functions, placement densities and acceptance probabilities
Assumption 4.4.
We assume that for all , the reaction rate kernel is uniformly bounded for all , and denote generic constants dependent upon this bound by .
Assumption 4.5.
The reaction kernel is assumed to have the explicit dependence that
for any . See [28] for motivation and further details on this choice.
Assumption 4.6.
We assume that for any and , the placement density is uniformly bounded in and , and is a probability density in , i.e., .
To define placement densities in terms of delta-functions in a mathematically rigorous way, we introduce the displacement (i.e., smoothing) range parameter in order to mollify the limiting Dirac delta densities in the standard way.
Definition 4.1.
For , let denote a standard positive mollifier and . That is, is a smooth function on satisfying the following four requirements
-
(1)
;
-
(2)
is compactly supported in , the unit ball in ;
-
(3)
;
-
(4)
, where is the Dirac delta function and the limit is taken in the space of Schwartz distributions.
The allowable forms of the placement density for each possible reaction are summarized below.
Assumption 4.7.
The distributional limit of as is given by , a linear combination of Dirac delta functions, for any and .
-
(1)
For a first order reaction of the form , we assume that the placement density takes the mollified form of
with the distributional limit as given by
-
(2)
For a first-order reaction of the form , we assume that the unbinding displacement density is in the mollified form of
and the distributional limit as is given by
with for and .
-
(3)
For a second order reaction of the form we assume that the binding placement density takes the mollified form of
and the distributional limit as is given by
with for and .
-
(4)
For a second order reaction of the form ,we assume that the placement density takes the mollified form of
and the distributional limit as is given by
with
Remark 4.1.
We mention here that even though in Assumption 4.7 the placement density is assumed to depend only on the regularizing parameter , it is physically possible that it can also depend on the scaling parameter . We will see such an instance in Remark 6.3. It will be shown there the dependence is typically such that it is inconsequential for the limit as , and as such, we have chosen not to explicitly denote it for simplicity of exposition.
Assumption 4.8.
For (4.6) to be true, we will need the probability density to be normalized, i.e.
Since is a probability density, the previous condition implies that the tail probability
for any when is chosen sufficiently large.
Finally, we summarize assumed properties of the pre- and post-limit acceptance probabilities, and respectively. An explicit example of such probabilities is provided in Section 6. Let be the space of finite measures endowed with the weak topology and be the space of càdlàg paths with values in endowed with Skorokhod topology. As we will work with subsets of in which the measure of is uniformly bounded, we also let
| (10) |
Definition 4.2.
For a complete measurable space , we define the variation norm of finite measures on as
One can show via a density argument that an equivalent formulation is (see step 4 of Theorem 3.2 of [34])
Assumption 4.9.
We assume that for any and , both in , the acceptance probability is bounded and Lipschitz continuous with Lipschitz constant , i.e.,
| (11) |
Assumption 4.10.
We assume that for any and , the acceptance probability is bounded and Lipschitz continuous with Lipschitz constant , i.e.,
| (12) |
Assumption 4.11.
We assume that for any and , converges to uniformly as with respect to ; equivalently,
| (13) |
5. Mean field limit and examples.
Denote by
the limiting measures. Our main result is then
Theorem 5.1.
Remark 5.1.
If the limiting measures have marginal densities , then these marginals solve, in a weak sense, the following reaction-diffusion PIDEs
We now present a few examples to illustrate the limiting PIDEs for basic reaction types:
Example 5.1.
Consider a system with three species, , , and that can undergo the reversible reaction . Define the measures for , , and particles at time respectively as and .
Let be the forward reaction , with the probability per unit time one particle at position and one particle at position bind. Once reaction fires, we generate a new particle at position following the placement density . Reaction is then accepted with probability . For , the substrates are particles of species and , so and . The product is one particle , so and
Let be the backward reaction , with the probability per time one particle at position unbinds. Once reaction fires, we generate a new particle at position and a new particle at position following the placement density . Reaction is accepted with the acceptance probability . For , the substrate is a particle, so and . The products are and particles, so and
If the limiting spatially distributed measures for species and have marginal densities respectively, they solve the system (1) with the molar concentrations .
Example 5.2.
Consider a system with four species, and that can undergo the reversible reaction Define the measures for A, B, C, and D particles at time respectively as and .
Let be the forward reaction , with the probability per time one particle at position and one particle at position bind. Once reaction fires, we generate one new particle at position and one new particle at position following the placement density . Reaction is then accepted with probability . For , the substrates are particles of species and , so and . The products are one particle and one particle , so and
Let be the backward reaction , with the probability per time one particle at position and one particle at position bind. Once reaction fires, we generate a new particle at position and a new particle at position following the placement density . Reaction is accepted with the acceptance probability . For , the substrates are one particle and one particle, so and . The products are one particle and one particle, so and
If the limiting spatially distributed measures for species and have marginal densities respectively, they must solve the following reaction-diffusion equations in a weak sense:
Example 5.3.
Consider a system with two species, and that can undergo the reversible dimerization reaction Define the measures for A and B particles at time respectively as and .
Let be the forward reaction , with the probability per time one particle at position and another particle at position bind. Once reaction fires, we generate a new particle at position following the placement density . Reaction is then accepted with probability . For , the substrates are particles of species , so and . The product is one particle , so and
Let be the backward reaction , with the probability per time one particle at position unbinds. Once reaction fires, we generate two new particles at and following the placement density . Reaction is accepted with the acceptance probability . For , the substrate is one particle, so and . The products are two particles, so and .
If the limiting spatially distributed measures for species and have marginal densities respectively, they must solve the following reaction-diffusion equations in a weak sense:
6. A specific example: Fröhner-Noé Model
In this section, we study an example based on the specific acceptance probabilities, , proposed in Fröhner-Noé in [13]. We derive a specific formulation of the acceptance probability which preserves the detailed balance condition for general reversible reactions, present the corresponding acceptance probabilities, and illustrate their large population limit for general systems involving one- and two-body interactions.
To illustrate the particular acceptance probability in the generalized Fröhner-Noé model, consider the reaction , where one particle at binds with one particle at to produce one particle at , and the other non-substrate and non-product particles are located at . Denote the total potential energy of the system before by and after by . We assume that the total potential function depends on the system size parameter and consists of only one- and two-body potentials. We then represent the total potential energy in the system prior to by
and the total potential energy in the system after by
Here, denotes the total potential interactions between the non-substrate and non-product particles at ; , and represent all one-body interactions involving the substrates at and and the product at , respectively; , and denote all pairwise interactions between each substrate/product and the non-substrate and non-product particles at ; finally, represents the specific two-body interaction between the two substrate particles.
Let denote the pre-reaction state of the system, consistent with the state corresponding to having the two substrates at and the non-reactant particles at . The Fröhner-Noé acceptance probability of takes the form
In the next section we will demonstrate why it is appropriate to treat as a function of , , , and . The acceptance probability always accepts a reaction where the potential energy, excluding the pairwise potential between the substrates, decreases from pre-reaction stage to post-reaction stage. On the other hand, if the potential difference is positive, then the reaction is only accepted a fraction of time. In Subsections 6.1 and 6.2 we present the specifics of these constructions and illustrate them in a number of examples.
6.1. Acceptance probability.
In this section we present the functional form of the acceptance probability in the generalized Fröhner-Noé model, illustrate why it can be written as a function of instead of the positions of the non-reactant particles, and discuss its limiting form as . The proof that this generalized Fröhner-Noé acceptance probability satisfies the assumptions of this paper is presented in the appendix.
Let represent the total one-body interactions involving each of the substrates at , where
Similarly, denote all one-body interactions involving each of the product particles at by , where
Recall that we denote one-body potentials by for each particle at of type and two-body potentials by between particles at of type and at of type for . We slightly abuse notation for the following discussion and use to represent the total pairwise interactions between the substrate particles at , where
is defined analogously to represent the total pairwise interactions between the product particles at , where
Here, the first term represents the pairwise potential between substrates/products of different types, and the second term accounts for the two-body interactions between substrates/products of the same type. The lower limit of the first summation, , and the upper limit of the second summation, , prevent counting the two-body potential between the substrates/products twice. Note that both and converge to as due to the assumed boundedness of the two-body potentials.
When the system state is given by , for substrates at we denote by the position vector for the non-reactant particles of type . That is, corresponds to the particle positions within
where are the subset of particle indices that are represented within . We then have .
With some abuse of notation, we write the sum of all pairwise interactions between the substrates at and the non-substrate and non-product particles at as . To encode information about particle types, we let denote all pairwise interactions between the sampled substrates of type at and the non-reactant particles of species at , with . Therefore
demonstrating that the two-body interactions between a set of substrates and non-reactant particles can be written solely in terms of the substrate positions and the components of .
We analogously denote by the total two-body interactions between the products at and the non-substrate and non-product particles at . To specify particle types, we let denote all pairwise interactions between the products of type sampled from and the non-substrate and non-product particles of species sampled from , with . We then obtain
demonstrating we can write these two-body interactions in terms of the substrate positions, the product positions, and the pre-reaction state measure, .
With the preceding definitions, we can represent the total potential for the system before for by
and the total potential for the system after for by
Remark 6.1.
Examining the preceding definitions, we see that we could alternatively write the potentials as functions of , , and , i.e., and respectively. We will subsequently make use of this representation to extend the pre-limit Fröhner-Noé acceptance probabilities to be functions of general finite measures in the Appendix. We use the notation in this section as it is more consistent with how potentials are written in the modeling literature.
For reversible reactions with differing numbers of substrates and products, for instance the reversible reactions and , we denote the acceptance probability for the binding reaction with and by
| (15) |
and for the unbinding reaction with and by
| (16) |
in order to satisfy the detailed balance condition and preserve symmetry for the reversible reaction [13, 17].
For other allowable reversible reaction types such as the reversible reactions and with products always placed at the positions of the substrates, we do not subtract the specific pairwise potential term between the substrates at from the total potential energy in the system prior to the forward reaction, nor subtract the specific pairwise potential term between the products at from the total potential energy in the system after the backward reaction, for the detailed balance condition to hold. Instead, we consider the acceptance probability of the form
| (17) |
When goes to zero, the pairwise potentials between substrates at and between the products at both vanish. The total two-body interactions between the substrates (products) and the non-reactant particles with and are then
and
where and denote the corresponding large population limits of and for . Substituting in these formulas, we obtain that the mean field limits of the three forms of acceptance probabilities coincide. More specifically, the mean field limit of for is
and the mean field limit of for is
As such, the mean field limit of all forms of the acceptance probabilities, , are
| (18) |
with and .
Remark 6.2.
Previously, the position vectors and referred to locations of the substrate and product particles in the th reaction. We now directly compare the forward and backward directions in one reversible reaction cycle where a set of substrates at are replaced by a set of products at and vice versa, with the non-reactant particles at . As such, in the forward reaction , the substrates are placed at with the products located at , and in the backward reaction , the substrates are placed at while the products are located at . In this case, we have that
where and .
Remark 6.3.
For such reversible reactions where the number of substrates and products differs, for example and , the placement densities for may be chosen to take the form of , which converges to in the mean field limit as , where and are the normalizing constants. We provide specific formulations of the placement densities for the reversible reaction in Example 6.1 below. We again have and . See [13] and [17] for more details.
6.2. Examples.
Example 6.1.
Consider a system with three species, , , and that can undergo the reversible reaction . Let be the forward reaction , where one particle at position and one particle at position bind to generate one particle at position . Assume the non-reactant particles that are unchanged by the reaction are located at as in the last section.
We denote the specific two-body interaction between the substrates by
and represent the total potential of the system before occurs by
where represents the system’s state before an reaction at time (i.e., with an particle that will react at , a particle that will react at , and non-reactant particles at ). The total potential energy of the system after is denoted by
where we have written the potential in terms of the pre-reaction state, . The acceptance probability for is thus
The mean field limit of is
and the mean field limit of is
Note that the pairwise potential term between the substrates converges to zero as . Therefore, the mean field limit of the acceptance probability for simplifies to
Let denote the backward reaction , where one particle at position unbinds to generate one particle at position and one particle at position and the non-reactant particles are again assumed to be at . Letting represent the state before the reaction, with a substrate particle at and the remaining non-reactant particles at , the total potential of the system before is defined to be
and we denote the total potential energy of the system after by
The acceptance probability for is thus
so that the mean field limit of is
and the mean field limit of is
As the pairwise potential term between the products converges to zero as , the mean field limit of the acceptance probability for is
Finally, for completeness we give specific formulas for the placement densities of the reversible reaction that are consistent with detailed balance holding, see [17]. For simplicity, we let the placement density for take the form
and as then converges to
for . To ensure detailed balance of reaction fluxes at equilibrium, see [17], and also maintain symmetry for reversible reactions, we then chose
where
then converges as a distribution to in the mean field limit as with
Example 6.2.
Consider a system with four species, and that can undergo the reversible reaction . Let be the forward reaction , where one particle at position and one particle at position react to generate one particle at position and one particle at position .
Analogous to the last section, we represent the total potential energy of the system before by
and the total potential energy of the system after by
The acceptance probability for is thus
The mean field limit of is
and the mean field limit of is
Therefore, the mean field limit of the acceptance probability for simplifies to
Let be the backward reaction , where one particle at position and one particle at position react to generate one particle at position and one particle at position . The total potential energy of the system before is defined to be
and we denote the total potential energy of the system after by
The acceptance probability for is thus
The mean field limit of is
and the mean field limit of is
Therefore, the mean field limit of the acceptance probability for is
Finally, we note that the placement densities, and , and their respective mean field limits, and , take the same forms as in Assumption 4.7.
Example 6.3.
Consider a system with two species, and that can undergo the reversible reaction . Let be the forward reaction , where two particles at and bind to generate one particle at position .
Denote the specific two-body interaction between the substrates by
We represent the total potential energy of the system before by
and the total potential energy of the system after by
The acceptance probability for is thus
The mean field limit of is
and the mean field limit of is
The pairwise potential term between the substrates converges to zero as . Therefore, the mean field limit of the acceptance probability for simplifies to
Let be the backward reaction , where one particle at position unbinds to generate two particles at and . The total potential energy of the system before is defined to be
and we denote the total potential energy of the system after by
The acceptance probability for is thus
The mean field limit of is
and the mean field limit of is
The pairwise potential term between the products converges to zero as . Therefore, the mean field limit of the acceptance probability for is
7. Simulations
We numerically solve the reaction for a periodic one-dimensional system to compare our derived PIDEs and the underlying PBSRDD model. We subsequently call these PIDEs the mean field model (MFM). The MFM is solved using a Fourier spectral method. We discretize the PBSRDD model in space to obtain a (convergent) jump process approximation to the stochastic process associated with the PBSRDD model via the Convergent Reaction Diffusion Master Equation (CRDME) [26, 30] using the approach developed for systems with drift due to interaction potentials in [16, 19].
We first present the model problem in Subsection 7.1 and then discuss the discretization schemes we employed for the MFM and PBSRDD model in the next two subsections. Finally, we present the numerical results and demonstrate that for the total molar mass (i.e., the integral or -norm of the molar concentration field) of the type particles, the mean field process gives an increasingly accurate approximation of the PBSRDD model as increases. For , the largest value of that we consider, the means for the two models agree up to statistical error. We also compare with the purely-diffusive case to demonstrate that including drift induced by potential interactions affects the behavior of the system in non-trivial ways.
7.1. Description of model problem
Our model follows the general form of Example 6.1, with some modifications. We restrict the reaction system to the periodic domain with . As in the example, we prescribe harmonic two-body potentials between each pair of particles which we choose as
| (19) |
where . Here and throughout this section, denotes the periodic distance between , i.e.,
The parameters , which control the interaction distance, and , which controls the interaction strength, are chosen large enough to make a clear contrast with the (i.e., no potentials) case. Note that for simplicity, we do not include single-body potentials in this model.
The drift-diffusion transport operator for each particle type is also scaled by a diffusion constant . We emphasize that this diffusion constant plays a slightly different role than in earlier sections; in particular, it scales both the drift and diffusion terms (see (21) and (22)), and compare the transport operators in the latter system of PIDEs with, e.g., those in (1)).
For reactions, we follow Example 6.1 except that we replace the Doi reaction kernel with a normalized Gaussian
with the kernel width and a normalization constant,
We also replace the placement density with the combination of -functions:
| (20) |
so that, e.g., in the event of an reaction the product is placed at the location of the or the with equal probability . The backward reaction placement density is likewise modified to incorporate our changes to the forward placement density and the reaction kernel, i.e.,
where
recalling the notation for . We note that, in the following simulations, we do not regularize this placement density, i.e., in the actual numerical implementation we work with the function densities directly.
We choose parameters and which control the relative rates at which forward and backward reactions occur. The rates are chosen so that prior to applying the detailed-balance enforcing rejection-acceptance mechanism, the forward rate for an at and a at to react is and the rate for a at to unbind is in the particle model.
Finally, we specify the values of the various parameters described above: , , , and . We choose the potential strength parameter , also making qualitative comparisons with the pure diffusion () case. Initial conditions are set proportionally to
where again we use periodic distances.
7.2. Discretization of particle models.
To solve the particle model, we use the CRDME, a convergent spatial discretization of the forward Kolmogorov equation associated with the PBSRDD model [26, 30]. The CRDME corresponds to the forward equation for a system of continuous-time jump processes on a mesh, and we therefore simulate the particle system via simulations of these jump processes using optimized versions of the stochastic simulation algorithm (SSA), also known as Gillespie’s method or Kinetic Monte Carlo [11]. The PBSRDD particles’ Brownian motions are then approximated by continuous-time random walks on a grid and their reactive interactions by jump processes that depend on the relative positions of reactants on the mesh. As discussed in [26, 30, 19, 16], statistics obtained from simulations of the CRDME should then converge to those of the underlying PBSRDD model as the mesh spacing is taken to zero.
For these simulations, we use a uniform mesh with nodes , where , , and . We denote the compartments, or voxels, that particles hop between by for . To initialize the particle positions at the start of each simulation, we first choose the number of and particles as , for . Then, we sample the position of each individual particle from the (unnormalized) discrete distributions , . We note that our choice of initial distribution implies that the initial error between the mean field model and the mean of the particle model is zero, up to discretization error.
Let be concentration measures for the nodal locations of the particles of type , so that if there are particles of type in voxel ,
Then, the total potential difference induced by a hop of one particle of type from voxel to voxel is given by:
where the latter terms remove self-interactions. The hopping rate for each particle of species in voxel to a neighboring voxel is then given by
| (21) |
The above formula can be derived by using a specific combination of quadrature rules on the transport operator appearing in the forward Kolmogorov equation of the particle model, as described in [19, 16].
Proposal reaction rates between a molecule of type in voxel and a molecule of type in voxel are computed as . The resulting is placed in voxel or with probability each. We then accept the proposed reaction with probability computed by the formula given in Example 6.1, where , , and are replaced with the proposed mesh nodes and particle positions are replaced with mesh nodes associated with their respective voxel sites.
The total rate of proposed unbinding reactions in the CRDME model at each voxel site is given by the discrete marginal integral of the reaction kernel,
We note that for our chosen parameters, the above sum is essentially (i.e., to numerical precision). After the unbinding of a particle at is proposed, a particle of type or of type is tentatively placed in with probability . The location of the other product particle is proposed by sampling the (unnormalized) discrete distributions over the voxel sites. Again, after reactions are proposed using the rates described above, they are accepted or rejected using the mechanism described in Example 6.1, with particle positions localized to mesh nodes.
Specifying the reaction and transport rates as we have just described preserves detailed balance and convergence of the CRDME to the underlying particle model [19, 16]. We note that, although in the simulation methodology described here potentials and reaction rates are always evaluated at mesh nodes, it may improve CRDME convergence in some cases (e.g., discontinuous reaction kernels) to employ other discretization strategies (e.g., involving voxel averages of the reaction kernel as done in [26, 30]).
7.3. Discretization of MFM
Let , and define the integral operator for a function by
The MFM for the reversible reaction is given by the system of PIDEs
| (22) |
where , , and are the mean field molar concentration fields for the corresponding particle types. As for the particle model, the acceptance-rejection factors are as described in Example 6.1.
The above PIDEs are solved using a Fourier collocation method [22] for the spatial discretization, with collocation points . We use a total of basis functions to represent the concentration fields for each of the three species. We convert between Fourier representations and values at collocation points using the SciPy fast Fourier transforms functions, and approximate the drift and reaction integral terms using the trapezoidal rule centered at the collocation points.
For the resulting spatially discretized reaction-drift-diffusion ODEs, the diffusion and drift terms are stiff whereas the reaction terms are non-stiff. We therefore adopt a one-step implicit-explicit (IMEX) Euler method to solve the system of ODEs arising from our spatial discretization, treating the reaction terms explicitly (forward Euler) and the transport operator implicitly (backward Euler). For the implicit terms, the nonlinear system of equations is solved at each timestep using the SciPy Newton-Krylov solver. To ensure convergence of the nonlinear solver, we dynamically reduce our timestep from an empirically chosen (for accuracy) maximum timestep of .
7.4. Numerical results
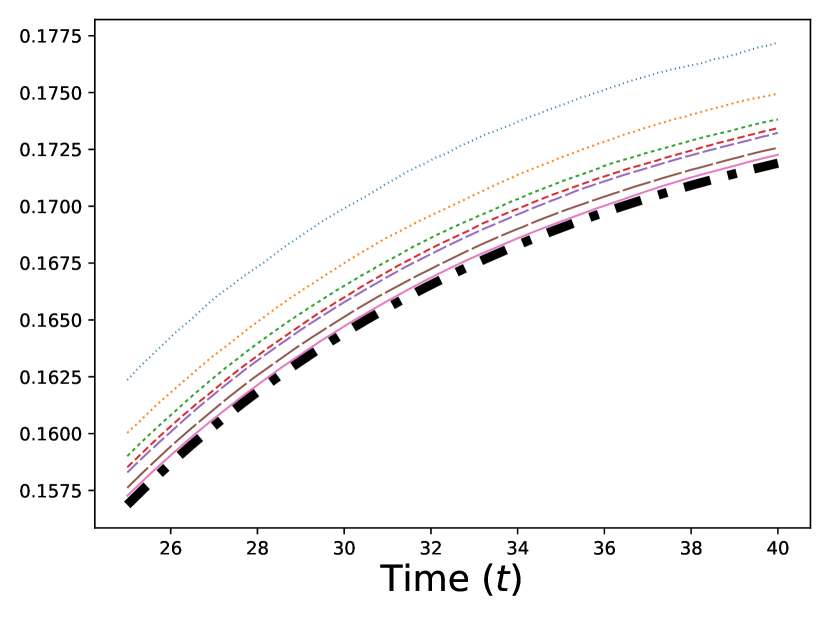
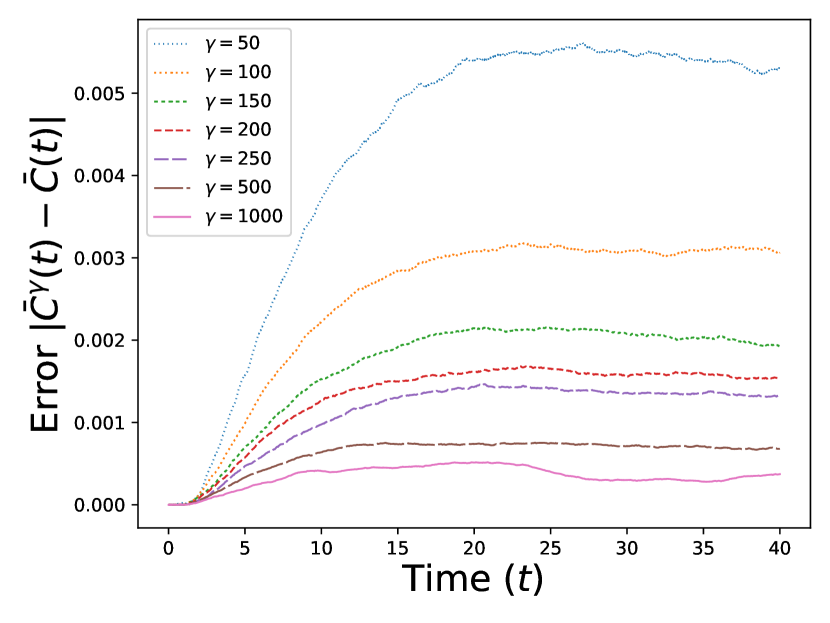
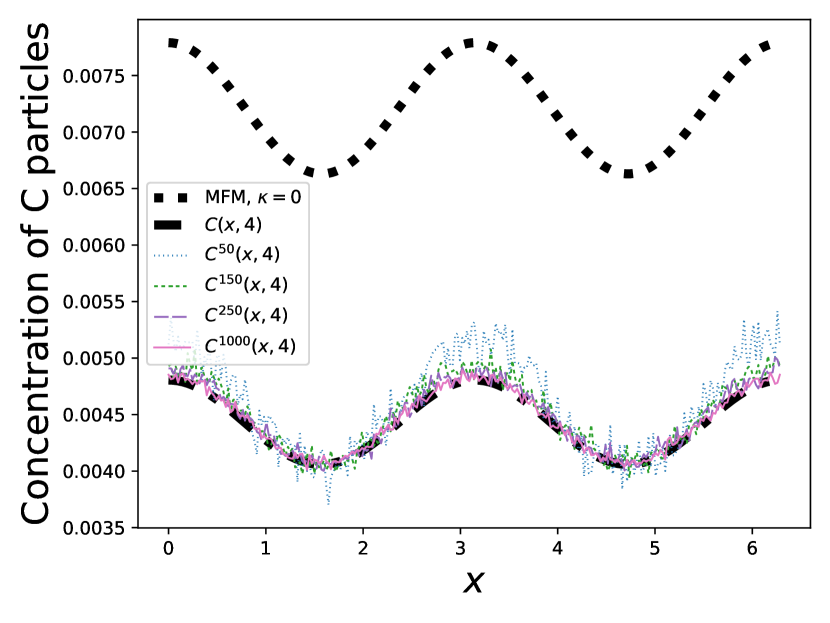
We present the results of our numerical studies in Figure 1. The first three subfigures (top left, top right, and bottom left) each compare the molar mass for the particles in the prelimit and limiting processes, denoted by for the MFM and for the CRDME model, over the time interval . The bottom-right subfigure compares the corresponding spatial distributions and at time .
For the MFM, the molar mass
is approximated from the spatial distribution at a series of discrete times by applying the trapezoidal rule to the numerically computed mean field solution. For the CRDME model, we compute by first averaging the number of particles in each voxel over 280,000 simulations to obtain , , at a series of discrete times . Then, the concentration fields shown in the bottom-right panel of Figure 1 can be computed from as the piecewise-linear interpolant of the grid function . Finally, the molar mass is computed from as
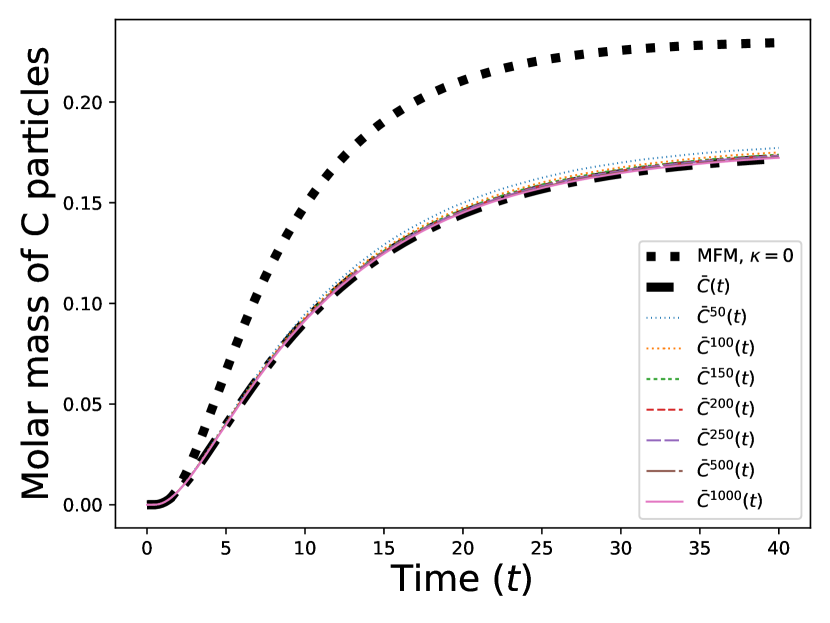
Starting with the top-left panel in Figure 1, we observe that, as expected, the CRDME molar masses converge to the MFM molar masses as . We have also included for comparsion the mean-field solution in the no-potentials case (i.e., ), observing that over time, the repulsive pair potential force reduces the effective forward reaction rate (relative to the backward), resulting in a significantly smaller molar mass at the final time.
The top-right and bottom-left panels further compare the molar masses and for the MFM and CRDME models in the case; the top-right panel shows a zoomed-in version of the top-left panel, with the solution removed and the time interval restricted to . We see more clearly the convergence of the CRDME molar masses to the MFM molar masses . Looking directly at the errors in the bottom-left panel, computed as for each time , we see that the maximum errors range from ( 3%) for to ( .15%) for .
Finally, in the bottom right figure, we compare the spatial distribution for the CRDME model with the MFM spatial distribution . Although the CRDME spatial distributions appear significantly noisier than the molar masses due to the relatively small number of particles in each voxel, we can still see that the MFM gives a good fit for the particle model, especially for larger values of . We have also once again included for comparison the MFM spatial distribution.
8. Proof of Theorem 5.1.
Without loss of generality, we assume that in this section. The case when follows by similar arguments as we now give in the case.
To rigorously determine the large population limit of the MVSP, we use the martingale problem approach for studying solutions to stochastic differential equations developed by Stroock and Varadhan [12, 46]. The proof is divided into four subsections. In Subsection 8.1, we provide the path level description of , and we derive equations for its expectation in Subsection 8.2. Tightness and identification of the limit are presented in Subsection 8.3. Lastly, we prove in Subsection 8.4 that the limit equation has a unique solution. Collectively, these results imply Theorem 5.1, see, for example, the proof of Theorem 5.5 in [28] for details.
8.1. Path level description.
For a test function and for each species , we obtain the coupled system
| (23) |
The exchangeability of the sum, the differentiation, and the Lebesgue integral here and in the next subsection are justified by the fact that for fixed is finite by Assumption (4.1), and that and its partial derivatives are uniformly bounded.
8.2. Taking expectations.
By taking expectation on (23), we have
Define the operator
| (24) |
and note in the remainder that for any test functions we consider
Using the operators and defined in (8) we then obtain
| (25) |
For this last equality, we switch integrals of the form to using the definitions of and (see equation (6) and Definition 2.6), and removing probability zero sets where two particles with the same type are simultaneously located at the same spatial location (see Definition 2.7). Note that by definition indices for particles of the same species are ordered by the allowable substrate index sampling space (see Definition 2.5). In converting from integrals involving the positions of individual particles with to integrals involving product measures , we need to remove the “diagonal” indices by means of integrating on (see Definition 2.7) and normalizing by the total number of index orderings .
8.3. Tightness and Identification of the limit.
We start by discussing relative compactness of the sequence . Recall that denotes the space of finite measures endowed with the weak topology.
Lemma 8.1.
The measure-valued processes are relatively compact on , the space of càdlàg paths with values in endowed with Skorokhod topology. Further, the corresponding weak limit of any convergent subsequence of as is in .
Proof.
The proof is exactly as in [28] with minor adjustments to account for the presence of the bounded one-body and two-body potential interactions. We omit the details for the sake of brevity. ∎
Given a sequence as , by Lemma 8.1 the sequence of marginal distribution vectors has a weakly convergent subsequence. Recall that we let be the corresponding limiting marginal distribution vector on and the corresponding limiting particle distribution on . We claim that for each , is then the unique solution to (14), which in the case that becomes
| (26) | ||||
where is defined in (24). Uniqueness of solutions to this equation is shown in Subsection 8.4. We now identify that the limit satisfies this equation.
Let be the collection of elements in the space of bounded functionals, , of the form
| (27) |
for some , some , and where each for and . Then separates points in (see Chapter of [12] and Proposition of [5]). To identify the limit, it suffices to show convergence of the martingale problem for functions of the form (27), given the existence and uniqueness of the limiting process.
For of the form and with each , the generator of (26) and of the limiting martingale problem for , is defined as
Lemma 8.2.
(Weak Convergence). For any and and , we have that
| (28) |
Proof.
For each , we can rewrite (7) as
where
and
Note that is a square integrable martingale (see Proposition in [24]) with quadratic variation
The quadratic variation of is thus uniformly bounded and goes to 0 as , due to the uniform boundedness of and its partial derivatives, and by Assumptions 4.4 and 4.6.
Now define , where
is the continuous martingale part, and
| (29) | ||||
is the martingale part coming from the stochastic integral with respect to the Poisson point processes.
Let . For simplicity of notation, we define
which represents the jumps and is uniformly bounded by . With some abuse of notation we shall write for the vector . Then (29) becomes
Applying Itô’s formula (see Theorem in [24]) to we obtain
| (30) |
where represents the th additive term on the right hand side. We now use the Skorokhod representation theorem (Theorem in [12]) which, for the purposes of identifying the limit and proving (28), allows us to assume that the aforementioned claimed convergence of holds with probability one in the topology of weak convergence of measures. The Skorokhod representation theorem involves the introduction of another probability space, but we ignore this distinction in the notation. To show (28), it is then sufficient to prove that the left-hand side of (30) goes to zero in probability. With this goal in mind, we proceed to prove convergence in probability to zero for for .
The fact that for converge to zero in probability follows from Section 7.3 in [28]. It remains to show that and converge to zero in probability. Note that
| (31) |
We note the following estimate proven in Appendix 9.2.
Lemma 8.3.
For any small enough, , and , there exists a constant such that
With the aid of Assumption 4.11, Lemma 8.3, and the assumptions that and its partial derivatives are uniformly bounded, we then have . Incorporating Assumption (4.3) we obtain
We then have that Thus, the left-hand side of (30) goes to zero in probability, concluding the proof of the lemma.
∎
We have shown that if the weak limit of the marginal distribution exists and is unique (uniqueness is shown in Subsection 8.4), then as goes to zero, it will converge to the limiting particle distribution in distribution with respect to the topology of weak convergence of measures.
8.4. Uniqueness of the limiting solution.
We now show that the solution to (26) is unique in . will subsequently denote a generic constant. Suppose, by contradiction, that we have two different solutions to (26), and , with the same initial condition . Parallel to Eq (26), for a test function of the form of , we get
| (32) | ||||
recalling (24).
Let , be the semigroup generated by . Choose , respectively for each , where , with . Using the semigroup property, we then have
and Eq (32) becomes
| (33) | ||||
We then get
| (34) |
Recall that solves
By the Bismut-Elworthy formula (see Proposition 9.22 and Corollary 9.23 of [41] or Theorem 3.2.4 of [45]), we have the following estimate for its gradient
for some finite constant . Consequently, we obtain
where . Note that as and is bounded by Assumption 4.3.
With and using the above estimates, we can further bound (34) by
| (35) |
Summing over all particle types, we get
for some unimportant constant . The integrable singularity of the kernel, , can be handled using either of the weakly singular Grönwall Inequalities Lemma 7.1.1 of [21] or Theorem 3.2 in [48]. We then obtain that
concluding the proof of the uniqueness of the limiting solution.
9. Appendix
9.1. Verifications of assumptions for the Fröhner-Noé model
We verify here that all forms of the acceptance probabilities for the generalized Fröhner-Noé model, i.e., (15), (16), and (17), satisfy Assumptions (4.9), (4.10) and (4.11). As such, they satisfy the conditions under which our main result, Theorem 5.1, holds.
We will prove the next two lemmas for the limit of the acceptance probability given by (15). Proofs for the other two cases are analogous. Consider for the following two proofs, and recall the definition of in (10).
Lemma 9.1.
Consider any and , both in . Then the acceptance probability is bounded and Lipschitz continuous with Lipschitz constant , i.e.,
| (36) |
Proof.
Recalling that the potentials are all assumed to be uniformly bounded, we have
The second inequality stems from the local Lipschitz continuity of exponential functions, the uniform bound on and , and the boundedness of the potentials implying global Lipschitz continuity. The last inequality is due to the uniform boundedness of the two-body potentials and the definition of the variation norm. ∎
Lemma 9.2.
Consider any and in . Then the acceptance probability is bounded and Lipschitz continuous with Lipschitz constant , i.e.,
| (37) |
Proof.
for some constant that may be changing from line to line. The second inequality stems from the local Lipschitz continuity of exponential functions, the uniform bound on , and the boundedness of the potentials implying global Lipschitz continuity. For the third inequality we used that the one-body potential is Lipschitz. We again used the boundedness of for all and the assumed global boundedness of the two-body potential in by Assumption 4.3. ∎
Lemma 9.3.
Proof.
We only demonstrate the proof of convergence of (16) to (18) as the other two cases are the same. Recall Remark 6.1, justifying why is well-defined as a function of general finite measures. For and , factoring out the one-body potential terms and using their uniform boundedness we find
The convergence result follows from the uniform boundedness of the two-body potentials and . ∎
9.2. Proof of Lemma 8.3.
For any small enough, , and , there exists a constant such that
Proof.
Case 1: Reaction of the form .
where Assumption 4.10 was used to derive the second to last inequality.
Case 2: Reaction of the form .
where Assumption 4.10 was used to derive the second to last inequality.
Case 3: Reaction of the form .
Case 4: Reaction of the form .
where Assumption 4.10 was used to derive the second to last inequality. ∎
References
- [1] D.F. Anderson and T.G. Kurtz “Stochastic analysis of biochemical systems” Berlin: Springer, 2015
- [2] T. Arnold and M. Theodosopulu “Deterministic limit of the stochastic model of chemical reactions with diffusion” In Advances in Applied Probability 12.2, 1980, pp. 367–379
- [3] V. Bansaye and S. Méléard “Stochastic models for structured populations” Springer, 2015
- [4] M. Bruna, S.J. Chapman and M. Robinson “Diffusion of Particles with Short-Range Interactions” In SIAM Journal on Applied Mathematics 77.6, 2017, pp. 2294–2316
- [5] A. Capponi, X. Sun and D. Yao “A Dynamic Network Model of Interbank Lending: Systemic Risk and Liquidity Provisioning” Mathematics of Operations Research, 2020
- [6] P. Dai Pra and F. Hollander “Mckean-vlasov limit for interacting random processes in random media” In Journal of Statistical Physics 84.3–4, 1996, pp. 735–772
- [7] P. Dai Pra and M. Tolotti “Heterogeneous credit portfolios and the dynamics of the aggregate losses” In Stochastic Processes and their Applications 119.9, 2009, pp. 2913–2944
- [8] F. Delarue, J. Inglis, S. Rubenthaler and E. Tanre “Particle systems with a singular mean-field self-excitation. application to neuronal networks” In Stochastic Processes and their Applications 125, 2015, pp. 2451–2492
- [9] M. Doi “Second quantization representation for classical many-particle system” In J. Phys. A: Math. Gen. 9.9, 1976, pp. 1465–1477
- [10] M. Doi “Stochastic theory of diffusion-controlled reaction” In J. Phys. A: Math. Gen. 9.9, 1976, pp. 1479–1495
- [11] Gillespie D.T. “A general method for numerically simulating the stochastic time evolution of coupled chemical reactions” In Journal of Computational Physics 22.4, 1976, pp. 403–434
- [12] S.N. Ethier and T.G. Kurtz “Markov Processes: Characterization and Convergence” New York: John Wiley & Sons Inc., 1986
- [13] C. Fröhner and F. Noé “Reversible Interacting-Particle Reaction Dynamics” In J. of Phys. Chem. B 122.49, 2018, pp. 11240–11250
- [14] K. Giesecke, K. Spiliopoulos and R.B. Sowers “Default clustering in large portfolios: Typical events” In Tha Annals of Applied Probability 23, 2013, pp. 348–385
- [15] K. Giesecke, K. Spiliopoulos, R.B. Sowers and J. Sirignano “Large portfolio asymptotics for loss from default” In Mathematical Finance 25, 2015, pp. 77–114
- [16] M. Heldman and S.A. Isaacson “Convergent Jump Process Approximations for Particle-Based Stochastic Reaction-Drift-Diffusion Models” In preparation for submission., 2023
- [17] M. Heldman, S.A. Isaacson, Q. Liu and K. Spiliopoulos “Detailed balance for particle-based reaction-drift-diffusion models.” In preparation for submission., 2023
- [18] M. Heldman, S. A. Isaacson, J. Ma and Spiliopoulos K. “Fluctuation Analysis for Particle-Based Stochastic Reaction-Diffusion Models” In Stochastic Processes and their Applications 167, 2024, pp. 61 pp
- [19] Max Heldman “Numerical Methods for Particle-Based Stochastic Reaction-Diffusion Systems”, 2023
- [20] J. Helfmann et al. “From interacting agents to density-based modeling with stochastic pdes” In Communications in Applied Mathematics and Computational Science 16.1, 2021, pp. 1–32
- [21] D. Henry “Geometric Theory of Semilinear Parabolic Equations” 840, Lecture Notes in Mathematics Springer-Verlag, Berlin-New York, 1981
- [22] J.S. Hesthaven, S. Gottlieb and Gottlieb D. “Spectral methods for time-dependent problems” Cambridge University Press, 2007
- [23] M. Hoffmann, C. Fröhner and F. Noé “ReaDDy 2: Fast and flexible software framework for interacting-particle reaction dynamics” In PLOS Computational Biology 15.2 Public Library of Science, 2019, pp. 1–26 DOI: 10.1371/journal.pcbi.1006830
- [24] N. Ikeda and S. Watanabe “Stochastic differential equations and diffusion processes” Elsevier, 2014
- [25] J. Inglis and D. Talay “Mean-field limit of a stochastic particle system smoothly interacting through threshold hitting-times and applications to neural networks with dendritic component” In SIAM Journal on Mathematical Analysis 47, 2015, pp. 3884–3916
- [26] S.A. Isaacson “A convergent reaction-diffusion master equation” In The Journal of chemical physics 139, 2013, pp. 054101
- [27] S.A. Isaacson, J. Ma and K. Spiliopoulos “How reaction-diffusion PDEs approximate the large-population limit of stochastic particle models” In SIAM J. Appl Math 81.6, 2021, pp. 2622–2657
- [28] S.A. Isaacson, J. Ma and K. Spiliopoulos “Mean field limits of particle-based stochastic reaction-diffusion models” In SIAM J. Math. Analysis 54.1, 2022, pp. 453–511
- [29] S.A. Isaacson, D.M. McQueen and C.S. Peskin “The influence of volume exclusion by chromatin on the time required to find specific DNA binding sites by diffusion” In PNAS 108.9, 2011, pp. 3815–3820
- [30] S.A. Isaacson and Zhang Y. “An unstructured mesh convergent reaction-diffusion master equation for reversible reactions” In Journal of Computational Physics 374, 2018, pp. 954–983
- [31] S.A. Isaacson and Y. Zhang “Detailed Balance for Particle Models of Reversible Reactions in Bounded Domains” In Journal of Chemical Physics 156.20, 2022, pp. 204105
- [32] S.A. Isaacson et al. “The Influence of Spatial Variation in Chromatin Density Determined by X-Ray Tomograms on the Time to Find DNA Binding Sites” In Bull. Math. Biol. 75.11, 2013, pp. 2093–2117
- [33] P.-E. Jabin and Z. Wang “Mean field limit for stochastic particle systems” In Active Particles, Volume 1: Advances in Theory, Models, and Applications, 2017, pp. 379–402
- [34] B. Jourdain, S. Méléard and W.A. Woyczynski “Lévy flights in evolutionary ecology” In Journal of mathematical biology 65.4, 2012, pp. 677–707
- [35] T.G. Kurtz “Lectures on stochastic analysis” Department of Mathematics and Statistics, University of Wisconsin, 2001
- [36] T.S. Lim, Y. Lu and J. Nolen “Quantitative propagation of chaos in the bimolecular chemical reaction-diffusion model” In SIAM J. Math. Anal. 52.2, 2020, pp. 2098–2133
- [37] O. Moynot and M. Samuelides “Large deviations and mean-field theory for asymmetric random recurrent neural networks” In Probability Theory and Related Fields 123, 2002, pp. 41–75
- [38] K. Oelschläger “On the derivation of reaction-diffusion equations as limit dynamics of systems of moderately interacting stochastic processes” In Probab. Th. Rel. Fields 82.4, 1989, pp. 565–586
- [39] A. Pazy “Semigroups of Linear Operators and Applications to Partial Differential Equations” 44, Applied Mathematical Sciences Springer-Verlag New York, 1983
- [40] L. Popovic and A. Véber “A spatial measure-valued model for chemical reaction networks in heterogeneous systems” In The Annals of Applied Probability 33.5, 2023
- [41] G. Prato “Introduction to Stochastic Analysis and Malliavin Calculus”, Publications of the Scuola Normale Superiore Edizioni della Normale Pisa, 2014
- [42] D.E. Shaw et al. “Millisecond-scale molecular dynamics simulations on Anton” In Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis 39, 2009
- [43] A. Siokis et al. “F-Actin-Driven CD28-CD80 Localization in the Immune Synapse” In Cell Reports 24.5, 2018, pp. 1151–1162
- [44] H. Sompolinsky, A. Crisanti and H. Sommers “Chaos in random neural networks” In Physical Review Letters 61, 1988, pp. 259
- [45] D.W. Stroock “Partial Differential Equations for Probabilists”, Cambridge Studies in Advanced Mathematics Cambridge University Press, 2008
- [46] D.W. Stroock and S.R.S. Varadhan “Multidimensional Diffusion Processes” Berlin Heidelberg: Springer-Verlang, 2006
- [47] E. Teramoto and N. Shigesada “Theory of bimolecular reaction processes in liquids” In Prog. Theor. Phys. 37.1, 1967, pp. 29–51
- [48] J.R.L. Webb “Weakly Singular Gronwall inequalities and applications to fractional differential equations” In Journal of Mathematical Analysis and Applications, 2019, pp. 692–711