![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/36972fb9-8cd9-417d-b8f4-0ec528dfe529/x1.png)
BELLE2-CONF-PH-2021-037
August 6, 2025
The Belle II Collaboration
Measurement of the branching ratio and with a fully reconstructed accompanying meson in 2019-2021 Belle II data
Abstract
We present a measurement of the () branching ratio and of the CKM parameter using signal decays accompanied by a fully reconstructed meson. The Belle II data set of electron-positron collisions at the resonance, corresponding to 189.3 fb-1 of integrated luminosity, is analyzed. With the Caprini-Lellouch-Neubert form factor parameterization, the parameters and are extracted, where is an electroweak correction, is a normalization factor and is a form factor shape parameter. We reconstruct 516 signal decays and thereby obtain , , and .
1 Introduction
A precise understanding of decays is important for future measurements of [1, 2] and of the magnitude of the Cabibbo-Kobayashi-Maskawa matrix element [3, 4], where persistent tensions exist between inclusive and exclusive measurements [1]. We study events, where the decay of the accompanying or is reconstructed in a hadronic final state using the full event interpretation algorithm (FEI) [5] and the signal bottom meson of opposite flavor is then reconstructed in the final state.
2 Belle II experiment
Belle II [6] is an experiment at the SuperKEKB super factory [7], an energy-asymmetric (4 GeV) (7 GeV) collider in Tsukuba, Japan. Collision data with an integrated luminosity corresponding to 189.3 fb-1 were collected from March 2019 to July 2021 at a center-of-mass (c.m.) energy of 10.58 GeV, corresponding to the mass of the resonance, as well as 18.0 fb-1 at 60 MeV below the nominal c.m. energy.
The Belle II detector consists of several nested detector subsystems arranged around the beam pipe in a cylindrical geometry. The innermost subsystem is the vertex detector, which includes one or two layers of silicon pixels and four outer layers of silicon strips. Outside the silicon, the central drift-chamber reconstructs charged-particles trajectories (tracks). Outside the chamber, a Cherenkov light-imaging and time-of-propagation detectors provide charged particle identification. Further out is an electromagnatic calorimeter with CsI(Tl) crystals. A uniform 1.5 T magnetic field aligned with the beam axis is provided by a superconducting solenoid. Multiple layers of scintillators and resistive plate chambers, located between the magnetic flux-return iron plates, detect and muons.
The analysis uses simulated Monte Carlo (MC) samples to determine the signal efficiency and background yields. These samples are generated using EvtGen [8] and consist of (generic) and processes, where indicates a or a meson and indicates an , , , or quark (continuum). The latter is simulated with KKMC [9] and PYTHIA [10]. The luminosity of the generic and continuum samples is 1 ab-1. The signal is modeled using the CLN form factor parameterization [11], and the time-integrated -mixing parameter [12]. All samples are analyzed with the basf2 framework [13, 14]. In this paper, the natural system of units with is used. The inclusion of charge-conjugated decay modes is implied unless otherwise stated.
3 Event selection
The reconstruction begins by fully reconstructing a or () in hadronic decay modes with the FEI algorithm [5]. The algorithm starts by selecting candidates for stable particles, which include muons, electrons, pions, protons, kaons, and photons, from tracks and electromagnetic energy deposits in each event. Subsequently, the algorithm carries out several stages of reconstruction of intermediate particles such as , , , and mesons, , , and baryons. Intermediate particles are reconstructed in specific decay modes from combinations of stable and other intermediate particle candidates. The final stage of the algorithm reconstructs the mesons in 31 hadronic modes, using boosted decision trees (BDTs). The candidates are required to have a BDT classifier output greater than 0.001, a beam constrained mass GeV , and an energy difference in the interval [-0.15, 0.1] GeV, where is half of the collision energy, and and are the momentum and energy of the candidate, all in the center-of-mass frame. The efficiency of the FEI is calibrated with decays [5].
An event-level selection requires more than three tracks, between 2 and 7 GeV of total energy in the electromagnetic calorimeter, and a ratio of the second to zeroth order Fox Wolfram moments, R2 [15], to be smaller than 0.4. The remaining or meson (the signal side ) is reconstructed in its decay of ( , ). Charged particles are required to originate from the interaction point and have a transverse momentum greater than 0.2 GeV. To identify electrons and muons, a likelihood-ratio like quantity for each particle hypothesis is calculated, which combines information from several detector subsystems. The likelihood performance is calibrated with well-known physics processes. In addition, electron and muon momenta are required to be greater than 1.0 GeV in the center-of-mass frame to reject continuum background. Kaon and pion candidates are combined to reconstruct candidates whose invariant mass is required to be within the interval [1.85, 1.88] GeV. The candidates are combined with an additional low-momentum pion to reconstruct candidates restricted to the - mass difference in the range [0.143, 0.149] GeV. Subsequently, candidates are reconstructed by combining candidates with either or candidates. At least one combination of and candidates is required with no remaining tracks. The missing neutrino mass squared (, where denotes a four vector) is required to be in the range [-0.5, 0.5] GeV2. If multiple combinations of and candidates are found in an event, the candidate with the largest BDT output for the and the best for the is selected. Figure 1 shows the , , and distributions. The figures include data points with statistical uncertainties and histograms for simulated signal and background candidates scaled to the equivalent data luminosity. The signal yield is estimated by counting the number of selected events on data from which simulated background is subtracted. Checks based on data in the sidebands show good agreement between simulated and experimental background distributions.
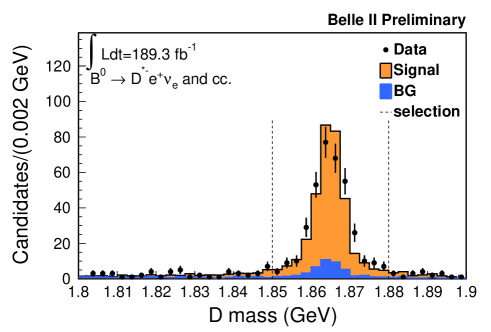
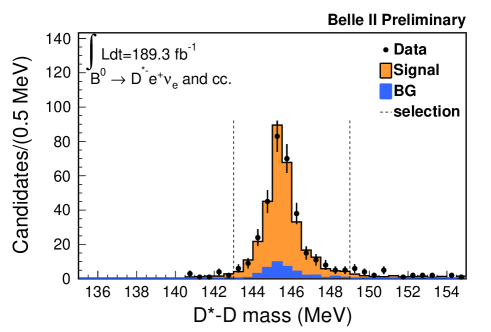
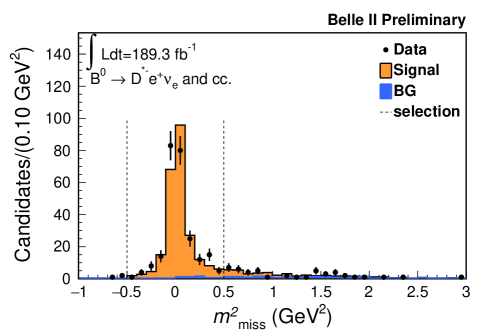
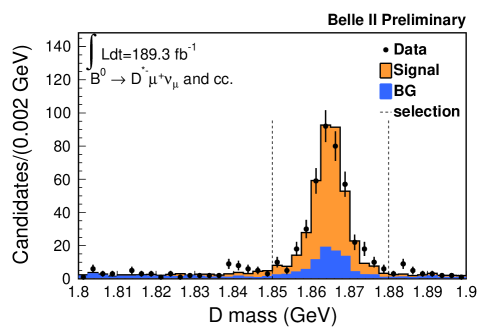
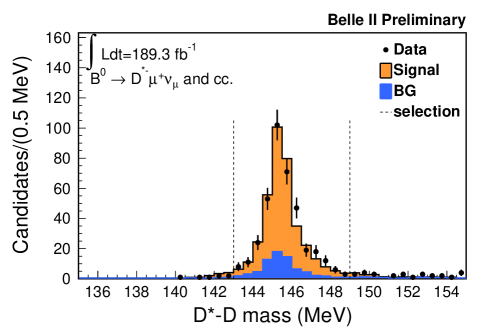
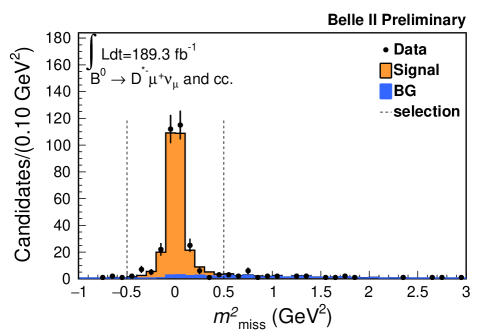
4 Measurement of branching ratio
The branching ratio for the decay is estimated as
| (1) |
where is the number of reconstructed events in data, is the number of reconstructed background events, is the signal reconstruction efficiency, is the number of produced pairs, and is the ratio of the number of produced and pairs. In Eq. 1, the values corresponding to electron and muon modes are averaged. The values of and are estimated from the background and signal simulation. The value of is determined using the R2 distribution after a subtraction of the continuum background using off-resonance data. The values for , , , and fraction of mixed and unmixed are taken from Ref. [12]. The input values for the branching fraction measurement are summarized in Table 1.
| Variables | Values |
|---|---|
| (data) | |
5 Measurement of
Figure 2 shows distribution of the recoil variable
| (2) |
where and are the known masses of the indicated particles. The decay-width differential in is as follows [4, 16]:
| (3) |
Here, is an electroweak correction (calculated to be in Ref. [17]). From lattice QCD, is calculated as [17]. The product describes the phase-space factor and the form factor, which is parameterized with in the CLN approach [11]. The CKM matrix element is determined by fitting the distribution with the form factor parameters. However, here the product is measured instead, in order to separate theory uncertainty of and . In this paper, the and values are taken from external measurements [1], as shown in Table 2.
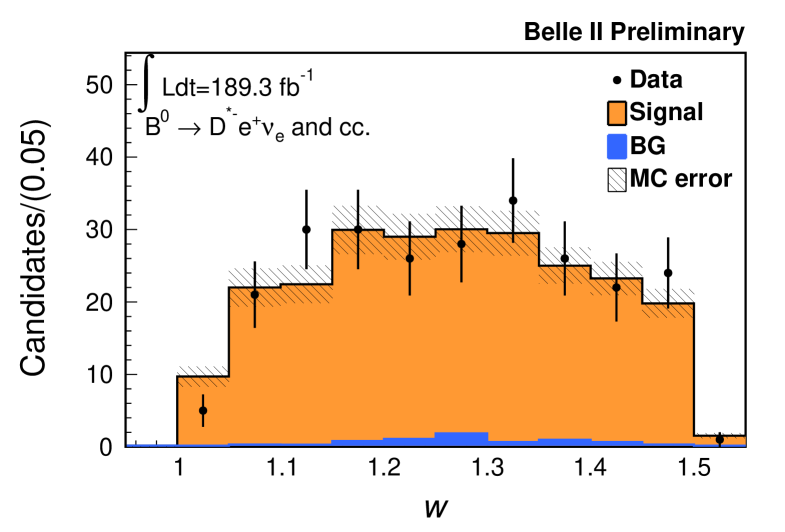
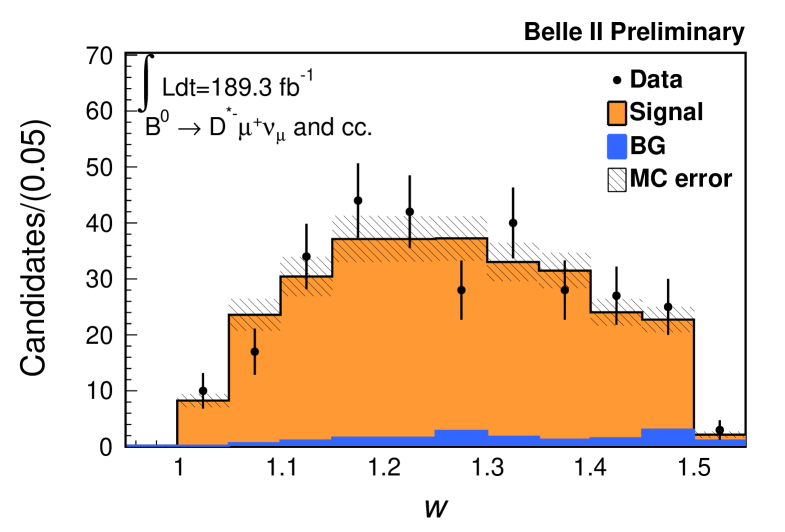
| 1.270 0.026 | |
| 0.852 0.018 | |
| Correlation coefficient of and | -0.715 |
5.1 Unfolding method
In order to estimate the true distribution from the observed values, an iterative unfolding method is used [18]. The number of signal events populating bin, , is estimated from the reconstructed variables as follows:
| (4) |
where is the bin number. We define 10 bins in the range each with a width of 0.05. The matrix models the probability that events reconstructed in the bin are in the true- bin , which is calculated by Bayes’ theorem according to
| (5) |
Here, is estimated with simulation. To avoid bias from the simulated signal, is calculated using the reconstructed distribution on data as follows.
-
1.
is assumed uniform ( for all bins).
-
2.
is calculated by using Eq.(5).
-
3.
is set to .
-
4.
Steps 2. and 3. are repeated 10 times, until converges.
The unfolding performance is validated with the simulation.
5.2 Fitting method
To determine , a binned maximum likelihood fit is performed using
| (6) |
where denotes the bin, is the number of observed events in the th bin, is a systematic parameter defined as the normalization uncertainty in the th reconstructed- bin, is the deviation of the systematic parameters from the nominal value, and is the covariance of the systematic parameters, modeled by multivariate Gaussians functions. Finally, is the expected yield in the th bin, which is written as follows:
| (7) |
where is the signal reconstruction efficiency in the th bin. The differential distribution is obtained using Eq.(3). In the fit there are two free parameters, and , and ten nuisance parameters . The two-dimensional contour of and is estimated by using a marginalized likelihood [19],
| (8) |
where and is the expected yield in the th bin with the th set of nuisance parameters, which is generated following the covariance matrix. The fitter performance is validated with simplified simulated experiments.
6 Systematic uncertainties
Systematic uncertainties are evaluated for several sources associated with the detector response, MC modeling, and physics inputs. For the branching ratio measurement, the systematic uncertainty of each source is propagated to the result based on Eq.(1) and summarized in Table 3. The reconstruction efficiency with the FEI algorithm is studied using decays and a systematic uncertainty of 3.9% is assigned [5]. The tracking efficiency is studied with decays and the maximum data-simulation difference of 0.3% is taken as systematic uncertainty for each track in the final state. The reconstruction efficiency of the low momentum is studied by using decays. The data-MC ratio of the momentum distribution is evaluated relative to the high momentum distribution; a 3–4% systematic uncertainty is assigned in each momentum bin, which is dominated by the statistical uncertainty of the control samples. Electron and muon identification efficiencies and misidentification rates are studied by using , , , decays of , , , and . The lepton identification and misidentification uncertainties associated with the size of the control samples, background contamination, modeling of the fitting function, trigger, and the difference of the results across samples are evaluated as a functions of each lepton angle and the absolute value of the lepton momentum. These uncertainties are propagated to the branching fraction measurement resulting in a total 2.0% systematic error. The potential variations in the amount of background from decays, hadronic decays and misreconstructed mesons are evaluated to propagate the uncertainty of the branching fraction of the background processes and of beam backgrounds resulting in a 1.2% systematic uncertainty. The number of produced pairs is estimated from the R2 distribution after a subtraction of the continuum background using off-resonance data. A systematic uncertainty of 2.9% is assigned to account for the limited statistics of off-resonance data, operation conditions of the detector and accelerator including beam energy, and selection efficiencies. A systematic uncertainty for the event-level selection is estimated to be 1.0%, to cover the maximum data-simulation difference of the total energy in the electromagnetic calorimeter. The uncertainty from the limited size of simulated samples is estimated to be 1.8%. The following sources of systematic uncertainty are from external measurements: the ratio of the number of produced and pairs (1.2%), the ratio of the number of mixed and unmixed (0.9%), the branching fractions of (0.7%) and (0.8%), and form factors (0.1%) [12]. The uncertainties from the various sources are assumed to be independent and the quadratic sum is taken as a total systematic uncertainty. For the measurement of and , the effect of the systematic uncertainty is included in the likelihood calculation (the second term in Eq.(6)) with the covariance matrix
| (9) |
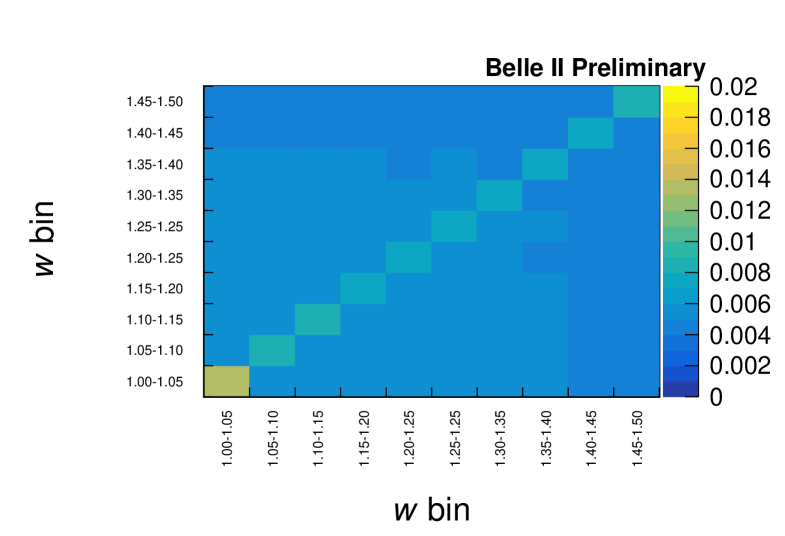
Here, runs over the sources of uncertainties, is the mean of the expected yield in the th bin, is the variation of the expected yield in the th bin for the th source of uncertainties. Figure 3 shows the estimated covariance matrix.
| Systematic sources | Relative uncertainty (%) |
|---|---|
| FEI efficiency | 3.9 |
| Low momentum efficiency | 4.1 |
| Tracking efficiency | 0.9 |
| Lepton particle identification | 2.0 |
| Background | 1.2 |
| 2.9 | |
| 1.2 | |
| Number of mixed | 0.9 |
| 0.7 | |
| 0.8 | |
| ECL energy | 1.0 |
| Form factor | 0.1 |
| MC sample size | 1.8 |
| Total | 7.3 |
7 Results and conclusion
The result for the branching fraction is
| (10) |
while the results for are
| (11) | ||||
| (12) |
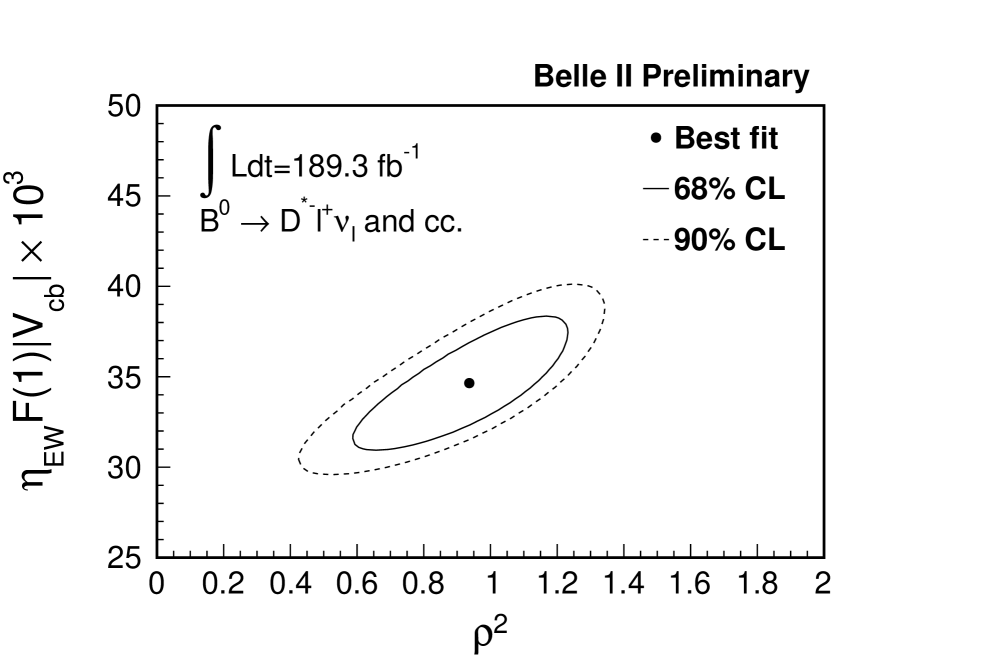
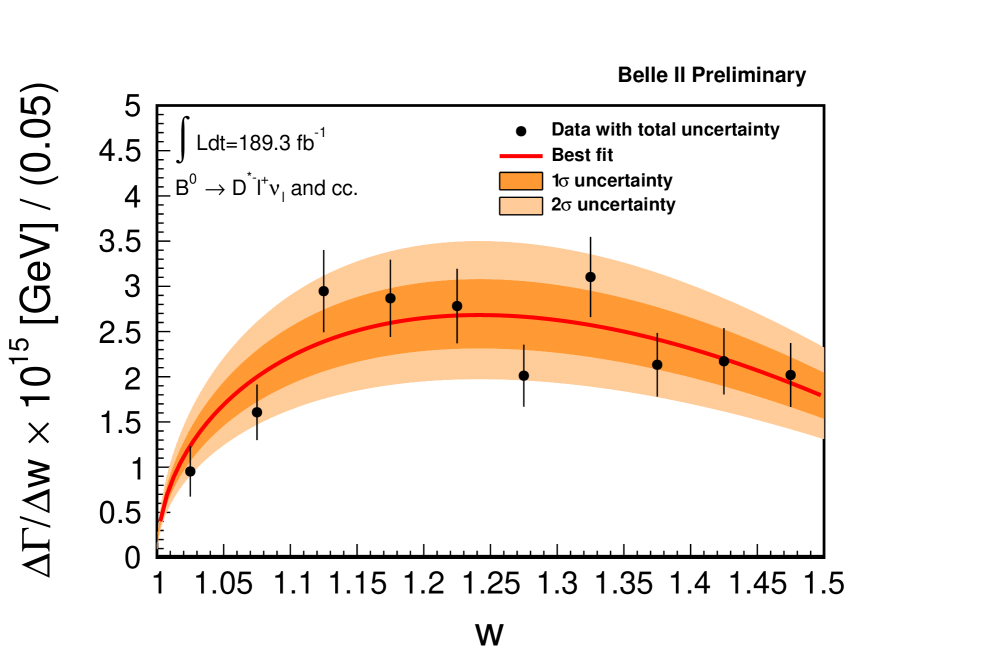
The two-dimensional probability contours for and are shown in Fig. 4. The observed values are shown in Fig. 5 with the best fit function overlaid. The reduced of the fit is 1.6 with p-value of 40.7, which is estimated by simulation. Under the assumption that and [17], we obtain . The results are consistent with the world averages of and based on exclusive decays within one standard deviation [1].
8 Acknowledgement
These acknowledgements are not to be interpreted as an endorsement of any statement made by any of our institutes, funding agencies, governments, or their representatives.
We thank the SuperKEKB team for delivering high-luminosity collisions; the KEK cryogenics group for the efficient operation of the detector solenoid magnet; the KEK computer group and the NII for on-site computing support and SINET6 network support; and the raw-data centers at BNL, DESY, GridKa, IN2P3, INFN, and the University of Victoria for offsite computing support.
References
- [1] Y. S. Amhis et al., HFLAV, Averages of b-hadron, c-hadron, and -lepton properties as of 2018, Eur. Phys. J. C 81 (2021) no. 3, 226, arXiv:1909.12524 [hep-ex].
- [2] F. U. Bernlochner, M. F. Sevilla, D. J. Robinson, and G. Wormser, Semitauonic b-hadron decays: A lepton flavor universality laboratory, Rev. Mod. Phys. 94 (2022) no. 1, 015003, arXiv:2101.08326 [hep-ex].
- [3] N. Cabibbo, Unitary Symmetry and Leptonic Decays, Phys. Rev. Lett. 10 (Jun, 1963) 531–533.
- [4] M. Kobayashi and T. Maskawa, CP Violation in the Renormalizable Theory of Weak Interaction, Prog. Theor. Phys. 49 (1973) 652–657.
- [5] F. Abudinén et al., Belle-II, A calibration of the Belle II hadronic tag-side reconstruction algorithm with decays, arXiv:2008.06096 [hep-ex].
- [6] T. Abe et al., Belle-II, Belle II Technical Design Report, arXiv:1011.0352 [physics.ins-det].
- [7] K. Akai, K. Furukawa, and H. Koiso, SuperKEKB, SuperKEKB Collider, Nucl. Instrum. Meth. A 907 (2018) 188–199, arXiv:1809.01958 [physics.acc-ph].
- [8] D. J. Lange, The EvtGen particle decay simulation package, Nucl. Instrum. Meth. A 462 (2001) 152–155.
- [9] B. F. L. Ward, S. Jadach, and Z. Was, Precision calculation for e+ e- — 2f: The KK MC project, Nucl. Phys. B Proc. Suppl. 116 (2003) 73–77, arXiv:hep-ph/0211132.
- [10] T. Sjostrand, S. Mrenna, and P. Z. Skands, A Brief Introduction to PYTHIA 8.1, Comput. Phys. Commun. 178 (2008) 852–867, arXiv:0710.3820 [hep-ph].
- [11] I. Caprini, L. Lellouch, and M. Neubert, Dispersive bounds on the shape of form factors, .
- [12] P. Zyla et al., Particle Data Group, Review of Particle Physics, PTEP 2020 (2020) no. 8, 083C01.
- [13] T. Kuhr, C. Pulvermacher, M. Ritter, T. Hauth, and N. Braun, Belle-II Framework Software Group, The Belle II Core Software, Comput. Softw. Big Sci. 3 (2019) no. 1, 1, arXiv:1809.04299 [physics.comp-ph].
- [14] The Belle II Collaboration, Belle II Analysis Software Framework (basf2), https://doi.org/10.1007/s41781-018-0017-9.
- [15] G. C. Fox and S. Wolfram, Observables for the Analysis of Event Shapes in e+ e- Annihilation and Other Processes, Phys. Rev. Lett. 41 (1978) 1581.
- [16] M. Neubert, Heavy quark symmetry, Phys. Rept. 245 (1994) 259–396, arXiv:hep-ph/9306320.
- [17] J. A. Bailey et al., Fermilab Lattice, MILC, Update of from the form factor at zero recoil with three-flavor lattice QCD, Phys. Rev. D 89 (2014) no. 11, 114504, arXiv:1403.0635 [hep-lat].
- [18] G. Cowan, A survey of unfolding methods for particle physics, Conf. Proc. C 0203181 (2002) 248–257.
- [19] K. A. Olive et al., Particle Data Group, Review of Particle Physics, Chin. Phys. C 38 (2014) 090001.