Measurement of the cross section for $e^{+}e^{-}\rightarrow\Lambda\bar{\Lambda}$ and evidence of the decay $\psi(3770)\rightarrow\Lambda\bar{\Lambda}$

Two-body baryonic decays of vector ($J^{PC}=1^{--}$) charmonium(-like) resonances provide a testing ground of predictions from quantum chromodynamics Farrar ; Briceno . The $\psi(3770)$ vector meson is believed to be a conventional $c\bar{c}$ state located above the open-charm threshold and is expected to decay into a $D\bar{D}$ meson pair with a branching fraction of at least 99% Eichten . However, the decay modes to light quark systems would be considerably enhanced if the $\psi(3770)$ would include gluonic or light quark and antiquark constituents  Close:2005iz . In 2003, the BES collaboration observed the first non-$D\bar{D}$ decay of $\psi(3770)$ into $J/\psi\pi^{+}\pi^{-}$ hepnp28_325 ; hepnp28_325-1 . Subsequently, the CLEO collaboration confirmed the observation and found more non-$D\bar{D}$ decays of $\psi(3770)$ prl96_082004 ; prl96_082004-1 ; prl96_082004-2 and the first decay into light-quark hadrons $\psi(3770)\rightarrow\phi\eta$ prd73_012002 .

The production of light quark baryon-antibaryon ($B\bar{B}$) final states leads to relatively simple topologies. In an early study, the BESIII collaboration found evidence for the interference effect in $e^{+}e^{-}\rightarrow p\bar{p}$ in the vicinity of $\psi(3770)$ Ablikim:2014jrz . However, the data did not allow to uncover the mechanism of $\psi(3770)$ charmless decays. Thus, the experimental study of $e^{+}e^{-}\rightarrow B\bar{B}$ will be a good search-ground for clarifying the nature of the charmless decays and even non-$D\bar{D}$ decays of $\psi(3770)$ Wan:2021vny ; Cao:2021asd ; Xia:2015mga .

In the past two decades, several vector states were observed at energies between 3.7 and 4.7 GeV at various $e^{+}e^{-}$ colliders. Four charmonium(-like) states predicted by potential models Farrar $\psi(3770)$, $\psi(4040)$, $\psi(4160)$ and $\psi(4415)$ have been observed as enhancements in the inclusive hadronic cross section PDG2016 ; Wang:2019ugd . In addition, new states such as $Y(4230)$, $Y(4260)$, $Y(4360)$, $X(4390)$, and $Y(4660)$, were reported using the initial state radiation (ISR) processes $e^{+}e^{-}\rightarrow\gamma_{ISR}\pi^{+}\pi^{-}J/\psi(\psi(3686))$ at the BABAR BABAR01 ; BABAR01-1 ; BABAR01-2 ; BABAR01-3 and Belle BELLE01 ; BELLE01-1 ; BELLE01-2 ; BELLE01-3 ; BELLE01-4 experiments, or in energy-scan experiments at the CLEO-c CLEO and BESIII BESIIIAB ; BESIIIAB01 ; BESIIIAB03 ; BESIIIAB04 ; BESIIIAB05 ; BESIIIAB06 experiments. Up to now, no evidence for decay modes into light-quark baryon–antibaryon pairs of these charmonium(-like) states has been found. The overpopulation of vector charmonium(-like) resonances with respect to predictions from potential models, and the difficulty in describing the properties of these states make them attractive candidates for exotic states QCD . In addition, knowledge of the vector charmonium(-like) coupling to the $B\bar{B}$ final states is crucial for understanding the electromagnetic structure of the baryons. In Refs. Dobbs:2014ifa ; Dobbs:2014ifa-1 , the timelike electromagnetic form factors for the ground-state octet baryons were determined based on the CLEO-c data. They assumed that the branching fractions of $\psi(3770)$ to the $B\bar{B}$ final states scale with the decay widths into a pair of electrons (electronic decay widths) when comparing to the $\psi(3686)$ state, e.g., one estimates a negligible branching fraction ${\cal B}(\psi(3770)\to\Lambda\bar{\Lambda})\approx 5\times 10^{-7}$.

In this paper, we present a measurement of the Born cross section for the $e^{+}e^{-}\rightarrow\Lambda\bar{\Lambda}$ process using data corresponding to a total integrated luminosity of 20.0 fb^-1 ABC ; Ablikim:2015nan ; Ablikim:2015zaa collected at center-of-mass (c.m.) energies $\sqrt{s}$ between 3.51 and 4.60 GeV with the BESIII detector Wang:2007tv ; Wang:2007tv-1 at the BEPCII collider BESIII . We extract the $\Lambda$ effective form factor and report an evidence of the $\psi(3770)\rightarrow\Lambda\bar{\Lambda}$ process by fitting the $e^{+}e^{-}\rightarrow\Lambda\bar{\Lambda}$ dressed cross section.

Candidates for $e^{+}e^{-}\rightarrow\Lambda\bar{\Lambda}$ events are reconstructed using the $\Lambda\rightarrow p\pi^{-}$ and $\bar{\Lambda}\rightarrow\bar{p}\pi^{+}$ decay modes. The detection efficiency is determined by Monte Carlo (MC) simulations. A sample of 100,000 events is simulated for each of the 33 c.m. energy points. The production process is simulated by the kkmc generator kkmc ; kkmc-1 that includes corrections for ISR effects. The $\Lambda$ and $\bar{\Lambda}$ decays are handled by the evtgen evt2 ; evt2-01 program. The response of the BESIII detector is modeled with MC simulations using a framework based on geant4 geant4 ; geant4-01 .

Tracks of charged particles are reconstructed in the multilayer drift chamber with a helical fit requiring a good quality Asner:2008nq . These tracks should be within $|\cos\theta|<0.93$, where $\theta$ is the polar angle with respect to the $e^{+}$ beam direction. Events with two successfully reconstructed negatively charged and two positively charged particles are kept for further analysis.

To reconstruct $\Lambda(\bar{\Lambda})$ candidates, we apply a secondary vertex fit XUM to all pairs of positive and negative charged particles. The corresponding $\chi^{2}$ value is required to be less than $500$. The track combination with minimum ${|M_{p\pi^{-}}-m_{\Lambda}|^{2}+|M_{\bar{p}\pi^{+}}-m_{\Lambda}|^{2}}$ is selected, where $M_{p\pi^{-}}(M_{\bar{p}\pi^{+}})$ is the invariant mass of the $p\pi^{-}(\bar{p}\pi^{+})$ pair, and $m_{\Lambda}$ is the world-average $\Lambda$ mass value from the Particle Data Group (PDG) PDG2016 . To further suppress background from non-$\Lambda$ processes, the $\Lambda$ decay length is required to be larger than zero, where the observed negative decay lengths are caused by the limited detector resolution. Here the misreconstruction ratio for $\Lambda$ particle is found to be less than 1% based on the study of MC simulation.

To further suppress the background and to improve the mass resolution, a four-constraint (4C) kinematic fit imposing energy-momentum conservation is applied for the $\Lambda\bar{\Lambda}$ hypothesis. The $\chi^{2}_{4C}$ of the fit is required to be less than 200, which can improve the resolutions of signals significantly in addition to suppressing backgrounds for a soft $\pi^{0}$ and radiated photons event. Figure 1 shows the distribution of $M_{p\pi^{-}}$ versus $M_{\bar{p}\pi^{+}}$ of the accepted candidates from all data samples. Clear peaks around the $\Lambda$ known mass can be discerned.

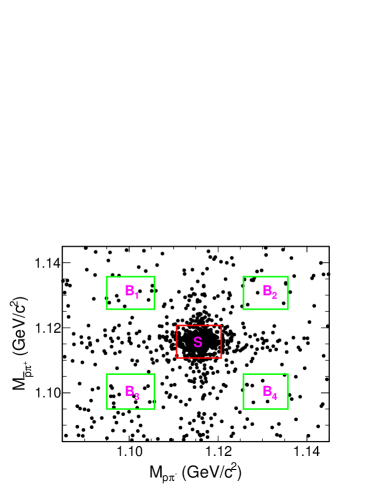
The invariant mass $M_{p\pi^{-}}$ is required to be within 5 MeV/$c^{2}$ of the known $\Lambda(\bar{\Lambda})$ mass (signal region marked by $S$). After applying the above selection criteria, the survived background events are mainly from non-$\Lambda(\bar{\Lambda})$ events, such as $e^{+}e^{-}\rightarrow\pi^{+}\pi^{-}p\bar{p}$. The background yield in the signal region is estimated using four sideband regions $B_{i}$, where $i=1,2,3,4$, each with the same area as the signal region. The regions are shown in Fig. 1, and the exact ranges are given in the Supplemental Material ABC . The signal yield $N_{obs}$ for $e^{+}e^{-}\rightarrow\Lambda\bar{\Lambda}$ events at each energy point can then be extracted by subtracting the number of events in the sideband regions from the number of events in the signal region, $N_{S}$: $N_{obs}=N_{S}-\frac{1}{4}\sum^{4}_{i=1}N_{B_{i}}$, and they are listed in Table 1.

The ISR corrected (“dressed”) cross section $\sigma^{\rm dr}$ for the process $e^{+}e^{-}\rightarrow\Lambda\bar{\Lambda}$ is defined as

$$\sigma^{\rm dr}(s)=\frac{N_{obs}}{{\cal{L}}(1+\delta)\epsilon\ {\cal B}^{2}(\Lambda\rightarrow p\pi^{-})}\ ,$$

(1)

where ${\cal{L}}$ is the integrated luminosity at given c.m.  energy $\sqrt{s}$, $(1+\delta)$ is the ISR correction factor Jadach:2000ir ; kkmc-1 , $\epsilon$ is the detection efficiency, and the branching fraction ${\cal B}(\Lambda\rightarrow p\pi^{-})=(63.9\pm 0.5)\%$ is taken from PDG. The ISR correction factor is obtained using the calculation described in Ref. Kuraev:1985hb , where the dressed cross sections are adopted as initial input and are iterated to obtain stable result. The dressed cross section is related to the Born cross section via the vacuum polarization factor $\frac{1}{|1-\Pi|^{2}}$ Actis:2010gg as $\sigma^{\rm dr}=\ \sigma^{B}/|1-\Pi|^{2}$ (further details are provided in the Supplemental Material ABC ).

Systematic uncertainties on the cross section measurement mainly come from the luminosity measurement, the $\Lambda$ reconstruction, the 4C kinematic fit, the branching fraction for the decay $\Lambda\rightarrow p\pi^{-}$, the line-shape description, and the physical model dependence. The uncertainty due to the vacuum polarization is negligible. The integrated luminosity is measured by $e^{+}e^{-}\rightarrow(\gamma)e^{+}e^{-}$ events with a similar method to Ref. Ablikim:2015nan with an uncertainty of 1.0%. The systematic uncertainty of the $\Lambda(\bar{\Lambda})$ reconstruction incorporating the tracking, the mass window of $\Lambda(\bar{\Lambda})$, and the decay length of $\Lambda(\bar{\Lambda})$ is studied using a control sample of $\psi(3686)\rightarrow\Lambda\bar{\Lambda}$ decay ($\sim$ 20000 events) with the same method as introduced in Refs. Ablikim:2016iym ; Ablikim:2016iym-1 ; Ablikim:2016iym-2 ; Ablikim:2016iym-3 ; Ablikim:2016iym-4 ; Ablikim:2016iym-5 ; BESIII:2021gca . The signal MC sample is simulated using a DIY model evt2 implementing the joint angular distribution from Refs. Faldt:2017kgy ; nature . The efficiency difference between data and MC simulation is found to be 0.5% for the $\Lambda$ reconstruction and 1.5% for the $\bar{\Lambda}$ reconstruction. The uncertainty from the 4C kinematic fit is studied using the control sample of $\psi(3686)\rightarrow\Lambda\bar{\Lambda}$ decays with and without performing a 4C kinematic fit. The relative change of 1.0% is assigned as the systematic uncertainty. The uncertainty of the branching fraction for $\Lambda\rightarrow p\pi^{-}$ from the PDG PDG2016 is 0.8%, and is propagated to the final result. The uncertainty from the line-shape description is estimated with an alternative input cross section line shape based on a simple power-law function. The change of the efficiency, 2.6%, is taken as the systematic uncertainty. The uncertainty due to the physical model dependence is estimated to be 2.5% by comparing the efficiencies between phase space and the DIY model incorporating the $\Lambda$ transverse polarization and spin correlation based on the control sample of $\psi(3770)\rightarrow\Lambda\bar{\Lambda}$ decays. Assuming all sources are independent, the total systematic uncertainty on the cross section measurement is determined to be 4.3% by adding these sources in quadrature. The correlations for the different points are negligible due to the limited statistics.

The extracted Born cross sections at each energy point are listed in Table 1 and shown in Fig. 2(top) together with the CLEO-c results at 3.770 and 4.160 GeV Dobbs:2014ifa ; Dobbs:2014ifa-1 . Our results are significantly lower than those of CLEO-c at both energy points. Figure 2 (bottom) shows the extracted energy dependence of the $\Lambda$ effective form factor $G_{\rm eff}(s)$ defined as Ablikim:2019kkp

$$G_{\rm eff}(s)=\sqrt{\frac{3s\tau\sigma^{B}}{2\pi\alpha^{2}\beta(2\tau+1)}}\ ,$$

(2)

where $\alpha$ is the fine-structure constant, $\beta=\sqrt{(\tau-1)/\tau}$ is the $\Lambda$ velocity and $\tau={s}/({4m^{2}_{\Lambda}})$.

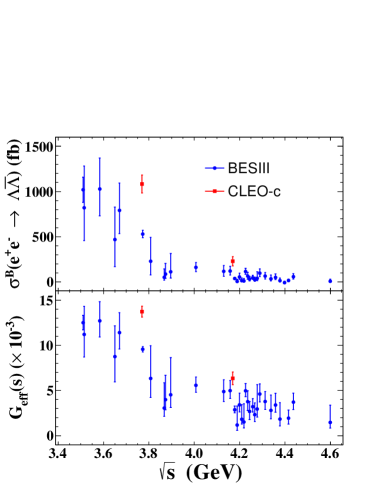
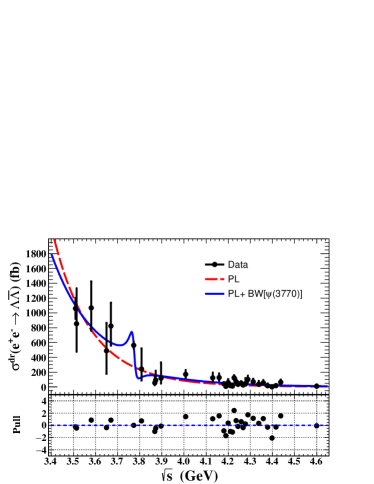
The dressed cross section for the continuum $e^{+}e^{-}\rightarrow\Lambda\bar{\Lambda}$ process is expected to have an asymptotic power-law behavior $\propto s^{-n}$ with the exponent $n\approx 10$ Ablikim:2019kkp ; Lepage:1980fj ; Lepage:1980fj-1 . A least-$\chi^{2}$ fit including statistical and systematic uncertainties to the power-law distribution describes the data points reasonably well, as shown with the dashed line in Fig. 3. The fitted value of the exponent $n$ is not close to 10 within the uncertainty of 1$\sigma$, as shown in the column “Fit I” in Table 2. A fit with the coherent sum of the power-law function and a Breit-Wigner (BW) function

$$\sigma^{\rm dr}({s})=\left|\sqrt{\sigma_{\rm 0}}{\left(\frac{M}{\sqrt{s}}\right)^{n}}+e^{i\phi}{\rm BW}({s})\right|^{2}$$

(3)

is applied, where $M$ is the $\psi(3770)$ mass, $\sigma_{0}$ is the value of the continuum cross section at $\psi(3770)$ and $\phi$ is the relative phase between the continuum and the resonance. The BW function is

$${\rm BW}({s})=\frac{\sqrt{\sigma_{\psi}}M\Gamma}{s-M^{2}+iM\Gamma}\ {\rm with}\ \sigma_{\psi}\!=\!\frac{{12\pi(\hbar c)^{2}{\Gamma}_{ee}{\cal{B}}}}{\Gamma M^{2}}\ ,$$

(4)

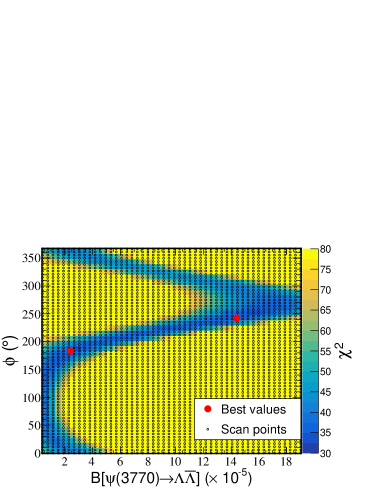
where $\Gamma$ and ${\Gamma}_{ee}$ are the total and the electronic width of the $\psi(3770)$ resonance, respectively, and ${\cal{B}}$ denotes the branching fraction to $\Lambda\bar{\Lambda}$. The solid line in Fig. 3 and the column ”Fit II” in Table 2 shows the result of the fit with two solutions, where the mass and width of $\psi(3770)$ are fixed according to the PDG values PDG2016 , and $\sigma_{0}$, $n$, $\phi$ and $\sigma_{\psi}$ parameters are free. The improvement of the $\chi^{2}$ value gives a significance of 4.6$-$4.9$\sigma$ for the hypothesis with the $\psi(3770)$ resonance including the systematic uncertainty. The correlation coefficient between the resonance cross section $\sigma_{\psi}$ and the phase $\phi$ is almost equal to one. In the Fit II, two solutions are expected according to mathematical calculation Zhu:2011ha ; Zhu:2011ha-1 , but fits give the consistent results within the uncertainty of 1$\sigma$ due to statistics limitation. Figure 4 shows the contour of ${\cal{B}}$ and $\phi$ on the distribution of $\chi^{2}$ values for each set of parameters. Our results can be summarized by giving 90% C.L. intervals $24<\sigma_{\psi}<1800$ fb and $2.4\times 10^{-6}<{\cal B}<1.8\times 10^{-4}$. This represents the first evidence of the decay $\psi(3770)\rightarrow\Lambda\bar{\Lambda}$. This result is larger by at least an order of magnitude than the prediction based on a scaling from the electronic branching fraction value. This implies, that the $\psi(3770)$ resonance needs to be considered when interpreting the CLEO-c data. Note that the systematic uncertainties due to beam energy, mass and width of the $\psi(3770)$ resonance have been considered by varying the known value within one standard deviation, and they turn out to be negligible.

Finally, we have included an additional charmonium(-like) state (i.e. $\psi(4040)$, $\psi(4160)$, $Y(4260)$, or $\psi(4415)$) in the fit, one at a time. It turns out that the exponent and significance for the $\psi(3770)$ state are consistent with a single resonance assumption. Since the significance of each mentioned state is smaller than 3$\sigma$, we quote upper limits at the 90% C.L. for the $\Gamma_{ee}{\cal B}$ products: $<5.5\times 10^{-3}$ eV for $\psi(4040)$, $<0.7\times 10^{-3}$ eV for $\psi(4160)$, $<0.8\times 10^{-3}$ eV for $Y(4260)$ and $<1.8\times 10^{-3}$ eV for $\psi(4415)$ including the systematic uncertainty. These results provide important information to understand the nature of charmonium(-like) states above the open charm threshold. In particular this concerns their coupling to the $B\bar{B}$ final states and insight into the puzzle of large non-$D\bar{D}$ component of $\psi(3770)$.