The Belle and Belle II Collaborations

Electroweak penguin quark transitions mediated by flavor changing neutral currents (FCNCs) such as $b\rightarrow s\,\ell^{+}\ell^{-}$, $b\rightarrow d\,\ell^{+}\ell^{-}$, and $c\rightarrow u\,\ell^{+}\ell^{-}$ (where $\ell^{\pm}$ is an electron or muon) are forbidden at tree level in the standard model (SM) ¹¹1The inclusion of the charge-conjugate decay mode is implemented throughout the letter unless otherwise stated.. The FCNCs proceed through electroweak box or loop diagrams and are thus highly suppressed, and thus $c\rightarrow u\,\ell^{+}\ell^{-}$ decays probe beyond the standard model (BSM) physics that could affect the decay rate and other variables. The BSM amplitudes can interfere with the SM amplitudes, altering physics observables from the SM predictions such as total and differential decay rates, and affecting tests of lepton flavor universality (LFU) [2, 3, 4, 5, 6].
The decays $c\rightarrow u\,\ell^{+}\ell^{-}$ are FCNC transitions of a charm quark to an up quark and a lepton pair. Compared to $b\rightarrow s\,\ell^{+}\ell^{-}$ and $b\rightarrow d\,\ell^{+}\ell^{-}$ decays, these transitions are further suppressed due to the Glashow–Iliopoulos–Maiani mechanism and the small quark masses relative to the top quark in the loop [7]. The decays $D^{0}\rightarrow X^{0}\ell^{+}\ell^{-}$, where $X^{0}$ is a light-quark system, can have contributions from both short-distance (SD) and long-distance (LD) amplitudes, as shown in Fig. 1. The SD decay amplitudes are suppressed, with branching fractions ($\mathcal{B}$) reaching only the $2\times 10^{-9}$ level [8]. However, LD contributions from photon pole or vector meson dominance (VMD) amplitudes, which proceed through the decays $D^{0}\rightarrow X^{0}(\gamma^{*}/V^{0})\rightarrow X^{0}\ell^{+}\ell^{-}$, where $\gamma^{*}$ is an off-shell virtual photon and $V^{0}$ is an intermediate vector meson ($\rho,\,\omega,\,\phi$), can reach values of up to 2 $\times$ 10^-6 [8] for the Cabibbo-favored decay $D^{0}$ $\rightarrow$ $K^{-}\pi^{+}e^{+}e^{-}$.

We reconstruct $D^{0}\rightarrow K^{-}\pi^{+}e^{+}e^{-}$, $\pi^{+}\pi^{-}e^{+}e^{-}$, and $K^{+}K^{-}e^{+}e^{-}$ signal candidates from the selected kaon, pion, and electron candidates. Candidates with $D^{0}$ invariant mass $m_{hh^{(\prime)}ee}$ in the range 1.80 $<m_{hh^{(\prime)}ee}<$ 1.93 ${\mathrm{\,Ge\kern-1.00006ptV\!/}c^{2}}$ are combined with a $\pi^{+}$ candidate to form a $D^{*+}$ candidate. The requirement of a $D^{*+}$ tagged $D^{0}$ suppresses the background from random track combinations. Candidates must have a $D^{*+}$ momentum in the center-of-mass frame $p^{*}(D^{*+})>2.5$ ${\mathrm{\,Ge\kern-1.00006ptV\!/}c}$ to reduce the combinatorial background from $B$ decays and a mass difference between $D^{*+}$ and $D^{0}$ candidates $\Delta m$ within 0.5 ${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$ of the nominal value [34] to be consistent with the decay $D^{*+}\rightarrow D^{0}\pi^{+}$. We also apply a vertex fit to the decay chain $D^{*+}\rightarrow D^{0}\pi^{+}$, $D^{0}$ $\rightarrow$ $hh^{(\prime)}ee$, with the $D^{*}$ production vertex constrained to the interaction point. We discard candidates that fail this fit.

The decay $\pi^{0}/\eta\rightarrow e^{+}e^{-}\gamma$ can produce a complicated background shape, which is difficult to model. The electron bremsstrahlung recovery can mistakenly include a photon originating from a $\pi^{0}/\eta$ decay so that the reconstructed $m(hh^{(\prime)}ee\gamma)$ will fake the signal. Such decays will also contribute to a background in the $m_{hh^{(\prime)}ee}$ region below the $D^{0}$ mass, resulting in a non-linear background shape. To suppress these backgrounds, we apply the selection $m_{ee}>200$ ${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$. In addition, we do not apply electron bremsstrahlung recovery for candidates with $m_{ee}$ in the $\eta$ mass region (520, 560${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$). The $m_{ee}$ $>$ 560 ${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$ is applied to the $K^{-}\pi^{+}e^{+}e^{-}$ for searching the signal not in the resonant region to suppress the $D^{0}\rightarrow K^{-}\pi^{+}\eta\,\,[\rightarrow e^{+}e^{-}\gamma]$ background.

Some candidates include electrons originating from photon conversions. In order to veto these events, we combine the $e^{\pm}$ from the signal ($D^{0}$) candidate with another oppositely charged track from the event to form a candidate $e^{+}e^{-}$ pair. We require a converged vertex fit for the photon conversion candidates $(e^{+}e^{-})$ and discard the corresponding $D^{0}$ candidate if the angle between the $e^{+}e^{-}$ tracks in the lab frame is less than 0.07 radians or the invariant mass of $e^{+}e^{-}$ tracks is less than 100 ${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$.

Hadronic $D^{0}$ decays in which one or more of the $D^{0}$ daughters are misidentified as leptons also contribute to the background. In each event, we reconstruct $D^{*+}\rightarrow D^{0}\pi^{+}_{s}$ with $D^{0}\rightarrow K^{-}\pi^{+}\pi^{-}\pi^{+}$, $D^{0}\rightarrow\pi^{+}\pi^{-}\pi^{+}\pi^{-}$, and $D^{0}\rightarrow K^{+}K^{-}\pi^{+}\pi^{-}$ decays in addition to the signal modes $hh^{(\prime)}e^{+}e^{-}$. We discard the corresponding signal candidate if any of the reconstructed hadronic $D^{0}$ decay candidates have invariant mass and $\Delta m$ within 3 ${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$ and 0.4 ${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$, respectively, of the corresponding nominal values.

For each signal mode, we optimize the selection criteria for $p^{*}(D^{*+})$, $\Delta m$, PID, photon conversion and hadronic $D^{0}$ vetos in the $\eta$ (520, 560), $\rho/\omega$ (675, 875), and $\phi$ (990, 1035${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$) mass regions in order to search for potential $ee$ resonant decays. We also search for $D^{0}$ $\rightarrow$ $h^{-}h^{(\prime)+}e^{+}e^{-}$ decays in the $m_{ee}$ spectrum not included in the resonant regions defined above which we refer to as ”non-resonant”. The $m_{ee}$ regions mentioned above are not individually optimized, with the $m_{ee}$ ranges covering about 80% of the corresponding $ee$ resonance regions. For events with more than one signal candidate, the candidate with $\Delta m$ closest to the known value is selected. We optimize the cuts by maximizing a figure-of-merit ${S}/{\sqrt{S+B}}$ for each $m_{ee}$ region, where $S$ and $B$ are the expected number of signal candidates in data estimated from PDG [34] branching fractions and background yields estimated using background MC samples, respectively. Since the $D^{0}$ production rate is not precisely known, we measure the signal branching fractions relative to the normalization decay $D^{0}$ $\rightarrow$ $K^{-}\pi^{+}\pi^{-}\pi^{+}$, with similar selections applied such as PID.

We calculate the signal branching fractions and upper limits using the equation

where $N$ are the yields, and $\epsilon$ are the reconstruction efficiencies. We measure the branching fractions or set branching fraction upper limits for various $m_{ee}$ regions in each $hh^{(\prime)}ee$ mode.

We use a one-dimensional unbinned extended maximum likelihood fit to $m_{hh^{(\prime)}ee}$ to extract the signal yield for each decay mode in the $\eta$ (520, 560), $\rho/\omega$ (675, 875), $\phi$ (990, 1035${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$), and remaining $m_{ee}$ regions. The signal probability density function (PDF) is a Gaussian-like function with different resolutions above and below the $D^{0}$ mass ²²2The normalization mode signal PDF is a sum of the signal PDF used for the signal channels and a Gaussian with a shared mean for the $D^{0}$ mass.. We obtain the signal PDF parameters from fits to the signal MC distributions, and we fix these parameters for the signal yield extraction. We model the background using a linear function, where the slope parameter is floated in the fit. We do not examine any signal mode distributions until the analysis procedure is finalized to minimize potential biases on the measured quantities.

We show the signal mode $m_{hh^{(\prime)}ee}$ distributions with projections of the fits superimposed for each $m_{ee}$ region in Fig. 2.

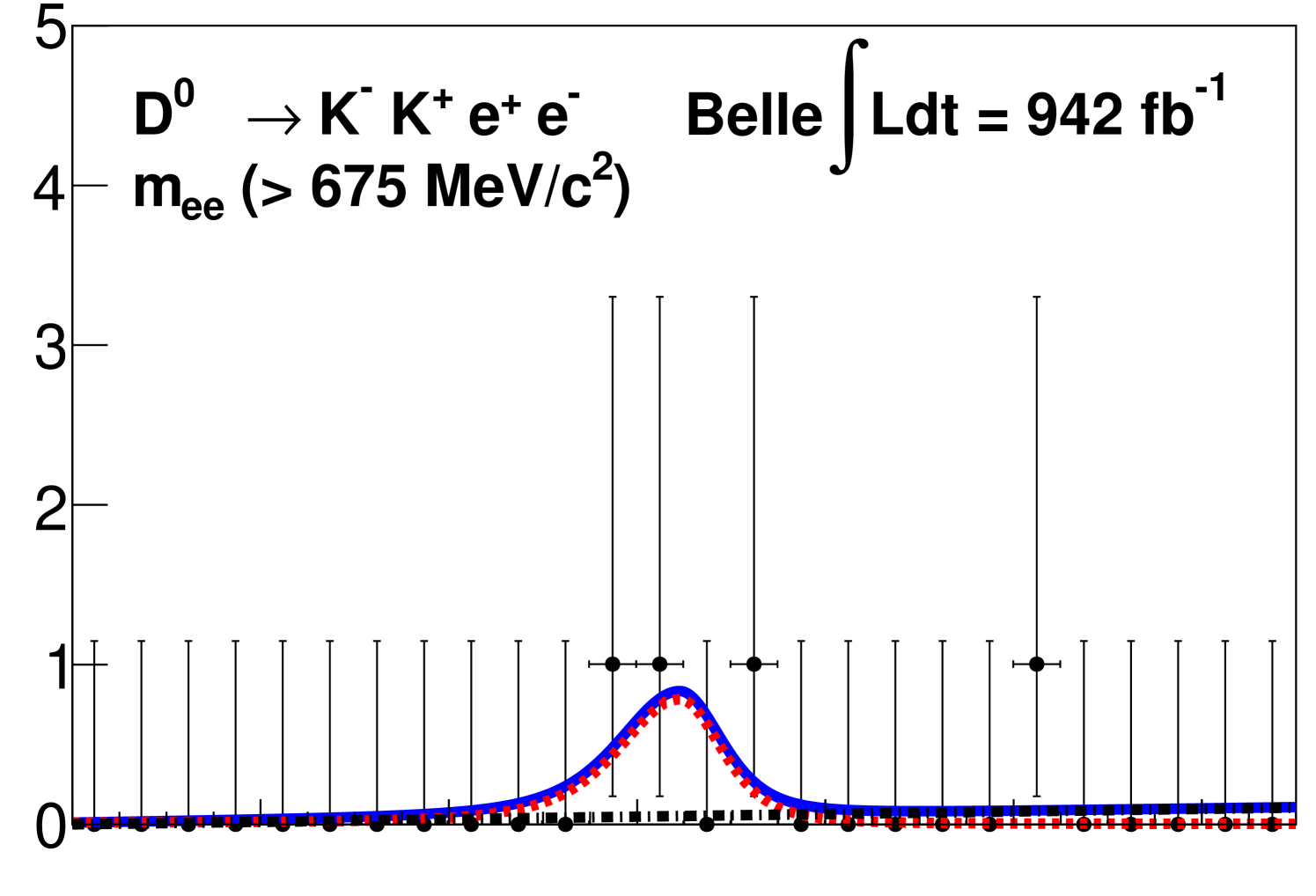
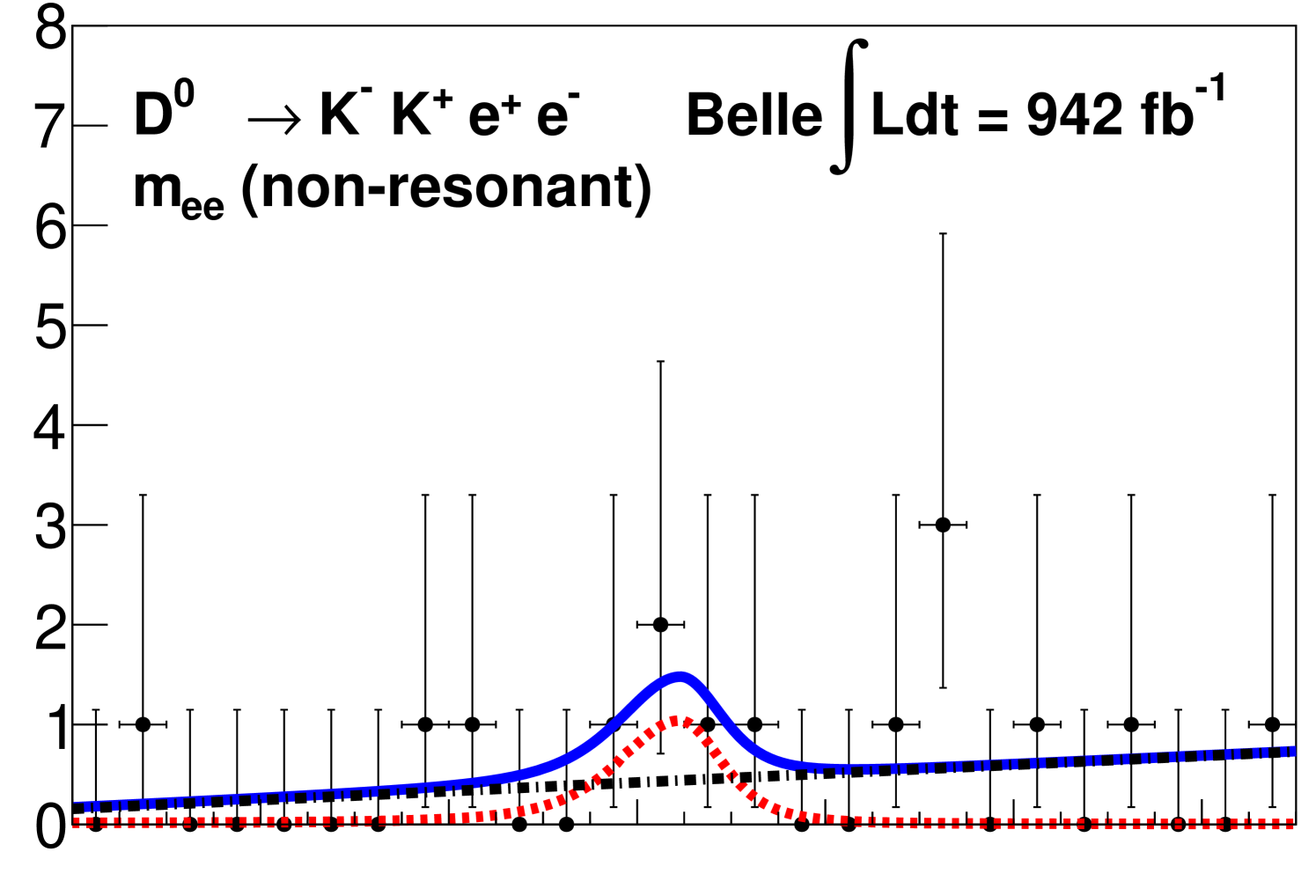
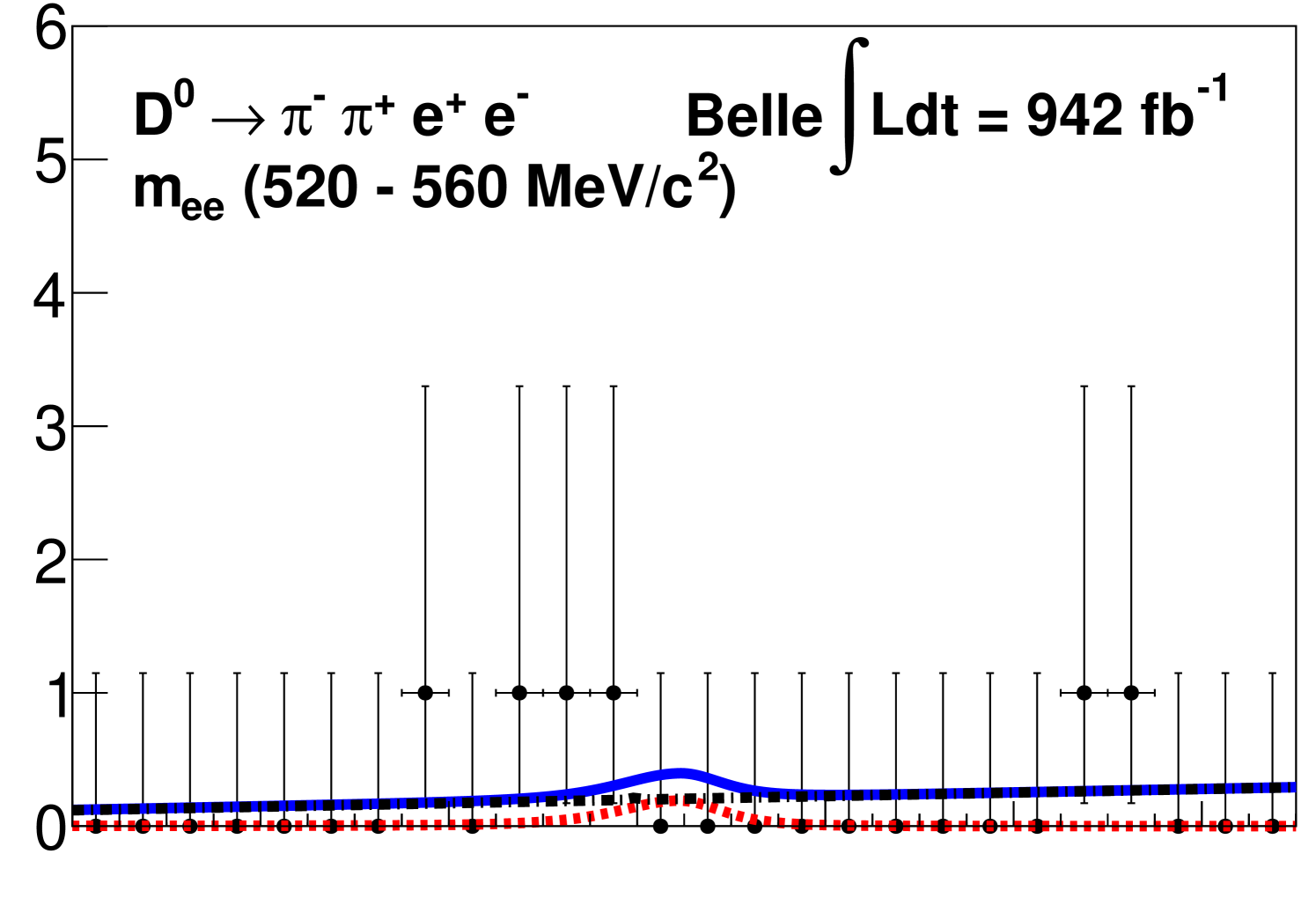
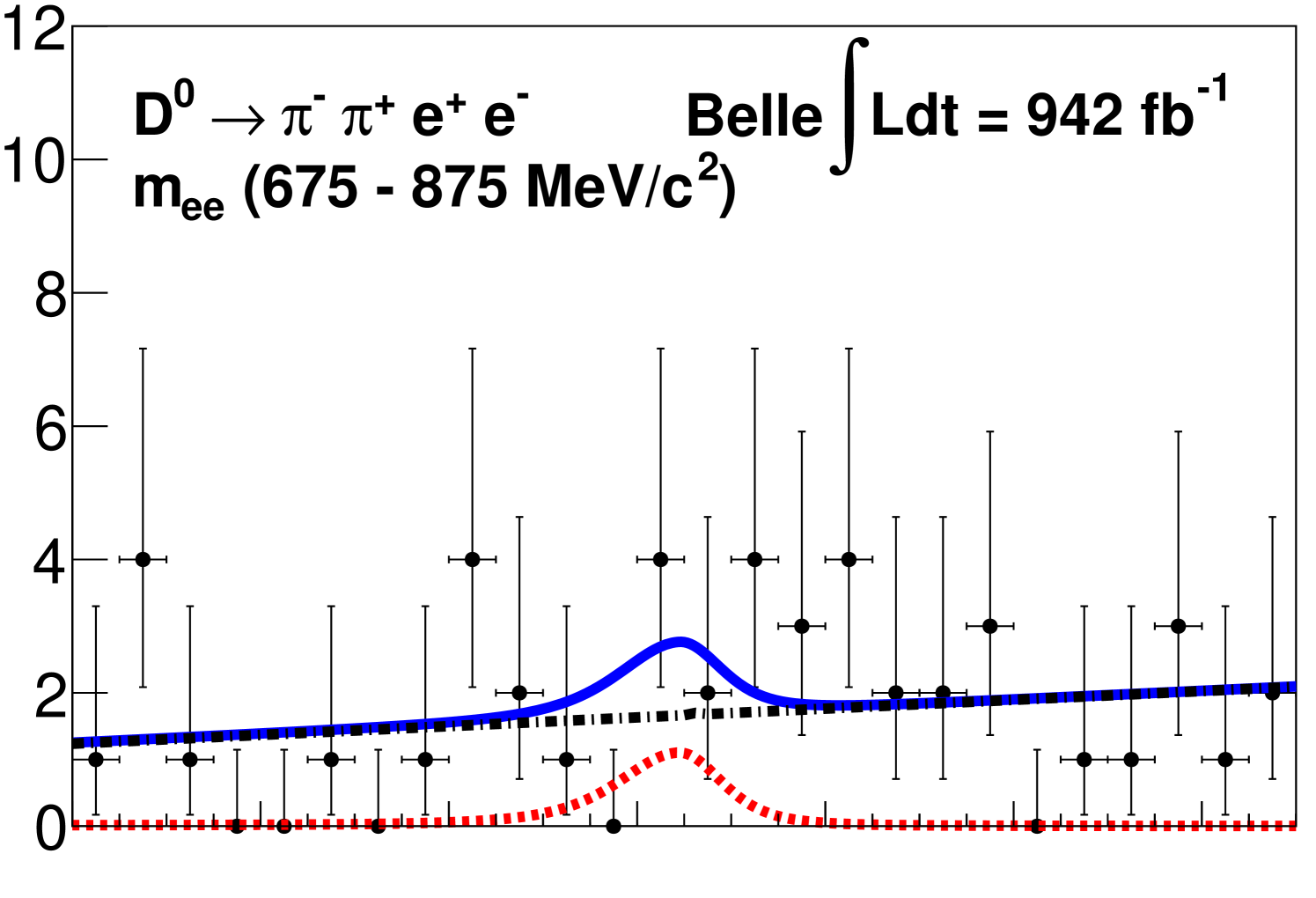
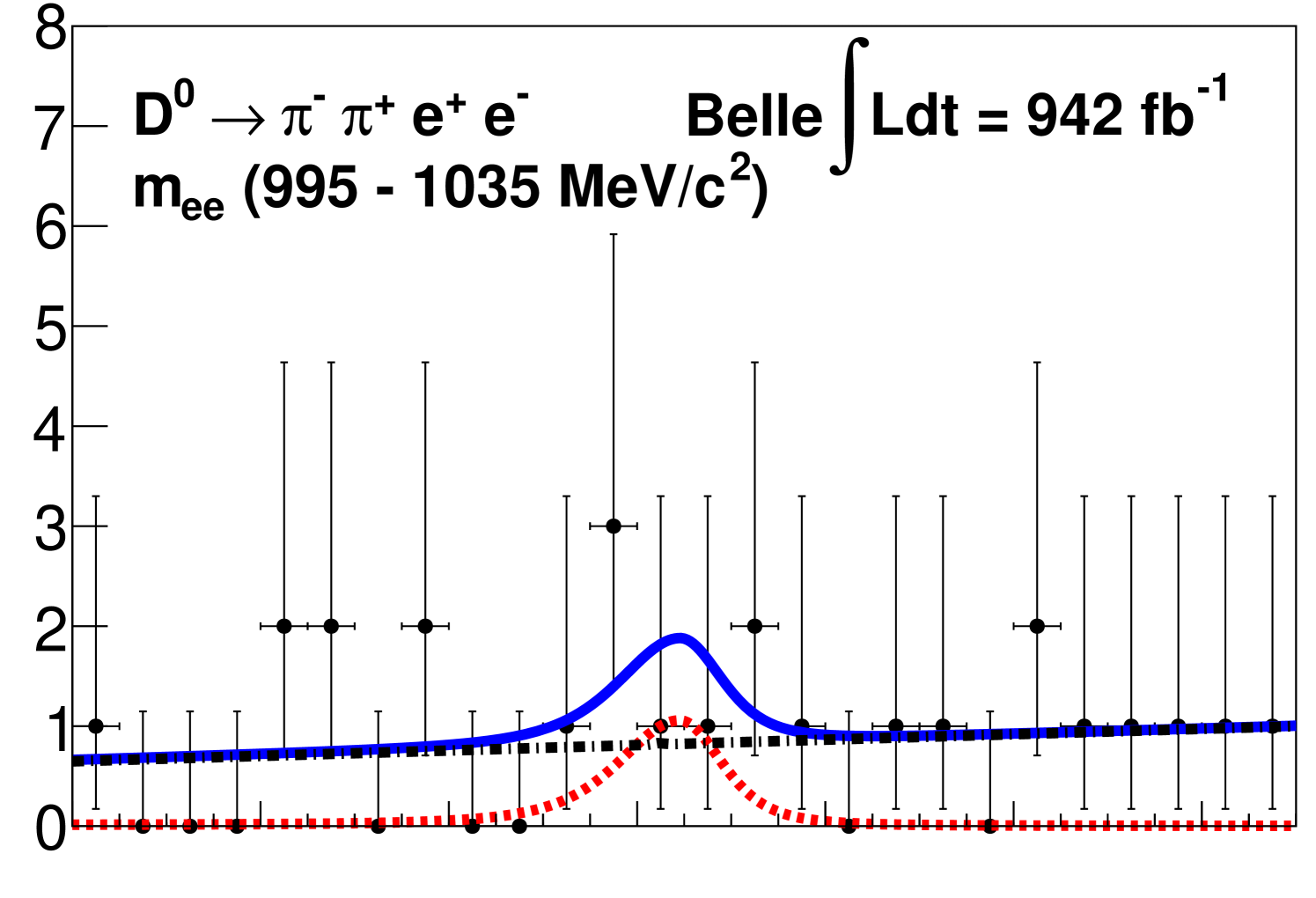
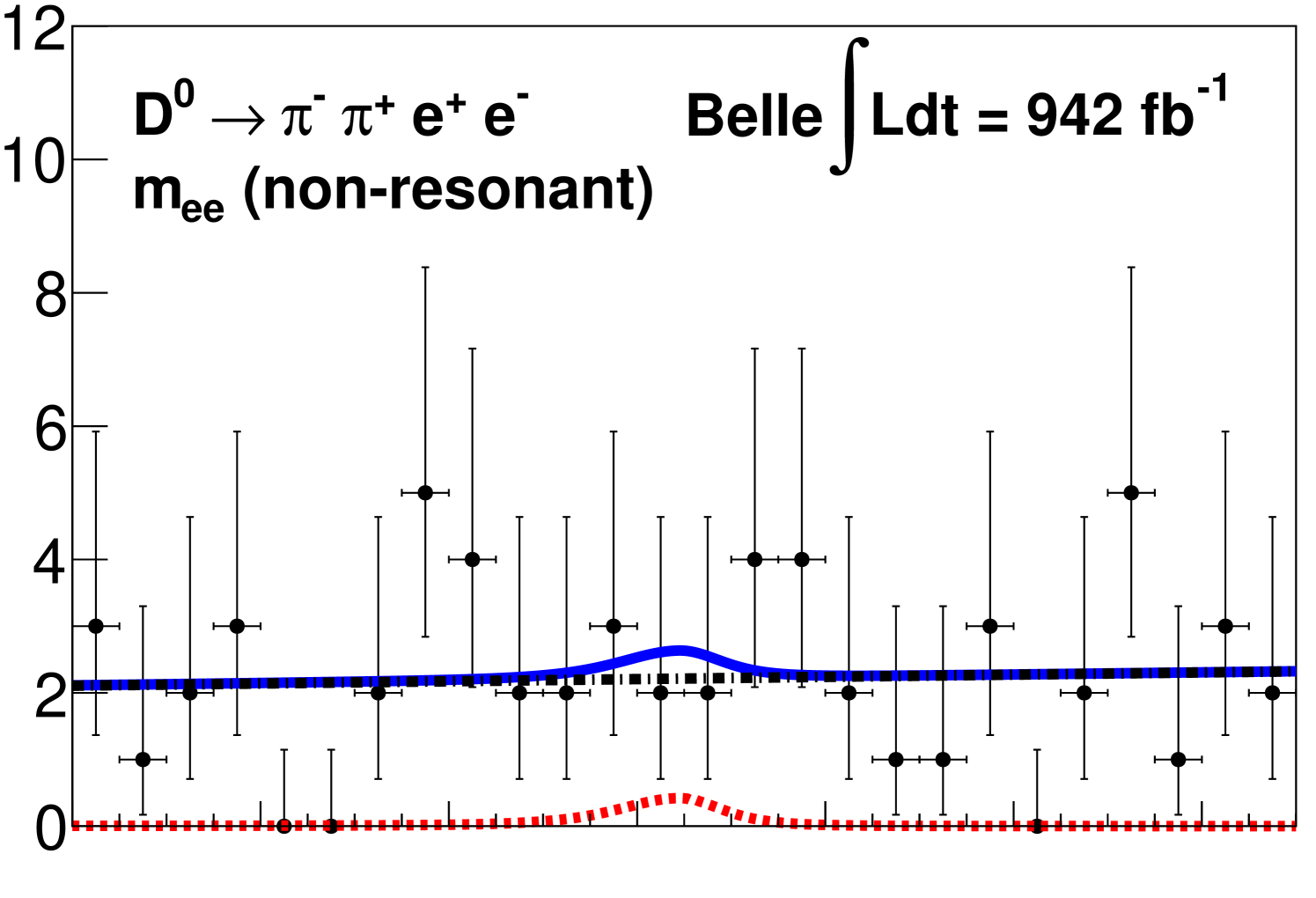
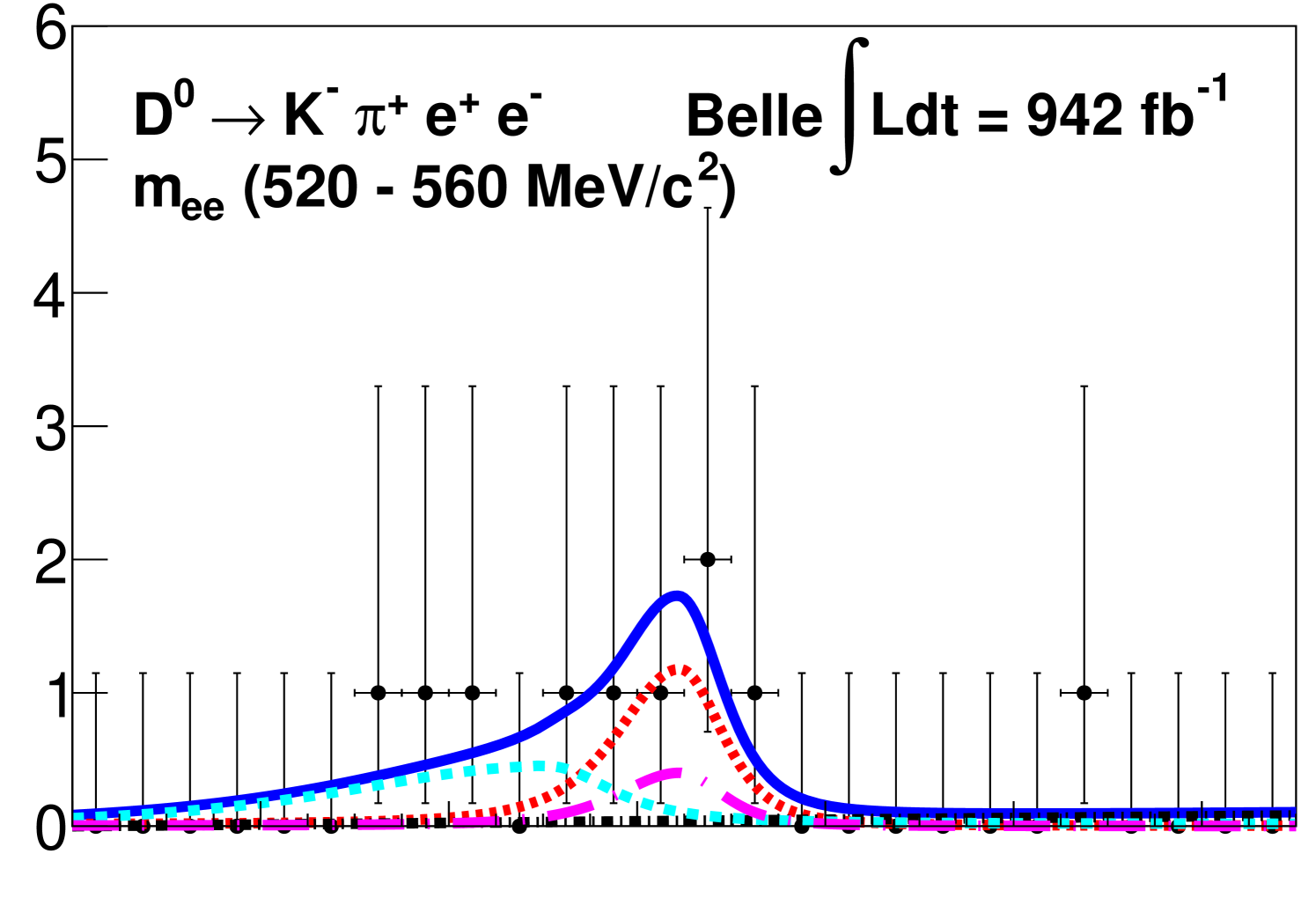
For each signal channel, we provide the branching fractions, and the corresponding significance $S=\sqrt{-2\Delta\mathrm{ln}\mathcal{L}}$, where $\Delta$ln$\mathcal{L}$ is the difference in the log-likelihood from the maximum value with respect to the value from the background-only hypothesis. We measure the branching fraction of $D^{0}$ $\rightarrow$ $K^{-}\pi^{+}e^{+}e^{-}$ in the $m_{ee}$ range $675<m_{ee}<875$ ${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$ to be $(39.6\pm 4.5\pm 2.9)$ $\times$ 10^-7, where the first uncertainty is statistical and the second is systematic with a significance of 11.8$\sigma$. We set 90% CL upper limits using the CL_s method [36] for the channels with no significant signal; these results are in the range from $(2.3-8.1)$ $\times$ 10^-7. The extracted signal yields, significances, efficiencies, and branching fractions, or branching fraction upper limits for each $m_{ee}$ region are given in Table 1.

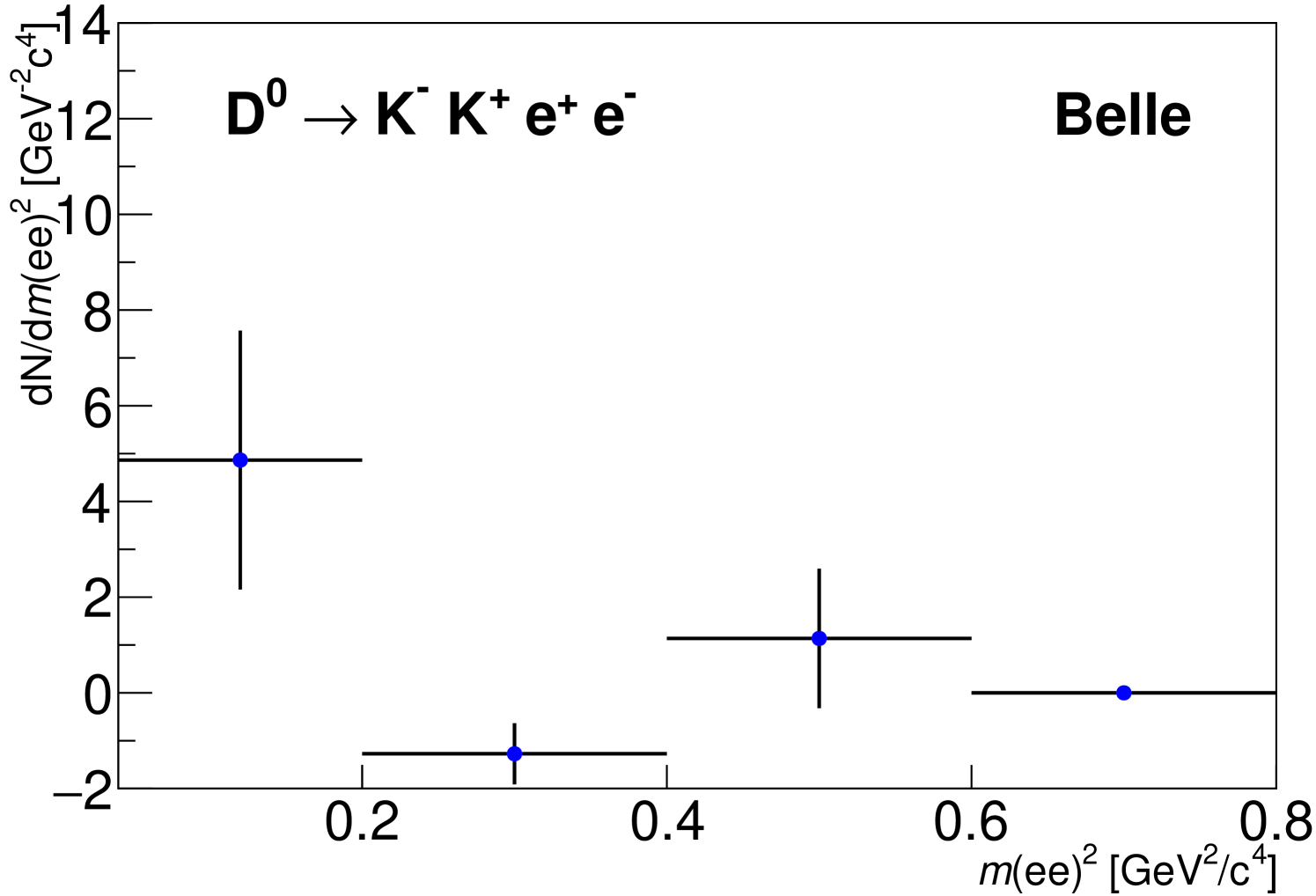
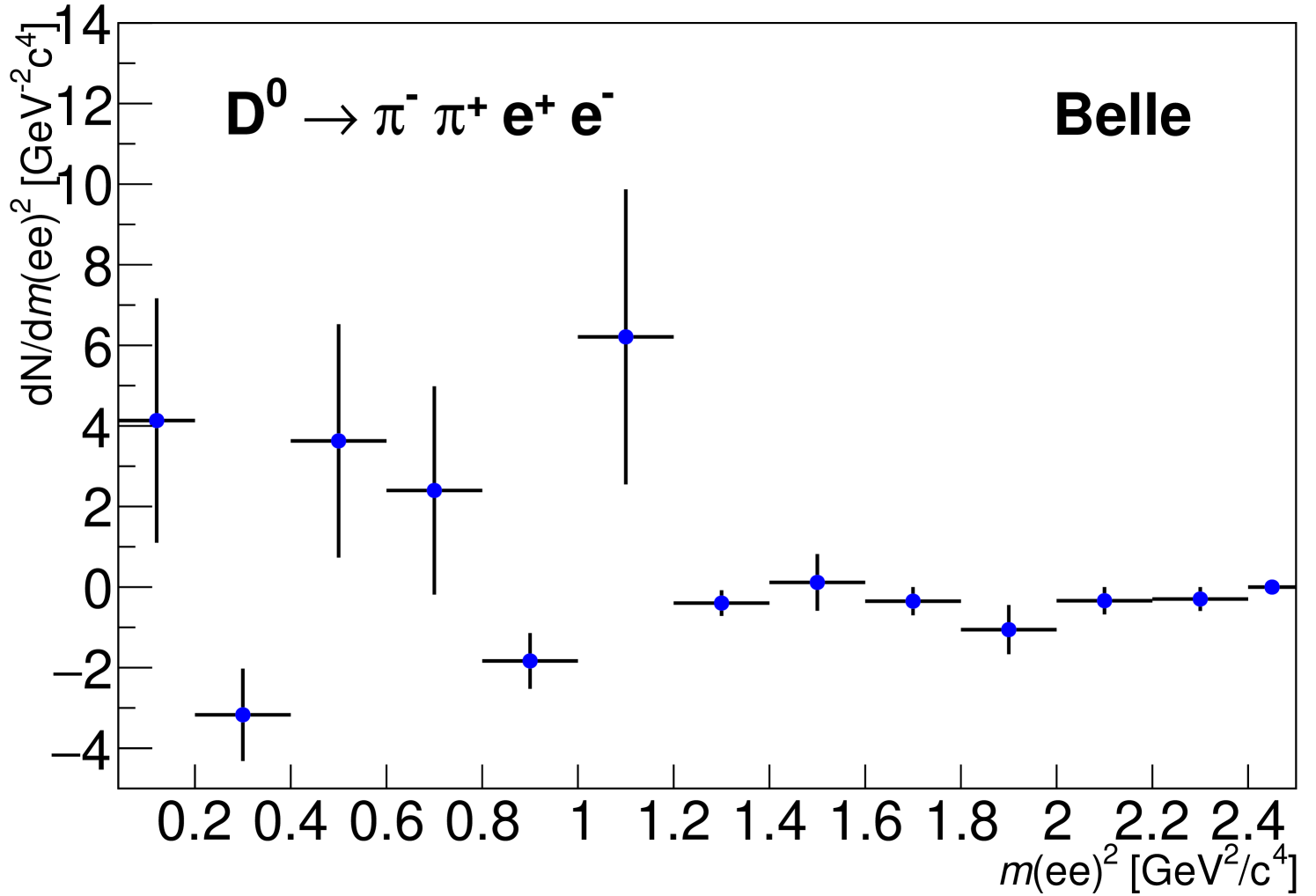
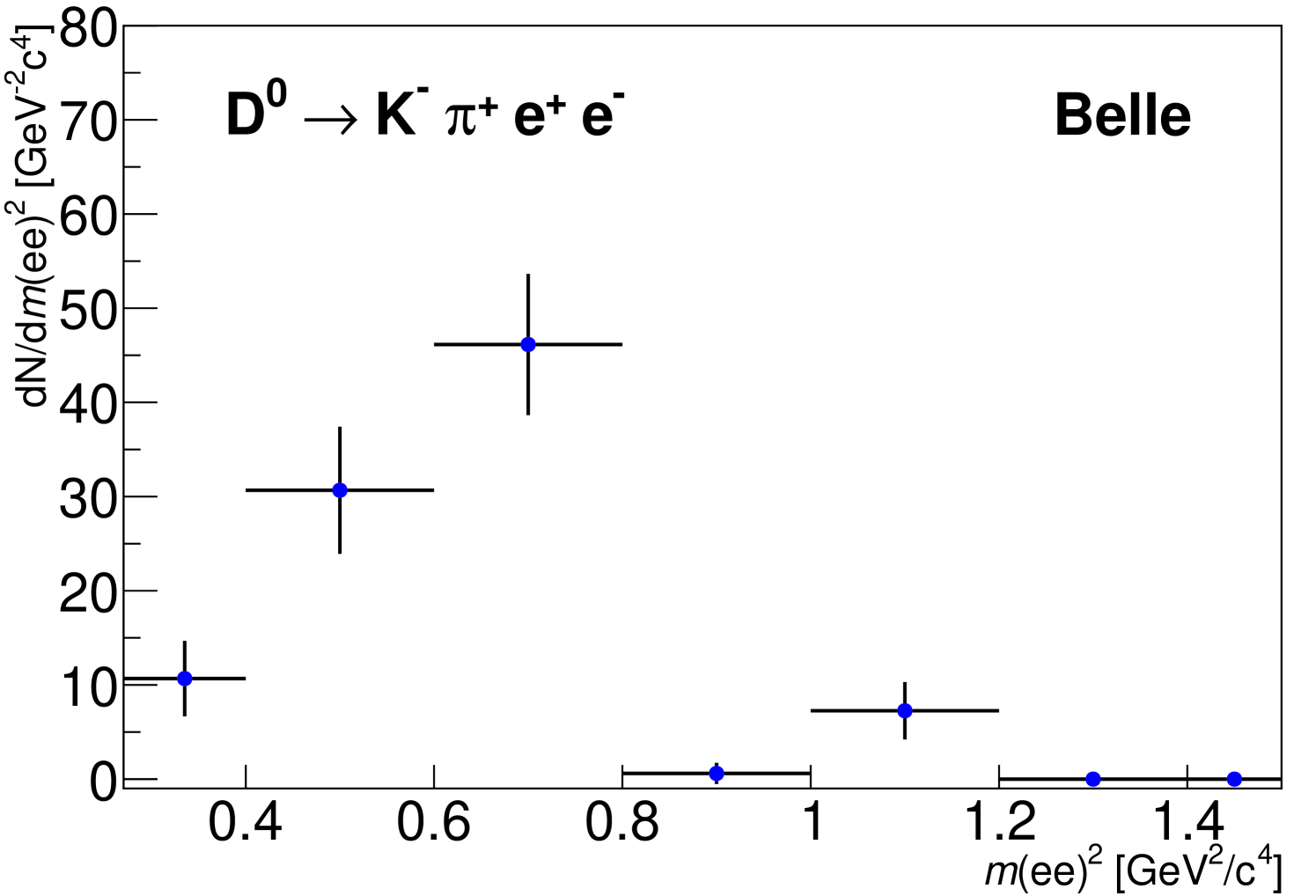
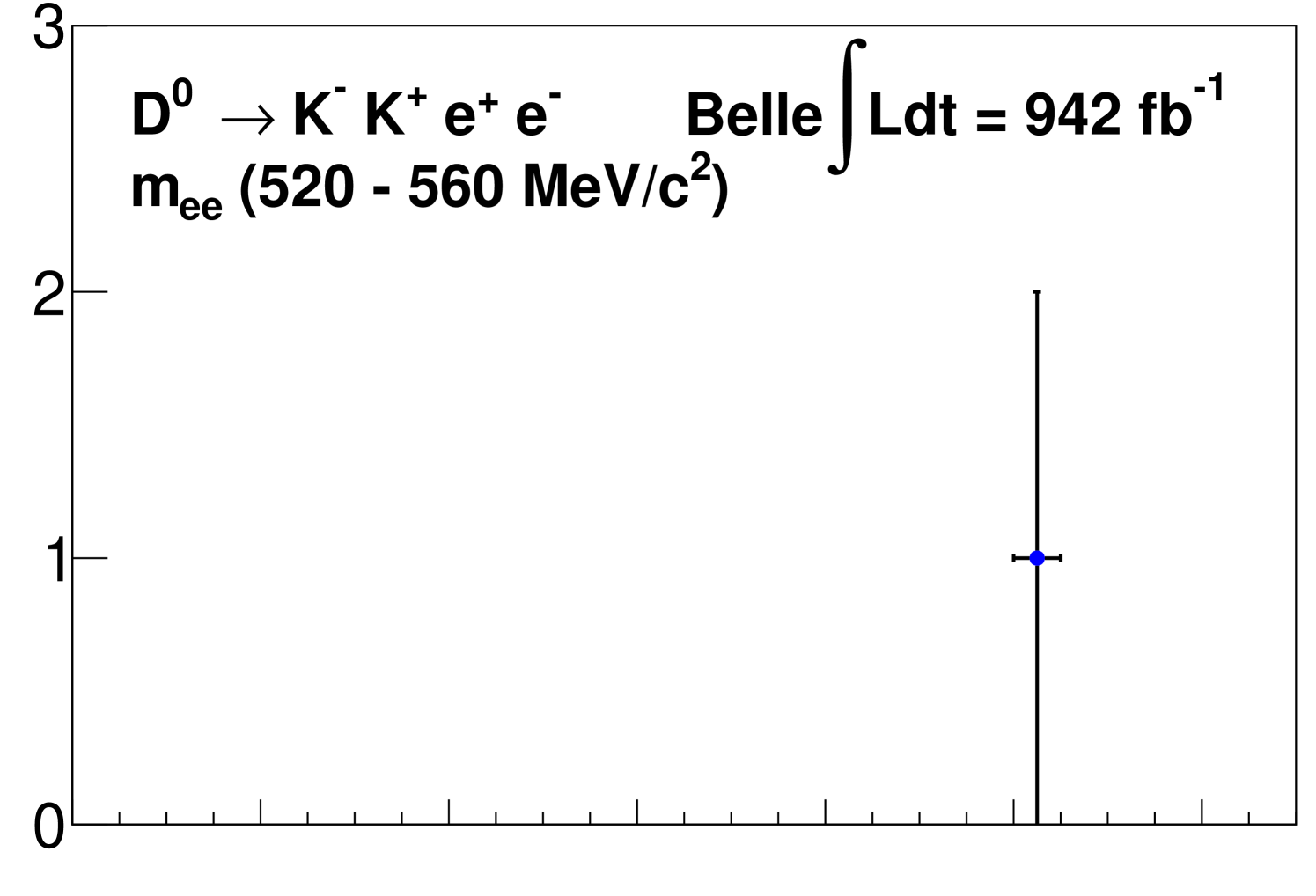
In the supplemental material, we show the projection of the fit on the $D^{0}$ $\rightarrow$ $h^{-}h^{(\prime)+}e^{+}e^{-}$ distribution as a function of $m_{ee}^{2}$ with the background subtracted using the $s\mathcal{P}lot$ technique [37].
Systematic uncertainties can be divided into multiplicative and additive categories. The additive systematic uncertainties affect the determination of the signal and normalization mode yields and the corresponding significance. Multiplicative systematic uncertainties include PID and tracking efficiencies. The systematic uncertainty of tracking efficiency is 0.35% for each track, obtained from a study of a $D^{*+}\rightarrow D^{0}(\pi^{+}\pi^{-}K^{0}_{\scriptscriptstyle S})\pi^{+}$ data control sample. The systematic uncertainty due to $K$ identification is 1.0%, determined from a study of a $D^{*+}\rightarrow D^{0}(K^{-}\pi^{+})\pi^{+}$ control sample. The electron identification efficiency uncertainty is determined from $e^{+}e^{-}\rightarrow e^{+}e^{-}e^{+}e^{-}$ processes and found to be 2.0% for each track. The PID efficiency corrections are applied for the normalization mode and for each signal channel, and the particle identification systematics are about 5%, which depend on the decay channel. We do not include a systematic uncertainty for the PID fake rates as the $D^{0}$ candidate invariant mass of misidentified $h^{-}h^{(\prime)+}e^{+}e^{-}$ decays do not peak near the $D^{0}$ mass after final selections according to MC simulations of hadronic $D^{0}$ decays. To account for the potential non-resonant decay contribution in the $m_{ee}$ resonance regions, the signal efficiency differences obtained using the signal MC between non-resonant and resonant decays are included in the systematic uncertainty.
The uncertainty in yield extraction contributes to the additive systematic uncertainty, which affects the significance of the branching fraction. We obtain the PDF-related uncertainties by varying the PDF shapes and parameters for both signal and background. As alternative PDFs, we use two double-sided Crystal Ball functions [38] with a shared mean for the signal and a second-order Chebyshev polynomial for the background PDF functions to determine the signal yield systematics from the PDF shapes. In addition, the yield differences between the signal PDF parameters, fixed and floated, are incorporated into the systematic uncertainty. The additive systematic uncertainty for the background originating from the signal channel $D^{0}$ $\rightarrow$ $h^{-}h^{(\prime)+}e^{+}e^{-}$ with $ee$ from $\rho$ resonant decay is negligible for other $ee$ resonance regions. To incorporate the systematic uncertainties into the upper limits, the likelihood function is convolved with two Gaussian functions whose widths are the total multiplicative and additive systematic uncertainties and a third Gaussian with a width that is the sum in quadrature of the additive systematic uncertainties from the normalization mode.

In summary, we have measured the branching fraction of $D^{0}$ $\rightarrow$ $K^{-}\pi^{+}e^{+}e^{-}$ in the $m_{ee}$ range $675<m_{ee}<875$ ${\mathrm{\,Me\kern-1.00006ptV\!/}c^{2}}$ to be

with a significance of 11.8$\sigma$ using 942 $\mbox{\,fb}^{-1}$ of Belle data. The measured branching fraction is consistent with and more precise than the BABAR measurement [13]. For the other $ee$ resonant and non-resonant regions, we do not observe any significant signal and set 90% CL upper limits on the branching fractions. These limits range from 2.3 $\times$ 10^-7 to 8.1 $\times$ 10^-7. Our $D^{0}$ $\rightarrow$ $K^{-}\pi^{+}e^{+}e^{-}$ limits are more restrictive than the BABAR [14] and BES III [16] limits.

Note added:
While this manuscript was being finalized, LHCb published new results on $D^{0}\rightarrow\pi^{+}\pi^{-}e^{+}e^{-}$ and $D^{0}\rightarrow K^{+}K^{-}e^{+}e^{-}$ decays. They observe the former in two $m_{ee}$ mass regions and set upper limits on the latter that are 1.4–7.7 times more stringent than ours [25].

Supplemental material to $D^{0}\rightarrow h^{-}h^{(\prime)+}e^{+}e^{-}$