Jefferson Lab E97-110 Collaboration

The nucleon is the basic building block of nature, accounting for about 99% of the universe’s visible mass. Understanding its properties, e.g., mass and spin, is thus crucial. Those are mainly determined by the Strong Interaction, which is described by Quantum Chromodynamics (QCD) with quarks and gluons as the fundamental degrees of freedom. The nucleon structure is satisfactorily understood at high $Q^{2}$ (short space-time scales, see Fig. 1 for the definition of kinematic variables), since there QCD is calculable using perturbation methods (perturbative QCD) and tested by numerous experimental measurements. At lower $Q^{2}$, the strong coupling $\alpha_{s}$ becomes too large for perturbative QCD to be applicable [5]. Yet, calculations are critically needed since the Strong Interaction’s chiral symmetry breaks in this region. Chiral symmetry and its breaking is one of the most important properties of the Strong Interaction and is believed to lead to the emergence of the nucleon’s global properties. To understand how the underlying structure leads to the emergence of these global properties, non-perturbative methods must be used. A method using the fundamental quark and gluon degrees of freedom is lattice QCD. However, calculations from this method are often intractable for spin observables at low $Q^{2}$ [6]. Another solution is to employ effective theories. Chiral effective field theory ($\chi$EFT) capitalizes on QCD’s approximate chiral symmetry and uses the emergent hadronic degrees of freedom. Therein lies $\chi$EFT’s strengths and challenges: while the nucleon and the pion are used for first-order calculations, this is often insufficient to describe the data, and heavier hadrons, such as the nucleon’s first excited state $\Delta(1232)$, become needed. This complicates $\chi$EFT calculations, and theorists are still seeking the best way to include the $\Delta(1232)$ in their calculations. It is therefore crucial to perform precision measurements at low enough $Q^{2}$ to test $\chi$EFT calculations. Spin observables, among them the generalized spin-polarizabilities that are reported here, provide an extensive set of tests to benchmark $\chi$EFT calculations [6].

Polarizabilities describe how the components of an object collectively react to external electromagnetic fields. In particular, spin-polarizabilities quantify the object’s spin precession under an electromagnetic field. The spin-polarizabilities, initially defined with real photons, can be generalized to virtual photons such as those used to probe the neutron in our experiment. Accordingly, generalized spin-polarizabilities are extracted by scattering polarized electrons off polarized nucleons and measuring how the cross-section changes when the relative orientation between the electron and nucleon spins is varied (see Fig. 1).

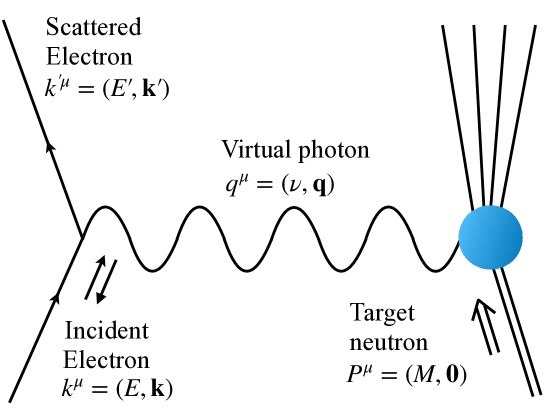
The energy-momentum transferred between the electron and neutron is $(\nu,\bm{q})$, with $Q^{2}=\bm{q}^{2}-\nu^{2}$ characterizing the space-time scale at which we probe the neutron. While real photons ($Q^{2}=0$) only have transverse polarizations, mediating virtual photons ($Q^{2}\neq 0$) are transversely ($\mathrm{T}$) or longitudinally ($\mathrm{L}$) polarized. Thus, two contributions to the spin-polarizability arise: one from the transverse-transverse ($\mathrm{TT}$) interference called the forward spin-polarizability $\gamma_{0}(Q^{2})$, and the other from the longitudinal-transverse ($\mathrm{LT}$) interference, called the Longitudinal-Transverse interference polarizability $\delta_{\mathrm{LT}}(Q^{2})$, which is available only with virtual photons. The additional longitudinal polarization direction and the ensuing interference term offer extra latitude to test theories describing the Strong Interaction.

The theoretical basis to measure $\delta_{\mathrm{LT}}(Q^{2})$ originates from a work of Gell-Mann, Goldberger and Thirring [7, 8]. This work led to relations between the cross-sections measured in polarized electron-nucleon scattering (Fig. 1) and the spin-polarizabilities:

where $\kappa_{\gamma}=\nu-\nicefrac{{Q^{2}}}{{2M}}$ [9] is the photon flux factor, $\nu_{0}$ the photoproduction threshold, and $\sigma_{\mathrm{TT}}$ and $\sigma_{\mathrm{LT}}$ are respectively the $\mathrm{TT}$ and $\mathrm{LT}$ interference cross-sections. They are obtained from [6, 10]:

where $\Delta\sigma_{||}$ ($\Delta\sigma_{\bot}$) is the difference between the cross sections when the beam and target spin directions are parallel and antiparallel (perpendicular), $\alpha$ is the electromagnetic coupling constant, $\epsilon=1/[1+2(1+\nicefrac{{Q^{2}}}{{4M^{2}x^{2}}})\tan^{2}(\nicefrac{{\theta}}{{2}})]$ with $x=\nicefrac{{Q^{2}}}{{2m\nu}}$ the Bjorken scaling variable and $\theta$ the electron scattering angle in the laboratory frame, $\eta=\nicefrac{{\epsilon Q}}{{(E-E^{\prime}\epsilon)}}$ and $\zeta=\nicefrac{{\eta(1+\epsilon)}}{{2\epsilon}}$. The $\sigma_{\mathrm{TT}}$ and $\sigma_{\mathrm{LT}}$, shown in Figs. 2 and 3,

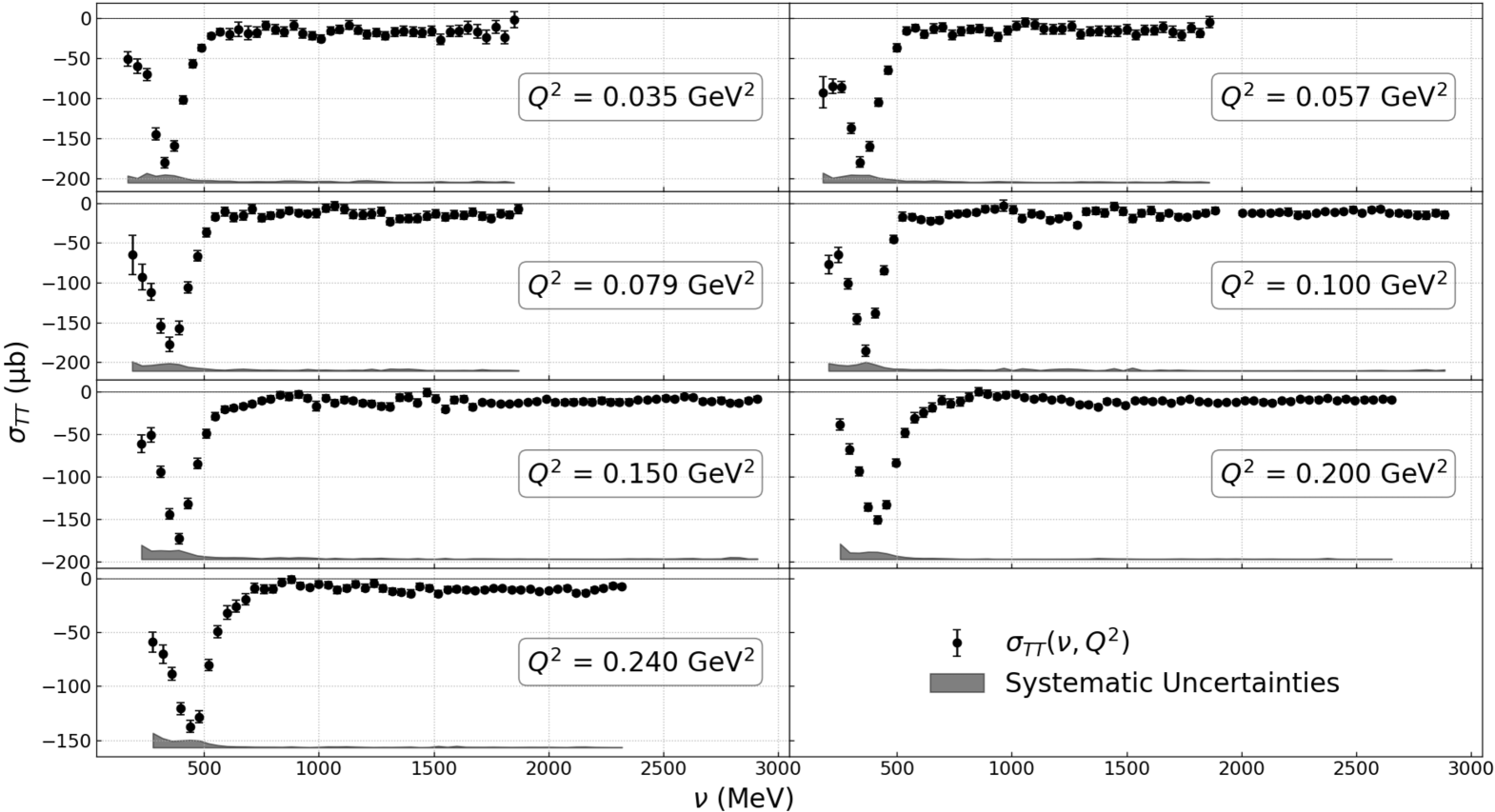
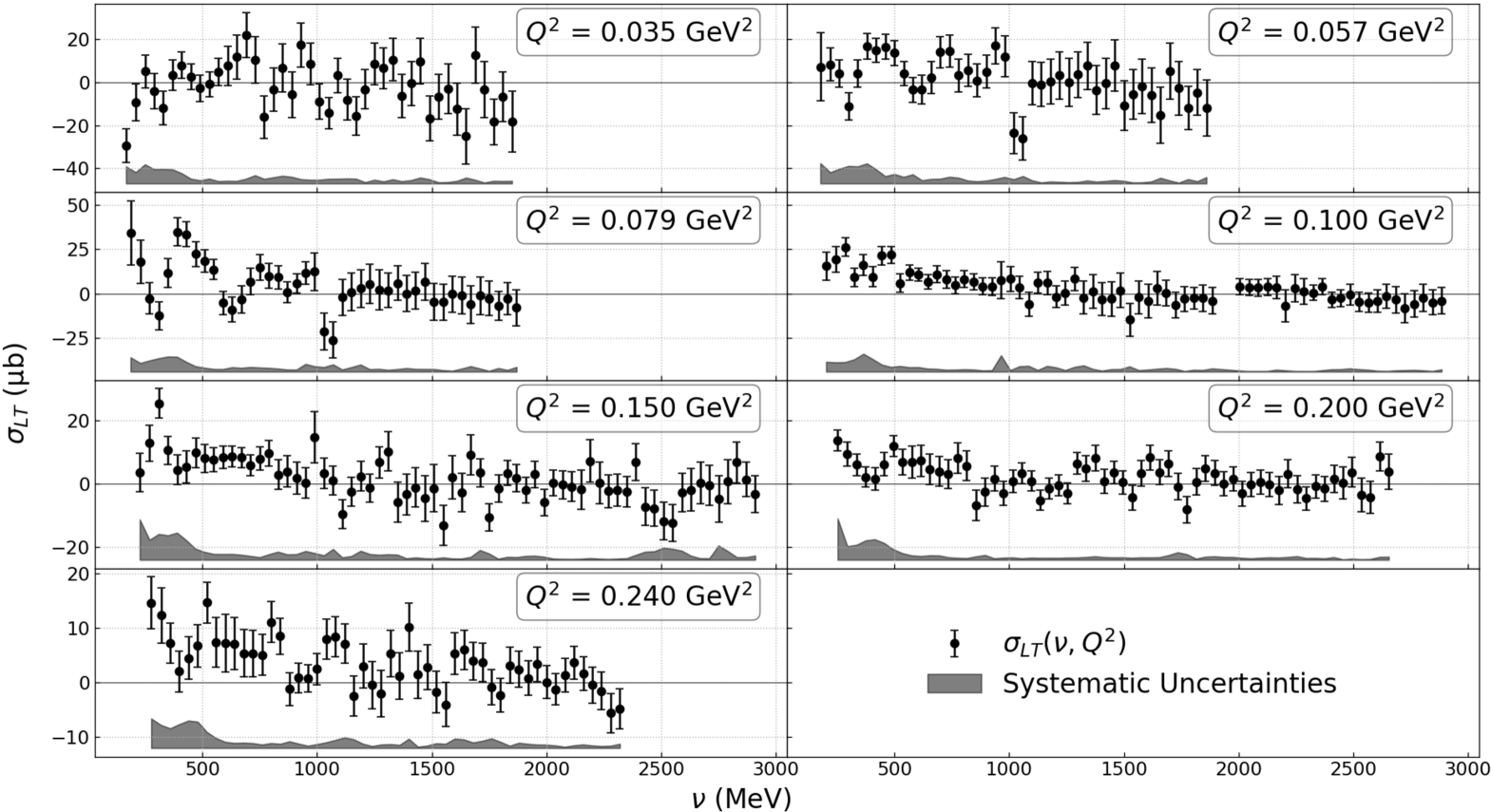
were integrated according to Eqs. (1) and (2) to obtain $\gamma_{0}(Q^{2})$ and $\delta_{\mathrm{LT}}(Q^{2})$. The unmeasured part of the integrals at large $\nu$ is often negligible due to the $\nu$-weighting.

An outstanding feature of $\delta_{\mathrm{LT}}(Q^{2})$ at low $Q^{2}$ is that the $\Delta(1232)$ is not expected to appreciably contribute to the LT-interference cross section, since exciting the $\Delta(1232)$ overwhelmingly involves transverse photons. This should alleviate the difficulty of including the $\Delta(1232)$ in $\chi$EFT calculations, making them more robust. However, the first measurement of $\delta_{\mathrm{LT}}(Q^{2})$ from JLab experiment E94-010 [11] done at $Q^{2}\geq 0.1$ GeV² strongly disagreed with $\chi$EFT calculations [12, 13]. This surprising result, known as the “$\delta_{\mathrm{LT}}$ puzzle” [10], triggered improved $\chi$EFT calculations [14] which now explicitly include the $\Delta(1232)$ [2, 3, 4], and measurements of $\delta_{\mathrm{LT}}$ at lower $Q^{2}$ where $\chi$EFT can be best tested. New data of $\delta_{\mathrm{LT}}$ on the neutron at very low $Q^{2}$ are presented next, which were taken during experiment JLab E97-110.

Eq. (2) allows measuring $\delta_{\mathrm{LT}}^{n}(Q^{2})$ (the superscript $n$ indicates neutron quantities) by scattering polarized electrons off polarized neutrons in ³He nuclei. The data were acquired in Hall A [15] of Jefferson Lab (JLab) during experiment E97-110 [16]. The probing virtual photons were produced by a longitudinally polarized electron beam during its scattering off a polarized ³He target [15]. The beam polarization, flipped pseudo-randomly at 30 Hz and monitored by Møller and Compton polarimeters, was (75.0 $\pm$ 2.3)%. The beam energies ranged from 1.1 to 4.4 GeV, and the beam current was typically a few $\mu$A. Since free neutrons are unstable, we used ³He nuclei as an effective polarized neutron target. To first-order, polarized ³He nuclei can be treated as effective polarized neutrons together with unpolarized protons because the ³He’s nucleons (two protons and one neutron) are mostly in an $S$-state, and so the Pauli exclusion principle dictates that in the S-state the proton spins point oppositely, yielding no net contribution to the ³He spin. The gaseous ($\approx 12$ atm) ³He was contained in a 40 cm-long glass cylinder and polarized by spin-exchange optical pumping of Rubidium atoms. Helmholtz coils provided a longitudinal or transverse 2.5 mT field used to maintain the polarization, to orient it longitudinally or transversely (in-plane) to the beam direction, and to aid in performing polarimetry. The average target polarization in-beam was (39.0 $\pm$ 1.6)%. The scattered electrons from the reaction $\vec{\rm{{}^{3}He}}$($\vec{\rm{e}},\rm{e^{\prime}}$) were detected by a High Resolution Spectrometer (HRS) [15] supplemented by a dipole magnet [17] allowing us to detect electrons scattered at angles down to 6^∘. Behind the HRS, drift chambers provided particle tracking, scintillator planes enabled the data acquisition trigger, and a gas Cherenkov counter and electromagnetic calorimeters ensured the identification of the particle type.

The measured $\sigma_{\mathrm{TT}}$ ($\sigma_{\mathrm{LT}}$) on ³He is shown in Fig. 2 (Fig. 3). Its values with their uncertainties are available in the Supplementary Data Files. While polarized ³He nuclei are effectively polarized neutrons to good approximation, nuclear corrections are needed to obtain genuine neutron information. The prescription of Ref. [18] was used for the correction. The effect of the nuclear correction, which can be obtained from Tables I-III in the Supplementary Data Files, is relatively small. In particular it does not appreciably affect the $Q^{2}$ trend seen for the uncorrected ³He integrals. The relative uncertainty on this correction is estimated to be 6 to 14% relative to the correction, the higher uncertainties corresponding to our lowest $Q^{2}$ values. The quasi-elastic contamination was corrected following the procedure described in [16]. The correction is small for $\delta_{\mathrm{LT}}^{n}$, but important for $\gamma_{0}^{n}$ and was estimated using [19]. No calculation uncertainty is provided in [19] and using another quasi-elastic calculation [20] may shift the lowest-$Q^{2}$ $\gamma_{0}^{n}$ data points by as much as our total systematic uncertainty. The other main systematic uncertainties come from the absolute cross-sections (3.5 to 4.5%), target and beam polarizations (3 to 5% and 3.5%, respectively), and radiative corrections (3 to 7%).

Our $\delta_{\mathrm{LT}}^{n}(Q^{2})$ data are shown in the left panel of Fig. 4. They agree with earlier data from E94-010 at larger $Q^{2}$ [11] while reaching much lower $Q^{2}$ where the $\chi$EFT is expected to work well. The measurement can be compared to $\chi$EFT calculations [12, 13, 2, 4] and a model parameterization of the world photo- and electro-production data called MAID [21].

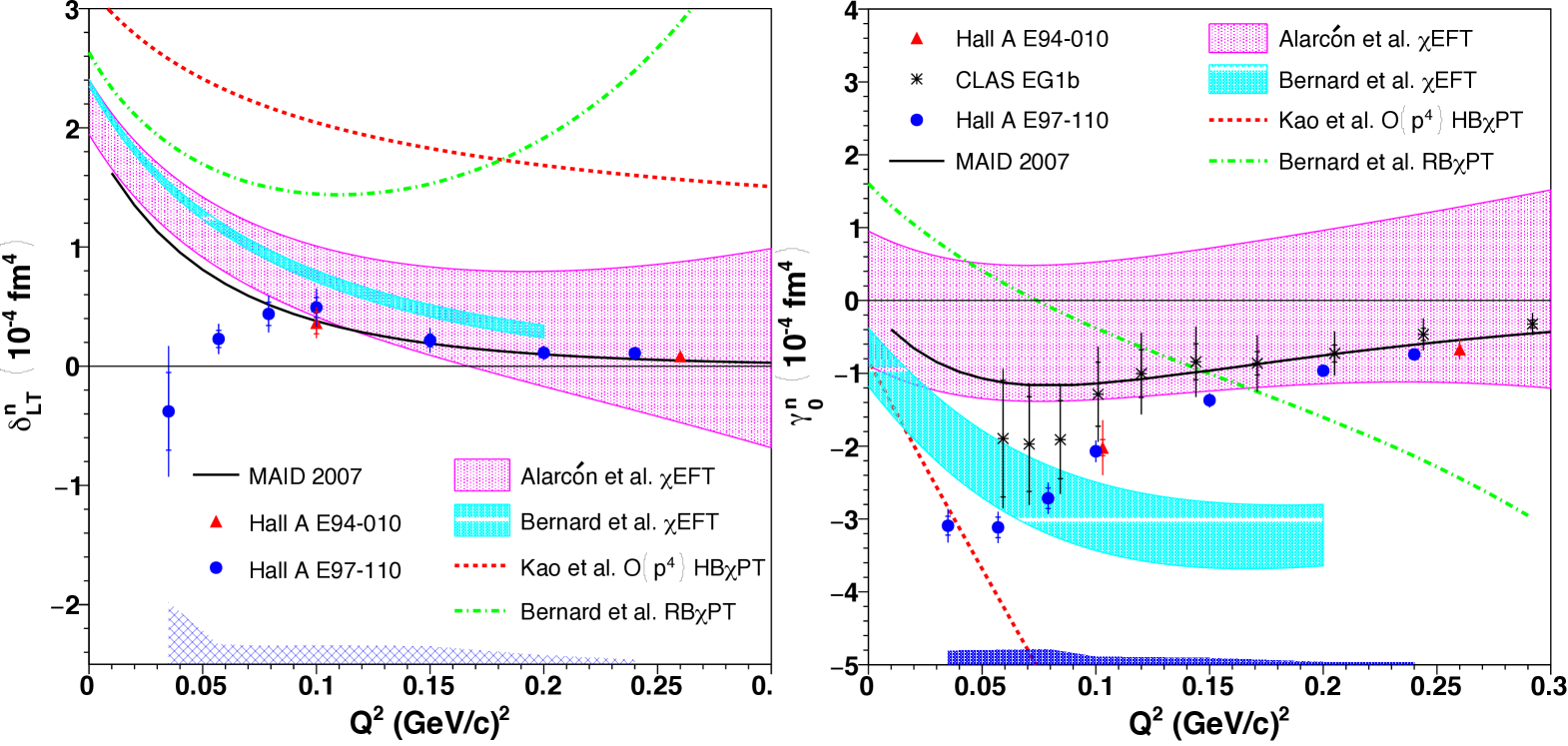
Earlier $\chi$EFT calculations [12, 13] used different approaches (Heavy Baryon and Relativistic Baryon chiral perturbation theory: HB$\chi$PT and RB$\chi$PT, respectively), and furthermore either neglected the $\Delta(1232)$ degrees of freedom, or included it approximately. Newer calculations [2, 3, 4], which are all fully relativistic, account for the $\Delta(1232)$ explicitly by using a perturbative expansion, but they differ in their choice of expansion parameter. Despite this theoretical improvement and the small-$Q^{2}$ reach that places our data well in the validity domain of $\chi$EFT, our $\delta_{\mathrm{LT}}^{n}(Q^{2})$ starkly disagrees with the predictions. This is even more surprising because the latest $\chi$EFT calculations of $\delta_{\mathrm{LT}}^{n}$ agree with each other, suggesting that calculations for this particular observable should be under control. However, our data reveal an opposite trend with $Q^{2}$ to that of all the $\chi$EFT calculations.

This startling discrepancy demanded further scrutinization of our data. They are compatible with the E94-010 data where they overlap. This is also true for $\gamma_{0}^{n}(Q^{2})$, which we measured concurrently and show in the right panel of Fig. 4. The measured $\gamma_{0}^{n}(Q^{2})$ also agrees with data from CLAS experiment EG1 [22], which used a target and detectors that are very different from E97-110 and E94-010. Our $\gamma_{0}^{n}(Q^{2})$ data generally disagree with $\chi$EFT calculations. Since $\gamma_{0}(Q^{2})$ does not benefit from the suppression of the $\Delta(1232)$ contribution, and since $\gamma^{n}_{0}(Q^{2})$ predictions do not reach a consensus, this disagreement is not entirely surprising, in contrast to the unexpected $\delta_{\mathrm{LT}}^{n}(Q^{2})$ disagreement. Interestingly, we can also study with our data the Schwinger relation [23], which has a similar definition but without $\nu^{-2}$ weighting in its integrand:

Schwinger predicted that $I_{\mathrm{LT}}(Q^{2})\xrightarrow[Q^{2}\to 0]{~}\kappa e_{t}$, with $\kappa$ the anomalous magnetic moment of the target particle and $e_{t}$ its electric charge. This prediction is general, e.g. it does not use $\chi$EFT. $I_{\mathrm{LT}}(Q^{2})$ having no $\nicefrac{{1}}{{\nu^{2}}}$-weighting, the large $\nu$ contribution to the integral is not negligible. Since this contribution to the integral cannot be measured, a parameterization based on the model described in [24] completed by a Regge-based parameterization [25] for the largest $\nu$ part was used to extrapolate it. Our measurement of $I^{n}_{\mathrm{LT}}(Q^{2})$ is shown in Fig. 5. Our measurement of $I^{n}_{\mathrm{LT}}(Q^{2})$ without the Regge-based parameterization [25] for the large-$\nu$ part (open symbols), which is suppressed in $\delta_{\mathrm{LT}}(Q^{2})$, displays a similar pattern as $\delta_{\mathrm{LT}}^{n}(Q^{2})$. The Gerasimov-Drell-Hearn (GDH) relation [28, 29] can be used to extrapolate our $I^{n}_{\mathrm{LT}}(Q^{2})$ to $Q^{2}=0$; and provided that the GDH relation is valid, which is widely expected and supported by dedicated experimental studies [30], our data satisfy Schwinger’s prediction that $I^{n}_{\mathrm{LT}}(0)=0$ [23]. Our trend contrasts with the MAID model and presumably the $\chi$EFT calculations, since MAID tracks those (see Fig. 4). This suggests that the problem lies in the theoretical description of the neutron structure.

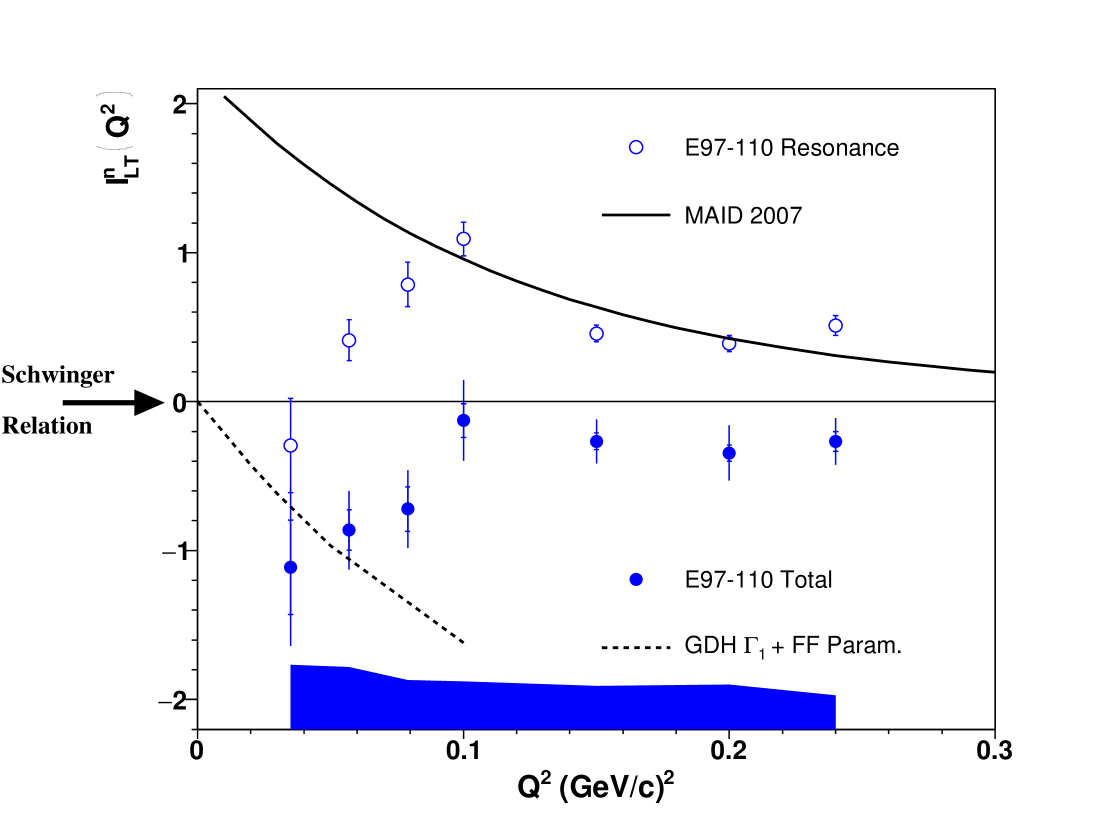
The measured $I_{\mathrm{LT}}(Q^{2})$ displays a similar $Q^{2}$-behavior as $\delta_{\mathrm{LT}}$, irrespective of the different $\nu$-weighting. Other integrals without $\nu^{-2}$ weighting formed using our data and reported in [16] did not display the surprisingly strong disagreement with the predictions seen here. The values of $\gamma_{0}^{n}$, $\delta_{\mathrm{LT}}^{n}$ and $I_{\mathrm{LT}}^{n}$ with their uncertainties are available in the Supplementary Data Files.

Our data indicate that both the TT and LT interferences of the electromagnetic field’s components induce a clear spin precession of the neutron. While it was predicted by all calculations and models that the LT term influence should intensify at small $Q^{2}$, our data reveal the opposite trend. This notable disagreement is perplexing since our measurements were done well into the domain where $\chi$EFT is expected to describe reliably the nucleon properties, especially the “gold-plated” $\delta_{\mathrm{LT}}$. Lattice QCD calculations of $\delta_{\mathrm{LT}}(Q^{2})$ are possible [31], but not yet available. Our data motivate such calculations since the measured generalized spin-polarizabilities underline a current lack of reliable quantitative descriptions of the Strong Interaction at the nucleon-size scale.