Also at ]Novosibirsk State University Also at ]Oak Ridge National Laboratory Also at ]The Cockcroft Institute of Accelerator Science and Technology Also at ]Shanghai Key Laboratory for Particle Physics and CosmologyAlso at ]Key Lab for Particle Physics, Astrophysics and Cosmology (MOE) Also at ]Lebedev Physical Institute and NRNU MEPhI Also at ]Shanghai Key Laboratory for Particle Physics and CosmologyAlso at ]Key Lab for Particle Physics, Astrophysics and Cosmology (MOE) Also at ]The Cockcroft Institute of Accelerator Science and Technology Also at ]Shanghai Key Laboratory for Particle Physics and CosmologyAlso at ]Key Lab for Particle Physics, Astrophysics and Cosmology (MOE) ††thanks: Deceased Also at ]The Cockcroft Institute of Accelerator Science and Technology Also at ]Shanghai Key Laboratory for Particle Physics and CosmologyAlso at ]Key Lab for Particle Physics, Astrophysics and Cosmology (MOE) Also at ]Shenzhen Technology University Also at ]Shanghai Key Laboratory for Particle Physics and CosmologyAlso at ]Key Lab for Particle Physics, Astrophysics and Cosmology (MOE) Also at ]Novosibirsk State University ††thanks: Deceased Also at ]The Cockcroft Institute of Accelerator Science and Technology ††thanks: Deceased Also at ]Oregon State University Also at ]Novosibirsk State University Also at ]The Cockcroft Institute of Accelerator Science and Technology Also at ]The Cockcroft Institute of Accelerator Science and Technology The Muon Collaboration
Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm
Abstract
We present the first results of the Fermilab Muon Experiment for the positive muon magnetic anomaly . The anomaly is determined from the precision measurements of two angular frequencies. Intensity variation of high-energy positrons from muon decays directly encodes the difference frequency between the spin-precession and cyclotron frequencies for polarized muons in a magnetic storage ring. The storage ring magnetic field is measured using nuclear magnetic resonance probes calibrated in terms of the equivalent proton spin precession frequency in a spherical water sample at 34.7∘C. The ratio , together with known fundamental constants, determines (0.46 ppm). The result is 3.3 standard deviations greater than the standard model prediction and is in excellent agreement with the previous Brookhaven National Laboratory (BNL) E821 measurement. After combination with previous measurements of both and , the new experimental average of (0.35 ppm) increases the tension between experiment and theory to 4.2 standard deviations.
I Introduction
The magnetic moments of the electron and muon
() have played an important role in the development of the standard model (SM). One of the triumphs of the Dirac equation [1] was its prediction for the electron that . Motivated in part by anomalies in the hyperfine structure of hydrogen [2, 3], Schwinger [4] proposed an additional contribution to the electron magnetic moment from a radiative correction, predicting the anomaly 111The scalar quantity is the magnetic anomaly, but is also commonly referred to as the “anomaly” or the “anomalous magnetic moment” in the literature. in agreement with experiment [6].
The first muon spin rotation experiment that observed parity violation in muon decay [7] determined that, to within 10%, , which was subsequently measured with higher precision [8]. A more precise experiment [9] confirmed Schwinger’s prediction for the muon anomaly and thereby established for the first time the notion that a muon behaved like a heavy electron in a magnetic field. This evidence, combined with the discovery of the muon neutrino [10], pointed to the generational structure of the SM.
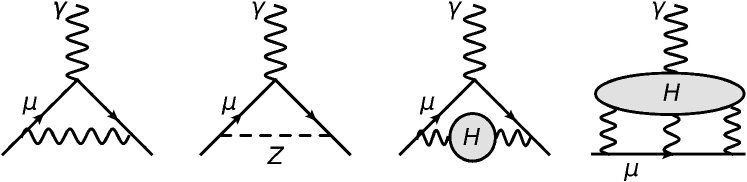
The SM contributions to the muon anomaly, as illustrated in Fig. 1, include electromagnetic, strong, and weak interactions that arise from virtual effects involving photons, leptons, hadrons, and the , , and Higgs bosons [11]. Recently, the international theory community published a comprehensive 222The value is based on evaluating hadronic vacuum polarization contributions via data. Lattice QCD calculations of the hadronic vacuum polarization show promising improvements [13, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79]. The lattice world average determined in Ref. [13] is consistent with the data-driven result used for the number in the main text, but has a higher central value and larger uncertainty. Further scrutiny and improvements of lattice results are expected. SM prediction [13] for the muon anomaly, finding (0.37 ppm). It is based on state-of-the-art evaluations of the contributions from quantum electrodynamics (QED) to tenth order [14, 15], hadronic vacuum polarization [16, 17, 18, 19, 20, 21, 22], hadronic light-by-light [23, 24, 25, 26, 27, 28, 29, 30, 31, 11, 32, 33, 34, 35, 36], and electroweak processes [37, 38, 39, 40, 41].
The measurement of has become increasingly precise through a series of innovations employed by three experimental campaigns at CERN [42, 43, 44] and more recently at Brookhaven (BNL E821) [45]. The BNL net result, with its 0.54 ppm precision, is larger than by 3.7 standard deviations (). While the electron magnetic anomaly has been measured to fractions of a part per billion [46], the relative contribution of virtual heavy particles in many cases scales as . This is the case e.g. for the and bosons of the SM and many hypothetical new particles, and it gives the muon anomaly a significant advantage when searching for effects of new heavy physics. Because the BNL result hints at physics not included in the SM, Experiment E989 [47] at Fermilab was constructed to independently confirm or refute that finding. In this paper, we report our first result with a precision of 0.46 ppm. Separate papers provide analysis details on the muon precession [48], the beam dynamics corrections [49], and the magnetic field [50] determination.
II Experimental Method
The experiment follows the BNL concept [45] and uses the same 1.45 T superconducting storage ring (SR) magnet [51], but it benefits from substantial improvements. These include a 2.5 times improved magnetic field intrinsic uniformity, detailed beam storage simulations, and state-of-the-art tracking, calorimetry, and field metrology for the measurement of the beam properties, precession frequency, and magnetic field [47].
The Fermilab Muon Campus delivers 16 highly polarized, 3.1 GeV/, ns long positive muon beam bunches every 1.4 s into the SR. A fast pulsed-kicker magnet deflects the muon bunch into a 9-cm-diameter storage aperture, resulting in stored muons per fill. The central orbit has a radius of m and the cyclotron period is 149.2 ns. Four sections of electrostatic quadrupole (ESQ) plates provide weak focusing for vertical confinement.
The muon spins precess in the magnetic field at a rate greater than the cyclotron frequency. The anomalous precession frequency 333The rate of change of the angle between spin and momentum vectors is equal to only if and are parallel. The angle between and is always small, and the rate of oscillation of out of pure circular motion is fast compared to . in the presence of the electric and magnetic fields of the SR is
| (1) | ||||
For horizontally circulating muons in a vertical magnetic field, ; this condition is approximately met in our SR. At the muon central momentum , set such that , the third term vanishes.
In-vacuum straw tracker stations located at azimuthal angle and with respect to the injection point provide nondestructive, time-in-fill dependent beam profiles by extrapolation of decay positron trajectories to their upstream radial tangency points within the storage aperture 444The coordinate system is with respect to the center of the storage volume at radius , with radially outward, vertically up, and increasing clockwise when viewed from above.. These profiles determine the betatron oscillation parameters necessary for beam dynamics corrections and the precession data fits discussed below.
Twenty-four calorimeters [54, 55, 56], each containing a array of PbF2 crystals, detect the inward-spiraling decay positrons. When a signal in a silicon photomultiplier (SiPM) viewing any crystal exceeds MeV, the data-acquisition system stores the 54 waveforms from that calorimeter in a set time window around the event. Decay positron hit times and energies are derived from reconstruction of the waveforms.
The magnetic field is measured using pulsed proton NMR, calibrated in terms of the equivalent precession frequency of a proton shielded in a spherical sample of water at a reference temperature C. The magnetic field is determined from the precession frequency and shielded proton magnetic moment, using . The muon anomaly can then be obtained from 555We use the shielded proton-to-electron magnetic moment ratio [80] and the electron -factor [81] measurement. The CODATA-2018 result is used for the muon-to-electron mass ratio [82], which is determined from bound-state QED theory and measurements described in [83]. The QED factor is computed by theory with negligible uncertainty [82].
| (2) |
where our collaboration measures the two quantities to form the ratio
| (3) |
The Run-1 data, collected in 2018, are grouped into four subsets (a – d) that are distinguished by unique kicker and ESQ voltage combinations. The ratio can be conceptually written in terms of measured quantities and corrections as
| (4) |
The numerator includes the master clock unblinding factor , the measured precession frequency , and four beam-dynamics corrections, . We deconstruct into the absolute NMR calibration procedure (indicated by ) and the field maps, which are weighted by the detected positrons and the muon distribution averaged over several timescales (). The result must be corrected for two fast magnetic transients that are synchronized to the injection.
Damage to two of the 32 ESQ high-voltage resistors was discovered after completion of Run-1. This led to slower-than-designed charging of one of the quadrupole sections, spoiling the symmetry of the electric field early in each fill. The impact of this is accounted for in the analysis presented. Brief summaries of the terms in Eq. 4 follow.
III Anomalous precession frequency
: A single 10 MHz, GPS-disciplined master clock drives both the and measurements. The clock has a one-week Allan deviation [58] of 1 ppt. Two frequencies derived from this clock provide the 61.74 MHz field reference and a blinded “ MHz” used for the precession measurement. A blinding factor in the range ppm was set and monitored by individuals external to our collaboration. is the unblinding conversion factor; its uncertainty is negligible.
: The signature of muon spin precession stems from parity violation in decay, which correlates the muon spin and the positron emission directions in the rest frame. When boosted to the lab frame, this correlation modulates the energy () spectrum at the relative precession frequency between the muon spin and momentum directions. The rate of detected positrons with as a function of time into the muon fill then varies as
| (5) |
where is the time-dilated muon lifetime (s), is the normalization, is the average weak-decay asymmetry, and is the ensemble average phase angle at injection. The latter three parameters all depend on . The terms model effects from betatron oscillations of the beam, and are not required in their absence. This beam motion couples with detector acceptance to modulate the rate and the average energy, and hence the average asymmetry and phase, at specific frequencies. The coherent betatron oscillation (CBO) in the radial direction dominates the modulation.
The CBO, aliased vertical width (VW), and vertical mean () frequencies are well measured, and the terms are well modeled and minimally correlated in fits for .
An accurate fit to the data also requires accounting for the continuous loss of muons over a fill, also weakly coupled to . Coincident minimum-ionizing energies in three sequential calorimeters provide a signal to determine the time dependence of muon losses.
Two complementary reconstruction algorithms transform the digitized SiPM waveforms into positron energies and arrival times. In the “local” approach, waveforms are template-fit to identify all pulses in each crystal, which are then clustered based on a time window. In the “global” approach, waveforms in a array of crystals centered on a local maximum in time and position are template-fit simultaneously. After subtraction of the fit from the waveforms, that algorithm iterates to test for any missed pulses from multiparticle pileup. To avoid biasing , we stabilize the calorimeter energy measurement within a muon fill by correcting the energy reconstruction algorithm on the SiPM pixel recovery timescale (up to tens of nanoseconds) and the fill timescale (700 s) using a laser-based monitoring system [59]. The system also provides long-term (many-days) gain corrections. The two reconstructed positron samples are used in four independent extractions of in which each contribution to the time series is weighted by its energy-dependent asymmetry; this is the optimal approach [60]. Seven other determinations using additional methods agree well [48]. Each time series is modified to statistically correct for contributions of unresolved pileup clusters that result from multiple positrons proximate in space and time. The analyses employ one of three data-driven techniques to correct for pileup, which would otherwise bias .
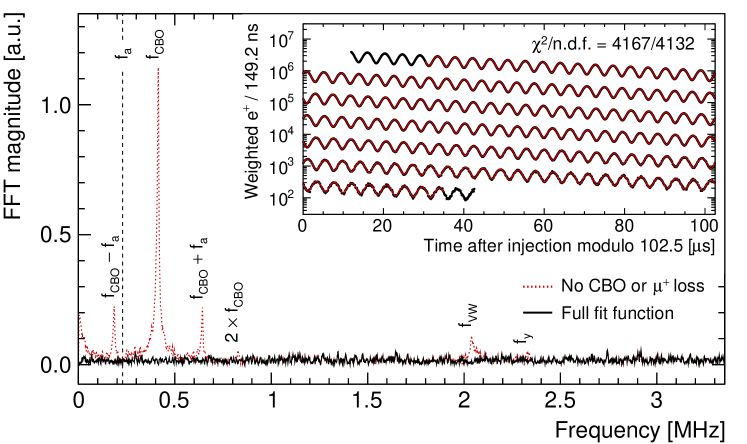
A minimization of the data model of Eq. 5 to the reconstructed time series determines the measured () quantity . The model fits the data well (see inset to Fig. 2), producing reduced s consistent with unity. Fourier transforms of the fit residuals show no unmodeled frequency components, see Fig. 2. Without the terms and the muon loss function in the model, strong signals emerge in the residuals at expected frequencies.
The dominant systematic uncertainties on arise from uncertainties in the pileup and gain correction factors, the modeling of the functional form of the CBO decoherence, and in the model. Scans varying the fit start and stop times and across individual calorimeter stations showed no significant variation in any of the four run groups [48].
The measured frequency requires four corrections, , for interpretation as the anomalous precession frequency of Eq. 2. The details are found in Ref. [49].
: The electric-field correction from the last term in Eq. 1 depends on the distribution of equilibrium radii , which translates to the muon beam momentum distribution via , where is the field index determined by the ESQ voltage [49]. A Fourier analysis [61, 49] of the decoherence rate of the incoming bunched beam as measured by the calorimeters provides the momentum distribution and determines the mean equilibrium radius mm and the width mm. The final correction factor is , where .
: A pitch correction is required to account for the vertical betatron oscillations that lead to a nonzero average value of the term in Eq. 1. The expression determines the pitch correction factor [62, 49]. The acceptance-corrected vertical amplitude distribution in the above expression is measured by the trackers.
Extensive simulations determined the uncertainties and arising from the geometry and alignment of the plates, as well as their voltage uncertainties and nonlinearities. The nonuniform kicker time profile applied to the finite-length incoming muon bunch results in a correlation introducing the largest uncertainty on .
: Any bias in the average phase of muons that are lost compared to those that remain stored creates a time dependence to the phase factor in Eq. 5. Beamline simulations predict a phase-momentum correlation mrad and losses are known to be momentum dependent. We verified the correlation by fitting precession data from short runs in which the storage ring magnetic field, and thus the central stored momentum , varied by compared to its nominal setting. Next, we measured the relative rates of muon loss () versus momentum in dedicated runs in which muon distributions were heavily biased toward high or low momenta using upstream collimators. Coupling the measured rate of muon loss in Run-1 to these two correlation factors determines the correction factor .
: The phase term in Eq. 5 depends on the muon decay coordinate and positron energy, but the precession frequency does not. If the stored muon average transverse distribution and the detector gains are stable throughout a fill, that average phase remains constant. The two damaged resistors in the ESQ system caused slow changes to the muon distribution during the first s of the measuring period. An extensive study of this effect involved: a) generation of phase, asymmetry, and acceptance maps for each calorimeter as a function of muon decay coordinate and positron energy from simulations utilizing our GEANT-based model of the ring (gm2ringsim); b) extraction of the time dependence of the optical lattice around the ring from the COSY simulation package and gm2ringsim; c) folding the azimuthal beam distribution derived from tracker and optics simulations with the phase, asymmetry, and acceptance maps to determine a net effective phase shift versus time-in-fill, ; and d) application of this time-dependent phase shift to precession data fits to determine the phase-acceptance () correction . The use of multiple approaches confirmed the conclusions; for details, see Ref. [49]. The damaged resistors were replaced after Run-1, which significantly reduces the dominant contribution to and the overall magnitude of muon losses.
IV Magnetic field determination
A suite of pulsed-proton NMR probes, each optimized for a different function in the analysis chain, measures the magnetic field strength [50]. Every 3 days during data taking, a 17-probe NMR trolley [63] measures the field at about 9000 locations in azimuth to provide a set of 2D field maps. 378 pulsed-NMR probes, located 7.7 cm above and below the storage volume, continuously monitor the field at 72 azimuthal positions, called stations. The trolley and fixed probes use petroleum jelly as an NMR sample. The probe signals are digitized and analyzed [64] to extract a precession frequency proportional to the average magnetic field over the NMR sample volume. A subset of probes is used to provide feedback to the magnet power supply to stabilize the field.
Calibration procedure : The primary calibration uses a probe with a cylindrical water sample. Corrections are required to relate its frequencies to the precession frequency expected from a proton in water at the reference temperature 34.7∘C. Studies of the calibration probe in an MRI solenoid precisely determine corrections for sample shape, temperature, and magnetization of probe materials to an uncertainty of 15 ppb. Cross-calibrations to an absolute 3He magnetometer [65] confirm the corrections to better than 38 ppb.
The calibration probe is installed on a translation stage in the SR vacuum. We repeatedly swap the calibration probe and a trolley probe into the same location, compensating for changes of the SR field. This procedure determines calibration offsets between individual trolley probes and the equivalent values. The offsets are due primarily to differences in diamagnetic shielding of protons in water versus petroleum jelly, sample shape, and magnetic perturbations from magnetization of the materials used in the probes and trolley body. The trolley probe calibration offsets are determined with an average uncertainty of 30 ppb.
Field Tracking (): The 14 Run-1 trolley field measurements bracket muon storage intervals to . They provide a suite of 2D multipole moments (dipole, normal quadrupole, skew quadrupole, …), which the fixed probes track. The fixed probes provide five independent moments (four moments for some stations) that track the field over 5∘ in azimuth for each station. The trolley moments are interpolated for times between the trolley runs, and the fixed probes continuously track changes to five lower-order moments [50]. The fixed probe and trolley measurements are synchronized when the trolley passes, averaged over each 5∘ azimuthal segment. The trolley run at time yields a second set of moments . The fixed probe moments are used to interpolate the field during muon storage between the trolley runs. The uncertainty on the interpolation is estimated from both the and maps and a Brownian bridge random walk model. The procedure produces interpolated storage volume field maps in terms of the equivalent shielded proton frequency throughout the Run-1 data-taking periods.
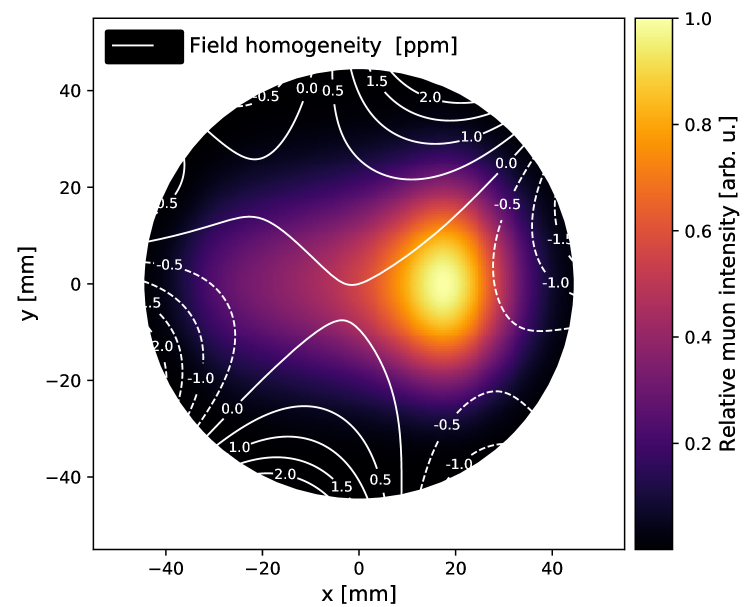
Muon weighting (): Averaging of the magnetic field weighted by the muon distribution in time and space uses the detected positron rates and the muon beam distribution measured by the trackers. The interpolated field maps are averaged over periods of roughly 10 s and weighted by the number of detected positrons during the same period. The SR guide fields introduce azimuthal dependencies of the muon distribution . We determine the muon-weighted average magnetic field by summing the field moments multiplied by the beam-weighted projections for every three-hour interval over which the tracker maps and field maps are averaged. Along , the beam is highly symmetric and centered, and the skew field moments (derivatives with respect to ) are relatively small. The azimuthally averaged centroid of the beam is displaced radially, leading to relative weights for the field dipole, normal quadrupole, and normal sextupole of , and , respectively. An overlay of the azimuthally averaged field contours on the muon distribution is shown in Fig. 3. The combined total uncertainty of from probe calibrations, field maps, tracker alignment and acceptance, calorimeter acceptance, and beam dynamics modeling is 56 ppb.
and : Two fast transients induced by the dynamics of charging the ESQ system and firing the SR kicker magnet slightly influence the actual average field seen by the beam compared to its NMR-measured value as described above and in Ref. [50]. An eddy current induced locally in the vacuum chamber structures by the kicker system produces a transient magnetic field in the storage volume. A Faraday magnetometer installed between the kicker plates measured the rotation of polarized light in a terbium-gallium-garnet crystal from the transient field to determine the correction .
The second transient arises from charging the ESQs, where the Lorentz forces induce mechanical vibrations in the plates that generate magnetic perturbations. The amplitudes and sign of the perturbations vary over the two sequences of eight distinct fills that occur in each 1.4 s accelerator supercycle. Customized NMR probes measured these transient fields at several positions within one ESQ and at the center of each of the other ESQs to determine the average field throughout the quadrupole volumes. Weighting the temporal behavior of the transient fields by the muon decay rate, and correcting for the azimuthal fractions of the ring coverage, 8.5% and 43% respectively, each transient provides final corrections and to as listed in Table 2.
V Computing and Conclusions
| Run | [Hz] | [Hz] | |
|---|---|---|---|
| 1a | 229081.06(28) | 61791871.2(7.1) | 3.7073009(45) |
| 1b | 229081.40(24) | 61791937.8(7.9) | 3.7073024(38) |
| 1c | 229081.26(19) | 61791845.4(7.7) | 3.7073057(31) |
| 1d | 229081.23(16) | 61792003.4(6.6) | 3.7072957(26) |
| Run-1 | 3.7073003(17) |
Table 1 lists the individual measurements of and , inclusive of all correction terms in Eq. 4, for the four run groups, as well as their ratios, (the latter multiplied by 1000). The measurements are largely uncorrelated because the run-group uncertainties are dominated by the statistical uncertainty on . However, most systematic uncertainties for both and measurements, and hence for the ratios , are fully correlated across run groups. The net computed uncertainties (and corrections) are listed in Table 2. The fit of the four run-group results has a , corresponding to ; we consider the to be a plausible statistical outcome and not indicative of incorrectly estimated uncertainties. The weighted-average value is = 0.0037073003(16)(6), where the first error is statistical and the second is systematic 666The E821 results for the field measurements were expressed in terms of the equivalent free proton precession frequency, resulting in . Expressing the field instead in terms of the proton shielded in water at C results in (BNL) = 0.0037073019(20).. From Eq. 2, we arrive at a determination of the muon anomaly
where the statistical, systematic, and fundamental constant uncertainties that are listed in Table 2 are combined in quadrature. Our result differs from the SM value by and agrees with the BNL E821 result. The combined experimental (Exp) average777We have carefully assessed any and all possible correlations to E821 at BNL and have concluded there are no important correlations that would impact a weighted average to obtain a correct combined result.There are also no non-negligible correlations between and . is
The difference, , has a significance of . These results are displayed in Fig. 4.
| Quantity | Correction terms | Uncertainty |
| (ppb) | (ppb) | |
| (statistical) | – | 434 |
| (systematic) | – | 56 |
| 489 | 53 | |
| 180 | 13 | |
| -11 | 5 | |
| -158 | 75 | |
| – | 56 | |
| -27 | 37 | |
| -17 | 92 | |
| – | 10 | |
| – | 22 | |
| – | 0 | |
| Total systematic | – | 157 |
| Total fundamental factors | – | 25 |
| Totals | 544 | 462 |
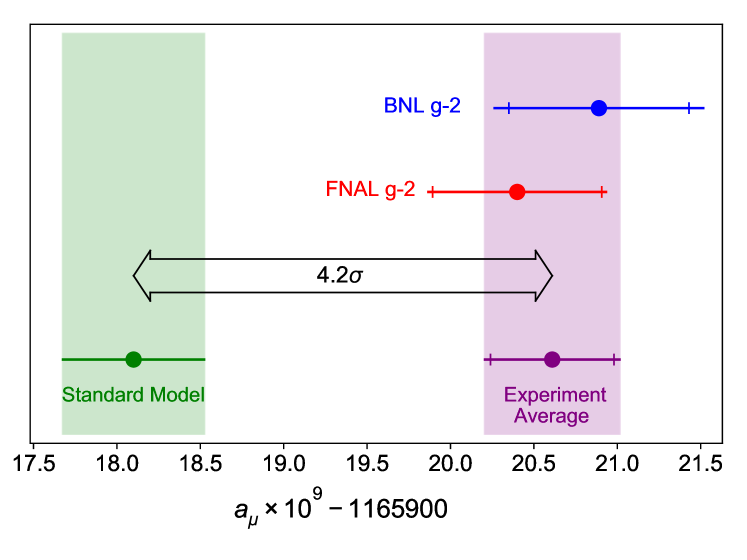
In summary, the findings here confirm the BNL experimental result and the corresponding experimental average increases the significance of the discrepancy between the measured and SM predicted to . This result will further motivate the development of SM extensions, including those having new couplings to leptons.
Following the Run-1 measurements, improvements to the temperature in the experimental hall have led to greater magnetic field and detector gain stability. An upgrade to the kicker enables the incoming beam to be stored in the center of the storage aperture, thus reducing various beam dynamics effects. These changes, amongst others, will lead to higher precision in future publications.
VI Acknowledgments
We thank the Fermilab management and staff for their strong support of this experiment, as well as the tremendous support from our university and national laboratory engineers, technicians, and workshops. We are indebted to Akira Yamamoto, Lou Snydstrup and Chien Pai who provided critical advice and engineering about the storage ring magnet and helped shepherd its transfer from Brookhaven to Fermilab. Greg Bock and Joe Lykken set the blinding clock and diligently monitored its stability. This result could not be interpreted without the worldwide theoretical effort to establish the standard model prediction, and in particular the recent work by the Muon Theory Initiative.
The Muon Experiment was performed at the Fermi National Accelerator Laboratory, a U.S. Department of Energy, Office of Science, HEP User Facility. Fermilab is managed by Fermi Research Alliance, LLC (FRA), acting under Contract No. DE-AC02-07CH11359. Additional support for the experiment was provided by the Department of Energy offices of HEP and NP (USA), the National Science Foundation (USA), the Istituto Nazionale di Fisica Nucleare (Italy), the Science and Technology Facilities Council (UK), the Royal Society (UK), the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant Agreements No. 690835, No. 734303, the National Natural Science Foundation of China (Grant No. 11975153, 12075151), MSIP, NRF and IBS-R017-D1 (Republic of Korea), and the German Research Foundation (DFG) through the Cluster of Excellence PRISMA+ (EXC 2118/1, Project ID 39083149).
References
- Dirac [1928] P. A. M. Dirac, The Quantum theory of electron. Part II, Proc. Roy. Soc. Lond. A118, 351 (1928).
- Nagel et al. [1947] D. E. Nagel, R. S. Julian, and J. R. Zacharias, The Hyperfine Structure of Atomic Hydrogen and Deuterium, Phys. Rev. 72, 971 (1947).
- Nafe et al. [1947] J. E. Nafe, E. B. Nelson, and I. I. Rabi, The Hyperfine Structure of Atomic Hydrogen and Deuterium, Phys. Rev. 71, 914 (1947).
- Schwinger [1948] J. S. Schwinger, On Quantum electrodynamics and the magnetic moment of the electron, Phys. Rev. 73, 416 (1948).
- Note [1] The scalar quantity is the magnetic anomaly, but is also commonly referred to as the “anomaly” or the “anomalous magnetic moment” in the literature.
- Kusch and Foley [1948] P. Kusch and H. M. Foley, The Magnetic Moment of the Electron, Phys. Rev. 74, 250 (1948).
- Garwin et al. [1957] R. L. Garwin, L. M. Lederman, and M. Weinrich, Observations of the Failure of Conservation of Parity and Charge Conjugation in Meson Decays: The Magnetic Moment of the Free Muon, Phys. Rev. 105, 1415 (1957).
- Cassels et al. [1957] J. M. Cassels, T. W. O’Keeffe, M. Rigby, A. M. Wetherell, and J. R. Wormald, Experiments with a polarized muon beam, Proceedings of the Physical Society. Section A 70, 543 (1957).
- Garwin et al. [1960] R. L. Garwin, D. P. Hutchinson, S. Penman, and G. Shapiro, Accurate Determination of the Magnetic Moment, Phys. Rev. 118, 271 (1960).
- Danby et al. [1962] G. Danby et al., Observation of High-Energy Neutrino Reactions and the Existence of Two Kinds of Neutrinos, Phys. Rev. Lett. 9, 36 (1962).
- Jegerlehner [2017] F. Jegerlehner, The Anomalous Magnetic Moment of the Muon, Vol. 274 (Springer, Cham, 2017).
- Note [2] The value is based on evaluating hadronic vacuum polarization contributions via data. Lattice QCD calculations of the hadronic vacuum polarization show promising improvements [13, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79]. The lattice world average determined in Ref. [13] is consistent with the data-driven result used for the number in the main text, but has a higher central value and larger uncertainty. Further scrutiny and improvements of lattice results are expected.
- Aoyama et al. [2020] T. Aoyama et al., The anomalous magnetic moment of the muon in the Standard Model, Phys. Rept. 887, 1 (2020), arXiv:2006.04822 [hep-ph] .
- Aoyama et al. [2012] T. Aoyama, M. Hayakawa, T. Kinoshita, and M. Nio, Complete Tenth-Order QED Contribution to the Muon , Phys. Rev. Lett. 109, 111808 (2012), arXiv:1205.5370 [hep-ph] .
- Aoyama et al. [2019] T. Aoyama, T. Kinoshita, and M. Nio, Theory of the Anomalous Magnetic Moment of the Electron, Atoms 7, 28 (2019).
- Davier et al. [2017] M. Davier, A. Hoecker, B. Malaescu, and Z. Zhang, Reevaluation of the hadronic vacuum polarisation contributions to the Standard Model predictions of the muon and using newest hadronic cross-section data, Eur. Phys. J. C77, 827 (2017), arXiv:1706.09436 [hep-ph] .
- Keshavarzi et al. [2018] A. Keshavarzi, D. Nomura, and T. Teubner, Muon and : a new data-based analysis, Phys. Rev. D97, 114025 (2018), arXiv:1802.02995 [hep-ph] .
- Colangelo et al. [2019] G. Colangelo, M. Hoferichter, and P. Stoffer, Two-pion contribution to hadronic vacuum polarization, JHEP 02, 006, arXiv:1810.00007 [hep-ph] .
- Hoferichter et al. [2019] M. Hoferichter, B.-L. Hoid, and B. Kubis, Three-pion contribution to hadronic vacuum polarization, JHEP 08, 137, arXiv:1907.01556 [hep-ph] .
- Davier et al. [2020] M. Davier, A. Hoecker, B. Malaescu, and Z. Zhang, A new evaluation of the hadronic vacuum polarisation contributions to the muon anomalous magnetic moment and to , Eur. Phys. J. C 80, 241 (2020), [Erratum: Eur.Phys.J.C 80, 410 (2020)], arXiv:1908.00921 [hep-ph] .
- Keshavarzi et al. [2020] A. Keshavarzi, D. Nomura, and T. Teubner, The of charged leptons, and the hyperfine splitting of muonium, Phys. Rev. D101, 014029 (2020), arXiv:1911.00367 [hep-ph] .
- Kurz et al. [2014] A. Kurz, T. Liu, P. Marquard, and M. Steinhauser, Hadronic contribution to the muon anomalous magnetic moment to next-to-next-to-leading order, Phys. Lett. B734, 144 (2014), arXiv:1403.6400 [hep-ph] .
- Melnikov and Vainshtein [2004] K. Melnikov and A. Vainshtein, Hadronic light-by-light scattering contribution to the muon anomalous magnetic moment revisited, Phys. Rev. D70, 113006 (2004), arXiv:hep-ph/0312226 [hep-ph] .
- Masjuan and Sánchez-Puertas [2017] P. Masjuan and P. Sánchez-Puertas, Pseudoscalar-pole contribution to the : a rational approach, Phys. Rev. D95, 054026 (2017), arXiv:1701.05829 [hep-ph] .
- Colangelo et al. [2017] G. Colangelo, M. Hoferichter, M. Procura, and P. Stoffer, Dispersion relation for hadronic light-by-light scattering: two-pion contributions, JHEP 04, 161, arXiv:1702.07347 [hep-ph] .
- Hoferichter et al. [2018] M. Hoferichter, B.-L. Hoid, B. Kubis, S. Leupold, and S. P. Schneider, Dispersion relation for hadronic light-by-light scattering: pion pole, JHEP 10, 141, arXiv:1808.04823 [hep-ph] .
- Gérardin et al. [2019] A. Gérardin, H. B. Meyer, and A. Nyffeler, Lattice calculation of the pion transition form factor with Wilson quarks, Phys. Rev. D100, 034520 (2019), arXiv:1903.09471 [hep-lat] .
- Bijnens et al. [2019] J. Bijnens, N. Hermansson-Truedsson, and A. Rodríguez-Sánchez, Short-distance constraints for the HLbL contribution to the muon anomalous magnetic moment, Phys. Lett. B798, 134994 (2019), arXiv:1908.03331 [hep-ph] .
- Colangelo et al. [2020] G. Colangelo, F. Hagelstein, M. Hoferichter, L. Laub, and P. Stoffer, Longitudinal short-distance constraints for the hadronic light-by-light contribution to with large- Regge models, JHEP 03, 101, arXiv:1910.13432 [hep-ph] .
- Pauk and Vanderhaeghen [2014] V. Pauk and M. Vanderhaeghen, Single meson contributions to the muon’s anomalous magnetic moment, Eur. Phys. J. C74, 3008 (2014), arXiv:1401.0832 [hep-ph] .
- Danilkin and Vanderhaeghen [2017] I. Danilkin and M. Vanderhaeghen, Light-by-light scattering sum rules in light of new data, Phys. Rev. D95, 014019 (2017), arXiv:1611.04646 [hep-ph] .
- Knecht et al. [2018] M. Knecht, S. Narison, A. Rabemananjara, and D. Rabetiarivony, Scalar meson contributions to from hadronic light-by-light scattering, Phys. Lett. B787, 111 (2018), arXiv:1808.03848 [hep-ph] .
- Eichmann et al. [2020] G. Eichmann, C. S. Fischer, and R. Williams, Kaon-box contribution to the anomalous magnetic moment of the muon, Phys. Rev. D101, 054015 (2020), arXiv:1910.06795 [hep-ph] .
- Roig and Sánchez-Puertas [2020] P. Roig and P. Sánchez-Puertas, Axial-vector exchange contribution to the hadronic light-by-light piece of the muon anomalous magnetic moment, Phys. Rev. D101, 074019 (2020), arXiv:1910.02881 [hep-ph] .
- Blum et al. [2020] T. Blum, N. Christ, M. Hayakawa, T. Izubuchi, L. Jin, C. Jung, and C. Lehner, The hadronic light-by-light scattering contribution to the muon anomalous magnetic moment from lattice QCD, Phys. Rev. Lett. 124, 132002 (2020), arXiv:1911.08123 [hep-lat] .
- Colangelo et al. [2014] G. Colangelo, M. Hoferichter, A. Nyffeler, M. Passera, and P. Stoffer, Remarks on higher-order hadronic corrections to the muon , Phys. Lett. B735, 90 (2014), arXiv:1403.7512 [hep-ph] .
- Jackiw and Weinberg [1972] R. Jackiw and S. Weinberg, Weak interaction corrections to the muon magnetic moment and to muonic atom energy levels, Phys. Rev. D5, 2396 (1972).
- Bars and Yoshimura [1972] I. Bars and M. Yoshimura, Muon magnetic moment in a finite theory of weak and electromagnetic interaction, Phys. Rev. D6, 374 (1972).
- Fujikawa et al. [1972] K. Fujikawa, B. W. Lee, and A. I. Sanda, Generalized Renormalizable Gauge Formulation of Spontaneously Broken Gauge Theories, Phys. Rev. D6, 2923 (1972).
- Czarnecki et al. [2003] A. Czarnecki, W. J. Marciano, and A. Vainshtein, Refinements in electroweak contributions to the muon anomalous magnetic moment, Phys. Rev. D67, 073006 (2003), [Erratum: Phys. Rev. D73, 119901 (2006)], arXiv:hep-ph/0212229 [hep-ph] .
- Gnendiger et al. [2013] C. Gnendiger, D. Stoeckinger, and H. Stoeckinger-Kim, The electroweak contributions to after the Higgs boson mass measurement, Phys. Rev. D88, 053005 (2013), arXiv:1306.5546 [hep-ph] .
- Charpak et al. [1962] G. Charpak, F. J. M. Farley, and R. L. Garwin, A New Measurement of the Anomalous Magnetic Moment of the Muon, Phys. Lett. 1, 16 (1962).
- Bailey et al. [1968] J. Bailey et al., Precision measurement of the anomalous magnetic moment of the muon, Phys. Lett. B28, 287 (1968).
- Bailey et al. [1979] J. Bailey et al. (CERN-Mainz-Daresbury), Final Report on the CERN Muon Storage Ring Including the Anomalous Magnetic Moment and the Electric Dipole Moment of the Muon, and a Direct Test of Relativistic Time Dilation, Nucl. Phys. B150, 1 (1979).
- Bennett et al. [2006] G. Bennett et al. (Muon Collaboration), Final Report of the Muon E821 Anomalous Magnetic Moment Measurement at BNL, Phys.Rev. D73, 072003 (2006), arXiv:hep-ex/0602035 [hep-ex] .
- Hanneke et al. [2008] D. Hanneke, S. Fogwell, and G. Gabrielse, New Measurement of the Electron Magnetic Moment and the Fine Structure Constant, Phys. Rev. Lett. 100, 120801 (2008), arXiv:0801.1134 [physics.atom-ph] .
- Grange et al. [2015] J. Grange et al. (Muon ), Muon Technical Design Report, (2015), arXiv:1501.06858 [physics.ins-det] .
- Albahri et al. [2021a] T. Albahri, A. Anastasi, A. Anisenkov, K. Badgley, S. Baeßler, I. Bailey, V. A. Baranov, E. Barlas-Yucel, T. Barrett, A. Basti, et al. (Muon ), Measurement of the anomalous precession frequency of the muon in the Fermilab Muon experiment, Phys. Rev. D 103, 072002 (2021a).
- Albahri et al. [2021b] T. Albahri, A. Anastasi, K. Badgley, S. Baeßler, I. Bailey, V. A. Baranov, E. Barlas-Yucel, T. Barrett, F. Bedeschi, M. Berz, et al. (Muon ), Beam dynamics corrections to the Run-1 measurement of the muon anomalous magnetic moment at Fermilab, Phys. Rev. Accel. Beams (to be published) (2021b).
- Albahri et al. [2021c] T. Albahri, A. Anastasi, K. Badgley, S. Baeßler, I. Bailey, V. A. Baranov, E. Barlas-Yucel, T. Barrett, F. Bedeschi, M. Berz, et al. (Muon ), Measurement of the anomalous precession frequency of the muon in the Fermilab Muon experiment, Phys. Rev. A 103, 042208 (2021c).
- Danby et al. [2001] G. T. Danby et al., The Brookhaven muon storage ring magnet, Nucl. Instrum. Meth. A457, 151 (2001).
- Note [3] The rate of change of the angle between spin and momentum vectors is equal to only if and are parallel. The angle between and is always small, and the rate of oscillation of out of pure circular motion is fast compared to .
- Note [4] The coordinate system is with respect to the center of the storage volume at radius , with radially outward, vertically up, and increasing clockwise when viewed from above.
- Fienberg et al. [2015] A. T. Fienberg et al., Studies of an array of PbF2 Cherenkov crystals with large-area SiPM readout, Nucl. Instrum. Meth. A783, 12 (2015), arXiv:1412.5525 [physics.ins-det] .
- Khaw et al. [2019] K. S. Khaw et al. (Muon ), Performance of the Muon calorimeter and readout systems measured with test beam data, Nucl. Instrum. Meth. A945, 162558 (2019), arXiv:1905.04407 [physics.ins-det] .
- Kaspar et al. [2017] J. Kaspar et al., Design and performance of SiPM-based readout of PbF2 crystals for high-rate, precision timing applications, JINST 12 (01), P01009, arXiv:1611.03180 [physics.ins-det] .
- Note [5] We use the shielded proton-to-electron magnetic moment ratio [80] and the electron -factor [81] measurement. The CODATA-2018 result is used for the muon-to-electron mass ratio [82], which is determined from bound-state QED theory and measurements described in [83]. The QED factor is computed by theory with negligible uncertainty [82].
- Allan [1966] D. W. Allan, Statistics of Atomic Frequency Standards, Proceedings of the IEEE 54, 221 (1966).
- Anastasi et al. [2019] A. Anastasi et al. (Muon ), The laser-based gain monitoring system of the calorimeters in the Muon experiment at Fermilab, JINST 14, P11025, arXiv:1906.08432 [physics.ins-det] .
- Bennett et al. [2007] G. W. Bennett et al. (Muon ), Statistical equations and methods applied to the precision muon experiment at BNL, Nucl. Instrum. Meth. A 579, 1096 (2007).
- Orlov et al. [2002] Y. Orlov et al., Muon revolution frequency distribution from a partial-time Fourier transform of the signal in the muon experiment, Nucl. Instrum. Meth. A482, 767 (2002).
- Farley [1972] F. J. M. Farley, Pitch correction in experiments, Phys. Lett. 42B, 66 (1972).
- Corrodi et al. [2020] S. Corrodi, P. De Lurgio, D. Flay, J. Grange, R. Hong, D. Kawall, M. Oberling, S. Ramachandran, and P. Winter (Muon ), Design and performance of an in-vacuum, magnetic field mapping system for the Muon experiment, JINST 15 (11), P11008, arXiv:2003.06244 [physics.ins-det] .
- Hong et al. [2021] R. Hong et al., Systematic and statistical uncertainties of the hilbert-transform based high-precision FID frequency extraction method, J. Magn. Reson XYZ, xyx (2021).
- Farooq et al. [2020] M. Farooq, T. Chupp, J. Grange, A. Tewsley-Booth, D. Flay, D. Kawall, N. Sachdeva, and P. Winter, Absolute Magnetometry with He3, Phys. Rev. Lett. 124, 223001 (2020).
- [66] See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevLett.126.141801/ for additional details on the measurements.
- Note [6] The E821 results for the field measurements were expressed in terms of the equivalent free proton precession frequency, resulting in . Expressing the field instead in terms of the proton shielded in water at \tmspace+.1667emC results in (BNL) = 0.0037073019(20).
- Note [7] We have carefully assessed any and all possible correlations to E821 at BNL and have concluded there are no important correlations that would impact a weighted average to obtain a correct combined result.There are also no non-negligible correlations between and .
- Chakraborty et al. [2018] B. Chakraborty et al. (Fermilab Lattice, LATTICE-HPQCD, MILC), Strong-Isospin-Breaking Correction to the Muon Anomalous Magnetic Moment from Lattice QCD at the Physical Point, Phys. Rev. Lett. 120, 152001 (2018), arXiv:1710.11212 [hep-lat] .
- Borsanyi et al. [2018] S. Borsanyi et al. (Budapest-Marseille-Wuppertal), Hadronic vacuum polarization contribution to the anomalous magnetic moments of leptons from first principles, Phys. Rev. Lett. 121, 022002 (2018), arXiv:1711.04980 [hep-lat] .
- Blum et al. [2018] T. Blum, P. A. Boyle, V. Gülpers, T. Izubuchi, L. Jin, C. Jung, A. Jüttner, C. Lehner, A. Portelli, and J. T. Tsang (RBC, UKQCD), Calculation of the hadronic vacuum polarization contribution to the muon anomalous magnetic moment, Phys. Rev. Lett. 121, 022003 (2018), arXiv:1801.07224 [hep-lat] .
- Giusti et al. [2019] D. Giusti, V. Lubicz, G. Martinelli, F. Sanfilippo, and S. Simula, Electromagnetic and strong isospin-breaking corrections to the muon from Lattice QCD+QED, Phys. Rev. D 99, 114502 (2019), arXiv:1901.10462 [hep-lat] .
- Shintani and Kuramashi [2019] E. Shintani and Y. Kuramashi (PACS), Hadronic vacuum polarization contribution to the muon with 2+1 flavor lattice QCD on a larger than (10 fm lattice at the physical point, Phys. Rev. D 100, 034517 (2019), arXiv:1902.00885 [hep-lat] .
- Davies et al. [2020] C. T. H. Davies et al. (Fermilab Lattice, LATTICE-HPQCD, MILC), Hadronic-vacuum-polarization contribution to the muon’s anomalous magnetic moment from four-flavor lattice QCD, Phys. Rev. D 101, 034512 (2020), arXiv:1902.04223 [hep-lat] .
- Gérardin et al. [2019] A. Gérardin, M. Cè, G. von Hippel, B. Hörz, H. B. Meyer, D. Mohler, K. Ottnad, J. Wilhelm, and H. Wittig, The leading hadronic contribution to from lattice QCD with flavours of O() improved Wilson quarks, Phys. Rev. D 100, 014510 (2019), arXiv:1904.03120 [hep-lat] .
- Aubin et al. [2020] C. Aubin, T. Blum, C. Tu, M. Golterman, C. Jung, and S. Peris, Light quark vacuum polarization at the physical point and contribution to the muon , Phys. Rev. D 101, 014503 (2020), arXiv:1905.09307 [hep-lat] .
- Giusti and Simula [2019] D. Giusti and S. Simula, Lepton anomalous magnetic moments in Lattice QCD+QED, PoS LATTICE2019, 104 (2019), arXiv:1910.03874 [hep-lat] .
- Borsanyi et al. [2020] S. Borsanyi et al., Leading hadronic contribution to the muon 2 magnetic moment from lattice QCD, (2020), arXiv:2002.12347 [hep-lat] .
- Lehner and Meyer [2020] C. Lehner and A. S. Meyer, Consistency of hadronic vacuum polarization between lattice QCD and the R-ratio, Phys. Rev. D 101, 074515 (2020), arXiv:2003.04177 [hep-lat] .
- Phillips et al. [1977] W. D. Phillips, W. E. Cooke, and D. Kleppner, Magnetic moment of the proton in H2O in bohr magnetons, Metrologia 13, 179 (1977).
- Hanneke et al. [2011] D. Hanneke, S. F. Hoogerheide, and G. Gabrielse, Cavity Control of a Single-Electron Quantum Cyclotron: Measuring the Electron Magnetic Moment, Phys. Rev. A 83, 052122 (2011), arXiv:1009.4831 [physics.atom-ph] .
- [82] E. Tiesinga, P. J. Mohr, D. B. Newell, and B. N. Taylor, The 2018 CODATA Recommended Values of the Fundamental Physical Constants (Web Version 8.1), http://physics.nist.gov/constants.
- Liu et al. [1999] W. Liu et al., High precision measurements of the ground state hyperfine structure interval of muonium and of the muon magnetic moment, Phys. Rev. Lett. 82, 711 (1999).