The BLAST collaboration
Measurement of the Vector and Tensor Asymmetries at Large Missing
Momentum in Quasielastic Electron Scattering from Deuterium
Abstract
We report the measurement of the beam-vector and tensor asymmetries and in quasielastic electrodisintegration of the deuteron at the MIT-Bates Linear Accelerator Center up to missing momentum of 500 MeV/c. Data were collected simultaneously over a momentum transfer range (GeV/c)2 with the Bates Large Acceptance Spectrometer Toroid using an internal deuterium gas target, polarized sequentially in both vector and tensor states. The data are compared with calculations. The beam-vector asymmetry is found to be directly sensitive to the -wave component of the deuteron and have a zero-crossing at a missing momentum of about 320 MeV/c, as predicted. The tensor asymmetry at large missing momentum is found to be dominated by the influence of the tensor force in the neutron-proton final-state interaction. The new data provide a strong constraint on theoretical models.
pacs:
13.40.-f, 13.40.Gp, 13.85.Dz, 13.88.+e, 25.30.Bf, 27.10.+hUnderstanding the structure and properties of the nucleon-nucleon system is a cornerstone of nuclear physics. Classic studies of the properties of the bound state, (the deuteron) like the magnetic and quadrupole moments, have elucidated the non-relativistic - and -state wave function components. However, modern polarized beams and targets provide new tools to revisit this subject to provide more stringent tests of our understanding. Spin-dependent quasielastic electron scattering from both vector and tensor polarized deuterium provides unique access to the orbital angular momentum structure of the deuteron, which is inaccessible in unpolarized scattering Boeglin:2014gda . The combination of a pure, highly polarized gas target internal to a storage ring with an intense, highly polarized electron beam and a large acceptance detector allows the simultaneous measurement of the asymmetries as a function of initial-state proton momentum and momentum transfer. To see the direct effects of the -state, initial-state momenta up to 500 MeV/c are required. Further, nucleon-nucleon correlations with high relative momenta are known to play a significant role in nuclear structure Hen2016 . The tensor force between the neutron and proton can be probed via final-state interaction (FSI) effects in spin-dependent quasielastic at large initial-state momenta Jeschonnek:2017 ; Mayer:2016zmv . In this Letter, we report on new measurements of the vector and tensor asymmetries in quasielastic scattering from deuterium over a broad range of kinematics and compare with theoretical calculations.
The deuteron’s simple structure enables reliable calculations to be performed in sophisticated theoretical frameworks. These calculations use nucleon-nucleon potentials as input, which show that the ground-state wave function is dominated by the -state at low relative proton-neutron momentum . The tensor component of the NN interaction generates an additional -state component. Models predict that the and state components strongly depend on . In the reaction, energy and three-momentum are transferred to the deuteron. The cross section can be measured as a function of the missing momentum , where is the measured momentum of the ejected proton.
The cross section can be written in terms of the unpolarized cross section multiplied by asymmetries diluted by various combinations of the beam’s longitudinal polarization , the target vector polarization , and the target tensor polarization Aren1992 as:
| (1) | |||||
In the Born approximation , , and are all zero. In a purely -state is also zero but will vary from zero as -state contributions become important providing a measure of the tensor component of the NN interaction. Similarly, will vary from as -state contributions become significant.
Previous measurements of the asymmetries up to 150 MeV/c NIKHEF:1999 and of up to 350 MeV/c NIKHEF:2002 were carried out at NIKHEF. These pioneering measurements did not have the kinematic reach to observe the effects of the -state in or the FSI effects in .
Our experiment was carried out with the Bates Large Acceptance Spectrometer Toroid (BLAST) Hasell:2009 ; Hasell:2011 . The BLAST experiment; including details on the detector, the South Hall Ring (SHR) of the MIT-Bates Linear Accelerator Center, the longitudinal polarized electron beam, the atomic beam source Cheever:2006 (ABS) that produced the vector and tensor polarized deuterium, and the experimental operation; has been described extensively in the cited references and will not be repeated here.
The target spin states were switched every 5 minutes. The longitudinal beam polarization was reversed every injection cycle and was monitored continuously using a Compton back-scattering polarimeter. The average polarization was .
The data were taken in two separate running periods and acquired simultaneously with the BLAST measurements of Geis:2008 and Zhang:2011 . The average target spin angles were and with respect to the beam axis for the two run periods. The target spin angle was in the horizontal plane pointing into the left sector and was determined using elastic electron-deuteron scattering Zhang:2011 . Electrons scattered into the right (left) sector delivered momentum transfer predominantly parallel (perpendicular) to the target spin vector, so-called same sector (opposing sector) kinematics.
The average product of beam and target polarization was determined from measuring in the reaction in the quasielastic limit (low missing momentum, GeV/c) where the reaction is close to elastic scattering. The results were in the first run and in the second run. In parallel, was similarly determined from the quasielastic reaction and was found to be in good agreement.
The target tensor polarizations were determined from fits to the elastic electron-deuteron observable Zhang:2011 using parameterizations to previous data Abbott:2000 . The results were and , where the three uncertainties are statistical, systematic, and due to the parametrization of , in that order.
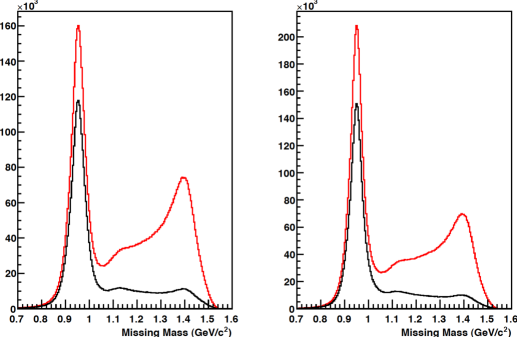
The event selection is described in detail in the theses of A. Maschinot Maschinot and A. DeGrush DeGrush . Briefly, electron-proton coincidence events were selected using a series of PID, timing, and vertex cuts. Events were chosen with two oppositely charged (curvature) tracks in opposing sectors. The Čerenkov detectors were used to distinguish electrons from and time of flight was used to select proton events while rejecting events with or a deuteron. To ensure that the two particles came from the same event, a cut was placed on the relative separation of their vertices in the target cm. Once these events were selected each track’s kinematic variables, for the electron and for the proton, were used to determine the variables . The quasielastic events were selected by placing a cut around the peak of the missing mass spectrum (see Fig. 1) representing the remaining neutron.
After background subtraction and correcting for false asymmetries determined from the empty target runs the resulting yield in the various and bins could be determined for the combinations of beam and deuterium vector and tensor orientations (1, 1 or 0, +1 or -2) for which data was collected. The charge normalized yields or event rates could be combined to give the desired asymmetries. For this paper:
| (2) | |||||
| (3) | |||||
| (4) | |||||
where is the charge normalized yield or event rate for each spin orientation combination.
Radiative corrections to the asymmetries were calculated using the MASCARAD code MASCARAD and all found to be less than 1%. Thus, no corrections were applied to the asymmetries but a systematic uncertainty of % was included. Background arose predominantly from beam collisions with the target cell wall. Estimates for this rate were made by acquiring data with and without gas in the target cell. Background was subtracted on a bin-by-bin basis and increased from a typical value of % at low to of order 10% at the highest .
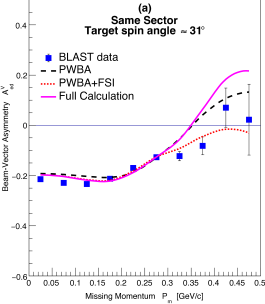
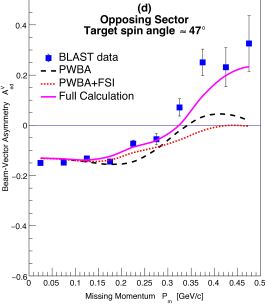
The beam-vector asymmetries for the runs with the two target spin orientations are shown in Fig. 2. The data are shown in same sector and opposing sector kinematics as a function of the missing momentum for momentum transfers (GeV/c)2. The values of extend up to about 500 MeV/c and the data are compared with theoretical calculations based on the model of Arenhövel, Leidemann, and Tomusiak Aren2005 . The model was calculated for the kinematics of the experiment folding in the detector acceptances and efficiencies in a comprehensive GEANT simulation. The curves shown in each plot correspond to a plane-wave Born approximation (PWBA) which includes the coupling to the neutron, a PWBA with final state interactions (FSI) and a full calculation beyond PWBA+FSI including the effects of meson-exchange currents (MEC), isobar configurations (IC) and relativistic corrections (RC). The two-body wave functions needed for the calculation of the observables are based on the realistic Bonn potential Bonn1987 , which is defined in purely nucleonic space. The theoretical calculations were found to be insensitive to the choice of different realistic potentials (e.g. Reid Reid:1968 , Paris Paris:1980 , Argonne V14 and V18 Argonne:1995 ). The treatment of MEC, IC, and RC is done consistently according to Aren2005 ; Bonn1997 .
At the limit the opposing sector asymmetries are directly proportional to the product , a key parameter that has been determined with better than 1% absolute accuracy. The target vector polarization is directly related to the polarization of the proton or neutron bound in the deuteron such that Aren1988
| (5) |
where and are the - and -state probabilities of the deuteron, respectively. This illustrates the fact that the polarization of a nucleon in the -state is opposite to that of a nucleon in the -state, as expected from angular momentum considerations for a system like the deuteron. The present results for the asymmetries show for the first time the evolution going from the -state to the -state in momentum space. The are constant up to about MeV/c which is consistent with an -state, then as increases, the presence of the -state lowers the proton polarization in the deuteron until it changes sign when .
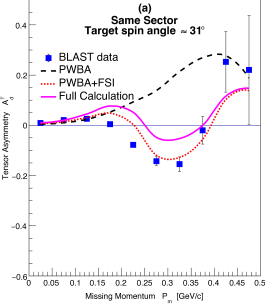
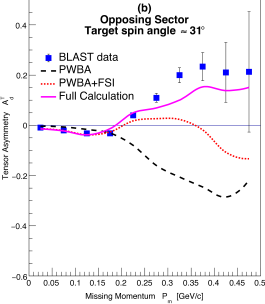
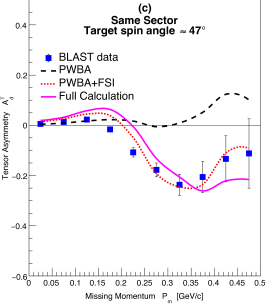
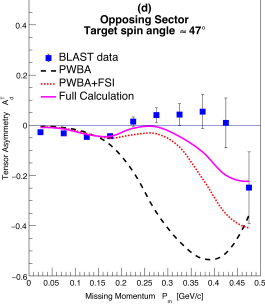
Figure 2 shows that the experimental asymmetries are in good agreement with the full theoretical calculations over a wide range of and . The only previous measurement of was carried out in perpendicular kinematics at NIKHEF NIKHEF:2002 up to of about 300 MeV/c, although with limited statical precision after 200 MeV/c. The BLAST data in the region of around 200 MeV/c, where the - and -states strongly interfere, are very well described by the full theoretical calculation in contrast to the claim in NIKHEF:2002 where the data suggested an underestimation by the theory. The asymmetries directly relate to the deuteron momentum distribution for the spin states. It has been pointed out Forest1996 that the momentum distribution has a zero around 300 MeV/c, which in a simple picture can be related to the dimensions of the toroidal shape of the density distribution. The Fourier transform of the deuteron density calculated in the model of Ref. Forest1996 yields a zero at 320 MeV/c for the momentum distribution DeGrush , which is where the asymmetries in Fig. 2 have their zero-crossings. This zero crossing was also predicted by Jeschonnek and Donnelly Donnelly1998 using an improved treatment of the non-relativistic reduction of the electromagnetic current operator.
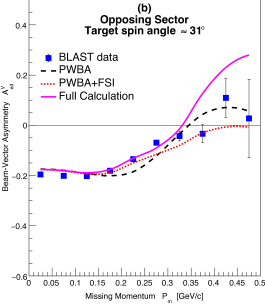
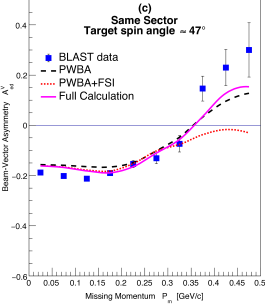
Figure 3 shows the tensor analyzing powers as a function of for the same kinematics and target spin orientations as that of Fig. 2, and compared also with the same theoretical model folded with the detector acceptances and efficiencies. Just as for the only previous measurement of was carried out in parallel kinematics at NIKHEF NIKHEF:1999 up to of only 150 MeV/c with limited statistics. The BLAST data extend up to = 500 MeV/c and for the first time into the region where the -state dominates over the -state. As expected, where the -state dominates, the are small and well described by the theoretical calculations, including the simple PWBA. Beyond about = 150 MeV/c grows, indicating the effect of the tensor polarization. The PWBA calculations show that the sign is different for the in same sector and opposing sector kinematics.
As shown in Fig. 3, in contrast to the vector asymmetries , the tensor asymmetries are significantly modified by the effects of the FSI for MeV/c. In same sector kinematics, the effects of FSI bring the calculations into reasonable agreement with the present data. In opposing sector kinematics, the effects of the FSI are also sizable but not sufficient to agree with the data; the effects of MEC and IC contribute equally after FSI to produce the full calculations of Fig. 3. The kinematic reach of the BLAST data is such that the proton-neutron interaction is sampled via the FSI over a large spatial range: from short distances, where the nucleons are expected to overlap, to long distances where the interaction is dominated by one-pion-exchange. The data at MeV/c are particularly sensitive to the tensor part of the interaction at short distances, where it has significant model dependence Forest1996 . It is to be noted that the theoretical model used here works well, given that it is mainly based on nucleon degrees of freedom.
We have presented data for the vector and tensor spin asymmetries from the deuteron for (GeV/c)2. The asymmetries were mapped out for quasielastic kinematics over a range of up to MeV/c. The data were taken using an internal deuterium gas target polarized in both vector and tensor spin states that minimized systematic errors. This was done simultaneously with precise measurements of the elastic Zhang:2011 and the Geis:2008 channels that also permitted measurements of and . The new data are in good agreement with theoretical calculations and provide a strong constraint on our understanding of deuteron structure and the tensor force between a neutron and a proton. The -state contribution is clearly evident in both asymmetries as increases and highlights the importance of measurements at large . The tensor asymmetries with same and opposing sector kinematics probes the proton-neutron interaction over a large spatial range. These results and approach are important for future theoretical calculations and experiments that study the deuteron and details of the proton-neutron interaction.
Acknowledgements.
We thank the staff at the MIT-Bates Linear Accelerator Center for the high quality electron beam and their technical support. We thank H. Arenhövel for many enlightening discussions. This work has been supported in part by the US Department of Energy Office of Nuclear Physics and by the National Science Foundation.References
- (1) W.U. Boeglin, J. Phys. Conf. Ser. 543 012011, (2014).
- (2) O. Hen, G. Miller, E. Piasetzky and L.B. Weinstein, arXiv: 1611.09748, to be published in Reviews of Modern Physics.
- (3) S. Jeschonnek and J.W. Van Orden, Phys. Rev. C95, 044001 (2017).
- (4) M. Mayer et al., Phys. Rev. C95, 024005 (2017)
- (5) H. Arenhövel, W. Leidemann, and E.L. Tomusiak, Phys. Rev. C46, 455 (1992).
- (6) Z.L. Zhou et al., Phys. Rev. Lett. 82, 687 (1999).
- (7) I. Passchier et al., Phys. Rev. Lett. 88, 102302 (2002).
- (8) D.K. Hasell et al., Nucl. Instr. and Meth. A603, 247 (2009).
- (9) D.K. Hasell et al., Ann. Rev. Nucl. Sci. 61, 409 (2011).
- (10) D. Cheever et al., Nucl. Instr. and Meth. A556, 410 (2006).
- (11) E. Geis et al. (The BLAST Collaboration), Phys. Rev. Lett. 101, 042501 (2008).
- (12) C. Zhang et al. (The BLAST Collaboration), Phys. Rev. Lett. 107, 252501 (2011).
- (13) D. Abbott et al., Eur. Phys. J. A7, 421 (2000).
- (14) A. Maschinot, Ph.D. thesis, MIT (2005), http://hdl.handle.net/1721.1/34390.
- (15) A. DeGrush, Ph.D. thesis, MIT (2010), http://hdl.handle.net/1721.1/62644.
- (16) A. Afanasev, I. Akushevich, and N. Merenkov, Phys. Rev. D64, 113009 (2001).
- (17) H. Arenhövel, W. Leidemann, and E.L. Tomusiak, Eur. Phys. J. A23, 147–190 (2005).
- (18) R. Machleidt, K. Holinde, Ch. Ester, Phys. Rep. 149, 1 (1987).
- (19) R. Reid, Ann. Phys. 50, 411 (1968).
- (20) M. Lacombe et al., Phys. Rev. C21 861 (1980).
- (21) R. Wiringa, V.G.J. Stoks, and R. Schiavilla, Phys. Rev. C51 38 (1995).
- (22) F. Ritz, H. Goller, T. Wilbois, H. Arenhovel, Phys. Rev. C55, 2214 (1997).
- (23) H. Arenhövel, W. Leidemann, and E.L. Tomusiak, Z. Phys. Rev. A331, 123–138 (1988).
- (24) J.L. Forest et al., Phys. Rev. C54, 646 (1996).
- (25) S. Jeschonnek and T.W. Donnelly, Phys. Rev. C57, 2438 (1998).