Measuring the Stellar and Planetary Parameters of the 51 Eridani System \righttitleA. Elliott et al.
110 \jnlDoiYr2023 \doival10.1017/pasa.xxxx.xx
A. Elliott, Email: aelli76@lsu.edu
(Received xx xx xxxx; revised xx xx xxxx; accepted xx xx xxxx)
Measuring the Stellar and Planetary Parameters of the 51 Eridani System
Abstract
In order to study exoplanets, a comprehensive characterization of the fundamental properties of the host stars - such as angular diameter, temperature, luminosity, and age, is essential, as the formation and evolution of exoplanets are directly influenced by the host stars at various points in time. In this paper, we present interferometric observations taken of directly imaged planet host 51 Eridani at the CHARA Array. We measure the limb-darkened angular diameter of 51 Eridani to be mas and combining with the Gaia zero-point corrected parallax, we get a stellar radius of R⊙. We use the PARSEC isochrones to estimate an age of Myr and a mass of M⊙. The age and mass agree well with values in the literature, determined through a variety of methods ranging from dynamical age trace-backs to lithium depletion boundary methods. We derive a mass of MJup for 51 Eri b using the Sonora Bobcat models, which further supports the possibility of 51 Eri b forming under either the hot-start formation model or the warm-start formation model.
keywords:
exoplanets, interferometry, fundamental properties, young stars1 Introduction
Young, nearby stars are of major interest to scientists as they can provide insight into stellar evolution, as well as planetary formation. The exoplanet host 51 Eridani has been an object of interest in the astronomical community for a number of years. 51 Eridani is a F0 spectral type, mag star and has a binary pair companion, GJ 3305A,B (both M0 dwarfs). 51 Eridani and GJ 3305A,B have a separation of 66′′, or roughly 2000 au, and the system components are co-moving together in a hierarchical relationship (Feigelson et al.,, 2006). The exoplanet, 51 Eri b, has a semi-major axis of au, an inclination of deg, an eccentricity of , and an orbital period of years, all determined by fits of SPHERE and GPI data by Maire et al., (2019).
51 Eridani is a member of the Pictoris moving group (), which is one of the youngest and closest moving groups to Earth. Zuckerman et al., (2001) determined that the Pictoris Moving Group consisted of 17 star systems. Since then, there are now a few hundred candidate systems belonging to the (Miret-Roig et al.,, 2020). The age estimates for the include Myr (Mamajek and Bell,, 2014) using the lithium depletion boundary method and isochronal ages for FGMK stars, which is consistent with the age estimate of 51 Eridani, Myr (Macintosh et al.,, 2015) using the group’s lithium depletion boundary age. A more recent dynamical age estimate developed by Miret-Roig et al., (2020) presents an age of Myr. This estimate is a dynamical trace-back age that reconciles other trace-back estimates with other methods such as lithium depletion, isochronal ages, and other dynamical estimates.
Macintosh et al., (2015) presented the discovery of the directly imaged planet 51 Eri b by the Gemini Planet Imager (GPI). Follow-up work by GPI and NIRC2 at the W. M. Keck 2 telescope (Wizinowich et al.,, 2000) have confirmed and refined the orbit and planetary properties of the system. The most current study of this system by Dupuy et al., (2022) determined an upper limit for the planet mass of MJup within a interval and an orbital separation of au derived using joint fitting of the Hipparcos-Gaia Catalog of Accelerations (HGCA-EDR3) proper motions and relative astrometry. Samland et al., (2017) determined a planetary effective temperature of K, and a radius of RJup from fitting spectro-photometry from VLT/SPHERE. Brown-Sevilla et al., (2023) recently published updated parameters on 51 Eri b using observations from VLT/SPHERE. A radiative transfer model fit using petitRADTRANS resulted in a planetary effective temperature of K along with a radius of RJup, and a mass of MJup. For the mass of the planet, Brown-Sevilla et al., (2023) reported three possible masses: MJup as the nominal result, MJup as a mass using evolutionary models by Baraffe et al., (2002) with an age of 10 Myr, and MJup with an age of 20 Myr. These ages were taken from age estimates published by Lee et al., (2022) and Macintosh et al., (2015), respectively.
Given the young age of the system (both star and planet) determined by several literature sources, 51 Eri b is a perfect candidate to study a planet that is both young and still being influenced by its initial conditions of formation (Macintosh et al.,, 2015). There are two main planet formation scenarios that most planets discovered fit into: the cold-start model and the hot-start model. The cold-start model is described by core accretion and usually results in lower entropy and a smaller radius of the planet. The hot-start model is described by disk instability which results in a planet with a higher entropy, a higher effective temperature, and a larger radius (Spiegel and Burrows, 2012a, ). A third formation scenario, cleverly named the warm-start model, involves a combination of the hot and cold start formation criteria (Spiegel and Burrows, 2012b, ). The warm-start model is a spectrum of initial conditions motivated by the observed preference of core accretion with gas giants forming closer to their stars and the recent observations of young exoplanets that are hotter than the cold-start model predictions but colder than the hot-start model predictions (Spiegel and Burrows, 2012b, ). A planet’s luminosity can provide insights into its formation because it is a function of age, mass, and initial conditions (Marley et al.,, 2007; Spiegel and Burrows, 2012a, ). Macintosh et al., (2015)’s initial observations and study of 51 Eri b noted that the core-accretion theory explains the formation of this planet due to the derived low luminosity range (log(). Samland et al., (2017) explored all three scenarios and ruled out the cold-start models due to the new luminosity ranges (log() derived and found that the planet mass favored the hot- or warm- start models. Dupuy et al., (2022) also ruled out the cold-start formation with their derivation of a lower limit on the initial specific entropy. Further study of this planet and its star can continue to explain its formation.
Characterizing exoplanet host stars is key to understanding the exoplanet itself. The directly measured fundamental properties of a star, i.e. radius, effective temperature, and luminosity, lead to more precise characterization of the exoplanet. The habitable zone of a planet is heavily influenced by its host star, so in order to constrain the habitable zone boundaries and planets’ effective temperature, one must know the host star’s fundamental properties (von Braun and Boyajian, 2017a, ). The derived age of a star from the directly measured fundamental properties can provide information about the formation of the exoplanet.
There are several indirect methods to determine stellar fundamental properties, such as atmospheric modeling and stellar evolutionary models. These models have been shown to have difficulties reproducing observations (Boyajian et al.,, 2012, 2013). Long baseline optical/infrared interferometry provides high angular resolution measurements of stars, allowing astronomers to calculate fundamental properties without relying on models.
Interferometric observations allow us to measure the stellar angular diameter, which when combined with the parallax, gives a direct measurement of the stellar radii, one of the fundamental parameters of an astronomical object. Optical interferometry achieves a higher resolution (on the order of milli-arcseconds) than most large telescopes by combining light from several pairs of telescopes that are separated across a variety of baselines, or the separation between telescopes. The resolution capability of an interferometer increases the precision of an angular diameter measurement which then lowers the uncertainty of stellar parameters that can be derived from the angular diameter, i.e. stellar effective temperature and linear radius.
Similar to 51 Eridani and its planet, several other systems of stars with directly imaged exoplanets have been characterized with the CHARA Array. One such system is the Andromedae and its exoplanet, And b by Jones et al., (2016). Jones et al., (2016) took into account the oblate nature and gravity darkening caused by And’s rapid rotation through the use of modeling interferometric observations. The model results were used to determine fundamental stellar parameters, such as temperatures at the poles and equator, surface gravities, luminosity, stellar age and mass, and planetary age and mass.
Baines et al., (2012) used high resolution interferometric observations to study HR 8799, which hosts 4 directly imaged companions (Marois et al.,, 2008). The classification of the 4 companions, which is highly dependent on the age of the planet (inferred from the age of the star), is the subject of debate amongst astronomers (see Table 1 in Baines et al., 2012). Baines et al., (2012) combined the angular diameter, parallax, and photometry to determine stellar parameters, such as linear radius, stellar effective temperature, and luminosity. The effective temperature calculated revealed two possible age scenarios of HR 8799: either the star is contracting onto the zero-age main sequence (ZAMS) or expanding away from it. Baines et al., (2012) used the Yonsei-Yale evolutionary models to investigate both possibilities. The resulting young ages (less than 0.1 Gyr) from either scenario highly favored the classification of planet for the 4 companions, not brown dwarf. Additional recent works that use interferometric radii to determine planet properties are as follows but not limited to: Caballero et al., (2022), Ellis et al., (2021), and Ligi et al., (2019) with more references tabulated in the von Braun and Boyajian, 2017b compilation. Other works demonstrating the wide utility of interferometric data are Korolik et al., (2023) and Roettenbacher et al., (2022), which demonstrate analyzing stellar activity and co-alignment of systems and Ibrahim et al., (2023) which studies the inner au disk of Herbig Be star HD 190073.
In this paper, we present new stellar and planetary properties of the 51 Eridani system. This paper is organized as follows: the interferometric observations in Section 2, the directly determined stellar properties in Section 3, the derived stellar and planetary properties in Section 4, and a discussion of the results presented in this paper in comparison with the results published in the literature in Section 5.
2 Interferometric Observations
The Center for High Angular Resolution Astronomy (CHARA) is a long baseline, optical/IR interferometer located at Mt. Wilson, CA. The CHARA Array (ten Brummelaar et al.,, 2005) comprises of six 1-meter telescopes arranged in a Y-shape configuration, with three arms: East (E), West (W), and South (S), each having two telescopes labeled 1 (outermost) and 2 (innermost). Baselines for the interferometer are formed by pairs of telescopes, such as E1/W1 (outermost East and West telescopes). We observed 51 Eridani in 2015 and 2016 using the Precision Astronomical Visible Observations (PAVO) beam combiner (Ireland et al.,, 2008), which measures interference fringes over a 630-950 nm dispersed bandwidth with 2 telescopes (as indicated in Table 1). We observed 51 Eridani in 2021 using the CLASSIC (Ten Brummelaar et al.,, 2013) beam combiner, which operates in the near-infrared -band.
An observation sequence consists of the target star, or science star, and a selection of calibrator stars. Observations of calibrator stars allow for the removal of atmospheric and instrumentation noise from the observations of the science star. Data were taken in the following pattern: calibrator star - science star - calibrator star. This pattern is referred to as a bracket. The observations taken adhere to a minimum 2 night, 2 calibrator, 2 baseline requirement to reduce and/or eliminate unknown systematic errors in the visibility data.
We use the Jean-Marie Mariotti Center Stellar Diameter Catalog (JSDC) (Chelli et al., (2016), Bourgés et al., (2014))111Available at https://www.jmmc.fr/english/tools/data-bases/jsdc-72/ to find suitable calibrator stars for our science target. The calibrator stars are chosen such that they are unresolved, nearby to the science star on the sky (), and have no known companions or rapid rotation. A summary of observations can be found in Table 1 and a list of calibrator stars used can be found in Table 2.
We reduce and calibrate data for each night of PAVO observations using the PAVO software available through CHARA’s Remote Data Reduction Machine (Ireland et al.,, 2008). In the calibration process, we found that that the calibrator star, HD 29335, showed spurious results indicating that it was a bad calibrator. The amount of usable observations diminished after the removal of this calibrator from the observing sequence (seen in the parentheses in the column “Brackets” in Table 1).
We reduce and calibrate data for each night of the CLASSIC observations using the CLASSIC/CLIMB reduction software redfluor, accessed through CHARA’s Remote Data Reduction Machine (ten Brummelaar, 2014a, , ten Brummelaar, 2014b, ). For the first two nights of observations, only one observation of the science star and one observation of a calibrator star was made. We found that the calibrator was more resolved than the science star. Due to this trend, we suspect that this calibrator (HD 26912) is a bad calibrator and did not use in our analysis.
| Date [UT] | Wavelength [m] | Baseline | Brackets | Calibrators |
|---|---|---|---|---|
| 2015-10-11 | 0.630-0.950 | E1/W1 | 7 (5) | HD28375, HD27563, HD29335∗ |
| 2015-10-12 | 0.630-0.950 | S2/E2 | 9 (7) | HD28375, HD27563, HD29335∗ |
| 2015-11-06 | 0.630-0.950 | E2/W1 | 3 (1) | HD27563, HD29335∗ |
| 2016-11-09 | 0.630-0.950 | W2/E2 | 3 (1) | HD27563, HD29335∗ |
| 2021-08-25 | 1.6731 | S1/E1 | 1 (0) | HD26912∗ |
| 2021-08-26 | 1.6731 | S1/E1 | 1 (0) | HD26912∗ |
| 2021-08-27 | 1.6731 | S1/E1 | 4 (3) | HD29248, HD28736 |
| Calibrator | mag | [mas] |
|---|---|---|
| HD 28375 | 5.531 | |
| HD 27563 | 5.891 | |
| HD 29335∗ | 5.345 | |
| HD 26912∗ | 4.250 | |
| HD 29248 | 8.687 | |
| HD 28736 | 5.979 |
3 Directly Determined Stellar Properties
An interferometer produces interference fringes that allow us to measure two basic pieces of information: the amplitude of the fringes and the phase shift of the peaks. The amplitudes allow us to measure visibilities, which describe the fringe contrast of the interference pattern. The visibility of a star can tell us about the star’s size, shape, and any surface features. Normalized visibilities are measured between 0 and 1, with a visibility of 0 indicating a completely resolved star and a visibility of 1 indicating a completely unresolved star.
When observing a star, it is important to remember that a star’s brightness is not uniform across the star. Optical depth and effective temperature gradients across the disk of a star combine to create an effect called limb darkening. To an observer, a star is brighter in the center and then as you move out from the center, the brightness goes down until it is 0 at the apparent edge of the star. A star’s uniform disk diameter does not take into account the limb darkening effect while the limb darkened diameter does.
In order to determine the angular diameter of a star, the visibility squared as a function of baseline (), angular diameter (either uniform, , or limb darkened, ), and wavelength () is used to fit the interferometric visibilities using Equation 1.
| (1) |
where and is the limb-darkening coefficient (LDC). The first iteration of this fit is applied using a value of 0, which corresponds to a uniform disk diameter, .
To estimate the bolometric flux () of 51 Eridani, we use the spectral-energy distribution using available photometry from Gaia (Gaia Collaboration,, 2020; Lindegren et al.,, 2021), the Two-Micron All-Sky Survey (2MASS; Skrutskie et al.,, 2006), Tycho-2 (Høg et al.,, 2000), the Wide-field Infrared Survey Explorer (WISE; Cutri and et al.,, 2014), and the General Catalog of Photometric Data (GCPD; Mermilliod et al.,, 1997). We combine the spectrum of 51 Eridani from the STIS Next Generation Spectral Library (NGSL; Heap and Lindler,, 2007) (covering the near UV and optical) with one from Cool Stars library (Rayner et al.,, 2009) (covering the near-infrared), filling any additional gaps with a stellar atmosphere (Allard et al.,, 2011). We scaled the combined spectrum to match the photometry, yielding an absolutely calibrated spectrum. The final fit is shown in Figure 1 and our bolometric flux measurement is in Table 3. More details on this fitting procedure, including our treatment of systematic uncertainties in the photometry and spectra are given in Mann et al., (2015) and Mann et al., (2016).
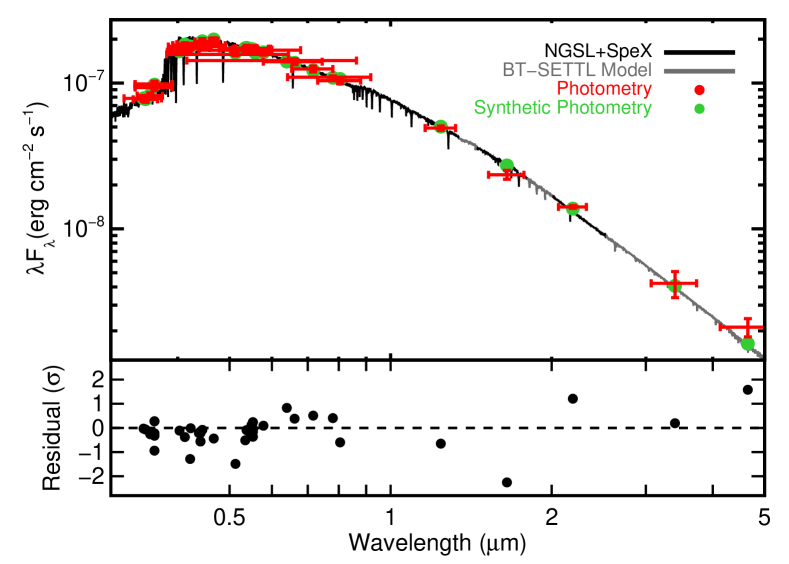
From the angular diameter and , the stellar effective temperature, , is calculated using the following form of the Stefan-Boltzmann equation:
| (2) |
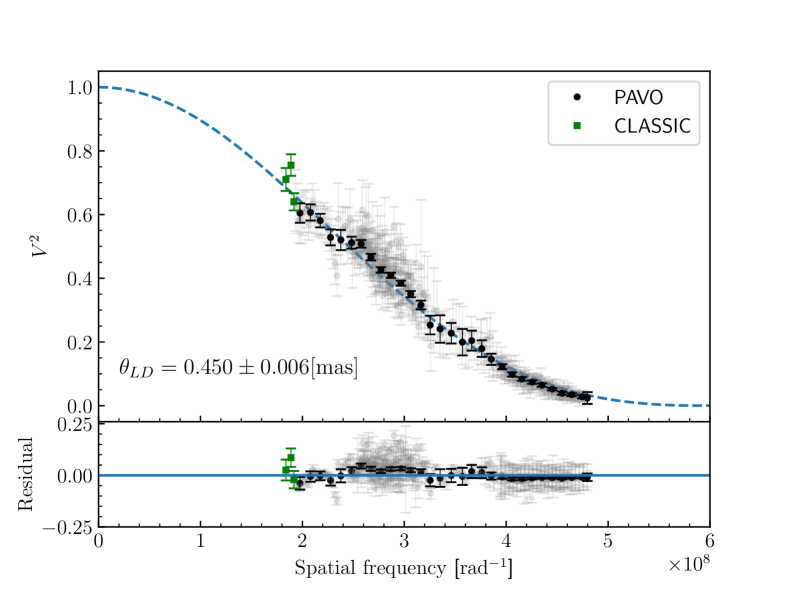
In Equation 2, the bolometric flux is in units of and is in units of mas. In the first initial calculation of , refers to the uniform disk angular diameter. In order to account for limb darkening, we use the Limb Darkening Coefficients table (Claret and Bloemen,, 2011) to solve for a linear -band LDC with initial guesses of the star’s , , and [Fe/H]. This value is used in a subsequent fit (Equation 1) and a new temperature is derived using Equation 2 where is now referring to the limb-darkened angular diameter, . We iterate on this process twice when no changes are seen. We determine the error for sampling the angular diameter in a Monte Carlo simulation, varying on a normal distribution of the uncertainties for wavelength ( nm), calibrator diameters ( of the diameter), and limb-darkening coefficients (). The resulting limb-darkened angular diameter is mas.
Systematic variations (i.e. due to atmospheric effects or instrument alignments) can occur between nights. To investigate any systematic variations, we solve for the angular diameter using the data for each night separately, and found that they all agreed with of each other. We took a weighted average of the angular diameters from each individual night and found mas, which agrees with the diameter from the combined fit within . The weights for this average are where is the associated uncertainty for each data point. For the final limb-darkened angular diameter, we add the uncertainties from the combined diameter fit and the weighted average diameter in quadrature which can be found in Table 3.
Figure 2 displays the PAVO binned and calibrated visibilities, the CLASSIC data, and the final fit for angular diameter. The CLASSIC data presented are not used in the final fit for angular diameter because the observations do not adhere to the recommended observing minimum requirements of 2 nights, 2 calibrators, 2 baselines (Boyajian et al.,, 2012). The data shown in Figure 2 are there to demonstrate where CLASSIC lies on the curve (see Section 5 for further discussion.)
A stellar luminosity, is calculated using Equation 3
| (3) |
where is the distance (seen in Table 3) and is the bolometric flux (seen also in Table 3). The distance, , is calculated using the zero-point corrected parallax, mas (Gaia Collaboration, (2020), Lindegren et al., (2021)). This yields a distance of pc. The linear radius is then calculated using this new distance and Equation 4 below:
| (4) |
where is the limb-darkened angular diameter and is the zero-point corrected distance. The final parameters are presented in Table 3.
| Property | Value | Source |
| Section 3 | ||
| Section 3 | ||
| Gaia Collaboration, (2020), | ||
| Lindegren et al., (2021) | ||
| Gaia Collaboration, (2020), | ||
| Lindegren et al., (2021) | ||
| Swastik et al., (2021) | ||
| log | Arentsen et al., (2019) | |
| Section 3 | ||
| Section 3 | ||
| Section 3 | ||
| Section 4.1 | ||
| Section 4.1 | ||
| Brown-Sevilla et al., (2023) | ||
| Section 4.1 |
4 Modeled Stellar and Planetary Properties
Using our measured effective temperature, luminosity, and radius, we estimate the age and mass of the star using stellar evolutionary models. Improved age estimates for the star means the age of the planet, 51 Eri b, is also improved given that the system is coeval. We then estimate the planet’s mass through evolutionary modeling and provide further insight on how the planet formed.
51 Eridani falls in a unique spot in the HR diagram. Previous works (summarized in the Introduction of Mamajek and Bell, 2014) indicated that the consisted of pre-main sequence (PMS) stars. Mamajek and Bell, (2014) analyzed the kinematics of the and concluded that the majority of the A0-F0 stars are either near or on the zero-age main sequence (ZAMS), which includes 51 Eridani.
4.1 Age and Mass Using Isochronal Modeling
To estimate the age and mass of 51 Eridani, we use stellar evolution models: the PAdova and TRieste Stellar Evolution Code (PARSEC) (Bressan et al.,, 2012) and the Garching Stellar Evolution Code (GARSTEC) (Weiss and Schlattl,, 2008).
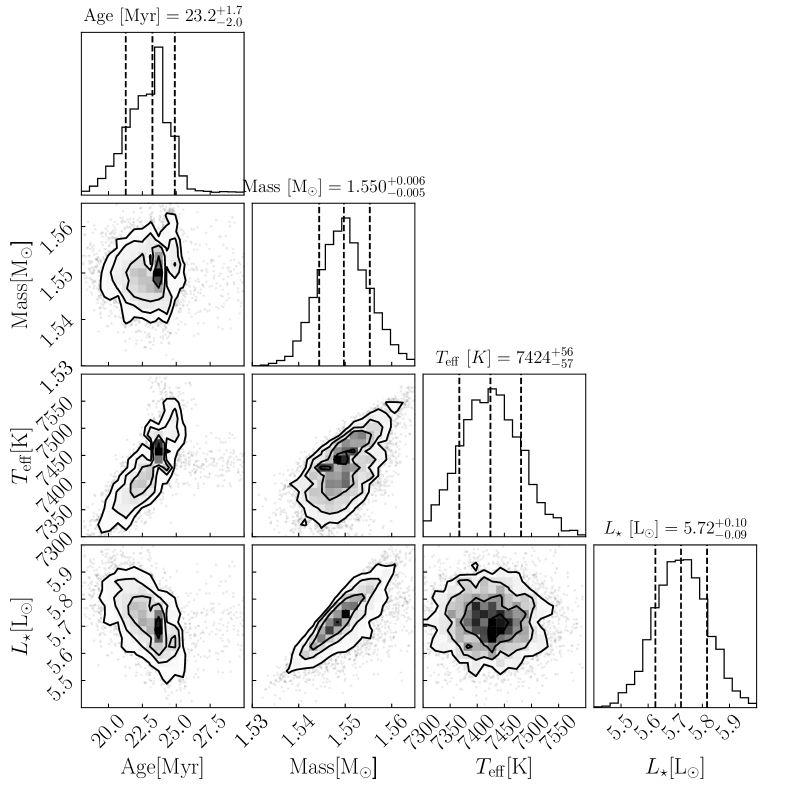
We use the PARSEC version 1.2S model222Available at http://stev.oapd.inaf.it/cgi-bin/cmd developed by Bressan et al., (2012) to create stellar isochrones given stellar priors. We generated isochrones for a range of ages between 0 and 50 Myr in steps of 0.5 Myrs in log space using a metal fraction of (Table 3). We interpolated the outputted isochrones to obtain a finer grid of points along each isochrone track. We then performed two separate two-dimensional interpolations over L⊙) and ; one to extract an age and the other to extract a mass. We use a Monte Carlo simulation to obtain the errors for the age and mass estimates by sampling the and luminosity in a normal distribution. The posterior distributions are shown in Figure 3. The final solution results in an age of Myr and a mass of M⊙.
We then used the GARSTEC models (Weiss and Schlattl,, 2008) through the implementation of bagemass. bagemass (Maxted et al.,, 2015) is a program written in Fortran that uses stellar evolution models to estimate the mass and age of a star and produces posterior probability distributions calculated using Bayesian methods. The GARSTEC model chosen has an mixing length of 1.78 and a He-enhancement value of 0. The priors used are , L⊙), and [Fe/H] (Table 3). We fixed the metallicity and the age is given a range between 0 and 50 Myr. The posterior distributions are shown in Figure 4. The final solution determined gives an age of Myr and a mass of M⊙.
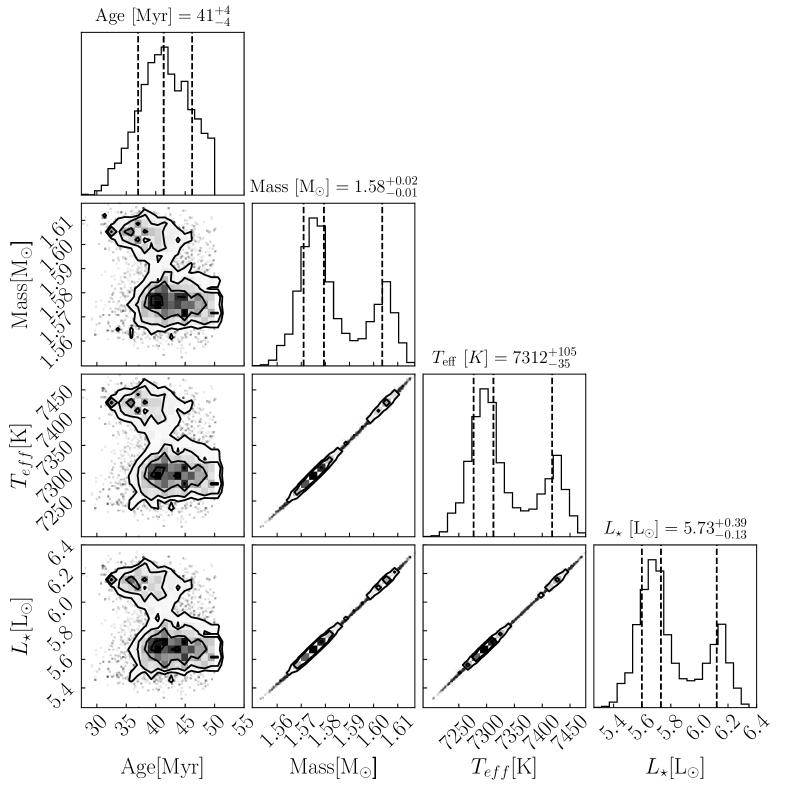
The age and mass estimates determined by the PARSEC model and the GARSTEC model are vastly different, with the GARSTEC model estimating an age almost twice that of the PARSEC model. The GARSTEC model could not return the prior distributions for and log(L⊙) within the uncertainties or stay within the range of [Fe/H] priors given. Looking at the posterior distributions, we see that the GARSTEC model returns a bimodal solution and skews the priors, reflecting the model not returning the priors sufficiently well enough. This bimodal distribution could be due to the star’s location on the HR diagram. Although both models incorporate the PMS phase and the ZAMS phase of stellar evolution, the position of this star being right at the transition point could cause each model to either favor the pre-main sequence (PMS) side or the early zero-age main sequence (ZAMS) side of this transition point. However, the PARSEC model is able to return the priors well and produce a single mode solution. We adopt for the final results of this work, the PARSEC age and mass of Myr and M⊙.
The determination of age and mass is reliant on the priors of effective temperature and luminosity, so it is logical that the uncertainties of age and mass would be in turn reliant on these priors. In addition to the effect from temperature and luminosity, the uncertainties for age and mass are reliant on the choice in model chosen to determine these parameters (Tayar et al.,, 2022). The age is more affected by the choice in model, especially for stars closer to the ZAMS or PMS, where Tayar et al., (2022) describes the differences in age being near in these regions of parameter space. The differences between the PARSEC and the GARSTEC models used to estimate the age of 51 Eridani is another example of the discrepancy in age between models.
4.2 Analysis of the Planetary Companion 51 Eri b
The next step in the analysis of 51 Eri b is to estimate a mass using the assumption that the planet is the same age as the star (see Section 4.1). We use the Sonora Bobcat models (Marley et al.,, 2021) which were developed to study L-, Y-, and T- type brown dwarfs and self-luminous exoplanets. 51 Eri b is considered to be a self-luminous planet but it has been debated on whether 51 Eri b is an L- or T- type brown dwarf given its unique strong methane absorption features that are also seen in T- type brown dwarfs and similar near-IR colors to L-type brown dwarfs (Macintosh et al.,, 2015).
The Sonora Bobcat models produce evolutionary tables that hold either age, mass, or bolometric luminosity fixed. For this paper’s purpose, we use the model holding mass fixed. In our analysis, we use the planet’s effective temperature of K (Brown-Sevilla et al.,, 2023). Figure 5 shows the Sonora Bobcat models as age vs along with the position of 51 Eri b. To determine a mass, we first perform a one-dimensional interpolation to create a finer grid of points for each of the iso-mass lines. We then perform an additional two-dimensional interpolation over the effective temperature and age and find the corresponding mass. To obtain uncertainties for the mass, we ran a Monte Carlo simulation, sampling the age and on a normal distribution. For the age, an asymmetrical normal distribution was created to account for the uneven uncertainties. Figure 6 shows the posterior distribution for this simulation. The final mass of 51 Eri b is MJup.
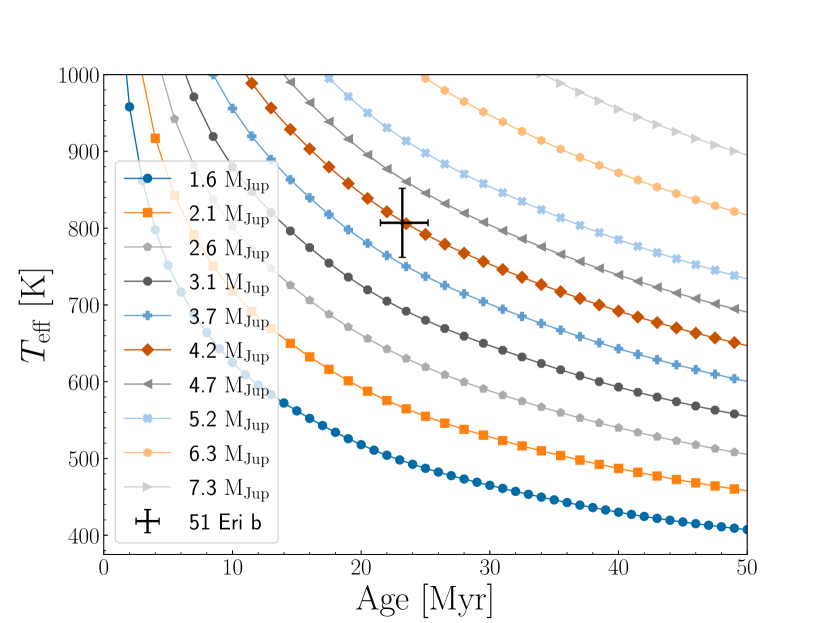
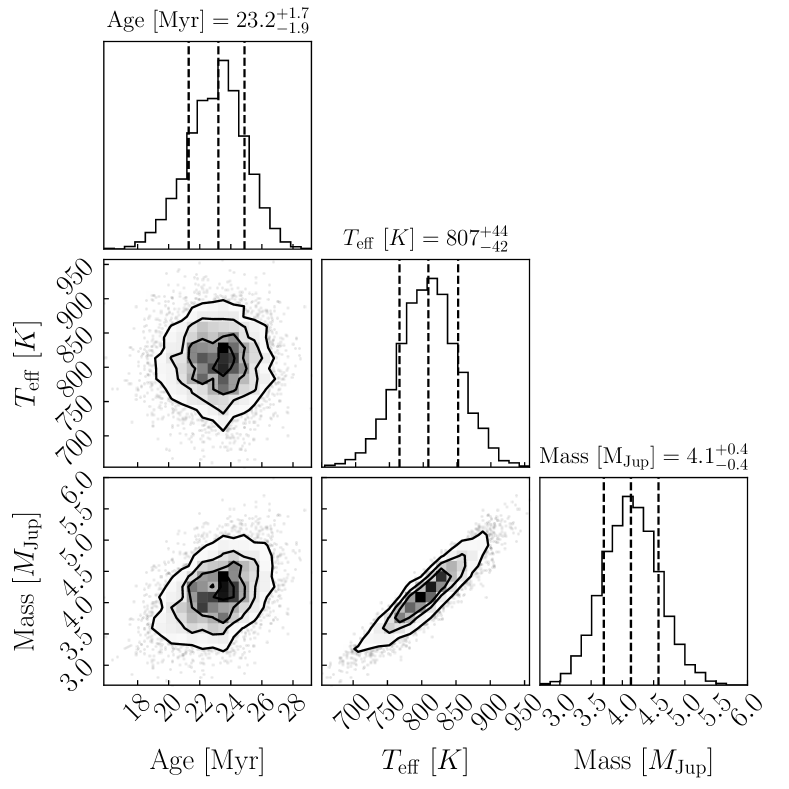
5 Discussion
5.1 Stellar Parameters
We measure a limb-darkened angular diameter for 51 Eridani of mas (Section 4). We also measure an angular diameter of mas using a limb-darkening coefficient of from our CLASSIC data alone, which is consistent with the PAVO diameter within . The PAVO measurement has a precision of less than , compared to the CLASSIC measurement which has a precision of just over . This is due to the greater spatial frequency coverage obtained with PAVO’s multiple wavelengths channels, as well as sampling further down the visibility curve to higher spatial frequencies. More coverage, especially at higher spatial frequencies, ensures that the visibility squared fit is more accurate. Simon and Schaefer, (2011) measure an angular diameter of 51 Eridani also using CHARA’s CLASSIC beam combiner. Their measurements were taken in both - and -band on the E1/W1 baseline (314 m). Simon and Schaefer, (2011)’s angular diameter of mas is over off from our PAVO angular diameter. We suspect that this disagreement is due to the observation strategy used by Simon and Schaefer, (2011) who observed on a single baseline (E1/W1) and only used one calibrator in their analysis. This observation strategy is dangerously insensitive to verifying whether or not the single calibrator they used is good. In contrast, our measurements were taken using multiple calibrators over multiple nights (see Table 1). The angular diameter of 51 Eridani is near the resolution limit () of the CHARA Array on the longest baselines in the near-infrared. Analysis in the literature shows that interferometric measurements of under-resolved stars tend to systematically over-estimate their angular diameters (Casagrande et al., (2014), White et al., (2018), Tayar et al., (2022)). However, our observations using CLASSIC data alone do not support this trend as they are in agreement within of the PAVO observations.
Simon and Schaefer, (2011) also performed an analysis to estimate the age and mass of 51 Eridani. This analysis used the PMS evolution models developed by Siess et al., (2000) and the Yonsei-Yale (Y2) models (Yi et al.,, 2003). Simon and Schaefer, (2011) compared their absolute angular diameter (angular diameter scaled to a distance at 10 pc) with those predicted by both models and found an average age of Myr and a mass of M⊙. Our age is almost twice that of Simon and Schaefer, (2011) and our mass is off of Simon and Schaefer, (2011)’s. If we scale our angular measurement to a distance of 10 pc, it would fall closer to the older isochrones in Figure 3 in Simon and Schaefer, (2011) for the same , suggesting that the difference in angular diameter seems to be the main source of discrepancy. Additional errors are subject to arise in transforming the theoretical properties calculated by the models to observational quantities, such as magnitudes and color indexes from color tables. Comparing our directly measured and luminosity to the model predictions ensures that any ambiguous errors that result from the color tables will not affect our results.
Simon and Schaefer, (2011) also used a vs. diagram to estimate age and mass of 51 Eridani. The mass results were around M⊙smaller than their initial analysis of comparing the model-predicted angular diameters and yielded older ages (around 5 Myr), creating a noted discrepancy between the two methods for age and mass. However, the vs. result estimates align with our results.
The age we determine with the PARSEC model ( Myr) agrees with the age estimates found in the literature of both the star itself and that of the . These age estimates have been determined through a variety of methods from isochronal ages to lithium depletion methods. Mamajek and Bell, (2014) conclude with an isochronal age of Myr, where their value compares favorably to several lithium depletion boundary ages from Binks and Jeffries, (2014) ( Myr) and Malo et al., (2014) ( Myr).
A more recent study on the from Miret-Roig et al., (2020) concludes with an age estimate of Myr through dynamical age trace-back methods using precise Gaia DR2 astrometry and ground based radial velocities. Couture et al., (2023) developed a method to correct the trace-back age method that reduces the systemic errors from a combination of uncorrected gravitational red-shift and convective blue-shift absolute radial velocity measurements and the random errors from the parallax, proper motion, and additional radial velocity measurements. Their final resulting age is Myr for the . Our age estimate compares favorably to Couture et al., (2023)’s dynamical age estimates of the .
5.2 A quick look at available TESS data
The Transiting Exoplanet Survey Satellite (TESS: Ricker et al., (2015)) observed 51 Eridani in two sectors: Sector 5 and Sector 32. Sepulveda et al., (2022) investigated the variability seen in the TESS light curve data and concluded that 51 Eridani is a -Dor pulsator. We downloaded the available 2 minute cadence data using lightkurve (Lightkurve Collaboration et al.,, 2018). The data were flattened and binned. From these data, we constructed a periodogram of the processed TESS data to search for significant exoplanet signals. We extracted significant frequencies and tested to see if a possible planet signal could be found. There were no significant possible planet signals. The light curves did show significant variability which does corroborate the findings of Sepulveda et al., (2022) in 51 Eridani being a -Dor pulsator.
5.3 Planetary Parameters
We derive a mass for 51 Eri b to be MJup through the Sonora Bobcat evolutionary models (Section 4.2). Other studies have estimated the mass of 51 Eri b through a variety of methods, such as atmospheric modeling and evolutionary modeling. Several works present exploration of both methods, i.e. using atmospheric modeling to obtain planetary parameters such as effective temperature, surface gravity, luminosity, and radius, and using these parameters along with an adopted age in evolutionary models to estimate a mass.
The initial discovery announcement of 51 Eri b (Macintosh et al.,, 2015) performed atmospheric modeling to estimate the planet parameters, such as effective temperature and luminosity. Macintosh et al., (2015) used two separate models, a cloud-free and a partial cloudy model to obtain these parameters. The cloud-free model resulted in a K and a log(. The partial cloudy model gave a K and a log(. Macintosh et al., (2015) determined that the luminosity derived from the models does not change much with either model and used the luminosity along with age to estimate a mass based off of formation models. Given hot-start formation, the mass of 51 Eri b is MJup. With a cold-start formation, the mass falls in a range of 2-12 MJup. Our mass of MJup is well within the cold-start formation range of ages but is over double that of the hot-start formation age.
Samland et al., (2017) presented the first spectro-photometric measurements in the - and - bands of 51 Eri b using VLT/SPHERE. This study used atmospheric modeling using petitCODE - Cloudy to obtain planetary parameters. The resulting temperature, K, radius of RJup, and surface gravity of (cgs-units) are used in a variety of methods to obtain mass estimates. Samland et al., (2017) used surface gravity and radius relations to get a mass of MJup which is Samland et al., (2017) also used radius and effective temperature relations to derive a luminosity and a planet formation model which relates luminosity and mass. The range in luminosity rules out the cold-start formation model and resulted in masses between 2.4 and 5 MJup for the hot-start model and a larger spread of masses between 2 and 12 MJup for the warm-start model. Our mass also agrees with both mass ranges for the hot-start and warm-start models.
Dupuy et al., (2022) performed a cross calibration of Hipparcos-GAIA astrometry and the orbit fitting code orvara. Their results provided orbital parameters as well as an upper limit on the mass of 51 Eri b of MJup. Through private communication, another run of the orvara fit was made using the new age and mass of 51 Eridani presented in this paper. The new upper limit constraint on the mass of 51 Eri b is 9.5 MJup. Our mass of MJup clearly falls under this upper limit. Dupuy et al., (2022)’s result also indicated that the cold-start formation is ruled out given the derived initial entropy. They suggested that 51 Eri b formed similarly to other directly imaged planets which indicate either the warm or hot-start scenarios.
The most recent study of 51 Eri b, done by Brown-Sevilla et al., (2023), revisited the work by Samland et al., (2017) and obtained new observations of 51 Eri b with VLT/SPHERE at a higher S/N than Samland et al., (2017)’s original data. Brown-Sevilla et al., (2023) used a new atmospheric retrieval code, petitRADTRANS, to update the and the resulting posterior distributions for the log and planet radius to obtain a mass of MJup. Brown-Sevilla et al., (2023) labeled this result as the nominal model. Brown-Sevilla et al., (2023) also performed an analysis using evolutionary models from Baraffe et al., (2002) with two separate ages: 10 Myr (Lee et al.,, 2022) and 20 Myr (Macintosh et al.,, 2015), where they found masses of MJup and MJup respectively. The mass presented in this work ( MJup) agrees well with the nominal result obtained by Brown-Sevilla et al., (2023).
Our mass falls within the ranges of both the hot-start and the warm-start models as described by both Samland et al., (2017) and Brown-Sevilla et al., (2023). With our analysis, we can rule out a purely core accretion model as the main formation mechanism. Either scenario is likely but future observations and analyses are needed to further test each model and develop a more conclusive argument.
6 Conclusion
In this work, we present interferometric observations of the directly imaged exoplanet host star 51 Eridani taken with both the PAVO and CLASSIC beam combiners at the CHARA Array. These observations resulted in a highly precise angular diameter measurement of 51 Eridani, mas. From this angular diameter, we calculate the effective temperature, K, luminosity, L⊙, and linear radius, R⊙. We use the PARSEC isochrones to derive an age of Myr and mass of M⊙ of 51 Eridani. For 51 Eri b, we estimate a mass of is MJup using the Sonora Bobcat evolutionary models.
Future analysis is encouraged using the JWST data taken in 2022 with NIRCAM and MIRI. Additional spectra can provide more constraints on planet composition, effective temperature, and luminosity when used with the atmospheric retrievals developed for JWST. Brown-Sevilla et al., (2023) suggested the use of the Mid-Infrared ELT Imager and Spectrograph (Quanz et al.,, 2015) which will increase the wavelength coverage up to 13.
Observations of other members of the can help further the age constraints on these objects. In Table A1 in Alonso-Floriano et al., (2015)’s paper, they list 185 members and candidate members of the . At least two F type stars are observable with PAVO at the CHARA Array and with future instruments being commissioned, such as the SPICA instrument (Mourard et al., (2017), Mourard et al., (2022)), the increased sensitivity will allow for more targets in this group to be observed. In addition, there are four stars that are accessible in the southern sky with VLTI, that have angular diameters ranging between 0.46 mas and 0.75 mas (estimated using the surface brightness relationships in Adams et al., 2018). Two of these stars are observable with the current instrumentation available at VLTI. With the planned improvements to VLTI, such as adding the BIFROST (Kraus et al.,, 2022) instrument, the other two stars could be observable in the near future. Observing and characterizing more stars within the PMG will help to estimate the age of the group and the individual stars within, giving us more insight on stellar evolution.
Acknowledgements
This work is based upon observations obtained with the Georgia State University Center for High Angular Resolution Astronomy Array at Mount Wilson Observatory. The CHARA Array is supported by the National Science Foundation under Grant No. AST-1636624 and AST-2034336. Institutional support has been provided from the GSU College of Arts and Sciences and the GSU Office of the Vice President for Research and Economic Development.
CHARA telescope time was granted by NOIRLab through the Mid-Scale Innovations Program (MSIP). MSIP is funded by NSF.
CHARA Array time was granted through the NOIRLab community-access program (NOIRLab Prop. ID: 2021A-0141; PI: T. Boyajian).
CHARA Array time was granted through the NOIRLab community-access program (NOIRLab Prop. ID: 2021A-0247; PI: T. Ellis).
We thank Dr. Gururaj A. Wagle for his assistance in understanding interpolation and Henry Ngo for the extremely helpful suggestions in debugging interpolation code. We also thank Nageeb Zaman and Dr. Jonas Klüter for their assistance in developing an asymmetrical normal distribution for Monte Carlo simulations used in this work.
This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France (DOI : 10.26093/cds/vizier). The original description of the VizieR service was published in 2000, A&AS 143, 23 (Ochsenbein et al.,, 2000).
This research has made use of the Jean-Marie Mariotti Center JSDC catalogue 333Available at http://www.jmmc.fr/catalogue_jsdc.html.
This research has made use of the Jean-Marie Mariotti Center Aspro 444Available at http://www.jmmc.fr/aspro service.
This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA’s Science Mission Directorate.
This research made use of Lightkurve, a Python package for Kepler and TESS data analysis (Lightkurve Collaboration et al.,, 2018).
Financial Support
A.E. and T.S.B. acknowledge support by the National Support Foundation under Grant No. AST-2205914.
Conflicts of Interests
None
Data Availability
All interferometric data are available in the CHARA archive555Available at https://www.chara.gsu.edu/observers/database. The TESS observations are available in the Barbara A. Mikulski Archive for Space Telescopes (MAST) archive.
References
- Adams et al., (2018) Adams, A. D., Boyajian, T. S., & von Braun, K. 2018, Predicting stellar angular diameters from V, IC, H and K photometry. MNRAS, 473(3), 3608–3614.
- Allard et al., (2011) Allard, F., Homeier, D., & Freytag, B. Model Atmospheres From Very Low Mass Stars to Brown Dwarfs. In Johns-Krull, C., Browning, M. K., & West, A. A., editors, 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun 2011,, volume 448 of Astronomical Society of the Pacific Conference Series, 91.
- Alonso-Floriano et al., (2015) Alonso-Floriano, F. J., Caballero, J. A., Cortés-Contreras, M., Solano, E., & Montes, D. 2015, Reaching the boundary between stellar kinematic groups and very wide binaries. III. Sixteen new stars and eight new wide systems in the Pictoris moving group. A&A, 583, A85.
- Arentsen et al., (2019) Arentsen, A., Prugniel, P., Gonneau, A., Lançon, A., Trager, S., Peletier, R., Lyubenova, M., Chen, Y.-P., Falcón Barroso, J., Sánchez Blázquez, P., & Vazdekis, A. 2019, Stellar atmospheric parameters for 754 spectra from the X-shooter Spectral Library. A&A, 627, A138.
- Baines et al., (2012) Baines, E. K., White, R. J., Huber, D., Jones, J., Boyajian, T., McAlister, H. A., ten Brummelaar, T. A., Turner, N. H., Sturmann, J., Sturmann, L., Goldfinger, P. J., Farrington, C. D., Riedel, A. R., Ireland, M., von Braun, K., & Ridgway, S. T. 2012, The CHARA Array Angular Diameter of HR 8799 Favors Planetary Masses for its Imaged Companions. ApJ, 761(1), 57.
- Baraffe et al., (2002) Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 2002, Evolutionary models for low-mass stars and brown dwarfs: Uncertainties and limits at very young ages. A&A, 382, 563–572.
- Binks and Jeffries, (2014) Binks, A. S. & Jeffries, R. D. 2014, A lithium depletion boundary age of 21 Myr for the Beta Pictoris moving group. MNRAS, 438(1), L11–L15.
- Bourgés et al., (2014) Bourgés, L., Lafrasse, S., Mella, G., Chesneau, O., Bouquin, J. L., Duvert, G., Chelli, A., & Delfosse, X. The JMMC Stellar Diameters Catalog v2 (JSDC): A New Release Based on SearchCal Improvements. In Manset, N. & Forshay, P., editors, Astronomical Data Analysis Software and Systems XXIII 2014,, volume 485 of Astronomical Society of the Pacific Conference Series, 223.
- Boyajian et al., (2013) Boyajian, T. S., von Braun, K., van Belle, G., Farrington, C., Schaefer, G., Jones, J., White, R., McAlister, H. A., ten Brummelaar, T. A., Ridgway, S., Gies, D., Sturmann, L., Sturmann, J., Turner, N. H., Goldfinger, P. J., & Vargas, N. 2013, Stellar Diameters and Temperatures. III. Main-sequence A, F, G, and K Stars: Additional High-precision Measurements and Empirical Relations. ApJ, 771(1), 40.
- Boyajian et al., (2012) Boyajian, T. S., von Braun, K., van Belle, G., McAlister, H. A., ten Brummelaar, T. A., Kane, S. R., Muirhead, P. S., Jones, J., White, R., Schaefer, G., Ciardi, D., Henry, T., López-Morales, M., Ridgway, S., Gies, D., Jao, W.-C., Rojas-Ayala, B., Parks, J. R., Sturmann, L., Sturmann, J., Turner, N. H., Farrington, C., Goldfinger, P. J., & Berger, D. H. 2012, Stellar Diameters and Temperatures. II. Main-sequence K- and M-stars. ApJ, 757(2), 112.
- Bressan et al., (2012) Bressan, A., Marigo, P., Girardi, L., Salasnich, B., Dal Cero, C., Rubele, S., & Nanni, A. 2012, PARSEC: stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. MNRAS, 427(1), 127–145.
- Brown-Sevilla et al., (2023) Brown-Sevilla, S. B., Maire, A. L., Mollière, P., Samland, M., Feldt, M., Brandner, W., Henning, T., Gratton, R., Janson, M., Stolker, T., Hagelberg, J., Zurlo, A., Cantalloube, F., Boccaletti, A., Bonnefoy, M., Chauvin, G., Desidera, S., D’Orazi, V., Lagrange, A. M., Langlois, M., Menard, F., Mesa, D., Meyer, M., Pavlov, A., Petit, C., Rochat, S., Rouan, D., Schmidt, T., Vigan, A., & Weber, L. 2023, Revisiting the atmosphere of the exoplanet 51 Eridani b with VLT/SPHERE. A&A, 673, A98.
- Caballero et al., (2022) Caballero, J. A., González-Álvarez, E., Brady, M., Trifonov, T., Ellis, T. G., Dorn, C., Cifuentes, C., Molaverdikhani, K., Bean, J. L., Boyajian, T., Rodríguez, E., Sanz-Forcada, J., Zapatero Osorio, M. R., Abia, C., Amado, P. J., Anugu, N., Béjar, V. J. S., Davies, C. L., Dreizler, S., Dubois, F., Ennis, J., Espinoza, N., Farrington, C. D., López, A. G., Gardner, T., Hatzes, A. P., Henning, T., Herrero, E., Herrero-Cisneros, E., Kaminski, A., Kasper, D., Klement, R., Kraus, S., Labdon, A., Lanthermann, C., Le Bouquin, J. B., López González, M. J., Luque, R., Mann, A. W., Marfil, E., Monnier, J. D., Montes, D., Morales, J. C., Pallé, E., Pedraz, S., Quirrenbach, A., Reffert, S., Reiners, A., Ribas, I., Rodríguez-López, C., Schaefer, G., Schweitzer, A., Seifahrt, A., Setterholm, B. R., Shan, Y., Shulyak, D., Solano, E., Sreenivas, K. R., Stefánsson, G., Stürmer, J., Tabernero, H. M., Tal-Or, L., ten Brummelaar, T., Vanaverbeke, S., von Braun, K., Youngblood, A., & Zechmeister, M. 2022, A detailed analysis of the Gl 486 planetary system. A&A, 665, A120.
- Casagrande et al., (2014) Casagrande, L., Portinari, L., Glass, I. S., Laney, D., Silva Aguirre, V., Datson, J., Andersen, J., Nordström, B., Holmberg, J., Flynn, C., & Asplund, M. 2014, Towards stellar effective temperatures and diameters at 1 per cent accuracy for future surveys. MNRAS, 439(2), 2060–2073.
- Chelli et al., (2016) Chelli, A., Duvert, G., Bourgès, L., Mella, G., Lafrasse, S., Bonneau, D., & Chesneau, O. 2016, Pseudomagnitudes and differential surface brightness: Application to the apparent diameter of stars. A&A, 589, A112.
- Claret and Bloemen, (2011) Claret, A. & Bloemen, S. 2011, Gravity and limb-darkening coefficients for the Kepler, CoRoT, Spitzer, uvby, UBVRIJHK, and Sloan photometric systems. A&A, 529, A75.
- Couture et al., (2023) Couture, D., Gagné, J., & Doyon, R. 2023, Addressing Systematics in the Traceback Age of the Pictoris Moving Group. ApJ, 946(1), 6.
- Cutri and et al., (2014) Cutri, R. M. & et al. 2014, VizieR Online Data Catalog: AllWISE Data Release (Cutri+ 2013). VizieR Online Data Catalog,, II/328.
- Dupuy et al., (2022) Dupuy, T. J., Brandt, G. M., & Brandt, T. D. 2022, Limits on the mass and initial entropy of 51 Eri b from Gaia EDR3 astrometry. MNRAS, 509(3), 4411–4419.
- Ellis et al., (2021) Ellis, T. G., Boyajian, T., von Braun, K., Ligi, R., Mourard, D., Dragomir, D., Schaefer, G. H., & Farrington, C. D. 2021, Directly Determined Properties of HD 97658 from Interferometric Observations. AJ, 162(3), 118.
- Feigelson et al., (2006) Feigelson, E. D., Lawson, W. A., Stark, M., Townsley, L., & Garmire, G. P. 2006, 51 Eridani and GJ 3305: A 10-15 Myr old Binary Star System at 30 Parsecs. AJ, 131(3), 1730–1739.
- Gaia Collaboration, (2020) Gaia Collaboration 2020, VizieR Online Data Catalog: Gaia EDR3 (Gaia Collaboration, 2020). VizieR Online Data Catalog,, I/350.
- Heap and Lindler, (2007) Heap, S. R. & Lindler, D. J. Hubble’s Next Generation Spectral Library (NGSL). In Vallenari, A., Tantalo, R., Portinari, L., & Moretti, A., editors, From Stars to Galaxies: Building the Pieces to Build Up the Universe 2007,, volume 374 of Astronomical Society of the Pacific Conference Series, 409.
- Høg et al., (2000) Høg, E., Fabricius, C., Makarov, V. V., Urban, S., Corbin, T., Wycoff, G., Bastian, U., Schwekendiek, P., & Wicenec, A. 2000, The Tycho-2 catalogue of the 2.5 million brightest stars. A&A, 355, L27–L30.
- Ibrahim et al., (2023) Ibrahim, N., Monnier, J. D., Kraus, S., Le Bouquin, J.-B., Anugu, N., Baron, F., Brummelaar, T. T., Davies, C. L., Ennis, J., Gardner, T., Labdon, A., Lanthermann, C., Mérand, A., Rich, E., Schaefer, G. H., & Setterholm, B. R. 2023, Imaging the Inner Astronomical Unit of the Herbig Be Star HD 190073. ApJ, 947(2), 68.
- Ireland et al., (2008) Ireland, M. J., Mérand, A., ten Brummelaar, T. A., Tuthill, P. G., Schaefer, G. H., Turner, N. H., Sturmann, J., Sturmann, L., & McAlister, H. A. Sensitive visible interferometry with PAVO. In Schöller, M., Danchi, W. C., & Delplancke, F., editors, Optical and Infrared Interferometry 2008,, volume 7013 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 701324.
- Jones et al., (2016) Jones, J., White, R. J., Quinn, S., Ireland, M., Boyajian, T., Schaefer, G., & Baines, E. K. 2016, The Age of the Directly Imaged Planet Host Star Andromedae Determined from Interferometric Observations. ApJ, 822(1), L3.
- Korolik et al., (2023) Korolik, M., Roettenbacher, R. M., Fischer, D. A., Kane, S. R., Perkins, J. M., Monnier, J. D., Davies, C. L., Kraus, S., Le Bouquin, J.-B., Anugu, N., Gardner, T., Lanthermann, C., Schaefer, G. H., Setterholm, B., Brewer, J. M., Llama, J., Zhao, L. L., Szymkowiak, A. E., & Henry, G. W. 2023, Refining the Stellar Parameters of Ceti: a Pole-on Solar Analog. AJ, 166(3), 123.
- Kraus et al., (2022) Kraus, S., Mortimer, D., Chhabra, S., Lu, Y., Codron, I., Gardner, T., Anugu, N., Monnier, J. D., Le Bouquin, J.-B., Ireland, M., Martinache, F., Defrère, D., & Martinod, M.-A. High spectral-resolution interferometry down to one micron with Asgard/BIFROST at VLTI: science drivers and project overview. In Mérand, A., Sallum, S., & Sanchez-Bermudez, J., editors, Optical and Infrared Interferometry and Imaging VIII 2022,, volume 12183 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 121831S.
- Lee et al., (2022) Lee, J., Song, I., & Murphy, S. J. 2022, Low-mass members of nearby young stellar moving groups from Gaia EDR3. MNRAS, 511(4), 6179–6192.
- Lightkurve Collaboration et al., (2018) Lightkurve Collaboration, Cardoso, J. V. d. M., Hedges, C., Gully-Santiago, M., Saunders, N., Cody, A. M., Barclay, T., Hall, O., Sagear, S., Turtelboom, E., Zhang, J., Tzanidakis, A., Mighell, K., Coughlin, J., Bell, K., Berta-Thompson, Z., Williams, P., Dotson, J., & Barentsen, G. 2018,. Lightkurve: Kepler and TESS time series analysis in Python. Astrophysics Source Code Library.
- Ligi et al., (2019) Ligi, R., Dorn, C., Crida, A., Lebreton, Y., Creevey, O., Borsa, F., Mourard, D., Nardetto, N., Tallon-Bosc, I., Morand, F., & Poretti, E. 2019, From the stellar properties of HD 219134 to the internal compositions of its transiting exoplanets. A&A, 631, A92.
- Lindegren et al., (2021) Lindegren, L., Bastian, U., Biermann, M., Bombrun, A., de Torres, A., Gerlach, E., Geyer, R., Hernández, J., Hilger, T., Hobbs, D., Klioner, S. A., Lammers, U., McMillan, P. J., Ramos-Lerate, M., Steidelmüller, H., Stephenson, C. A., & van Leeuwen, F. 2021, Gaia Early Data Release 3. Parallax bias versus magnitude, colour, and position. A&A, 649, A4.
- Macintosh et al., (2015) Macintosh, B., Graham, J. R., Barman, T., De Rosa, R. J., Konopacky, Q., Marley, M. S., Marois, C., Nielsen, E. L., Pueyo, L., Rajan, A., Rameau, J., Saumon, D., Wang, J. J., Patience, J., Ammons, M., Arriaga, P., Artigau, E., Beckwith, S., Brewster, J., Bruzzone, S., Bulger, J., Burningham, B., Burrows, A. S., Chen, C., Chiang, E., Chilcote, J. K., Dawson, R. I., Dong, R., Doyon, R., Draper, Z. H., Duchêne, G., Esposito, T. M., Fabrycky, D., Fitzgerald, M. P., Follette, K. B., Fortney, J. J., Gerard, B., Goodsell, S., Greenbaum, A. Z., Hibon, P., Hinkley, S., Cotten, T. H., Hung, L. W., Ingraham, P., Johnson-Groh, M., Kalas, P., Lafreniere, D., Larkin, J. E., Lee, J., Line, M., Long, D., Maire, J., Marchis, F., Matthews, B. C., Max, C. E., Metchev, S., Millar-Blanchaer, M. A., Mittal, T., Morley, C. V., Morzinski, K. M., Murray-Clay, R., Oppenheimer, R., Palmer, D. W., Patel, R., Perrin, M. D., Poyneer, L. A., Rafikov, R. R., Rantakyrö, F. T., Rice, E. L., Rojo, P., Rudy, A. R., Ruffio, J. B., Ruiz, M. T., Sadakuni, N., Saddlemyer, L., Salama, M., Savransky, D., Schneider, A. C., Sivaramakrishnan, A., Song, I., Soummer, R., Thomas, S., Vasisht, G., Wallace, J. K., Ward-Duong, K., Wiktorowicz, S. J., Wolff, S. G., & Zuckerman, B. 2015, Discovery and spectroscopy of the young jovian planet 51 Eri b with the Gemini Planet Imager. Science, 350(6256), 64–67.
- Maire et al., (2019) Maire, A. L., Rodet, L., Cantalloube, F., Galicher, R., Brandner, W., Messina, S., Lazzoni, C., Mesa, D., Melnick, D., Carson, J., Samland, M., Biller, B. A., Boccaletti, A., Wahhaj, Z., Beust, H., Bonnefoy, M., Chauvin, G., Desidera, S., Langlois, M., Henning, T., Janson, M., Olofsson, J., Rouan, D., Ménard, F., Lagrange, A. M., Gratton, R., Vigan, A., Meyer, M. R., Cheetham, A., Beuzit, J. L., Dohlen, K., Avenhaus, H., Bonavita, M., Claudi, R., Cudel, M., Daemgen, S., D’Orazi, V., Fontanive, C., Hagelberg, J., Le Coroller, H., Perrot, C., Rickman, E., Schmidt, T., Sissa, E., Udry, S., Zurlo, A., Abe, L., Origné, A., Rigal, F., Rousset, G., Roux, A., & Weber, L. 2019, Hint of curvature in the orbital motion of the exoplanet 51 Eridani b using 3 yr of VLT/SPHERE monitoring. A&A, 624, A118.
- Malo et al., (2014) Malo, L., Doyon, R., Feiden, G. A., Albert, L., Lafrenière, D., Artigau, É., Gagné, J., & Riedel, A. 2014, BANYAN. IV. Fundamental Parameters of Low-mass Star Candidates in Nearby Young Stellar Kinematic Groups—Isochronal Age Determination using Magnetic Evolutionary Models. ApJ, 792(1), 37.
- Mamajek and Bell, (2014) Mamajek, E. E. & Bell, C. P. M. 2014, On the age of the Pictoris moving group. MNRAS, 445(3), 2169–2180.
- Mann et al., (2015) Mann, A. W., Feiden, G. A., Gaidos, E., Boyajian, T., & von Braun, K. 2015, How to Constrain Your M Dwarf: Measuring Effective Temperature, Bolometric Luminosity, Mass, and Radius. ApJ, 804, 64.
- Mann et al., (2016) Mann, A. W., Newton, E. R., Rizzuto, A. C., Irwin, J., Feiden, G. A., Gaidos, E., Mace, G. N., Kraus, A. L., James, D. J., Ansdell, M., Charbonneau, D., Covey, K. R., Ireland, M. J., Jaffe, D. T., Johnson, M. C., Kidder, B., & Vanderburg, A. 2016, Zodiacal Exoplanets in Time (ZEIT). III. A Short-period Planet Orbiting a Pre-main-sequence Star in the Upper Scorpius OB Association. AJ, 152, 61.
- Marley et al., (2007) Marley, M. S., Fortney, J. J., Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2007, On the Luminosity of Young Jupiters. ApJ, 655(1), 541–549.
- Marley et al., (2021) Marley, M. S., Saumon, D., Visscher, C., Lupu, R., Freedman, R., Morley, C., Fortney, J. J., Seay, C., Smith, A. J. R. W., Teal, D. J., & Wang, R. 2021, The Sonora Brown Dwarf Atmosphere and Evolution Models. I. Model Description and Application to Cloudless Atmospheres in Rainout Chemical Equilibrium. ApJ, 920(2), 85.
- Marois et al., (2008) Marois, C., Macintosh, B., Barman, T., Zuckerman, B., Song, I., Patience, J., Lafrenière, D., & Doyon, R. 2008, Direct Imaging of Multiple Planets Orbiting the Star HR 8799. Science, 322(5906), 1348.
- Maxted et al., (2015) Maxted, P. F. L., Serenelli, A. M., & Southworth, J. 2015, Bayesian mass and age estimates for transiting exoplanet host stars. A&A, 575, A36.
- Mermilliod et al., (1997) Mermilliod, J.-C., Mermilliod, M., & Hauck, B. 1997, The General Catalogue of Photometric Data (GCPD). II. A&AS, 124, 349–352.
- Miret-Roig et al., (2020) Miret-Roig, N., Galli, P. A. B., Brandner, W., Bouy, H., Barrado, D., Olivares, J., Antoja, T., Romero-Gómez, M., Figueras, F., & Lillo-Box, J. 2020, Dynamical traceback age of the Pictoris moving group. A&A, 642, A179.
- Mourard et al., (2022) Mourard, D., Berio, P., Pannetier, C., Nardetto, N., Allouche, F., Bailet, C., Dejonghe, J., Geneslay, P., Jacqmart, E., Lagarde, S., Lecron, D., Morand, F., Rousseau, S., Salabert, D., Spang, A., Albrecht, S., Anugu, N., Bourgès, L., ten Brummelaar, T. A., Creevey, O., Deheuvels, S., Domiciano de Souza, A., Gies, D., Ligi, R., Mella, G., Perraut, K., Schaefer, G., & Wittkowski, M. CHARA/SPICA: a six-telescope visible instrument for the CHARA Array. In Mérand, A., Sallum, S., & Sanchez-Bermudez, J., editors, Optical and Infrared Interferometry and Imaging VIII 2022,, volume 12183 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 1218308.
- Mourard et al., (2017) Mourard, D., Bério, P., Perraut, K., Clausse, J.-M., Creevey, O., Martinod, M.-A., Meilland, A., Millour, F., & Nardetto, N. 2017, SPICA, Stellar Parameters and Images with a Cophased Array: a 6T visible combiner for the CHARA array. Journal of the Optical Society of America A, 34(5), A37.
- Ochsenbein et al., (2000) Ochsenbein, F., Bauer, P., & Marcout, J. 2000, The VizieR database of astronomical catalogues. A&AS, 143, 23–32.
- Quanz et al., (2015) Quanz, S. P., Crossfield, I., Meyer, M. R., Schmalzl, E., & Held, J. 2015, Direct detection of exoplanets in the 3–10 m range with e-elt/metis. International Journal of Astrobiology, 14(2), 279–289.
- Rayner et al., (2009) Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, The Infrared Telescope Facility (IRTF) Spectral Library: Cool Stars. ApJS, 185(2), 289–432.
- Ricker et al., (2015) Ricker, G. R., Winn, J. N., Vanderspek, R., Latham, D. W., Bakos, G. Á., Bean, J. L., Berta-Thompson, Z. K., Brown, T. M., Buchhave, L., Butler, N. R., Butler, R. P., Chaplin, W. J., Charbonneau, D., Christensen-Dalsgaard, J., Clampin, M., Deming, D., Doty, J., De Lee, N., Dressing, C., Dunham, E. W., Endl, M., Fressin, F., Ge, J., Henning, T., Holman, M. J., Howard, A. W., Ida, S., Jenkins, J. M., Jernigan, G., Johnson, J. A., Kaltenegger, L., Kawai, N., Kjeldsen, H., Laughlin, G., Levine, A. M., Lin, D., Lissauer, J. J., MacQueen, P., Marcy, G., McCullough, P. R., Morton, T. D., Narita, N., Paegert, M., Palle, E., Pepe, F., Pepper, J., Quirrenbach, A., Rinehart, S. A., Sasselov, D., Sato, B., Seager, S., Sozzetti, A., Stassun, K. G., Sullivan, P., Szentgyorgyi, A., Torres, G., Udry, S., & Villasenor, J. 2015, Transiting Exoplanet Survey Satellite (TESS). Journal of Astronomical Telescopes, Instruments, and Systems, 1, 014003.
- Roettenbacher et al., (2022) Roettenbacher, R. M., Cabot, S. H. C., Fischer, D. A., Monnier, J. D., Henry, G. W., Harmon, R. O., Korhonen, H., Brewer, J. M., Llama, J., Petersburg, R. R., Zhao, L. L., Kraus, S., Le Bouquin, J.-B., Anugu, N., Davies, C. L., Gardner, T., Lanthermann, C., Schaefer, G., Setterholm, B., Clark, C. A., Jorstad, S. G., Kuehn, K., & Levine, S. 2022, EXPRES. III. Revealing the Stellar Activity Radial Velocity Signature of Eridani with Photometry and Interferometry. AJ, 163(1), 19.
- Samland et al., (2017) Samland, M., Mollière, P., Bonnefoy, M., Maire, A. L., Cantalloube, F., Cheetham, A. C., Mesa, D., Gratton, R., Biller, B. A., Wahhaj, Z., Bouwman, J., Brandner, W., Melnick, D., Carson, J., Janson, M., Henning, T., Homeier, D., Mordasini, C., Langlois, M., Quanz, S. P., van Boekel, R., Zurlo, A., Schlieder, J. E., Avenhaus, H., Beuzit, J. L., Boccaletti, A., Bonavita, M., Chauvin, G., Claudi, R., Cudel, M., Desidera, S., Feldt, M., Fusco, T., Galicher, R., Kopytova, T. G., Lagrange, A. M., Le Coroller, H., Martinez, P., Moeller-Nilsson, O., Mouillet, D., Mugnier, L. M., Perrot, C., Sevin, A., Sissa, E., Vigan, A., & Weber, L. 2017, Spectral and atmospheric characterization of 51 Eridani b using VLT/SPHERE. A&A, 603, A57.
- Sepulveda et al., (2022) Sepulveda, A. G., Huber, D., Zhang, Z., Li, G., Liu, M. C., & Bedding, T. R. 2022, The Directly Imaged Exoplanet Host Star 51 Eridani is a Gamma Doradus Pulsator. ApJ, 938(1), 49.
- Siess et al., (2000) Siess, L., Dufour, E., & Forestini, M. 2000, An internet server for pre-main sequence tracks of low- and intermediate-mass stars. A&A, 358, 593–599.
- Simon and Schaefer, (2011) Simon, M. & Schaefer, G. H. 2011, Measured Diameters of Two F Stars in the Pic Moving Group. ApJ, 743(2), 158.
- Skrutskie et al., (2006) Skrutskie, M. F., Cutri, R. M., Stiening, R., Weinberg, M. D., Schneider, S., Carpenter, J. M., Beichman, C., Capps, R., Chester, T., Elias, J., Huchra, J., Liebert, J., Lonsdale, C., Monet, D. G., Price, S., Seitzer, P., Jarrett, T., Kirkpatrick, J. D., Gizis, J. E., Howard, E., Evans, T., Fowler, J., Fullmer, L., Hurt, R., Light, R., Kopan, E. L., Marsh, K. A., McCallon, H. L., Tam, R., Van Dyk, S., & Wheelock, S. 2006, The Two Micron All Sky Survey (2MASS). AJ, 131, 1163–1183.
- (58) Spiegel, D. S. & Burrows, A. 2012,a Spectral and Photometric Diagnostics of Giant Planet Formation Scenarios. ApJ, 745a(2), 174.
- (59) Spiegel, D. S. & Burrows, A. 2012,b Spectral and Photometric Diagnostics of Giant Planet Formation Scenarios. ApJ, 745b(2), 174.
- Swastik et al., (2021) Swastik, C., Banyal, R. K., Narang, M., Manoj, P., Sivarani, T., Reddy, B. E., & Rajaguru, S. P. 2021, Host Star Metallicity of Directly Imaged Wide-orbit Planets: Implications for Planet Formation. AJ, 161(3), 114.
- Tayar et al., (2022) Tayar, J., Claytor, Z. R., Huber, D., & van Saders, J. 2022, A Guide to Realistic Uncertainties on the Fundamental Properties of Solar-type Exoplanet Host Stars. ApJ, 927(1), 31.
- (62) ten Brummelaar, T. The CLASSIC/CLIMB Data Reduction: The Math. In EAS Publications Series 2014,a, volume 69-70 of EAS Publications Series, pp. 75–99.
- (63) ten Brummelaar, T. The CLASSIC/CLIMB Data Reduction: The Software. In EAS Publications Series 2014,b, volume 69-70 of EAS Publications Series, pp. 101–131.
- ten Brummelaar et al., (2005) ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., Bagnuolo, W. G., J., Turner, N. H., Sturmann, L., Sturmann, J., Berger, D. H., Ogden, C. E., Cadman, R., Hartkopf, W. I., Hopper, C. H., & Shure, M. A. 2005, First Results from the CHARA Array. II. A Description of the Instrument. ApJ, 628(1), 453–465.
- Ten Brummelaar et al., (2013) Ten Brummelaar, T. A., Sturmann, J., Ridgway, S. T., Sturmann, L., Turner, N. H., McAlister, H. A., Farrington, C. D., Beckmann, U., Weigelt, G., & Shure, M. 2013, The Classic/climb Beam Combiner at the CHARA Array. Journal of Astronomical Instrumentation, 2(2), 1340004.
- (66) von Braun, K. & Boyajian, T. 2017,a. Extrasolar Planets and Their Host Stars.
- (67) von Braun, K. & Boyajian, T. 2017,b Extrasolar Planets and Their Host Stars. arXiv e-prints,, arXiv:1707.07405.
- Weiss and Schlattl, (2008) Weiss, A. & Schlattl, H. 2008, GARSTEC—the Garching Stellar Evolution Code. The direct descendant of the legendary Kippenhahn code. Ap&SS, 316(1-4), 99–106.
- White et al., (2018) White, T. R., Huber, D., Mann, A. W., Casagrande, L., Grunblatt, S. K., Justesen, A. B., Silva Aguirre, V., Bedding, T. R., Ireland, M. J., Schaefer, G. H., & Tuthill, P. G. 2018, Interferometric diameters of five evolved intermediate-mass planet-hosting stars measured with PAVO at the CHARA Array. MNRAS, 477(4), 4403–4413.
- Wizinowich et al., (2000) Wizinowich, P., Acton, D. S., Shelton, C., Stomski, P., Gathright, J., Ho, K., Lupton, W., Tsubota, K., Lai, O., Max, C., Brase, J., An, J., Avicola, K., Olivier, S., Gavel, D., Macintosh, B., Ghez, A., & Larkin, J. 2000, First Light Adaptive Optics Images from the Keck II Telescope: A New Era of High Angular Resolution Imagery. PASP, 112(769), 315–319.
- Yi et al., (2003) Yi, S. K., Kim, Y.-C., & Demarque, P. 2003, The Y2 Stellar Evolutionary Tracks. ApJS, 144(2), 259–261.
- Zuckerman et al., (2001) Zuckerman, B., Song, I., Bessell, M. S., & Webb, R. A. 2001, The Pictoris Moving Group. ApJ, 562(1), L87–L90.