Membrane-Protein Interactions in a Generic Coarse-Grained Model for Lipid Bilayers

We employ a simple generic lipid model (Schmid et al., 2007) that has been shown to reproduce the characteristic high-temperature phase transitions of monolayers (Stadler et al., 1999; Düchs and Schmid, 2001) and bilayers (Lenz and Schmid, 2007). The lipids are represented by chains of seven beads with one head bead of diameter $\sigma_{h}$ followed by six tail beads of diameter $\sigma_{t}$. Beads, that are not direct neighbors in a chain interact, via a truncated and lifted Lennard-Jones potential:

$$V_{\text{bead}}(r)=\left\{\begin{array}[]{rl}V_{\text{LJ}}(r/\sigma)-V_{\text{LJ}}(r_{c}/\sigma)&\text{ if $r<r_{c}$}\\ 0&\text{ otherwise}\end{array}\right.$$

(1)

with

$$V_{\text{LJ}}(x)=\epsilon\left(x^{-12}-2x^{-6}\right)$$

(2)

where $\sigma$ is the mean diameter of the two interacting beads, $\sigma_{ij}=(\sigma_{i}+\sigma_{j})/2$ ($i,j=h$ or $t$). Head-head and head-tail interactions are purely repulsive ($r_{c}=\sigma$) while tail-tail interactions also have an attractive contribution ($r_{c}=2\sigma$). Within a “lipid” chain beads are connected to each other by FENE (Finitely Extensible Nonlinear Elastic) springs with the spring potential

$$V_{\text{FENE}}(r)=-\frac{1}{2}\epsilon_{{}_{\text{FENE}}}(\Delta r_{\text{max}})^{2}\log\left(1-\left(\frac{r-r_{0}}{\Delta r_{\text{max}}}\right)^{2}\right),$$

(3)

where $r_{0}$ is the equilibrium distance, $\Delta r_{\text{max}}$ the maximal deviation, and $\epsilon_{\text{FENE}}$ the FENE spring constant. In addition, the chains are given bending stiffness by means of a bond-angle potential

$$V_{BA}(\theta)=\epsilon_{BA}(1-\cos(\theta)).$$

(4)

The aqueous environment of the membrane is modeled with “phantom” solvent beads (Lenz and Schmid, 2005), which interact with lipids like head beads ($\sigma_{s}=\sigma_{h}$), but have no interactions with each other. Much like an implicit solvent, the phantom solvent is structureless and does not impart unwanted correlations onto the bilayers, and it is very cheap from a computational point of view. At sufficiently low temperatures it forces the lipids to spontaneously self-assemble into stable bilayers (Lenz and Schmid, 2005).

Specifically our model parameters are (Düchs and Schmid, 2001; Schmid et al., 2007) $\sigma_{h}=1.1\sigma_{t}$, $r_{0}=0.7\sigma_{t}$, $\Delta r_{\text{max}}=0.2\sigma_{t}$, $\epsilon_{{}_{\text{FENE}}}=100\epsilon/\sigma_{t}^{2}$, and $\epsilon_{BA}=4.7\epsilon$. The simulations were carried out at constant pressure $P=2.\epsilon/\sigma_{t}^{3}$ and temperature $k_{B}T=1.3\epsilon$, which is well in the fluid phase region of the bilayer. (The bilayer undergoes a main transition to a tilted gel phase $L_{\beta^{\prime}}$ via a ripple phase $P_{\beta^{\prime}}$ at the temperature $k_{B}T=1.2\epsilon$ (Lenz and Schmid, 2007).) Comparing the monolayer thickness, $t_{0}\sim 3\sigma_{t}$, and the area per lipid, $a_{0}\sim 1.36\sigma_{t}^{2}$, with the corresponding numbers for real lipid bilayers in the fluid $L_{\alpha}$ phase, we find that the values in our model roughly reproduce those of DPPC (dipalmitoyl phosphatidylcholine) bilayers, if we set $\sigma_{t}\sim 6$Å (Lenz, 2007). By matching the temperatures of the main transition ($T_{m}=42^{\circ}$C in DPPC) we can also identify an energy scale: $\epsilon\sim 0.36\cdot 10^{-20}$J.

The proteins are modeled as cylinders with the radius $R=1.5\sigma_{t}$, which have fixed orientation along the bilayer normal (the $z$-axis). We impose the orientation in order to realize the situation considered in the elastic theory as closely as possible – proteins cannot respond to hydrophobic mismatch by tilting. In a real membrane, this would correspond to a situation where the orientation of the transmembrane domain of a protein is kept fixed by external factors, e.g., geometrical constraints in the extramembrane domain. For comparison, selected simulations were also conducted for proteins which were allowed to tilt (unconstrained orientations). As in other model studies Brannigan and Brown (2006); de Meyer et al. (2008), the effect of orientation fluctuations on the results was found to be rather small (see section Three).

The interaction between proteins and lipid or solvent beads has a purely repulsive contribution, which is described by a radially shifted and truncated Lennard-Jones potential

$$V_{\text{rep}}(r)=\left\{\begin{array}[]{rl}V_{\text{LJ}}(\frac{r-\sigma_{0}}{\sigma})-V_{\text{LJ}}(1)&\text{ if $r-\sigma_{0}<\sigma$}\\ 0&\text{ otherwise}\end{array}\right.,$$

(5)

where $r=\sqrt{x^{2}+y^{2}}$ denotes the distance of the interacting partners in the $(xy)$-plane, the parameter $\sigma$ is given by $\sigma=(\sigma_{t}+\sigma_{i})/2$ for interactions with beads of type $i$ ($i=h,t$, and $s$ for head, tail, and solvent beads, respectively), $\sigma_{0}=\sigma_{t}$, and $V_{\text{LJ}}$ has been defined above (Eq. (2)). The direct protein-protein interactions have the same potential (5) with $\sigma=\sigma_{t}$ and $\sigma_{0}=2\sigma_{t}$.

In addition, protein cylinders attract tail beads on a “hydrophobic” section of length $L$. This is described by an additional attractive potential that depends on the $z$-distance between the tail bead and the protein center. The total potential reads

$$V_{\text{pt}}(r,z)=\epsilon_{pt}\ \Big{(}V_{\text{rep}}(r)+V_{\text{attr}}(r)\cdot W_{\text{P}}(z)\Big{)}$$

(6)

with the attractive Lennard-Jones contribution

$$V_{\text{attr}}(r)=\left\{\begin{array}[]{rl}V_{\text{LJ}}(1)-V_{\text{LJ}}(2)&\text{ if $r-\sigma_{0}<\sigma$}\\ V_{\text{LJ}}(\frac{r-\sigma_{0}}{\sigma})-V_{\text{LJ}}(2)&\text{ if $\sigma<r-\sigma_{0}<2\sigma$}\\ 0&\text{ otherwise}\end{array}\right.$$

(7)

and a weight function $W_{\text{P}}(z)$, which is unity on a stretch of length $L-2\sigma_{t}$ and crosses smoothly over to zero over a distance $\sigma_{t}$ at both sides. Specifically, we use

$$W_{\text{P}}(z)=\left\{\begin{array}[]{rl}1&\text{ if $|z|\leq l$}\\ \cos^{2}[3/2(|z|-l)]&\text{ if $l<|z|<l+\pi/3$}\\ 0&\text{ otherwise}\end{array}\right.$$

(8)

with $l=L/2-\sigma_{t}$. The parameter $\epsilon_{pt}$ tunes the strength of the lipid-protein interaction, i.e., the hydrophobicity of the protein. It was varied between $\epsilon_{pt}=1$ and $\epsilon_{pt}=6$. The hydrophobicity $\epsilon_{pt}=1$ was sufficient to trap the center of the protein inside the membrane: The fluctuations of its $z$-position relative to the height of the membrane $h$ were of the order $\langle(z_{\text{protein}}-h)^{2}\rangle\stackrel{{\scriptstyle<}}{{\sim}}0.5\sigma_{t}$ for all values of $\epsilon_{pt}$. The proteins with unconstrained orientation were modeled as spherocylinders of length $L$ with essentially the same interaction potentials, except that the $z$-axis is replaced by the protein axis, and the variable $r$ by the closest distance to the protein.

The system is studied using Monte Carlo simulations at constant pressure and temperature with periodic boundary conditions in a simulation box of variable size and shape: The simulation box is a parallelepiped spanned by the vectors $(L_{x},0,0),(s_{yx}L_{x},L_{y},0),(s_{zx}L_{x},s_{zy}L_{y},L_{z})$, and all $L_{i}$ and $s_{j}$ are allowed to fluctuate. This ensures that the membranes have no interfacial tension. The system sizes ranged from $200$ to $3200$ lipids, and the simulations were run up to $8$ million Monte Carlo steps, where one Monte Carlo step corresponds to one Monte Carlo move per bead. Moves that alter the simulation box were attempted every $50$th Monte Carlo step. To generate the initial configurations, we set up a perfectly ordered bilayer in the $(xy)$-plane with straight chains pointing in the $z$-direction and simulated it until it was equilibrated, i.e., all observables of the system fluctuated about the equilibrium value and none of the observables shows a trend. Typical equilibration times where $1$ million Monte Carlo steps ($4$ million Monte Carlo steps in simulations where we looked at large-scale height fluctuations). Due to this procedure, the bilayers were oriented in the $(xy)$-plane.

Fig. 1 shows two snapshots of a system containing two inclusions whose thickness roughly matches that of the bilayer ($L=6\sigma_{t}$), with different hydrophobicity parameters $\epsilon_{pt}$. They illustrate the existence of membrane-mediated attractive interactions even in the absence of hydrophobic mismatch. At low values of $\epsilon_{pt}$, the proteins touch. At higher values of $\epsilon_{pt}$, they are separated by a single lipid layer.

Before proceeding to a more quantitative discussion of the simulation results, we shall now briefly recollect the main assumptions and results of the analytical theories which we use to analyze our data.

One of the oldest theoretical approaches to studying lipid-mediated interactions between inclusions is based on a Landau-de Gennes expansion of the free energy in powers of the lipid area or membrane thickness variations Owicki et al. (1978); Owicki and McConnell (1979); Sperotto and Mouritsen (1991); Jensen and Mouritsen (2004). In the simplest case, this expansion reads Jensen and Mouritsen (2004)

$$F_{\mbox{\tiny{LdG}}}=\int\mbox{d}^{2}r\Big{\{}\frac{a}{2}(2\phi_{\mbox{\tiny{LdG}}})^{2}+\frac{c}{2}(2\nabla\phi_{\mbox{\tiny{LdG}}})^{2}\Big{\}}$$

(9)

with the boundary condition $\phi_{\mbox{\tiny{LdG}}}=t_{R}$ at the surface of the inclusion, where $\phi_{\mbox{\tiny{LdG}}}$ denotes the local deviation of the monolayer thickness from its equilibrium value $t_{0}$ in the unperturbed membrane, and $2(t_{R}+t_{0})$ is the hydrophobic thickness of the inclusion. The first term in Eq. (9) accounts for the area compressibility $k_{A}$ of the bilayer ($k_{A}=a(2t_{0})^{2}$), and the second term penalizes spatial thickness variations, i.e., the variable $c$ is taken to be positive. Minimizing this free energy for a membrane containing a single inclusion at $r=0$ yields the deformation profile

$$\phi_{\mbox{\tiny{LdG}}}(r)=t_{R}\frac{K_{0}(r/\xi)}{K_{0}(R/\xi)},$$

(10)

where $R$ is the radius of the inclusion, $\xi=\sqrt{c/a}$ the correlation length, and $K_{0}$ is the modified Bessel function of the second kind. For $r\xi>1$, Eq. (10) can be approximated by an exponential decay

$$\phi_{\mbox{\tiny{LdG}}}(r)\approx t_{R}\exp{\left(-\frac{r-R}{\xi}\right)}\>\sqrt{\frac{R}{r}}.$$

(11)

Such exponential laws have often been used to fit data from simulations or molecular theories for membranes with inclusions Sperotto and Mouritsen (1991); Fattal and Ben-Shaul (1993, 1995); Venturoli et al. (2005); Venturoli (2004). Eq. (9) can also be used to deduce an equation for the monolayer thickness fluctuation spectrum

$$\langle|\phi_{\mbox{\tiny{LdG}}}(q)|^{2}\rangle=\frac{k_{B}T}{4(a+cq^{2})}.$$

(12)

Another popular approach is the elastic theory of coupled monolayers Huang (1986, 1995); Harroun et al. (1999b); Helfrich and Jakobsson (1990); Nielsen et al. (2000); Nielsen and Andersen (2000); Dan et al. (1993, 1994); Aranda-Espinoza et al. (1996); Brannigan and Brown (2006, 2007). Here the membrane is treated as a system of two coupled elastic monolayer sheets. The basic structure of the different theories is very similar – they differ mainly in the choice of the boundary conditions and the number of elastic terms that they include. For example, early theories have often disregarded the possibility that the individual monolayers may have a spontaneous curvature, whereas this is usually accounted for in more recent work. Here we shall use a recent version of the elastic theory developed by Brannigan and Brown (Brannigan and Brown, 2006, 2007), which is fairly “complete” in the sense that it includes all known elastic terms.

We consider a flat lipid bilayer in the $(xy)$-plane. The two constituting monolayers are described by four independent fluctuating fields – two accounting for mesoscopic bending deformations, and two for the microscopic protrusions. We assume that the volume of lipids is locally conserved, and that the mesoscopic bilayer height and thickness fluctuations and the protrusions basically decouple. The latter requirement may seem all-too rigid and is actually not imposed in the original model (Brannigan and Brown, 2006), but it leads to a considerable simplification of the resulting theory and will be justified a posteriori by the fact that it describes the fluctuation spectra of our model bilayers in an excellent way.

The quantities of interest for us are the local bilayer height $h$, the local monolayer thickness $t$, and the local field $\phi_{\mbox{\tiny{el}}}$ which denotes just the contribution of bending deformations to the thickness, without the microscopic protrusions. This field is defined in analogy to the field $\phi_{\mbox{\tiny{LdG}}}$ in Eq. (9). With the assumptions mentioned above, the spectra of the bilayer height and monolayer thickness fluctuations in Fourier space, $\langle|h(q)|^{2}\rangle$ and $\langle|t(q)|^{2}\rangle$, are given by (Brannigan and Brown, 2006)

	$\displaystyle\langle|h(q)|^{2}\rangle=$	$\displaystyle\frac{k_{B}T}{k_{c}q^{4}}+\frac{k_{B}T}{2(k_{\lambda}+\gamma_{\lambda}q^{2})},$		(13)
	$\displaystyle\begin{split}\langle|t(q)|^{2}\rangle=&\frac{k_{B}T}{k_{c}q^{4}-4k_{c}\zeta q^{2}/t_{0}+k_{A}/t_{0}^{2}}\\ +&\frac{k_{B}T}{2(k_{\lambda}+\gamma_{\lambda}q^{2})},\end{split}$			(14)

where $k_{c}$ and $k_{A}$ are the bending and the compressibility modulus of the bilayer, $\zeta$ is related to the spontaneous curvature (not, a), $t_{0}$ is the mean monolayer thickness, and the parameters $\gamma_{\lambda}$ and $k_{\lambda}$ characterize the protrusions. Fitting our simulation data to these theoretical spectra allows us to (i) test the validity of the theory and (ii) extract the elastic parameters $k_{c}$, $k_{A}$, and $\zeta$, which we need for the subsequent analysis of protein-lipid interactions.

Within the decoupling approximation, the protrusions and the height fluctuations do not contribute to the protein-induced membrane deformations. The free energy of monolayer thickness deformations can be expressed as (Brannigan and Brown, 2007)

$$\begin{split}F_{el,0}=&\int\mbox{d}^{2}r\>\bigg{\{}\frac{k_{A}}{2t_{0}^{2}}\phi_{\mbox{\tiny{el}}}^{2}+2k_{c}c_{0}\nabla^{2}\phi_{\mbox{\tiny{el}}}+2k_{c}\zeta\frac{\phi_{\mbox{\tiny{el}}}}{t_{0}}\nabla^{2}\phi_{\mbox{\tiny{el}}}\\ &\qquad+\>\frac{k_{c}}{2}(\nabla^{2}\phi_{\mbox{\tiny{el}}})^{2}+k_{G}\det(\partial_{ij}\phi_{\mbox{\tiny{el}}})\bigg{\}},\end{split}$$

(15)

where $(\phi_{\mbox{\tiny{el}}}+t_{0})$ is the locally smoothed monolayer thickness (without the protrusions), and we have introduced the spontaneous curvature of the monolayers $c_{0}$ and the Gaussian rigidity $k_{G}$. According to the Gauss-Bonnet theorem, the latter only contributes an uninteresting constant in homogeneous planar sheets and is thus often omitted; in the presence of inclusions (holes), however, it has to be taken into account Brannigan and Brown (2007).

We consider inclusions with radius $R$ that enforce a certain membrane thickness $2t_{R}$ at their surface. To calculate the deformation profile of the bilayer in the vicinity of such an inclusion centered at $r=0$, we minimize the free energy $F_{el,0}$ with respect to the profile $\phi_{\mbox{\tiny{el}}}(r)$ while keeping the membrane deformation at the surface of the inclusion fixed, $\phi_{\mbox{\tiny{el}}}^{\text{surface}}\equiv t_{R}$. This leads to the Euler-Lagrange equation

$$\frac{k_{A}}{k_{c}t_{0}^{2}}\phi_{\mbox{\tiny{el}}}+\frac{4\zeta}{t_{0}}\nabla^{2}\phi_{\mbox{\tiny{el}}}+\nabla^{4}\phi_{\mbox{\tiny{el}}}=0$$

(16)

with the boundary conditions

	$\displaystyle\phi_{\mbox{\tiny{el}}}(R)$	$\displaystyle=$	$\displaystyle t_{R}$		(17)
	$\displaystyle\nabla_{r}^{2}\phi_{\mbox{\tiny{el}}}|_{R}$	$\displaystyle=$	$\displaystyle-\frac{k_{G}}{k_{c}R}t_{R}^{\prime}-2\left(c_{0}+{\zeta}\frac{t_{R}}{t_{0}}\right)$		(18)

at the surface of the inclusion, and

$$\partial_{r}\phi_{\mbox{\tiny{el}}}(r)|_{r\to\infty}=\nabla_{r}^{3}\phi_{\mbox{\tiny{el}}}(r)|_{r\to\infty}=0$$

(19)

at infinity, where $\nabla^{2}_{r}=(1/r)\partial_{r}r\partial_{r}$ and $\nabla^{3}_{r}=\partial_{r}\nabla^{2}_{r}$, and we have defined $t_{R}^{\prime}=\partial_{r}\phi_{\mbox{\tiny{el}}}|_{R}$. For a single inclusion, these equations can be solved analytically, giving (Aranda-Espinoza et al., 1996)

$$\begin{split}\phi_{\mbox{\tiny{el}}}(r)&=A_{1}J_{0}(\alpha_{+}r)+A_{2}Y_{0}(\alpha_{+}r)\\ &+A_{3}J_{0}(\alpha_{-}r)+A_{4}Y_{0}(\alpha_{-}r)\end{split}$$

(20)

with (not, b)

$$\alpha_{\pm}=\sqrt{\frac{2\zeta}{t_{0}}\pm\sqrt{\left(\frac{2\zeta}{t_{0}}\right)^{2}-\frac{k_{A}}{k_{c}t_{0}^{2}}}},$$

(21)

where $J_{0}(x)$ and $Y_{0}(x)$ are the zeroth order Bessel functions of the first and second kind, and the coefficients $A_{i}$ are determined by the boundary conditions.

The elastic model presented so far only uses material properties of free, bulk membranes. Inclusions may locally alter the lipid properties, e.g., the lipid volume, the lipid ordering etc., which may in turn affect the elastic properties (e.g., the equilibrium thickness, the spontaneous curvature, the bending rigidity, the compression modulus) of the membrane. In Ref. (Brannigan and Brown, 2007), Brannigan and Brown have demonstrated for the case of varying lipid volume that such effects can be incorporated into the theory in a relatively straightforward way (Brannigan and Brown, 2007).

Here we will discuss this from a more general perspective: Consider some scalar quantity $q(r)$ that is distorted from its bulk value $q_{0}$ by the inclusion and locally alters the membrane properties. By symmetry, it will introduce two new terms in Eq. (15),

	$\displaystyle F_{el,q}$	$\displaystyle=$	$\displaystyle F_{el,0}+F_{q}\qquad\mbox{with}$
	$\displaystyle F_{q}$	$\displaystyle=$	$\displaystyle\int\mbox{d}^{2}r\left\{K_{1}\frac{\delta q}{q_{0}}\phi_{\mbox{\tiny{el}}}+K_{2}\frac{\delta q}{q_{0}}\nabla^{2}\phi_{\mbox{\tiny{el}}}\right\}.$		(22)

Here $\delta q/q_{0}$ denotes the relative deviation of $q$, and terms that do not depend on $\phi_{\mbox{\tiny{el}}}$ or that are of higher than quadratic order in the deviations $\phi_{\mbox{\tiny{el}}}$ and $\delta q/q_{0}$ have been disregarded. In general, the additional free energy contribution $F_{q}$ will change the Euler-Lagrange equations, and the solution (20) is no longer valid close to the inclusion. The situation however simplifies considerably if we make the reasonable assumption that the local distortion $\delta q(r)$ decays to zero on a length scale which is much smaller than the characteristic length scales of the elastic profile. For an inclusion centered at $r=0$, we can then replace $\phi_{\mbox{\tiny{el}}}(r)$ by $t_{R}+t_{R}^{\prime}(r-R)$ in Eq. (22), and the free energy $F_{q}$ turns into a surface term,

$$\begin{split}{F_{q}}&=t_{R}\ K_{1}\int_{R}^{\infty}2\pi\mbox{d}r\ r\frac{\delta q(r)}{q_{0}}\\ &+t_{R}^{\prime}\int_{R}^{\infty}\mbox{d}r2\pi\frac{\delta q(r)}{q_{0}}(K_{1}\>r(r-R)+K_{2}),\end{split}$$

(23)

which only changes the boundary condition (18): The local distortion $\delta q(r)$ renormalizes the spontaneous curvature term in Eq. (18) according to

$$\tilde{c_{0}}=c_{0}-\frac{1}{2k_{c}R}\int_{R}^{\infty}\mbox{d}r\ \frac{\delta q(r)}{q_{0}}\ (K_{1}\ r(r-R)+K_{2}).$$

(24)

Inserting that into Eq. (22) with (15) and exploiting the Euler Lagrange equation (16), we find that the free energy of the deformation is given by

$$F_{el,q}=\pi k_{c}R\Big{(}t_{R}\nabla_{r}^{3}\phi_{\mbox{\tiny{el}}}|_{R}-2t_{R}^{\prime}\big{(}\tilde{c_{0}}-\zeta\ t_{R}/t_{0}\big{)}\Big{)}+\mbox{const.},$$

(25)

where the constant does not depend on the deformation profile.

This result can readily be generalized to situations where several scalar quantities $q_{\alpha}(r)$ affect the membrane simultaneously. Within our linear approximation, each of them will contribute a separate surface term $F_{q_{\alpha}}$ of the form (23) and the effect on the renormalized curvature term (24) will be additive. For given renormalized curvature $\tilde{c_{0}}$, Eq. (25) still remains valid.

Our findings agree qualitatively with those of Brannigan and Brown in Ref. (Brannigan and Brown, 2007), who also conclude that lipid volume deviations $v(r)/v_{0}$ at the surface of the inclusion effectively renormalize the spontaneous curvature term. The actual expression for $\tilde{c_{0}}$ given in that paper is different from ours. The discrepancy is due to an error in the original analysis.

The elastic theory sketched in the previous section is an effective interface theory, i.e., the main degrees of freedom are the positions of the fluctuating interfaces between the monolayers and the surrounding solvent. A number of authors have put forward elastic theories which include the local tilt of chains as supplementary degrees of freedom in the spirit of the Landau-de Gennes theory for smectic liquid crystals Fournier (1998, 1999); Bohinc et al. (2003); Fošnarič et al. (2006). These theories introduce new elastic parameters which describe, e.g., the splay, twist, and bend modes of the tilt order parameter, and their coupling to the interfacial degrees of freedom. Due to the difficulty of accessing the additional parameters, they are not included in the present analysis.

Another entirely different type of approach is pursued by the molecular theories Fattal and Ben-Shaul (1993, 1995); Harries and Ben-Shaul (1997); May and Ben-Shaul (2000); Lagüe et al. (1998, 2000, 2001). They account for the chain character of lipids explicitly and calculate the packing interactions between proteins and membranes by different sophisticated mean field methods. Since the results depend on the chain model, which is different from ours, they can only be compared to our simulation data at a qualitative level (see next section).

One of the most powerful approaches to looking at elastic membrane properties is the analysis of fluctuation spectra (Goetz et al., 1999; Lindahl and Edholm, 2000a; Marrink and Mark, 2001; Loison et al., 2003). To determine the spectra for our membranes, we have basically followed the procedure outlined in Ref. (Loison et al., 2003). We have carried out simulations of a bilayer containing $3200$ lipids (and $24615$ solvent beads). The system was divided in $N_{x}\times N_{y}$ bins in the $(xy)$-plane with $N_{x}=N_{y}=20$. In each bin, the $z$-value of the mean head position in the $z$-direction was determined for both monolayers separately. The average and the difference of the two values give the bilayer height spectrum $h(x,y)$ and monolayer thickness spectrum $t(x,y)$, respectively. The two spectra were then Fourier transformed according to

$$f_{q_{x},q_{y}}=\frac{L_{x}L_{y}}{N_{x}N_{y}}\sum_{x,y}f(x,y)e^{-i(q_{x}x+q_{y}y)},$$

(26)

and the values of $|h_{q}|^{2}$ and $|t_{q}|^{2}$ were collected in $q$-bins of size $0.1$. The binning was made necessary by the fact that the dimensions of the simulation box and hence the $q$-values fluctuate. In each bin, the averages $\langle|h_{q}|^{2}\rangle$ and $\langle|t_{q}|^{2}\rangle$ were evaluated.

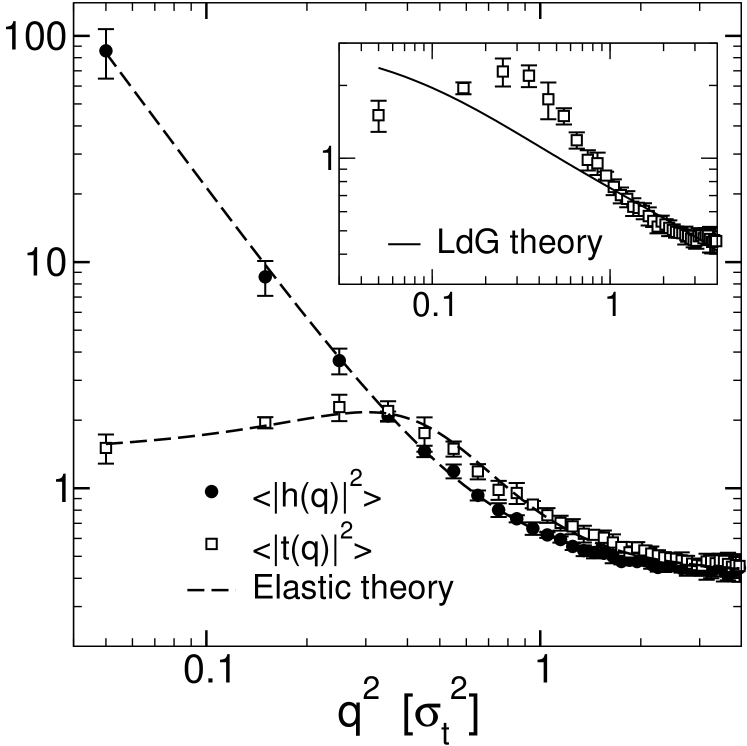
The results are shown in Fig. 2. The data illustrates the characteristic features of the spectra: The height fluctuations are Goldstone modes, hence the height spectrum diverges for small wavelength modes. In contrast, the monolayer thickness spectrum is limited by the equilibrium thickness and tends towards a constant value for small wavevector values (Lindahl and Edholm, 2000a). It exhibits a characteristic peak at $q^{2}\sigma_{t}^{2}\sim 0.4$, corresponding to a soft peristaltic mode with wavelength $\sim 10\sigma_{t}$. At small $q^{2}$, the fluctuation spectra are dominated by bending deformations. For larger values of $q^{2}$, the spectra are dominated by the protrusion modes and are equal for the height and the monolayer thickness fluctuations.

The solid line in Fig. 2 (main frame) shows the fit to the elastic theory, Eqs. (13) and (14), with fit parameters $k_{c}$, $\zeta/t_{0}$, $k_{A}/t_{0}^{2}$, $k_{\lambda}$, and $\gamma_{\lambda}$. The results of the fit are given in Table 1. The elastic theory describes the data in an excellent way. This confirms the validity of the underlying assumptions, most notably, the decoupling approximations (see above). The strength of the coupling between bending modes and protrusion modes can be estimated by looking at the coupling parameter $\gamma_{\lambda}^{2}/k_{\lambda}k_{c}$. Our fit gives $\gamma_{\lambda}^{2}/k_{\lambda}k_{c}=5\cdot 10^{-6}$, which is indeed much smaller than unity. The inset of Fig. 2 shows the fit of the monolayer thickness spectrum to the Landau-de Gennes theory (solid line). To make the analyses comparable, we have included a protrusion contribution and fitted the monolayer thickness deformations to

$$\langle|t(q)|^{2}\rangle=\frac{k_{B}T}{4(a+cq^{2})}+\frac{k_{B}T}{2(k_{\lambda}+\gamma_{\lambda}q^{2})},$$

(27)

(cf. Eq. (12)) and the bending deformations to Eq. (13) simultaneously, with fit parameters $a$, $c$, $k_{c}$, $k_{\lambda}$, and $\gamma_{\lambda}$. Not suprisingly, the Landau-de Gennes theory cannot reproduce the peak at nonzero $q$ in $\langle|t(q)|^{2}\rangle$, hence it misses one important characteristic of the thickness spectrum.

Turning back to the elastic theory, the analysis of fluctuation spectra yields the values of three elastic parameters that are needed in the subsequent analysis: the bending rigidity $k_{c}$, the compressibility modulus $k_{A}$, and the extrapolated curvature $\zeta$. The two remaining elastic parameters in Eq. (15) are the spontaneous curvature $c_{0}$, and the Gaussian rigidity $k_{G}$. Under the (admittedly bold) assumption that the two monolayer slabs can be treated as elastic continua subject to internal stress, these quantities can be calculated from the first and the second moment of the surface tension profile across the monolayers (Safran, 1994) via

	$\displaystyle k_{c}\,c_{0}$	$\displaystyle=-\int_{0}^{\infty}\mbox{d}z\ \gamma_{\text{int}}(z)\ (z-z_{0})$		(28)
	$\displaystyle k_{G}$	$\displaystyle=2\int_{0}^{\infty}\mbox{d}z\ \gamma_{\text{int}}(z)\ (z-z_{0})^{2}.$		(29)

Here $\gamma_{\text{int}}(z)$ denotes the intrinsic surface tension profile, which is defined as the difference between the normal and the tangential components of the local pressure tensor. The integration starts at the bilayer midplane $z=0$, and the reference plane $z=z_{0}$ is the “inextensibility plane”, i.e., the plane in which an infinitesimal volume element is not compressed or extended if the monolayer is bent. For symmetric bilayers with overall tensionless monolayers, one has $\int_{0}^{\infty}\mbox{d}z\ \gamma_{\text{int}}(z)=0$, and the result for $c_{0}$ is independent of $z_{0}$. The value obtained for $k_{G}$, however, depends sensitively on the choice of $z_{0}$.

In the simulation, the pressure tensor is obtained using the virial theorem,

$$\mathcal{P}_{\alpha\beta}=\frac{Nk_{B}T}{V}\delta_{\alpha\beta}+\frac{1}{2V}\left\langle\sum_{i}r^{\alpha}_{i}F^{\beta}_{i}\right\rangle,$$

(30)

where $\mathbf{r}_{i}$ is the position of particle $i$, $\mathbf{F}_{i}$ the force acting on this particle, $N$ the number of particles, $T$ the temperature, and $V$ the volume. Because of the periodic boundaries, care must be taken to use a version of the expression (30) that does not depend on absolute positions, e.g., by rewriting the contribution of pairwise forces as $\sum_{i<j}(r_{i}^{\alpha}-r_{j}^{\alpha})F_{ij}^{\alpha}$, etc. The pressure tensor of the whole equilibrated system is diagonal, $\mathcal{P}_{\alpha\beta}=\delta_{\alpha\beta}P$, where $P$ is the applied pressure. Nevertheless, it varies spatially on the molecular scale. In order to measure the local pressure profile, we divide the system along the $z$-axis in slices of length $\delta z=0.125\sigma$. The contributions of pairwise forces to the total virial are parcelled out on the bins according to the Irving-Kirkwood convention (Irving and Kirkwood, 1950), i.e., they are distributed evenly on the line connecting the two interaction partners. The contributions of our only multibody interactions, the bond-angle potentials (Eq. (4)), are distributed evenly on the two participating bonds. Alternatively, Goetz and Lipowsky (Goetz and Lipowsky, 1998) have proposed a method where the contribution of multibody forces is spread evenly on all lines connecting the participating partners (the bond-angle virials would then be distributed on triangles). We have also implemented this definition, and found that the effect on the pressure profile was negligible. The interfacial tension profile is given by

$$\gamma(z)=\mathcal{P}_{zz}(z)-\frac{1}{2}(\mathcal{P}_{xx}(z)+\mathcal{P}_{yy}(z)).$$

(31)

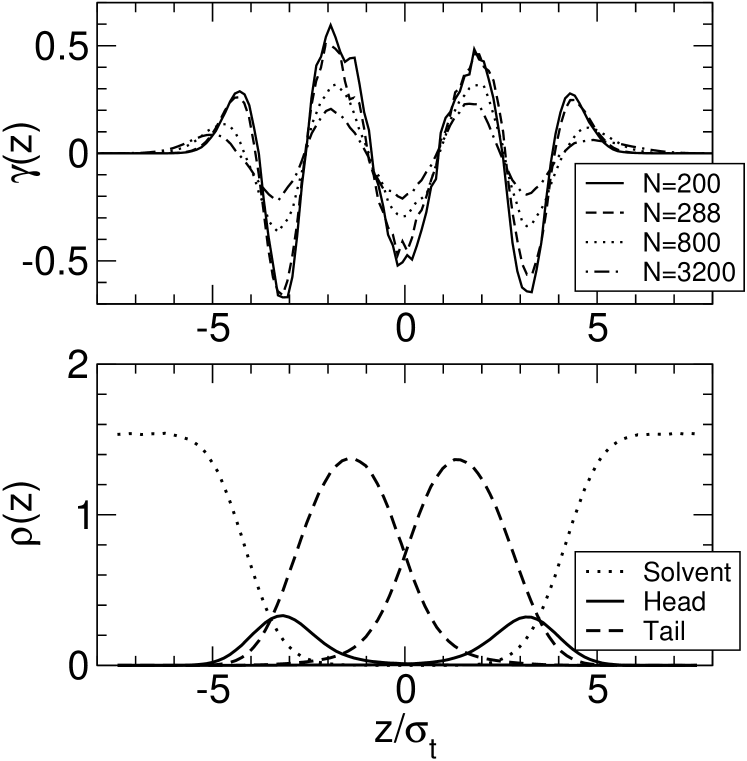
Figure 3 shows the surface tension profiles of a pure model membrane for four system sizes. Qualitatively, it exhibits the same features as the stress profile obtained with the similarly simple coarse-grained lipid model of Goetz and Lipowsky (Goetz and Lipowsky, 1998). Most notably, the surface tension features a negative peak in the bilayer midplane (at $z=0$), indicating that the monolayers are strongly bound to each other, in agreement with atomistic and coarse-grained simulations of DPPC bilayers Lindahl and Edholm (2000b); Venturoli (2004); Marrink et al. (2007); not (c).

Due to the height fluctuations, $\gamma(z)$ depends on the lateral system size: All profiles are broadened in large systems. In contrast, the expressions (28) and (29) are based on a hypothetical intrinsic surface tension profile $\gamma_{\text{int}}(z)$. If such an intrinsic profile exists, the actual tension profile $\gamma(z)$ should be given by the convolution of $\gamma_{\text{int}}(z)$ with the distribution of interface heights $W(z^{\prime})$,

$$\gamma(z)=\int\mbox{d}z^{\prime}\ W(z^{\prime})\ \gamma_{\text{int}}(z-z^{\prime}).$$

(32)

In this case, one easily verifies that the integral $\Gamma_{0}=\int\mbox{d}z\>\gamma(z)$ is still zero for tensionless membranes, and the second moment $\Gamma_{2}=\int\mbox{d}z\>z^{2}\>\gamma(z)$ does not depend on the shape of the function $W(z)$ for symmetric tensionless bilayers with $\int\mbox{d}z\>z\>\gamma(z)=0$. This prediction can be used to test the convolution hypothesis, Eq. (32). The integral $\Gamma_{0}$ is close to zero in all systems as expected ($\Gamma_{0}\ \sigma_{t}^{2}/\epsilon=-0.018,-0.003,-0.04$, and $0.02$ for the system with $N=200,288,800$, and $3200$ lipids, respectively). The values of the second moment are $\Gamma_{2}/\epsilon=2.8,2.7,2.0$, and $2.8$. Hence $\Gamma_{2}$ does not depend on the system size, which confirms the existence of an intrinsic tension profile.

We note that the integral for the Gaussian rigidity (29) still depends on the system size, since the lower integration bound is finite. Both Eqs. (28) and (29) are only applicable in sufficiently small systems. Therefore, we proceed by evaluating them in the smallest system with $N=200$ lipids. For the monolayer curvature, we obtain a small negative value, $k_{c}c_{0}=-0.3\pm 0.1\epsilon/\sigma_{t}$. This may seem surprising, given the fact that the heads in our model are larger than the tail beads, and that the tails have to tilt in the low temperature phase (the $L_{\beta^{\prime}}$ phase) in order to accommodate this mismatch. Indeed, the spontaneous curvature is found to be positive in the gel state (West, ). At higher temperature, the tails disorder and occupy more membrane area, and $c_{0}$ decreases and changes sign as a result. Negative curvatures have also been found in more realistic models of DPPC bilayers (Marrink et al., 2007). The calculated result for the Gaussian rigidity depends on the position of the “inextinsibility plane” $z_{0}$, which is not known unambiguously. Depending on our choice of $z_{0}$, we obtain $k_{G}$ values that range between $\pm 2.8\epsilon$. Among these, the positive values can be excluded: Positive Gaussian rigidity would imply that the bilayers tend to assume saddle-shaped configurations, which destabilizes flat bilayer structures on large scales and promotes interconnected structures, i.e., cubic phases or sponge-like structures. Our model bilayers remained flat for all system sizes. Therefore, only negative values of $k_{G}$ are physically reasonable. In previous work (Brannigan and Brown, 2007), $z_{0}$ was taken to be the “neutral” plane where $\gamma(z)$ crosses zero, i.e., $z_{0}=2.6\sigma_{t}$ in our system (cf. Fig. (3)). Using this value, we obtain $k_{G}=-0.26\epsilon$.

To summarize this subsection, the Landau-de Gennes theory does not describe the fluctuations of our model membranes very well. It misses a soft peristaltic mode in the monolayer thickness spectrum, which is clearly present in the simulation data. In contrast, the elastic theory fits the data excellently. We have extracted values for the elastic parameters that describe the bending deformations in monolayers from the fluctuation spectra and the surface tension profiles of bilayers. They are given in Table 1. Using the identifications $\sigma_{t}\sim 6$Å and $\epsilon\sim 0.36\cdot 10^{-20}$J (see section 2), we can relate our model to real lipid bilayers. The values of our elastic parameters in SI units (see Table 1) have the same order of magnitude than those obtained based on all-atom simulations of DPPC (Lindahl and Edholm, 2000a), $k_{c}\sim 4\cdot 10^{-20}$J, $k_{A}/t_{0}^{2}\sim 1.1\cdot 10^{-20}$J/nm⁴, $\zeta/t_{0}\sim 0.18$nm^-2 (Brannigan and Brown, 2006), and $c_{0}\sim-0.04$ – $-0.05$ nm^-1 (Marrink et al., 2007), and those based on experimental estimates (Marsh, 2006), $k_{c}\sim 5-20\cdot 10^{-20}$J, $k_{A}/t_{0}^{2}\sim 6\cdot 10^{-20}$J/nm⁴, $c_{0}\sim-0.04$ nm^-1, and $k_{G}/k_{c}\sim-0.8$.

Next we investigate the deformation of a bilayer by a single inclusion. To this end, we consider the radial profiles of the membrane thickness $2\phi$, which we define as the mean $z$-distance between the head positions in the upper and the lower monolayer. Two parameters are varied, the hydrophobicity parameter $\epsilon_{pt}$ (cf. Eq. (6)) and the hydrophobic thickness $L$ of the inclusion. The results for $\epsilon_{pt}=2$ and $6$ are shown in Fig. 4 for proteins with freely fluctuating orientations and for proteins with orientation constrained to the the $z$-axis. The deformation profiles induced by proteins with fixed and free orientiations are identical within the error. This is due to the fact that proteins with free orientations were hardly tilted – the tilt angles were always smaller than $\theta\stackrel{{\scriptstyle<}}{{\sim}}0.08$. In the following, we shall only show data for proteins with fixed orientation.

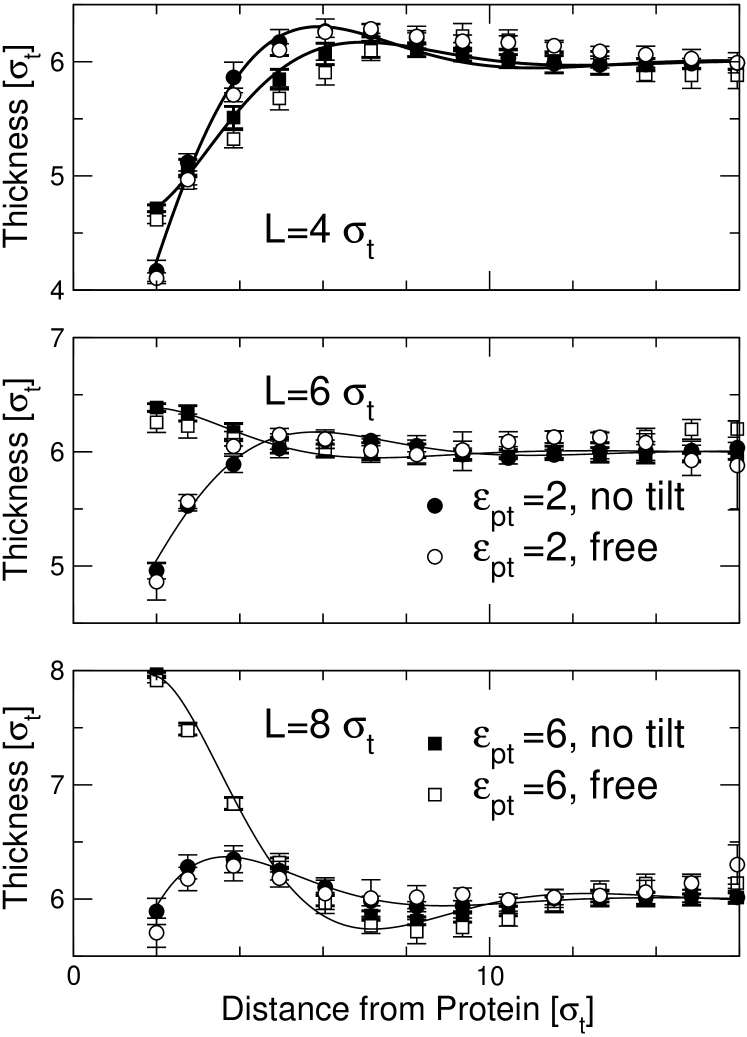
Looking at Fig. 4, we first observe that the membrane thickness profiles are not strictly monotonic, but exhibit a characteristic over- or undershoot at the distance $r\sim 6\sigma_{t}$ from the protein. Such a weakly oscillatory behavior has also been observed in previous coarse-grained Venturoli et al. (2005) and atomistic Cordomi and Perez (2007) simulations of protein-induced membrane deformations. In our case, the wavelength of the oscillation is roughly $\sim 10\sigma_{t}$, hence it can be related to the soft peristaltic mode in the fluctuation spectrum.

The second observation is that the protein hydrophobicity parameter $\epsilon_{pt}$ must exceed a certain value in order to produce classical hydrophobic mismatch. If $\epsilon_{pt}$ is too small, the protein effectively repels the lipids, and the membrane thickness is reduced at the surface of the protein regardless of the value of $L$. The hydrophobic section of the protein pins the membrane thickness for hydrophobicity parameters larger than $\epsilon_{pt}\sim 4$. This can be rationalized by noting that $\epsilon_{pt}\sim 4$ is the critical value where touching the protein surface is about as favorable for tail beads, from an energetic point of view, as being immersed in the bulk: The maximal contact energy of a tail bead in contact with a plane of tail beads is $4\epsilon$.

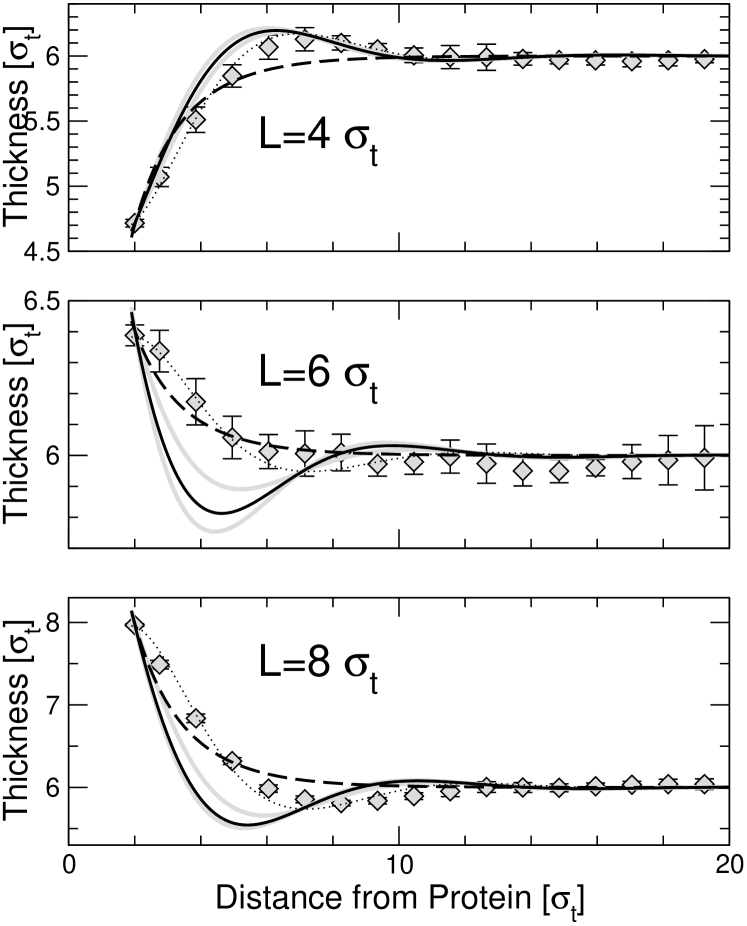
We proceed by fitting the profiles to the prediction of the analytical theories. Since the hydrophobicity of the inclusion must be larger than $\epsilon_{pt}>4$ in order to cleave the membrane, we focus on the data for $\epsilon_{pt}=6$. Fig. 5 compares them with fits to the prediction of the Landau-de Gennes theory (Eq. (10) and the elastic theory (Eq. (20) with the boundary conditions Eq. (18)). In the Landau-de Gennes case, the three curves were fitted simultaneously with one common fit parameter $\xi$ and three separate fit parameters $t_{R}=t_{R}^{\mbox{\tiny LdG}}$. Not surprisingly, the Landau-de Genens fit cannot reproduce the oscillatory component of the profiles; otherwise, the fit is quite reasonable (Fig. 5, dashed line).

The thick solid lines in Fig. 5 show the fits to the elastic theory with $t_{R}=:t_{R}^{\mbox{\tiny el}}$ as sole fit parameter. None of them is satisfactory. Hence the ”pure” version of the elastic theory, which explains the profiles in terms of bulk membrane properties only, is not sufficient. In contrast, the data can be fitted very nicely if we release the constraint on the value of $c_{0}$, i.e., replace the spontaneous curvature by a renormalized curvature $\tilde{c_{0}}$ (thin dotted lines in Fig. 5, solid lines in Fig. 4). The resulting fit parameter values are essentially the same for $\epsilon_{pt}=6$ (Fig. 5) and $\epsilon_{pt}=5$ (data not shown) and given in Table 2.

From the fit results for $t_{R}$, we can infer the effective hydrophobic thickness $L_{\text{eff}}=2(t_{0}+t_{R})$ of the inclusions. We note that the exact relation between $t_{R}$ and the model parameter $L$ is not a priori clear, since the lipid-protein potential is smooth and varies on the length scale $\sigma_{t}$. In all cases, the values for $L_{\text{eff}}$ are reasonably close to $L$, i.e., well within $1\sigma_{t}$. The fit parameters for $\tilde{c_{0}}$, however, deviate considerably from the spontaneous curvature $c_{0}=-0.05\pm 0.02\sigma_{t}^{-1}$ (see Table 1) and depend on $L$. This clearly demonstrates that the local structure of the lipids that surround the inclusion indeed contributes to the boundary conditions, as has been discussed in the theory section (Eq. (24)).

A similar effect has been observed by Brannigan and Brown in a different coarse-grained model in Ref. (Brannigan and Brown, 2007), and could be explained satisfactorily by the effect of nonconstant lipid volume. The volume per lipid in that model varies substantially over a range of $r$. In our model, the lipid volume (i.e., the lipid density inside the membrane) is almost constant throughout the system. Fig. 6 (upper left) shows profiles of the lipid bead density in the membrane for different hydrophobic thicknesses $L$ at $\epsilon_{pt}=6$. Here the lipid bead density $\rho_{l}$ is defined as the number of lipid beads per area divided by the membrane thickness, and it is directly related to the local lipid volume $v_{l}$ via $v_{l}=n/\rho_{l}$ with the chain length $n=7$. Apart from an enhancement directly at the protein surface, which reflects the attractive protein-lipid interaction, and a very shallow depletion zone thereafter, the lipid density is nearly constant. Moreover, the curves for different hydrophobic thickness $L$ are almost identical. Hence lipid volume effects contribute at most an $L$-independent constant to the renormalized curvature (24).

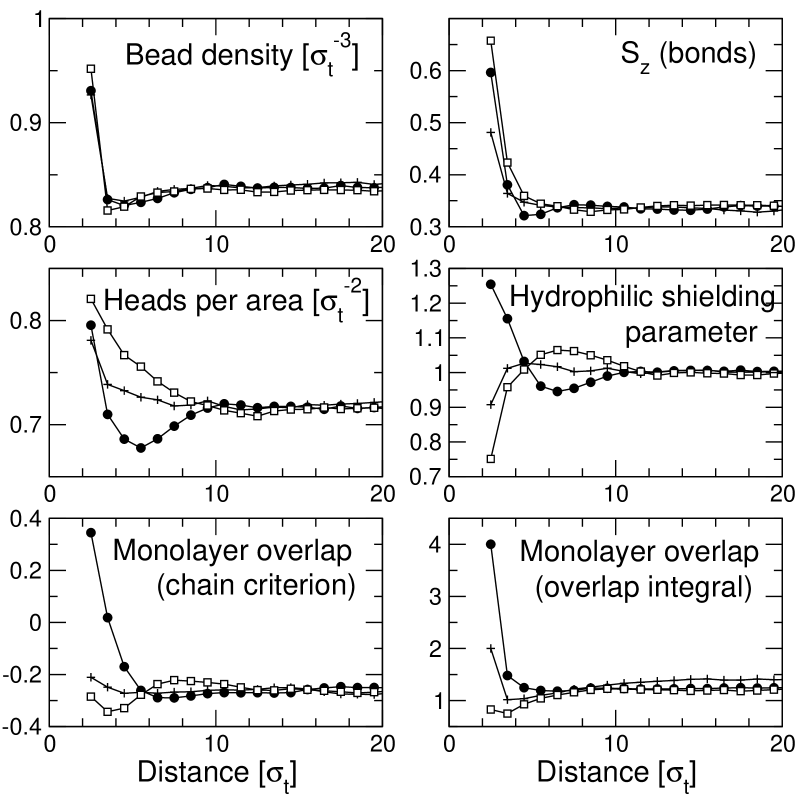
Fig. 6 also displays profiles of other candidate quantities that might affect the membrane properties and renormalize the curvature term at the surface. The upper right panel shows the nematic order parameter for single bonds, $S_{z}=\langle 3(u_{z}/u)^{2}-1)\rangle/2$, where $u$ refers to the bond vectors. The profiles show that the nematic order is enhanced in the vicinity of the inclusion. This is partly related to the increase of lipid density at the inclusion, since both quantities are correlated. The details of the nematic order profile, however, cannot be explained by the density profile alone. The ordering effect is highest for positively mismatched inclusions. Suprisingly, negatively mismatched inclusions induce higher order at the boundary than hydrophobically matching inclusions. This may seem counter-intuitive at first, but becomes plausible in view of the fact that the monolayers also overlap in the vicinity of negatively mismatched inclusions. At larger distances from the inclusion, the bond order decays monotonically for hydrophobically matching and positively mismatched inclusions, and exhibits a non-monotonic dip for negatively mismatched inclusions.

The middle panel in Fig. 6 shows two quantities that are related to the shielding of the hydrophobic membrane interior from the solvent. Since shielding is achieved by the heads, the areal head density gives a direct measure of the effectiveness of shielding. At constant lipid volume, however, the areal head density depends directly on the monolayer thickness $t(r)$ and thus does not qualify as independent field $\delta q(r)$ in the elastic theory, i.e., it cannot contribute directly to Eq. (24). Instead, we must consider a renormalized shielding parameter, such as, e.g., the “hydrophilic shielding parameter” introduced by de Meyer et al. in Ref. (de Meyer et al., 2008). It is defined as the areal head density divided by the areal tail density, normalized such that it becomes one far from the inclusion. In the original version of the elastic theory, this parameter would be constant. Our data show that the areal head density is enhanced directly at the surface of the inclusion for all $L$ – an indirect consequence of the attractive protein-tail interaction. The subsequent behavior depends on the type of mismatch: For positively mismatched inclusions, the areal head density goes up, for negatively mismatched inclusions, it goes down (Fig. 6, middle left panel). The hydrophilic shielding parameter (middle right panel) shows the same behavior at intermediate distances from the inclusion: Overshielding for positively mismatched inclusions, undershielding for negatively mismatched inclusions. Close to the inclusion, the curves turn around, in qualitative agreement with the observations of de Meyer et al. in Ref. (de Meyer et al., 2008). The resulting integral $\int\mbox{d}r\>\delta q(r)/q_{0}$ (the $K_{2}$ term in Eq. (24)) is roughly zero for $L=6\sigma_{t}$ and $8\sigma_{t}$ and positive for $L=4\sigma_{t}$.

The bottom panel in Fig. 6 shows profiles of the monolayer overlap, which measures the amount of interdigitation between monolayers. It has been calculated following two different conventions: The left graph shows a chain-related overlap parameter originally introduced by Kranenburg et al. in Ref. (Kranenburg et al., 2003): It is defined as $O_{\mbox{\tiny chain}}=\langle 2(l_{z}-t_{0})/l_{z}\rangle$, where $l_{z}$ is the $z$-component of the end to end vector of chains and $t_{0}$ the monolayer thickness. Far from the inclusion, this parameter is negative, indicating that the two monolayers are well separated. Close to the inclusion, it becomes positive for negatively mismatched inclusions – the inclusions pull the lipids inwards and enforce a certain amount of interdigitation. For hydrophobically matching inclusions and for positively mismatched inclusions, it remains negative and roughly constant. The right graph shows a monomer-related overlap parameter which is defined as the overlap integral of the density profiles of the two monolayers, $O_{\mbox{\tiny bead}}=\int\mbox{d}z(\rho_{\mbox{\tiny tail}}^{\mbox{\tiny upper}}(z)-\rho_{\mbox{\tiny tail}}^{\mbox{\tiny lower}}(z))$, where $\rho_{\mbox{\tiny tail}}$ denotes the density of tail beads. The curves for $O_{\mbox{\tiny bead}}$ are qualitatively similar to those for $O_{\mbox{\tiny chain}}$, except that they are shifted to positive values – even far from inclusions, the monolayer densities have some overlap in the center of the bilayer (cf. Fig. 3).

To summarize this section, we find that the thickness deformation profiles around single inclusions can be fitted reasonably well with the exponential law predicted by the Landau-de Gennes theory. The fit with the pure version of the elastic theory is not good, but the elastic fit becomes much better and far superior to the Landau-de Gennes fit, if we allow for the possibility of curvature renormalization in the vicinity of the inclusion. We have identified a number of quantities which could conceivably contribute to this renormalization, i.e., they vary substantially close to the inclusion and they show a sizeable $L$-dependence. However, we cannot pinpoint an obvious single culprit. According to Table 2, the renormalized curvature $\tilde{c_{0}}$ exhibits an almost perfect linear dependence on the hydrophobic thickness $L$ of the inclusion: The relation $\tilde{c_{0}}-c_{0}\approx 0.078/\sigma_{t}+0.0825(L-2t_{0})/\sigma_{t}^{2}$ describes the data in Table 2 within $4\%$. None of the quantities shown in Fig. 6 produces such a linear behavior in an obvious way. We conclude that we have either still missed the truly relevant quantity, or that the observed linear relation is accidental and results from an interplay of various curvature-renormalizing factors. ¿From a physical point of view, it seems likely that most or all of the quantities discussed above will affect the local membrane properties, and most notably, the spontaneous curvature: Monolayer overlap will favor negative spontaneous curvature, since the area per tail increases. Variations in the hydrophilic shielding parameter will change the local pressure profile and hence affect the local curvature. Chain order will favor positive spontaneous curvature, since the structure in the chain region resembles that in the gel state, where the spontaneous curvature is large and positive.

Finally, we turn to studying the membrane-mediated interactions between inclusions. We study the dilute protein limit, i.e., we do not consider effects from multibody interactions between several proteins. In order to determine the potential of mean force, we have carried out simulations of membranes containing two inclusions and determined their radial pair distribution function. The effective potential $w(r)$ is

$$w(r)=-k_{B}T\ln g(r),$$

(33)

where $k_{B}$ is the Boltzmann constant and $T$ the temperature. Since the function $g(r)$ varies over several orders of magnitude, we have used umbrella sampling and reweighting to determine it accurately at all distances $r$.

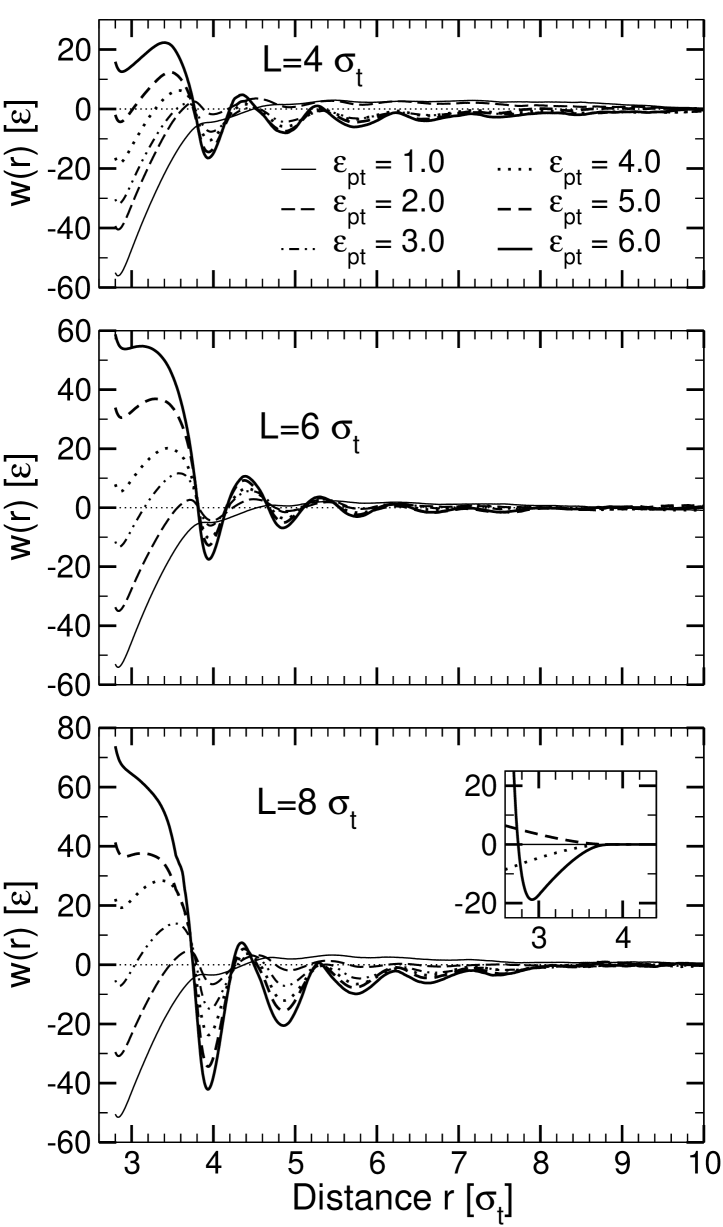
The resulting potential curves are shown in Fig. 7 for several values of the hydrophobicity parameter $\epsilon_{pt}$ and the hydrophobic thickness $L$. The most striking feature of these profiles is their distinctly oscillatory shape. The oscillations have a wavelength of roughly $1\sigma_{t}$ in all systems, which indicates that they are caused by lipid packing in the vicinity of the inclusions. Only for the lowest value of the hydrophobicity parameter, $\epsilon_{pt}=1$, the oscillatory structure disappears. Here, we recover qualitatively the behavior observed in the simulations of purely repulsive inclusions by Sintes and Baumgärtner (Sintes and Baumgärtner, 1997) and predicted by the corresponding molecular mean-field theories (Lagüe et al., 2000, 2001; May and Ben-Shaul, 2000): The potential of mean force exhibits a minimum at close inclusion distances followed by a shallow maximum.

Beyond $r>3.5\>\sigma_{t}$, all layering minima obey the general rule that they become more shallow with increasing protein separation $r$ and/or decreasing hydrophobicity parameter $\epsilon_{pt}$. The layering effects are most pronounced at high $\epsilon_{pt}$, indicating that lipids pack more tightly if they move closer to the protein surface. In contrast, the first potential minimum at $r\sim 3\ \sigma_{t}$ features the opposite behavior: It deepens as $\epsilon_{pt}$ decreases and disappears for high $\epsilon_{pt}$. This minimum results from a number of effects that are not directly related to layering: (i) The direct protein-protein interaction and the solvent-induced depletion interaction between the hydrophilic protein section located outside of the membrane: This contribution is roughly constant and can be calculated analytically (inset of Fig. 7). (ii) A depletion-type interaction induced by the lipids: By pushing the proteins towards each other, they maximize their translational and conformational entropy. This effect is strongest at low $\epsilon_{pt}$, where the protein and the lipids effectively repel each other. (iii) A bridging interaction induced by the lipids: At higher $\epsilon_{pt}$, the lipids gain from being in contact with the proteins. Therefore, they tend to squeeze themselves between the proteins, pushing them apart, and the height of the first minimum goes up.

The competition between the depletion interaction and the lipid bridging effect accounts for the phenomenon reported earlier (Fig. 1), that the preferred arrangement of inclusions in the membrane depends on $\epsilon_{pt}$: Weakly hydrophobic inclusions tend to touch each other, whereas strongly hydrophobic inclusions favor a larger distance where they are separated by one single lipid layer.

The influence of hydrophobic mismatch on the potential of mean force can be assessed by comparing the potential curves for different hydrophobic thickness $L$. On the one hand, hydrophobic mismatch affects the local features of the potential – the packing interaction (the strength of the layering) and the effective contact energy of proteins. On the other hand, it also contributes a smooth attractive interaction for mismatched proteins with $L=4\sigma_{t}$ and $8\sigma_{t}$, which superimposes the oscillatory packing interaction at $r>4\sigma_{t}$. It is worth noting that the sign of the additional term is independent of the type of mismatch – it is attractive for both positively and negatively mismatched inclusions. This smooth long-range contribution to the potential can now be compared with the predictions of the analytical theories.

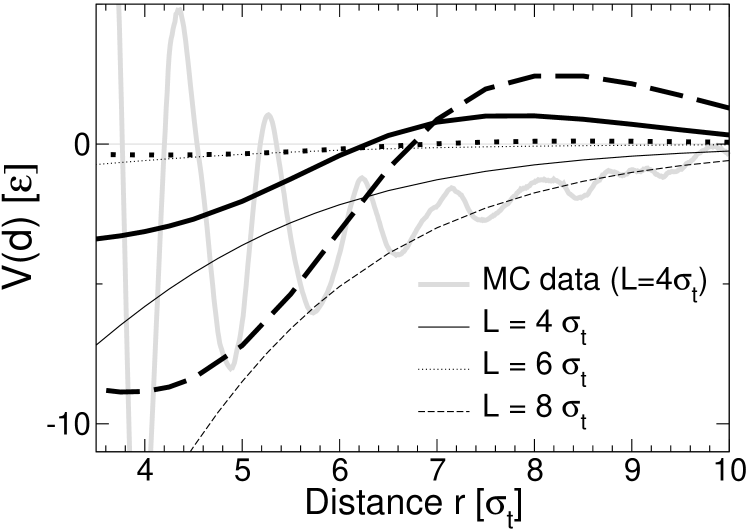
Fig. 8 shows the corresponding curves for the Landau-de Gennes theory (thin lines) and the elastic theory (thick lines). They were calculated numerically by minimizing the free energy – Eq. (9) or Eq. (15) with $\tilde{c_{0}}$ replacing ${c_{0}}$ – for systems containing two inclusions at given distance $r$, with the boundary condition $\phi=t_{R}$ at the surface of the inclusion. The model parameters were taken from Table 1 and 2. In the Landau-de Gennes calculation, the parameter $4a$ in Eq. (9) was identified with the reduced area compressibility coefficient $k_{A}/t_{0}^{2}$ in Table 1. This may seem inconsistent, since the latter was originally determined from a fit of the fluctuation spectra to the elastic theory. Unfortunately, the fit of the spectra to the Landau-de Gennes theory (Fig. (2)) did not produce dependable parameters $a$ and $c$. The value of $k_{A}$ in Table 1 is compatible with independent simulation data on the lipid area increase at finite surface tension Neder and was thus considered to be more reliable. The value for $c$ then follows from $c=\xi^{2}a$, using the value $\xi=2.0\sigma_{t}$ determined from the fit to the membrane thickness profiles around single inclusions.

To calculate the free energy, we have discretized the corresponding integrals in real space using a square grid with spatial discretization parameter $h$ and a second order difference scheme to evaluate the derivatives. The boundary condition was implemented by setting $\phi=t_{R}$ inside the inclusion. (The other boundary condition of the elastic theory, Eq. (18), follows automatically from the energy minimization). The energy was minimized via a steepest descent method, using a relaxation scheme introduced in Ref (Schmid and Schick, 1995). The final accuracy was $\int\mbox{d}^{2}r|\delta F/\delta\phi|\leq 10^{-6}$. The curves shown in Fig. 8 were obtained using the spatial discretization $h=0.25\sigma_{t}$ and a system of size $30\times 20\sigma_{t}^{2}$ with periodic boundary conditions, which corresponds to the situation in the Monte Carlo simulations. Calculations for $h=0.5\sigma_{t}$ and system sizes up to $70\times 50\sigma_{t}^{2}$ produced the same curves, hence discretization errors and finite size effects are negligible.

Both the Landau-de Gennes theory and the elastic theory predict an attractive interaction at distances $r<6\sigma_{t}$, in agreement with the trend observed in the simulation data. For larger distances, the elastic theory predicts the potential of mean force to become positive and exhibit a peak at $r\sim 8\sigma_{t}$. The simulation data show no indication for the existence of such a positive peak. Apparently, the elastic theory fails to reproduce the trend of the simulation data at large distances, which is surprising, since this is where one would expect it to work best. The potential predicted by the Landau-de Gennes theory is negative and attractive everywhere and thus better compatible with the data. However, this should not be overrated, given the overall poorer performance of this approach when looking at pure membranes and membrane interactions with single inclusions. The weakly oscillatory behavior of the potential of mean force in the elastic theory is generated by the soft peristaltic mode in the fluctuation spectrum, which has been shown to leave a clear signature in the shape of the distortion profiles around single proteins. The simulation data suggest that the effect of this mode on the lipid-mediated interactions between two proteins is destroyed by some yet unknown mechanism.

We thank Grace Brannigan and Jörg Neder for very helpful discussions. This work was funded by the German Science Foundation (DFG) within the SFB 613. F. B. is partially supported by the NSF (CHE-0349196). F. B. is a Sloan Research Fellow and a Camille Dreyfus Teacher-Scholar. The simulations were mostly carried out at the Paderborn center for parallel computing (PC2) and the NIC computer center in Jülich.